Crystallisation Dynamics in Large-Scale Extrusion Additive Manufacturing: An Analysis with and without Temperature Modification
Abstract
:1. Introduction
2. Methods
2.1. Thermal Simulation of LS-MEX
2.2. Material Polyamide 6 Reinforced with 40 wt.% Carbon Fibres
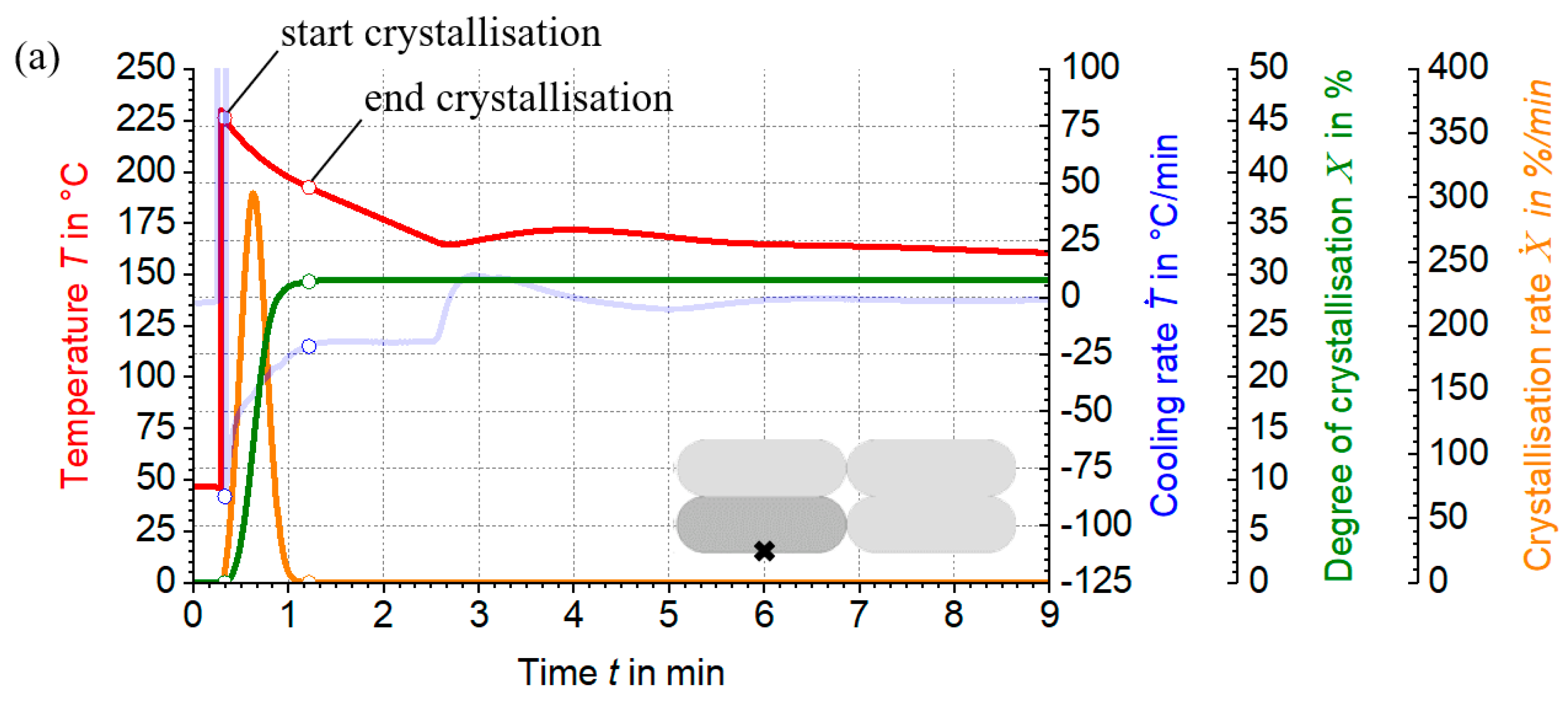
2.3. Procedure for the Experimental Analysis of Crystallisation Kinetics
2.4. Semi-Empirical Characterisation of Crystallisation Kinetics
2.5. Simulation Model Setup
3. Results
3.1. Verification of the Thermal Simulation Results
3.2. Crystallisation Kinetics of Polyamide 6 wt.%40 Carbon Fibres
3.3. Modification of the Temperature Profiles through Additional Peripherals
3.4. Investigation of Crystallisation Kinetics in the LS-MEX Process
4. Conclusions
5. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Large Scale Material Extrusion | LS-MEX |
| Polyamide 6 with 40% carbon fibres | PA6 wt.%40 CF |
| Finite element method | FEM |
Appendix A. Material Properties for Thermal Process Simulation

| Thermal Properties Wood | Unit | Value |
|---|---|---|
Appendix B. Model Parameters (Nakamura Model)

References
- Pintos, P.B.; de León, A.S.; Molina, S.I. Large format additive manufacturing of polyethylene terephthalate (PET) by material extrusion. Addit. Manuf. 2024, 79, 103908. [Google Scholar] [CrossRef]
- Duty, C.E.; Kunc, V.; Compton, B.; Post, B.; Erdman, D.; Smith, R.; Lind, R.; Lloyd, P.; Love, L. Structure and mechanical behavior of Big Area Additive Manufacturing (BAAM) materials. Rapid Prototyp. J. 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Choo, K.; Friedrich, B.; Daugherty, T.; Schmidt, A.; Patterson, C.; Abraham, M.A.; Conner, B.; Rogers, K.; Cortes, P.; MacDonald, E. Heat retention modeling of large area additive manufacturing. Addit. Manuf. 2019, 28, 325–332. [Google Scholar] [CrossRef]
- Friedrich, B.K.; Choo, K. Thermal-Stress Characteristics of a Large Area Additive Manufacturing. Heat Transf. Eng. 2022, 44, 1083–1098. [Google Scholar] [CrossRef]
- Kugele, D.; Dörr, D.; Wittemann, F.; Hangs, B.; Rausch, J.; Kärger, L.; Henning, F. Modeling of the non-isothermal crystallization kinetics of polyamide 6 composites during thermoforming. In AIP Conference Proceedings; AIP Publishing LLC.: Melville, NY, USA, 2017; Volume 1896. [Google Scholar] [CrossRef]
- Kulkarni, S.; Reuvers, M.-C.; Brepols, T.; Reese, S.; Johlitz, M.; Lion, A. Characterization of crystallization kinetics in Polyamide 6 with a focus on modeling the thermoforming process: Experiments, modeling, simulations. Contin. Mech. Thermodyn. 2024, 36, 415–431. [Google Scholar] [CrossRef]
- Leubecher, D.; Vitale, P.; Musil, B.; Brier, S.; Höfer, P. Analysis and interpretation of the temperature field in additive material extrusion process for small and large scale components: A numerical study. In 11. Landshuter Leichtbaukolloquium; Leichtbau-Cluster: Landshut, Germany, 2023; ISBN 978-3-9818439-7-2. [Google Scholar]
- Gersten, K.; Herwig, H. Strömungsmechanik: Grundlagen der Impuls-, Wärme- und Stoffübertragung aus asymptotischer Sicht. In Springer eBook Collection Computer Science and Engineering; Springer Vieweg: Wiesbaden, Germany, 1992. [Google Scholar]
- Owens, J.T.; Das, A.; Bortner, M.J. Accelerating heat transfer modeling in material extrusion additive manufacturing: From desktop to big area. Addit. Manuf. 2022, 55, 102853. [Google Scholar] [CrossRef]
- Collins, D.; Turner, C. Initial Development of a Simulation Model of a Radiation-based Print Heating System for Fused Deposition Modeling. In Proceedings of the Solid Freeform Fabrication 2021: 32nd Annual International Solid Freeform Fabrication Symposium, Virtual, 2–4 August 2021. [Google Scholar]
- Ovlaque, P.; Bayart, M.; Soulestin, J.; Trolez, Y.; Olivier, D.; Bujeau, B.; Charlon, S. On the temperature evolution and related crystallinity of polypropylene parts processed via material extrusion. Addit. Manuf. 2022, 58, 103065. [Google Scholar] [CrossRef]
- Bengfort, P. Entwicklung einer Prozessmodifikation für teilkristalline Thermoplaste im Fused Layer Modeling. Ph.D. Thesis, Technical University Dortmund, Dortmund, Germany, 2023. [Google Scholar]
- Deshpande, A.; Ravi, A.; Kusel, S.; Churchwell, R.; Hsu, K. Interlayer thermal history modification for interface strength in fused filament fabricated parts. Prog. Addit. Manuf. 2019, 4, 63–70. [Google Scholar] [CrossRef]
- Kishore, V.; Ajinjeru, C.; Nycz, A.; Post, B.; Lindahl, J.; Kunc, V.; Duty, C. Infrared preheating to improve interlayer strength of big area additive manufacturing (BAAM) components. Addit. Manuf. 2017, 14, 7–12. [Google Scholar] [CrossRef]
- Tagscherer, N.; Osswald, T.A.; Drechsler, K. Targeted Temperature Manipulation and Analysis of the Influence on Mechanical Properties in Large-Scale Extrusion Additive Manufacturing. Appl. Sci. 2022, 12, 2998. [Google Scholar] [CrossRef]
- Tagscherer, N.; Consul, P.; Kottenstedde, I.L.; Latiri, H.; Zaremba, S.; Drechsler, K. Investigation of nonisothermal fusion bonding for extrusion additive manufacturing of large structural parts. Polym. Compos. 2021, 42, 5209–5222. [Google Scholar] [CrossRef]
- Dörr, D. Simulation of the thermoforming process of UD fiber-reinforced thermoplastic tape laminates. KIT Scientific Publishing: 78. Ph.D. Thesis, Institute of Vehicle System Technology (FAST), Karlsruhe, Germany, 2021. [Google Scholar] [CrossRef]
- Papadopoulou, K.; Tarani, E.; Chrissafis, K.; Mašek, O.; Bikiaris, D.N. Non-Isothermal Crystallization Kinetics of PBSu/Biochar Composites Studied by Isoconversional and Model Fitting Methods. Polymers 2023, 15, 1603. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Yu, B.; Sun, H.; Wang, N.; Liu, P.; Feng, J.; Cui, X. Isothermal and Non-Isothermal Crystallization Kinetics of Poly(ethylene chlorotrifluoroethylene). Polymers 2022, 14, 2630. [Google Scholar] [CrossRef] [PubMed]
- Costa, S.; Duarte, F.; Covas, J. Thermal conditions affecting heat transfer in FDM/FFE: A contribution towards the numerical modelling of the process. Virtual Phys. Prototyp. 2015, 10, 35–46. [Google Scholar] [CrossRef]
- Ramos, N.; Mittermeier, C.; Kiendl, J. Experimental and numerical investigations on heat transfer in fused filament fabrication 3D-printed specimens. Int. J. Adv. Manuf. Technol. 2022, 118, 1367–1381. [Google Scholar] [CrossRef]
- Groth, C.; Müller, G.; Stelzmann, U. FEM für Praktiker: Basiswissen und Arbeitsbeispiele zur Finite-Element-Methode mit dem FE-Programm ANSYS Rev. 5.5; Expert-Verl.: Renningen-Malmsheim, Germany, 2009. [Google Scholar]
- Sakin, M.; Kaymak-Ertekin, F.; Ilicali, C. Convection and radiation combined surface heat transfer coefficient in baking ovens. J. Food Eng. 2009, 94, 344–349. [Google Scholar] [CrossRef]
- Arunkumar, M.; Dhinakaran, V.; Shanmugam, N.S. Numerical prediction of temperature distribution and residual stresses on plasma arc welded thin titanium sheets. Int. J. Model. Simul. 2021, 41, 146–162. [Google Scholar] [CrossRef]
- Herwig, H.; Moschallski, A. Wärmeübertragung; Springer Science and Business Media LLC: Dordrecht, Netherlands, 2019. [Google Scholar] [CrossRef]
- Kaiser, W. Kunststoffchemie für Ingenieure; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2015; pp. 1–32. [Google Scholar]
- Tagscherer, N.; Schromm, T.; Drechsler, K. Foundational Investigation on the Characterization of Porosity and Fiber Orientation Using XCT in Large-Scale Extrusion Additive Manufacturing. Materials 2022, 15, 2290. [Google Scholar] [CrossRef] [PubMed]
- Iroh, J.O.; Berry, J. Heterogeneous nucleation of short glass fibre-polypropylene composites. Polymer 1993, 34, 4747–4751. [Google Scholar] [CrossRef]
- ISO 11357-7:2022-03; Plastics—Differential scanning calorimetry (DSC)—Part 7: Determination of crystallization kinetics. DIN-Normenausschuss Kunststoffe: Berlin, Germany, 2022.
- Brahmia, N.; Bourgin, P.; Boutaous, M.; Garcia, D. Numerical Simulation with “Comsol Multiphysics” of Crystallization Kinetics of Semi-Crystalline Polymer during Cooling: Application to Injection Moulding Process. In Proceedings of the COMSOL Users Conference, Paris, France, 7 November 2006. [Google Scholar]
- Zaldua, N.; Maiz, J.; de la Calle, A.; García-Arrieta, S.; Elizetxea, C.; Harismendy, I.; Tercjak, A.; Müller, A.J. Nucleation and Crystallization of PA6 Composites Prepared by T-RTM: Effects of Carbon and Glass Fiber Loading. Polymers 2019, 11, 1680. [Google Scholar] [CrossRef]
- Seo, J.; Zhang, X.; Schaake, R.P.; Rhoades, A.M.; Colby, R.H. Dual Nakamura model for primary and secondary crystallization applied to nonisothermal crystallization of poly(ether ether ketone). Polym. Eng. Sci. 2021, 61, 2416–2426. [Google Scholar] [CrossRef]
- Zholkov, Y.A. Thermal inertia of thermocouples. Meas. Technol. 1961, 4, 983–985. [Google Scholar] [CrossRef]
- Descher, S.; Wünsch, O. Simulation framework for crystallization in melt flows of semi-crystalline polymers based on phenomenological models. Arch. Appl. Mech. 2022, 92, 1859–1878. [Google Scholar] [CrossRef]
- Mileva, D.; Kolesov, I.; Androsch, R. Morphology of cold-crystallized polyamide 6. Colloid Polym. Sci. 2012, 290, 971–978. [Google Scholar] [CrossRef]
- Consul, P.; Chaplin, A.; Tagscherer, N.; Zaremba, S.; Drechsler, K. Interlaminar strength in large-scale additive manufacturing of slow crystallizing polyaryletherketone carbon composites. Polym. Int. 2021, 70, 1099–1108. [Google Scholar] [CrossRef]
- Srinivas, V.; Van Hooy-Corstjens, C.S.; Rastogi, S.; Harings, J.A. Promotion of molecular diffusion and/or crystallization in fused deposition modeled poly(lactide) welds. Polymer 2020, 202, 122637. [Google Scholar] [CrossRef]
- Soldner, D.; Steinmann, P.; Mergheim, J. Modeling crystallization kinetics for selective laser sintering of polyamide 12. GAMM-Mitteilungen 2021, 44, e202100011. [Google Scholar] [CrossRef]












| Manufacturing Parameters | Unit | Value |
|---|---|---|
| Extrudate temperature, | ||
| Print bed temperature, | ||
| Ambient temperature, | ||
| Printing speed, | ||
| Layer width, | ||
| Layer height, | ||
| Power density—Cooling element, | ||
| Power density—Heating element, | ||
| Nozzle-periphery distance, | ||
| Manufactured Part Dimensions | Unit | Value |
| Length, | ||
| Width, | ||
| Height, | ||
| Thermal Boundary Condition | Unit | Value |
| Heat transfer coefficient—Polymer, | ||
| Heat transfer coefficient—Print bed, | ||
| Emissivity, | ||
| Discretisation Parameters | Unit | Value |
| Mesh length and width, and | ||
| Mesh height, | ||
| Time step, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leubecher, D.; Brier, S.; Vitale, P.; Musil, B.; Höfer, P. Crystallisation Dynamics in Large-Scale Extrusion Additive Manufacturing: An Analysis with and without Temperature Modification. Materials 2024, 17, 2243. https://doi.org/10.3390/ma17102243
Leubecher D, Brier S, Vitale P, Musil B, Höfer P. Crystallisation Dynamics in Large-Scale Extrusion Additive Manufacturing: An Analysis with and without Temperature Modification. Materials. 2024; 17(10):2243. https://doi.org/10.3390/ma17102243
Chicago/Turabian StyleLeubecher, Dominik, Steffen Brier, Pablo Vitale, Bruno Musil, and Philipp Höfer. 2024. "Crystallisation Dynamics in Large-Scale Extrusion Additive Manufacturing: An Analysis with and without Temperature Modification" Materials 17, no. 10: 2243. https://doi.org/10.3390/ma17102243






