Research on the Effect Mechanism of Re on Interface Dislocation Networks of Ni–Based Single Crystal Alloys
Abstract
:1. Introduction
2. Experimental Tests and Molecular Dynamics Simulation
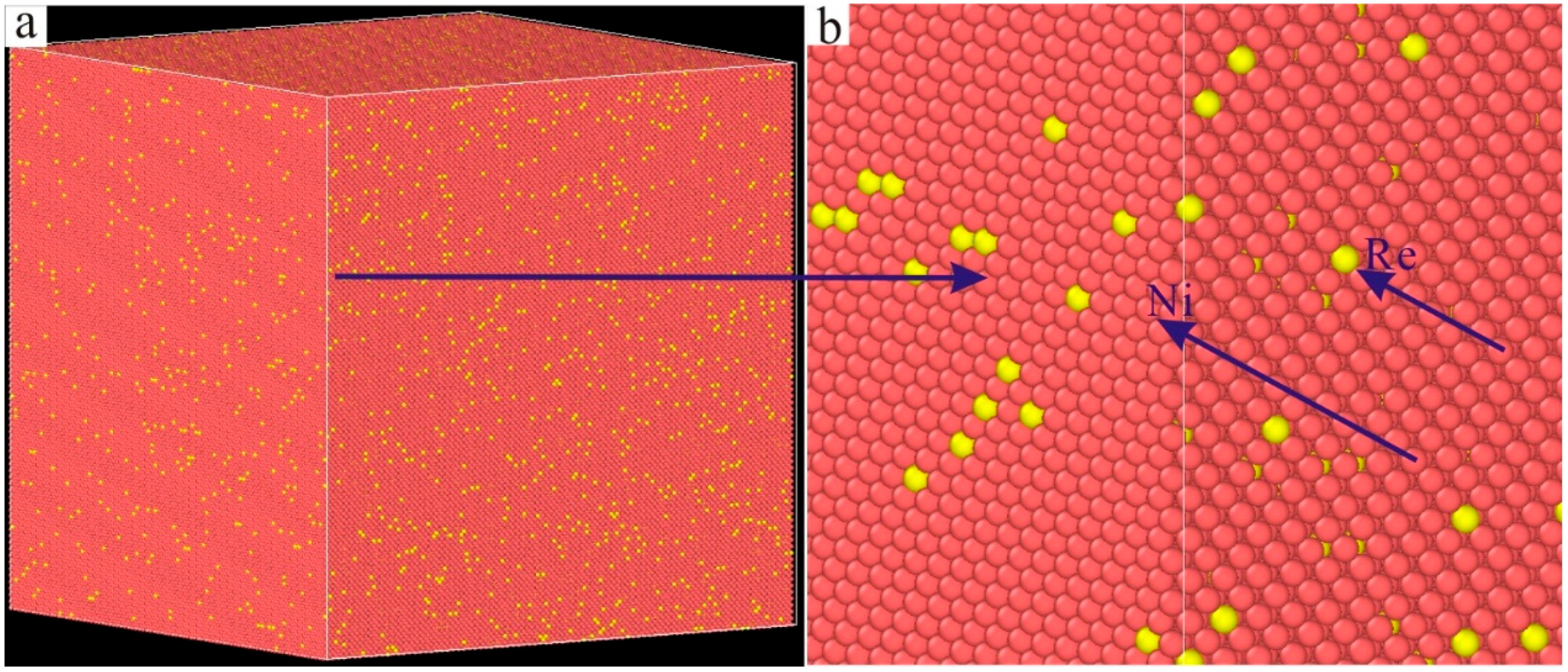
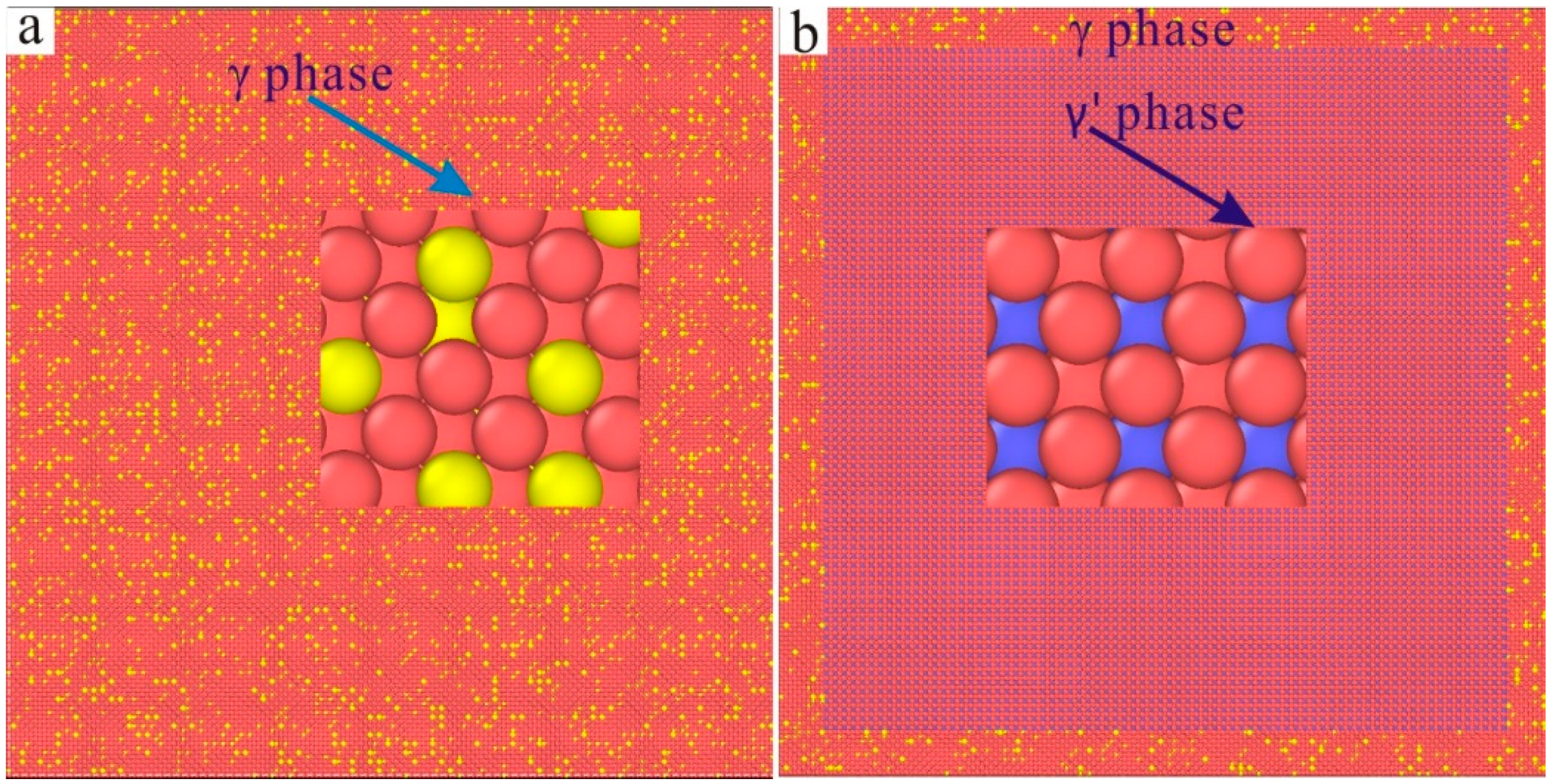
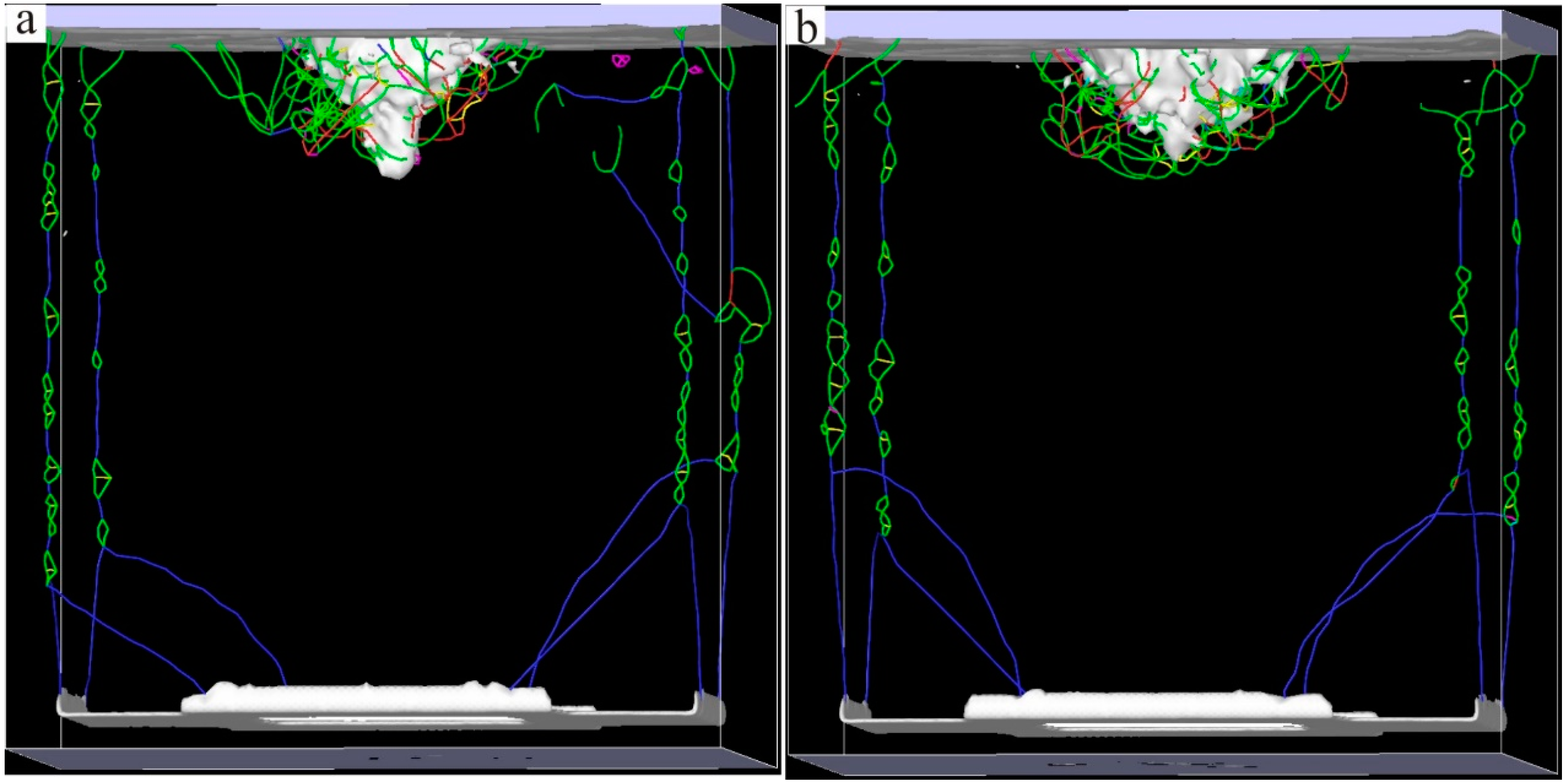
3. Results and Discussion
4. Conclusions
- (1)
- The mechanical properties of Ni–based single crystal alloys can be enhanced after the integration of Re, and with the increase in the content of Re, the hardnesses of the six kinds of new Ni–based single crystal alloys containing Re showed a nonlinear increasing trend.
- (2)
- The density of the interface dislocation network improved with the increase in the content of Re, and the nonlinear characteristic parameter was proportional to the dislocation density. Thus, the increase in the density of the interface dislocation network was further verified by nonlinear ultrasonic lamb wave tests.
- (3)
- A new model was constructed using the molecular dynamics method, which is closer to the real state of Ni–based single crystal alloys. The number of atoms in this model increased by six to seven times compared with that of the traditional model, and the strengthening mechanism of Re on the square interface dislocation network was analyzed using this model.
- (4)
- After the new Ni–based single crystal alloy was integrated with Re, the interface dislocation network enhanced the blocking ability of γ phase dislocations cutting into the γ′ phase. The analysis of the total lengths of the dislocation loops of the six models showed that the inhibition of the dislocation movement was strengthened by the increase in the number of Re atoms.
- (5)
- The analysis of the atomic potential energy showed that the potential energy of Re atoms at the interface was the lowest, which affected the reduction of the potential energy of other atoms at the interface. Thus, the potential energy of the model system was reduced, and the stability of the model was improved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Huang, H.Z.; Zhang, X.; Zhang, K. A multiaxial probabilistic fatigue life prediction method for nickel-based single crystal turbine blade considering mean stress correction. Qual. Reliab. Eng. Int. 2023, 39, 1735–1755. [Google Scholar] [CrossRef]
- Fan, Y.S.; Yang, X.G.; Shi, D.Q.; Tan, L.; Huang, W.Q. Quantitative mapping of service process–microstructural degradation–property deterioration for a Ni–based superalloy based on chord length distribution imaging process. Mater. Des. 2021, 203, 109561. [Google Scholar] [CrossRef]
- Bezold, A.; Volz, N.; Lenz, M.; Karpstein, N.; Zenk, C.H.; Spiecker, E.; Göken, M.; Neumeier, S. Quantification of the temperature–dependent evolution of defect structures in a CoNi–base superalloy. Acta Mater. 2022, 227, 117702–117714. [Google Scholar] [CrossRef]
- Yu, J.; Li, J.R.; Liu, S.Z.; Han, M.; Xiong, J.C. Anisotropic Tensile Properties in Ni–Based Single–Crystal Superalloy DD6 near [001] Orientation at 760 °C. Mater. Sci. Forum 2022, 1072, 79–86. [Google Scholar] [CrossRef]
- Soares Janeiro, I.; Franchet, J.M.; Cormier, J.; Bozzolo, N. Dynamic Precipitation during Forging of a γ–γ′ Nickel–Based Superalloy. Metall. Mater. Trans. A 2023, 54, 2052–2070. [Google Scholar] [CrossRef]
- Yang, X.; Hu, X.; Zhang, X. Atomistic simulation for the γ′–phase volume fraction dependence of the interfacial behavior of Ni–base superalloy. Appl. Surf. Sci. 2013, 264, 563–569. [Google Scholar] [CrossRef]
- Yue, E.L.; Yu, T.; Wang, Y.J.; Wang, C.Y. Synergistic strengthening mechanisms of rhenium in nickel–based single crystal superalloys. Intermetallics 2021, 132, 107133–107139. [Google Scholar] [CrossRef]
- Gruber, H.; Hryha, E.; Lindgren, K.; Cao, Y.; Rashidi, M.; Nyborg, L. The effect of boron and zirconium on the microcracking susceptibility of IN–738LC derivatives in laser powder bed fusion. Appl. Surf. Sci. 2022, 573, 151541. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Li, B. Research on the Relationship between Surface Defects and Preparation Quality Evaluation of Ni–Based Single Crystal Alloy. J. Mater. Eng. Perform. 2022, 32, 1612–1626. [Google Scholar] [CrossRef]
- Gorgannejad, S.; Estrada Rodas, E.A.; Neu, R.W. Employing sequential experiments to gain insights on the interaction between creep and fatigue damage in Ni–base superalloys. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 1981–1994. [Google Scholar] [CrossRef]
- Nasajpour, A.; Mirsalehi, S.E.; Farzadi, A. Diffusion brazing of Nicrofer 5520 (IN-617) superalloy using an amorphous Ni–Cr–Si–B interlayer: Microstructural characterization and mechanical properties. Kov. Mater. Met. Mater. 2022, 60, 89–107. [Google Scholar] [CrossRef]
- Hagen, S.P.; Weiser, M.; Abu–Khousa, B.; Virtanen, S. Influence of the Co/Ni Ratio Dendritic Segregations on the High–Temperature Oxidation Resistance of Multinary Co–Rich Superalloys at 850 °C and 1050 °C. Metall. Mater. Trans. A 2022, 53, 1552–1571. [Google Scholar] [CrossRef]
- Sakaguchi, M.; Okamoto, R.; Karato, T.; Suzuki, K. Effect of rafted microstructure and its temperature dependency on fatigue crack propagation in a single-crystal Ni-base superalloy. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 590–602. [Google Scholar] [CrossRef]
- Perez, T.; Monceau, D.; Desgranges, C. Kinetic oxidation model including the transient regime for a single crystal nickel–based superalloy over the temperature range 750–1300 °C. Corros. Sci. 2022, 206, 110485. [Google Scholar] [CrossRef]
- Schneiderman, B.; Hansen, A.; Chuang, A.C.; Yu, Z. Influence of oxygen on performance of multi–principal element alloy as braze filler for Ni–base alloys. J. Manuf. Process. 2023, 87, 25–35. [Google Scholar] [CrossRef]
- Geranmayeh, A.; Malekan, M.; Forghani, F.; Ghorbani, H. Microstructural mechanical investigations on the heat treatment rejuvenation of a long–term service–exposed GTD–111 Ni–based superalloy. Mater. Sci. Eng. A 2023, 862, 144381. [Google Scholar] [CrossRef]
- Koundinya, N.; Karnati, A.K.; Sahadevan, A.; Murty, S.N.; Kottada, R.S. Assessment of the post–dynamic recrystallization effects on the overall dynamic recrystallization kinetics in a Ni–base superalloy. J. Alloys Compd. 2023, 930, 167412–167423. [Google Scholar] [CrossRef]
- Kreins, M.; Büßenschütt, K.; Wesselmecking, S.; Krupp, U. On the impact of nanoscale γ″ precipitates on the Bauschinger effect in single–and polycrystal Ni–base superalloy 718. Mater. Sci. Eng. A 2022, 856, 144008. [Google Scholar] [CrossRef]
- Bessa, S.M.; de Oliveira, C.A.S. Effects of a high temperature artificial aging on microstructure and mechanical properties of the Ni–base superalloy GTD–111. Mater. Charact. 2023, 201, 112966–112977. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.R.; Yao, B.N.; Legut, D.; Zhang, R.F. Atomic insights into interface–mediated plasticity and engineering principles for heterogeneous serrated interfaces. Int. J. Plast. 2023, 160, 103498. [Google Scholar] [CrossRef]
- Pan, A.; Wang, W.; Xie, J.; Zhang, H.; Hao, S. Molecular dynamics simulations of interface structure and deformation mechanisms in metal/ceramic composites under tension. Mech. Mater. 2023, 184, 104688. [Google Scholar] [CrossRef]













| Samples | Re | Al | Ti | Cr | Co | Ni | Mo | Ta | W |
|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 0 | 6.16 | 1.73 | 9.67 | 6.10 | 62.41 | 2.99 | 3.70 | 7.25 |
| Sample 2 | 1 | 6.16 | 1.73 | 9.67 | 6.10 | 61.41 | 2.99 | 3.70 | 7.25 |
| Sample 3 | 2 | 6.16 | 1.73 | 9.67 | 6.10 | 60.41 | 2.99 | 3.70 | 7.25 |
| Sample 4 | 3 | 6.16 | 1.73 | 9.67 | 6.10 | 59.41 | 2.99 | 3.70 | 7.25 |
| Sample 5 | 4 | 6.16 | 1.73 | 9.67 | 6.10 | 58.41 | 2.99 | 3.70 | 7.25 |
| Sample 6 | 5 | 6.16 | 1.73 | 9.67 | 6.10 | 57.41 | 2.99 | 3.70 | 7.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhou, H. Research on the Effect Mechanism of Re on Interface Dislocation Networks of Ni–Based Single Crystal Alloys. Materials 2024, 17, 2361. https://doi.org/10.3390/ma17102361
Li B, Zhou H. Research on the Effect Mechanism of Re on Interface Dislocation Networks of Ni–Based Single Crystal Alloys. Materials. 2024; 17(10):2361. https://doi.org/10.3390/ma17102361
Chicago/Turabian StyleLi, Ben, and Hongyan Zhou. 2024. "Research on the Effect Mechanism of Re on Interface Dislocation Networks of Ni–Based Single Crystal Alloys" Materials 17, no. 10: 2361. https://doi.org/10.3390/ma17102361




