Reinforcement Effects on Tensile Behavior of Ultra-High-Performance Concrete (UHPC) with Low Steel Fiber Volume Fractions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Property
2.2. Specimen Design
2.3. Test Setup
3. Local Fiber Distribution
4. Mechanical Properties
4.1. Failure Modes
4.2. Load–Displacement Response
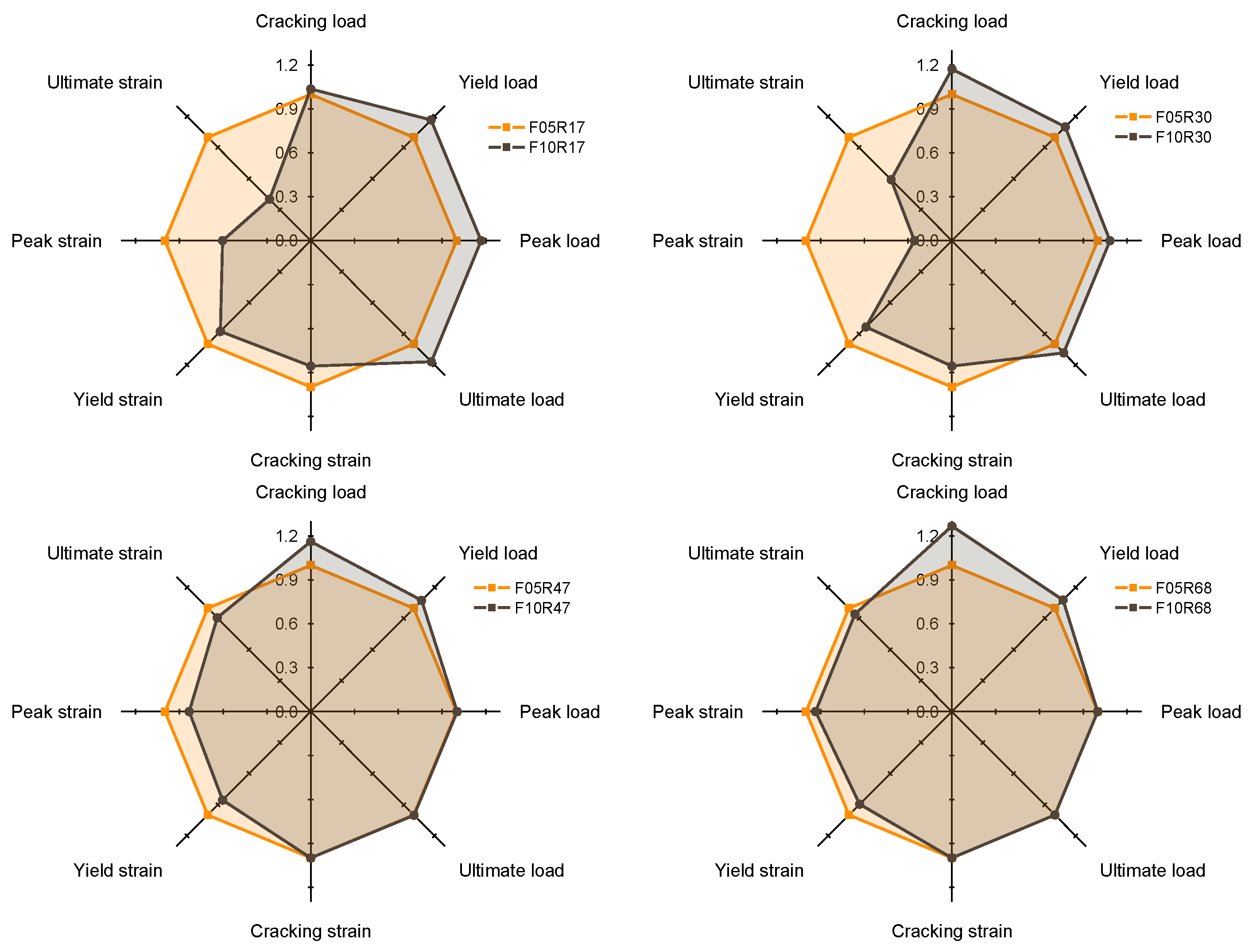
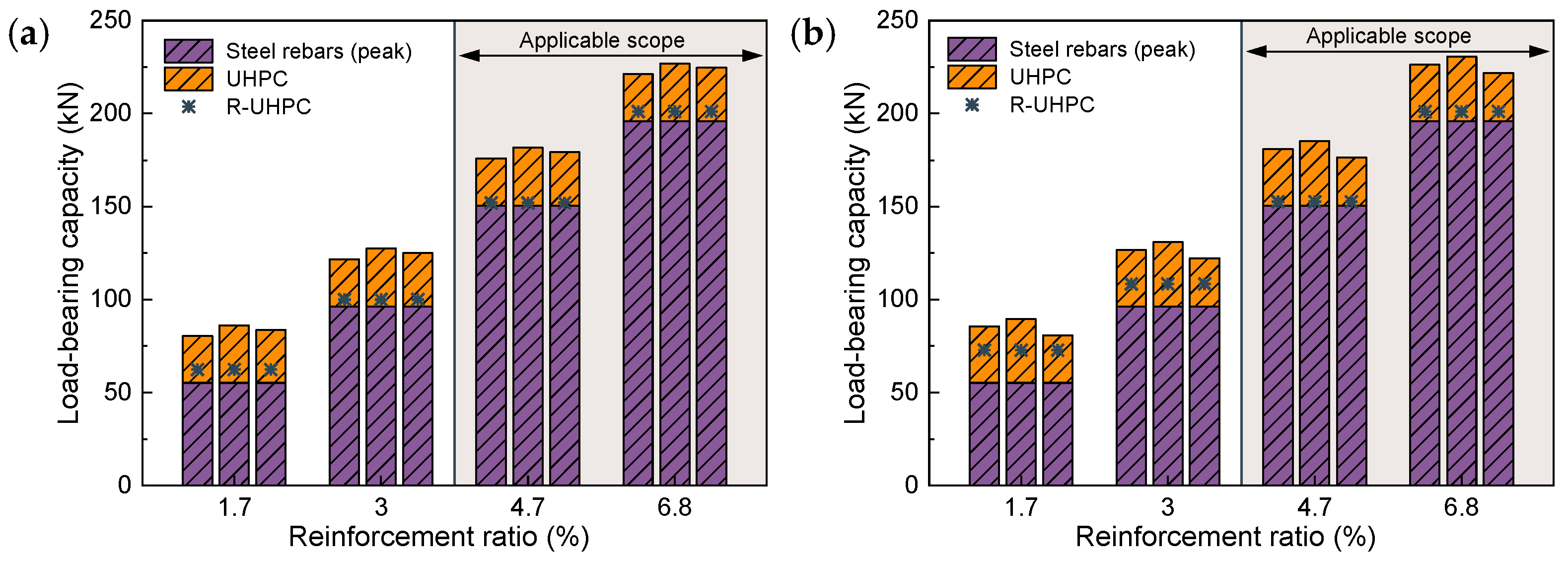
4.3. Load-Bearing Capacity
- The rebar component, due to excessive localized deformation, enters the yielding stage prior to the UHPC component reaching its load-bearing capacity.
- Upon the UHPC component reaching its load-bearing capacity, the rebar component enters the strength hardening stage, or just reaches ultimate strength, or enters the necking stage.
- Both the UHPC component and the rebar component concurrently reach their load-bearing capacities.
- When the load-bearing capacity of the UHPC component declines due to many fibers being pulled out, the rebar component continues in the strain-hardening stage.
5. Cracking Behavior
5.1. Cracking Process
5.2. Cracks Number and Spacing
5.3. Maximum Crack Width
5.4. Fiber Efficiency in Restricting Maximum Crack Propagation
6. Conclusions
- Adopting UHPC with a low fiber volume fraction can significantly mitigate the ductility deterioration of R-UHPC, and both increasing the reinforcement ratio and decreasing the fiber volume fraction contribute to the improvement of ductility.
- Reducing the fiber volume fraction was particularly effective in improving the ductility of R-UHPC with low reinforcement ratios; for R-UHPC with reinforcement ratios of 1.7% and 3.0%, the reduction of the fiber volume fraction from 1.0% to 0.5% resulted in an increase in peak ductility of 55.4% and 287.7%, respectively. The ductility of R-UHPC with low fiber volume fraction increases approximately linearly with increasing reinforcement ratio.
- The failure modes of R-UHPC are determined by the ratio of reinforcement ratio and fiber volume fraction, rather than a single parameter, which also means that R-UHPC with different parameters may require different methods to predict tensile load-bearing capacity. For R-UHPC with significant ductility degradation, the load-bearing capacity can be calculated by superimposing the tensile load-bearing capacity of the UHPC component and the yielding load-bearing capacity of the rebar component. For R-UHPC with no substantial ductility degradation, the load-bearing capacity can be calculated by considering the contribution of rebars only.
- Incorporating steel rebars into UHPC with a low fiber volume fraction can significantly improve its capacity to restrict the maximum crack propagation. With maximum crack width up to 0.20 mm, the strains experienced by R-UHPC with fiber volume fractions of 0.5% and 1.0% increased by at least 145.5% and 43.5%, respectively, compared to unreinforced UHPC. Compared to whether rebars are incorporated, varying the reinforcement ratio does not remarkably affect the ability of R-UHPC to restrict the maximum crack propagation.
- Increasing the fiber volume fraction from 0.5% to 1.0% results in R-UHPC demonstrating better multi-cracking behavior, yet there is only a marginal enhancement in its ability to restrict maximum crack propagation. Enhancing the ability of R-UHPC to restrict the maximum crack propagation by augmenting the fiber volume fraction is inefficient.
- If excellent ductility is essential, R-UHPC with a reinforcement ratio greater than 4.7% combined with a 0.5% fiber volume fraction can be adopted. If the capacity to restrict maximum crack propagation is primarily required, R-UHPC with a reinforcement ratio of 1.7% combined with a 0.5% fiber volume fraction is more appropriate. Increasing the fiber volume fraction from 0.5% to 1.0% at the same reinforcement ratio will yield little benefit other than increased load-bearing capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hung, C.; El-Tawil, S.; Chao, S. A Review of Developments and Challenges for UHPC in Structural Engineering: Behavior, Analysis, and Design. J. Struct. Eng. 2021, 147, 3121001. [Google Scholar] [CrossRef]
- Kravanja, G.; Mumtaz, A.R.; Kravanja, S. A Comprehensive Review of the Advances, Manufacturing, Properties, Innovations, Environmental Impact and Applications of Ultra-High-Performance Concrete (UHPC). Buildings 2024, 14, 382. [Google Scholar] [CrossRef]
- Gong, J.; Ma, Y.; Fu, J.; Hu, J.; Ouyang, X.; Zhang, Z.; Wang, H. Utilization of fibers in ultra-high performance concrete: A review. Compos. Part B 2022, 241, 109995. [Google Scholar] [CrossRef]
- Bahmani, H.; Mostofinejad, D. A review of engineering properties of ultra-high-performance geopolymer concrete. Dev. Built Environ. 2023, 14, 100126. [Google Scholar] [CrossRef]
- Zou, Y.; Zheng, K.; Zhou, Z.; Zhang, Z.; Guo, J.; Jiang, J. Experimental study on flexural behavior of hollow steel-UHPC composite bridge deck. Eng. Struct. 2023, 274, 115087. [Google Scholar] [CrossRef]
- Li, C.; Shi, Y.; Zhou, J.; Fang, C.; He, J.; He, L. Experimental investigation on UHPC shrinkage of full-scale steel-UHPC composite bridge deck. Dev. Built Environ. 2023, 16, 100281. [Google Scholar] [CrossRef]
- Huang, B.; Dai, J.; Weng, K.; Zhu, J.; Shah, S.P. Flexural performance of UHPC–concrete–ECC composite member reinforced with perforated steel plates. J. Struct. Eng. 2021, 147, 4021065. [Google Scholar] [CrossRef]
- Huang, B.; Zhu, J.; Weng, K.; Huang, J.; Dai, J. Prefabricated UHPC-concrete-ECC underground utility tunnel reinforced by perforated steel plate: Experimental and numerical investigations. Case Stud. Constr. Mater. 2022, 16, e856. [Google Scholar] [CrossRef]
- Liu, X.; Pan, M.; Li, W.; Jing, C.; Chang, W.; Zhang, H. Experimental Study and Bearing Capacity Calculation of Compression-Reinforced Concrete Columns Strengthened with Ultra-High-Performance Concrete. Appl. Sci. 2024, 14, 1911. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, J.; Shao, X.; Li, L.; Sun, J.; Wang, X. The feasibility of using ultra-high performance concrete (UHPC) to strengthen RC beams in torsion. J. Mater. Res. Technol. 2023, 24, 9961–9983. [Google Scholar] [CrossRef]
- Shah, H.A.; Yuan, Q.; Photwichai, N. Use of materials to lower the cost of ultra-high-performance concrete—A review. Constr. Build. Mater. 2022, 327, 127045. [Google Scholar] [CrossRef]
- Wang, J.; Ji, W.; Li, W.; Zhao, T. Experimental Research on Fatigue Behavior of Reinforced UHPC-NC Composite Beams under Cyclic Loading. Materials 2024, 17, 747. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, P.; Wang, J.; Hu, S. Influence of fibers on the mechanical properties and durability of ultra-high-performance concrete: A review. J. Build. Eng. 2022, 52, 104370. [Google Scholar] [CrossRef]
- Ravichandran, D.; Prem, P.R.; Kaliyavaradhan, S.K.; Ambily, P.S. Influence of fibers on fresh and hardened properties of Ultra High Performance Concrete (UHPC)—A review. J. Build. Eng. 2022, 57, 104922. [Google Scholar] [CrossRef]
- Liu, J.; Han, F.; Cui, G.; Zhang, Q.; Lv, J.; Zhang, L.; Yang, Z. Combined effect of coarse aggregate and fiber on tensile behavior of ultra-high performance concrete. Constr. Build. Mater. 2016, 121, 310–318. [Google Scholar] [CrossRef]
- Ren, G.M.; Wu, H.; Fang, Q.; Liu, J.Z. Effects of steel fiber content and type on static mechanical properties of UHPCC. Constr. Build. Mater. 2018, 163, 826–839. [Google Scholar] [CrossRef]
- Qiu, M.; Shao, X.; Zhu, Y.; Hussein, H.H.; Li, F.; Li, X. Effect of Aspect Ratios of Hooked End and Straight Steel Fibers on the Tensile Strength of UHPFRC. J. Mater. Civ. Eng. 2022, 34, 4022131. [Google Scholar] [CrossRef]
- Yang, J.; Chen, B.; Wu, X.; Xu, G. Quantitative analysis of steel fibers on UHPFRC uniaxial tensile behavior using X-CT and UTT. Constr. Build. Mater. 2023, 368, 130349. [Google Scholar] [CrossRef]
- Wille, K.; Kim, D.J.; Naaman, A.E. Strain-hardening UHP-FRC with low fiber contents. Mater. Struct. 2011, 44, 583–598. [Google Scholar] [CrossRef]
- Pyo, S.; Kim, H.; Lee, B.Y. Effects of coarser fine aggregate on tensile properties of ultra high performance concrete. Cem. Concr. Compos. 2017, 84, 28–35. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, R.; Tian, Y.; Dou, G.; Du, X. Experimental investigation on static and dynamic mechanical properties of steel fiber reinforced ultra-high-strength concretes. Constr. Build. Mater. 2018, 178, 102–111. [Google Scholar] [CrossRef]
- Su, Y.; Wu, C.; Li, J.; Li, Z.; Li, W. Development of novel ultra-high performance concrete: From material to structure. Constr. Build. Mater. 2017, 135, 517–528. [Google Scholar] [CrossRef]
- Abbas, S.; Soliman, A.M.; Nehdi, M.L. Exploring mechanical and durability properties of ultra-high performance concrete incorporating various steel fiber lengths and dosages. Constr. Build. Mater. 2015, 75, 429–441. [Google Scholar] [CrossRef]
- Aghdasi, P.; Heid, A.E.; Chao, S. Developing Ultra-High-Performance Fiber-Reinforced Concrete for Large-Scale Structural Applications. ACI Mater. J. 2016, 113, 559–570. [Google Scholar] [CrossRef]
- Kunieda, M.; Hussein, M.; Ueda, N.; Nakamura, H. Enhancement of Crack Distribution of UHP-SHCC under Axial Tension Using Steel Reinforcement. J. Adv. Concr. Technol. 2010, 8, 49–57. [Google Scholar] [CrossRef]
- Bian, C.; Wang, J. Mechanical and damage mechanisms of reinforced ultra high performance concrete under tensile loading. Constr. Build. Mater. 2019, 226, 259–279. [Google Scholar] [CrossRef]
- Qiu, M.; Zhang, Y.; Qu, S.; Zhu, Y.; Shao, X. Effect of reinforcement ratio, fiber orientation, and fiber chemical treatment on the direct tension behavior of rebar-reinforced UHPC. Constr. Build. Mater. 2020, 256, 119311. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Bian, C. Synergistic tensile response of reinforced ultra high performance concrete with low fiber contents. Case Stud. Constr. Mater. 2022, 17, e1629. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, S.; Li, A.; Zhang, D. Fiber content optimization of UHPC and R-UHPC oriented to tensile behavior and cost reduction. Constr. Build. Mater. 2023, 395, 132314. [Google Scholar] [CrossRef]
- Hung, C.; Lee, H.; Chan, S.N. Tension-stiffening effect in steel-reinforced UHPC composites: Constitutive model and effects of steel fibers, loading patterns, and rebar sizes. Compos. Part B 2019, 158, 269–278. [Google Scholar] [CrossRef]
- Kang, S.; Tan, K.H.; Zhou, X.; Yang, B. Influence of reinforcement ratio on tension stiffening of reinforced engineered cementitious composites. Eng. Struct. 2017, 141, 251–262. [Google Scholar] [CrossRef]
- Shao, Y.; Billington, S.L. Utilizing full UHPC compressive strength in steel reinforced UHPC beams. In International Interactive Symposium on Ultra-High Performance Concrete; Iowa State University Digital Press: Ames, IA, USA, 2019. [Google Scholar]
- Shao, Y.; Billington, S.L. Impact of UHPC Tensile Behavior on Steel Reinforced UHPC Flexural Behavior. J. Struct. Eng. 2022, 148, 4021244. [Google Scholar] [CrossRef]
- Yang, I.H.; Joh, C.; Kim, B. Structural behavior of ultra high performance concrete beams subjected to bending. Eng. Struct. 2010, 32, 3478–3487. [Google Scholar] [CrossRef]
- Hasgul, U.; Turker, K.; Birol, T.; Yavas, A. Flexural behavior of ultra-high-performance fiber reinforced concrete beams with low and high reinforcement ratios. Struct. Concr. 2018, 19, 1577–1590. [Google Scholar] [CrossRef]
- Turker, K.; Hasgul, U.; Birol, T.; Yavas, A.; Yazici, H. Hybrid fiber use on flexural behavior of ultra high performance fiber reinforced concrete beams. Compos. Struct. 2019, 229, 111400. [Google Scholar] [CrossRef]
- Yoo, D.; Yoon, Y. Structural performance of ultra-high-performance concrete beams with different steel fibers. Eng. Struct. 2015, 102, 409–423. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Soleimani-Dashtaki, S.; Oh, T.; Chun, B.; Banthia, N.; Lee, S.J.; Yoon, Y.S. Strain-hardening effect on the flexural behavior of ultra-high-performance fiber-reinforced concrete beams with steel rebars. Dev. Built Environ. 2024, 17, 100343. [Google Scholar] [CrossRef]
- Dong, S.; Wang, D.; Wang, X.; D’Alessandro, A.; Ding, S.; Han, B.; Ou, J. Optimizing flexural cracking process of ultra-high performance concrete via incorporating microscale steel wires. Cem. Concr. Compos. 2022, 134, 104830. [Google Scholar] [CrossRef]
- Al-Osta, M.A.; Sharif, A.M.; Ahmad, S.; Adekunle, S.K.; Al-Huri, M.; Sharif, A.M. Effect of hybridization of straight and hooked steel fibers and curing methods on the key mechanical properties of UHPC. J. Mater. Res. Technol. 2021, 15, 3222–3239. [Google Scholar] [CrossRef]
- GB/T228.1; Metallic materials-Tensile Testing—Part 1: Method of Test at Room Temperature. Standardization Administration of the People’s Republic of China: Beijing, China, 2021.
- Luo, X.; Zhang, S.; Li, A.; Yang, X.; Liang, Z. Steel rebar effect on tensile and cracking behavior of UHPFRC based on direct tensile tests and digital image correlation. Cem. Concr. Compos. 2023, 137, 104940. [Google Scholar] [CrossRef]
- Hafiz, M.A.; Denarié, E. Tensile response of UHPFRC under very low strain rates and low temperatures. Cem. Concr. Res. 2020, 133, 106067. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, B.; Chen, W.; Liu, H. Multi-scale analysis on the tensile properties of UHPC considering fiber orientation. Compos. Struct. 2022, 280, 114835. [Google Scholar] [CrossRef]
- Song, Q.; Yu, R.; Shui, Z.; Wang, X.; Rao, S.; Lin, Z. Optimization of fibre orientation and distribution for a sustainable Ultra-High Performance Fibre Reinforced Concrete (UHPFRC): Experiments and mechanism analysis. Constr. Build. Mater. 2018, 169, 8–19. [Google Scholar] [CrossRef]
- Miletić, M.; Kumar, L.M.; Arns, J.Y.; Agarwal, A.; Foster, S.J.; Arns, C.; Perić, D. Gradient-based fibre detection method on 3D micro-CT tomographic image for defining fibre orientation bias in ultra-high-performance concrete. Cem. Concr. Res. 2020, 129, 105962. [Google Scholar] [CrossRef]
- Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing. Bull. N. Z. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
- Khorami, M.; Navarro-Gregori, J.; Serna, P. Tensile behaviour of reinforced UHPFRC elements under serviceability conditions. Mater. Struct. 2021, 54, 43. [Google Scholar] [CrossRef]
- Teng, L.; Khayat, K.H. Effect of overlay thickness, fiber volume, and shrinkage mitigation on flexural behavior of thin bonded ultra-high-performance concrete overlay slab. Cem. Concr. Compos. 2022, 134, 104752. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; Khayat, K.H. Investigation of mechanical properties and shrinkage of ultra-high performance concrete: Influence of steel fiber content and shape. Compos. Part B 2019, 174, 107021. [Google Scholar] [CrossRef]























| Fiber Volume Fraction (vol%) | Tensile Strength ft (MPa) | Compressive Strength fc (MPa) | Elastic Modulus E (GPa) |
|---|---|---|---|
| 0.5 | 5.7 ± 0.6 | 143.9 ± 5.8 | 41.6 ± 1.3 |
| 1.0 | 6.0 ± 0.9 | 145.7 ± 4.8 | 43.3 ± 0.9 |
| Diameter d (mm) | Elastic Modulus E (GPa) | Yield Strength fy (MPa) | Ultimate Strength fu (MPa) | Ultimate Strain εu (%) |
|---|---|---|---|---|
| 6 | 206 | 483 | 649 | 11.0 |
| 8 | 212 | 504 | 640 | 9.3 |
| 10 | 202 | 473 | 639 | 11.1 |
| 12 | 208 | 434 | 597 | 13.8 |
| Types | Specimen | Fiber Volume Fraction Vf (vol%) | Reinforcement Ratio ρ (%) |
|---|---|---|---|
| UHPC | F05R00 | 0.5 | 0 |
| F10R00 | 1.0 | 0 | |
| R-UHPC | F05R17 | 0.5 | 1.7 |
| F05R30 | 0.5 | 3.0 | |
| F05R47 | 0.5 | 4.7 | |
| F05R68 | 0.5 | 6.8 | |
| F10R17 | 1.0 | 1.7 | |
| F10R30 | 1.0 | 3.0 | |
| F10R47 | 1.0 | 4.7 | |
| F10R68 | 1.0 | 6.8 |
| Specimens | F05R17 | F05R30 | F05R47 | F05R68 |
|---|---|---|---|---|
| Cracking load Fcr (kN) | 19.4 ± 0.07 | 17.9 ± 3.0 | 14.3 ± 0.9 | 13.5 ± 2.1 |
| Cracking strain εcr (%) | 0.007 ± 0.001 | 0.007 ± 0.000 | 0.005 ± 0.000 | 0.005 ± 0.001 |
| Yield load Fy (kN) | 53.0 ± 1.3 | 87.7 ± 1.2 | 125.0 ± 5.3 | 157.8 ± 1.8 |
| Yield strain εy (%) | 0.418 ± 0.001 | 0.476 ± 0.019 | 0.482 ± 0.008 | 0.477 ± 0.020 |
| Peak load Fp (kN) | 62.4 ± 1.2 | 100.0 ± 3.0 | 152.0 ± 0.0 | 201.1 ± 0.4 |
| Peak strain εp (%) | 1.804 ± 0.385 | 4.436 ± 0.084 | 12.845 ± 1.027 | 25.941 ± 0.395 |
| Ultimate load Fu (kN) | 53.0 ± 1.0 | 85.0 ± 2.5 | 129.2 ± 0.0 | 171.0 ± 0.4 |
| Specimens | F10R17 | F10R30 | F10R47 | F10R68 |
|---|---|---|---|---|
| Cracking load Fcr (kN) | 20.1 ± 3.6 | 21.0 ± 2.1 | 16.6 ± 1.8 | 17.1 ± 1.0 |
| Cracking strain εcr (%) | 0.006 ± 0.002 | 0.006 ± 0.001 | 0.005 ± 0.000 | 0.005 ± 0.000 |
| Yield load Fy (kN) | 61.8 ± 1.8 | 96.5 ± 0.7 | 134.2 ± 0.7 | 170.1 ± 1.0 |
| Yield strain εy (%) | 0.366 ± 0.013 | 0.397 ± 0.010 | 0.412 ± 0.016 | 0.427 ± 0.022 |
| Peak load Fp (kN) | 72.9 ± 2.2 | 108.4 ± 1.3 | 152.5 ± 1.0 | 201.2 ± 0.3 |
| Peak strain εp (%) | 1.091 ± 0.150 | 1.144 ± 0.215 | 10.700 ± 1.192 | 24.232 ± 0.353 |
| Ultimate load Fu (kN) | 62.0 ± 1.9 | 92.2 ± 1.1 | 129.6 ± 0.8 | 171.0 ± 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Zhang, S.; Li, A.; Zhang, C.; Zhang, Y. Reinforcement Effects on Tensile Behavior of Ultra-High-Performance Concrete (UHPC) with Low Steel Fiber Volume Fractions. Materials 2024, 17, 2418. https://doi.org/10.3390/ma17102418
Luo X, Zhang S, Li A, Zhang C, Zhang Y. Reinforcement Effects on Tensile Behavior of Ultra-High-Performance Concrete (UHPC) with Low Steel Fiber Volume Fractions. Materials. 2024; 17(10):2418. https://doi.org/10.3390/ma17102418
Chicago/Turabian StyleLuo, Xianzhi, Sumei Zhang, Aidong Li, Chenming Zhang, and Yuchen Zhang. 2024. "Reinforcement Effects on Tensile Behavior of Ultra-High-Performance Concrete (UHPC) with Low Steel Fiber Volume Fractions" Materials 17, no. 10: 2418. https://doi.org/10.3390/ma17102418





