Development of a Measurement Device for Micro Gas Flowrate Based on Laminar Flow Element with Micro-Curved Surface
Abstract
:1. Introduction
2. Working Principle of the Curved Surface Gap LFM
3. Physical Model and Simulation Analysis
3.1. Physical Model of the Flow Meter
3.2. Simulation Parameter Setting
3.3. Analysis of Simulation Results
3.3.1. Analysis of Velocity Distribution in the Flow Field
3.3.2. Internal Flow Loss
4. Experimental Tests
4.1. Experimental Model
4.2. Experimental Test Method
4.3. Laminar Flow Sensor Calibration Experiment and Analysis
4.3.1. Calibration of K
4.3.2. Three Kinds of Surface Structure Data Test
4.4. Uncertainty Analysis
5. Conclusions
- (1)
- Introduction of curved surface gap structure: In contrast to traditional flat designs, the flowmeter incorporates a curved surface gap structure, effectively increasing the length of the flow channel while saving space. This innovative design offers a novel approach to addressing challenges in micro gas measurement.
- (2)
- Adjustable radius of curvature: By varying the radius of curvature, the length of the surface segment can be adjusted to meet measurement requirements across different ranges. This flexible design allows the curved surface gap laminar flowmeter to adapt to various applications and measurement ranges.
- (3)
- Comparable measurement accuracy to established brands: Experimental testing demonstrates that the curved surface gap laminar flowmeter, with a curvature radius of 6 mm, achieves a measurement deviation within ±0.8%, comparable to the established Alicat brand of main gas laminar flowmeters. The test results across the three structures consistently exhibit small measurement deviations, fulfilling the design requirement of ±1%.
- (4)
- Expanded measurement range and improved accuracy: The proposed design effectively expands the measurement range and enhances measurement accuracy. This study holds significant implications for the industrial application of laminar flowmeters flow metering technology.
- (5)
- Unaffected by deformation: Resolution of leakage and deformation issues in vane flowmeters: Vane flowmeters commonly encounter problems such as leakage and deformation. The study addresses these challenges by designing and testing three sample pieces using a sonic nozzle standard device, showcasing the superior measurement accuracy of the curved surface gap laminar flowmeter. The experimental findings confirm that the laminar flow element of the curved surface gap laminar flowmeter remains unaffected by deformation. Even without nonlinear correction, the differential pressure and flow rate maintain a strong linear relationship across all three structures, validating the rationality of the design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sagi, H.; Zhao, Y.; Wereley, S.T. Wide Range Flow Sensor—Vacuum through Viscous Flow Conditions. J. Vac. Sci. Technol. Vac. Surf. Films 2004, 22, 1992–1999. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, N.; Cao, Q.; Du, Y. Evaluation Approach to Dynamic Characteristic of Turbine Flowmeters Considering Calibration System Response. Flow Meas. Instrum. 2018, 64, 126–132. [Google Scholar] [CrossRef]
- Kudva, J.; Scott, M.; Jacob, J.; Smith, S.; Asheghian, L. Development of a Novel Low Stored Volume High-Altitude Wing Design. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
- Suga, S.; Okajima, M.; Fujiwara, K.; Yoshida, J.-I. “Cation Flow” Method: A New Approach to Conventional and Combinatorial Organic Syntheses Using Electrochemical Microflow Systems. J. Am. Chem. Soc. 2001, 123, 7941–7942. [Google Scholar] [CrossRef] [PubMed]
- Kametani, H.; Takao, M.; Setoguchi, T. Characteristic Evaluation of the Flowmeter Using the Wells Turbine for Measurement of Respiration. In Proceedings of the 41st SICE Annual Conference, SICE 2002, Osaka, Japan, 5–7 August 2002; Volume 1, pp. 531–534. [Google Scholar]
- Kreith, F.; Eisenstadt, R. Pressure Drop and Flow Characteristics of Short Capillary Tubes at Low Reynolds Numbers. Trans. Am. Soc. Mech. Eng. 2022, 79, 1070–1074. [Google Scholar] [CrossRef]
- Berg, R.F.; Tison, S.A. Laminar flow of four gases through a helical rectangular duct. AIChE J. 2001, 47, 263–270. [Google Scholar] [CrossRef]
- Berg, R.F. Simple Flow Meter and Viscometer of High Accuracy for Gases. Metrologia 2005, 42, 11. [Google Scholar] [CrossRef]
- Cobu, T.; Berg, R.F.; Wright, J.D.; Moldover, M.R. Modeling Laminar flow meters for process gases. In Proceedings of the 15th Proceedings of FLOMECO, Taipei, Taiwan, 13–15 October 2010. [Google Scholar]
- Pena, F.L.; Diaz, A.D.; Lema, M.R.; Rodriguez, S.V. A New Approach to Laminar Flow Meters. Sensors 2010, 10, 10560–10570. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.-C.; Lin, W.-T.; Yang, C.-T. Laminar Flow Meter with Straight Glass Capillary. MAPAN 2011, 26, 237–245. [Google Scholar] [CrossRef]
- Nuszkowski, J.; Schwamb, J.; Esposito, J. A Novel Gas Divider Using Nonlinear Laminar Flow. Flow Meas. Instrum. 2016, 52, 255–260. [Google Scholar] [CrossRef]
- Wright, J.D. What is the “Best” Transfer Standard for Gas Flow? In Proceedings of the 12th International Conference on Flow Measurement (FLOMECO), Groningen, The Netherlands, 12–14 May 2003. [Google Scholar]
- Wang, B.N. Contributions on laminar flowmeter and intake flowrate of ICE by academician Shih S.H. Trans. CSICE 2001, 19, 531–534. [Google Scholar] [CrossRef]
- Nishimura, R.; Kawashima, K.; Kagawa, T. Analysis of Laminar Flow Meter with Flute-Type Cross Section Laminar Elements. In Proceedings of the 2008 Asia Simulation Conference—7th International Conference on System Simulation and Scientific Computing, Beijing, China, 10–12 October 2008; pp. 1110–1114. [Google Scholar]
- Liu, F.-B.; Tsai, Y.-C. An Experimental and Numerical Investigation of Fluid Flow in a Cross-Corrugated Channel. Heat Mass Transf. 2010, 46, 585–593. [Google Scholar] [CrossRef]
- Variable Property Effects of Fully Developed Laminar Flow in Concentric Annuli. Heat Mass Transf. 1988, 110, 314–320. [CrossRef]
- Qingqing, W.; Guozhan, L.; Dongfei, Z.; Caolang, C.; Hongjun, Z. Study on the Parallel Pressure Differential Type Gas Laminar Flow Sensing Technique. Flow Meas. Instrum. 2021, 81, 102046. [Google Scholar] [CrossRef]
- Huang, H.-Q.; Zhao, P.; Li, G.-Z.; Zhang, H.-J. Research on pressure potential differential laminar flow sensing technology. J. Chin. J. Sci. Instrum. 2020, 41, 72–79. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Jiang, Y.; Zhang, K. Rectangle-Gap-Type Laminar Flow Meter with Inward Pressure Taps. Flow Meas. Instrum. 2021, 79, 101893. [Google Scholar] [CrossRef]
- Wright, J.D.; Cobu, T.; Berg, R.F.; Moldover, M.R. Calibration of Laminar Flow Meters for Process Gases. Flow Meas. Instrum. 2012, 25, 8–14. [Google Scholar] [CrossRef]
- Zhong, H.; He, Y.; Yang, E.; Bi, Y.; Yang, T. Modeling of Microflow during Viscoelastic Polymer Flooding in Heterogenous Reservoirs of Daqing Oilfield. J. Pet. Sci. Eng. 2022, 210, 110091. [Google Scholar] [CrossRef]
- JJG 736-2012; Gas Laminar Flow Sensor. MTC3: Beijing, China, 2012.

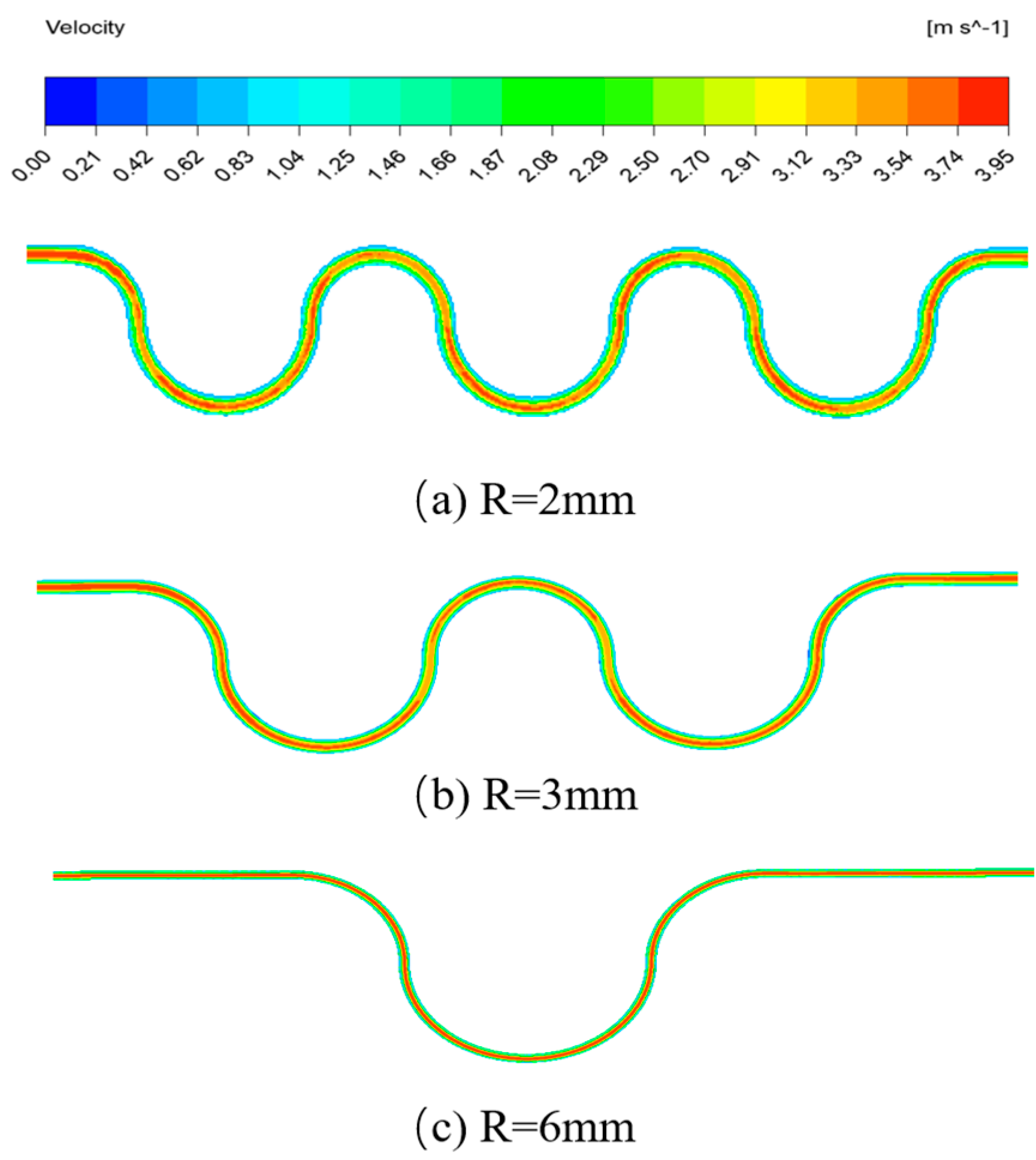
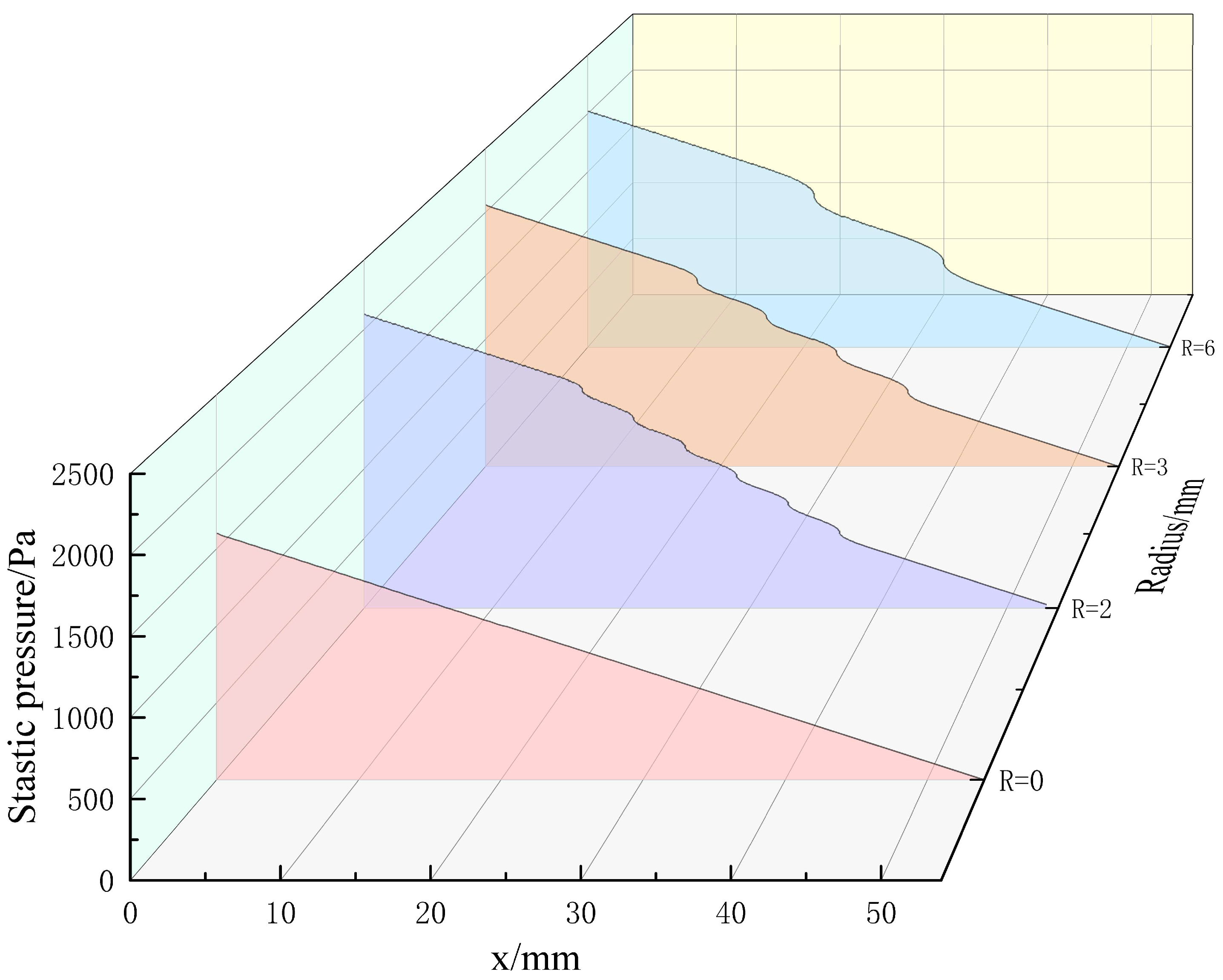






| Symbol | Units | Design Value |
|---|---|---|
| R | mm | 0/2/3/6 |
| W | mm | 2 |
| D | mm | 0.2 |
| mm | 10 | |
| mm | 10 | |
| L | mm | 54 |
| de | mm | 0.36 |
| - | 560 | |
| m/s | 22.48 | |
| mL/min | 539.52 | |
| Pa | 6515.8 |
| No. | Calibration Point | /Pa | /sccm | /sccm | K |
|---|---|---|---|---|---|
| 1 | 20% | 1027.3 | 108.1 | 108.98 | 0.9922 |
| 2 | 40% | 2078.1 | 216.5 | 220.46 | 0.9813 |
| 3 | 60% | 3080.1 | 324.1 | 326.76 | 0.9920 |
| 4 | 80% | 3802.0 | 400.7 | 403.35 | 0.9934 |
| 5 | 100% | 5144.6 | 540.2 | 545.77 | 0.9898 |
| No. | Source | Sensitivity | Relative Uncertainty |
|---|---|---|---|
| 1 | 1 | 0.25 | |
| 2 | ur () | −1 | 0.01 |
| 3 | ur () | 1 | 0.01 |
| 4 | ur () | 1 | 0.023 |
| 5 | ur () | −1 | 0.023 |
| 6 | ur () | 1 | 0.046 |
| 7 | ur () | 1 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Xu, Y.; Liu, T.; Huang, Z.; Xie, D. Development of a Measurement Device for Micro Gas Flowrate Based on Laminar Flow Element with Micro-Curved Surface. Micromachines 2024, 15, 660. https://doi.org/10.3390/mi15050660
Wang Z, Xu Y, Liu T, Huang Z, Xie D. Development of a Measurement Device for Micro Gas Flowrate Based on Laminar Flow Element with Micro-Curved Surface. Micromachines. 2024; 15(5):660. https://doi.org/10.3390/mi15050660
Chicago/Turabian StyleWang, Zixuan, Ya Xu, Tiejun Liu, Zhenwei Huang, and Dailiang Xie. 2024. "Development of a Measurement Device for Micro Gas Flowrate Based on Laminar Flow Element with Micro-Curved Surface" Micromachines 15, no. 5: 660. https://doi.org/10.3390/mi15050660





