Sidewall Corrugation-Modulated Phase-Apodized Silicon Grating Filter
Abstract
:1. Introduction
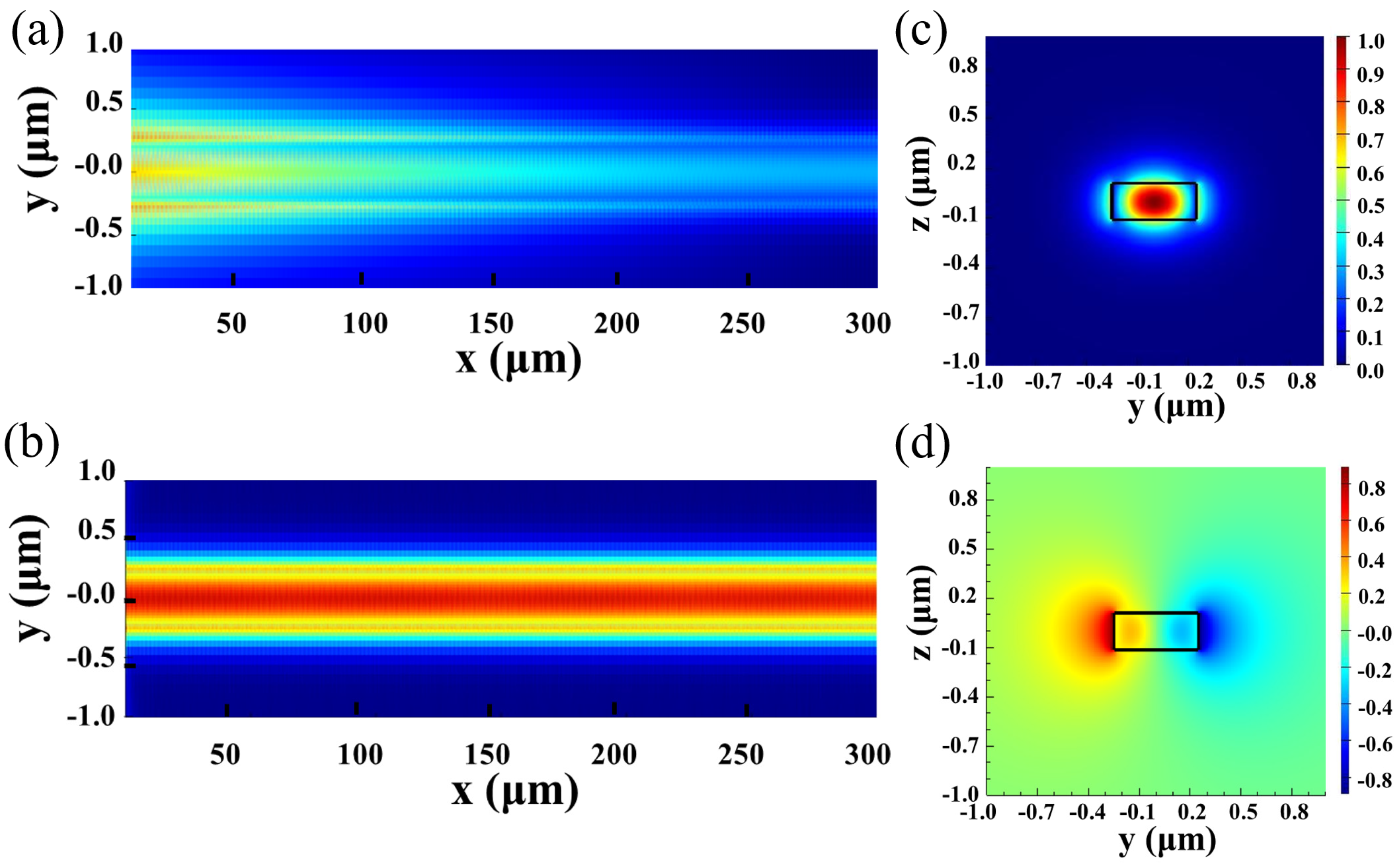
2. Device Design and Principle
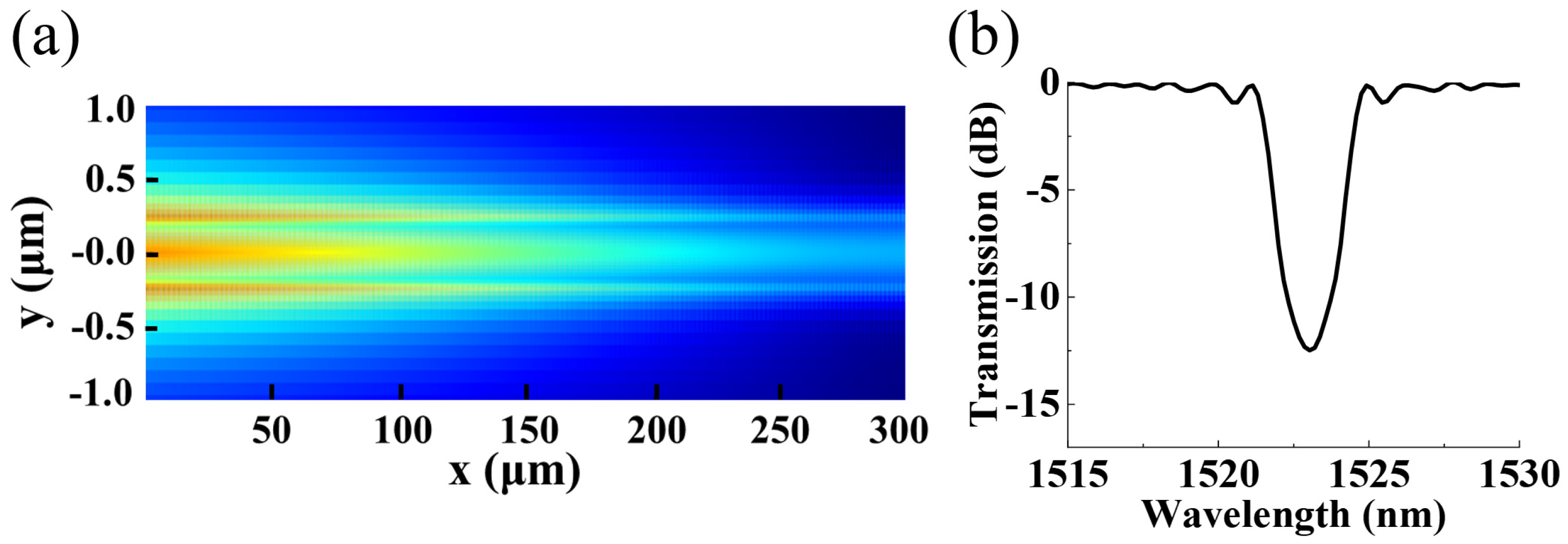
3. Device Fabrication and Characterization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Yao, J. A fully reconfigurable waveguide Bragg grating for programmable photonic signal processing. Nat. Commun. 2018, 9, 139. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Chang, K.-C.; Xie, Z.; Sarihan, M.C.; Lee, Y.S.; Li, Y.; Xu, X.; Vinod, A.K.; Kocaman, S.; Yu, M.; et al. A chip-scale polarization-spatial-momentum quantum SWAP gate in silicon nanophotonics. Nat. Photonics 2023, 17, 656–665. [Google Scholar] [CrossRef]
- Ren, W.; Liang, Q.; Feng, J.; Liu, H.; Hu, J.; Yuan, S.; Xia, X.; Jiang, W.; Zhan, Q.; Zeng, H. Free-space beam shaping and steering based on a silicon optical phased array. Photonics Res. 2023, 11, 2093–2099. [Google Scholar] [CrossRef]
- Gao, W.; Lee, W.S.L.; Fumeaux, C.; Withayachumnankul, W. Effective-medium-clad Bragg grating filters. APL Photonics 2021, 6, 076105. [Google Scholar] [CrossRef]
- Han, C.; Zheng, Z.; Shu, H.; Jin, M.; Qin, J.; Chen, R.; Tao, Y.; Shen, B.; Bai, B.; Yang, F.; et al. Slow-light silicon modulator with 110-GHz bandwidth. Sci. Adv. 2023, 9, eadi5339. [Google Scholar] [CrossRef] [PubMed]
- Nambiar, S.; Ranganath, P.; Kallega, R.; Selvaraja, S.K. High efficiency DBR assisted grating chirp generators for silicon nitride fiber-chip coupling. Sci. Rep. 2019, 9, 18821. [Google Scholar] [CrossRef] [PubMed]
- Watts, S. Optical microchip sensors. Nat. Photonics 2010, 4, 433–434. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, J.; Zhou, Y. Silicon-based wavelength division multiplexer using asymmetric grating-assisted couplers. Opt. Express 2019, 27, 23234–23249. [Google Scholar] [CrossRef]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef]
- Wu, Y.; Shi, Y.; Zhao, Y.; Li, L.; Wu, P.; Dai, P.; Fang, T.; Chen, X. On-chip optical narrowband reflector based on anti-symmetric Bragg grating. Opt. Express 2019, 27, 38541–38552. [Google Scholar] [CrossRef]
- Cheben, P.; Čtyroký, J.; Schmid, J.H.; Wang, S.; Lapointe, J.; Wangüemert-Pérez, J.G.; Molina-Fernández, Í.; Ortega-Moñux, A.; Halir, R.; Melati, D.; et al. Bragg filter bandwidth engineering in subwavelength grating metamaterial waveguides. Opt. Lett. 2019, 44, 1043–1046. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yu, H.; Qiu, H.; Zhang, Q.; Fu, Z.; Xia, P.; Chen, B.; Guo, X.; Wang, Y.; Jiang, X.; et al. Hitless and gridless reconfigurable optical add drop (de)multiplexer based on looped waveguide sidewall Bragg gratings on silicon. Opt. Express 2020, 28, 14461–14475. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Shi, W.; Yun, H.; Grist, S.; Jaeger, N.A.F.; Chrostowski, L. Narrow-band waveguide Bragg gratings on SOI wafers with CMOS-compatible fabrication process. Opt. Express 2012, 20, 15547–15558. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, Y.; Flueckiger, J.; Bojko, R.; Liu, A.; Reid, A.; Pond, J.; Jaeger, N.A.F.; Chrostowski, L. Precise control of the coupling coefficient through destructive interference in silicon waveguide Bragg gratings. Opt. Lett. 2014, 39, 5519–5522. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Piramidowicz, R. Small Footprint and High Extinction Ratio Cladding-Modulated Bragg Grating Structure as a Wideband Bandstop Filter. Photonics 2024, 11, 158. [Google Scholar] [CrossRef]
- Wang, X.; Shi, W.; Vafaei, R.; Jaeger, N.A.F.; Chrostowski, L. Uniform and Sampled Bragg Gratings in SOI Strip Waveguides with Sidewall Corrugations. IEEE Photonics Technol. Lett. 2011, 23, 290–292. [Google Scholar] [CrossRef]
- Kaushal, S.; Cheng, R.; Ma, M.; Mistry, A.; Burla, M.; Chrostowski, L.; Azaña, J. Optical signal processing based on silicon photonics waveguide Bragg gratings: Review. Front. Optoelectron. 2018, 11, 163–188. [Google Scholar] [CrossRef]
- Cheng, R.; Chrostowski, L. Apodization of Silicon Integrated Bragg Gratings Through Periodic Phase Modulation. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–15. [Google Scholar] [CrossRef]
- Klitis, C.; Cantarella, G.; Strain, M.J.; Sorel, M. High-extinction-ratio TE/TM selective Bragg grating filters on silicon-on-insulator. Opt. Lett. 2017, 42, 3040–3043. [Google Scholar] [CrossRef]
- Ma, M.; Chen, Z.; Yun, H.; Wang, Y.; Wang, X.; Jaeger, N.A.F.; Chrostowski, L. Apodized Spiral Bragg Grating Waveguides in Silicon-on-Insulator. IEEE Photonics Technol. Lett. 2018, 30, 111–114. [Google Scholar] [CrossRef]
- Paul, S.; Vartiainen, I.; Roussey, M.; Saastamoinen, T.; Tervo, J.; Honkanen, S.; Kuittinen, M. Add-drop filter based on TiO2 coated shifted Bragg grating. Opt. Express 2016, 24, 26901–26910. [Google Scholar] [CrossRef]
- Liu, D.; He, J.; Zhu, M.; Xiang, Y.; Zhang, L.; Zhang, M.; Xu, Y.; Dai, D. High-Performance Silicon Photonic Filter Using Subwavelength-Structure Multimode Waveguide Gratings. Laser Photonics Rev. 2023, 17, 2300485. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, Z.; Xie, Z.; Wang, R.; Qi, T.; Hu, F.; Kim, H.; Xiao, Q.; Fu, X.; Wu, Q.H.; et al. Versatile on-chip light coupling and (de)multiplexing from arbitrary polarizations to controlled waveguide modes using an integrated dielectric metasurface. Photonics Res. 2020, 8, 564–576. [Google Scholar] [CrossRef]
- Meng, Y.; Chen, Y.; Lu, L.; Ding, Y.; Cusano, A.; Fan, J.A.; Hu, Q.; Wang, K.; Xie, Z.; Liu, Z.; et al. Optical meta-waveguides for integrated photonics and beyond. Light Sci. Appl. 2021, 10, 235. [Google Scholar] [CrossRef] [PubMed]
- Paul, S.; Kuittinen, M.; Roussey, M.; Honkanen, S. Multi-wavelength add-drop filter with phase-modulated shifted Bragg grating. Opt. Lett. 2018, 43, 3144–3147. [Google Scholar] [CrossRef] [PubMed]
- Sahu, S.; Ali, J.; Yupapin, P.P.; Singh, G. Porous Silicon Based Bragg-Grating Resonator for Refractive Index Biosensor. Photonic Sens. 2018, 8, 248–254. [Google Scholar] [CrossRef]
- Bazargani, H.P.; Burla, M.; Chrostowski, L.; Azaña, J. Photonic Hilbert transformers based on laterally apodized integrated waveguide Bragg gratings on a SOI wafer. Opt. Lett. 2016, 41, 5039–5042. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, D.; Duan, F.; Yu, Y. Enhanced direct modulation bandwidth in a tunable DBR laser with an equivalent phase shift grating. Opt. Laser Technol. 2022, 149, 107830. [Google Scholar] [CrossRef]
- Butt, M.A. Numerical investigation of a small footprint plasmonic Bragg grating structure with a high extinction ratio. Photonics Lett. Pol. 2020, 12, 82–84. [Google Scholar] [CrossRef]
- Okayama, H.; Onawa, Y.; Shimura, D.; Yaegashi, H.; Sasaki, H. Polarization insensitive silicon waveguide wavelength filter using polarization rotator and mode conversion Bragg grating with resonator cavity. Jpn. J. Appl. Phys. 2020, 59, 128002. [Google Scholar] [CrossRef]
- Yuan, S.; Feng, J.; Yu, Z.; Chen, J.; Liu, H.; Chen, Y.; Guo, S.; Huang, F.; Akimoto, R.; Zeng, H. Silicon Nanowire-Assisted High Uniform Arrayed Waveguide Grating. Nanomaterials 2023, 13, 182. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wu, Q.; Xiong, K.; Ji, J.; Zhang, H.; Zhai, H. Phase-Shifted Fiber Bragg Grating Sensing Network and its Ultrasonic Sensing Application. IEEE Sens. J. 2019, 19, 9790–9797. [Google Scholar] [CrossRef]
- Liang, X.; Cheng, R.; Shen, X.; Yu, P.; Dai, T.; Qiu, H. Spectral-Distortionless, Flat-Top, Drop-Filter Based on Complementarily-Misaligned Multimode-Waveguide Bragg Gratings. J. Light. Technol. 2020, 38, 6600–6604. [Google Scholar] [CrossRef]
- Qiu, H.; Jiang, J.; Yu, P.; Dai, T.; Yang, J.; Yu, H.; Jiang, X. Silicon band-rejection and band-pass filter based on asymmetric Bragg sidewall gratings in a multimode waveguide. Opt. Lett. 2016, 41, 2450–2453. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Qiu, H.; Wang, G.; Li, Y.; Dai, T.; Mu, D.; Yu, H.; Yang, J.; Jiang, X. Silicon lateral-apodized add–drop filter for on-chip optical interconnection. Appl. Opt. 2017, 56, 8425–8429. [Google Scholar] [CrossRef]
- Liu, H.; Feng, J.; Chen, J.; Zhou, W.; Bi, Q.; Zeng, H. Silicon nano-bridge waveguide assisted polarizing beam splitter. Opt. Laser Technol. 2023, 167, 109684. [Google Scholar] [CrossRef]





| Grating Parameters | Geometric Parameters |
|---|---|
| Waveguide width (W) | 500 nm |
| Waveguide height | 220 nm |
| Period (Λ) | 400 nm |
| Corrugations etching depth (ΔW) | 25 nm |
| Grating length (L) | 300 μm |
| Sidewall ripple width (P1) | 200 nm |
| Sidewall ripple width (P2) | 150, 200, 250 nm |
| Sidewall corrugation location offset (ΔP) | 0, 50, 100, 150, 200 nm |
| Rejection Bandwidth | Resonance Wavelength | Extinction Ratio | Fine Tuning | Footprint | |
|---|---|---|---|---|---|
| Tradition grating [16] | 5 nm | 1493 nm | 15 dB | No | 620 × 0.5 μm2 |
| Misaligned corrugation grating [14] | ~20 nm | 1547 nm | 28 dB | No | 92 × 0.55 μm2 |
| Cladding-Modulated Bragg Grating [15] | ~50 nm | 1523 nm | 7.98 dB | No | 16.4 × 3 μm2 |
| π-phase shift grating [28] | ~4 nm | 1620 nm | 15 dB | No | 100 × 0.6 μm2 |
| This work | 2.03 nm | 1517.05 nm | 8.79 dB | Yes | 300 × 0.5 μm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Feng, J.; Yuan, S.; Liu, H.; Yu, Z.; Yang, C.; Ren, W.; Xia, X.; Wang, Z.; Huang, F. Sidewall Corrugation-Modulated Phase-Apodized Silicon Grating Filter. Micromachines 2024, 15, 666. https://doi.org/10.3390/mi15060666
Jiang W, Feng J, Yuan S, Liu H, Yu Z, Yang C, Ren W, Xia X, Wang Z, Huang F. Sidewall Corrugation-Modulated Phase-Apodized Silicon Grating Filter. Micromachines. 2024; 15(6):666. https://doi.org/10.3390/mi15060666
Chicago/Turabian StyleJiang, Wei, Jijun Feng, Shuo Yuan, Haipeng Liu, Zhiheng Yu, Cunliang Yang, Wenbo Ren, Xincheng Xia, Zhengjie Wang, and Fengli Huang. 2024. "Sidewall Corrugation-Modulated Phase-Apodized Silicon Grating Filter" Micromachines 15, no. 6: 666. https://doi.org/10.3390/mi15060666





