ETE-SRSP: An Enhanced Optimization of Tramp Ship Routing and Scheduling
Abstract
:1. Introduction
- Addressing the intricate decision-making and multifaceted challenges inherent in achieving sustainable maritime transportation, we introduce an innovative model named ETE-SRSP (efficiency–time–emission multi-optimization algorithm). This model incorporates a comprehensive approach, accommodating various constraints to streamline the optimization process.
- The ETE-SRSP model is engineered for the precise alignment of ship-to-cargo matching and the refinement of shipping schedules, factoring in a multitude of conditions such as total cargo load, ship capacity, initial positioning of ships, distances across ports, and the timing of loading and unloading operations. This approach innovatively determines effective sailing routes for the fleet.
- Leveraging the NSGA (non-dominated sorting genetic algorithm) for multi-objective optimization, our strategy adeptly mediates between the objectives of sailing time efficiency and CO2 emission reduction. This detailed exploration of the interplay between these objectives and operational expenses substantially improves the model’s utility and adaptability for addressing the complex challenges of shipping logistics, underscoring the significance of simultaneous multi-objective optimization in maritime operational management.
- Innovatively including both ballast and fully loaded sailing speeds as variables in the decision-making process, we ascertain optimal speeds that exhibit a capacity for emission reduction while managing expenses effectively. Particularly under typical temporal considerations, this methodology serves as an impactful fleet management method, facilitating the pursuit of both financial and environmental objectives. Experiments demonstrate the effectiveness of the ETE-SRSP algorithm in optimizing sailing speed, particularly evident when adjusted to typical weights, where it successfully strikes a balance between operating cost control and emission reduction. This finding offers fleet management a viable strategy that considers environmental protection while pursuing economic benefits.
2. Literary Review
3. Background
3.1. Description of the Tramp Ship Routing and Scheduling Problem
3.2. Mathematical Formulations
4. Proposed Model
4.1. Preparation of Parameter and Variable Sets
4.2. Description of Assumptions
- The shipping company operates a heterogeneous fleet, each ship characterized by specific attributes such as effective payload, ballast speed, full load speed, lightship weight, initial port, and initial time [25].
- Throughout their voyage, each ship must adhere to established speed ranges for ballast or meet speed requirements under fully loaded conditions [23].
- Within the consideration period of the model, fuel prices are assumed to be constant to eliminate the impact of fuel cost fluctuations on shipping economics, allowing the model to concentrate on optimizing routes and schedules.
4.3. Route Generation
4.4. Objective Function and Constraints
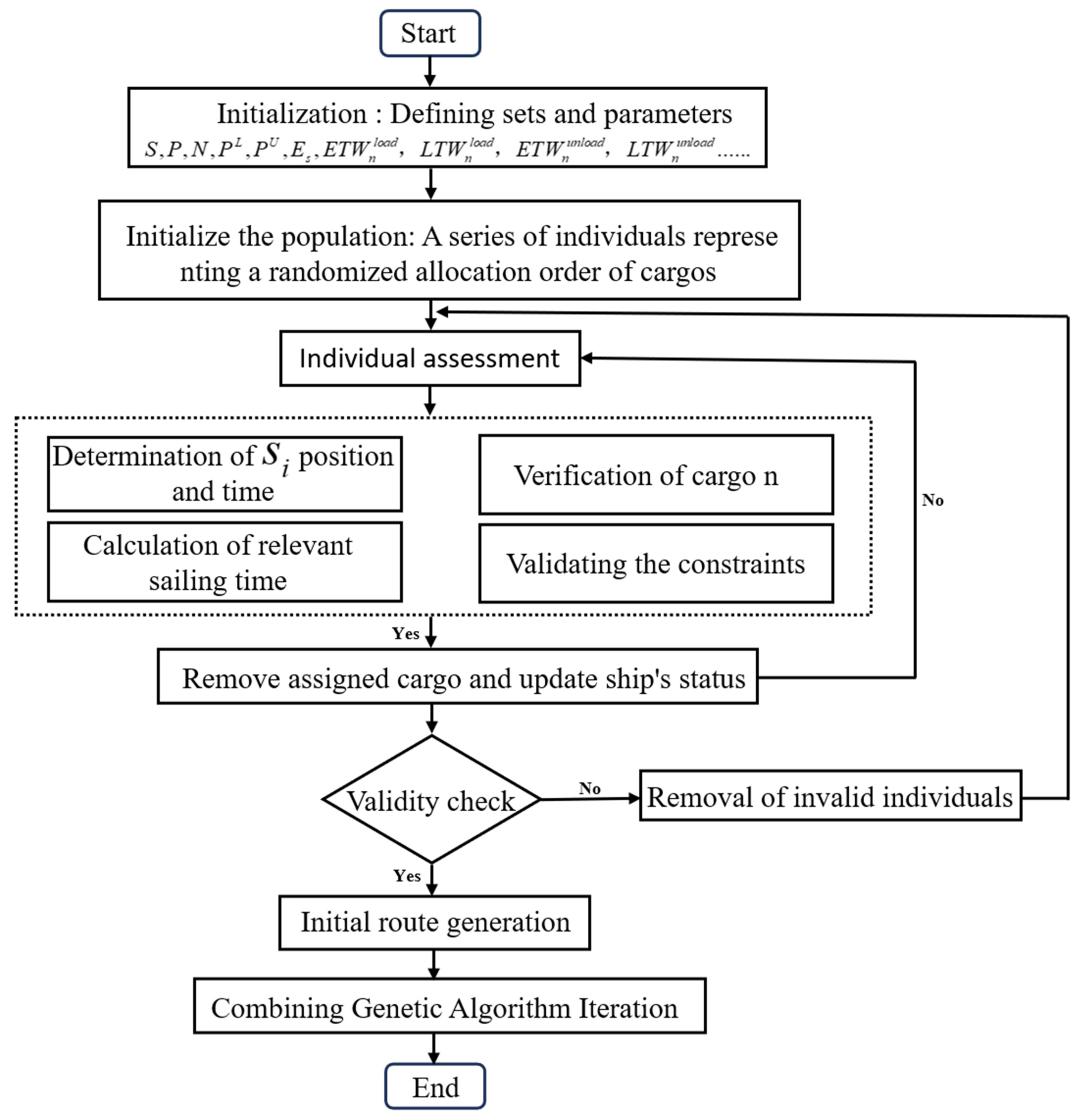
4.5. Model Logic
| Algorithm 1: The procedure of ETE-SRSP Algorithm. |
| 1: Initialization: Ship collection S, port collection P, cargo collection N…… 2: Input: Parameter settings of ETE-SRSP; Parameter settings of ETE-SRSP: see Table 1 3: Constructing ship route scheduling environment to generate route network topology 4: Repeat n 5: Evaluate the fitness of each individual 6: for m = 1: individual 7: if check_time_e(i) < ship_time(k,s) + sailing_time(k,i) < check_time_l(i) 8: check_time(i) < ship_time(i,s) + sailing_time(i,j) < check_time(j) 9: W(s) < ship(s)_capacity 10: Constraint 11: end 12: Update route, cargo, ship 13: end 14: Repeat end 15: Generate the set of optimal true_routes 16: Define the objective function using calculate Objectives (), true_routes, shipData, cargoData, Distances, alpha, lambda, fuel cost 17: Execution of multi-objective algorithm 18: For each solution in the optimal solution 19: Visualize the Pareto front and the optimal solution 20: end 21: Return |
5. Experimental Results and Analysis
5.1. Environment and Data
5.2. Results
5.3. Comparative Experimental Analysis
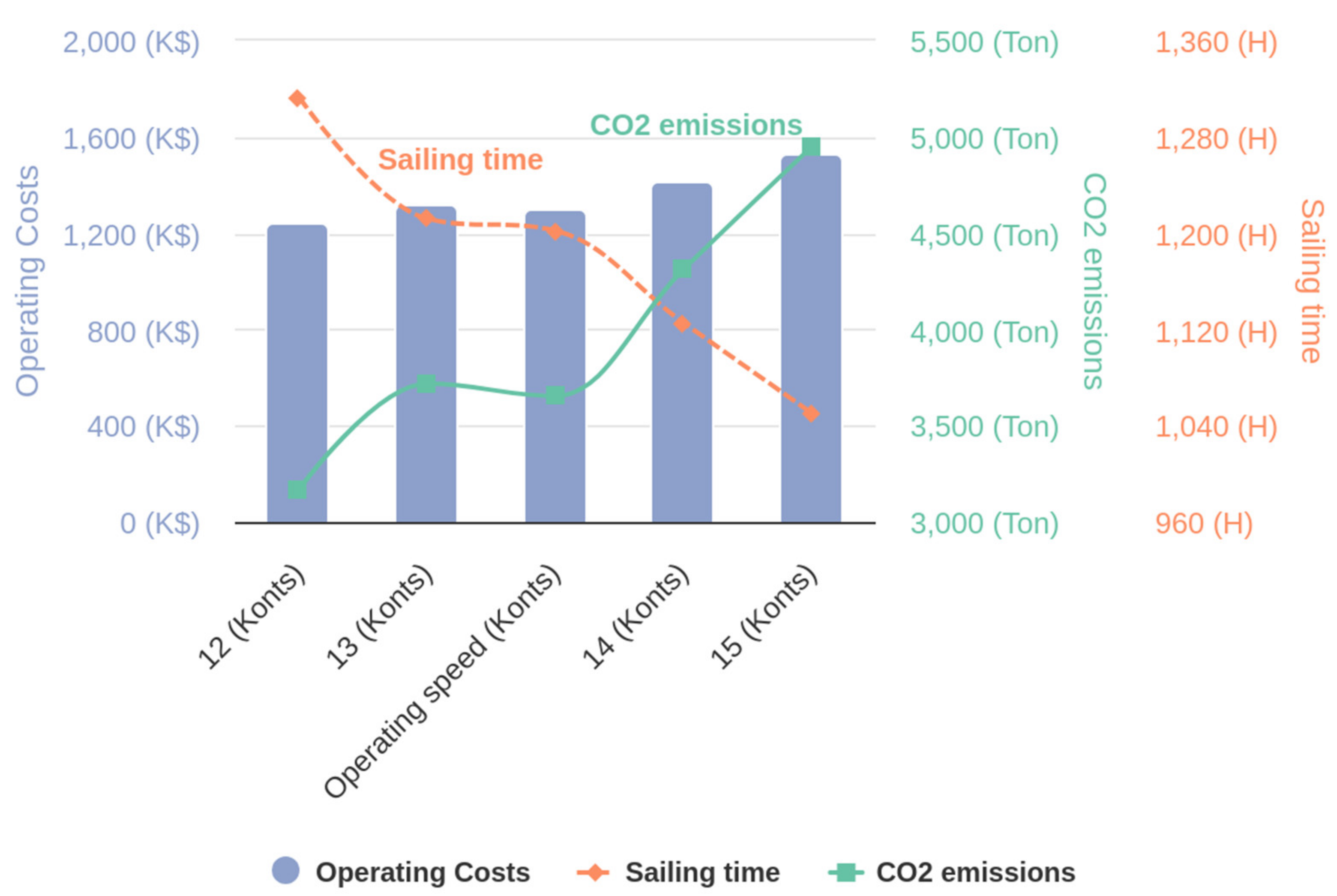
5.3.1. Multi-Speed
5.3.2. Multi-Decision
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | Reference | Objectives | Method |
|---|---|---|---|
| 1 | Lee and Kim. [17] | Min (Cost) | A mixed-integer programming model and an adaptive large neighborhood search-based heuristic algorithm are proposed, effectively reducing operating costs. |
| 2 | Charlotte et al. [20] | Min (Cost) | To introduce a novel exact branch-and-price procedure incorporating voyage separation requirements for tramp ship routing and scheduling, significantly enhancing profit maximization and inventory cost minimization |
| 3 | Min et al. [19] | Min (Cost) | To study a proposed mixed-integer linear programming and set packing method, demonstrating significant profit improvements and sensitivity to fuel prices based on real-life data. |
| 4 | Jiang et al. [22] | Min (Cost) | To present a mixed-integer linear programming model that optimizes liner shipping routes and schedules by incorporating port time windows, resulting in significant improvements in total operating costs. |
| 5 | Yu et al. [23] | Min (Cost) and Satisfaction | To propose a bi-objective model that simultaneously optimizes minimum operating costs and maximum shipper satisfaction, as well as determines the optimal speed on each leg of a given ship route. |
| 6 | Gao et al. [1] | Max (Profits) | To develop a mixed-integer programming model for optimizing ship scheduling, routing, and sailing speeds in dry bulk shipping to maximize operational revenue, demonstrating its effectiveness through numerical experiments on both illustrative. |
| 7 | Hemmat et al. [16] | Min (Cost) | To develop a benchmark suite for industrial and tramp ship routing and scheduling problems |
| 8 | Arijit et al. [14] | Min (Cost) and consideration of CO2 | This research introduces a mixed-integer non-linear programming (MINLP) model for sustainable ship routing and scheduling. |
| 9 | Fan et al. [25] | Min (Cost) and consideration of CO2 | To establish a multi-type tramp ship scheduling and speed optimization model considering carbon emissions to minimize total shipping cost. |
| 10 | Li et al. [15] | Min (Cost) and consideration of CO2 | A two-stage stochastic programming model is proposed, considering potential carbon tax schemes to evaluate its impact on CO2 emission reduction and gross margin improvement. |
| 11 | Wang et al. [26] | Min (Cost) | To introduce a voyage optimization method combining dynamic programming and genetic algorithms to optimize ship engine power for fuel and emissions reduction. |
| 12 | Wen et al. [27] | Min (Cost) and consideration of CO2 | To develop a branch and price algorithm and a constraint programming model that incorporate factors like fuel consumption, fuel price, freight rate, and cargo inventory cost |
| 13 | Wang et al. [28] | Min (Cost) and consideration of CO2 | This paper presents a new method that optimizes the sailing route and speed under complex conditions, achieving a reduction of approximately 4% in fuel consumption and CO2 emissions. |
| 14 | Henrik et al. [24] | Max (Profits) | A mathematical formulation and three solution methods are proposed to address the complexity of routing and scheduling unique cargoes with coupling and synchronization constraints, achieving maximum revenue. |
| 15 | Gao et al. [23] | Min (Cost) | A branch-and-price framework is used for effective solutions, and computational experiments validate the method’s effectiveness and practical benefits. |
References
- Gao, Y.; Sun, Z. Tramp ship routing and speed optimization with tidal berth time windows. Transp. Res. Part E Logist. Transp. Rev. 2023, 178, 103268. [Google Scholar] [CrossRef]
- Homsi, G.; Martinelli, R.; Vidal, T.; Fagerholt, K. Industrial and Tramp Ship Routing Problems: Closing the Gap for Real-Scale Instances. arXiv 2018, arXiv:abs/1809.10584. [Google Scholar] [CrossRef]
- Ksciuk, J.; Kuhlemann, S.; Tierney, K.; Koberstein, A. Uncertainty in maritime ship routing and scheduling: A Literature review. Eur. J. Oper. Res. 2023, 308, 499–524. [Google Scholar] [CrossRef]
- De, A.; Choudhary, A.K.; Tiwari, M.K. Multiobjective Approach for Sustainable Ship Routing and Scheduling with Draft Restrictions. IEEE Trans. Eng. Manag. 2019, 66, 35–51. [Google Scholar] [CrossRef]
- Gavalas, D.; Syriopoulos, T.; Tsatsaronis, M. COVID–19 impact on the shipping industry: An event study approach. Transp. Policy 2021, 116, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Alharbi, A.; Davy, P. Liner ship route schedule design with port time windows. Transp. Res. Part C Emerg. Technol. 2014, 41, 1–17. [Google Scholar] [CrossRef]
- Monge, M.; Romero Rojo, M.F.; Gil-Alana, L.A. The impact of geopolitical risk on the behavior of oil prices and freight rates. Energy 2023, 269, 126779. [Google Scholar] [CrossRef]
- Han, D.; Pan, N.; Li, K.C. A Traceable and Revocable Ciphertext-Policy Attribute-based Encryption Scheme Based on Privacy Protection. IEEE Trans. Dependable Secur. Comput. 2022, 19, 316–327. [Google Scholar] [CrossRef]
- Wen, X.; Chen, Q.; Yin, Y.Q.; Lau, Y.Y.; Dulebenets, M.A. Multi-Objective Optimization for Ship Scheduling with Port Congestion and Environmental Considerations. J. Mar. Sci. Eng. 2024, 12, 114. [Google Scholar] [CrossRef]
- Chen, C.; Han, D.; Shen, X. CLVIN: Complete language-vision interaction network for visual question answering. Knowl. Based Syst. 2023, 275, 110706. [Google Scholar] [CrossRef]
- Yan, R.; Wang, S.; Psaraftis, H.N. Data analytics for fuel consumption management in maritime transportation: Status and perspectives. Transp. Res. Part E Logist. Transp. Rev. 2021, 155, 102489. [Google Scholar] [CrossRef]
- Yu, B.; Peng, Z.; Tian, Z.; Yao, B. Sailing speed optimization for tramp ships with fuzzy time window. Flex. Serv. Manuf. J. 2019, 31, 308–330. [Google Scholar] [CrossRef]
- Aydin, N.; Lee, H.; Mansouri, S.A. Speed optimization and bunkering in liner shipping in the presence of uncertain service times and time windows at ports. Eur. J. Oper. Res. 2017, 259, 143–154. [Google Scholar] [CrossRef]
- De, A.; Mamanduru, V.K.; Gunasekaran, A.; Subramanian, N.; Tiwari, M.K. Composite particle algorithm for sustainable integrated dynamic ship routing and scheduling optimization. Comput. Ind. Eng. 2016, 96, 201–215. [Google Scholar] [CrossRef]
- Li, M.; Fagerholt, K.; Schütz, P. Stochastic tramp ship routing with speed optimization: Analyzing the impact of the Northern Sea Route on CO2 emissions. Ann. Oper. Res. 2022. [Google Scholar] [CrossRef]
- Hemmati, A.; Hvattum, L.M.; Fagerholt, K.; Norstad, I. Benchmark Suite for Industrial and Tramp Ship Routing and Scheduling Problems. INFOR Inf. Syst. Oper. Res. 2014, 52, 28–38. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.I. Industrial ship routing problem with split delivery and two types of vessels. Expert Syst. Appl. 2015, 42, 9012–9023. [Google Scholar] [CrossRef]
- Vilhelmsen, C.; Lusby, R.; Larsen, J. Tramp ship routing and scheduling with integrated bunker optimization. EURO J. Transp. Logist. 2014, 3, 143–175. [Google Scholar] [CrossRef]
- Wen, M.; Ropke, S.; Petersen, H.; Larsen, R.; Madsen, O. Full-shipload tramp ship routing and scheduling with variable speeds. Comput. Oper. Res. 2016, 70, 1–8. [Google Scholar] [CrossRef]
- Vilhelmsen, C.; Lusby, R.M.; Larsen, J.B. Tramp ship routing and scheduling with voyage separation requirements. OR Spectr. 2017, 39, 913–943. [Google Scholar] [CrossRef]
- Norstad, I.; Fagerholt, K.; Laporte, G. Tramp ship routing and scheduling with speed optimization. Transp. Res. Part C Emerg. Technol. 2011, 19, 853–865. [Google Scholar] [CrossRef]
- Jiang, X.; Mao, H.; Zhang, H. Simultaneous Optimization of the Liner Shipping Route and Ship Schedule Designs with Time Windows. Math. Probl. Eng. 2020, 2020, 3287973. [Google Scholar] [CrossRef]
- Gao, J.; Wang, J.; Liang, J.P. A unified operation decision model for dry bulk shipping fleet: Ship scheduling, routing, and sailing speed optimization. Optim. Eng. 2023, 25, 301–324. [Google Scholar] [CrossRef]
- Andersson, H.; Duesund, J.M.; Fagerholt, K. Ship routing and scheduling with cargo coupling and synchronization constraints. Comput. Ind. Eng. 2011, 61, 1107–1116. [Google Scholar] [CrossRef]
- Fan, H.; Yu, J.; Liu, X. Tramp Ship Routing and Scheduling with Speed Optimization Considering Carbon Emissions. Sustainability 2019, 11, 6367. [Google Scholar] [CrossRef]
- Wang, H.; Lang, X.; Mao, W. Voyage optimization combining genetic algorithm and dynamic programming for fuel/emissions reduction. Transp. Res. Part D Transp. Environ. 2021, 90, 102670. [Google Scholar] [CrossRef]
- Wen, M.; Pacino, D.; Kontovas, C.; Psaraftis, H. A multiple ship routing and speed optimization problem under time, cost and environmental objectives. Transp. Res. Part D Transp. Environ. 2017, 52, 303–321. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Huang, L.; Ma, R.; Jiang, X.; Yuan, Y.; Mwero, N.A.; Negenborn, R.R.; Sun, P.; Yan, X. A novel method for joint optimization of the sailing route and speed considering multiple environmental factors for more energy efficient shipping. Ocean Eng. 2020, 216, 107591. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Lee, H.; Aluko, O. Multi-objective decision support to enhance environmental sustainability in maritime shipping: A review and future directions. Transp. Res. Part E Logist. Transp. Rev. 2015, 78, 3–18. [Google Scholar] [CrossRef]
- Han, D.; Zhu, Y.; Li, D.; Liang, W.; Souri, A.; Li, K.-C. A Blockchain-Based Auditable Access Control System for Private Data in Service-Centric IoT Environments. IEEE Trans. Ind. Inform. 2022, 18, 3530–3540. [Google Scholar] [CrossRef]
- Chen, C.; Han, D.; Chang, C.C. MPCCT: Multimodal vision-language learning paradigm with context-based compact Transformer. Pattern Recognit. 2023, 147, 110084. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Kontovas, C.A. Ship speed optimization: Concepts, models and combined speed-routing scenarios. Transp. Res. Part C Emerg. Technol. 2014, 44, 52–69. [Google Scholar] [CrossRef]
- Degiuli, N.; Martić, I.; Farkas, A.; Gospić, I. The impact of slow steaming on reducing CO2 emissions in the Mediterranean Sea. Energy Rep. 2021, 7, 8131–8141. [Google Scholar] [CrossRef]
- Han, Y.; Ma, W.; Ma, D. Green maritime: An improved quantum genetic algorithm-based ship speed optimization method considering various emission reduction regulations and strategies. J. Clean. Prod. 2023, 385, 135814. [Google Scholar] [CrossRef]









| Tag | Description |
|---|---|
| Set | |
| S | Set of ships, S = 1, 2, 3… |
| P | Set of ports, P = 1, 2, 3… |
| Set of loading ports | |
| Set of unloading ports | |
| N | Set of cargoes |
| L | Set of feasible voyage routes, L = 1, 2, 3… |
| Set of empty weights for ship s | |
| Parameters | |
| Fuel consumption for voyage route l of ship | |
| Emission factor, a constant | |
| A constant | |
| Cargo weight carried by ship s | |
| o(s) | Initial position of ship s |
| d(s) | Destination node in the solution or the destination port of the ship s |
| Earliest loading time for cargo n | |
| Latest loading time for cargo n | |
| Earliest unloading time for cargo n | |
| Latest unloading time for cargo n | |
| Fuel price | |
| Daily fixed cost | |
| Distance from port i to port j | |
| m | Number of ships, a constant |
| Variables | |
| Variable defining ship s sailing from i to j as 0,1 | |
| Total sailing time for the fleet | |
| Sailing time for the current voyage | |
| Ballast speed of ship s | |
| Fully loaded speed of ship s | |
| CO2 emissions for voyage route l of the ship | |
| Operating costs for ship | |
| CO2 emissions for voyage route l of the ship | |
| Total CO2 emissions for the fleet |
| Ship ID | Initial Port | Initial Time (H) | Speed Range (Knots) | Capacity (Tons) | Empty Weight (Tons) | Daily Cost ($) | |
|---|---|---|---|---|---|---|---|
| Min | Max | ||||||
| 1 | Sydney | 288 | 11.5 | 17 | 31,760 | 13,382 | 5200 |
| 2 | Belem | 96 | 11 | 16 | 32,800 | 14,295 | 5800 |
| 3 | New Orleans | 24 | 11 | 17 | 31,770 | 11,936 | 5300 |
| 4 | Rotterdam | 168 | 10 | 16 | 34,650 | 14,273 | 6200 |
| Cargo ID | Cargo Weight (Tons) | Load Port | Unload Port | Load Time Start (H) | Load Time End (H) | Unload Time Start (H) | Unload Time End (H) | Charter Cost (K$) |
|---|---|---|---|---|---|---|---|---|
| 1 | 27,050 | Sydney | Ho Chi Minh | 270 | 298 | 572 | 667 | 872 |
| 2 | 24,728 | Rotterdam | Fujairah | 150 | 220 | 576 | 693 | 633 |
| 3 | 24,814 | Belem | Qingdao | 94 | 144 | 815 | 1026 | 926 |
| 4 | 29,304 | New Orleans | Le Havre | 22 | 126 | 330 | 422 | 437 |
| 5 | 30,576 | Vancouver | Dalian | 843 | 1063 | 1182 | 1485 | 517 |
| 6 | 24,975 | Vancouver | Guangzhou | 2011 | 2481 | 2392 | 2561 | 581 |
| 7 | 31,733 | Dunkerque | Port Klang | 983 | 1023 | 1528 | 1881 | 755 |
| 8 | 29,862 | Seattle | Tokyo | 1529 | 1921 | 1813 | 2270 | 409 |
| 9 | 30,616 | Sydney | Fujairah | 867 | 1031 | 1330 | 1605 | 639 |
| 10 | 28,879 | Vancouver | Ningbo | 1160 | 1447 | 1516 | 1866 | 511 |
| 11 | 27,365 | Seattle | Guangzhou | 1855 | 2298 | 2229 | 2573 | 550 |
| ID | Route | Cargoes | Ballast Speed (Knots) | Full Load Speed (Knots) | Fuel Consumption (Tons) | CO2 Quantity (Tons) | Time (H) | Time Cost (K$) | Fuel Cost (K$) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1-1-8 | 1 | - | 12.7 | 427.7 | 1154.7 | 347 | 141.82 | 256.60 |
| 1 | 8-1-9 | 9 | 14.9 | 12.4 | 925.5 | 2498.9 | 855 | 348.99 | 555.30 |
| 2 | 3-3-10 | 3 | - | 13 | 1048.8 | 2831.7 | 849 | 325.39 | 629.26 |
| 2 | 10-5-16 | 10 | 14.8 | 12.5 | 795.1 | 2146.7 | 747 | 286.33 | 477.05 |
| 2 | 16-7-13 | 11 | 14.7 | 12.3 | 840.0 | 2268.1 | 818 | 313.58 | 504.02 |
| 3 | 4-4-11 | 4 | - | 12.4 | 389.3 | 1051.0 | 377 | 135.16 | 233.56 |
| 3 | 11-5-12 | 5 | 14.9 | 12.3 | 828.4 | 2236.7 | 928 | 332.65 | 497.04 |
| 3 | 12-7-15 | 8 | 14.9 | 12.1 | 621.1 | 1676.9 | 700 | 250.98 | 372.65 |
| 4 | 2-2-9 | 2 | - | 12.3 | 604.9 | 1633.2 | 505 | 237.84 | 362.94 |
| 4 | 9-6-14 | 7 | 14.7 | 12.3 | 1236.6 | 3338.9 | 1075 | 506.12 | 741.99 |
| 4 | 14-5-13 | 6 | 14.8 | 12.6 | 1064.6 | 2874.5 | 946 | 445.20 | 638.78 |
| ID | Fuel Consumption (Tons) | CO2 Quantity (Tons) | Time (H) | Time Cost (K$) | Fuel Cost (K$) | Total Cost (K$) |
|---|---|---|---|---|---|---|
| 1 | 1353.2 | 3653.6 | 1202 | 490.8 | 811.9 | 1302.7 |
| 2 | 2683.9 | 7246.5 | 2414 | 925.3 | 1610.3 | 2535.6 |
| 3 | 1838.7 | 4964.6 | 2006 | 718.8 | 1103.2 | 1822.0 |
| 4 | 2906.2 | 7846.7 | 2526 | 1189.2 | 1743.7 | 2932.9 |
| Total | 8782.0 | 23,711.4 | 8147 | 3324.1 | 5269.2 | 8593.2 |
| Speed 12 Knots | Speed 13 Knots | Operating Speed | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ID | CO2 (Tons) | Time (H) | Cost (K$) | CO2 (Tons) | Time (H) | Cost (K$) | CO2 (Tons) | Time (H) | Cost (K$) |
| 1 | 3167.6 | 1313 | 1240.1 | 3717.5 | 1212 | 1321.0 | 3653.6 | 1202 | 1302.7 |
| 2 | 6088.8 | 2675 | 2378.6 | 7145.9 | 2470 | 2534.6 | 7246.5 | 2414 | 2535.6 |
| 3 | 4194.4 | 2244 | 1736.1 | 4922.5 | 2071 | 1836.1 | 4964.6 | 2006 | 1822.0 |
| 4 | 6719.7 | 2789 | 2806.2 | 7886.3 | 2574 | 2964.5 | 7846.7 | 2526 | 2932.9 |
| Speed 14 Knots | Speed 15 Knots | Operating Speed | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ID | CO2 (Tons) | Time (H) | Cost (K$) | CO2 (Tons) | Time (H) | Cost (K$) | CO2 (Tons) | Time (H) | Cost (K$) |
| 1 | 4311.4 | 1126 | 1417.7 | 4949.3 | 1050 | 1528.8 | 3653.6 | 1202 | 1302.7 |
| 2 | 8287.6 | 2293 | 2720.7 | 9513.8 | 2140 | 2934.6 | 7246.5 | 2414 | 2535.6 |
| 3 | 5709.0 | 1923 | 1957.8 | 6553.7 | 1795 | 2099.6 | 4964.6 | 2006 | 1822.0 |
| 4 | 9146.3 | 2390 | 3157.9 | 10,499.6 | 2231 | 3383.6 | 7846.7 | 2526 | 2932.9 |
| Keys | Option | |||
|---|---|---|---|---|
| Decision 1 | Decision 2 | Decision 3 | Decision 4 | |
| CO2 (Tons) | 16,948.8 | 17,480.1 | 19,131.0 | 23,711.4 |
| Time (H) | 9841 | 9624 | 9071 | 8147 |
| Cost (K$) | 7779.5 | 7804.2 | 7951.9 | 8593.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Liu, Y.; Sha, M.; Han, B.; Han, D.; Liu, H. ETE-SRSP: An Enhanced Optimization of Tramp Ship Routing and Scheduling. J. Mar. Sci. Eng. 2024, 12, 817. https://doi.org/10.3390/jmse12050817
Huang X, Liu Y, Sha M, Han B, Han D, Liu H. ETE-SRSP: An Enhanced Optimization of Tramp Ship Routing and Scheduling. Journal of Marine Science and Engineering. 2024; 12(5):817. https://doi.org/10.3390/jmse12050817
Chicago/Turabian StyleHuang, Xiaohu, Yuhan Liu, Mei Sha, Bing Han, Dezhi Han, and Han Liu. 2024. "ETE-SRSP: An Enhanced Optimization of Tramp Ship Routing and Scheduling" Journal of Marine Science and Engineering 12, no. 5: 817. https://doi.org/10.3390/jmse12050817





