The Machine Learning Attribution of Quasi-Decadal Precipitation and Temperature Extremes in Southeastern Australia during the 1971–2022 Period
Abstract
:1. Introduction
2. Materials and Methods
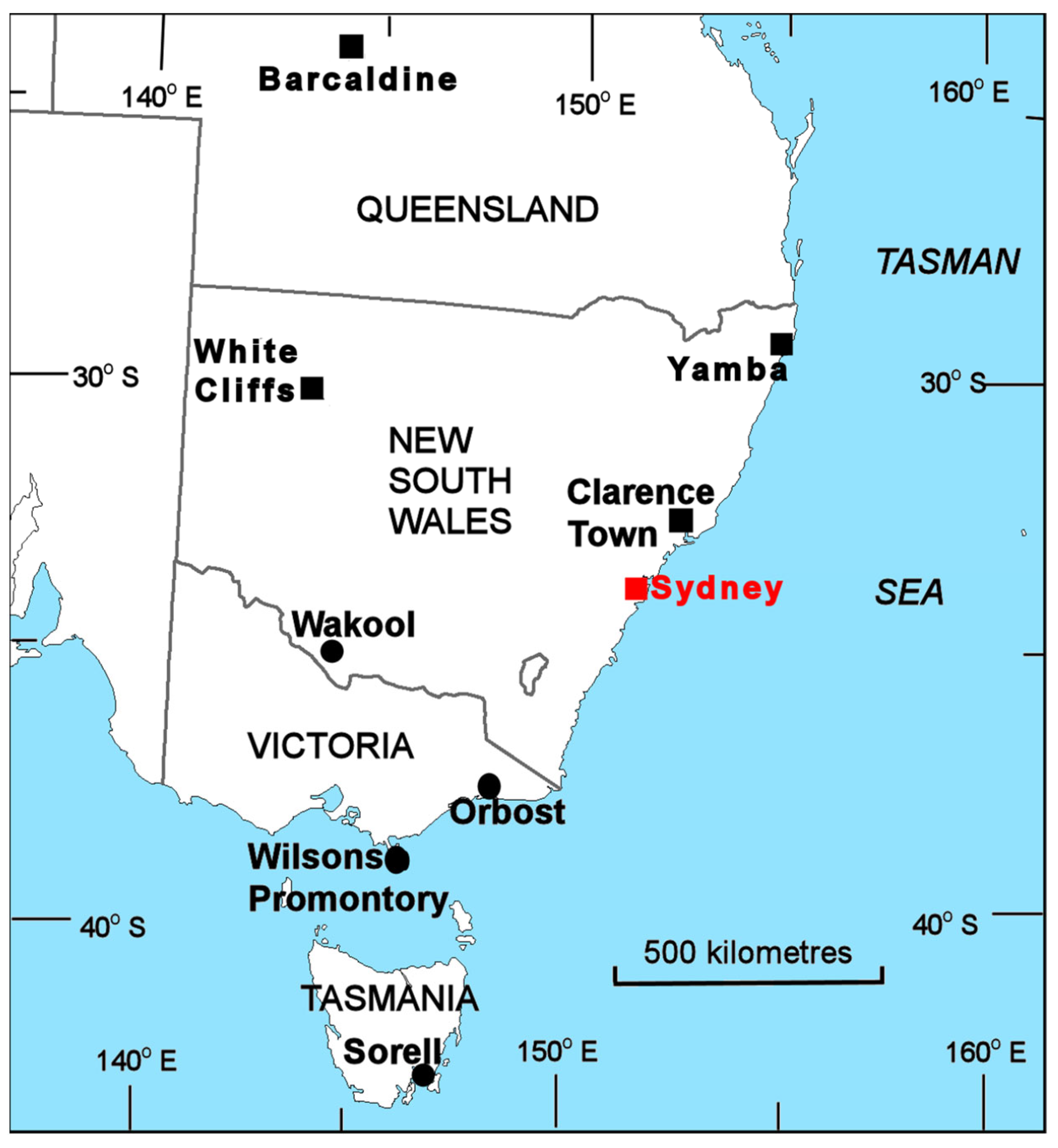
2.1. Study Area
2.2. Data
2.3. Methods
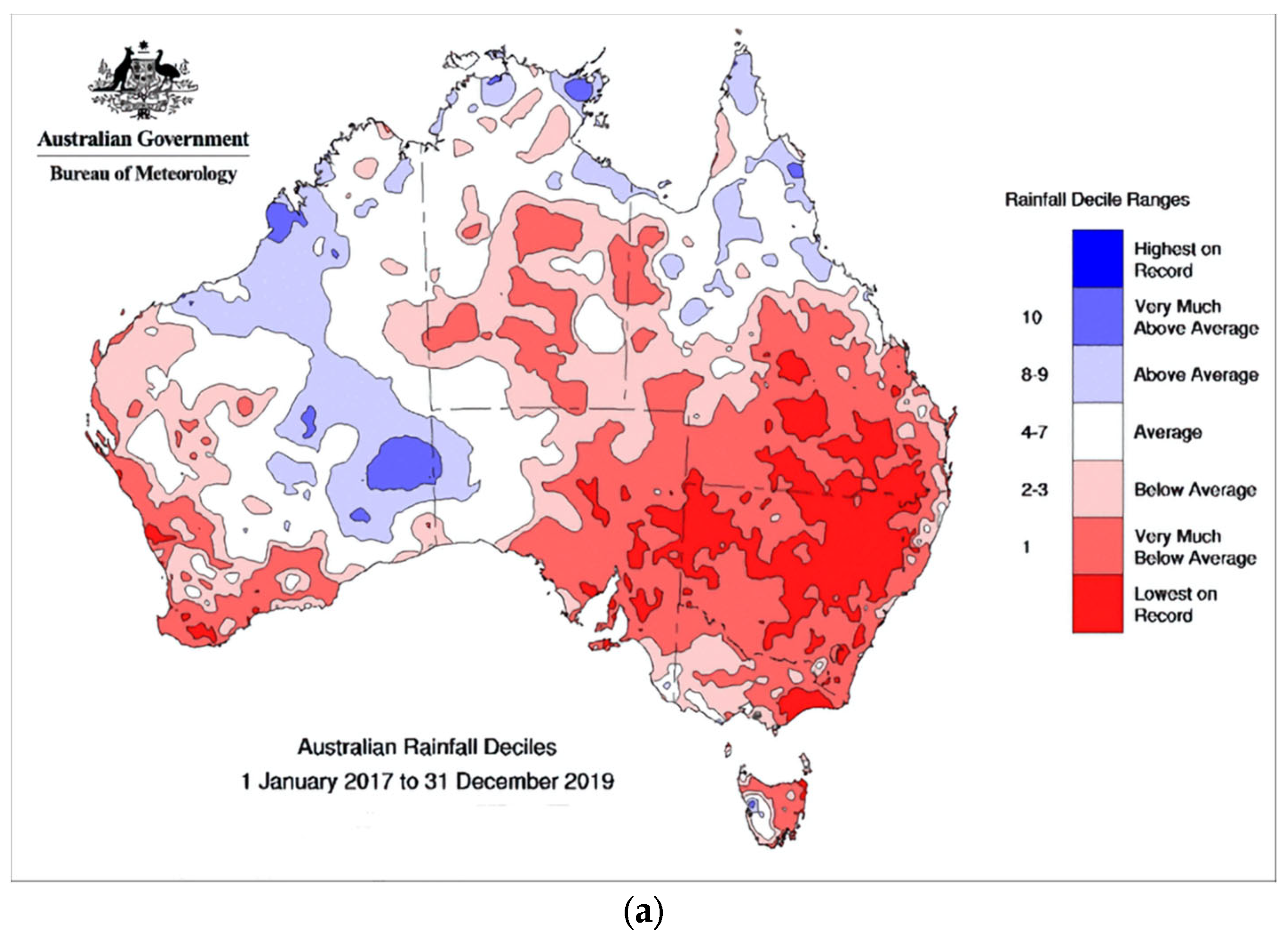
3. Results
3.1. Precipitation and TMax Time Series for SEAUS
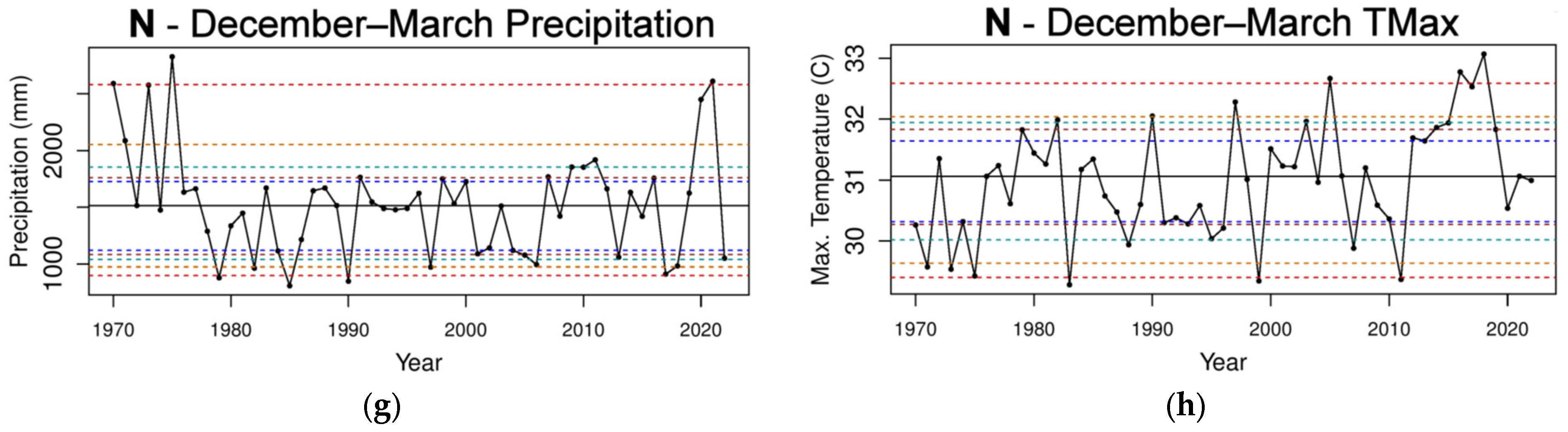
3.2. Total Precipitation and TMax Time Series of N
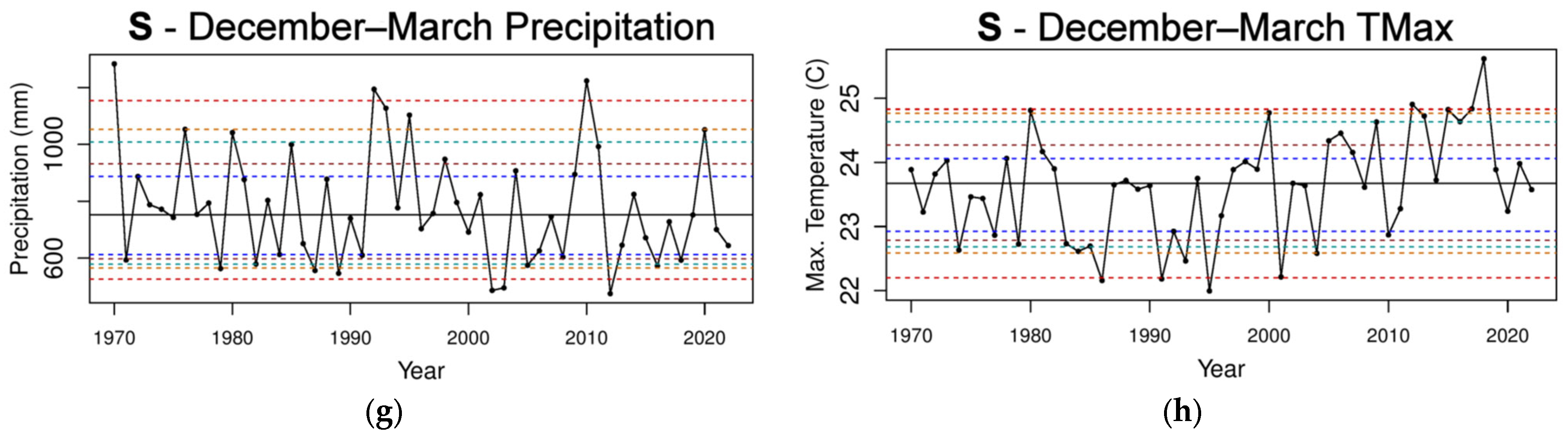
3.3. Total Precipitation and TMax Time Series of S
3.4. Total Precipitation and TMax p-Values for Six Quasi-Decadal Intervals
3.5. Attribute Selection
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BoM 2020. Australian Bureau of Meteorology and CSIRO. State of the Climate 2020. Available online: https://bom.gov.au/state-of-the-climate/ (accessed on 7 March 2024).
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Chen, Y., Goldfarb, L., Gomis, M.I., Matthews, J.B.R., Berger, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_SPM_final.pdf (accessed on 1 April 2024).
- NOAA. National Centers for Environmental Information, State of the Climate: Global Climate Report for 2019. Available online: https://www.ncdc.noaa.gov/sotc/global/201913/supplemental/page-3 (accessed on 7 March 2024).
- Speer, M.S.; Leslie, L.M.; Fierro, A.O. Australian east coast rainfall decline related to large scale climate drivers. Clim. Dyn. 2011, 36, 1419–1429. [Google Scholar] [CrossRef]
- Speer, M.; Hartigan, J.; Leslie, L. Machine Learning Assessment of the Impact of Global Warming on the Climate Drivers of Water Supply to Australia’s Northern Murray-Darling Basin. Water 2022, 14, 3073. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Thirty-Year Climate Normal. Understanding Climate Normals. Available online: https://www.noaa.gov/explainers/understanding-climate-normals (accessed on 7 May 2024).
- Cheng, L.; AghaKouchak, A. Nonstationary Precipitation Intensity-Duration-Frequency Curves for Infrastructure Design in a Changing Climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef] [PubMed]
- Slater, L.J.; Anderson, B.; Buechel, M.; Dadson, S.; Han, S.; Harrigan, S.; Kelder, T.; Kowal, K.; Lees, T.; Matthews, T.; et al. Nonstationary weather and water extremes: A review of methods for their detection, attribution, and management. Hydrol. Earth Syst. Sci. 2021, 25, 3897–3935. [Google Scholar] [CrossRef]
- Speer, M.; Leslie, L. Southeast Australia encapsulates the recent decade of extreme global weather and climate events. Acad. Environ. Sci. Sustain. 2023, 1. [Google Scholar] [CrossRef]
- Speer, M.; Leslie, L. Application of Machine Learning Techniques to Detect and Understand the Impacts of Global Warming on Southeast Australia. Georget. J. Int. Aff. 2023, 24, 260–266. [Google Scholar] [CrossRef]
- Record-Breaking La Niña Events. Available online: http://www.bom.gov.au/climate/enso/history/La-Nina-2010-12.pdf (accessed on 7 March 2024).
- Understanding the IOD. Available online: http://www.bom.gov.au/climate/about/?bookmark=iod (accessed on 7 March 2024).
- Southern Annular Mode. Available online: http://www.bom.gov.au/climate/about/?bookmark=sam (accessed on 7 March 2024).
- BoM Climate Data. Australian Bureau of Meteorology. Available online: http://www.bom.gov.au/climate/data/ (accessed on 7 March 2024).
- Tasman Sea Surface Temperature Anomalies. Available online: http://www.bom.gov.au/climate/change/?ref=ftr#tabs=Tracker&tracker=timeseries (accessed on 24 April 2024).
- Speer, M.S.; Leslie, L.M.; MacNamara, S.; Hartigan, J. From the 1990s climate change has decreased cool season catchment precipitation reducing river heights in Australia’s southern Murray-Darling Basin. Sci. Rep. 2021, 11, 16136. [Google Scholar] [CrossRef] [PubMed]
- Understanding ENSO. Available online: http://www.bom.gov.au/climate/about/?bookmark=enso (accessed on 7 March 2024).
- Speer, M.; Hartigan, J.; Leslie, L. Machine Learning Identification of Attributes and Predictors for a Flash Drought in Eastern Australia. Climate 2024, 12, 49. [Google Scholar] [CrossRef]
- Brownlee, J. Long Short-Term Memory Networks with Python Develop Sequence Prediction Models with Deep Learning; Machine Learning Mastery EBook: San Juan, PR, USA, 2017. [Google Scholar]
- Maldonado, S.; Weber, R. A wrapper method for feature selection using Support Vector Machines. Inf. Sci. 2009, 179, 2208–2217. [Google Scholar] [CrossRef]
- Annual Deciles of Actual Evapotranspiration 2018–2019. Available online: http://www.bom.gov.au/water/nwa/2019/mdb/climateandwater/climateandwater.shtml (accessed on 7 March 2024).
- Hartigan, J.; MacNamara, S.; Leslie, L.M. Application of machine learning to attribution and prediction of seasonal precipitation and temperature trends in Canberra, Australia. Climate 2020, 8, 76. [Google Scholar] [CrossRef]
- Hartigan, J.; MacNamara, S.; Leslie, L.; Speer, M. Attribution and prediction of precipitation and temperature trends within the Sydney catchment using machine learning. Climate 2020, 8, 120. [Google Scholar] [CrossRef]
- Robinson, A.; Lehmann, J.; Barriopedro, D.; Rahmstorf, S.; Coumou, D. Increasing heat and rainfall extremes now far outside the historical climate. npj Clim. Atmos. Sci. 2021, 4, 45. [Google Scholar] [CrossRef]
- Francis, J.A.; Vavrus, S.J. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012, 39, L06801. [Google Scholar] [CrossRef]
- Hendon, H.H.; Thompson, D.W.J.; Wheeler, M.C. Australian Rainfall and Surface Temperature Variations Associated with the Southern Hemisphere Annular Mode. J. Clim. 2007, 20, 2452–2467. [Google Scholar] [CrossRef]
- Lim, E.-P.; Hendon, H.H. Understanding and predicting the strong Southern Annular Mode and its impact on the record wet east Australian spring 2010. Clim Dyn. 2015, 44, 2807–2824. [Google Scholar] [CrossRef]
- Speer, M.; Geerts, B. A synoptic-mesoalpha scale climatology of flash floods in the Sydney metropolitan area. Aust. Meteorol. Mag. 1994, 43, 87–103. [Google Scholar]
- Holland, G.J.; Lynch, A.H.; Leslie, L.M. Australian east-coast cyclones. Part I: Synoptic overview and case study. Mon. Weather Rev. 1987, 115, 3024–3036. [Google Scholar] [CrossRef]
- Speer, M.; Wiles, P.; Pepler, A. Low pressure systems of the New South Wales coast and associated hazardous weather: Establishment of a database. Aust. Meteorol. Mag 2009, 58, 29–39. [Google Scholar] [CrossRef]
- Dowdy, A.J. Review of Australian east coast low pressure systems and associated extremes. Clim. Dyn. 2019, 53, 4887–4910. [Google Scholar] [CrossRef]
- Speer, M.; Leslie, L.; Hartigan, J.; MacNamara, S. Changes in Frequency and Location of East Coast Low Pressure Systems Affecting Southeast Australia. Climate 2021, 9, 44. [Google Scholar] [CrossRef]
- Risbey, J.S.; McIntosh, P.C.; Pook, M.J. Synoptic components of rainfall variability and trends in southeast Australia. Int. J. Climatol. 2013, 33, 2459–2472. [Google Scholar] [CrossRef]





| Area | Descriptive Statistic | p-Values for the Differences between the 1971–1996 and 1997–2022 Periods | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Annual | April–May | July–November | December–March | ||||||
| Precip. | TMax | Precip. | TMax | Precip. | TMax | Precip. | TMax | ||
| SEAUS | Mean | 0.38 | 0 | 0.13 | 0.07 | 0.73 | 0 | 0.58 | 0 |
| Variance | 0.56 | 0.68 | 0.055 | 0.24 | 0.25 | 0.88 | 0.62 | 0.47 | |
| N | Mean | 0.98 | 0 | 0.19 | 0.05 | 0.25 | 0 | 0.83 | 0 |
| Variance | 0.54 | 0.48 | 0.36 | 0.55 | 0.39 | 0.65 | 0.91 | 0.42 | |
| S | Mean | 0.06 | 0 | 0.2 | 0.19 | 0.075 | 0 | 0.28 | 0 |
| Variance | 0.48 | 0.91 | 0.086 | 0.46 | 0.94 | 0.72 | 0.80 | 0.77 | |
| Area | Time of Year | Descriptive Statistic | 1971–1983 and 1984–1996 | 1971–1983 and 1997–2009 | 1971–1983 and 2010–2022 | 1984–1996 and 1997–2009 | 1984–1996 and 2010–2022 | 1997–2009 and 2010–2022 |
|---|---|---|---|---|---|---|---|---|
| SEAUS | Annual | Mean | 0.31 | 0.088 | 0.68 | 0.30 | 0.64 | 0.24 |
| Variance | 0.071 | 0.091 | 0.61 | 0.81 | 0.056 | 0.12 | ||
| April–May | Mean | 0.58 | 0.17 | 0.13 | 0.53 | 0.41 | 0.76 | |
| Variance | 0.70 | 0.079 | 0.44 | 0.073 | 0.285 | 0.37 | ||
| July–November | Mean | 0.73 | 0.64 | 0.82 | 0.31 | 0.98 | 0.52 | |
| Variance | 0.083 | 0.18 | 0.23 | 0.77 | 0.015 | 0.81 | ||
| December–March | Mean | 0.26 | 0.11 | 0.8 | 0.49 | 0.46 | 0.22 | |
| Variance | 0.15 | 0.21 | 0.68 | 0.67 | 0.090 | 0.21 | ||
| N | Annual | Mean | 0.11 | 0.21 | 0.76 | 0.69 | 0.26 | 0.43 |
| Variance | 0.66 | 0.68 | 0.31 | 0.94 | 0.28 | 0.22 | ||
| April–May | Mean | 0.78 | 0.57 | 0.11 | 0.82 | 0.23 | 0.27 | |
| Variance | 0.70 | 0.69 | 0.54 | 0.56 | 0.44 | 0.78 | ||
| July–November | Mean | 0.62 | 0.66 | 0.48 | 0.37 | 0.25 | 0.73 | |
| Variance | 0.92 | 0.69 | 0.49 | 0.71 | 0.51 | 0.60 | ||
| December–March | Mean | 0.20 | 0.16 | 0.87 | 0.87 | 0.23 | 0.20 | |
| Variance | 0.10 | 0.12 | 0.84 | 0.75 | 0.26 | 0.31 | ||
| S | Annual | Mean | 0.88 | 0.077 | 0.64 | 0.0088 | 0.43 | 0.15 |
| Variance | 0.042 | 0.033 | 0.31 | 0.8 | 0.091 | 0.26 | ||
| April–May | Mean | 0.39 | 0.046 | 0.53 | 0.24 | 0.74 | 0.075 | |
| Variance | 0.44 | 0.042 | 0.16 | 0.14 | 0.50 | 0.74 | ||
| July–November | Mean | 0.33 | 0.27 | 0.72 | 0.030 | 0.16 | 0.46 | |
| Variance | 0.50 | 0.52 | 0.90 | 0.64 | 0.17 | 0.50 | ||
| December–March | Mean | 0.80 | 0.26 | 0.70 | 0.26 | 0.58 | 0.58 | |
| Variance | 0.11 | 0.98 | 0.33 | 0.06 | 0.76 | 0.43 |
| Area | Time of Year | Descriptive Statistic | 1971–1983 and 1984–1996 | 1971–1983 and 1997–2009 | 1971–1983 and 2010–2022 | 1984–1996 and 1997–2009 | 1984–1996 and 2010–2022 | 1997–2009 and 2010–2022 |
|---|---|---|---|---|---|---|---|---|
| SEAUS | Annual | Mean | 0.31 | 0.0078 | 0.0028 | 0 | 0.0002 | 0.24 |
| Variance | 0.24 | 0.62 | 0.64 | 0.98 | 0.49 | 0.044 | ||
| April–May | Mean | 0.84 | 0.36 | 0.10 | 0.44 | 0.11 | 0.44 | |
| Variance | 0.36 | 0.62 | 0.58 | 0.28 | 0.35 | 0.77 | ||
| July–November | Mean | 0.78 | 0.019 | 0.011 | 0.0018 | 0.0014 | 0.51 | |
| Variance | 0.083 | 0.60 | 0.96 | 0.77 | 0.42 | 0.31 | ||
| December–March | Mean | 0.18 | 0.12 | 0.026 | 0.0036 | 0.001 | 0.25 | |
| Variance | 0.21 | 0.74 | 0.53 | 0.73 | 0.41 | 0.18 | ||
| N | Annual | Mean | 0.77 | 0.026 | 0.012 | 0.0038 | 0.005 | 0.35 |
| Variance | 0.31 | 0.76 | 0.54 | 0.79 | 0.37 | 0.067 | ||
| April–May | Mean | 0.89 | 0.38 | 0.16 | 0.27 | 0.078 | 0.44 | |
| Variance | 0.47 | 0.97 | 0.708 | 0.65 | 0.55 | 0.63 | ||
| July–November | Mean | 0.91 | 0.038 | 0.023 | 0.011 | 0.0078 | 0.51 | |
| Variance | 0.28 | 0.71 | 0.72 | 0.80 | 0.38 | 0.23 | ||
| December–March | Mean | 0.85 | 0.22 | 0.039 | 0.088 | 0.014 | 0.34 | |
| Variance | 0.043 | 0.83 | 0.86 | 0.29 | 0.25 | 0.64 | ||
| S | Annual | Mean | 0.13 | 0.008 | 0.0002 | 0 | 0 | 0.18 |
| Variance | 0.57 | 0.75 | 0.79 | 0.68 | 0.97 | 0.25 | ||
| April–May | Mean | 0.61 | 0.46 | 0.13 | 0.77 | 0.27 | 0.49 | |
| Variance | 0.83 | 0.48 | 0.68 | 0.59 | 0.79 | 0.81 | ||
| July–November | Mean | 0.67 | 0.018 | 0.0062 | 0.0004 | 0.0006 | 0.57 | |
| Variance | 0.12 | 0.90 | 0.55 | 0.89 | 0.91 | 0.93 | ||
| December–March | Mean | 0.035 | 0.27 | 0.048 | 0.0058 | 0.001 | 0.29 | |
| Variance | 0.90 | 0.68 | 0.66 | 0.80 | 0.77 | 0.79 |
| Area of SEAUS | Annual | April–May | July–November | December–March |
|---|---|---|---|---|
| SEAUS | AMO*PMM Niño3.4 PMM*TPI AMO*IOD † AMO*TSSSTA † | AMO*TSSSTA IOD*PMM SAM GlobalSSTA*PMM Niño3.4 † IOD*SAM † | Nino3.4 IOD SOI PMM*TPI TPI † Niño3.4*TPI † | IOD*SAM PMM*SAM IOD*Niño3.4 GlobalSSTA † Niño3.4*SOI † PMM*SOI † |
| N | SOI PMM Niño3.4 Niño3.4*SOI † Niño3.4*TPI † | AMO*PMM Niño3.4 IOD*PMM IOD*Niño3.4 SAM | SAM TPI Niño3.4 SOI AMO*SAM | IOD*SAM PMM*TPI AMO*SAM † Niño3.4*SOI † SAM*TSSSTA † |
| S | IOD IOD*SAM SOI*TSSSTA AMO*IOD GlobalSSTA † Niño3.4*TPI † | AMO*TSSSTA Niño3.4*PMM † IOD*Nino3.4 † AMO*IOD AMO*PMM # AMO*TPI # PMM # IOD*SAM # | IOD AMO # AMO*PMM SOI † TSSSTA † IOD*Niño3.4 † PMM*SAM # SOI*TSSSTA † | SOI*TSSSTA AMO*GlobalT AMO*PMM † TPI † TPI*TSSSTA † |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speer, M.; Hartigan, J.; Leslie, L. The Machine Learning Attribution of Quasi-Decadal Precipitation and Temperature Extremes in Southeastern Australia during the 1971–2022 Period. Climate 2024, 12, 75. https://doi.org/10.3390/cli12050075
Speer M, Hartigan J, Leslie L. The Machine Learning Attribution of Quasi-Decadal Precipitation and Temperature Extremes in Southeastern Australia during the 1971–2022 Period. Climate. 2024; 12(5):75. https://doi.org/10.3390/cli12050075
Chicago/Turabian StyleSpeer, Milton, Joshua Hartigan, and Lance Leslie. 2024. "The Machine Learning Attribution of Quasi-Decadal Precipitation and Temperature Extremes in Southeastern Australia during the 1971–2022 Period" Climate 12, no. 5: 75. https://doi.org/10.3390/cli12050075







