Analysis of Heat Transfer for the Copper–Water Nanofluid Flow through a Uniform Porous Medium Generated by a Rotating Rigid Disk
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Equations
2.2. Similarity Transformations
2.3. Solution Methodology
3. Results
3.1. Heat Transfer Analysis
3.2. Analysis of the Velocity and Stresses
4. Discussion
5. Conclusions
- The temperature of the nanofluid exhibits an increase with higher values of velocity and temperature slip parameters.
- The effective viscosity and thermal conductivity of the nanofluid play a role in accounting for the slip effects within the system.
- The influence of the nanoparticle volume fraction on the nanofluid’s temperature is expected to be particularly notable in the presence of a heat source.
- Higher values of the velocity slip parameter lead to an increase in the radial velocity component, accompanied by a decrease in the azimuthal and axial velocity components.
- Increasing the nanoparticle fraction results in a decrease in the radial velocity component, with peak values observed near the disk at the same axial distance, which are lower than those under non-slip conditions. Additionally, the velocity decreases as the distance from the disk increases, reaching zero magnitude sooner than under non-slip conditions due to heightened viscosity resulting from an increased nanoparticle volume fraction. This induces centrifugal effects near the disk and results in higher fluid velocities near the disk compared to distant regions.
- The axial velocity reaches a uniform pattern earlier than under non-slip conditions, following a considerable reduction.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Int. Mech. Eng. Conger. Exposition 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. Thermal instability in a porous medium layer saturated by a nanofluid: A revised model. Int. J. Heat Mass Transf. 2014, 68, 211–214. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Alsaedi, A. Peristaltic transport of magneto-nanoparticles submerged in water: Model for drug delivery system. Phys. E Low-Dimens. Syst. Nanostructures 2015, 68, 123–132. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Ahmad, B. Peristalsis of silver-water nanofluid in the presence of Hall and Ohmic heating effects: Applications in drug delivery. J. Mol. Liq. 2015, 207, 248–255. [Google Scholar] [CrossRef]
- Cai, C.-J.; Shen, Z.-G.; Zheng, Y.-H.; Xing, Y.-S.; Ma, S.-L. A novel technology for powder dispersion and surface modification. J. Mater. Sci. 2007, 42, 3745–3753. [Google Scholar] [CrossRef]
- Zou, H.; Chen, C.; Zha, M.; Zhou, K.; Xiao, R.; Feng, Y.; Qiu, L.; Zhang, X.; Wang, Z. A Neural Regression Model for Predicting Thermal Conductivity of CNT Nanofluids with Multiple Base Fluids. J. Therm. Sci. 2021, 30, 1908–1916. [Google Scholar] [CrossRef]
- Mishra, S.; Mondal, H.; Behl, R.; Salimi, M. The Impact of Thermal Radiation on Mixed Convective Unsteady Nanofluid Flow in a Revolving Vertical Cone. Mathematics 2024, 12, 349. [Google Scholar] [CrossRef]
- Peter, F.; Sambath, P.; Dhanasekaran, S. Numerical Investigation of Radiative Hybrid Nanofluid Flows over a Plumb Cone/Plate. Mathematics 2023, 11, 4331. [Google Scholar] [CrossRef]
- Izadi, M.; Sheremet, M.A.; Mehryan, S.A.M. Natural convection of a hybrid nanofluid affected by an inclined periodic magnetic field within a porous medium. Chin. J. Phys. 2020, 65, 447–458. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Aly, E.H.; Shehzad, S.A.; Abbasi, F.M. Magnetized peristaltic transportation of Boron-Nitride and Ethylene-Glycol nanofluid through a curved channel. Int. J. Ambient. Energy 2022, 43, 3228–3236. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Gul, M.; Shanakhat, I.; Anjum, H.J.; Shehzad, S.A. Entropy generation analysis for magnetized peristaltic movement of nanofluid through a non-uniform asymmetric channel with variable thermal conductivity. Chin. J. Phys. 2022, 78, 111–131. [Google Scholar] [CrossRef]
- Rauf, A.; Mushtaq, T.; Javed, M.; Alahmadi, H.; Shehzad, S.A. Modeling and analysis of Bödewadt hybrid nanofluid flow triggered by a stretchable stationary disk under Hall current. Case Stud. Therm. Eng. 2023, 103315. [Google Scholar] [CrossRef]
- Datta, A.; Halder, P. Thermal efficiency and hydraulic performance evaluation on Ag-Al2O3 and SiC-Al2O3 hybrid nanofluid for circular jet impingement. Arch. Thermodyn. 2021, 42, 163–182. [Google Scholar]
- Von Kármán, T. Uber laminare und turbulente reibung. Z. Angew. Math Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Cochran, W.G. The flow due to a rotating disk. Proc. Camb. Philos. Soc. 1934, 30, 365–375. [Google Scholar] [CrossRef]
- Stuart, J.T. On the effects of uniform suction on the steady flow due to a rotating disk. Q. J. Mech. Appl. Mech. 1954, 7, 446–457. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Turkyilmazoglua, M. Fluid flow and heat transfer over a rotating and vertically moving disk. Phys. Fluids 2018, 30, 063605. [Google Scholar] [CrossRef]
- Mustafa, M. MHD nanofluid flow over a rotating disk with partial slip effects: Buongiorno model. Int. J. Heat Mass Transf. 2017, 108, 1910–1916. [Google Scholar] [CrossRef]
- Alkuhayli, N.A.M. Enhancing the Heat Transfer Due to Hybrid Nanofluid Flow Induced by a Porous Rotary Disk with Hall and Heat Generation Effects. Mathematics 2023, 11, 909. [Google Scholar] [CrossRef]
- Hussain, S.; Aziz, A.; Khalique, C.M.; Aziz, T. Numerical investigation of magnetohydrodynamic slip flow of power-law nanofluid with temperature dependent viscosity and thermal conductivity over a permeable surface. Open Phys. 2017, 15, 867–876. [Google Scholar] [CrossRef]
- Ramzan, M.; Riasat, S.; Chung, J.D.; Chu, Y.-M.; Sheikholeslami, M.; Kadry, S.; Howari, F. Upshot of heterogeneous catalysis in a nanofluid flow over a rotating disk with slip effects and Entropy optimization analysis. Sci. Rep. 2021, 11, 120. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Sharma, K. Entropy optimized radiative heat transfer of hybrid nanofluid over vertical moving rotating disk with partial slip. Chin. J. Phys. 2022, 77, 861–873. [Google Scholar] [CrossRef]
- Khan, I. Transportation of hybrid nanoparticles in forced convective Darcy Forchheimer flow by a rotating disk. Int. Commun. Heat Mass Transf. 2021, 122, 105177. [Google Scholar] [CrossRef]
- Abdulaziz, N.; Alkuhayli, M. Magnetohydrodynamic flow of copper-water nanofluid over a rotating rigid disk with Ohmic heating and Hall Effects. J. Magn. Magn. Mater. 2023, 575, 170709. [Google Scholar]
- Karimipour, A.; Esfe, M.H.; Safaei, M.R.; Semiromi, D.T.; Jafari, S.; Kazi, S.N. Mixed convection of copper–water nanofluid in a shallow inclined lid driven cavity using the lattice Boltzmann method. Phys. A Stat. Mech. Its Appl. 2014, 402, 150–168. [Google Scholar] [CrossRef]
- Santra, A.K.; Sen, S.; Chakraborty, N. Study of heat transfer due to laminar flow of copper–water nanofluid through two isothermally heated parallel plates. Int. J. Therm. Sci. 2009, 48, 391–400. [Google Scholar] [CrossRef]
- Kargarsharifabad, H. Experimental and numerical study of natural convection of Cu-water nanofluid in a cubic enclosure under constant and alternating magnetic fields. Int. Commun. Heat Mass Transf. 2020, 119, 104957. [Google Scholar] [CrossRef]
- Alahmadi, H.; Alkinidri, M.O. Exploring the Impact of Nanomaterials on Heat and Mass Transfer Properties of Carreau-Yasuda Fluid with Gyrotactic Bioconvection Peristaltic Phenomena. Mathematics 2023, 11, 1474. [Google Scholar] [CrossRef]
- Iqbal, J.; Abbasi, F.M.; Alkinidri, M.; Alahmadi, H. Heat and mass transfer analysis for MHD bioconvection peristaltic motion of Powell-Eyring nanofluid with variable thermal characteristics. Case Stud. Therm. Eng. 2023, 43, 102692. [Google Scholar] [CrossRef]
- Abdel-Wahed, M.S.; Emam, T.G. Effect of joule heating and hall current on MHD flow of a nanofluid due to a rotating disk with viscous dissipation. Therm. Sci. 2018, 22, 857–870. [Google Scholar] [CrossRef]
- Wang, T.; Song, B.; Qiao, K.; Huang, Y.; Wang, L. Effect of dimensions and agglomerations of carbon nanotubes on synchronous enhancement of mechanical and damping properties of epoxy nanocomposites. Nanomaterials 2018, 8, 996. [Google Scholar] [CrossRef]
- Zahmatkesh, I.; Sheremet, M.; Yang, L.; Heris, S.Z.; Sharifpur, M.; Meyer, J.P.; Ghalambaz, M.; Wongwises, S.; Jing, D.; Mahian, O. Effect of nanoparticle shape on the performance of thermal systems utilizing nanofluids: A critical review. J. Mol. Liq. 2021, 321, 114430. [Google Scholar] [CrossRef]











| , Density | , Thermal Conductivity | , Specific Heat | |
|---|---|---|---|
| Copper | 8933 | 401 | 385.0 |
| Water | 997.1 | 0.613 | 4179 |
| - | - | - | ||
| - | - | - | ||
| - | - | |||
| - | - | - | ||
| - | - | - | ||
| - | - | |||
| - | - | - | ||
| - | - | - | ||
| - | - | |||
| - | - | - | ||
| - | - | - |
| - | - | |||
| - | - | |||
| - | ||||
| - | - | |||
| - | - | |||
| - | ||||
| - | - | |||
| - | - |
| Studies | |
|---|---|
| from Wahed and Emam [34] for CuO nanoparticles. | |
| and for the present study, considering CuO nanoparticles and neglecting effective viscosity effects on the porous medium |
| Parameter | Range | Its Effect is Examined on: | Illustrations |
|---|---|---|---|
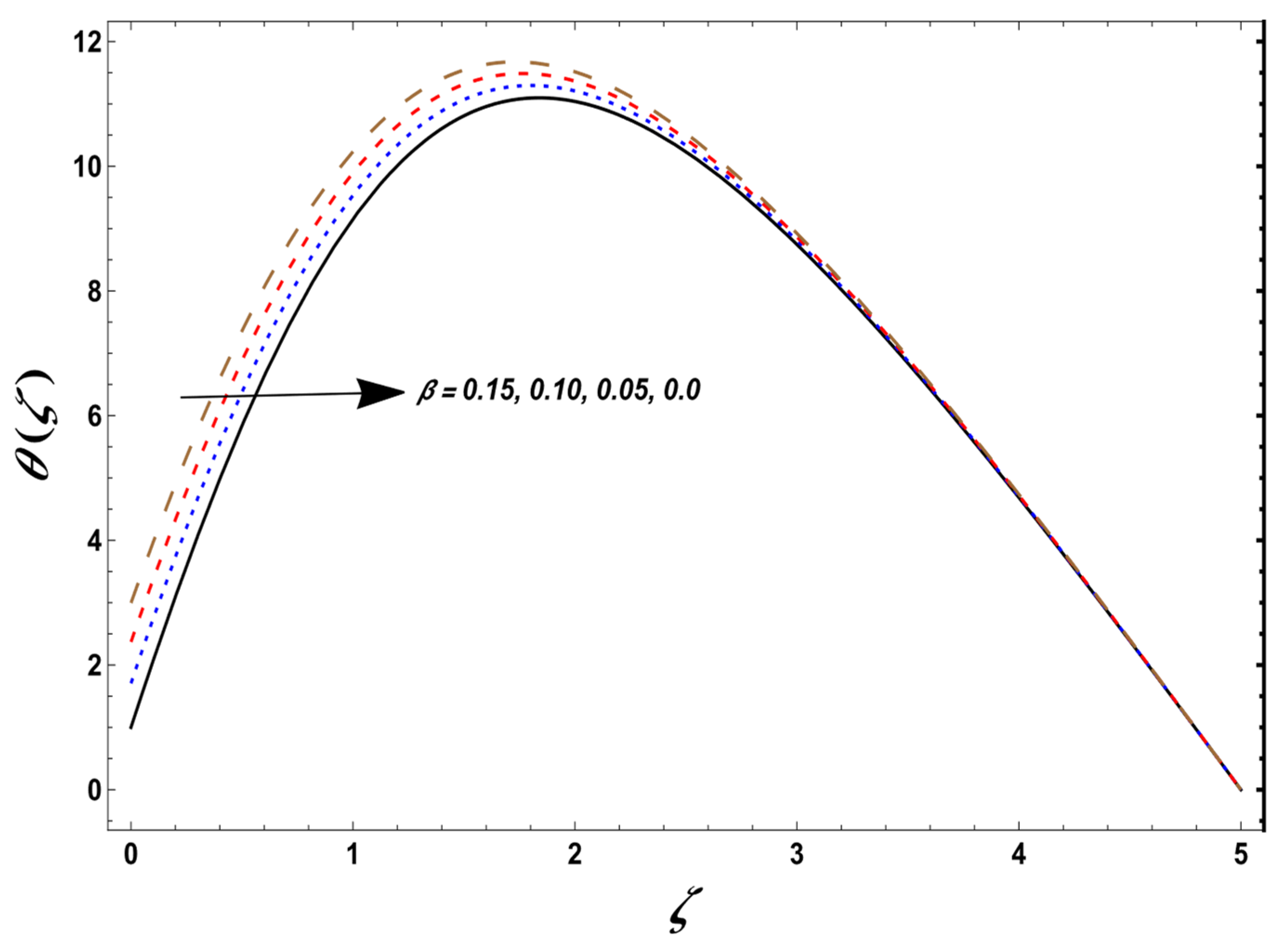
| Velocity slip parameter, | Temperature and velocities | Figure 2, Figure 7, Figure 8 and Figure 9 | |
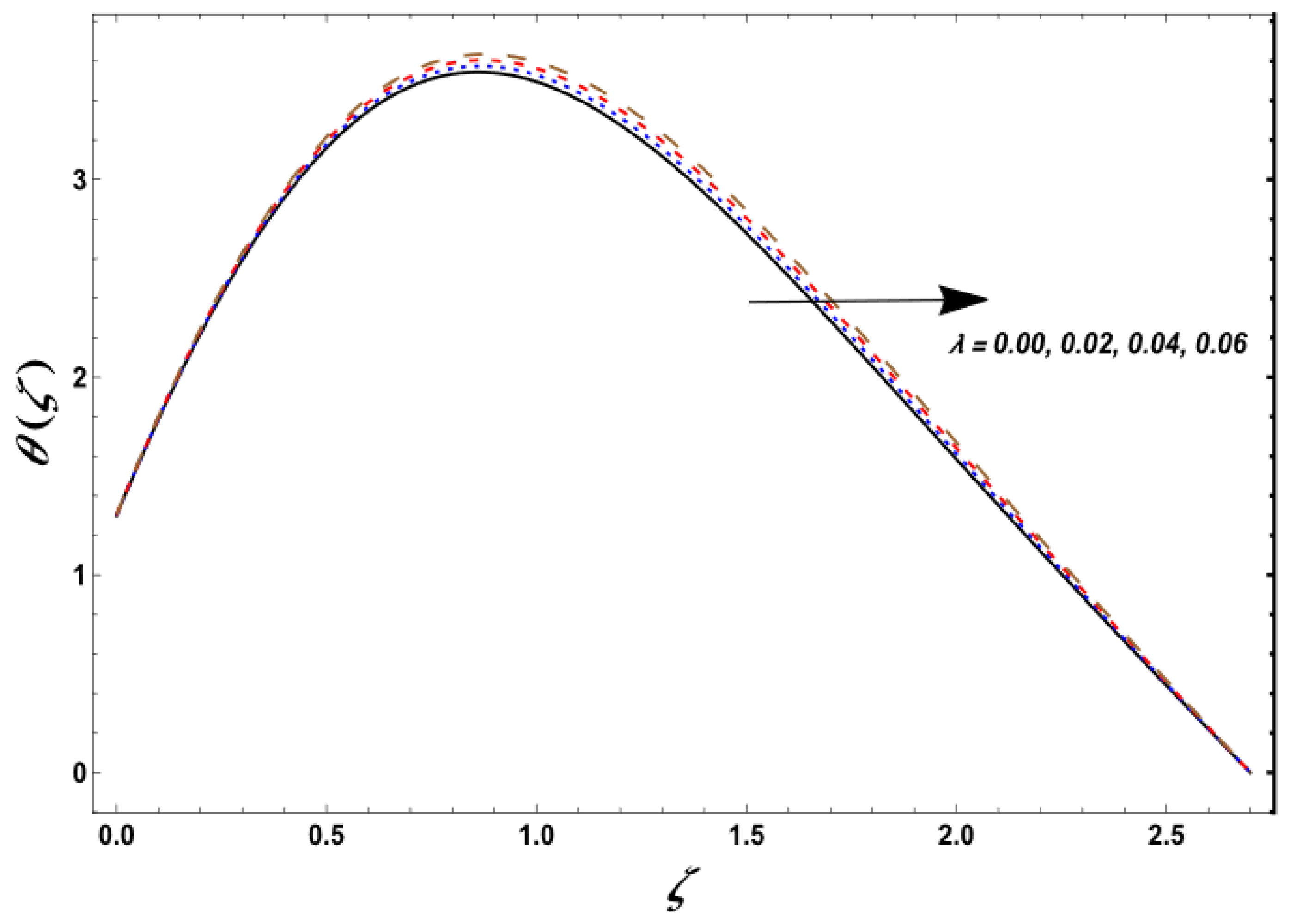
| Temperature slip parameter, | Temperature | Figure 3 | |
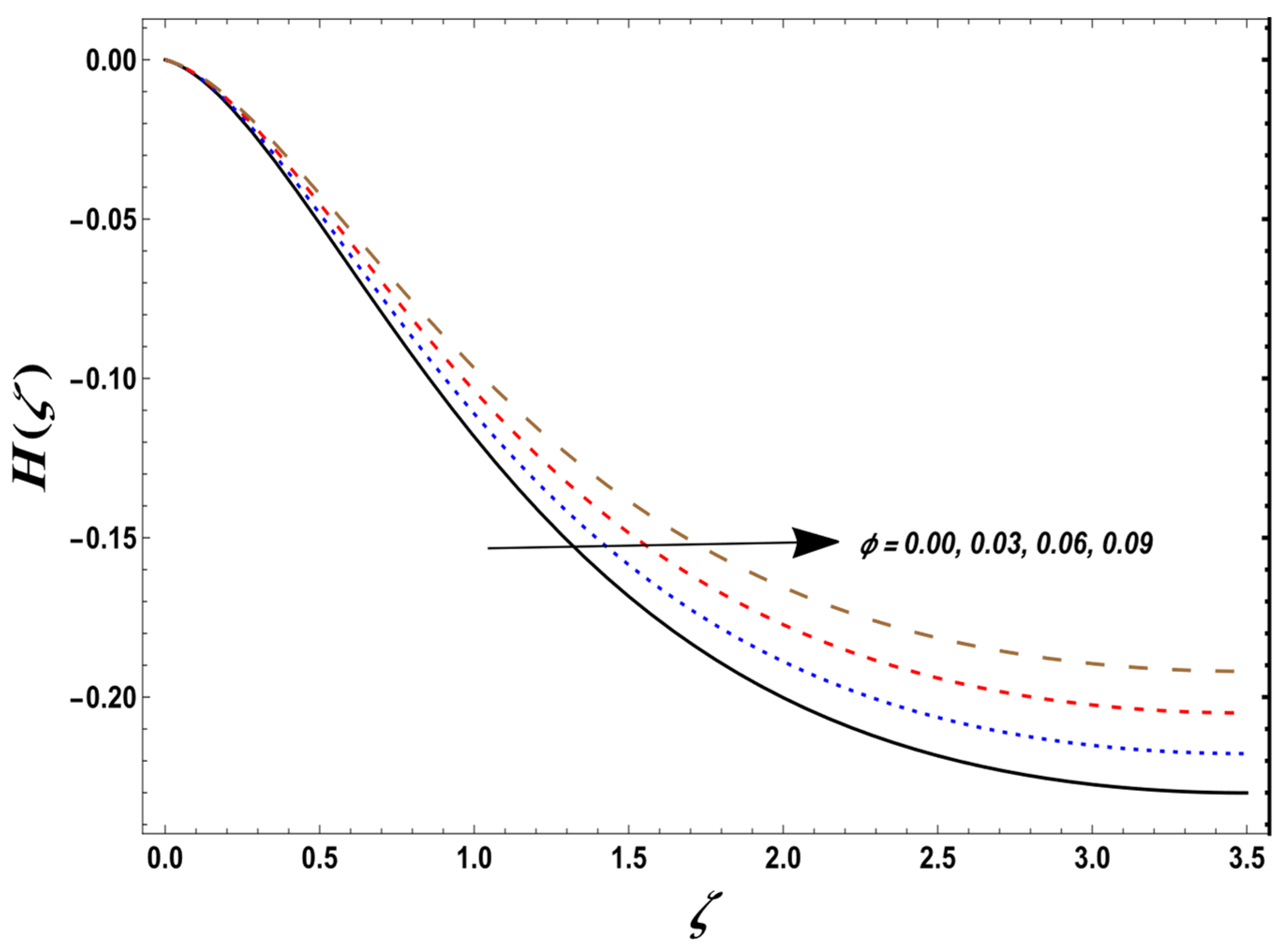
| Porosity parameter, | Temperature and velocities | Figure 4, Figure 13, Figure 14 and Figure 15 | |
| Heat generation parameter, | Temperature | Figure 5 | |
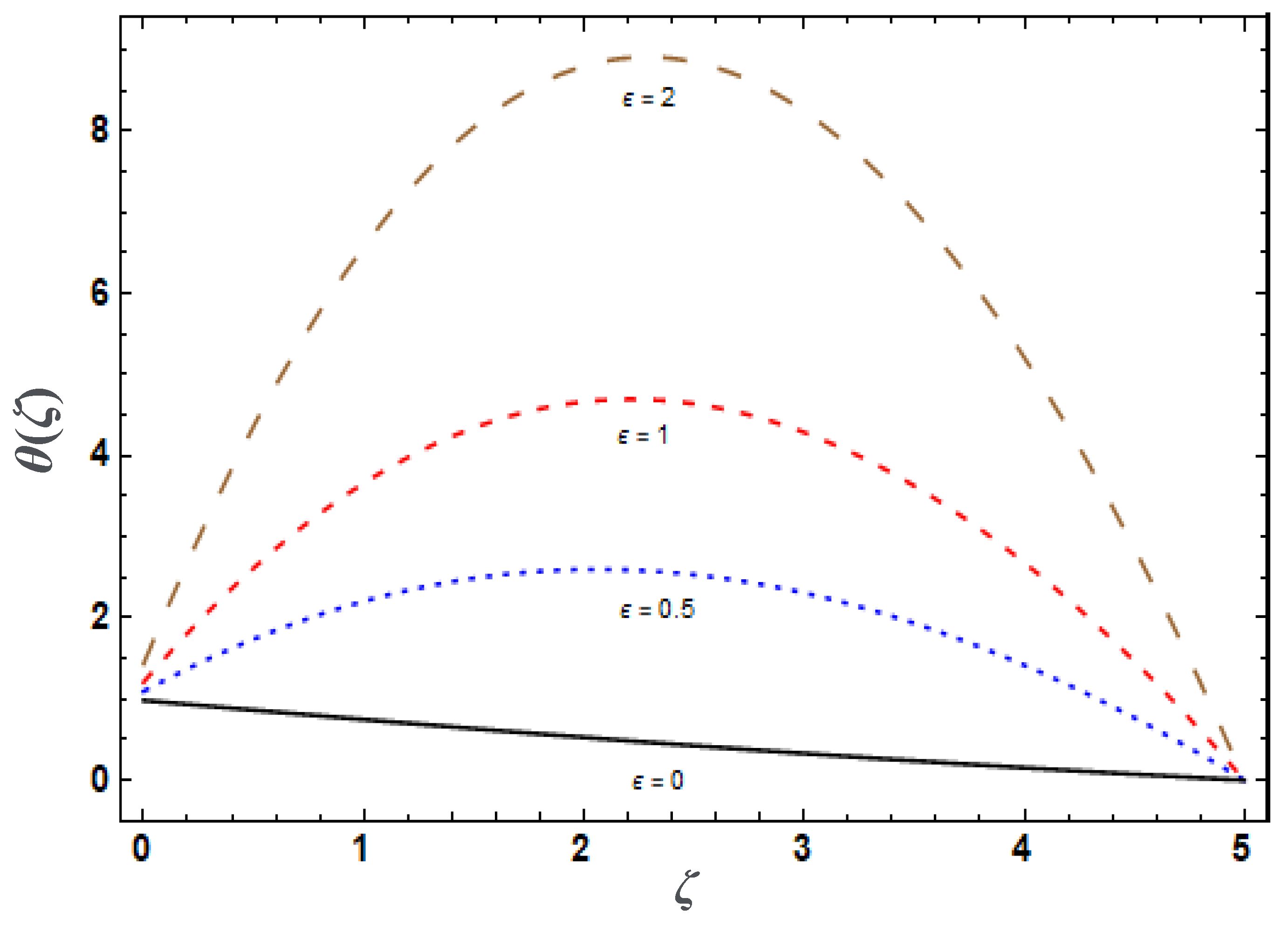
| Nanoparticle volume fraction, | Temperature and velocities | Figure 6, Figure 10, Figure 11 and Figure 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkuhayli, N.A.M.; Morozov, A. Analysis of Heat Transfer for the Copper–Water Nanofluid Flow through a Uniform Porous Medium Generated by a Rotating Rigid Disk. Mathematics 2024, 12, 1555. https://doi.org/10.3390/math12101555
Alkuhayli NAM, Morozov A. Analysis of Heat Transfer for the Copper–Water Nanofluid Flow through a Uniform Porous Medium Generated by a Rotating Rigid Disk. Mathematics. 2024; 12(10):1555. https://doi.org/10.3390/math12101555
Chicago/Turabian StyleAlkuhayli, Naif Abdulaziz M., and Andrew Morozov. 2024. "Analysis of Heat Transfer for the Copper–Water Nanofluid Flow through a Uniform Porous Medium Generated by a Rotating Rigid Disk" Mathematics 12, no. 10: 1555. https://doi.org/10.3390/math12101555





