The Phononic Properties and Optimization of 2D Multi-Ligament Honeycombs
Abstract
:1. Introduction
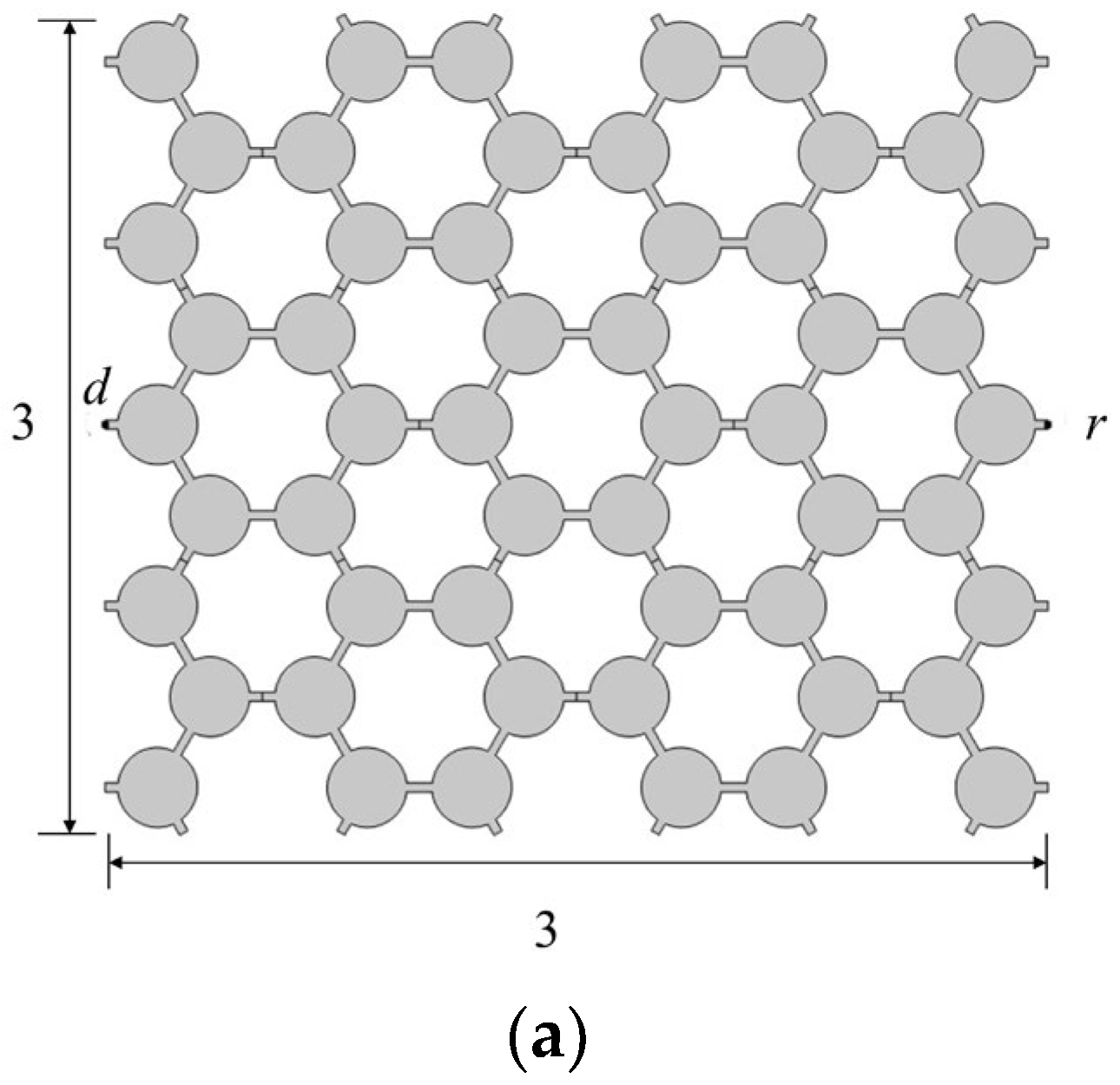
2. Geometry Parameters and Properties
3. Band Gap Properties of the Chiral Structures
3.1. Band Gap Properties with the Different Radius R of the Center Node
3.2. Band Gap Properties with the Different Ligament Width t of the Solid Ligament Structures
3.3. The Band Gap Properties of Symmetric Triligaments Structure
4. Transmission and Vibration Characteristics of Periodic Honeycomb Structure
4.1. Transmission Characteristics
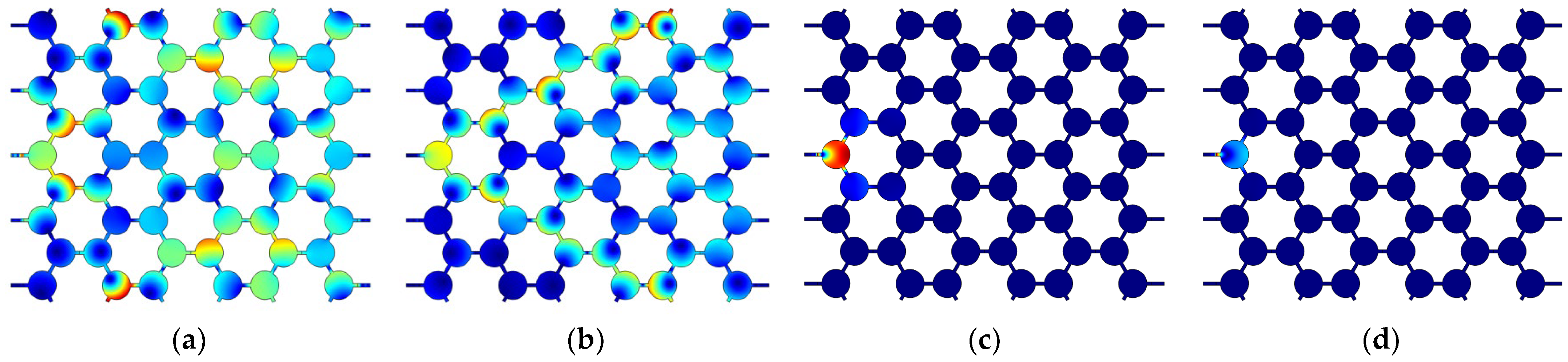
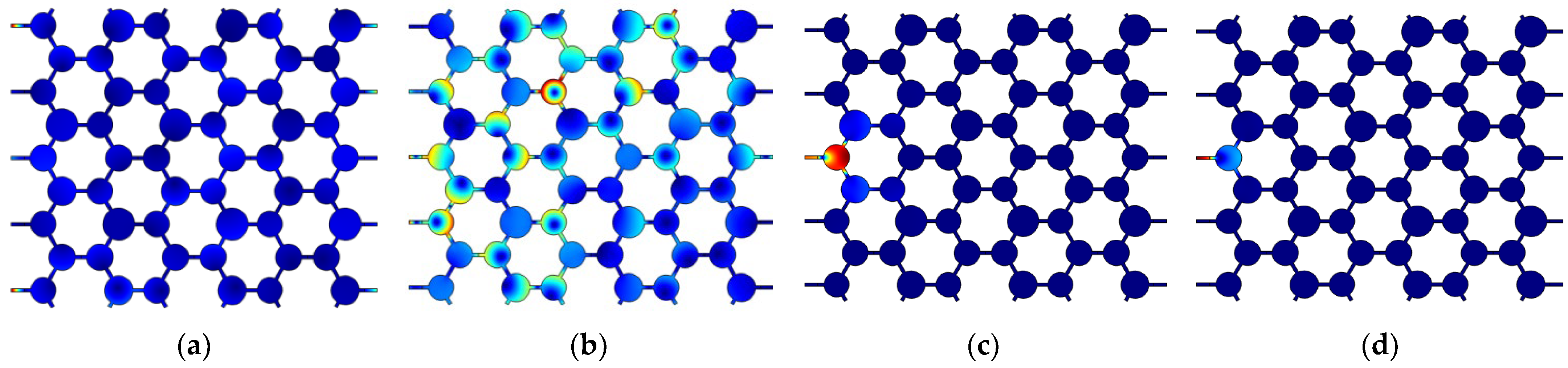
4.2. Vibration Mode Characteristics
5. Harmonic Response Analysis of Periodic Structures
6. Calculation of Transient Fluctuations in Periodic Structures
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jin, X.; Zhang, Z. Study on the Bandgap Characteristics and Vibration-Reduction Mechanism of Symmetric Power-Exponent Prismatic Phononic Crystal Plates. Crystals 2022, 12, 1125. [Google Scholar] [CrossRef]
- Chen, C.; Lei, J.; Liu, Z. A ternary seismic metamaterial for low frequency vibration attenuation. Materials 2022, 15, 1246. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Yang, Q.; Xiong, X.; Yin, R.; Jia, B.; Liang, Y.; Fang, H. Analysis of Vibration-Damping Characteristics and Parameter Optimization of Cylindrical Cavity Double-Plate Phononic Crystal. Materials 2023, 16, 4605. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Chen, M.; Qian, D.; Shi, Z. Influence mechanism of a new-style resonator on band gap of locally resonant phononic crystal double panel structure. Crystals 2022, 12, 609. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Scarpa, F.; Wang, L. Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys. Rev. Appl. 2017, 7, 024012. [Google Scholar] [CrossRef]
- Gonella, S.; Ruzzene, M. Analysis of in-plane wave propagation in hexagonal and re-entrant lattices. J. Sound Vib. 2008, 312, 125–139. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M.; Gonella, S.; Scarpa, F. Phononic properties of hexagonal chiral lattices. Wave Motion 2009, 46, 435–450. [Google Scholar] [CrossRef]
- Haghpanah, B.; Papadopoulos, J.; Mousanezhad, D.; Nayeb-Hashemi, H.; Vaziri, A. Bucking of regular, chiral and hierarchical Honeycombs under a general macroscopic stress state. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130856. [Google Scholar]
- Rosi, G.; Auffary, N. Anisotropic and dispersive wave propagation within strain-gradient framework. Wave Motion 2016, 63, 120–134. [Google Scholar] [CrossRef]
- Sun, Y.; Pugno, N.M. In plane stiffness of multifunctional hierarchical honeycombs with negative Poisson’s ratio sub-structures. Compos. Struct. 2013, 106, 681–689. [Google Scholar] [CrossRef]
- Shu, X.; Mao, Y.; Lei, M.; Da, D.; Hou, S.; Zhang, P. Toughness Enhancement of Honeycomb Lattice Structures through Heterogeneous Design. Mater. Des. 2022, 217, 110604. [Google Scholar] [CrossRef]
- Luo, H.C.; Ren, X.; Zhang, Y.; Zhang, X.Y.; Zhang, X.G.; Luo, C.; Cheng, X.; Xie, Y.M. Mechanical properties of foam-filled hexagonal and re-entrant honeycombs under uniaxial compression. Compos. Struct. 2022, 280, 114922. [Google Scholar] [CrossRef]
- Song, S.; Xiong, C.; Zheng, J.; Zou, Y.; Zhu, X. Compression, bending, energy absorption properties, and failure modes of composite Kagome honeycomb sandwich structure reinforced by PMI foams. Compos. Struct. 2021, 277, 114611. [Google Scholar] [CrossRef]
- Hou, J.; Li, D.; Dong, L. Mechanical behaviors of hierarchical cellular structures with negative Poisson’s ratio. J. Mater. Sci. 2018, 53, 10209–10216. [Google Scholar] [CrossRef]
- Zhang, Z.; Qian, D.; Zou, P. Study on Band Gap Characteristics of Phononic Crystal Double-Layer Beam Structure Attached by Multilayer Cylinder. Crystals 2023, 13, 638. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, M.; Zuo, S.; Huang, H.; Wu, H. An investigation on interior noise reduction using 2D locally resonant phononic crystal with point defect on car ceiling. J. Vib. Control 2019, 25, 386–396. [Google Scholar] [CrossRef]
- Cheong, T.W.; Zheng, L.W. Vibroacoustic performance of composite honeycomb structures. Noise Control Eng. J. 2006, 54, 251–262. [Google Scholar] [CrossRef]
- Peng, X.; Ji, J.; Jing, Y. Composite honeycomb metasurface panel for broadband sound absorption. J. Acoust. Soc. Am. 2018, 144, EL255–EL261. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.N.; Hu, G.K.; Sun, C.T.; Huang, G.L. Wave propagation characterization and design of two-dimensional elastic chiral metacomposite. J. Sound Vib. 2011, 330, 2536–2553. [Google Scholar] [CrossRef]
- Gokhale, A.A.; Prasad, N.E.; Basu, B. Light Weighting for Defense, Aerospace, and Transportation; Springer: Singapore, 2019. [Google Scholar]
- Wang, Y.; Yu, Y.; Wang, C.; Zhou, G.; Karamoozian, A.; Zhao, W. On the out-of-plane ballistic performances of hexagonal, reentrant, square, triangular and circular honeycomb panels. Int. J. Mech. Sci. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Mu, D.; Shu, H.; Zhao, L.; An, S. A review of research on seismic metamaterials. Adv. Eng. Mater. 2020, 22, 1901148. [Google Scholar] [CrossRef]
- Xia, H.; Sun, Q.; Wang, S. Influence of strain rate effect on energy absorption characteristics of bio-inspired honeycomb column thin-walled structure under impact loading. Case Stud. Constr. Mater. 2023, 18, e01761. [Google Scholar] [CrossRef]
- Zheng, T.; Yuan, L.; Zhao, C.; Shang, L.; Zhao, W. Research on seismic performance of honeycomb plate cylindrical reticulated shell structure. Case Stud. Constr. Mater. 2023, 18, e01897. [Google Scholar] [CrossRef]
- Yu, J.G.; Yang, Z.; Zhao, C.; Zhang, T.Y. Seismic performance of aluminum honeycomb sandwich panel buckling-restrained steel plate shear wall. J. Constr. Steel Res. 2024, 215, 108528. [Google Scholar] [CrossRef]
- Trainiti, G.; Rimoli, J.J.; Ruzzene, M. Wave propagation in undulated structural lattices. Int. J. Solids Struct. 2016, 97, 431–444. [Google Scholar] [CrossRef]
- Li, Y.; Yan, G. Vibration characteristics of innovative reentrant-chiral elastic metamaterials. Eur. J. Mech.—A Solids 2021, 90, 104350. [Google Scholar] [CrossRef]
- Jia, Z.; Chen, Y.; Yang, H.; Wang, L. Designing phononic crystals with wide and robust band gaps. Phys. Rev. Appl. 2018, 9, 044021. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, H.W.; Kim, J.T.; Kim, J.C. Sound insulation design of the corrugated steel panel considering local resonance. Trans. Korean Soc. Noise Vib. Eng. 2010, 20, 672–676. [Google Scholar] [CrossRef]
- McGurn, A.R. Introduction to Photonic and Phononic Crystals and Metamaterials; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Dal Poggetto, V.F.; Pugno, N.M.; Arruda, J.R.D.F. Bioinspired periodic panels optimized for acoustic insulation. Philos. Trans. R. Soc. A 2022, 380, 20210389. [Google Scholar] [CrossRef]
- Miranda, E.J.P., Jr.; Nobrega, E.D.; Ferreira, A.H.R.; Dos Santos, J.M.C. Flexural wave band gaps in a multi-resonator elastic metamaterial plate using Kirchhoff-Love theory. Mech. Syst. Signal Process. 2019, 116, 480–504. [Google Scholar] [CrossRef]
- Khelif, A.; Adibi, A. Phononic Crystals; Springer: Berlin/Heidelberg, Germany, 2015; Volume 10, pp. 978–979. [Google Scholar]
- Javid, F.; Wang, P.; Shanian, A.; Bertoldi, K. Architected materials with ultra-low porosity for vibration control. Adv. Mater. 2016, 28, 5943–5948. [Google Scholar] [CrossRef] [PubMed]
- Röhlig, D.; Kuhn, E.; Teichert, F.; Thränhardt, A.; Blaudeck, T. Function phononic crystals. Europhys. Lett. 2024, 145, 26001. [Google Scholar] [CrossRef]
- He, X.; Hu, H.; Wang, X. Finite difference modelling of dipole acoustic logs in a poroelastic formation with anisotropic permeability. Geophys. J. Int. 2013, 192, 359–374. [Google Scholar] [CrossRef]
- Karjanto, N.; Van Groesen, E. Note on wavefront dislocation in surface water waves. Phys. Lett. A 2007, 371, 173–179. [Google Scholar] [CrossRef]
- Karjanto, N. Wave group evolution and interaction. arXiv 2020, arXiv:2003.05742. [Google Scholar]






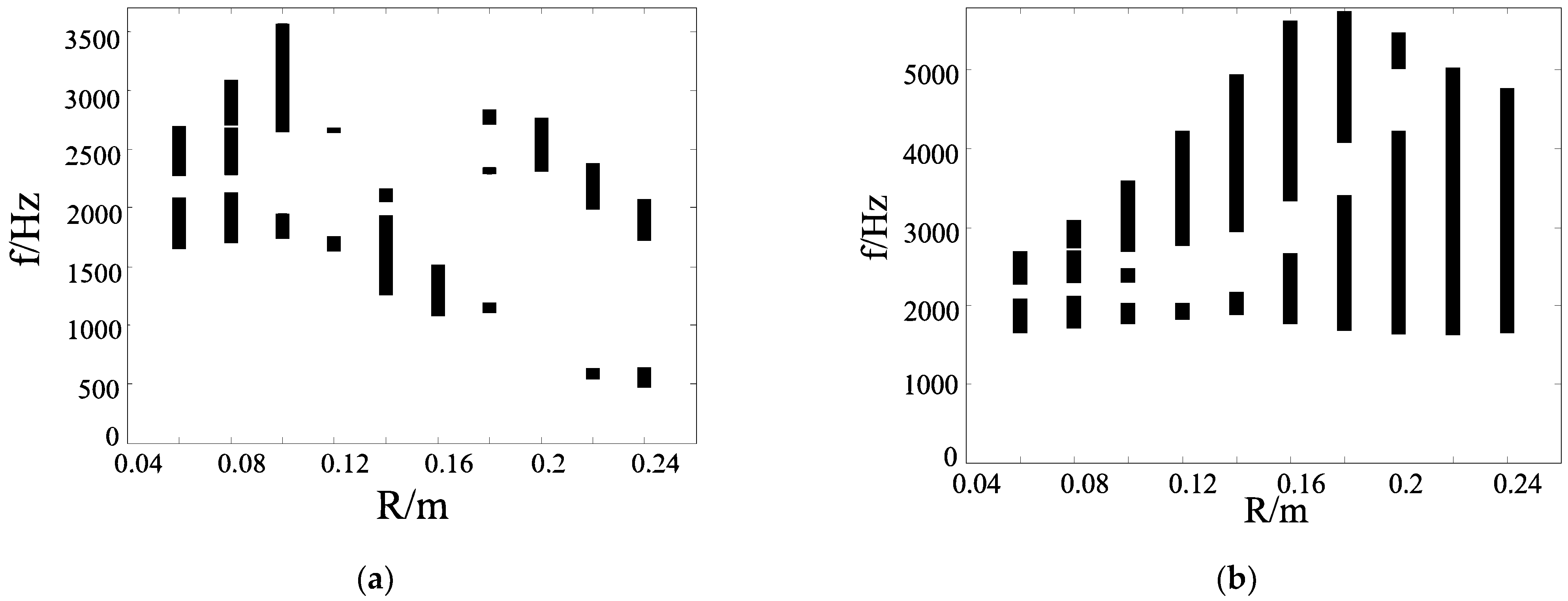







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Guan, W.; Kou, X. The Phononic Properties and Optimization of 2D Multi-Ligament Honeycombs. Materials 2024, 17, 2369. https://doi.org/10.3390/ma17102369
Yin Y, Guan W, Kou X. The Phononic Properties and Optimization of 2D Multi-Ligament Honeycombs. Materials. 2024; 17(10):2369. https://doi.org/10.3390/ma17102369
Chicago/Turabian StyleYin, Yiguo, Wei Guan, and Xing Kou. 2024. "The Phononic Properties and Optimization of 2D Multi-Ligament Honeycombs" Materials 17, no. 10: 2369. https://doi.org/10.3390/ma17102369




