Artificial Neuron Based on the Bloch-Point Domain Wall in Ferromagnetic Nanowires
Abstract
:1. Introduction
2. Methods
Simulation Details
3. Proof of Concept of the Artificial Neuron: Results and Discussion
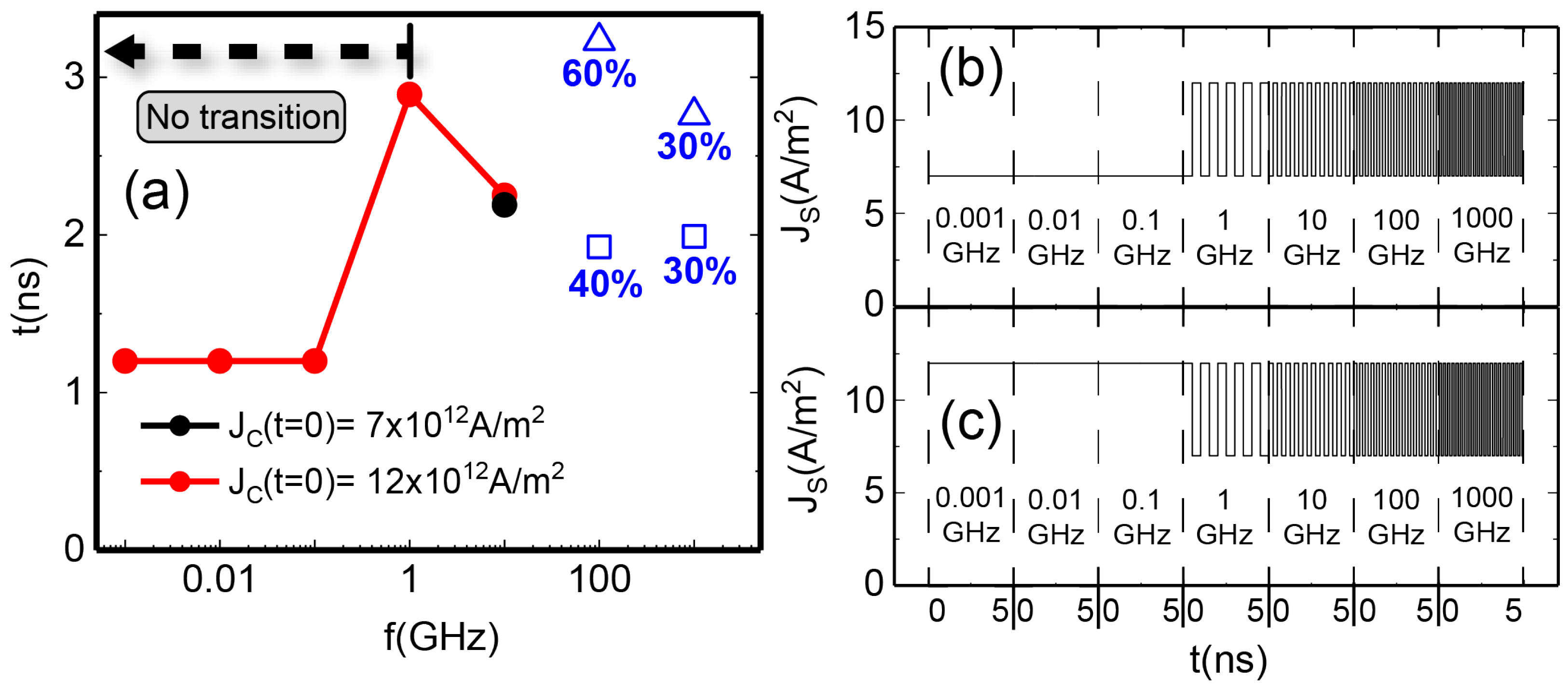
3.1. Integrate Functionality
3.2. Leak Functionality
3.3. Fire Functionality
3.4. Refractory Period
4. Device Implementation
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Magnetic State Stabilization with Changes in the Aspect Ratio of the NW
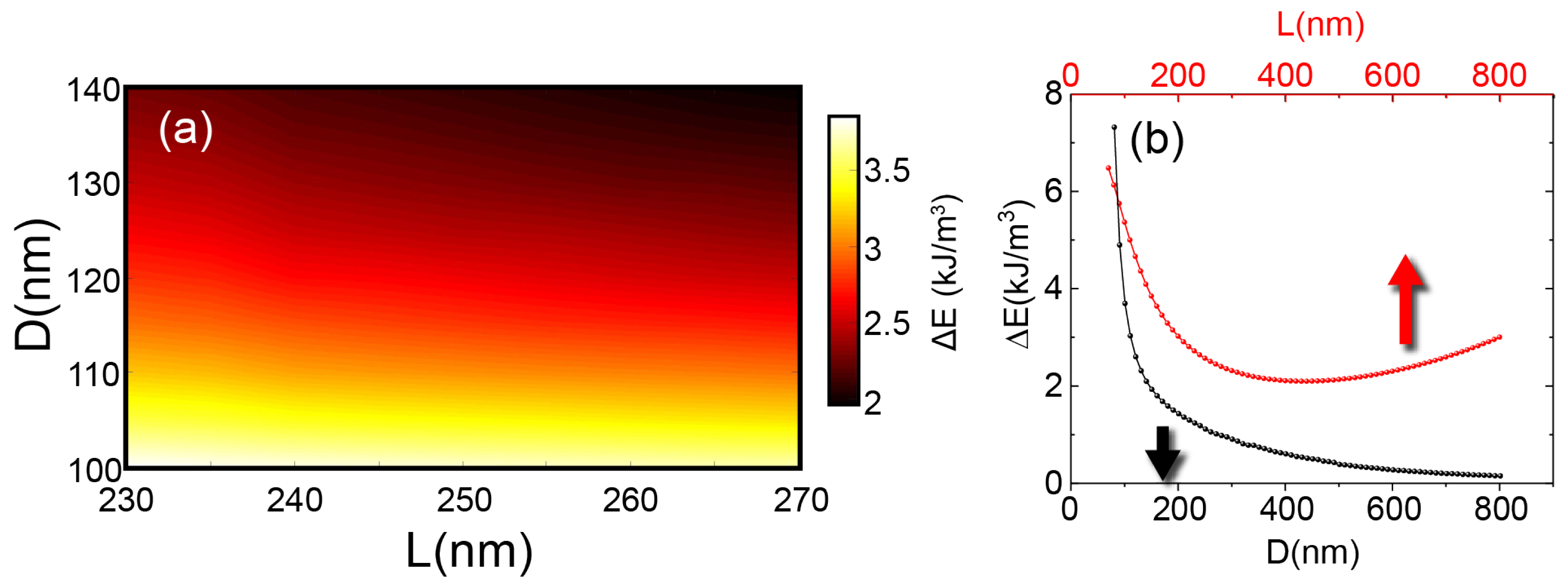
Appendix B. Eigenmodes of the NW in the BP-DW State

Appendix C. Estimation of the Maximum Working Time the Case of Implementation in an STT-Based Device
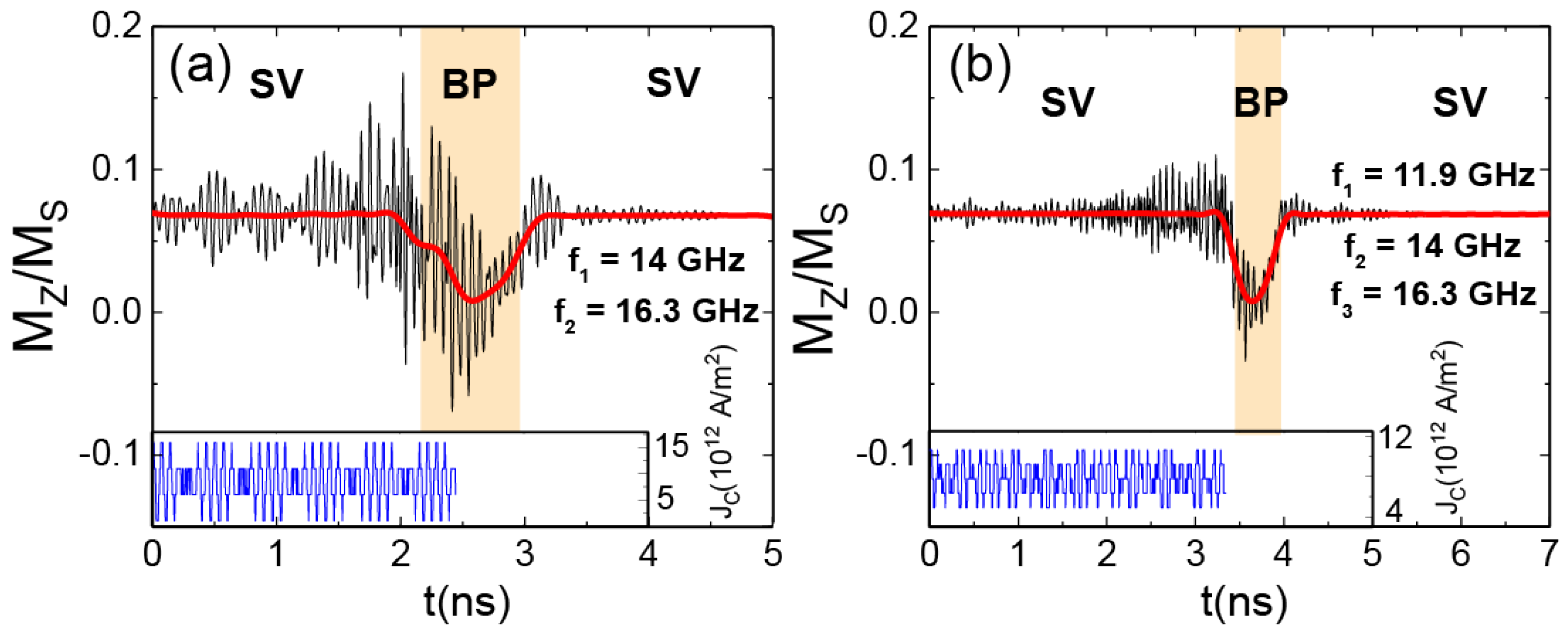
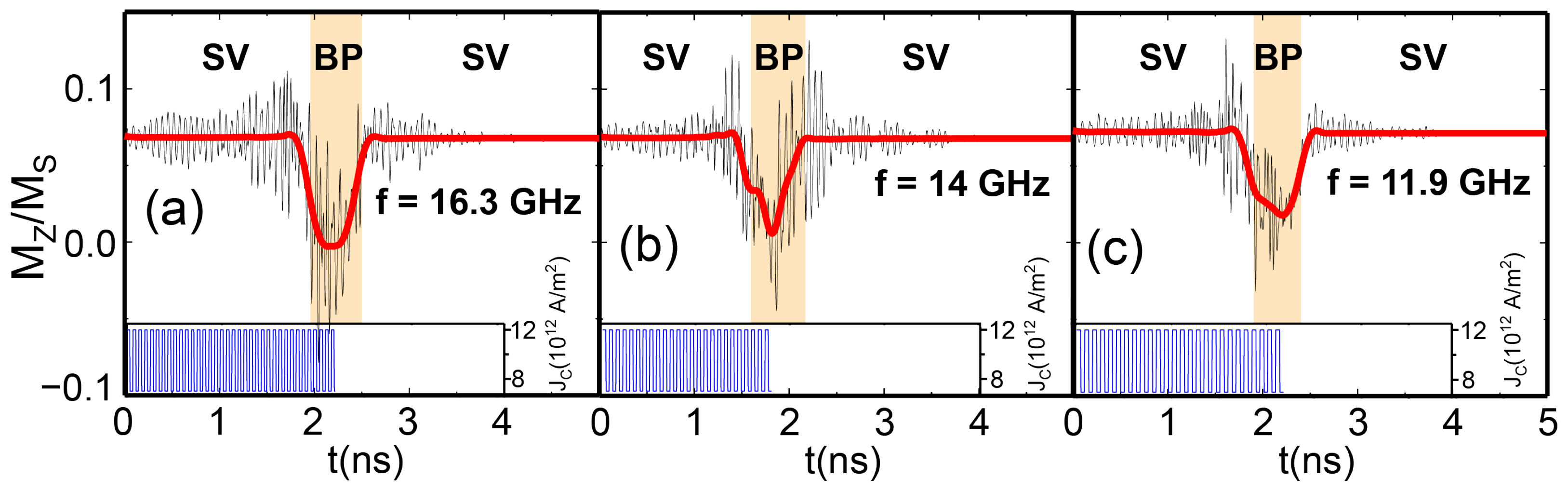
Appendix D. Neuron Behavior with an Input as the Sum of Various Signals
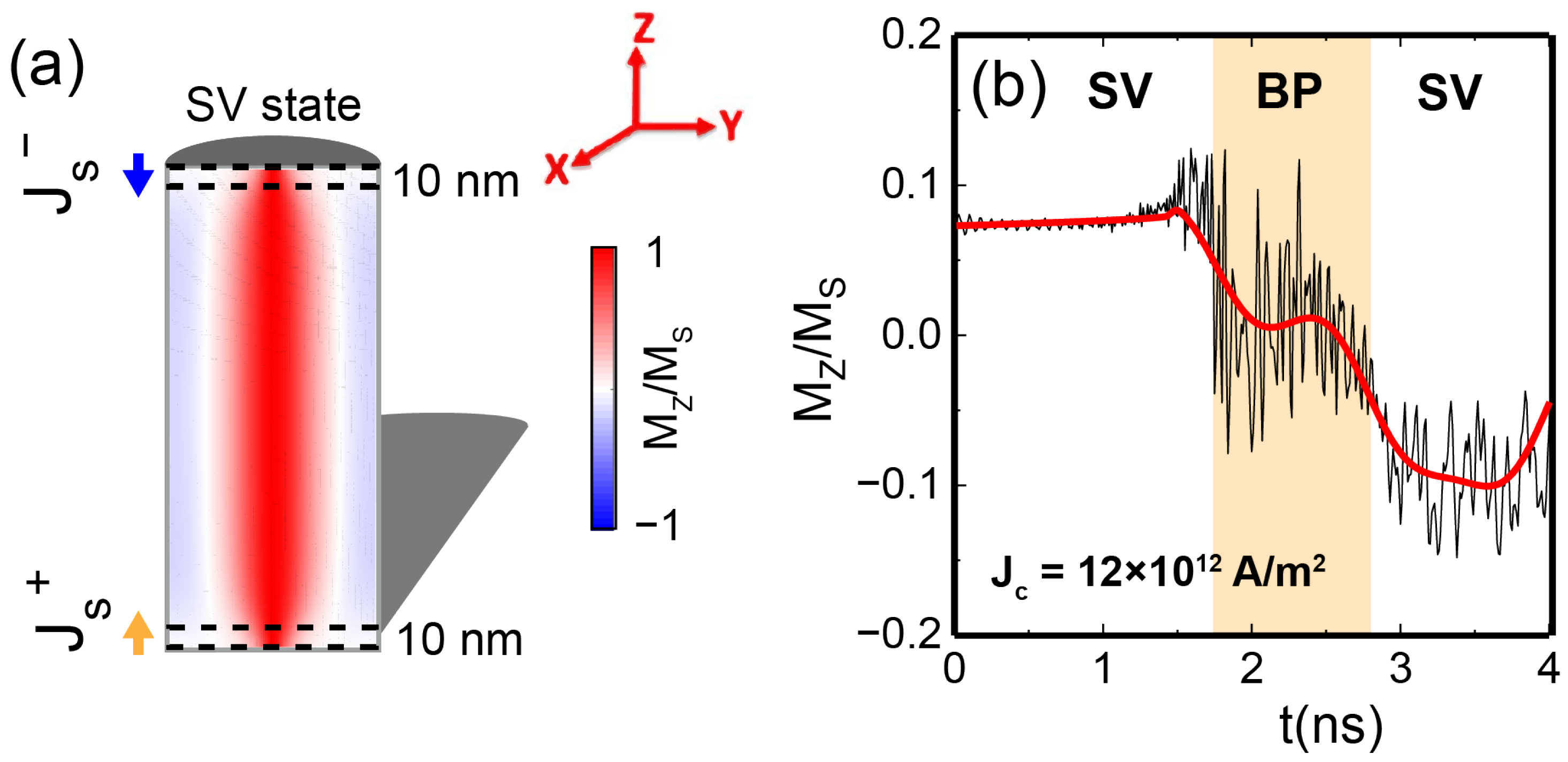
Appendix E. Spin Current Injection in a Thin Region of the NW
References
- van de Burgt, Y.; Santoro, F.; Tee, B.; Alibart, F. Editorial: Focus on organic materials, bio-interfacing and processing in neuromorphic computing and artificial sensory applications. Neuromorphic Comput. Eng. 2023, 3, 040202. [Google Scholar] [CrossRef]
- Li, S.; Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based artificial neuron device. Nanotechnology 2017, 28, 31LT01. [Google Scholar] [CrossRef]
- Marković, D.; Mizrahi, A.; Querlioz, D.; Grollier, J. Author Correction: Physics for neuromorphic computing. Nat. Rev. Phys. 2021, 3, 671. [Google Scholar] [CrossRef]
- del Valle, J.; Ramírez, J.G.; Rozenberg, M.J.; Schuller, I.K. Challenges in materials and devices for resistive-switching-based neuromorphic computing. J. Appl. Phys. 2018, 124, 211101. [Google Scholar] [CrossRef]
- Romera, M.; Talatchian, P.; Tsunegi, S.; Abreu Araujo, F.; Cros, V.; Bortolotti, P.; Trastoy, J.; Yakushiji, K.; Fukushima, A.; Kubota, H.; et al. Vowel recognition with four coupled spin-torque nano-oscillators. Nature 2018, 563, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Borders, W.A.; Pervaiz, A.Z.; Fukami, S.; Camsari, K.Y.; Ohno, H.; Datta, S. Integer factorization using stochastic magnetic tunnel junctions. Nature 2019, 573, 390–393. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; He, Y.; Xin, Y.; Yuan, Z.; Zhang, X.; Zhu, Z.; Liang, G. Unconventional computing based on magnetic tunnel junction. Appl. Phys. A 2023, 129, 236. [Google Scholar] [CrossRef]
- Chumak, A.V.; Kabos, P.; Wu, M.; Abert, C.; Adelmann, C.; Adeyeye, A.O.; Akerman, J.; Aliev, F.G.; Anane, A.; Awad, A.; et al. Advances in Magnetics Roadmap on Spin-Wave Computing. IEEE Trans. Magn. 2022, 58, 1–72. [Google Scholar] [CrossRef]
- Lara, A.; Robledo Moreno, J.; Guslienko, K.Y.; Aliev, F.G. Information processing in patterned magnetic nanostructures with edge spin waves. Sci. Rep. 2017, 7, 5597. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, A. Magnetic Elements for Neuromorphic Computing. Molecules 2020, 25, 2550. [Google Scholar] [CrossRef]
- Hong, J.Y.; Chen, C.Y.; Ling, D.C.; Martínez, I.; González-Ruano, C.; Aliev, F.G. Low-Frequency 1/f Noise Characteristics of Ultra-Thin AlOx-Based Resistive Switching Memory Devices with Magneto-Resistive Responses. Electronics 2021, 10, 2525. [Google Scholar] [CrossRef]
- Kuncic, Z.; Nakayama, T. Neuromorphic nanowire networks: Principles, progress and future prospects for neuro-inspired information processing. Adv. Phys. X 2021, 6, 1894234. [Google Scholar] [CrossRef]
- Zhu, R.; Lilak, S.; Loeffler, A.; Lizier, J.; Stieg, A.; Gimzewski, J.; Kuncic, Z. Online dynamical learning and sequence memory with neuromorphic nanowire networks. Nat. Commun. 2023, 14, 6697. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro de Assis, I.; Mertig, I.; Göbel, B. Biskyrmion-based artificial neuron. Neuromorphic Comput. Eng. 2023, 3, 014012. [Google Scholar] [CrossRef]
- Brigner, W.H.; Friedman, J.S.; Hassan, N.; Jiang-Wei, L.; Hu, X.; Saha, D.; Bennett, C.H.; Marinella, M.J.; Incorvia, J.A.C.; Garcia-Sanchez, F. Shape-Based Magnetic Domain Wall Drift for an Artificial Spintronic Leaky Integrate-and-Fire Neuron. IEEE Trans. Electron Devices 2019, 66, 4970–4975. [Google Scholar] [CrossRef]
- Mah, W.L.W.; Chan, J.P.; Ganesh, K.R.; Naik, V.B.; Piramanayagam, S.N. Leakage function in magnetic domain wall based artificial neuron using stray field. Appl. Phys. Lett. 2023, 123, 092401. [Google Scholar] [CrossRef]
- Lee, O.; Wei, T.; Stenning, K.D.; Gartside, J.C.; Prestwood, D.; Seki, S.; Aqeel, A.; Karube, K.; Kanazawa, N.; Taguchi, Y.; et al. Task-adaptive physical reservoir computing. Nat. Mater. 2023, 23, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Caso, D.; Tuero, P.; García, J.; Guslienko, K.Y.; Aliev, F.G. Dynamics and Reversible Control of the Bloch-Point Vortex Domain Wall in Short Cylindrical Magnetic Nanowires. Phys. Rev. Appl. 2023, 19, 064030. [Google Scholar] [CrossRef]
- Da Col, S.; Jamet, S.; Rougemaille, N.; Locatelli, A.; Mentes, T.O.; Burgos, B.S.; Afid, R.; Darques, M.; Cagnon, L.; Toussaint, J.C.; et al. Observation of Bloch-point domain walls in cylindrical magnetic nanowires. Phys. Rev. B 2014, 89, 180405. [Google Scholar] [CrossRef]
- Wartelle, A.; Trapp, B.; Staňo, M.; Thirion, C.; Bochmann, S.; Bachmann, J.; Foerster, M.; Aballe, L.; Menteş, T.O.; Locatelli, A.; et al. Bloch-point-mediated topological transformations of magnetic domain walls in cylindrical nanowires. Phys. Rev. B 2019, 99, 024433. [Google Scholar] [CrossRef]
- Sáez, G.; Díaz, P.; Vidal-Silva, N.; Escrig, J.; Vogel, E.E. Bloch points stabilization by means of diameter modulations in cylindrical nanowires. Results Phys. 2022, 39, 105768. [Google Scholar] [CrossRef]
- Sáez, G.; Saavedra, E.; Vidal-Silva, N.; Escrig, J.; Vogel, E.E. Dynamic susceptibility of a Bloch point singularity confined in a magnetic nanowire. Results Phys. 2022, 37, 105530. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; García-Sánchez, F.; Waeyenberge, B.V. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Berganza, E.; Bran, C.; Jaafar, M.; Vázquez, M.; Asenjo, A. Domain wall pinning in FeCoCu bamboo-like nanowires. Sci. Rep. 2016, 6, 29702. [Google Scholar]
- Bran, C.; Berganza, E.; Palmero, E.M.; Fernandez-Roldan, J.A.; Del Real, R.P.; Aballe, L.; Foerster, M.; Asenjo, A.; Fraile Rodríguez, A.; Vazquez, M. Spin configuration of cylindrical bamboo-like magnetic nanowires. J. Mater. Chem. C 2016, 4, 978–984. [Google Scholar] [CrossRef]
- Fernández-Roldán, J.A.; del Real, R.P.; Bran, C.; Vazquez, M.; Chubykalo-Fesenko, O. Magnetization pinning in modulated nanowires: From topological protection to the “corkscrew” mechanism. R. Soc. Chem. Nanoscale 2018, 10, 5923–5927. [Google Scholar] [CrossRef]
- Shaw, J.M.; Nembach, H.T.; Silva, T.J.; Boone, C.T. Precise determination of the spectroscopic g-factor by use of broadband ferromagnetic resonance spectroscopy. J. Appl. Phys. 2013, 114, 243906. [Google Scholar] [CrossRef]
- Park, J.P.; Eames, P.; Engebretson, D.M.; Berezovsky, J.; Crowell, P.A. Single-shot dynamics of spin–orbit torque and spin transfer torque switching in three-terminal magnetic tunnel junctions. Phys. Rev. B 2003, 67, 020403. [Google Scholar] [CrossRef]
- Brunel, N.; van Rossum, M.C.W. Quantitative investigations of electrical nerve excitation treated as polarization. Biol. Cybern. 2007, 97, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Pundir, Y.P.; Kumar Pal, P. Comparative analysis of STT and SOT based MRAMs for last level caches. J. Magn. Magn. Mater. 2022, 551, 169161. [Google Scholar] [CrossRef]
- da Câmara Santa Clara Gomes, T.; Marchal, N.; Abreu Araujo, F.; Piraux, L. Spin Caloritronics in 3D Interconnected Nanowire Networks. Nanomaterials 2020, 10, 2092. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.I.A.; Sisodia, N.; Muduli, P.K. Energy-efficient ultrafast nucleation of single and multiple antiferromagnetic skyrmions using in-plane spin polarized current. Sci. Rep. 2021, 11, 12332. [Google Scholar] [CrossRef] [PubMed]
- Shiino, T.; Oh, S.H.; Haney, P.M.; Lee, S.W.; Go, G.; Park, B.G.; Lee, K.J. Antiferromagnetic Domain Wall Motion Driven by Spin-Orbit Torques. Phys. Rev. Lett. 2016, 117, 087203. [Google Scholar] [CrossRef] [PubMed]
- Bhowmik, D.; Nowakowski, M.E.; You, L.; Lee, O.; Keating, D.; Wong, M.; Bokor, J.; Salahuddin, S. Deterministic Domain Wall Motion Orthogonal To Current Flow Due To Spin Orbit Torque. Sci. Rep. 2015, 5, 11823. [Google Scholar] [CrossRef] [PubMed]
- Kohno, R.; Sampaio, J.; Rohart, S.; Thiaville, A. Domain wall propagation by spin-orbit torques in in-plane magnetized systems. Phys. Rev. B 2020, 102, 020410. [Google Scholar] [CrossRef]
- Thiaville, A.; Rohart, S.; Jué, E.; Cros, V.; Fert, A. Dynamics of Dzyaloshinskii domain walls in ultrathin magnetic films. EPL (Europhys. Lett.) 2012, 100, 57002. [Google Scholar] [CrossRef]
- Ryu, K.S.; Thomas, L.; Yang, S.H.; Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 2013, 8, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Zahnd, G.; Vila, L.; Pham, V.T.; Cosset-Cheneau, M.; Lim, W.; Brenac, A.; Laczkowski, P.; Marty, A.; Attané, J.P. Spin diffusion length and polarization of ferromagnetic metals measured by the spin-absorption technique in lateral spin valves. Phys. Rev. B 2018, 98, 174414. [Google Scholar] [CrossRef]
- Moreno, R.; Carvalho-Santos, V.L.; Espejo, A.P.; Laroze, D.; Chubykalo-Fesenko, O.; Altbir, D. Oscillatory behavior of the domain wall dynamics in a curved cylindrical magnetic nanowire. Phys. Rev. B 2017, 96, 184401. [Google Scholar] [CrossRef]
- Vazquez, M. Cylindrical nanowire arrays: From advanced fabrication to static and microwave magnetic properties. J. Magn. Magn. Mater. 2022, 543, 168634. [Google Scholar] [CrossRef]
- Fangohr, H.; Chernyshenko, D.S.; Franchin, M.; Fischbacher, T.; Meier, G. Joule heating in nanowires. Phys. Rev. B 2011, 84, 054437. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez, C.; Caso, D.; Aliev, F.G. Artificial Neuron Based on the Bloch-Point Domain Wall in Ferromagnetic Nanowires. Materials 2024, 17, 2425. https://doi.org/10.3390/ma17102425
Sánchez C, Caso D, Aliev FG. Artificial Neuron Based on the Bloch-Point Domain Wall in Ferromagnetic Nanowires. Materials. 2024; 17(10):2425. https://doi.org/10.3390/ma17102425
Chicago/Turabian StyleSánchez, Carlos, Diego Caso, and Farkhad G. Aliev. 2024. "Artificial Neuron Based on the Bloch-Point Domain Wall in Ferromagnetic Nanowires" Materials 17, no. 10: 2425. https://doi.org/10.3390/ma17102425




