Analysis of Scalable Resonant DC–DC Converter Using GaN Switches for xEV Charging Stations
Abstract
:1. Introduction
- The modeling of a scalable iL2C resonant converter with operation is presented.
- A hybrid control strategy is suggested and derived to improve the regulations.
- Simulations are presented for various load and line regulating conditions to check the converter performances.
- The experimental setup is demonstrated using E-mode GaN technology at 3.3 kW as an EV charger with an efficiency of 98.2%.
2. Modeling and Operation of iL2C Converter Topology
3. Control Strategy
4. Simulation and Experimental Validation
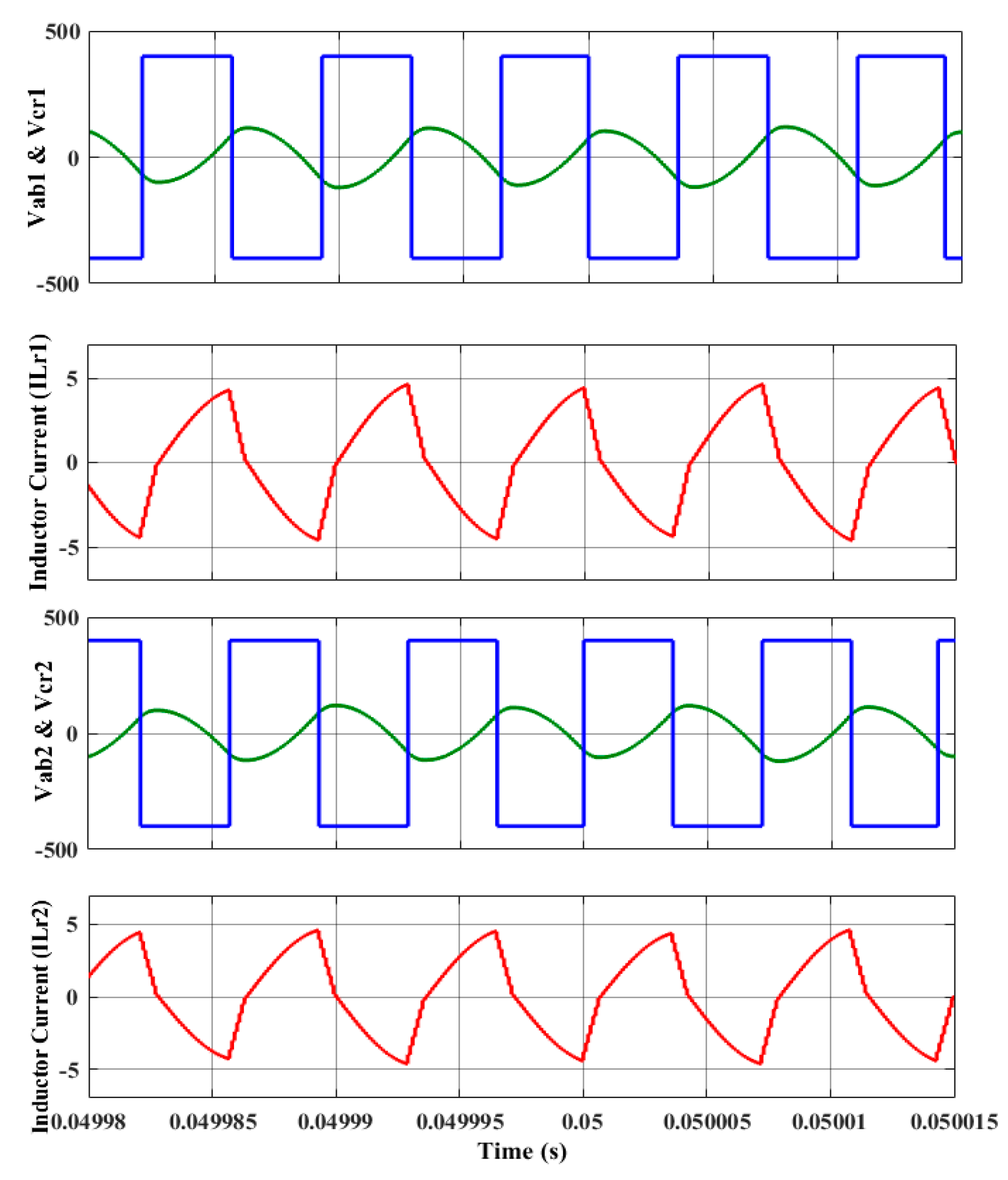
4.1. Dynamic Performance Analysis of iL2C Converter for 300 Vin–500 Vin under Various Load Conditions
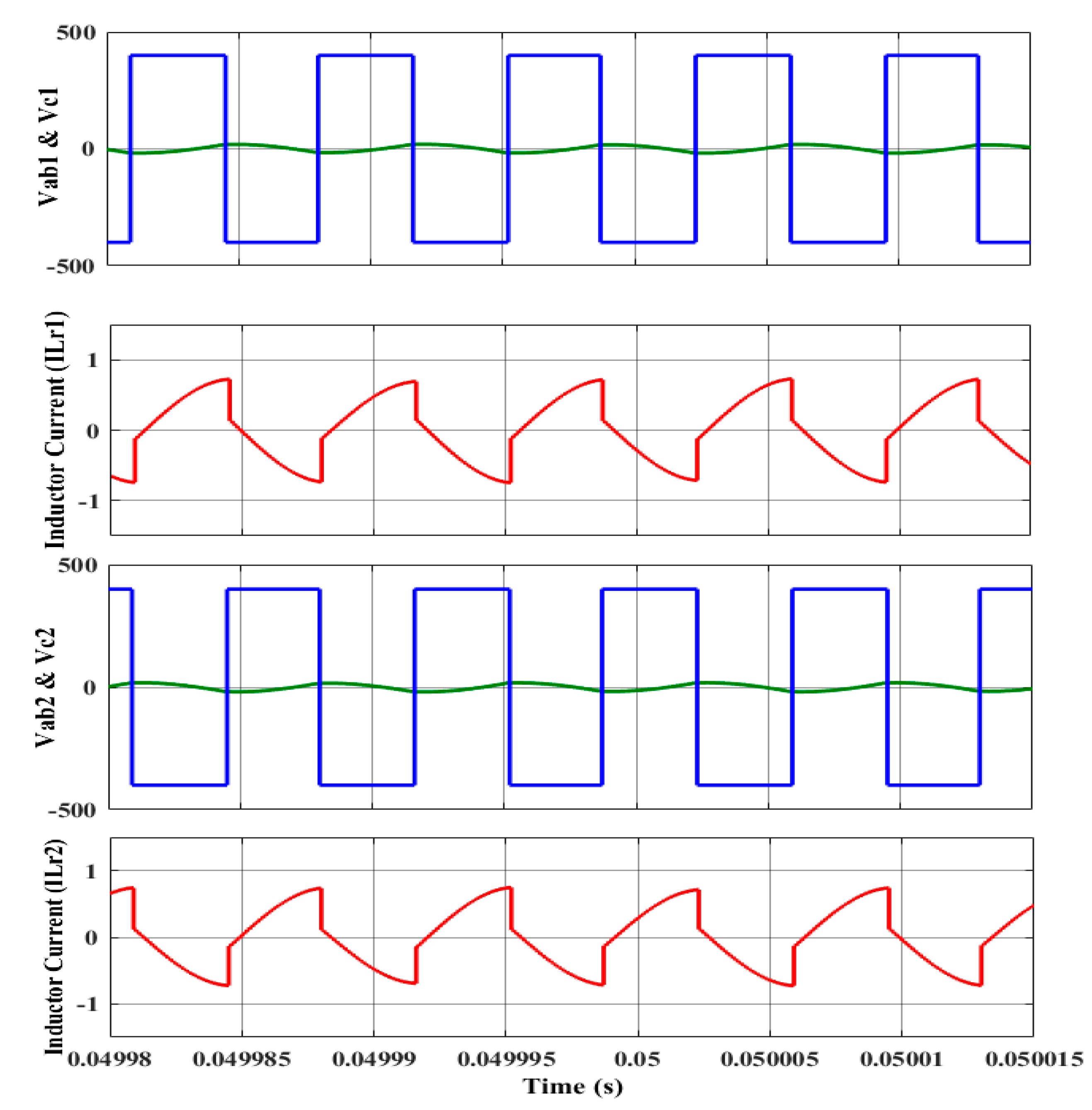
4.2. Dynamic Performance Analysis of iL2C Converter for 500 Vin–300 Vin under Various Load Conditions
4.3. Experimental Validation of iL2C Converter
5. Performance Analysis and Discussion
5.1. Steady-State Performance Analysis
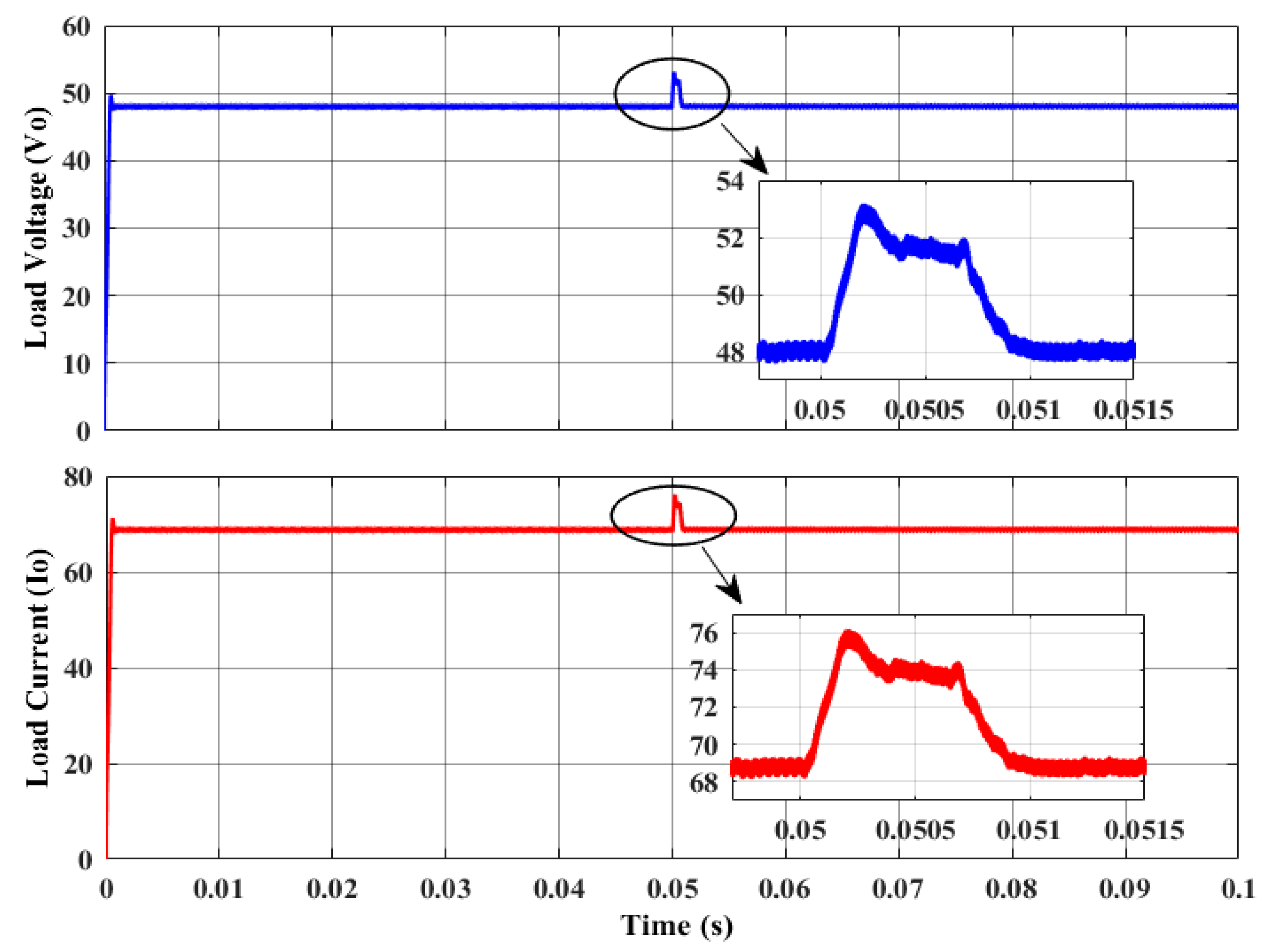
5.2. Transient Performance Analysis
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicle |
| ACR | Average Current Ripple |
| AVR | Average Voltage Ripple |
| E-mode | Enhancement Mode |
| EV | Electric Vehicle |
| FCEV | Fuel Cell Electric Vehicle |
| GaN | Gallium Nitride |
| HEV | Hybrid Electric Vehicle |
| ICE | Internal Combustion Engine |
| iL2C | Interleaved Inductor–Inductor–Capacitor |
| L2C | Inductor–Inductor–Capacitor |
| LCD | Load Current Deviation |
| LVD | Load Voltage Deviation |
| PHEV | Plugin Hybrid Electric Vehicle |
| SCEV | Super Capacitor Electric Vehicle |
| TCD | Transient Current Dip |
| TCR | Transient Current Ripple |
| TVD | Transient Voltage Dip |
| TVR | Transient Voltage Ripple |
| UCEV | Ultra-Capacitor Electric Vehicle |
| VCO | Voltage Control Oscillator |
| VFPSM | Variable Frequency Phase Shift Modulation |
| ZCS | Zero Current Switching |
| ZVS | Zero Voltage Switching |
References
- Mopidevi, S.; Narasipuram, R.P.; Aemalla, S.R.; Rajan, H. Emobility: Impacts and analysis of future transportation electrification market in economic, renewable energy and infrastructure perspective. Int. J. Powertrains 2022, 11, 264–284. [Google Scholar] [CrossRef]
- Zhou, K.; Wu, Y.; Wu, X.; Sun, Y.; Teng, D.; Liu, Y. Research and Development Review of Power Converter Topologies and Control Technology for Electric Vehicle Fast-Charging Systems. Electronics 2023, 12, 1581. [Google Scholar] [CrossRef]
- Shahjalal, M.; Shams, T.; Tasnim, M.N.; Ahmed, R.; Ahsan, M.; Haider, J. A Critical Review on Charging Technologies of Electric Vehicles. Energies 2022, 15, 8239. [Google Scholar] [CrossRef]
- Ilahi, T.; Izhar, T.; Zahid, M.; Rasool, A.; Tsamaase, K.; Zahid, T.; Khan, E.M. Design Analysis of High-Power Level 4 Smart Charging Infrastructure Using Next-Generation Power Devices for EVs and Heavy Duty EVs. World Electr. Veh. J. 2024, 15, 66. [Google Scholar] [CrossRef]
- Narasipuram, R.P.; Mopidevi, S. A technological overview & design considerations for developing electric vehicle charging stations. J. Energy Storage 2021, 43, 103225. [Google Scholar] [CrossRef]
- Deng, J.; Li, S.; Hu, S.; Mi, C.C.; Ma, R. Design Methodology of LLC Resonant Converters for Electric Vehicle Battery Chargers. IEEE Trans. Veh. Technol. 2014, 63, 1581–1592. [Google Scholar] [CrossRef]
- Domajnko, J.; Prosen, N. A Wireless Power Transfer System Using a Double DD Quadrature Coil Structure. Electronics 2023, 12, 890. [Google Scholar] [CrossRef]
- Far, M.F.; Miljavec, D.; Manko, R.; Pippuri-Mäkeläinen, J.; Ranta, M.; Keränen, J.; Kinder, J.; Vukotić, M. Modular and Scalable Powertrain for Multipurpose Light Electric Vehicles. World Electr. Veh. J. 2023, 14, 309. [Google Scholar] [CrossRef]
- Cervero, D.; Fotopoulou, M.; Muñoz-Cruzado, J.; Rakopoulos, D.; Stergiopoulos, F.; Nikolopoulos, N.; Voutetakis, S.; Sanz, J.F. Solid State Transformers: A Critical Review of Projects with Relevant Prototypes and Demonstrators. Electronics 2023, 12, 931. [Google Scholar] [CrossRef]
- Beiranvand, R.; Rashidian, B.; Zolghadri, M.R.; Alavi, S.M.H. A Design Procedure for Optimizing the LLC Resonant Converter as a Wide Output Range Voltage Source. IEEE Trans. Power Electron. 2012, 27, 3749–3763. [Google Scholar] [CrossRef]
- Musavi, F.; Craciun, M.; Gautam, D.S.; Eberle, W.; Dunford, W.G. An LLC resonant DC–DC converter for wide output voltage range battery charging applications. IEEE Trans. Power Electron. 2013, 28, 5437–5445. [Google Scholar] [CrossRef]
- Kim, B.-C.; Park, K.-B.; Kim, C.-E.; Moon, G.-W. Load sharing characteristic of two-phase interleaved LLC resonant converter with parallel and series input structure. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition (ECCE), San Jose, CA, USA, 20–24 September 2009; pp. 750–753. [Google Scholar]
- Guo, B.; Zhang, Y.; Zhang, J.; Gao, J. Hybrid Control Strategy of Phase-Shifted Full-Bridge LLC Converter Based on Digital Direct Phase-Shift Control. J. Power Electron. 2018, 18, 802–816. [Google Scholar]
- Zhou, B.; Zhao, C.; Luo, H.; Qiu, Y.; Chen, S.; Zang, T.; Zhou, Y.; Zhou, X.; Zhao, H. Hybrid Control Strategy for Single-Stage Interleaved Totem-Pole LLC AC-DC Converter With Input and Output Power Decoupling. IEEE Trans. Power Electron. 2024, 39, 5135–5154. [Google Scholar] [CrossRef]
- Yoo, K.-M.; Lee, J.-Y. A 10-kW Two-Stage Isolated/Bidirectional DC/DC Converter with Hybrid-Switching Technique. IEEE Trans. Ind. Electron. 2013, 60, 2205–2213. [Google Scholar] [CrossRef]
- Mortazavizadeh, S.A.; Palazzo, S.; Amendola, A.; De Santis, E.; Di Ruzza, D.; Panariello, G.; Sanseverino, A.; Velardi, F.; Busatto, G. High Frequency, High Efficiency, and High Power Density GaN-Based LLC Resonant Converter: State-of-the-Art and Perspectives. Appl. Sci. 2021, 11, 11350. [Google Scholar] [CrossRef]
- Shadnam Zarbil, M.; Khalifeh, M.; Vahedi, A. A real-time LabVIEW-based emulator for various types of electrical loads. Electr. Eng. 2022, 104, 4367–4378. [Google Scholar] [CrossRef]
- Maurya, R.; Arya, S.R.; Saini, R.K.; Gupta, J. On-board power quality charger for electric vehicles with minimized switching stresses. Electr. Eng. 2022, 104, 1667–1680. [Google Scholar] [CrossRef]
- Bayati, M.; Abedi, M.; Gharehpetian, G.B.; Farahmandrad, M. Two designs for DC–DC stage of electric vehicle charging stations. Electr. Eng. 2020, 102, 2389–2399. [Google Scholar] [CrossRef]
- Wang, H.; Dusmez, S.; Khaligh, A. Design and analysis of a full-bridge LLC-based PEV charger optimized for wide battery voltage range. IEEE Trans. Veh. Technol. 2014, 63, 1603–1613. [Google Scholar] [CrossRef]
- Narasipuram, R.P.; Mopidevi, S. A Novel Hybrid Control Strategy and Dynamic Performance Enhancement of a 3.3 kW GaN–HEMT-Based iL2C Resonant Full-Bridge DC–DC Power Converter Methodology for Electric Vehicle Charging Systems. Energies 2023, 16, 5811. [Google Scholar] [CrossRef]
- Narasipuram, R.P.; Mopidevi, S. Parametric Modelling of Interleaved Resonant DC–DC Converter with Common Secondary Rectifier Circuit for xEV Charging Applications. In Proceedings of the 2023 International Conference on Sustainable Emerging Innovations in Engineering and Technology (ICSEIET), Ghaziabad, India, 14–15 September 2023; pp. 842–846. [Google Scholar]
- Narasipuram, R.P.; Mopidevi, S. A Dual Primary Side FB DC-DC Converter with Variable Frequency Phase Shift Control Strategy for On/Off Board EV Charging Applications. In Proceedings of the 2023 9th IEEE India International Conference on Power Electronics (IICPE), Sonipat, India, 28–30 November 2023; pp. 1–5. [Google Scholar]
- Narasipuram, R.P.; Mopidevi, S. An industrial design of 400 V-48 V, 98.2% peak efficient charger using E-mode GaN technology with wide operating ranges for xEV applications. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3194. [Google Scholar] [CrossRef]
- Xi, J.; Si, H.; Gao, J. Optimization of a Shift Control Strategy for Pure Electric Commercial Vehicles Based on Driving Intention. World Electr. Veh. J. 2024, 15, 44. [Google Scholar] [CrossRef]
- Althurthi, S.B.; Rajashekara, K.; Debnath, T. Comparison of EV Fast Charging Protocols and Impact of Sinusoidal Half-Wave Fast Charging Methods on Lithium-Ion Cells. World Electr. Veh. J. 2024, 15, 54. [Google Scholar] [CrossRef]
- Zulauf, G.; Park, S.; Liang, W.; Surakitbovorn, K.N.; Rivas-Davila, J. COSS Losses in 600 V GaN Power Semiconductors in Soft-Switched, High- and Very-High-Frequency Power Converters. IEEE Trans. Power Electron. 2018, 33, 10748–10763. [Google Scholar] [CrossRef]
- Van Do, T.; Trovao, J.P.F.; Li, K.; Boulon, L. Wide-Bandgap Power Semiconductors for Electric Vehicle Systems: Challenges and Trends. IEEE Veh. Technol. Mag. 2021, 16, 89–98. [Google Scholar] [CrossRef]
- Gu, W.-J.; Harada, K. A new method to regulate resonant converters. IEEE Trans. Power Electron. 1988, 3, 430–439. [Google Scholar] [CrossRef]
- Bosshard, T.R.; Kolar, J.W. Performance comparison of a GaN GIT and a Si IGBT for high-speed drive applications. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014. [Google Scholar]
- Narasipuram, R.P.; Karkhanis, V.A.; Ellinger, M.; Saranath, K.M.; Alagarsamy, G.; Jadhav, R. Systems Engineering—A Key Approach to Transportation Electrification. Symposium on International Automotive Technology; SAE Technical Paper, 2024-26-0128; SAE International: Warrendale, PA, USA, 2024. [Google Scholar]
- Elrajoubi, A.M.; Ang, S.S.; George, K. Design and analysis of a new GaN-Based AC/DC converter for battery charging application. IEEE Trans. Ind. Appl. 2019, 55, 4044–4052. [Google Scholar] [CrossRef]
- Pushpakaran, B.N.; Subburaj, A.S.; Bayne, S.B. Commercial GaN-Based Power Electronic Systems: A Review. J. Electron. Mater. 2020, 49, 6247–6262. [Google Scholar] [CrossRef]
- Keshmiri, N.; Wang, D.; Agrawal, B.; Hou, R.; Emadi, A. Current Status and Future Trends of GaN HEMTs in Electrified Transportation. IEEE Access 2020, 8, 70553–70571. [Google Scholar] [CrossRef]
- Chellappan, S. Design Considerations of GaN Devices for Improving Power Converter Efficiency; Texas Instruments Inc.: Dallas, TX, USA, 2017. [Google Scholar]
- Yadlapalli, R.T.; Kotapati, A.; Kandipati, R.; Balusu, S.R.; Koritala, C.S. Advancements in energy efficient GaN power devices and power modules for electric vehicle applications: A review. Int. J. Energy Res. 2021, 45, 12638–12664. [Google Scholar] [CrossRef]
- Lidow, A.; Strydom, J.; Strittmatter, R.; Zhou, C. GaN: A Reliable Future in Power Conversion: Dramatic performance improvements at a lower cost. IEEE Power Electron. Mag. 2015, 2, 20–26. [Google Scholar] [CrossRef]
- Will, C.; Ocker, F. Flexibility Potential of Smart Charging Electric Trucks and Buses. World Electr. Veh. J. 2024, 15, 56. [Google Scholar] [CrossRef]
- Lei, H.; Hu, X.; Zhao, J.; Deng, D.; Wang, R. Research Progress and Prospects of Public Transportation Charging Station Layout Methods. World Electr. Veh. J. 2024, 15, 63. [Google Scholar] [CrossRef]
- Zheng, J.; Du, Y.; Chen, D.; Ying, W.; Zhao, H.; Liu, K.; Qiu, J. Resonant Gate Drive Circuit with Active Clamping to Increase Efficiency and Reliability. World Electr. Veh. J. 2024, 15, 74. [Google Scholar] [CrossRef]
- Bernard, K. Advantages of Using Gallium NitrideFETs in Satellite Applications; Renesas: Tokyo, Japan, 2018. [Google Scholar]
- Wang, Y.; Ding, Y.; Yin, Y. Reliability of Wide Band Gap Power Electronic Semiconductor and Packaging: A Review. Energies 2022, 15, 6670. [Google Scholar] [CrossRef]
- Al Attar, H.; Hamida, M.A.; Ghanes, M.; Taleb, M. LLC DC-DC Converter Performances Improvement for Bidirectional Electric Vehicle Charger Application. World Electr. Veh. J. 2022, 13, 2. [Google Scholar] [CrossRef]
- Bottaro, E.; Rizzo, S.A.; Salerno, N. Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review. Energies 2022, 15, 3415. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Wang, Z.; Mantooth, H.A. A Complete Step-by-Step Optimal Design for LLC Resonant Converter. IEEE Trans. Power Electron. 2021, 36, 3674–3691. [Google Scholar] [CrossRef]















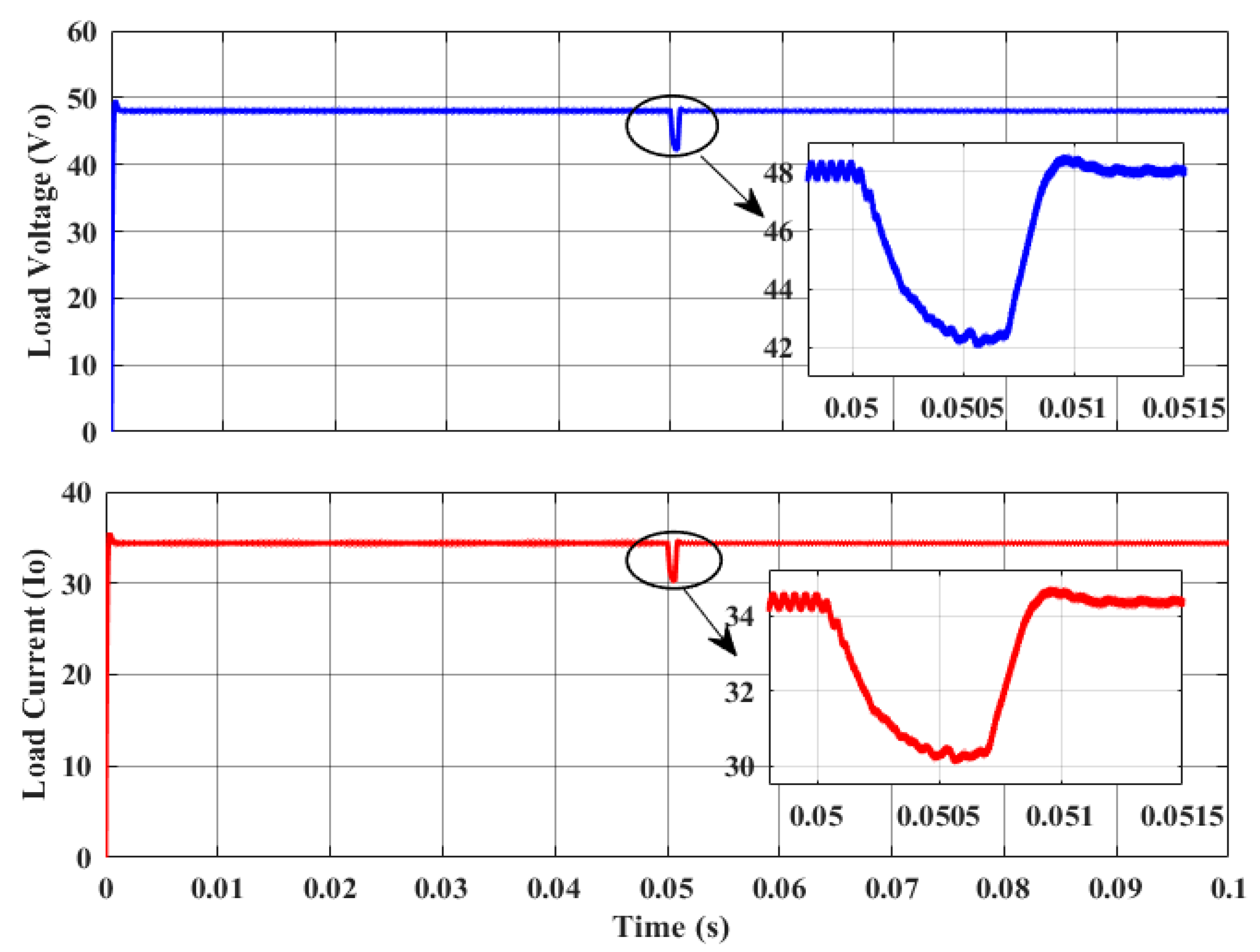



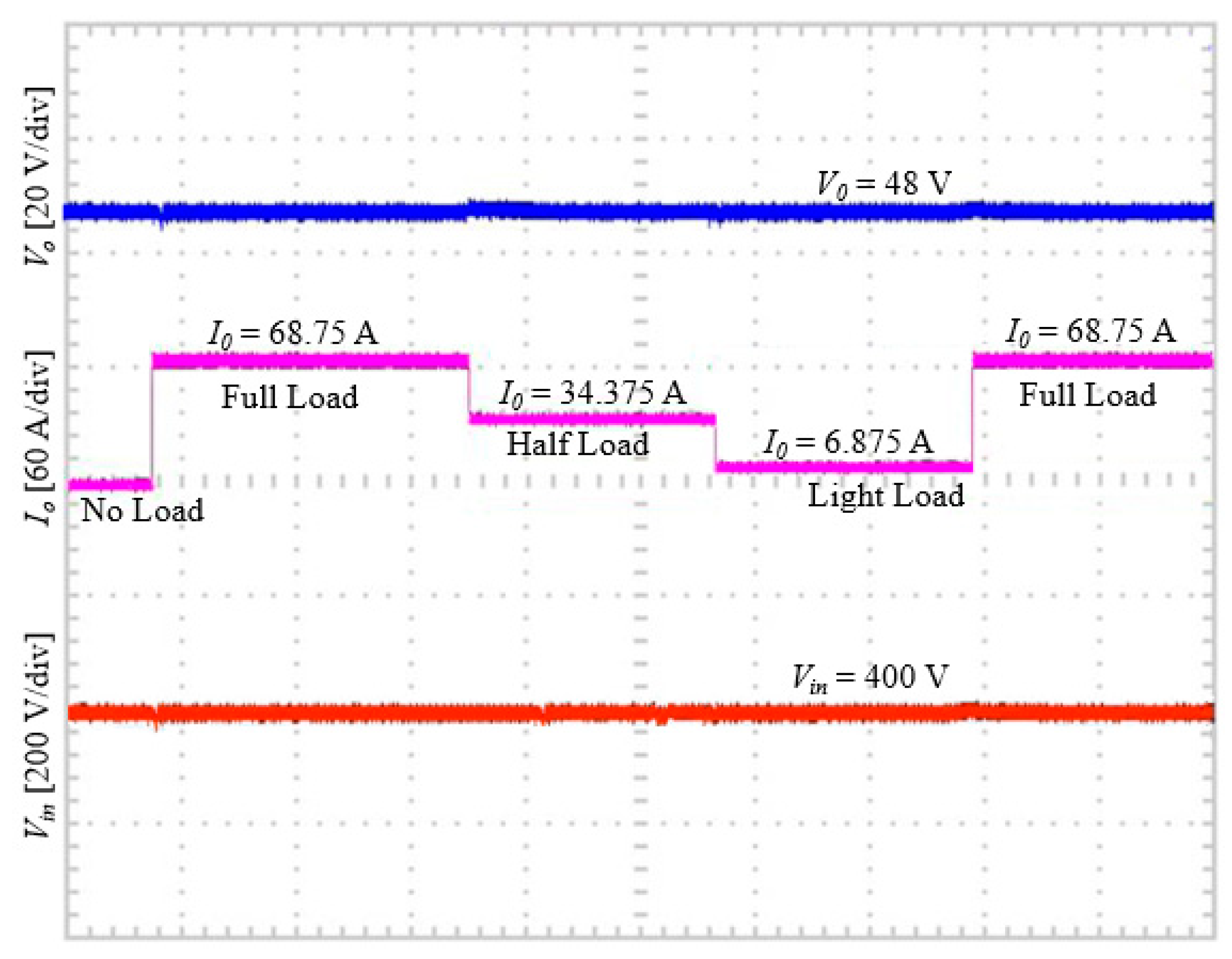

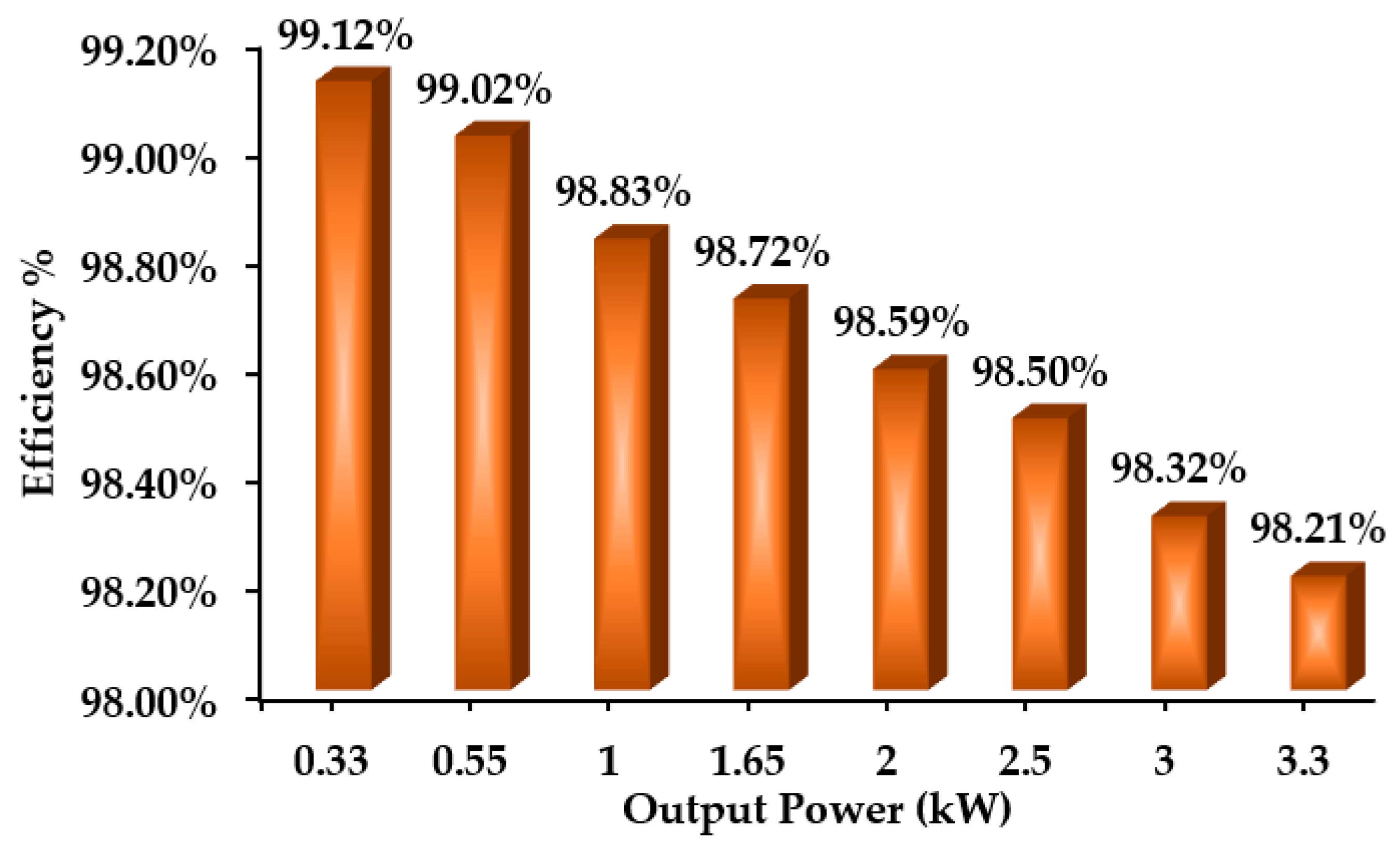
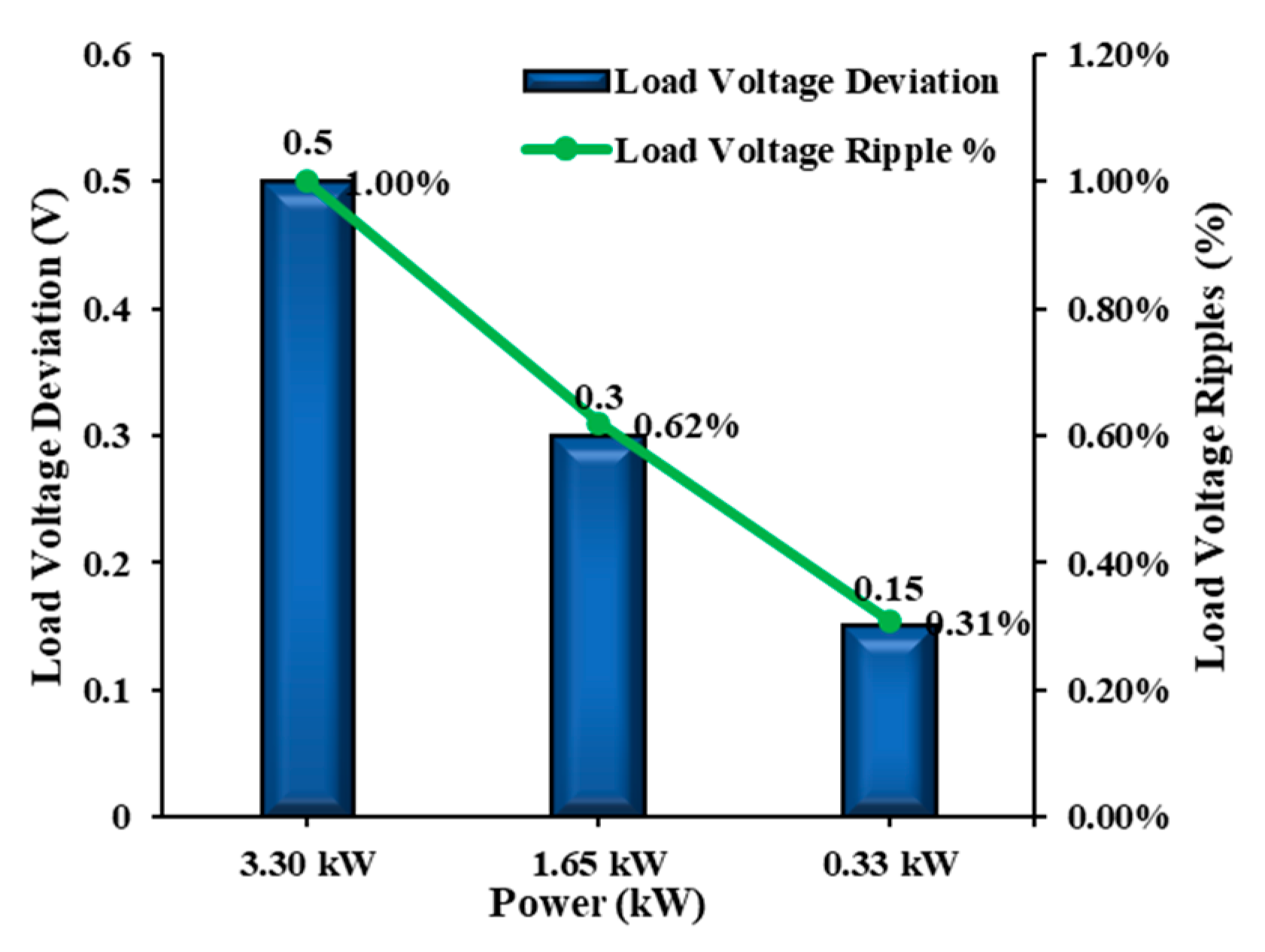



| Operation Attributes | Variable Input Voltage | Max. LVD | % ALVR | Transient Analysis | |||
|---|---|---|---|---|---|---|---|
| Voltage Dip | Avg % of Dip | Settling Time | |||||
| Load Variation | 3.3 kW | 300 V–500 V | +0.40 V | +0.830% | +5.2 V | +10.83% | 1.1 ms |
| 500 V–300 V | +0.42 V | +0.875% | −3.5 V | −7.29% | 1.2 ms | ||
| 1.65 kW | 300 V–500 V | +0.38 V | +0.791% | +4.8 V | +10.00% | 1.0 ms | |
| 500 V–300 V | +0.40 V | +0.833% | −5.8 V | −12.08% | 1.2 ms | ||
| 0.33 kW | 300 V–500 V | +0.37 V | +0.770% | +6.35 V | +13.23% | 1.33 ms | |
| 500 V–300 V | +0.38 V | +0.791% | −8.70 V | −18.12% | 1.40 ms | ||
| Operation Attributes | Variable Input Voltage | Max. LCD | % ALCR | Transient Analysis | |||
|---|---|---|---|---|---|---|---|
| Current Dip | Avg % of Dip | Settling Time | |||||
| Load Variation | 3.3 kW | 300 V–500 V | +0.59 A | +0.85% | +7.25 A | +10.54% | 1.1 ms |
| 500 V–300 V | +0.64 A | +0.93% | −4.75 A | −6.90% | 1.2 ms | ||
| 1.65 kW | 300 V–500 V | +0.57 A | +1.66% | +3.82 A | +11.11% | 1.0 ms | |
| 500 V–300 V | +0.62 A | +1.81% | −2.25 A | −6.54% | 1.2 ms | ||
| 0.33 kW | 300 V–500 V | +0.055 A | +0.8% | +1.85 A | +26.91% | 1.33 ms | |
| 500 V–300 V | +0.069 A | +1.0% | −1.87 A | −27.20% | 1.40 ms | ||
| Conditions | Max. LVD | %AVR | Max. LCD | %ACR |
|---|---|---|---|---|
| Simulations | +0.40 V | +0.83% | +0.59 A | +0.85% |
| Experimental | +0.76 V | +1.58% | +1.38 A | +2.00% |
| Conditions | Voltage Dip | Avg% of Dip | Current Dip | Avg% of Dip | Settling Time |
|---|---|---|---|---|---|
| Simulations | +5.20 V | +10.83% | +7.25 A | +10.54% | 1.1 ms |
| Experimental | +6.17 V | +12.85% | +8.29 A | +12.05% | 18 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narasipuram, R.P.; Mopidevi, S.; Dianov, A.; Tandon, A.S. Analysis of Scalable Resonant DC–DC Converter Using GaN Switches for xEV Charging Stations. World Electr. Veh. J. 2024, 15, 218. https://doi.org/10.3390/wevj15050218
Narasipuram RP, Mopidevi S, Dianov A, Tandon AS. Analysis of Scalable Resonant DC–DC Converter Using GaN Switches for xEV Charging Stations. World Electric Vehicle Journal. 2024; 15(5):218. https://doi.org/10.3390/wevj15050218
Chicago/Turabian StyleNarasipuram, Rajanand Patnaik, Subbarao Mopidevi, Anton Dianov, and Amit Singh Tandon. 2024. "Analysis of Scalable Resonant DC–DC Converter Using GaN Switches for xEV Charging Stations" World Electric Vehicle Journal 15, no. 5: 218. https://doi.org/10.3390/wevj15050218






