Frictional Behavior of Chestnut (Castanea sativa Mill.) Sawn Timber for Carpentry and Mechanical Joints in Service Class 2
Abstract
:1. Introduction
- Service Class 1: corresponds to conditions (20 °C and 65% relative humidity) where the average moisture content in most softwoods remains below 12%;
- Service Class 2: corresponds to conditions (20 °C and 85% relative humidity) where the average moisture content in most softwoods remains below 20%;
- Service Class 3: corresponds to conditions where the average moisture content in most softwoods exceeds 20%.
2. Materials and Methods
- Transverse plane (perpendicular to the fiber):
- (A) predominant direction of radial sliding (sliding parallel to the radius of the growth rings);
- (B) predominant direction of tangential sliding to the growth rings;
- Radial plane (defined by the axis of the three and a radius of the trunk):
- (C) sliding direction parallel to the fiber (i.e., radial surfaces);
- (D) sliding direction perpendicular to the fiber;
- Tangential plane (tangent to the growth rings):
- (E) sliding direction parallel to the fiber (i.e., tangential surfaces);
- (F) sliding direction perpendicular to the fiber.
3. Results and Discussion
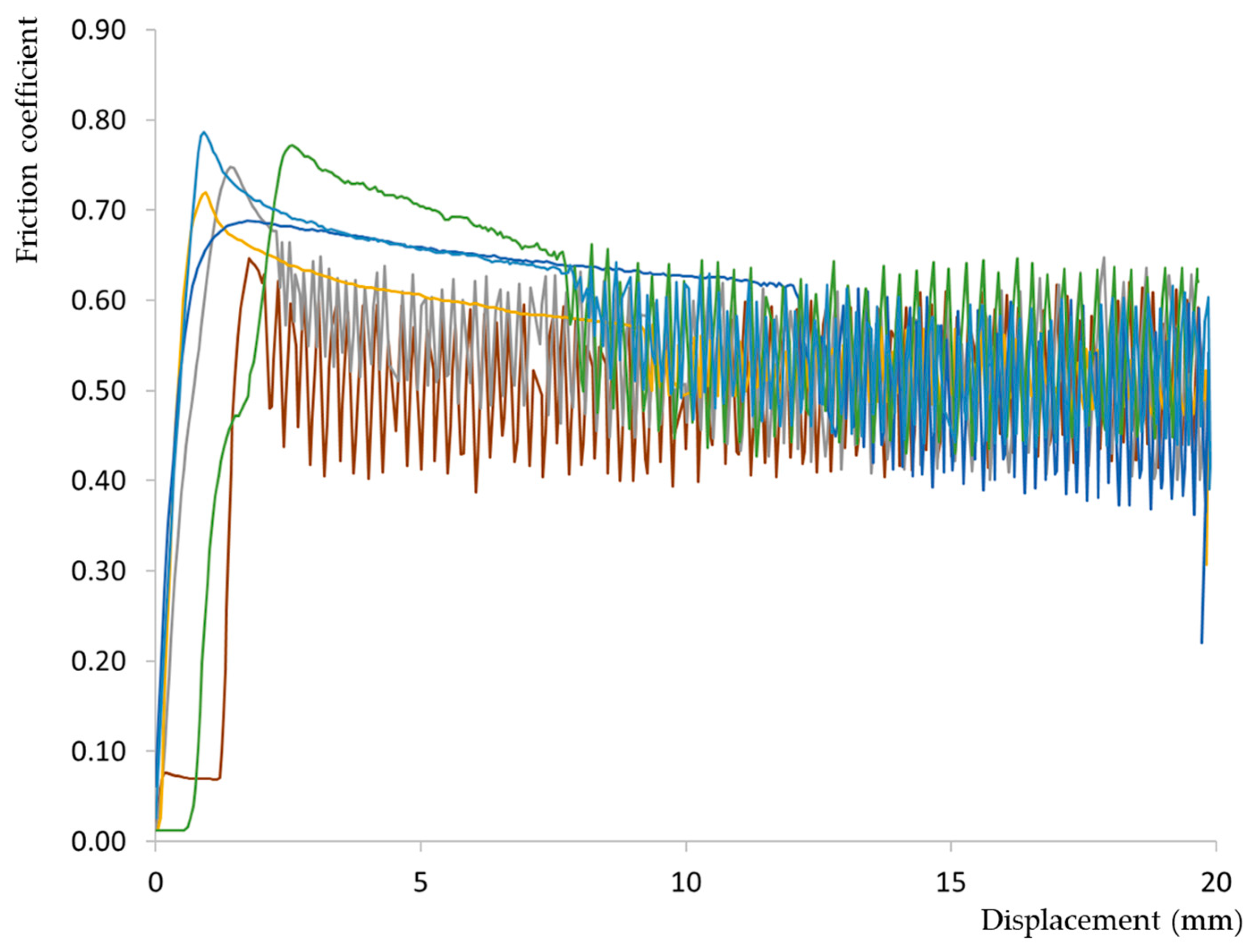
3.1. Timber-to-Timber Tests with Identical Orientations
3.2. Timber-to-Timber Tests with Different Orientations
3.3. Timber-to-Steel Tests
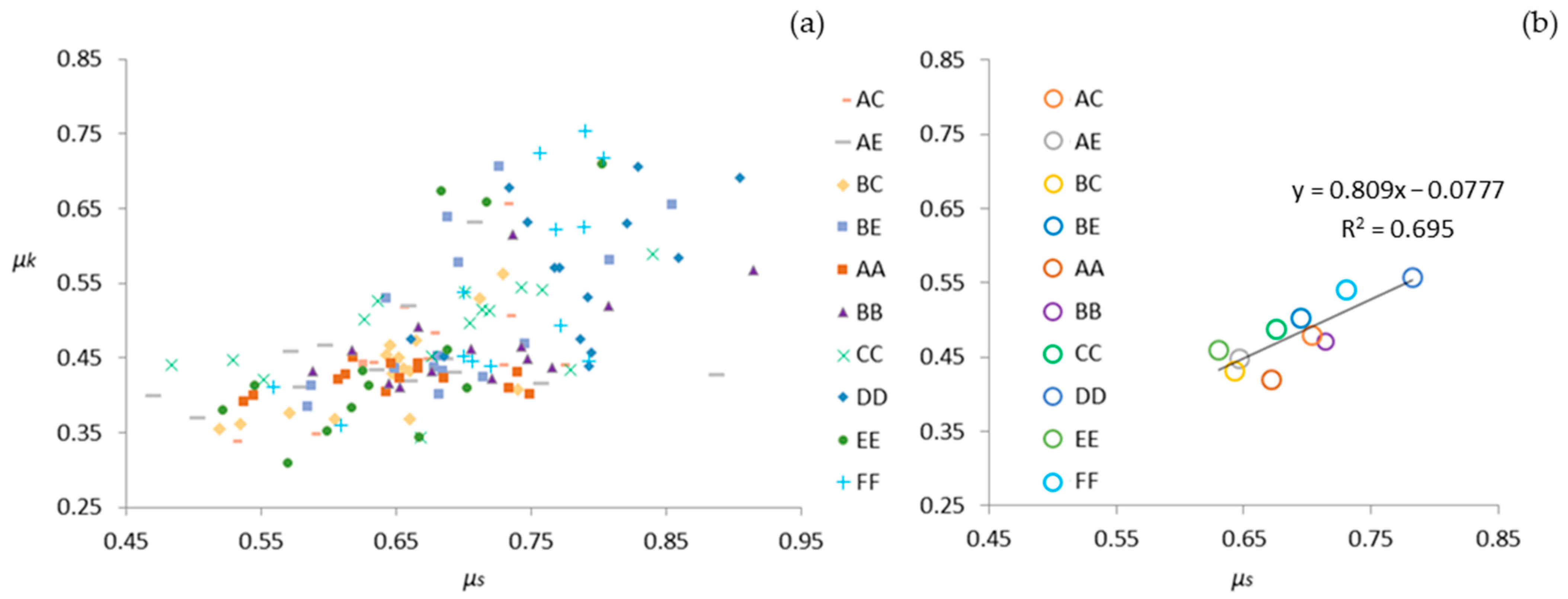
3.4. Correlation between μk and μs
3.5. Influence of Moisture Content on Friction Coefficients
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roos, A.; Woxblom, L.; McCluskey, D. The Influence of Architects and Structural Engineers on Timber in Construction–Perceptions and Roles. Silva Fenn. 2010, 44, 871–884. [Google Scholar] [CrossRef]
- Minunno, R.; O’Grady, T.; Morrison, G.M.; Gruner, R.L. Investigating the Embodied Energy and Carbon of Buildings: A Systematic Literature Review and Meta-Analysis of Life Cycle Assessments. Renew. Sustain. Energy Rev. 2021, 143, 110935. [Google Scholar] [CrossRef]
- Tonelli, C.; Grimaudo, M. Timber Buildings and Thermal Inertia: Open Scientific Problems for Summer Behavior in Mediterranean Climate. Energy Build. 2014, 83, 89–95. [Google Scholar] [CrossRef]
- Martínez-Alonso, C.; Berdasco, L. Carbon Footprint of Sawn Timber Products of Castanea Sativa Mill. in the North of Spain. J. Clean. Prod. 2015, 102, 127–135. [Google Scholar] [CrossRef]
- Arriaga, F.; Wang, X.; Íñiguez-González, G.; Llana, D.F.; Esteban, M.; Niemz, P. Mechanical Properties of Wood: A Review. Forests 2023, 14, 1202. [Google Scholar] [CrossRef]
- Conedera, M.; Tinner, W.; Krebs, P.; de Rigo, D.; Caudullo, G. Castanea Sativa in Europe: Distribution, Habitat, Usage and Threats. In European Atlas of Forest Tree Species; Publication Office of the European Union: Luxembourg, 2016; p. e0125e0+. [Google Scholar]
- Rodríguez-Guitián, M.; Rigueiro, A.; Real, C.; Blanco, J.; Ferreiro da Costa, J. El Habitat” 9269 Bosques de Castanea Sativa” En El Extremo Noroccidental Iberico: Primeros Datos Sobre La Variabilidad Floristica de Los” Soutos”. Bull. Société d’ Hist. Nat. Toulouse 2005, 141, 75–81. [Google Scholar]
- González-Varo, J.P.; López-Bao, J.V.; Guitián, J. Presence and Abundance of the Eurasian Nuthatch Sitta Europaea in Relation to the Size, Isolation and the Intensity of Management of Chestnut Woodlands in the NW Iberian Peninsula. Landsc. Ecol. 2008, 23, 79–89. [Google Scholar] [CrossRef]
- Council Directive 92/43/EEC On the Conservation of Natural Habitats and of Wild Fauna and Flora. Available online: http://data.europa.eu/eli/dir/1992/43/2013-07-01 (accessed on 7 March 2024).
- MITECO. Forest Statistics Yearbook 2021; Spnanish Ministry for Ecological Transition and Demographic Challenge: Madrid, Spain, 2022. [Google Scholar]
- Vega, A.; Dieste, A.; Guaita, M.; Majada, J.; Baño, V. Modelling of the Mechanical Properties of Castanea Sativa Mill. Structural Timber by a Combination of Non-Destructive Variables and Visual Grading Parameters. Eur. J. Wood Prod. 2012, 70, 839–844. [Google Scholar] [CrossRef]
- Beccaro, G.; Alma, A.; Bounous, G.; Gomes-Laranjo, J. (Eds.) The Chestnut Handbook: Crop & Forest Management; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2020; ISBN 978-0-429-44560-6. [Google Scholar]
- Carbone, F.; Moroni, S.; Mattioli, W.; Mazzocchi, F.; Romagnoli, M.; Portoghesi, L. Competitiveness and Competitive Advantages of Chestnut Timber Laminated Products. Ann. For. Sci. 2020, 77, 51. [Google Scholar] [CrossRef]
- Villar, J.R.; Guaita, M.; Vidal, P.; Arriaga, F. Analysis of the Stress State at the Cogging Joint in Timber Structures. Biosyst. Eng. 2007, 96, 79–90. [Google Scholar] [CrossRef]
- Sjödin, J.; Serrano, E.; Enquist, B. An Experimental and Numerical Study of the Effect of Friction in Single Dowel Joints. Holz. Roh. Werkst. 2008, 66, 363–372. [Google Scholar] [CrossRef]
- Koch, H.; Eisenhut, L.; Seim, W. Multi-Mode Failure of Form-Fitting Timber Connections—Experimental and Numerical Studies on the Tapered Tenon Joint. Eng. Struct. 2013, 48, 727–738. [Google Scholar] [CrossRef]
- Aira, J.R.; Íñiguez-González, G.; Guaita, M.; Arriaga, F. Load Carrying Capacity of Halved and Tabled Tenoned Timber Scarf Joint. Mater. Struct. 2016, 49, 5343–5355. [Google Scholar] [CrossRef]
- Villar-García, J.R.; Crespo, J.; Moya, M.; Guaita, M. Experimental and Numerical Studies of the Stress State at the Reverse Step Joint in Heavy Timber Trusses. Mater. Struct. 2018, 51, 17. [Google Scholar] [CrossRef]
- Domínguez, M.; Fueyo, J.G.; Villarino, A.; Anton, N. Structural Timber Connections with Dowel-Type Fasteners and Nut-Washer Fixings: Mechanical Characterization and Contribution to the Rope Effect. Materials 2021, 15, 242. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.M.M.; Leite, P.A.S.; Silva, L.D.S.; Silva, V.S.B.; Lopes, H.M. Parametric Study of Three Types of Timber Connections with Metal Fasteners Using Eurocode 5. Appl. Sci. 2022, 12, 1701. [Google Scholar] [CrossRef]
- UNE-EN 1995-1-1; Eurocódigo 5: Proyecto de Estructuras de Madera. Parte 1-1: Reglas Generales y Reglas Para Edificación. AENOR: Madrid, Spain, 2016.
- American Wood Council. The 2024 National Design Specification (NDS) for Wood Construction; American Wood Council: Leesburg, VA, USA, 2023. [Google Scholar]
- CSA O86; Engineering Design in Wood. Canadian Standards Association: Toronto, ON, Canada, 2019.
- EN 1995-2; Eurocode 5: Design of Timber Structures—Part 2: Bridges. CEN: Brussels, Belgium, 2016.
- Blass, H.; Aune, P.; Choo, B.; Görlacher, R.; Grifiths, D. Timber Engineering. STEP 1: Basis of Design, Material Properties, Structural Components and Joints; Centrum Hout: Almere, The Netherlands, 1995. [Google Scholar]
- Argüelles, R.; Arriaga, F.; Esteban, M.; Íñiguez, G.; Argüelles Bustillo, R. Timber Structures. Basis for Calculation [Estructuras de madera. Bases de cálculo]; AITIM. Technical Research Association of the Wood and Cork Industries: Madrid, Spain, 2013; ISBN 978-84-87381-44-7. [Google Scholar]
- Glass, S.V.; Zelinka, S.L. Chapter 4: Moisture Relations and Physical Properties of Wood. In Wood handbook: Wood as an Engineering Material; General Technical Report FPL-GTR-282; US Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010. [Google Scholar]
- Argüelles, R.; Arriaga, F.; Esteban, M.; Íñiguez, G.; Argüelles Bustillo, R. Timber Structures. Joints [Estructuras de madera. Uniones]; AITIM. Technical Research Association of the Wood and Cork Industries: Madrid, Spain, 2015; ISBN 978-84-87381-44-7. [Google Scholar]
- Fu, W.; Guan, H.; Chen, B. Investigation on the Influence of Moisture Content and Wood Section on the Frictional Properties of Beech Wood Surface. Tribol. Trans. 2021, 64, 830–840. [Google Scholar] [CrossRef]
- Villar-García, J.R.; Vidal-López, P.; Corbacho, A.J.; Moya, M. Determination of the Friction Coefficients of Chestnut (Castanea Sativa Mill.) Sawn Timber. Int. Agrophys. 2020, 34, 65–77. [Google Scholar] [CrossRef] [PubMed]
- Villar-García, J.R.; Vidal-López, P.; Rodríguez-Robles, D.; Moya Ignacio, M. Friction Coefficients of Chestnut (Castanea Sativa Mill.) Sawn Timber for Numerical Simulation of Timber Joints. Forests 2022, 13, 1078. [Google Scholar] [CrossRef]
- McKenzie, W.M.; Karpovich, H. The Frictional Behaviour of Wood. Wood Sci. Technol. 1968, 2, 139–152. [Google Scholar] [CrossRef]
- Dorn, M.; Habrová, K.; Koubek, R.; Serrano, E. Determination of Coefficients of Friction for Laminated Veneer Lumber on Steel under High Pressure Loads. Friction 2021, 9, 367–379. [Google Scholar] [CrossRef]
- EN 13183-1; Moisture Content of a Piece of Sawn Timber—Part 1: Determination by Oven Dry Method. CEN: Brussels, Belgium, 2002.
- ASTM G115-10; Standard Guide for Measuring and Reporting Friction Coefficients. ASTM International: West Conshohocken, PA, USA, 2018.
- Villar-García, J.R.; Vidal-López, P.; Moya Ignacio, M. Device to Perform Friction Tests between Solid Bodies. Utility Model U 201932027. 2020. Available online: https://patentscope.wipo.int/search/en/detail.jsf?docId=ES289318649 (accessed on 7 March 2024).
- Crespo, J.; Regueira, R.; Soilán, A.; Díez, M.R.; Guaita, M. Methodology to Determine the Coefficients of Both Static and Dynamic Friction Apply to Different Species of Wood. In Proceedings of the 1st Ibero-Latin American Congress on Wood in Construction (CIMAD), Coimbra, Portugal, 7–9 June 2011. [Google Scholar]
- Aira, J.R.; Arriaga, F.; Íñiguez-González, G.; Crespo, J. Static and Kinetic Friction Coefficients of Scots Pine (Pinus Sylvestris L.), Parallel and Perpendicular to Grain Direction. Mater. Construcción 2014, 64, e030. [Google Scholar] [CrossRef]
- Berman, A.; Ducker, W.; Israelachvili, J. Experimental and Theoretical Investigations of Stick-Slip Friction Mechanisms. In Physics of Sliding Friction; Persson, B.N.J., Tosatti, E., Eds.; NATO ASI Series; Springer: Dordrecht, The Netherlands, 1996; pp. 51–67. ISBN 978-94-015-8705-1. [Google Scholar]
- Möhler, K.; Herröder, W. Range of the coefficient of friction of spruce wood rough from sawing [Obere und untere Reibbeiwerte von sägerauhem Fichtenholz]. Holz. Roh. Werkstoff 1979, 37, 27–32. [Google Scholar] [CrossRef]
- Xu, M.; Li, L.; Wang, M.; Luo, B. Effects of Surface Roughness and Wood Grain on the Friction Coefficient of Wooden Materials for Wood–Wood Frictional Pair. Tribol. Trans. 2014, 57, 871–878. [Google Scholar] [CrossRef]







| Test | Static Friction Coefficient | Kinetic Friction Coefficient | Moisture Content | References |
|---|---|---|---|---|
| Timber-to-timber | 0.25 to 0.7 | 0.15 to 0.4 | Dry | Argüelles et al. [26,28] |
| Timber-to-timber | 0.5 to 0.71 | 0.3 to 0.65 | From 11.25% to 20% at different wood sections (tangential, diagonal, and radial) | Fu et al. [29] |
| Timber-to-timber | 0.36 to 052 | 0.25 to 0.34 | 12% at different orientation of the contact surfaces | Villar-García et al. [30] |
| Timber-to-timber | 0.44 to 0.51 | 0.33 to 0.39 | 12% at different orientation of the contact surfaces | Villar-García et al. [31] |
| Timber-to-steel | - | 0.1 to 0.3 | From 10% to 14% | McKenzie et al. [32] |
| - | 0.4 to 0.64 | At fiber saturation | ||
| Timber-to-steel | - | 0.3 to 0.5 | Dry | Glass and Zelinka [27] |
| - | 0.5 to 0.7 | Intermediate moisture | ||
| - | 0.7 to 0.9 | Close to saturation | ||
| Timber-to-steel | 0.156 to 0.238 | - | 12% at different fiber directions | Dorn et al. [33] |
| 0.121 to 0.176 | - | Oven-dried at different fiber directions | ||
| 0.280 to 0.344 | - | Saturated at different fiber directions | ||
| Timber-to-steel | 0.16 to 0.21 | 0.15 to 0.18 | 12% at different orientations of the contact surfaces | Villar-García et al. [31] |
| Mean (CoV %) | A-A | B-B | C-C | D-D | E-E | F-F |
|---|---|---|---|---|---|---|
| μs | 0.67 (15.3) | 0.71 (11.4) | 0.68 (14.4) | 0.78 (8.2) | 0.63 (13.9) | 0.73 (9.9) |
| μk | 0.42 (4.8) | 0.47 (12.7) | 0.49 (12.9) | 0.56 (16.7) | 0.46 (29.3) | 0.54 (24.6) |
| Mean (CoV %) | A-C | A-E | B-C | B-E |
|---|---|---|---|---|
| μs | 0.70 (18.1) | 0.65 (15.6) | 0.64 (9.9) | 0.70 (10.3) |
| μk | 0.48 (25.7) | 0.45 (13.6) | 0.43 (14.3) | 0.50 (20.7) |
| Mean (CoV %) | A-S | B-S | C-S | D-S | E-S | F-S |
|---|---|---|---|---|---|---|
| μs | 0.48 (2.5) | 0.49 (6.1) | 0.55 (4.6) | 0.53 (3.2) | 0.54 (4.9) | 0.52 (4.4) |
| μk | 0.45 (7.2) | 0.47 (7.2) | 0.53 (7.2) | 0.52 (3.1) | 0.53 (5.2) | 0.50 (5.3) |
| Mean (CoV %) | A-A | B-B | C-C | D-D | E-E | F-F |
|---|---|---|---|---|---|---|
| μs | 0.59 (6.3) | 0.61 (5.2) | 0.51 (33.1) | 0.69 (31.1) | 0.48 (7.5) | 0.70 (7.7) |
| μk | 0.37 (17.7) | 0.33 (11.8) | 0.37 (28.3) | 0.47 (26.3) | 0.37 (27.1) | 0.43 (6.4) |
| Mean (CoV %) | A-C | A-E | B-C | B-E |
|---|---|---|---|---|
| μs | 0.56 (32.0) | 0.57 (20.9) | 0.51 (26.5) | 0.56 (17.4) |
| μk | 0.44 (16.2) | 0.39 (31.7) | 0.40 (26.3) | 0.41 (25.9) |
| Mean (CoV %) | A-S | B-S | C-S | D-S | E-S | F-S |
|---|---|---|---|---|---|---|
| μs | 0.33 (7.3) | 0.34 (17.2) | 0.36 (10.6) | 0.35 (2.9) | 0.33 (8.8) | 0.37 (17.6) |
| μk | 0.31 (8.1) | 0.31 (5.5) | 0.32 (10.2) | 0.34 (5.7) | 0.32 (5.4) | 0.32 (15.9) |
| Interpolated value (error %) | A-A | B-B | C-C | D-D | E-E | F-F |
| μs | 0.56 | 0.55 | 0.54 | 0.65 | 0.50 | 0.64 |
| (−5.0%) | (−9.5%) | (6.4%) | (−5.7%) | (3.2%) | (−8.6%) | |
| μk | 0.37 | 0.36 | 0.40 | 0.45 | 0.37 | 0.47 |
| (−0.1%) | (9.2%) | (7.7%) | (−4.5%) | (0.0%) | (8.2%) | |
| Interpolated value (error %) | A-C | A-E | B-C | B-E | ||
| μs | 0.61 | 0.54 | 0.54 | 0.59 | ||
| (8.7%) | (−4.5%) | (6.8%) | (6%) | |||
| μk | 0.43 | 0.39 | 0.40 | 0.44 | ||
| (−1.2%) | (−0.4%) | (−0.9%) | (7%) | |||
| Interpolated value (error %) | A-S | B-S | C-S | D-S | E-S | F-S |
| μs | 0.34 | 0.33 | 0.37 | 0.37 | 0.37 | 0.35 |
| (2%) | (−3%) | (4%) | (6%) | (11%) | (−5%) | |
| μk | 0.30 | 0.32 | 0.35 | 0.35 | 0.35 | 0.34 |
| (−2%) | (2%) | (10%) | (3%) | (11%) | (6%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villar-García, J.R.; Moya Ignacio, M.; Vidal-López, P.; Rodríguez-Robles, D. Frictional Behavior of Chestnut (Castanea sativa Mill.) Sawn Timber for Carpentry and Mechanical Joints in Service Class 2. Sustainability 2024, 16, 3886. https://doi.org/10.3390/su16103886
Villar-García JR, Moya Ignacio M, Vidal-López P, Rodríguez-Robles D. Frictional Behavior of Chestnut (Castanea sativa Mill.) Sawn Timber for Carpentry and Mechanical Joints in Service Class 2. Sustainability. 2024; 16(10):3886. https://doi.org/10.3390/su16103886
Chicago/Turabian StyleVillar-García, José Ramón, Manuel Moya Ignacio, Pablo Vidal-López, and Desirée Rodríguez-Robles. 2024. "Frictional Behavior of Chestnut (Castanea sativa Mill.) Sawn Timber for Carpentry and Mechanical Joints in Service Class 2" Sustainability 16, no. 10: 3886. https://doi.org/10.3390/su16103886





