Data Assimilation of Satellite-Derived Rain Rates Estimated by Neural Network in Convective Environments: A Study over Italy
Abstract
:1. Introduction
2. Data and Methods
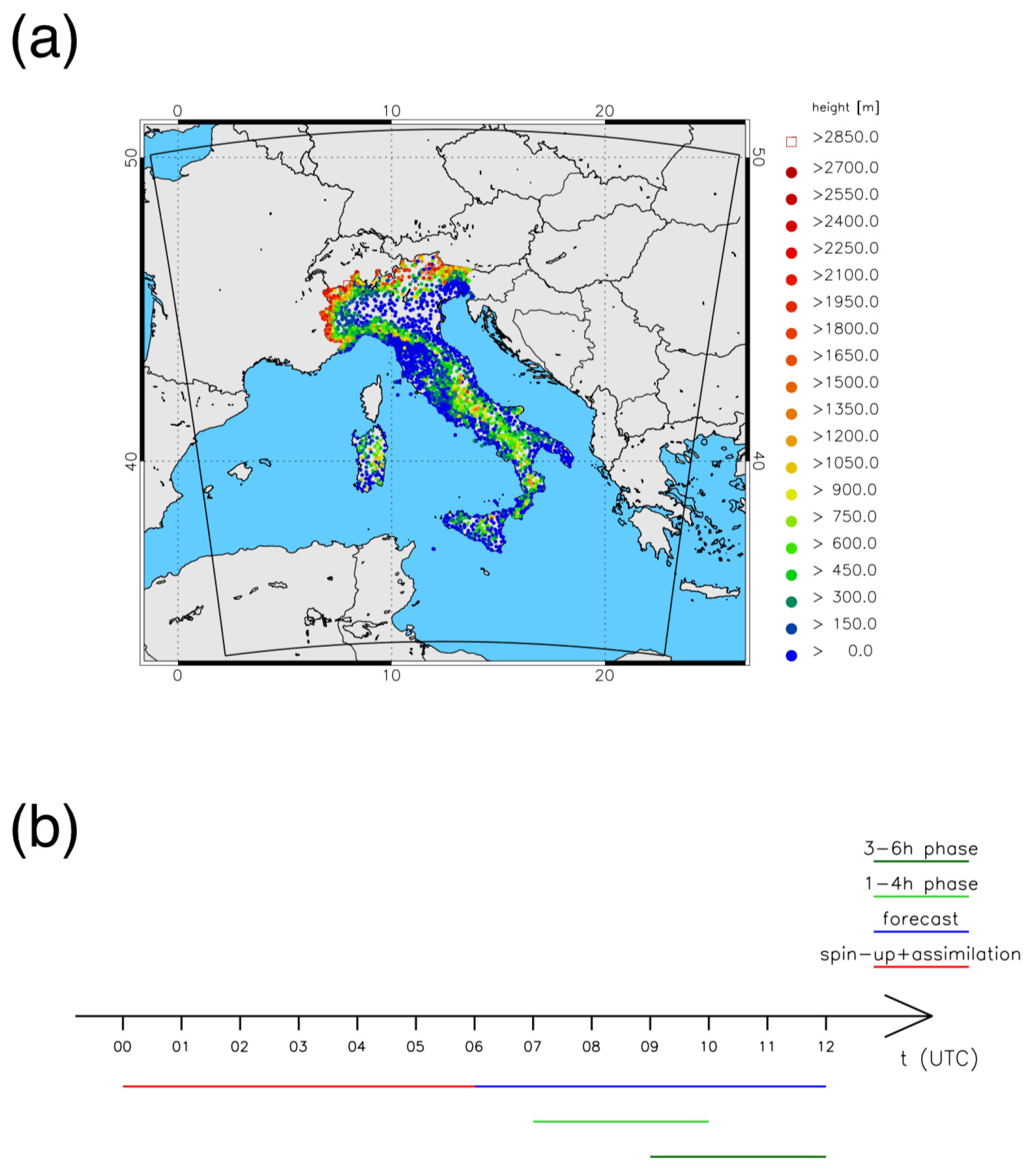
2.1. WRF Model Configuration and Experimental Set-Up
2.2. Rain Rate Products
2.3. Rain Rate Data Assimilation Method
2.4. Verification Procedure
- -
- hits (a): the precipitation forecast and rain gauge observation are both above or equal to the given threshold;
- -
- false alarms (b): the precipitation forecast is above or equal to the given threshold, while the rain gauge observation is below the given threshold;
- -
- misses (c): the precipitation forecast is below the given threshold, while the rain gauge observation is above or equal to the given threshold;
- -
- correct negatives (d): the precipitation forecast and observation are both below the given threshold.
- -
- Frequency bias (FBIAS), which is a measure of the frequency of predicted events above a certain rainfall threshold with respect to the observed frequency.
- -
- Probability of detection (POD), which accounts for the number of correctly predicted events upon the number of observed events. The POD gives the capability to the model for forecasting the exceedance of a certain rainfall threshold in the domain. Values close to one indicate that the experiment has a near-perfect performance, while in contrast, values near zero show that the model cannot correctly forecast the events.
- -
- Threat score (TS), which is the ratio between the number of events correctly predicted and the sum of the observed and predicted events.
- -
- False-alarm rate (FAR), which provides a measure of the fraction of rain forecast events that did not occur; therefore, a value of one signifies that only false alarms and no correct events were forecast; a value of zero denotes that only correct events and no false alarms were forecast.
3. Results
3.1. A Case Study
3.2. Scores for Summer and Fall
3.2.1. Scores for the 1–4 h Phase
3.2.2. Scores for the 3–6 h Phase
4. Discussion
5. Conclusions
- -
- a method to assimilate satellite-derived rain rates into the WRF model is presented;
- -
- neural networks can estimate rain rates from satellite data;
- -
- neural-network-derived rain rate data assimilation can improve precipitation forecasts;
- -
- H60-derived rain rate data assimilation improves the forecast for the lower thresholds in summer, while producing a high number of false alarms for the highest threshold (30 mm/3 h).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clark, P.A.; Roberts, N.; Lean, H.W.; Ballard, S.P.; Charlton-Perez, C. Convection-permitting models: A step-change in rainfall forecasting. Meteor. Appl. 2016, 23, 165–181. [Google Scholar] [CrossRef]
- Cuo, L.; Pagano, T.C.; Wang, Q.J. A review of quantitative precipitation forecasts and their use in short- to medium-range streamflow forecasting. J. Hydrometeorol. 2011, 12, 713–728. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Xue, M.; Wicker, L.J.; Kelleher, K.E.; Foster, M.P.; Schaefer, J.T.; Schneider, R.S.; Benjamin, S.G.; Weygandt, S.S.; Ferree, J.T.; et al. Convective-Scale Warn-on-Forecast System. Bull. Am. Meteorol. Soc. 2009, 90, 1487–1500. [Google Scholar] [CrossRef]
- Berner, J.; Fossell, K.R.; Ha, S.-Y.; Hacker, J.P.; Snyder, C. Increasing the skill of probabilistic forecasts: Understanding performance improvements from model-error representations. Mon. Weather Rev. 2015, 143, 1295–1320. [Google Scholar] [CrossRef]
- Dixon, M.; Li, Z.; Lean, H.W.; Roberts, N.M.; Ballard, S.P. Impact of data assimilation on forecasting convection over the United Kingdom using a high-resolution version of the Met Office Unified Model. Mon. Weather Rev. 2009, 137, 1562–1584. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American hourly assimilation and model forecast cycle: The rapid refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Federico, S.; Torcasio, R.C.; Avolio, E.; Caumont, O.; Montopoli, M.; Baldini, L.; Vulpiani, G.; Dietrich, S. The impact of lightning and radar reflectivity factor data assimilation on the very short-term rainfall forecasts of RAMS@ISAC: Application to two case studies in Italy. Nat. Hazards Earth Syst. Sci. 2019, 19, 1839–1864. [Google Scholar] [CrossRef]
- Gustafsson, N.; Janjić, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bučánek, A.; et al. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Q. J. R. Meteor. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteor. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Xue, J.; Bedi, H.S.; Ingles, K.; Oosterhof, D. Physical initialization for numerical weather prediction over the tropics. Tellus 1991, 43A, 53–81. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Bedi, H.S.; Ingles, K. Physical initialization using SSM/I rain rates. Tellus 1993, 45A, 247–269. [Google Scholar] [CrossRef]
- Manobianco, J.; Koch, S.; Karyampudi, V.M.; Negri, A.J. The impact of assimilating satellite-derived precipitation rates on numerical simulations of the ERICA IOP 4 cyclone. Mon. Weather Rev. 1994, 122, 341–365. [Google Scholar] [CrossRef]
- Jones, C.D.; Macpherson, B. A latent heat nudging scheme for the assimilation of precipitation data into the mesoscale model. Meteor. Appl. 1997, 4, 269–277. [Google Scholar] [CrossRef]
- Stephan, K.; Klink, S.; Schraff, C. Assimilation of radar-derived rain rates into the convective-scale model COSMO-DE at DWD. Q. J. R. Meteor. Soc. 2008, 134, 1315–1326. [Google Scholar] [CrossRef]
- Falkovich, A.; Kalnay, E.; Lord, S.; Muthur, M.B. A new method of observed rainfall assimilation in forecast models. J. Appl. Meteor. 2000, 39, 1282–1298. [Google Scholar] [CrossRef]
- Sokol, Z. Effects of an assimilation of radar and satellite data on a very-short-range forecast of heavy convective rainfalls. Atmos. Res. 2009, 93, 188–206. [Google Scholar] [CrossRef]
- Davolio, S.; Buzzi, A. A Nudging Scheme for the Assimilation of Precipitation Data into a Mesoscale Model. Weather Forecast. 2004, 19, 855–871. [Google Scholar] [CrossRef]
- Davolio, S.; Silvestro, F.; Gastaldo, T. Impact of rainfall assimilation on high-resolution hydrometeorological forecasts over Liguria, Italy. J. Hydrometeorol. 2017, 18, 2659–2680. [Google Scholar] [CrossRef]
- Torcasio, R.C.; Federico, S.; Comellas Prat, A.; Panegrossi, G.; D’Adderio, L.P.; Dietrich, S. Impact of Lightning Data Assimilation on the Short-Term Precipitation Forecast over the Central Mediterranean Sea. Remote Sens. 2021, 13, 682. [Google Scholar] [CrossRef]
- Comellas Prat, A.; Federico, S.; Torcasio, R.C.; Fierro, A.O.; Dietrich, S. Lightning data assimilation in the WRF-ARW model for short-term rainfall forecasts of three severe storm cases in Italy. Atmos. Res. 2021, 247, 105246. [Google Scholar] [CrossRef]
- Janjić, T.; Bormann, N.; Bocquet, M.; Carton, J.A.; Cohn, S.E.; Dance, S.L.; Losa, S.N.; Nichols, N.K.; Potthast, R.; Waller, J.A.; et al. On the representation error in data assimilation. Q. J. R. Meteor. Soc. 2017, 144, 1257–1278. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework. Meteor. Appl. 2008, 15, 51–64. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF, Version 4; No. NCAR/TN-556+STR, NCAR Technical Note; National Center for Atmospheric Research: Boulder, CO, USA, 2019; 145p. [Google Scholar]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Janjic, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res.-Space 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Crespi, A.; Brunetti, M.; Lentini, G.; Maugeri, M. 1961–1990 high-resolution monthly precipitation climatologies for Italy. Int. J. Clim. 2018, 38, 878–895. [Google Scholar] [CrossRef]
- H60 Users Manual. Available online: https://hsaf.meteoam.it/CaseStudy/GetDocumentUserDocument?fileName=saf_hsaf_atbd_60-63_1_0.pdf&tipo=ATBD (accessed on 13 May 2024).
- Sist, M.; Schiavon, G.; Del Frate, F. A New Data Fusion Neural Network Scheme for Rainfall Retrieval Using Passive Microwave and Visible/Infrared Satellite Data. Appl. Sci. 2021, 11, 4686. [Google Scholar] [CrossRef]
- Derrien, M.; Le Gléau, H. MSG/SEVIRI cloud mask and type from SAFNWC. Int. J. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- EUMETSAT. Cloud Mask Product User Guide. Available online: https://navigator.eumetsat.int/product/EO:EUM:DAT:MSG:CLM (accessed on 28 March 2024).
- Federico, S. Implementation of a 3D-Var system for atmospheric profiling data assimilation into the RAMS model: Initial results. Atmos. Meas. Tech. 2013, 6, 3563–3576. [Google Scholar] [CrossRef]
- Federico, S.; Torcasio, R.C.; Puca, S.; Vulpiani, G.; Comellas Prat, A.; Dietrich, S.; Avolio, E. Impact of Radar Reflectivity and Lightning Data Assimilation on the Rain- fall Forecast and Predictability of a Summer Convective Thunderstorm in Southern Italy. Atmosphere 2021, 12, 958. [Google Scholar] [CrossRef]
- Torcasio, R.C.; Papa, M.; Del Frate, F.; Dietrich, S.; Toffah, F.E.; Federico, S. Study of the Intense Meteorological Event Occurred in September 2022 over the Marche Region with WRF Model: Impact of Lightning Data Assimilation on Rainfall and Lightning Prediction. Atmosphere 2023, 14, 1152. [Google Scholar] [CrossRef]
- Marra, A.C.; Federico, S.; Montopoli, M.; Avolio, E.; Baldini, L.; Casella, D.; D’Adderio, L.P.; Dietrich, S.; Sanò, P.; Torcasio, R.C.; et al. The Precipitation Structure of the Mediterranean Tropical-Like Cyclone Numa: Analysis of GPM Observations and Numerical Weather Prediction Model Simulations. Remote Sens. 2019, 11, 1690. [Google Scholar] [CrossRef]
- Mascitelli, A.; Federico, S.; Fortunato, M.; Avolio, E.; Torcasio, R.C.; Realini, E.; Mazzoni, A.; Transerici, C.; Crespi, M.; Dietrich, S. Data assimilation of GNSS-ZTD into the RAMS model through 3D-Var: Preliminary results at the regional scale. Meas. Sci. Technol. 2019, 30, 055801. [Google Scholar] [CrossRef]
- Federico, S.; Torcasio, R.C.; Mascitelli, A.; Del Frate, F.; Dietrich, S. Preliminary Results of the AEROMET Project on the Assimilation of the Rain-Rate from Satellite Observations. In Computational Science and Its Applications—ICCSA 2022 Workshops; Gervasi, O., Murgante, B., Misra, S., Rocha, A.M.A.C., Garau, C., Eds.; ICCSA 2022, Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13380, Available online: https://www.doi.org/10.1007/978-3-031-10542-5_36 (accessed on 13 May 2024).
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Spectral Statis- tical Interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Davolio, S.; Ferretti, R.; Baldini, L.; Casaioli, M.; Cimini, D.; Ferrario, M.E.; Gentile, S.; Loglisci, N.; Maiello, I.; Manzato, A.; et al. The role of the Italian scientific community in the first HyMeX SOP: An outstanding multidisciplinary experience. Meteorol. Z. 2015, 24, 261–267. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmosph. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Gastaldo, T.; Poli, V.; Marsigli, C.; Cesari, D.; Alberoni, P.P.; Paccagnella, T. Assimilation of radar reflectivity volumes in a pre-operational framework. Quart. J. Roy. Meteor. Soc. 2021, 147, 1031–1054. [Google Scholar] [CrossRef]
- Craig, G.C.; Keil, C.; Leuenberger, D. Constraints on the impact of radar rainfall data assimilation on forecasts of cumulus convection. Quart. J. Roy. Meteor. Soc. 2012, 138, 340–352. [Google Scholar] [CrossRef]
- Emanuel, K.A. Atmospheric Convection; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Zimmer, M.; Craig, G.C.; Keil, C.; Wernli, H. 2011: Classification of precipitation events with a convective response timescale and their forecasting characteristics. Geophys. Res. Lett. 2011, 38, L05802. [Google Scholar] [CrossRef]
- Zeng, Y.; Janji’c, T.; Sommer, M.; de Lozar, A.; Blahak, U.; Seifert, A. Representation of model error in convective-scale data assimilation: Additive noise based on model truncation error. J. Adv. Model. Earth Syst. 2019, 11, 752–770. [Google Scholar] [CrossRef]





| Simulation Type | Rain Rate Assimilation | Assimilated Product | Minimum Threshold for the Assimilation |
|---|---|---|---|
| CTRL | No | None | None |
| NN_3th | Yes | Rain rate derived from neural network | 3 mm/h |
| NN_1th | Yes | Rain rate derived from neural network | 1 mm/h |
| H60_3th | Yes | Rain rate derived from HSAF H60 product | 3 mm/h |
| Summer 2022 | |
| June | 7; 8; 9; 10; 17 |
| July | 7; 8; 26; 27; 29 |
| August | 9; 12; 17; 18; 19 |
| Fall 2022 | |
| September | 15; 17; 22; 24; 25; 26; 29; 30 |
| October | 10; 13 |
| November | 4; 15; 16; 19; 22; 26; 29 |
| NN | Time | Total Samples | Training Samples | Validation Samples | Test Samples |
|---|---|---|---|---|---|
| NN1 | day | 24,471 | 17,129 | 3671 | 3671 |
| NN1 | night | 22,512 | 15,758 | 3377 | 3377 |
| NN2 | day | 8516 | 5960 | 1278 | 1278 |
| NN2 | night | 7774 | 5441 | 1167 | 1166 |
| Forecast | |||
|---|---|---|---|
| Yes | No | ||
| Observation | Yes | a | c |
| No | b | d | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torcasio, R.C.; Papa, M.; Del Frate, F.; Mascitelli, A.; Dietrich, S.; Panegrossi, G.; Federico, S. Data Assimilation of Satellite-Derived Rain Rates Estimated by Neural Network in Convective Environments: A Study over Italy. Remote Sens. 2024, 16, 1769. https://doi.org/10.3390/rs16101769
Torcasio RC, Papa M, Del Frate F, Mascitelli A, Dietrich S, Panegrossi G, Federico S. Data Assimilation of Satellite-Derived Rain Rates Estimated by Neural Network in Convective Environments: A Study over Italy. Remote Sensing. 2024; 16(10):1769. https://doi.org/10.3390/rs16101769
Chicago/Turabian StyleTorcasio, Rosa Claudia, Mario Papa, Fabio Del Frate, Alessandra Mascitelli, Stefano Dietrich, Giulia Panegrossi, and Stefano Federico. 2024. "Data Assimilation of Satellite-Derived Rain Rates Estimated by Neural Network in Convective Environments: A Study over Italy" Remote Sensing 16, no. 10: 1769. https://doi.org/10.3390/rs16101769






