Shaking Tables Test on Seismic Responses of a Long-Span Rigid-Framed Bridge Considering Traveling Wave Effect and Soil–Structure Interaction
Abstract
:1. Introduction
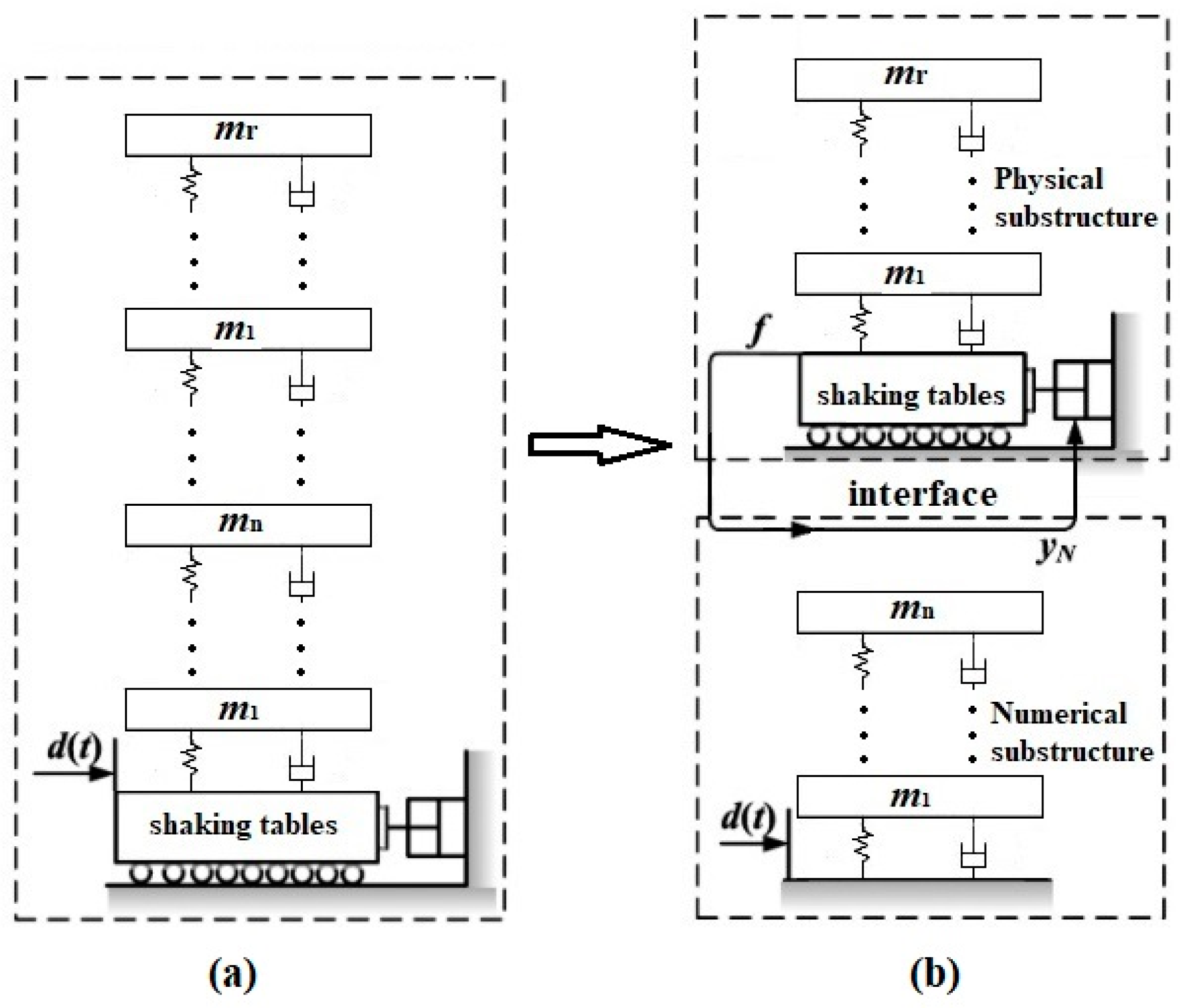
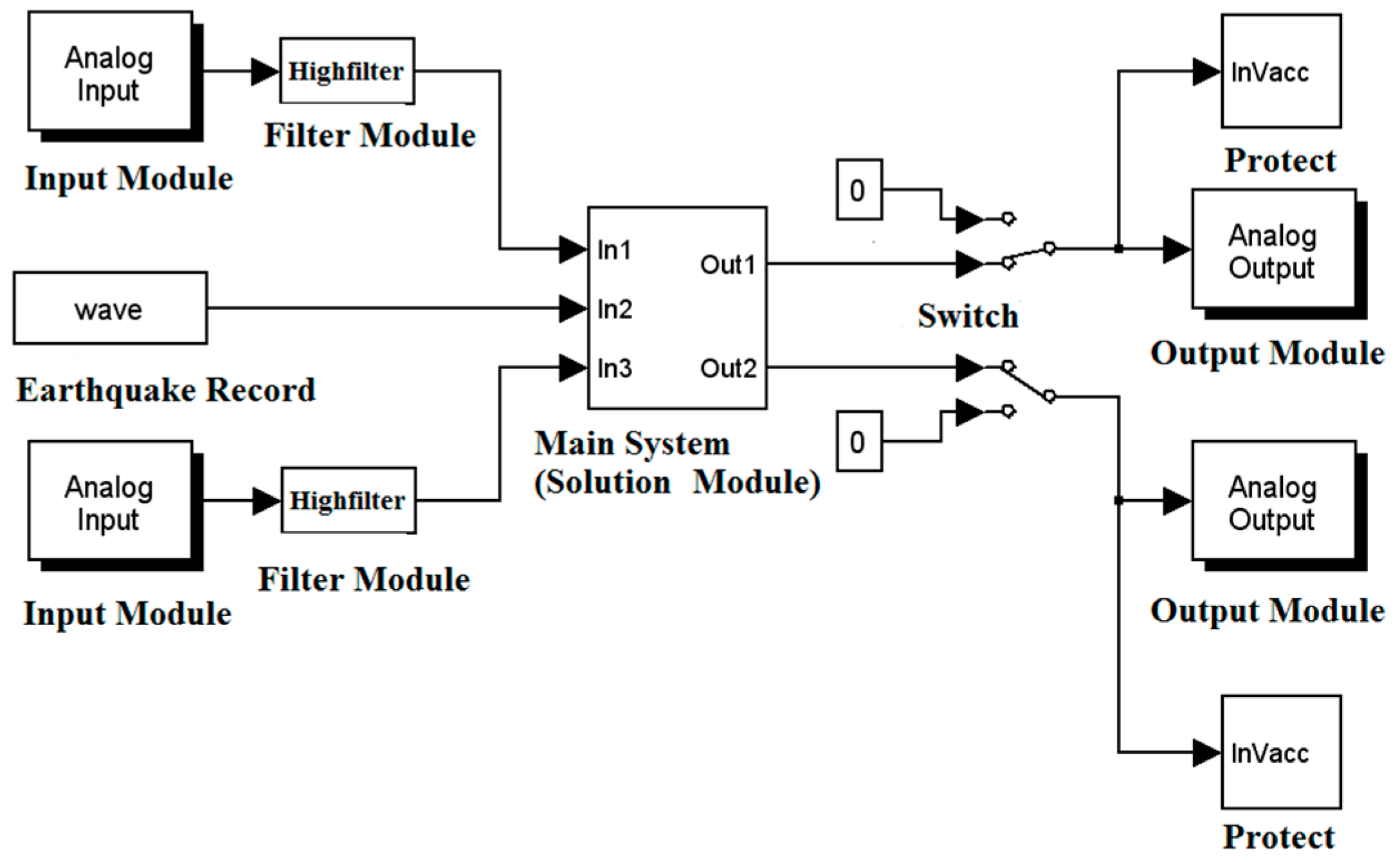
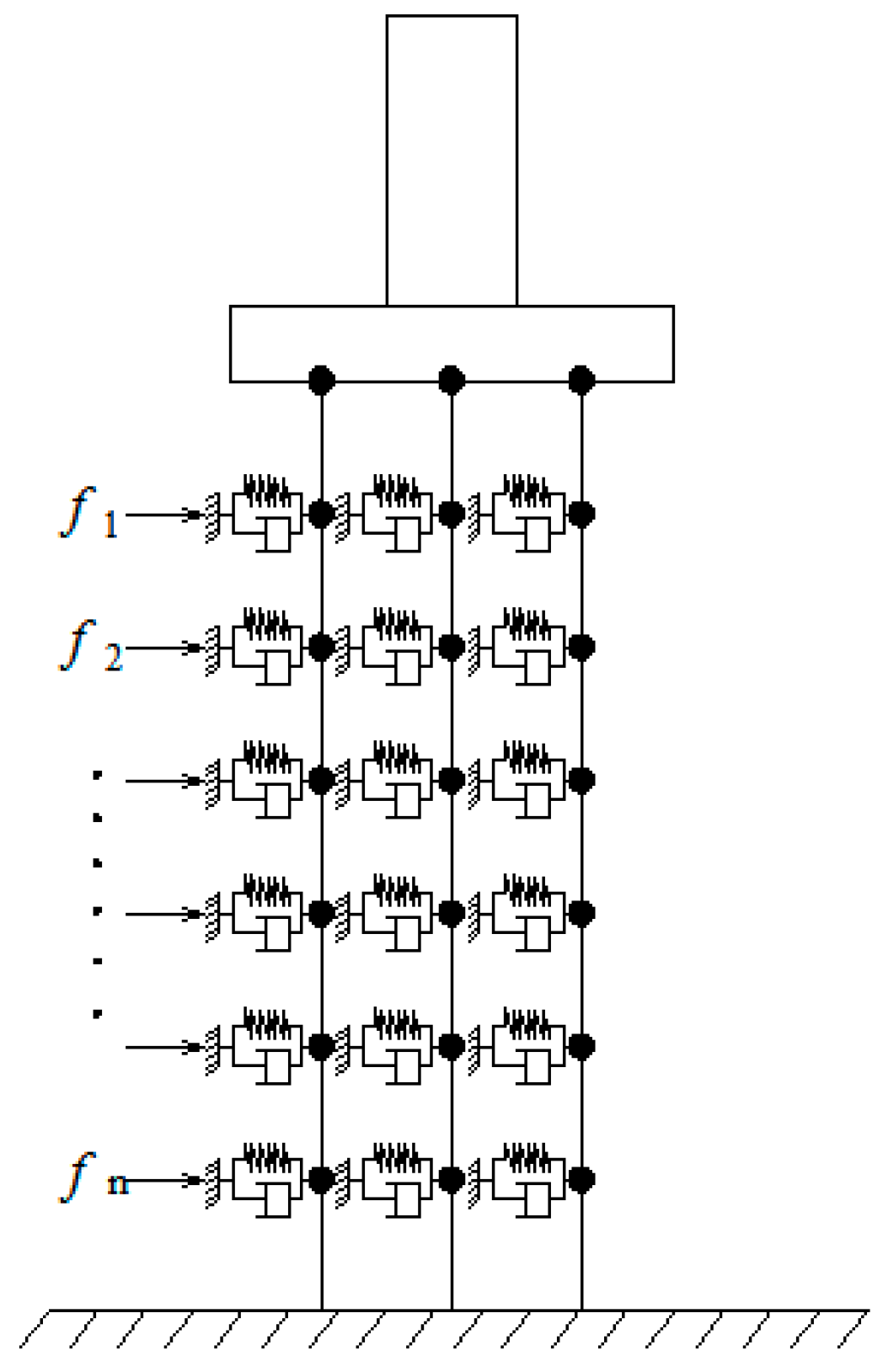
2. Substructure Hybrid Test Method for Soil–Structure Interaction
- Measuring the relative velocity and displacement of the bottom layer of the physical substructure to calculate the sum of bottom layer damping force and elastic restoring force;
- Measuring the strain of the bottom components of the physical substructure to determine the interface force, leveraging the linear relationship between interface force and strain;
- Installing sensors between the physical substructure and the shaking table to directly measure the interface force;
- Utilizing acceleration measurements of the specimen to calculate the total inertial force and subsequently derive the interface force.
3. Experiment Design
3.1. Model Design
3.1.1. Bridge Specimen
3.1.2. Construction
3.1.3. Soil Model Used in the Test
3.1.4. Instrumentation
3.1.5. Testing Schedule
4. Experimental Results and Discussion
4.1. Effect of Traveling Wave on Seismic Response
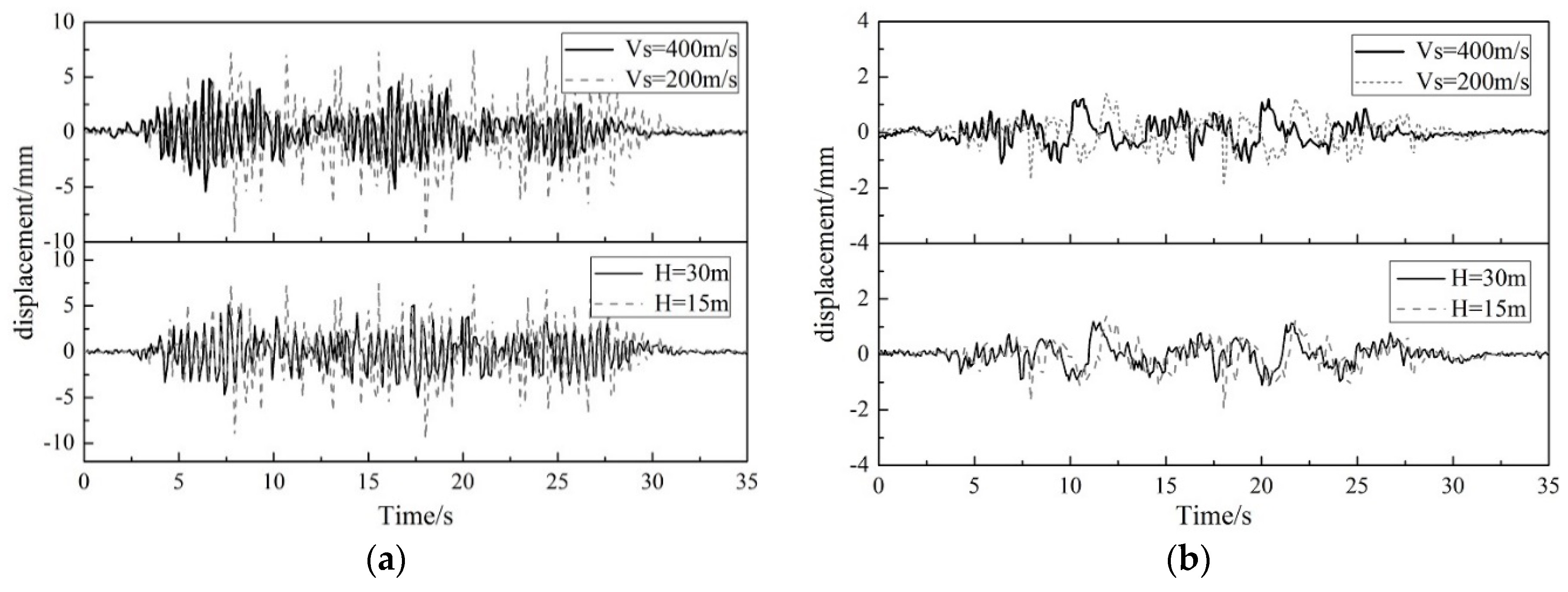
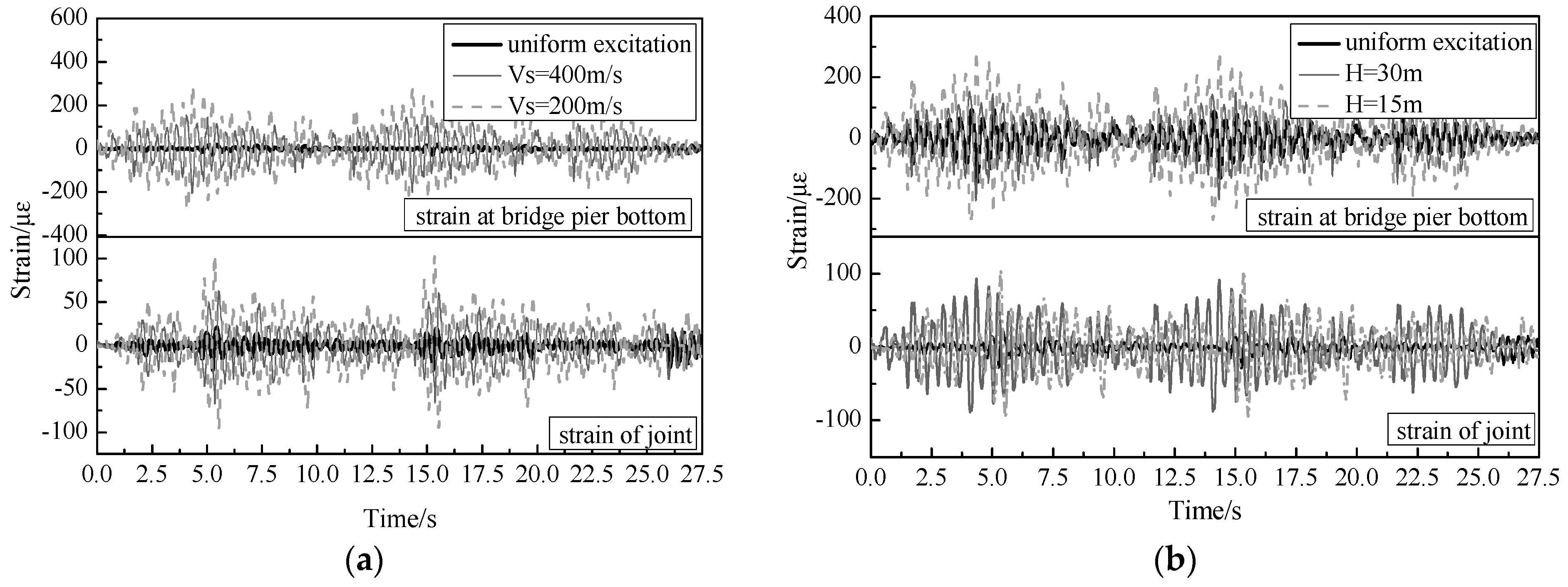
4.2. Effect of Soil–Structure Interaction on Seismic Response
4.2.1. Input Ground Motion
4.2.2. Displacement Response
4.2.3. Strain Response
4.3. Effect of Traveling Wave and Soil–Structure Interaction on Seismic Response
5. Conclusions
- (1)
- The seismic responses of the rigid-framed bridge could be increased by the traveling wave effect, when the apparent wave speed was small. The deformation of the pier and the strain at the bridge pier bottom were reduced as the apparent velocity increased, and then become almost the same to the dynamic response under uniform excitation. The apparent velocity and the constraint condition types had an influence on the traveling wave effect, and the seismic responses of the bottom of the pier were more sensitive to the traveling wave effect than the seismic responses of the joints.
- (2)
- There are many changes in the peak and spectrum characters of seismic input at the pier bottoms after considering the SSI, which result in a decrease in the predominant frequency and an increase in the peak of inputting acceleration. The SSI effect increased the seismic responses of the rigid-framed bridge, such as the deformation of bridge piers and the loading of pier bottoms, as well as the loading of clamped beam-pier joints. The velocity of shear waves and the thickness of soil layers were two important factors affecting SSI effects.
- (3)
- There is phase difference in the dynamic response, and the maximum value does not occur at the same time considering the coupling effect, traveling wave effects and SSI in the dynamic response of the continuous rigid-framed bridges. Consequently, its dynamic response amplitude is not a simple superposition of the dynamic response amplitudes under the separate action of the traveling wave effect and SSI.
- (4)
- The real-time substructure test method solved three problems. The traditional soil box experiment can be applied to the test of the large-scale model, the soil and bridge structure can meet the unified similarity ratio, and the boundary conditions can be simulated accurately. This provides a feasible method for the study of the SSI effect on long-span bridges.
- (5)
- In this paper, the bridge structure was considered as a physical substructure and the soil as a numerical substructure. And a simplified soil model applied by many scholars was used. It is well known that soils are highly dispersive, which poses a challenge for accurate simulations. This factor has a large impact on the accuracy of experimental results. Therefore, future research will focus on improving the soil model for more accurate simulations.
- (6)
- The spatial effect of ground vibration has various influencing factors, including the travelling wave effect, local site effect and coherence effect. In this paper, only the influence of the travelling wave effect was considered separately, and the influence of local site effect and coherence effect as well as their coupling with SSI effect will be further considered in the future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Huang, Y.; Guo, E. Recent advances on bridge seismic research from the 17th World Conference on Earthquake Engineering. Earthq. Eng. Eng. Dyn. 2022, 45, 26–39. (In Chinese) [Google Scholar]
- Jia, J.-F.; Wei, B.; Du, X.-L.; Guo, B.-L.; Guo, H. Research progress of seismic resilient girder bridges at home and aborad from WCEE. J. Traffic Transp. Eng. 2022, 22, 25–46. (In Chinese) [Google Scholar]
- Crespi, P.; Zucca, M.; Valente, M. On the collapse evaluation of existing RC bridges exposed to corrosion under horizontal loads. Eng. Fail. Anal. 2020, 116, 104727. [Google Scholar] [CrossRef]
- Crespi, P.; Zucca, M.; Valente, M.; Longarini, N. Influence of corrosion effects on the seismic capacity of existing RC bridges. Eng. Fail. Anal. 2022, 140, 106546. [Google Scholar] [CrossRef]
- Bonganoff, J.L.; Goldberg, J.E.; Schiff, A.J. The effect of ground transmission time on the response of long structures. Bull. Seismol. Soc. Am. 1965, 55, 627–640. [Google Scholar]
- Zhao, T.L.; Li, X.M.; Du, Y.F. Nonstationary elastoplastic response analysis of curved beam bridges under spatial variability of earthquake ground motion using absolute displacement method. Soil Dyn. Earthq. Eng. 2024, 181, 108626. [Google Scholar] [CrossRef]
- Parvanehro, P.; Shiravand, M.R.; Safi, M. A method for linear response analysis of long bridges under multi-support seismic excitation. Bull. Earthq. Eng. 2022, 20, 8381–8410. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Chen, X.; Wang, Y. Seismic response of the long-span steel truss arch bridge with the thrust under multidimensional excitation. Railw. Sci. 2022, 1, 40–55. [Google Scholar] [CrossRef]
- Shi, Y.; Fan, S.; Liu, C.; Lu, L.; Zuo, C.; Sun, X. Study on multidimensional and multipoint seafloor spatial ground motion simulation under an ice-water layer and the dynamic response of a cross-sea bridge. Ocean Eng. 2023, 281, 114901. [Google Scholar] [CrossRef]
- Li, X.; Jia, H.; Li, Q. Experimental study on long-span curved rigid frame bridge under near-fault ground motion. Vib. Shock 2017, 36, 199–207, 237. [Google Scholar]
- Cheng, M.; Li, Q.; Yan, L. Experimental study on seismic response of irregular high-pier curved bridge under multi-point excitation. J. Vib. Eng. 2016, 29, 874–880. [Google Scholar]
- Sextos, A.G.; Taskari, O. Influence of seismic wave angle of incidence over the response of long curved bridges considering soil-structure interaction. Dyn. Response Infrastruct. Environ. Induc. Loads 2017, 2, 1–17. [Google Scholar]
- Sung, Y.C.; Chao, K.H.; Chen, C.C.; Liu, X.Q.; Su, C.K. Effect of Soil–Structure Interaction on Inelastic Displacement Ratios of Bridge Structures Subjected to Pulse-Like Ground Motions. Int. J. Struct. Stab. Dyn. 2024, 24, 2450059. [Google Scholar] [CrossRef]
- Das, S.; Sil, A.; Naveen, B.P. Effects of Soil-Structure Interaction on Seismic Fragility of Railway Concrete Bridge, in India. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 353–372. [Google Scholar] [CrossRef]
- Roy, S.D.; Pandey, A.; Saha, R. Shake table study on seismic soil-pile foundation-structure interaction in soft clay. Structures 2021, 29, 1229–1241. [Google Scholar]
- Abd-Elhamed, A.; Mahmoud, S. Simulation analysis of TMD controlled building subjected to far- and near-fault records considering soil-structure interaction. J. Build. Eng. 2019, 26, 100930. [Google Scholar] [CrossRef]
- Tochaei, E.N.; Taylor, T.; Ansari, F. Effects of near-field ground motions and soil-structure interaction on dynamic response of a cable-stayed bridge. Soil Dyn. Earthq. Eng. 2020, 133, 106115. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Q.; Zhang, R.; Pan, C.; Jiang, Y. Optimal design of an inerter isolation system considering the soil condition. Eng. Struct. 2019, 196, 109324. [Google Scholar] [CrossRef]
- Xu, C.; Dou, P.; Du, X.; El Naggar, M.H.; Miyajima, M.; Chen, S. Seismic performance of pile group-structure system in liquefiable and non-liquefiable soil from large-scale shake table tests-ScienceDirect. Soil Dyn. Earthq. Eng. 2020, 138, 106299. [Google Scholar] [CrossRef]
- Xu, C.; Dou, P.; Du, X.; El Naggar, M.H.; Miyajima, M.; Chen, S. Large shaking table tests of pile-supported structures in different ground conditions. Soil Dyn. Earthq. Eng. 2020, 139, 106307. [Google Scholar] [CrossRef]
- Gallo, M.; Tomeo, R.; Nigro, E. The soil-structure interaction effect on the seismic vulnerability assessment and retrofitting of existing bridges. Procedia Struct. Integr. 2023, 44, 618–625. [Google Scholar] [CrossRef]
- Durante, M.G.; Di Sarno, L.; Mylonakis, G.; Taylor, C.A.; Simonelli, A.L. Soil-pile-structure interaction:Experimental outcomes from shaking table tests. Earthq. Eng. Struct. Dyn. 2016, 45, 1041–1047. [Google Scholar] [CrossRef]
- Yang, J.; Li, P.; Wu, W. Shaking Table Tests on Dynamic Characteristics of Pile-Soil-High Rise Structure System on Soft Soil Foundation. J. Tongji Univ. (Nat. Sci.) 2023, 51, 578–587. [Google Scholar]
- Tang, Z.; Dietz, M.; Hong, Y.; Li, Z. Performance extension of shaking table-based real-time dynamic hybrid testing through full state control via simulation. Struct. Control Health Monit. 2020, 27, e2611. [Google Scholar] [CrossRef]
- Tang, Z.; Dong, X.; Li, Z.; Du, X. Implementation of Real Time Hybrid Simulation Based on GPU Computing. Struct. Des. Tall Spec. Build. 2021, 31, e1942. [Google Scholar]
- Li, Z. Theory and Technology of Engineering Structure Testing; Tianjin University Press: Tianjin, China, 2004. [Google Scholar]
- Zhang, G. Structural Testing of Bridges; People’s Transportation Press: Beijing, China, 2002. [Google Scholar]
- Penzien, J.; Scheffey, C.F.; Parmelee, R.A. Seismic analysis of bridges on long piles. J. Eng. Mech. Div. 1964, 90, 223–254. [Google Scholar] [CrossRef]
- JTG/T 2231-01-20; Specifications for Seismic Design of Highway Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020.
- GB50011-2016; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development, People’s Republic of China: Beijing, China, 2016.









| Test ID | Wave Form | Peak Amplitude | Accessories Description |
|---|---|---|---|
| Case 1 | White noise | 0.05 g | |
| Case 2 | El-Centro Record | 0.385/1.1/1.5 g | Uniform excitation/Traveling wave excitation |
| Case 3 | Wenchuan Record | 0.385/1.1/1.5 g | Uniform excitation/Traveling wave excitation |
| Case 4 | Beijing Record | 0.385/1.1/1.5 g | Uniform excitation/Traveling wave excitation |
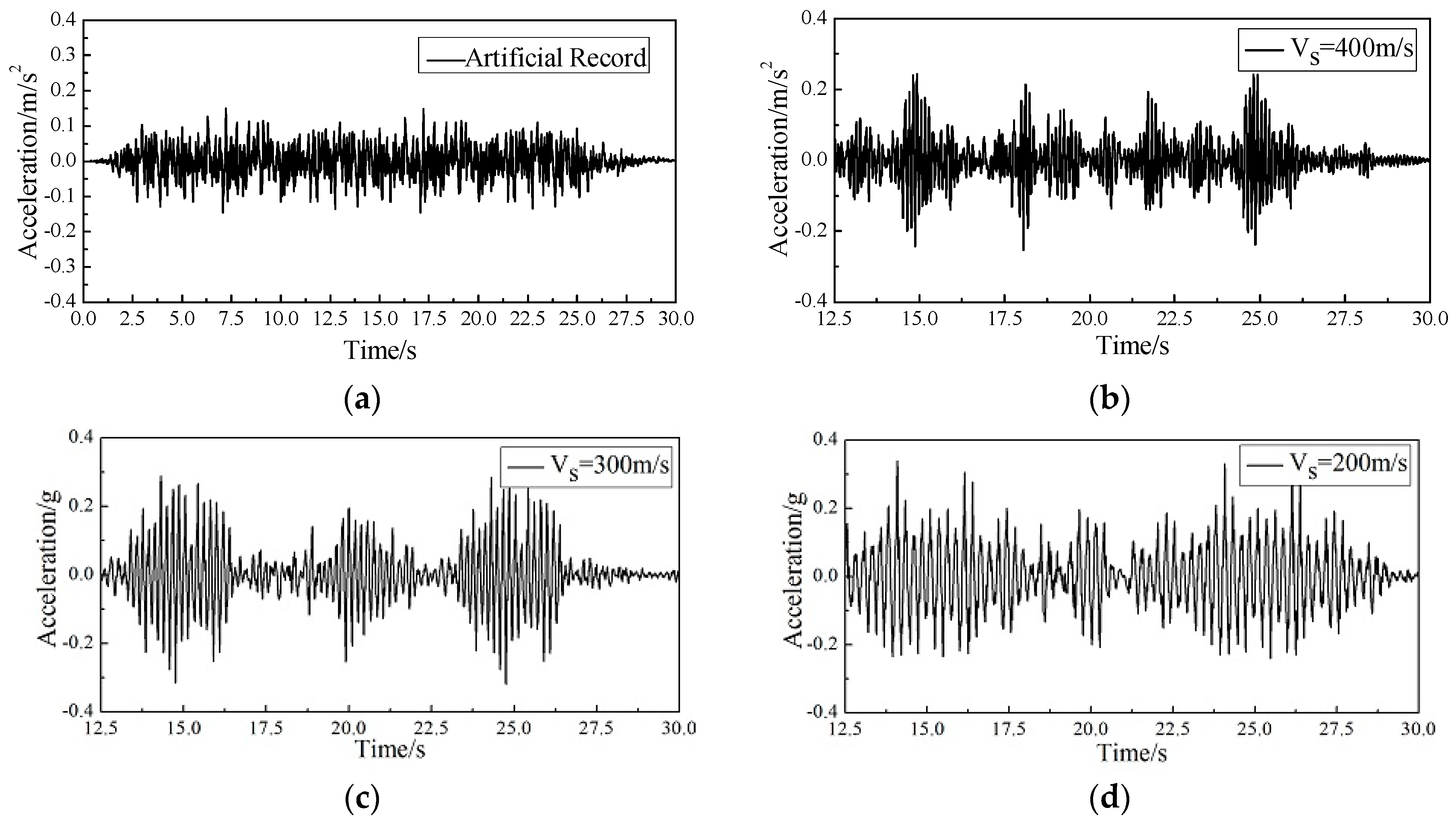
| Case 5 | Artificial wave I | 0.15 g | Shear wave velocity: 400 m/s, 300 m/s, 200 m/s |
| Case 6 | Artificial wave II | 0.15 g | Shear wave velocity: 400 m/s, 300 m/s, 200 m/s |
| Case 7 | Artificial wave III | 0.15 g | Shear wave velocity: 400 m/s, 300 m/s, 200 m/s |
| Groups for Seismic Design | Site Category | ||||
|---|---|---|---|---|---|
| I0 | I1 | II | III | IV | |
| The first group | 0.20 | 0.25 | 0.35 | 0.45 | 0.65 |
| The second group | 0.25 | 0.30 | 0.40 | 0.55 | 0.75 |
| The third group | 0.30 | 0.35 | 0.45 | 0.65 | 0.90 |
| Seismic Response | Pier 1 | Pier 2 | Pier 3 | Pier 4 | |||
|---|---|---|---|---|---|---|---|
Apparent Velocity | Stain at Pier Bottom/με | Stain at Pier Bottom/με | Displacement /mm | Stain at Pier Bottom/με | Displacement /mm | Stain at Pier Bottom/με | |
| Uniform excitation | El-Centro Record | 29.4 | 100.0 | 1.432 | 1.4 | 1.664 | 33.2 |
| Wenchuan Record | 67.9 | 155.0 | 3.864 | 165.0 | 4.183 | 73.8 | |
| Beijing Record | 66.9 | 163.7 | 6.732 | 209.0 | 6.656 | 78.8 | |
| 600 m/s | El-Centro Record | 30.8 | 104.4 | 1.498 | 133.2 | 1.692 | 34.5 |
| Wenchuan Record | 69.4 | 160.5 | 3.951 | 165.9 | 4.342 | 77.5 | |
| Beijing Record | 68.9 | 171.9 | 7.01 | 214.0 | 6.787 | 80.6 | |
| 400 m/s | El-Centro Record | 33.7 | 115.2 | 1.676 | 135.7 | 1.781 | 37.0 |
| Wenchuan Record | 74.0 | 172.2 | 4.232 | 171.0 | 4.838 | 79.1 | |
| Beijing Record | 74.7 | 191.7 | 7.228 | 226.1 | 7.197 | 86.6 | |
| 200 m/s | El-Centro Record | 41.3 | 139.9 | 1.829 | 141.4 | 1.847 | 46.3 |
| Wenchuan Record | 83.1 | 196.1 | 5.371 | 176.7 | 5.455 | 84.2 | |
| Beijing Record | 83.3 | 248.6 | 7.779 | 280.4 | 7.804 | 87.4 | |
| 100 m/s | El-Centro Record | 60.9 | 187.7 | 2.278 | 190.7 | 3.434 | 65.7 |
| Wenchuan Record | 106.8 | 225.7 | 6.253 | 226.6 | 6.229 | 110.5 | |
| Beijing Record | 135.7 | 341.0 | 8.501 | 344.6 | 8.761 | 143.3 | |
| Seismic Response | Strain of Joint 1 /με | Strain of Joint 2 /με | |
|---|---|---|---|
| Apparent Velocity | |||
| Uniform excitation | El-Centro Record | 31.6 | 18.1 |
| Wenchuan Record | 40.1 | 23.4 | |
| Beijing Record | 45.8 | 32.3 | |
| 400 m/s | El-Centro Record | 31.8 | 18.2 |
| Wenchuan Record | 40.3 | 23.6 | |
| Beijing Record | 46.1 | 33.2 | |
| 200 m/s | El-Centro Record | 32.9 | 20.3 |
| Wenchuan Record | 42.4 | 25.7 | |
| Beijing Record | 49.9 | 37.9 | |
| 100 m/s | El-Centro Record | 38.2 | 26.0 |
| Wenchuan Record | 58.5 | 35.7 | |
| Beijing Record | 74.2 | 52.8 |
| Characteristic Period/s | Shear Wave Velocity/m/s | Thickness of the Overburden/m | Displacement of Pier 3/mm | Displacement of Pier 2/mm | Deflection of Girder/mm |
|---|---|---|---|---|---|
| 0.25 | 400 | 15 | 4.831 | 3.202 | 1.006 |
| 0.4 | 5.919 | 4.469 | 1.094 | ||
| 0.65 | 7.378 | 4.375 | 1.564 | ||
| 0.25 | 300 | 15 | 5.617 | 3.263 | 1.161 |
| 0.4 | 11.757 | 6.159 | 1.244 | ||
| 0.65 | 10.486 | 6.333 | 1.640 | ||
| 0.25 | 200 | 30 | 5.112 | 3.428 | 1.190 |
| 0.4 | 9.454 | 5.464 | 1.273 | ||
| 0.65 | 8.263 | 5.693 | 1.587 | ||
| 0.25 | 15 | 7.509 | 4.648 | 1.405 | |
| 0.4 | 11.481 | 7.539 | 1.306 | ||
| 0.65 | 11.448 | 8.449 | 1.772 |
| Characteristic Period/s | Shear Wave Velocity/m/s | Thickness of Overburden/m | Strain at Pier 2 Bottom/με | Strain at Pier 3 Bottom/με | Strain at Mid-Span of Girder/με | Strain of Joint 1/με | Strain of Joint 2/με |
|---|---|---|---|---|---|---|---|
| 0.25 | Uniform excitation | 142.6 | 138.1 | 9.1 | 28.6 | 28.3 | |
| 0.4 | 161.8 | 141.3 | 10.466 | 37.8 | 38.0 | ||
| 0.65 | 221.4 | 155.4 | 15.3 | 49.4 | 48.0 | ||
| 0.25 | 400 | 15 | 205.5 | 166.1 | 16.4 | 66.7 | 60.5 |
| 0.4 | 261.3 | 229.2 | 18.1 | 91.1 | 84.7 | ||
| 0.65 | 291.4 | 219.5 | 18.2 | 96.0 | 86.3 | ||
| 0.25 | 300 | 15 | 210.1 | 244.6 | 18.2 | 78.5 | 70.3 |
| 0.4 | 285.5 | 237.9 | 19.4 | 111.2 | 122.3 | ||
| 0.65 | 318.3 | 292.4 | 18.3 | 107.7 | 137.6 | ||
| 0.25 | 200 | 30 | 216.4 | 263.5 | 18.9 | 92.9 | 97.3 |
| 0.4 | 394.2 | 303.1 | 21.1 | 113.2 | 148.8 | ||
| 0.65 | 382.5 | 313.9 | 20.9 | 138.2 | 179.2 | ||
| 0.25 | 15 | 284.3 | 282.7 | 20.9 | 104.2 | 124.8 | |
| 0.4 | 410.1 | 401.0 | 22.6 | 163.5 | 174.4 | ||
| 0.65 | 442.1 | 443.9 | 21.4 | 157.7 | 204.8 | ||
| Seismic Response | Pier 2 | Pier 3 | Joint 1 | Joint 2 | ||||
|---|---|---|---|---|---|---|---|---|
| Test Schedule | Displacement /mm | Strain /με | Displacement /mm | Strain /με | Strain /με | Strain /με | ||
| Uniform excitation | 2.514 | 142.6 | 3.716 | 138.1 | 28.6 | 28.3 | ||
| Traveling wave effect | apparent velocity 200 m/s | 3.217 | 174.3 | 4.468 | 170.5 | 34.0 | 34.7 | |
| apparent velocity 100 m/s | 3.571 | 218.4 | 5.328 | 202.0 | 42.5 | 41.7 | ||
| SSI effect | Vs = 400 m/s | 3.202 | 205.5 | 4.831 | 166.1 | 66.7 | 60.5 | |
| Vs = 200 m/s | 4.648 | 284.3 | 7.509 | 282.7 | 104.2 | 124.8 | ||
| Both of them | apparent velocity 200 m/s | Vs = 400 m/s | 5.311 | 316.5 | 8.045 | 302.9 | 82.4 | 85.7 |
| Vs = 200 m/s | 6.812 | 352.8 | 10.542 | 377.7 | 123.1 | 134.0 | ||
| apparent velocity 100 m/s | Vs = 400 m/s | 6.213 | 381.5 | 8.579 | 331.3 | 115.3 | 99.2 | |
| Vs = 200 m/s | 7.297 | 419.0 | 10.654 | 445.5 | 143.8 | 149.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.-Y.; Cao, S.-S.; Zhao, Z. Shaking Tables Test on Seismic Responses of a Long-Span Rigid-Framed Bridge Considering Traveling Wave Effect and Soil–Structure Interaction. Buildings 2024, 14, 1432. https://doi.org/10.3390/buildings14051432
Yan X-Y, Cao S-S, Zhao Z. Shaking Tables Test on Seismic Responses of a Long-Span Rigid-Framed Bridge Considering Traveling Wave Effect and Soil–Structure Interaction. Buildings. 2024; 14(5):1432. https://doi.org/10.3390/buildings14051432
Chicago/Turabian StyleYan, Xiao-Yu, Shan-Shan Cao, and Zhuo Zhao. 2024. "Shaking Tables Test on Seismic Responses of a Long-Span Rigid-Framed Bridge Considering Traveling Wave Effect and Soil–Structure Interaction" Buildings 14, no. 5: 1432. https://doi.org/10.3390/buildings14051432




