Deformation of Existing Shield Tunnel Adjacent to Deep Excavations: Simulation and Monitoring Analysis
Abstract
:1. Introduction
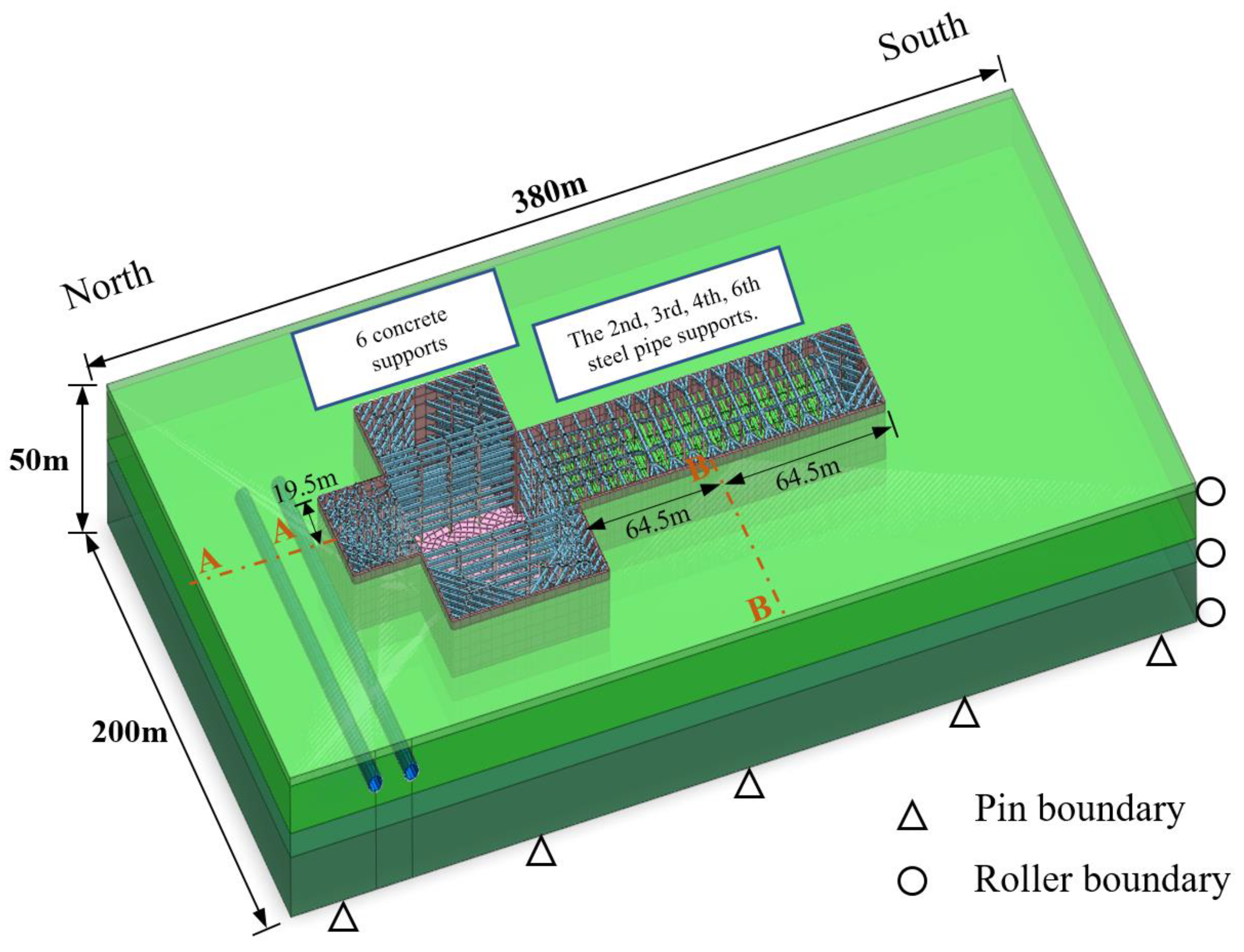
2. Engineering Background
3. Numerical Simulation
3.1. Description of the FE Model
3.2. Model Parameters
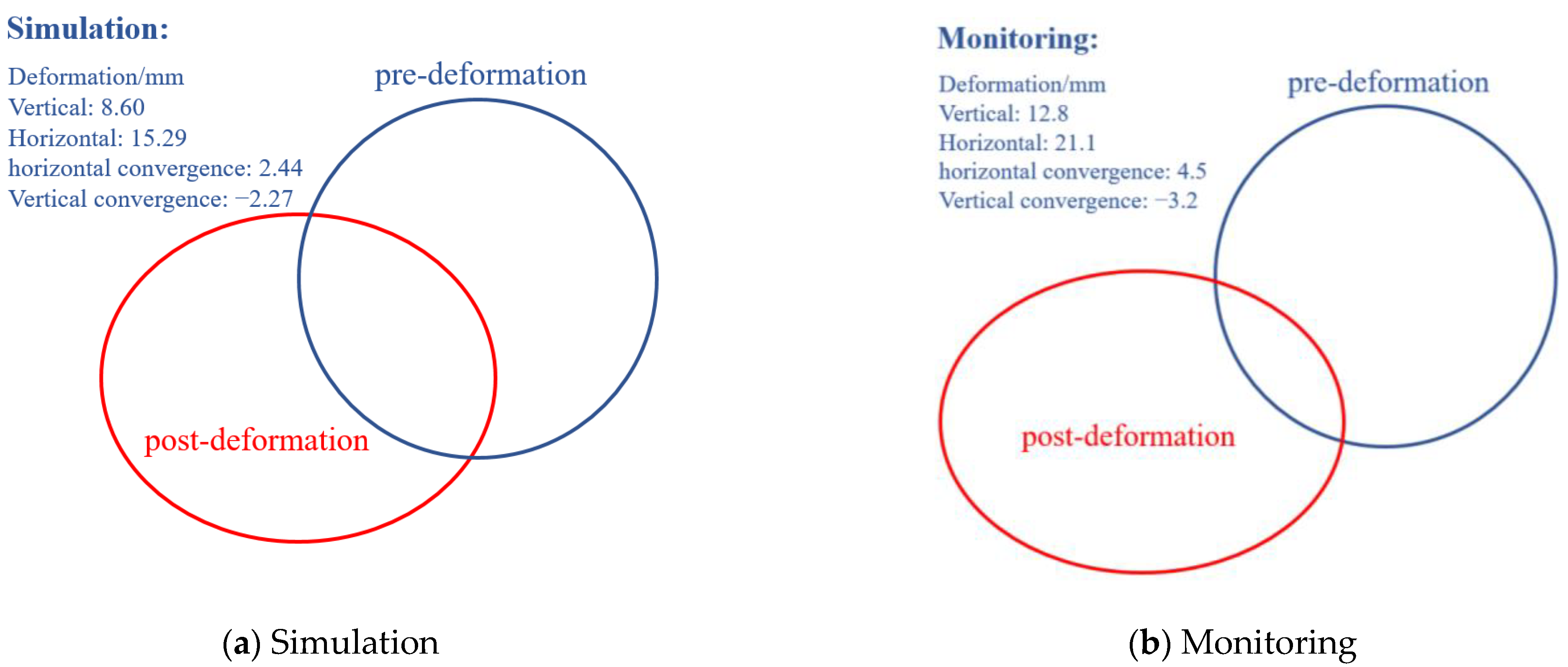
3.3. Model Validation
4. Simulation Results
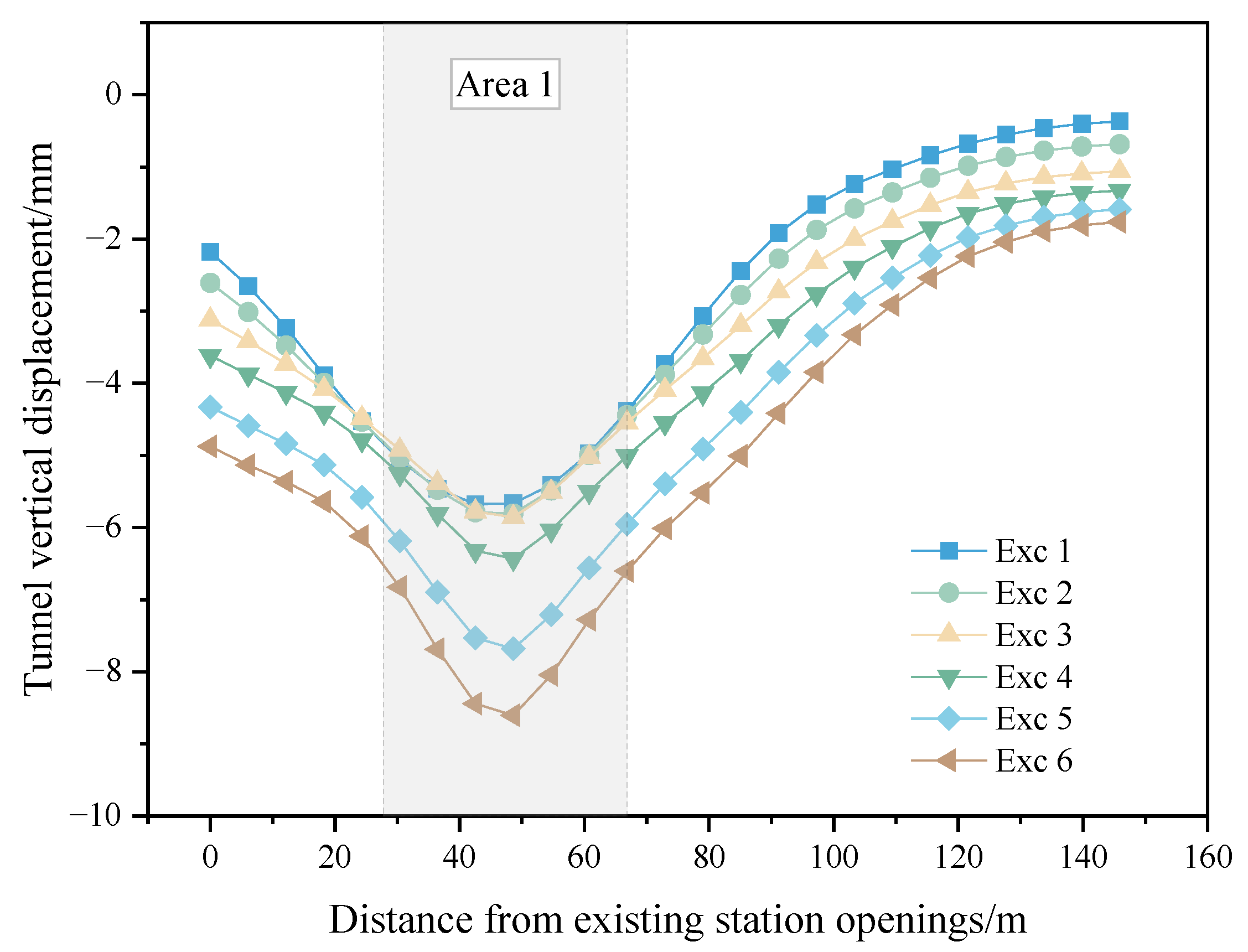
4.1. Tunnel Vertical Displacement
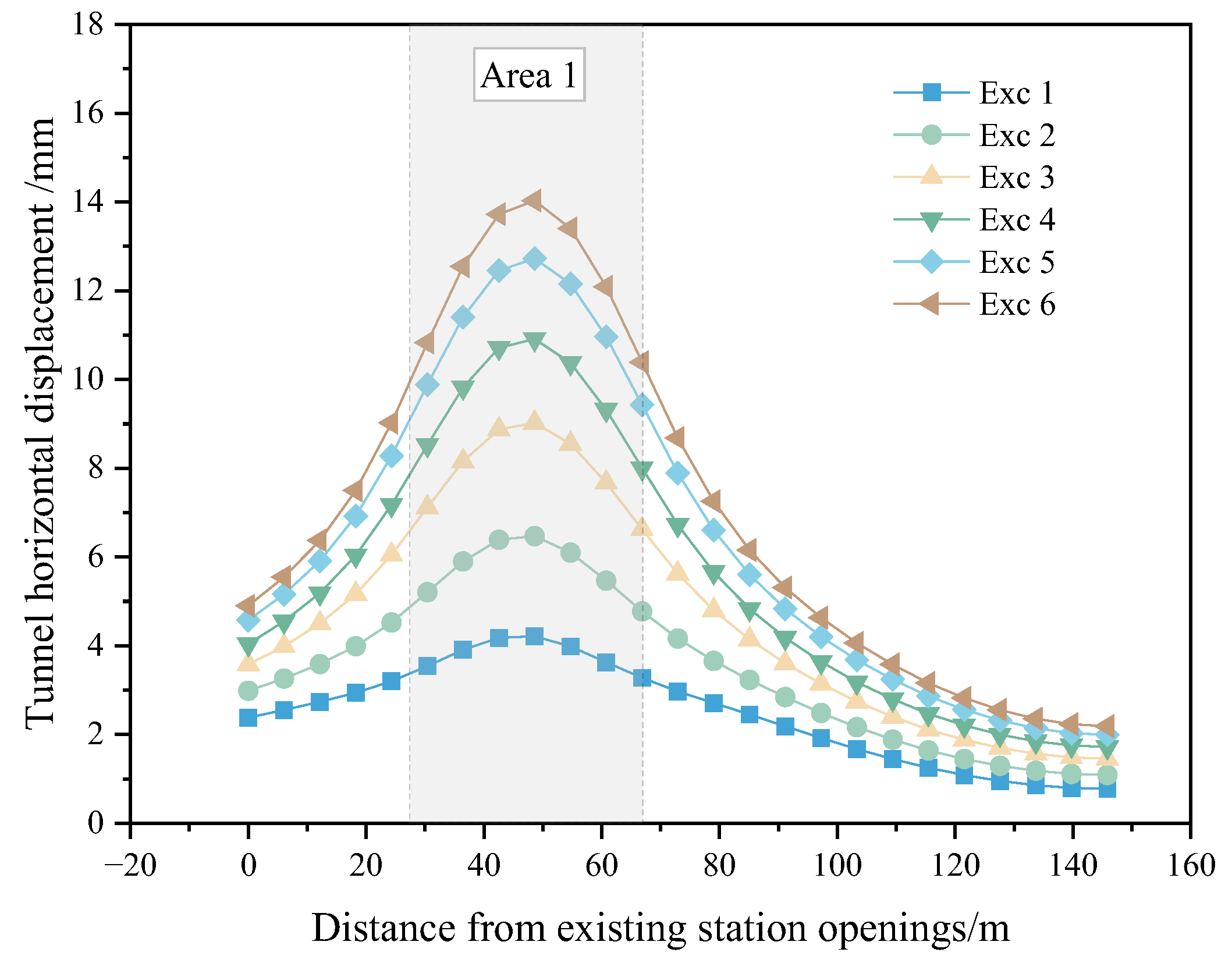
4.2. Tunnel Horizontal Displacement
4.3. Ground Displacement
5. Analysis of Factors Affecting Tunnel Deformation
5.1. Time Series Analysis of Field Measurements
5.2. Enclosure Deformation Pattern Effects
5.3. Sensitivity Analysis of Enclosure Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, J.T.; Jiang, J.; Zhou, X.J.; Zhang, Y.F.; Pan, Y.D. Analytical solution for evaluating deformation response of existing metro tunnel due to excavation of adjacent foundation pit. J. Cent. South Univ. 2021, 28, 1888–1900. [Google Scholar] [CrossRef]
- Quan, Y.; Tan, X.; Hu, Z.G.; Huang, M.H. Measurement and Analysis of Deformation of Underlying Tunnel Induced by Foundation Pit Excavation. Adv. Civ. Eng. 2023, 2023, 8897139. [Google Scholar] [CrossRef]
- Bian, X.C.; Hu, H.Q.; Zhao, C.; Ye, J.N.; Chen, Y.M. Protective effect of partition excavations of a large-deep foundation pit on adjacent tunnels in soft soils: A case study. Bull. Eng. Geol. Environ. 2021, 80, 5693–5707. [Google Scholar] [CrossRef]
- Dong, X.; Mei, L.; Yang, S.Y.; He, L. Deformation Response Research of the Existing Subway Tunnel Impacted by Adjacent Foundation Pit Excavation. Adv. Mater. Sci. Eng. 2021, 2021, 5121084. [Google Scholar] [CrossRef]
- Lu, C.R.; Huang, L. Study on the Effect of Foundation Pit Excavation on the Deformation of Adjacent Shield Tunnel. Adv. Civ. Eng. 2022, 2022, 8441758. [Google Scholar] [CrossRef]
- Wang, C.W.; Sun, H.S.; Zhang, J.H.; Lu, Y. Influence of Foundation Pit Excavation on Tunnels at Different Locations. Shock. Vib. 2022, 2022, 4282253. [Google Scholar] [CrossRef]
- Yu, Z.T.; Wang, H.Y.; Wang, W.J.; Ling, D.S.; Zhang, X.D.; Wang, C.; Qu, Y.H. Experimental and Numerical Investigation on the Effects of Foundation Pit Excavation on Adjacent Tunnels in Soft Soil. Math. Probl. Eng. 2021, 2021, 5587857. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, X.H.; Zhang, S.J.; Huang, F.; Xiao, H.; Ma, H.Z.; Luo, L.N.; Bao, H. Response Monitoring and Analysis in Deep Foundation Pit Excavation: A Case Study in Soft Soil at Subway Tunnel Intersections. Buildings 2023, 13, 1286. [Google Scholar] [CrossRef]
- Wei, G. Measurement and analysis of impact of foundation pit excavation on below existed shield tunnels. Rock Soil Mech. 2013, 34, 1421–1428. [Google Scholar]
- Zhao, Y.R.; Chen, X.S.; Hu, B.; Huang, L.P.; Lu, G.H.; Yao, H.L. Automatic monitoring and control of excavation disturbance of an ultra-deep foundation pit extremely adjacent to metro tunnels. Tunn. Undergr. Space Technol. 2023, 142, 105445. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wei, G.; Jiang, C.W. The Study for Longitudinal Deformation of Adjacent Shield Tunnel Due to Foundation Pit Excavation with Consideration of the Retaining Structure Deformation. Symmetry 2020, 12, 2103. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wei, G.; Lin, X.B.; Xia, C.; Wei, X.J. Transverse Force Analysis of Adjacent Shield Tunnel Caused by Foundation Pit Excavation Considering Deformation of Retaining Structures. Symmetry 2021, 13, 1478. [Google Scholar] [CrossRef]
- Li, M.-G.; Chen, J.-J.; Wang, J.-H.; Zhu, Y.-F. Comparative study of construction methods for deep excavations above shield tunnels. Tunn. Undergr. Space Technol. 2018, 71, 329–339. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Chen, R.P.; Meng, F.Y.; Li, Z.C.; Ye, Y.H.; Ye, J.N. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils. Tunn. Undergr. Space Technol. 2016, 58, 224–235. [Google Scholar] [CrossRef]
- Liu, B.H.; Lin, H.; Chen, Y.F.; Liu, J.S.; Guo, C. Deformation Stability Response of Adjacent Subway Tunnels considering Excavation and Support of Foundation Pit. Lithosphere 2022, 2022, 7227330. [Google Scholar] [CrossRef]
- Ye, S.H.; Zhao, Z.F.; Wang, D.Q. Deformation analysis and safety assessment of existing metro tunnels affected by excavation of a foundation pit. Undergr. Space 2021, 6, 421–431. [Google Scholar] [CrossRef]
- Liu, J.W.; Xue, B.S.; Wang, H.B.; Zhang, X.M.; Zhang, Y.X. Numerical Study on the Behavior of an Existing Tunnel during Excavating Adjacent Deep Foundation Pit. Sustainability 2023, 15, 9740. [Google Scholar] [CrossRef]
- Fu, H.L.; Deng, H.S.; Zhao, Y.B.; Chang, X.B.; Yi, H.D. Study on the Disturbance of Existing Subway Tunnels by Foundation Sloping Excavation. Appl. Sci. 2023, 13, 948. [Google Scholar] [CrossRef]
- Ter-Martirosyan, A.Z.; Kivliuk, V.P.; Isaev, I.O.; Rud, V.V. Projected Effects of a Deep Excavation Pit on the Existing Metro Tunnel and Findings of Geotechnical Monitoring: A Comparative Analysis. Buildings 2023, 13, 1320. [Google Scholar] [CrossRef]
- Liu, W.; Liang, J.X.; Xu, T. Tunnelling-induced ground deformation subjected to the behavior of tail grouting materials. Tunn. Undergr. Space Technol. 2023, 140, 105253. [Google Scholar] [CrossRef]
- Xie, X.Y.; Yang, Y.B.; Ji, M. Analysis of ground surface settlement induced by the construction of a large-diameter shield-driven tunnel in Shanghai, China. Tunn. Undergr. Space Technol. 2016, 51, 120–132. [Google Scholar] [CrossRef]
- Jia, S.; Chen, W.; Yang, J.; Chen, P. An elastoplastic constitutive model based on modified Mohr-Coulomb criterion and its numerical implementation. Rock Soil Mech. 2010, 31, 2051–2058. [Google Scholar]
- Simic-Silva, P.T.; Martínez-Bacas, B.; Galindo-Aires, R.; Simic, D. 3D simulation for tunnelling effects on existing piles. Comput. Geotech. 2020, 124, 103625. [Google Scholar] [CrossRef]
- Lin, X.T.; Chen, R.P.; Wu, H.N.; Cheng, H.Z. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar] [CrossRef]
- Huang, X.; Schweiger, H.F.; Huang, H.W. Influence of Deep Excavations on Nearby Existing Tunnels. Int. J. Geomech. 2013, 13, 170–180. [Google Scholar] [CrossRef]
- Zhong, X.; Zhang, J.; Qin, J.; Zhu, W. Simplified calculation model for longitudinal equivalent bending stiffness of shield tunnel and its influence factors’ analysis. Rock Soil Mech. 2011, 32, 132–136. [Google Scholar]
- Zheng, G.; Du, Y.; Diao, Y.; Deng, X.; Zhu, G.; Zhang, L. Influenced zones for deformation of existing tunnels adjacent to excavations. Chin. J. Geotech. Eng. 2016, 38, 599–612. [Google Scholar]
- He, Z.; Wang, P.; Wang, L.; Qiu, J. Influence of deep foundation pit construction on adjacent subway tunnel deformation and parameter sensitivity analysis. J. Chang. Univ. Nat. Sci. Ed. 2022, 42, 63–72. [Google Scholar]










| Monitoring Projects | Preliminary Alert Threshold | Alert Threshold | Control Limit |
|---|---|---|---|
| Absolute structural deformation | 6.0 mm | 8.0 mm | 10.0 mm |
| Stratigraphic Sequence | Unit Weight (kN/m3) | Compression Modulus (MPa) | Direct Shear | |
|---|---|---|---|---|
| Friction Angle (°) | Cohesion (kPa) | |||
| Stockpile soil | 18.2 | 5 | 15.0 | 12.0 |
| Gravelly clay | 18.1 | 6 | 23.0 | 22.0 |
| Strongly weathered granite | 18.9 | 12 | 27.0 | 25.5 |
| Fully weathered granite | 18.6 | 8 | 24.0 | 24.5 |
| Parameters | Basic Size/mm | Unit Weight (kN/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Element Type |
|---|---|---|---|---|---|
| lining | Diameter 6000 Thickness 300 | 24 | 34.5 | 0.1 | Plate |
| diaphragm wall | 1000/1200 | 24 | 31.5 | 0.2 | Plate |
| Bracing I | 600 × 600 | 24 | 31.5 | 0.2 | implantable truss |
| Bracing II | 1000 × 1200 | 24 | 31.5 | 0.2 | implantable truss |
| pipe support | Diameter 800 Thickness 20 | 76 | 250 | 0.25 | implantable truss |
| lattice column | 400 × 400 hollow | 76 | 250 | 0.25 | implantable beam |
| pile | 1200 | 24 | 31.5 | 0.2 | implantable truss |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Xu, Q.; Cui, Y. Deformation of Existing Shield Tunnel Adjacent to Deep Excavations: Simulation and Monitoring Analysis. Appl. Sci. 2024, 14, 4153. https://doi.org/10.3390/app14104153
Han Y, Xu Q, Cui Y. Deformation of Existing Shield Tunnel Adjacent to Deep Excavations: Simulation and Monitoring Analysis. Applied Sciences. 2024; 14(10):4153. https://doi.org/10.3390/app14104153
Chicago/Turabian StyleHan, Yufeng, Qianwei Xu, and Yuebang Cui. 2024. "Deformation of Existing Shield Tunnel Adjacent to Deep Excavations: Simulation and Monitoring Analysis" Applied Sciences 14, no. 10: 4153. https://doi.org/10.3390/app14104153




