Analyzing the Effect of Tethered Cable on the Stability of Tethered UAVs Based on Lyapunov Exponents
Abstract
:1. Introduction
2. Modeling of Tethered UAV Dynamics
2.1. Dynamics Modeling of UAV Platforms
2.1.1. Coordinate System Selection and Parameter Description
2.1.2. Modeling Assumptions for UAV Platforms
2.1.3. Force Analysis of the UAV Platform
2.1.4. Dynamical Modeling
2.2. Modeling of Tethered Cables
2.2.1. Modeling Assumptions for Tethered Cables
2.2.2. Force Analysis of Tethered Cable
2.2.3. Tension Formula
2.3. DynamiIing of Tethered UAVs
3. Stability Analysis Based on Lyapunov Exponential Method
3.1. Lyapunov Exponent Calculation Process
3.2. Parameterization of Dynamical Models
3.3. MATLAB Simulation Analysis
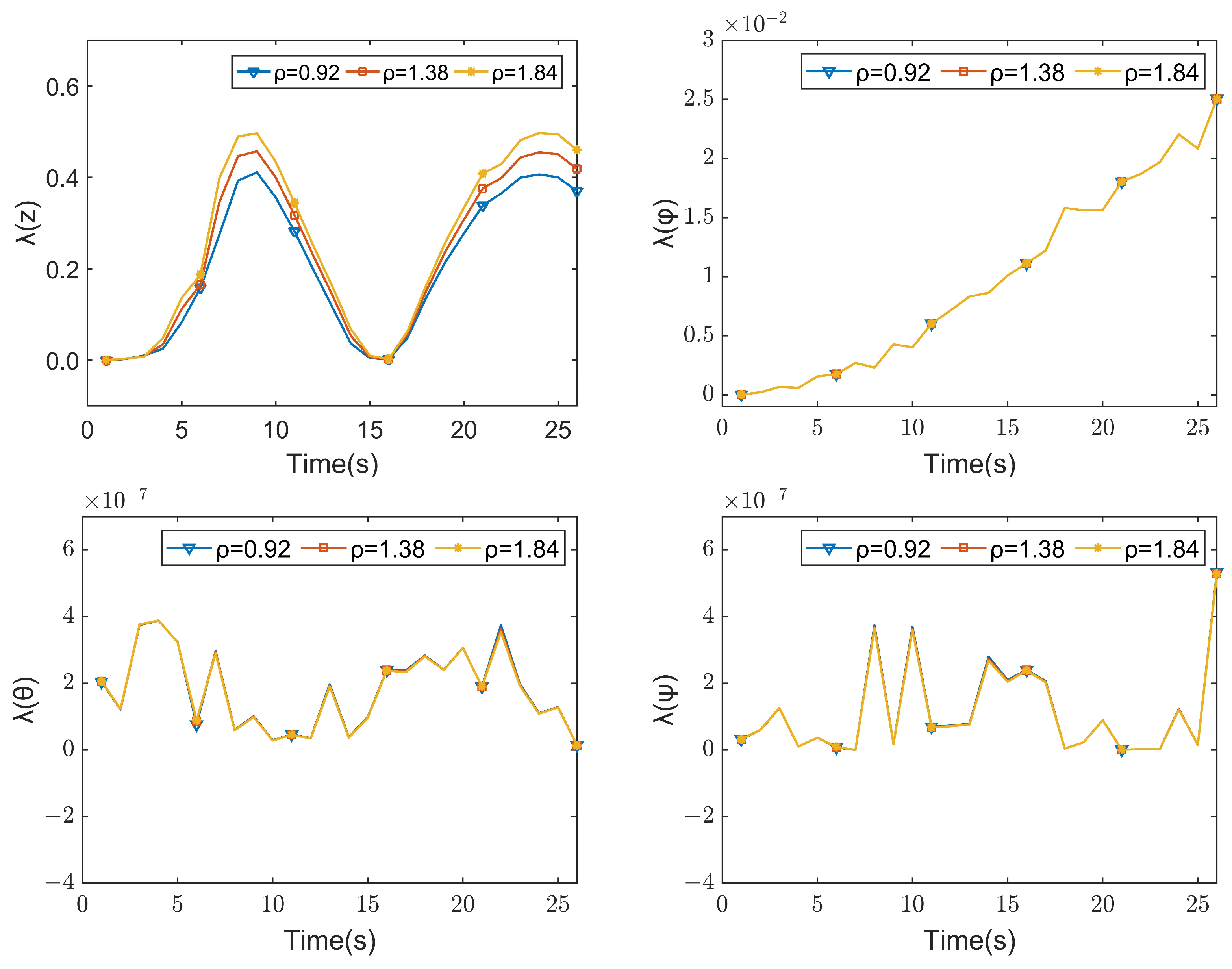
3.3.1. Takeoff Stage
3.3.2. Hovering Stage
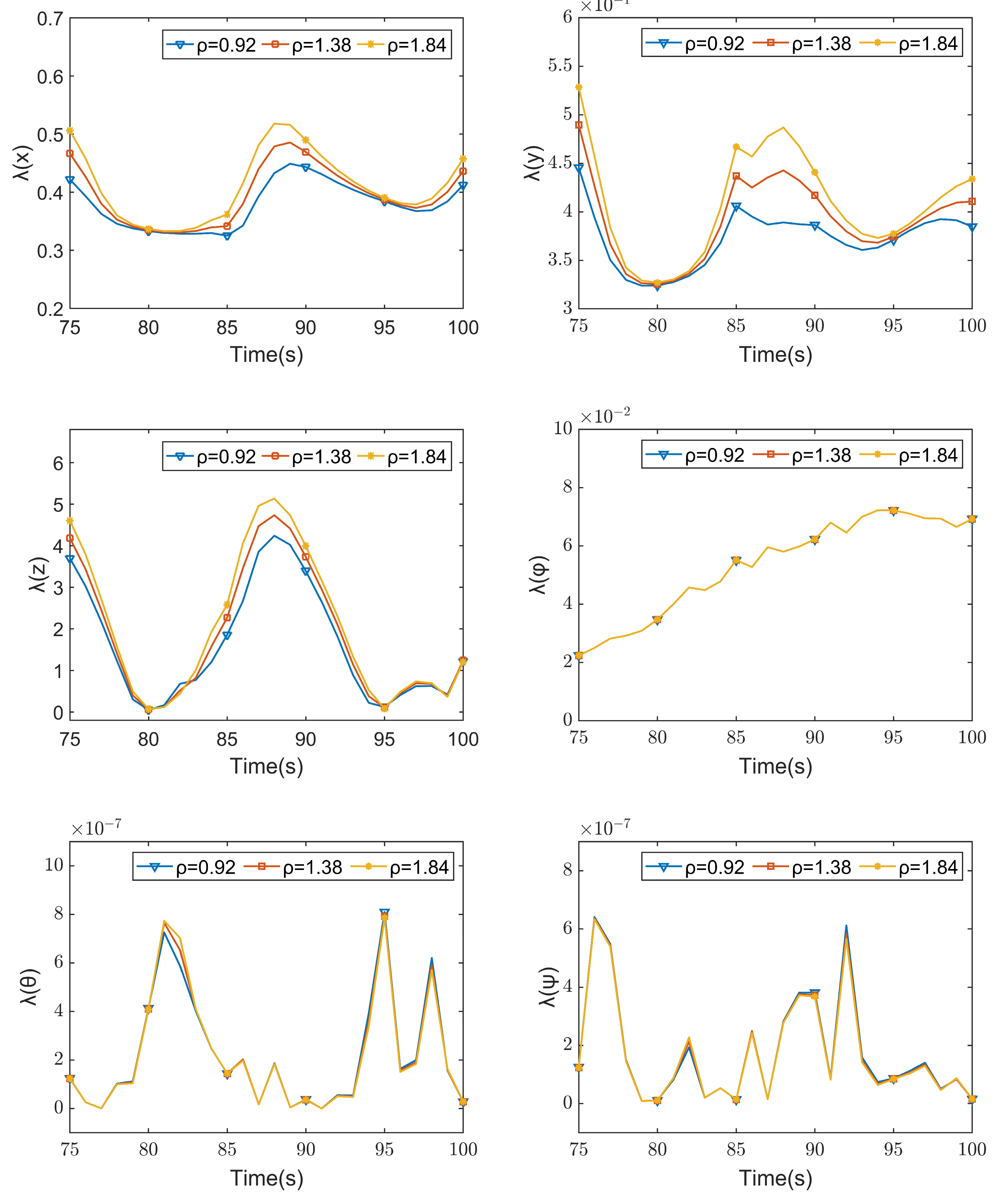
3.3.3. Landing Stage
4. Flight Tests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Radiansyah, S.; Kusrini, M.D.; Prasetyo, L.B. Quadcopter applications for wildlife monitoring. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 012066. [Google Scholar] [CrossRef]
- Senthilnath, J.; Kandukuri, M.; Dokania, A.; Ramesh, K.N. Application of UAV imaging platform for vegetation analysis based on spectral-spatial methods. Comput. Electron. Agric. 2017, 140, 8–24. [Google Scholar] [CrossRef]
- Fraundorfer, F.; Heng, L.; Honegger, D.; Lee, G.H.; Meier, L.; Tanskanen, P.; Pollefeys, M. Vision-based autonomous mapping and exploration using a quadrotor MAV. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems 2012, Algarve, Portugal, 7–12 October 2012; pp. 4557–4564. [Google Scholar]
- Faessler, M.; Fontana, F.; Forster, C.; Mueggler, E.; Pizzoli, M.; Scaramuzza, D. Autonomous, vision-based flight and live dense 3D mapping with a quadrotor micro aerial vehicle. J. Field Robot. 2016, 33, 431–450. [Google Scholar] [CrossRef]
- Moran, C.J.; Seielstad, C.A.; Cunningham, M.R.; Hoff, V.; Parsons, R.A.; Queen, L.; Sauerbrey, K.; Wallace, T. Deriving Fire Behavior Metrics from UAS Imagery. Fire 2019, 2, 36. [Google Scholar] [CrossRef]
- Anh, T.H.; Binh, N.T.; Song, J.W. In-Ground-Effect Model Based Adaptive Altitude Control of Rotorcraft Unmanned Aerial Vehicles. IEEE Robot. Autom. Lett. 2021, 7, 794–801. [Google Scholar] [CrossRef]
- Viegas, C.; Chehreh, B.; Andrade, J.; Lourenço, J. Tethered UAV with Combined Multi-rotor and Water Jet Propulsion for Forest Fire Fighting. J. Intell. Robot. Syst. 2022, 104, 20–21. [Google Scholar] [CrossRef]
- Chen, R.; Yuan, Y.; Thomson, D. A review of mathematical modelling techniques for advanced rotorcraft configurations. Prog. Aerosp. Sci. 2021, 120, 100681. [Google Scholar] [CrossRef]
- Abdelmaksoud, S.I.; Mailah, M.; Abdallah, A.M. Control Strategies and Novel Techniques for Autonomous Rotorcraft Unmanned Aerial Vehicles: A Review. IEEE Access 2020, 8, 195142–195169. [Google Scholar] [CrossRef]
- Amiri, N.; Ramirez-Serrano, A.; Davies, R.J. Integral Backstepping Control of an Unconventional Dual-Fan Unmanned Aerial Vehicle. J. Intell. Robot. Syst. 2013, 69, 147–159. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; El Saddik, A. Nonlinear adaptive control for quadrotor flying vehicle. Nonlinear Dyn. 2014, 78, 117–133. [Google Scholar] [CrossRef]
- Armiyoon, A.R.; Wu, C.Q. Lyapunov exponents-based stability analysis and integrated control of rollover mitigation and yaw stabilisation of ground vehicles. Int. J. Veh. Syst. Model. Test. 2016, 11, 343–362. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, C.; Wu, H.; Zhang, Y.; Mei, P. Structural stability analysis and optimization of the quadrotor unmanned aerial vehicles via the concept of Lyapunov exponents. Int. J. Adv. Manuf. Technol. 2018, 94, 3217–3227. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, Y.; Liu, Y.; Wang, L. Dynamics Modeling and Stability Analysis of Tilt Wing Unmanned Aerial Vehicle during Transition. Comput. Mater. Contin. 2019, 59, 833–851. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Wang, T.; Zhang, Y.; Mei, P. Quantitative stability of quadrotor unmanned aerial vehicles. Nonlinear Dyn. 2017, 87, 1819–1833. [Google Scholar] [CrossRef]
- Papachristos, C.; Alexis, K.; Tzes, A. Hybrid model predictive flight mode conversion control of unmanned quad-tiltrotors. In Proceedings of the 2013 European Control Conference (ECC) 2013, Zurich, Switzerland, 17–19 July 2013; pp. 1793–1798. [Google Scholar]
- Jain, A.; Rodriguez, G. Diagonalized Lagrangian robot dynamics. IEEE Trans. Robot. Autom. 1995, 11, 571–584. [Google Scholar] [CrossRef]
- Cheng, G.; Shan, X. Dynamics analysis of a parallel hip joint simulator with four degree of freedoms (3R1T). Nonlinear Dyn. 2012, 70, 2475–2486. [Google Scholar] [CrossRef]
- García Carrillo, L.R.; Dzul López, A.E.; Lozano, R.; Pégard, C.; García Carrillo, L.R.; Dzul López, A.E.; Pégard, C. Vision-based control of a quad-rotor uav. In Quad Rotorcraft Control: Vision-Based Hovering and Navigation; Springer: Berlin/Heidelberg, Germany, 2013; pp. 103–137. [Google Scholar]
- Chen, L.; Xiao, J.; Zheng, Y.; Alagappan, N.A.; Feroskhan, M. Design, Modeling, and Control of a Coaxial Drone. IEEE Trans. Robot. 2024, 40, 1650–1663. [Google Scholar] [CrossRef]
- Tao, Y.; Zhang, S. Research on the Vibration and Wave Propagation in Ship-Borne Tethered UAV Using Stress Wave Method. Drones 2022, 6, 349. [Google Scholar] [CrossRef]
- Qin, J.; Peng, F.; Qiao, L.; Jiang, M. Catenary method of helicopter live-line work in transmission line. In Proceedings of the 2016 International Conference on Advanced Electronic Science and Technology (AEST 2016) 2016, Shenzhen, China, 19–21 August 2016; pp. 969–974. [Google Scholar]












| Parameter | Meaning | Parameter Value |
|---|---|---|
| m | UAV platform weight | 1.365 kg |
| g | Gravity acceleration | 9.8 m/s2 |
| L | Boom length | 0.225 m |
| CT | Lift coefficient | 1.0792 × 10−5 |
| CQ | Reverse moment coefficient | 1.8992 × 10−5 |
| R | Blade radius | 0.127 m |
| Ix | Moment of inertia around the x-axis | 0.2868 kg/m2 |
| Iy | Moment of inertia around the y-axis | 0.3141 kg/m2 |
| Iz | Moment of inertia around the z-axis | 0.147 kg/m2 |
| ρa | Air density | 1.293 kg/m3 |
| ρ | Density of tethered cable | 1.29 kg/m3 |
| s | Cross-sectional area of a tethered cable | 0.002 m2 |
| Parameter | ρ = 0.92 | ρ = 1.38 | ρ = 1.84 |
|---|---|---|---|
| λ(x) | 0.42195 | 0.46652 (↑ 10.56%) | 0.50592 (↑ 19.9%) |
| λ(y) | 0.44627 | 0.49017 (↑ 9.84%) | 0.52917 (↑ 18.58%) |
| λ(z) | 0.36989 | 0.41851 (↑ 13.14%) | 0.46032 (↑ 24.45%) |
| λ(φ) | 0.02505 | 0.02505 (─) | 0.02505 (─) |
| λ(θ) | 1.39 × 10−8 | 1.38 × 10−8 (↑ 0.53%) | 1.38 × 10−8 (↓ 0.92%) |
| λ(ψ) | 5.33 × 10−7 | 5.30 × 10−7 (↑ 0.54%) | 5.28 × 10−7 (↓ 0.93%) |
| Parameter | ρ = 0.92 | ρ = 1.38 | ρ = 1.84 |
|---|---|---|---|
| λ(x) | 0.42187 | 0.46646 (↑ 10.57%) | 0.50588 (↑ 19.91%) |
| λ(y) | 0.44572 | 0.48955 (↑ 9.83%) | 0.52851 (↑ 18.58%) |
| λ(z) | 0.36967 | 0.41835 (↑ 13.17%) | 0.46020 (↑ 24.49%) |
| λ(φ) | 0.02244 | 0.02244 (─) | 0.02244 (─) |
| λ(θ) | 1.24 × 10−7 | 1.24 × 10−7 (↑ 0.54%) | 1.23 × 10−7 (↓ 0.92%) |
| λ(ψ) | 1.25 × 10−7 | 1.25 × 10−7 (↑ 0.54%) | 1.24 × 10−7 (↓ 0.94%) |
| Parameter | ρ = 0.92 | ρ = 1.38 | ρ = 1.84 |
|---|---|---|---|
| λ(x) | 0.41221 | 0.43593 (↑ 5.75%) | 0.45740 (↑ 10.96%) |
| λ(y) | 0.38481 | 0.41085 (↑ 6.77%) | 0.43391 (↑ 12.76%) |
| λ(z) | 1.22517 | 1.24377 (↑ 1.52%) | 1.20319 (↓ 1.79%) |
| λ(φ) | 0.06928 | 0.06928 (─) | 0.06928 (─) |
| λ(θ) | 2.78 × 10−8 | 2.79 × 10−8 (↑ 0.28%) | 2.82 × 10−8 (↑ 1.37%) |
| λ(ψ) | 1.59 × 10−8 | 1.60 × 10−8 (↑ 0.31%) | 1.61 × 10−8 (↑ 1.45%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Liu, C.; Jiang, H.; Hou, F.; Wang, S. Analyzing the Effect of Tethered Cable on the Stability of Tethered UAVs Based on Lyapunov Exponents. Appl. Sci. 2024, 14, 4253. https://doi.org/10.3390/app14104253
Tang Z, Liu C, Jiang H, Hou F, Wang S. Analyzing the Effect of Tethered Cable on the Stability of Tethered UAVs Based on Lyapunov Exponents. Applied Sciences. 2024; 14(10):4253. https://doi.org/10.3390/app14104253
Chicago/Turabian StyleTang, Zhiren, Chaofeng Liu, Hongbo Jiang, Feiyu Hou, and Shenglan Wang. 2024. "Analyzing the Effect of Tethered Cable on the Stability of Tethered UAVs Based on Lyapunov Exponents" Applied Sciences 14, no. 10: 4253. https://doi.org/10.3390/app14104253





