Modelling Context Effects in Exit Choice for Building Evacuations
Abstract
:1. Introduction
2. Related Works
2.1. Context Effects
2.2. Utility Function
2.3. Social Force Model
3. Methodology
3.1. Experimental Data
3.2. Model Description
3.2.1. UF-SF Model
3.2.2. CE-SF Model
3.2.3. Model Framework
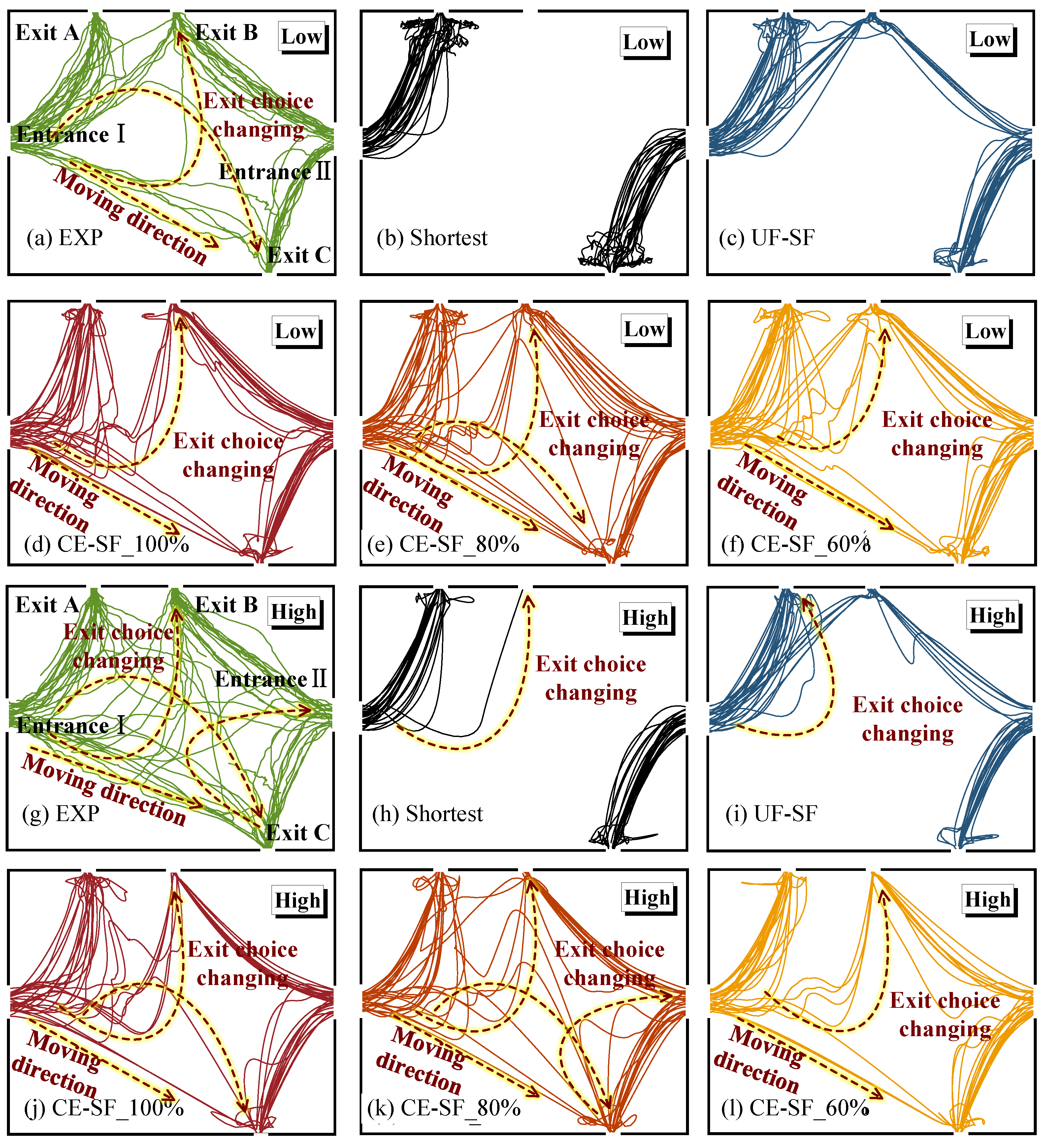
4. Results
4.1. Sensitivity Analysis of the UF-SF Model
4.2. Simulation Performance of the CE-SF Model
4.2.1. Sensitivity Analysis of the CE-SF Model
4.2.2. Different Percentages of Evacuees Affected by Context Effect
4.3. Evidenceof Context Effects in Experimental Data
5. Discussion
6. Conclusions and Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soomaroo, L.; Murray, V. Disasters at mass gatherings: Lessons from history. Plos Curr. 2012, 4, RRN1301. [Google Scholar] [CrossRef]
- Sharma, A.; McCloskey, B.; Hui, D.S.; Rambia, A.; Zumla, A.; Traore, T.; Shafi, S.; El-Kafrawy, S.A.; Azhar, E.I.; Zumla, A.; et al. Global mass gathering events and deaths due to crowd surge, stampedes, crush and physical injuries-lessons from the Seoul Halloween and other disasters. Travel Med. Infect. Dis. 2023, 52, 102524. [Google Scholar] [CrossRef] [PubMed]
- Haghani, M. Optimising crowd evacuations: Mathematical, architectural and behavioural approaches. Saf. Sci. 2020, 128, 104745. [Google Scholar] [CrossRef]
- Wang, P.; Cao, S. Simulation of pedestrian evacuation strategies under limited visibility. Phys. Lett. A 2019, 383, 825–832. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, Y.; Dong, S.; Zhang, M.; Mao, T. Simulation of pedestrian evacuation route choice using social force model in large-scale public space: Comparison of five evacuation strategies. PLoS ONE 2019, 14, e0221872. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Wang, Y.; Jiang, S. Optimization of building exit layout: Combining exit decisions of evacuees. Adv. Civ. Eng. 2021, 2021, 6622661. [Google Scholar] [CrossRef]
- Feng, Y.; Duives, D.C.; Hoogendoorn, S.P. Using virtual reality to study pedestrian exit choice behaviour during evacuations. Saf. Sci. 2021, 137, 105158. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, R.; Siu, M.F.F.; Luo, X. Human decision change in crowd evacuation: A virtual reality-based study. J. Build. Eng. 2023, 68, 106041. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Lovreglio, R.; Fonzone, A.; Dell’Olio, L.; Borri, D. A study of herding behaviour in exit choice during emergencies based on random utility theory. Saf. Sci. 2016, 82, 421–431. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, Z. Reserve capacity and exit choosing in pedestrian evacuation dynamics. J. Phys. A Math. Theor. 2010, 43, 105001. [Google Scholar] [CrossRef]
- Kinateder, M.; Warren, W.H. Social influence on evacuation behavior in real and virtual environments. Front. Robot. AI 2016, 3, 43. [Google Scholar] [CrossRef]
- Gao, D.L.; Xie, W.; Lee, E.W.M. Individual-level exit choice behaviour under uncertain risk. Phys. A Stat. Mech. Appl. 2022, 604, 127873. [Google Scholar] [CrossRef]
- Song, X.B.; Lovreglio, R. Investigating personalized exit choice behavior in fire accidents using the hierarchical Bayes estimator of the random coefficient logit model. Anal. Methods Accid. Res. 2021, 29, 100140. [Google Scholar] [CrossRef]
- Lovreglio, R.; Fonzone, A.; Dell’Olio, L. A mixed logit model for predicting exit choice during building evacuations. Transp. Res. Part A Policy Pract. 2016, 92, 59–75. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M.; Shahhoseini, Z. Evacuation behaviour of crowds under high and low levels of urgency: Experiments of reaction time, exit choice and exit-choice adaptation. Saf. Sci. 2020, 126, 104679. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Following the crowd or avoiding it? Empirical investigation of imitative behaviour in emergency escape of human crowds. Anim. Behav. 2017, 124, 47–56. [Google Scholar] [CrossRef]
- Lovreglio, R. Modelling Decision-Making in Fire Evacuation Based on Random Utility Theory. Ph.D. Thesis, Polytechnic University of Bari, Bari, Italy, 2016. [Google Scholar]
- Kahneman, D.; Sibony, O.; Sunstein, C.R. Noise: A Flaw in Human Judgment; Hachette: London, UK, 2021. [Google Scholar]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Klüpfel, H.; Schreckenberg, M.; Meyer-König, T. Models for crowd movement and egress simulation. In Traffic and Granular Flow’03; Springer: Berlin/Heidelberg, Germany, 2005; pp. 357–372. [Google Scholar]
- Thinking, C.H.O. Cambridge Handbook Of Thinking And Reasoning Ebook; Psychology Press: London, UK, 1999. [Google Scholar]
- Gao, S.; Li, N. Preference reversal and the evolution of cooperation. Appl. Math. Comput. 2023, 438, 127567. [Google Scholar] [CrossRef]
- Trueblood, J.S.; Brown, S.D.; Heathcote, A.; Busemeyer, J.R. Not just for consumers: Context effects are fundamental to decision making. Psychol. Sci. 2013, 24, 901–908. [Google Scholar] [CrossRef]
- Spektor, M.S.; Kellen, D.; Hotaling, J.M. When the good looks bad: An experimental exploration of the repulsion effect. Psychol. Sci. 2018, 29, 1309–1320. [Google Scholar] [CrossRef] [PubMed]
- O’Curry, Y.P.S.; Pitts, R. The attraction effect and political choice in two elections. J. Consum. Psychol. 1995, 4, 85–101. [Google Scholar]
- Doyle, J.R.; O’Connor, D.J.; Reynolds, G.M.; Bottomley, P.A. The robustness of the asymmetrically dominated effect: Buying frames, phantom alternatives, and in-store purchases. Psychol. Mark. 1999, 16, 225–243. [Google Scholar] [CrossRef]
- Trueblood, J.S.; Pettibone, J.C. The phantom decoy effect in perceptual decision making. J. Behav. Decis. Mak. 2017, 30, 157–167. [Google Scholar] [CrossRef]
- Gao, D.; Lee, E.W.M.; Lee, Y.Y. The influence of context effects on exit choice behavior during building evacuation combining virtual reality and discrete choice modeling. Adv. Eng. Inform. 2023, 57, 102072. [Google Scholar] [CrossRef]
- Cao, S.; Fu, L.; Song, W. Exit selection and pedestrian movement in a room with two exits under fire emergency. Appl. Math. Comput. 2018, 332, 136–147. [Google Scholar] [CrossRef]
- Guo, R.-Y.; Huang, H.-J. Logit-based exit choice model of evacuation in rooms with internal obstacles and multiple exits. Chin. Phys. B 2010, 19, 030501. [Google Scholar]
- Muñoz, M.A.; Pineda, S.; Morales, J.M. A bilevel framework for decision-making under uncertainty with contextual information. Omega 2022, 108, 102575. [Google Scholar] [CrossRef]
- Pirrone, A.; Reina, A.; Stafford, T.; Marshall, J.A.; Gobet, F. Magnitude-sensitivity: Rethinking decision-making. Trends Cogn. Sci. 2022, 26, 66–80. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, W.; Yuan, X.; Jiang, Y. Following Other People’s Footsteps: A Contextual-Attraction Effect Induced by Biological Motion. Psychol. Sci. 2022, 33, 1522–1531. [Google Scholar] [CrossRef]
- Spektor, M.S.; Bhatia, S.; Gluth, S. The elusiveness of context effects in decision making. Trends Cogn. Sci. 2021, 25, 843–854. [Google Scholar] [CrossRef] [PubMed]
- Simonson, I. Choice based on reasons: The case of attraction and compromise effects. J. Consum. Res. 1989, 16, 158–174. [Google Scholar] [CrossRef]
- Trueblood, J.S.; Brown, S.D.; Heathcote, A. The multiattribute linear ballistic accumulator model of context effects in multialternative choice. Psychol. Rev. 2014, 121, 179. [Google Scholar] [CrossRef] [PubMed]
- Tversky, A. Elimination by aspects: A theory of choice. Psychol. Rev. 1972, 79, 281. [Google Scholar] [CrossRef]
- Zalta, E.N.; Nodelman, U.; Allen, C.; Anderson, R.L. Stanford Encyclopedia of Philosophy; The Metaphysics Research Lab: Stanford, CA, USA, 2016. [Google Scholar]
- Huber, J.; Payne, J.W.; Puto, C. Adding asymmetrically dominated alternatives: Violations of regularity and the similarity hypothesis. J. Consum. Res. 1982, 9, 90–98. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.; Lee, J.; Kim, S.; Gonzalez-Jimenez, H.; Lee, J.; Choi, Y.K.; Lee, J.C.; Jang, S.; Franklin, D.; et al. COVID-19 and extremeness aversion: The role of safety seeking in travel decision making. J. Travel Res. 2022, 61, 837–854. [Google Scholar] [CrossRef]
- Milberg, S.J.; Silva, M.; Celedon, P.; Sinn, F. Synthesis of attraction effect research: Practical market implications? Eur. J. Mark. 2014, 48, 1413–1430. [Google Scholar] [CrossRef]
- Castillo, G. The attraction effect and its explanations. Games Econ. Behav. 2020, 119, 123–147. [Google Scholar] [CrossRef]
- Wu, C.; Cosguner, K. Profiting from the decoy effect: A case study of an online diamond retailer. Mark. Sci. 2020, 39, 974–995. [Google Scholar] [CrossRef]
- Arad, A.; Bachi, B.; Maltz, A. On the relevance of irrelevant strategies. Exp. Econ. 2023, 26, 1142–1184. [Google Scholar] [CrossRef]
- Shafir, S.; Waite, T.A.; Smith, B.H. Context-dependent violations of rational choice in honeybees (Apis mellifera) and gray jays (Perisoreus canadensis). Behav. Ecol. Sociobiol. 2002, 51, 180–187. [Google Scholar] [CrossRef]
- Latty, T.; Beekman, M. Irrational decision-making in an amoeboid organism: Transitivity and context-dependent preferences. Proc. R. Soc. B Biol. Sci. 2011, 278, 307–312. [Google Scholar] [CrossRef] [PubMed]
- Spektor, M.S.; Kellen, D.; Klauer, K.C. The repulsion effect in preferential choice and its relation to perceptual choice. Cognition 2022, 225, 105164. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.M.; Schley, D.R.; Muller, C.; Tsetsos, K. Competing theories of multialternative, multiattribute preferential choice. Psychol. Rev. 2018, 125, 329. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Zhou, R.; Cui, Y.; Wang, Y.; Jiang, J. Influencing factors for exit selection in subway station evacuation. Tunn. Undergr. Space Technol. 2022, 125, 104498. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, J.H.; Zhang, X.S.; Zhang, J.L.; Wang, Q.Z.; Zhang, Q. Pedestrians’ behavior in emergency evacuation: Modeling and simulation. Chin. Phys. B 2016, 25, 118901. [Google Scholar] [CrossRef]
- Veeraswamy, A. Computational Modelling of Agent Based Path Planning and the Representation of Human Wayfinding Behaviour within Egress Models. Ph.D. Thesis, University of Greenwich, London, UK, 2011. [Google Scholar]
- Kuffner, J.J., Jr. Goal-directed navigation for animated characters using real-time path planning and control. In International Workshop on Capture Techniques for Virtual Environments; Springer: Berlin/Heidelberg, Germany, 1998; pp. 171–186. [Google Scholar]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.; Lee, E.W.M.; Lee, Y.Y. Self-organisation phenomena in pedestrian counter flows and its modelling. Saf. Sci. 2022, 155, 105875. [Google Scholar] [CrossRef]
- Helbing, D.; Johansson, A. Pedestrian, crowd, and evacuation dynamics. arXiv 2013, arXiv:1309.1609. [Google Scholar]
- Chen, X.; Treiber, M.; Kanagaraj, V.; Li, H. Social force models for pedestrian traffic–state of the art. Transp. Rev. 2018, 38, 625–653. [Google Scholar] [CrossRef]
- Fu, L.; Qin, H.; He, Y.; Shi, Y. Application of the social force modelling method to evacuation dynamics involving pedestrians with disabilities. Appl. Math. Comput. 2024, 460, 128297. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, L.; Li, K. An improved social force model for pedestrian dynamics in shipwrecks. Appl. Math. Comput. 2019, 348, 355–362. [Google Scholar] [CrossRef]
- Xie, W.; Gao, D.; Lee, E.W. Detecting undeclared-leader-follower structure in pedestrian evacuation using transfer entropy. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17644–17653. [Google Scholar] [CrossRef]
- Hou, L.; Liu, J.G.; Pan, X.; Wang, B.H. A social force evacuation model with the leadership effect. Phys. A Stat. Mech. Appl. 2014, 400, 93–99. [Google Scholar] [CrossRef]
- Song, X.; Zhang, Z.; Peng, G.; Shi, G. Effect of authority figures for pedestrian evacuation at metro stations. Phys. A Stat. Mech. Appl. 2017, 465, 599–612. [Google Scholar] [CrossRef]
- Zheng, X.; Li, H.Y.; Meng, L.Y.; Xu, X.Y.; Chen, X. Improved social force model based on exit selection for microscopic pedestrian simulation in subway station. J. Cent. South Univ. 2015, 22, 4490–4497. [Google Scholar] [CrossRef]
- Fu, Y.; Shi, W.; Zeng, Y.; Zhang, H.; Liu, X.; Liu, Y. Simulation study on pedestrian evacuation optimization in a multi-exit building. J. Physics. Conf. Ser. 2021, 1780, 012024. [Google Scholar] [CrossRef]
- Boltes, M.; Seyfried, A.; Steffen, B.; Schadschneider, A. Automatic extraction of pedestrian trajectories from video recordings. In Pedestrian and Evacuation Dynamics 2008; Springer: Berlin/Heidelberg, Germany, 2010; pp. 43–54. [Google Scholar]
- Boltes, M.; Seyfried, A. Collecting pedestrian trajectories. Neurocomputing 2013, 100, 127–133. [Google Scholar] [CrossRef]
- Yuan, W.; Tan, K.H. An evacuation model using cellular automata. Phys. A Stat. Mech. Appl. 2007, 384, 549–566. [Google Scholar] [CrossRef]
- Li, H.; Zhang, J.; Xia, L.; Song, W.; Bode, N.W. Comparing the route-choice behavior of pedestrians around obstacles in a virtual experiment and a field study. Transp. Res. Part C Emerg. Technol. 2019, 107, 120–136. [Google Scholar] [CrossRef]
- Lovreglio, R.; Dillies, E.; Kuligowski, E.; Rahouti, A.; Haghani, M. Exit choice in built environment evacuation combining immersive virtual reality and discrete choice modelling. Autom. Constr. 2022, 141, 104452. [Google Scholar] [CrossRef]
- Liew, S.X.; Howe, P.D.; Little, D.R. The appropriacy of averaging in the study of context effects. Psychon. Bull. Rev. 2016, 23, 1639–1646. [Google Scholar] [CrossRef] [PubMed]
- Trueblood, J.S.; Brown, S.D.; Heathcote, A. The fragile nature of contextual preference reversals: Reply to Tsetsos, Chater, and Usher (2015). Psychol. Rev. 2015, 122, 848–853. [Google Scholar] [CrossRef]
- Luce, R.D.; Edwards, W. The derivation of subjective scales from just noticeable differences. Psychol. Rev. 1958, 65, 222. [Google Scholar] [CrossRef] [PubMed]
- Norwich, K.H. On the theory of Weber fractions. Percept. Psychophys. 1987, 42, 286–298. [Google Scholar] [CrossRef]
- Norman, J.F.; Todd, J.T.; Perotti, V.J.; Tittle, J.S. The visual perception of three-dimensional length. J. Exp. Psychol. Hum. Percept. Perform. 1996, 22, 173. [Google Scholar] [CrossRef] [PubMed]
- Gomez, D.M.; Dartnell, P. Psychophysical Distance between Visually-Presented Pairs of Ratios. Available online: https://osf.io/y4zmn/download/?format=pdf (accessed on 14 May 2024).
- Bode, N.W.; Kemloh Wagoum, A.U.; Codling, E.A. Human responses to multiple sources of directional information in virtual crowd evacuations. J. R. Soc. Interface 2014, 11, 20130904. [Google Scholar] [CrossRef] [PubMed]
- Bode, N.W.; Kemloh Wagoum, A.U.; Codling, E.A. Information use by humans during dynamic route choice in virtual crowd evacuations. R. Soc. Open Sci. 2015, 2, 140410. [Google Scholar] [CrossRef] [PubMed]
- Haghani, M.; Sarvi, M. Simulating dynamics of adaptive exit-choice changing in crowd evacuations: Model implementation and behavioural interpretations. Transp. Res. Part C Emerg. Technol. 2019, 103, 56–82. [Google Scholar] [CrossRef]
- Liao, W.; Kemloh Wagoum, A.U.; Bode, N.W. Route choice in pedestrians: Determinants for initial choices and revising decisions. J. R. Soc. Interface 2017, 14, 20160684. [Google Scholar] [CrossRef]
- Wollschlaeger, L.M.; Diederich, A. Similarity, attraction, and compromise effects: Original findings, recent empirical observations, and computational cognitive process models. Am. J. Psychol. 2020, 133, 1–30. [Google Scholar] [CrossRef]
- Spektor, M.S.; Gluth, S.; Fontanesi, L.; Rieskamp, J. How similarity between choice options affects decisions from experience: The accentuation-of-differences model. Psychol. Rev. 2019, 126, 52. [Google Scholar] [CrossRef] [PubMed]
- Pinger, P.; Ruhmer-Krell, I.; Schumacher, H. The compromise effect in action: Lessons from a restaurant’s menu. J. Econ. Behav. Organ. 2016, 128, 14–34. [Google Scholar] [CrossRef]
- Kuncel, N.R.; Dahlke, J.A. Decoy effects improve diversity hiring. Pers. Assess. Decis. 2020, 6, 5. [Google Scholar] [CrossRef]
- Lee, M.D.; Ke, M.Y. Framing effects and preference reversals in crowd-sourced ranked opinions. Decision 2022, 9, 153. [Google Scholar] [CrossRef]











| No. | UF-SF Model | |||
|---|---|---|---|---|
| Low Urgency | High Urgency | |||
| U1 | −0.3 | −10 | 1.6% | 3.8% |
| U2 | −0.3 | −1 | 9.4% | 3.8% |
| U3 | −1 | −1 | 11.1% | 10.0% |
| U4 | −10 | −0.3 | 2.2% | 2.2% |
| U5 | −1 | −0.3 | 9.6% | 13.2% |
| No. | (m) | (ped) | (m) | (ped) |
|---|---|---|---|---|
| C1 | 2 | 3 | 1.5 | 2 |
| C2 | 2 | 4 | 1.5 | 2 |
| C3 | 2 | 6 | 1.5 | 2 |
| C4 | 2 | 3 | 1 | 2 |
| C5 | 2 | 4 | 1 | 2 |
| C6 | 2 | 6 | 1 | 2 |
| C7 | 3 | 3 | 1.5 | 2 |
| C8 | 3 | 4 | 1.5 | 2 |
| C9 | 3 | 6 | 1.5 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Liang, X.; Chen, Q.; Qiu, H.; Lee, E.W.M. Modelling Context Effects in Exit Choice for Building Evacuations. Fire 2024, 7, 169. https://doi.org/10.3390/fire7050169
Gao D, Liang X, Chen Q, Qiu H, Lee EWM. Modelling Context Effects in Exit Choice for Building Evacuations. Fire. 2024; 7(5):169. https://doi.org/10.3390/fire7050169
Chicago/Turabian StyleGao, Dongli, Xuanwen Liang, Qian Chen, Hongpeng Qiu, and Eric Wai Ming Lee. 2024. "Modelling Context Effects in Exit Choice for Building Evacuations" Fire 7, no. 5: 169. https://doi.org/10.3390/fire7050169





