The Analysis of Mammalian Hearing Systems Supports the Hypothesis That Criticality Favors Neuronal Information Representation but Not Computation
Abstract
:1. Introduction
2. Universality and Criticality in Physics
3. Application to Biology
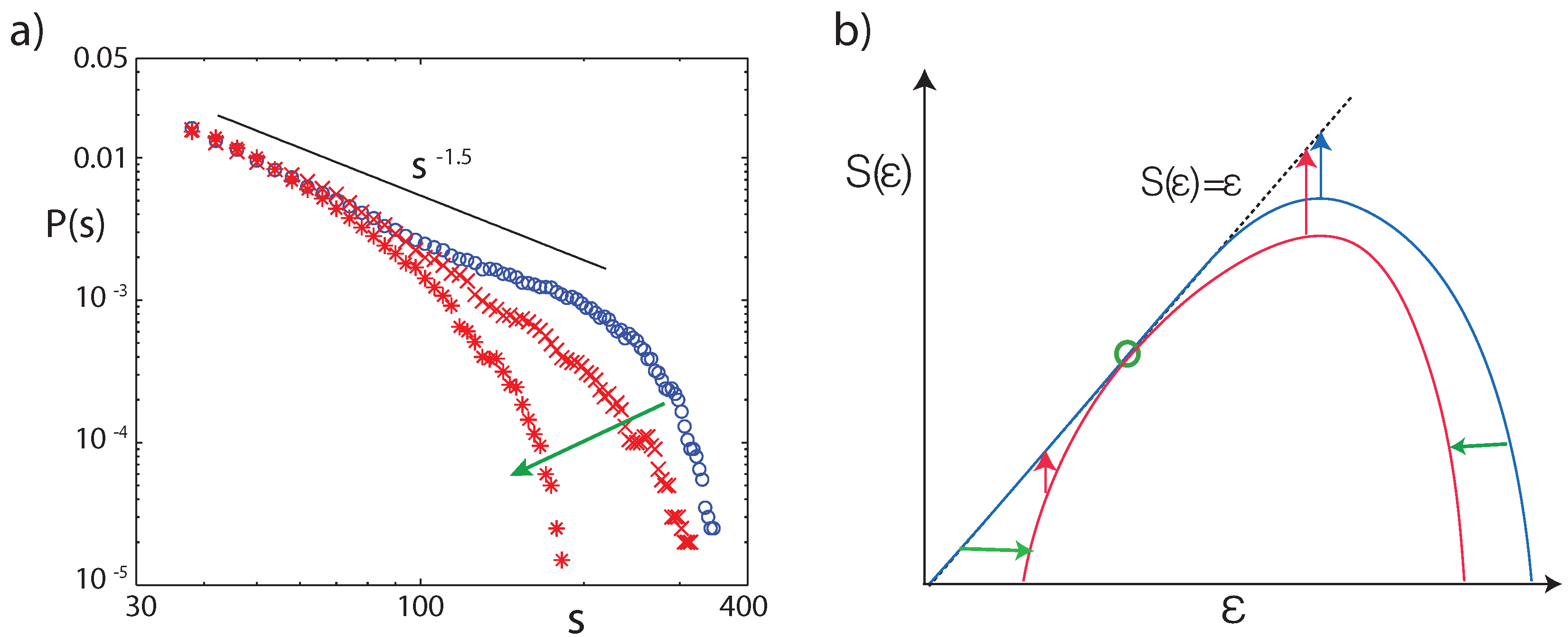
3.1. A List of Prominent Conjectures
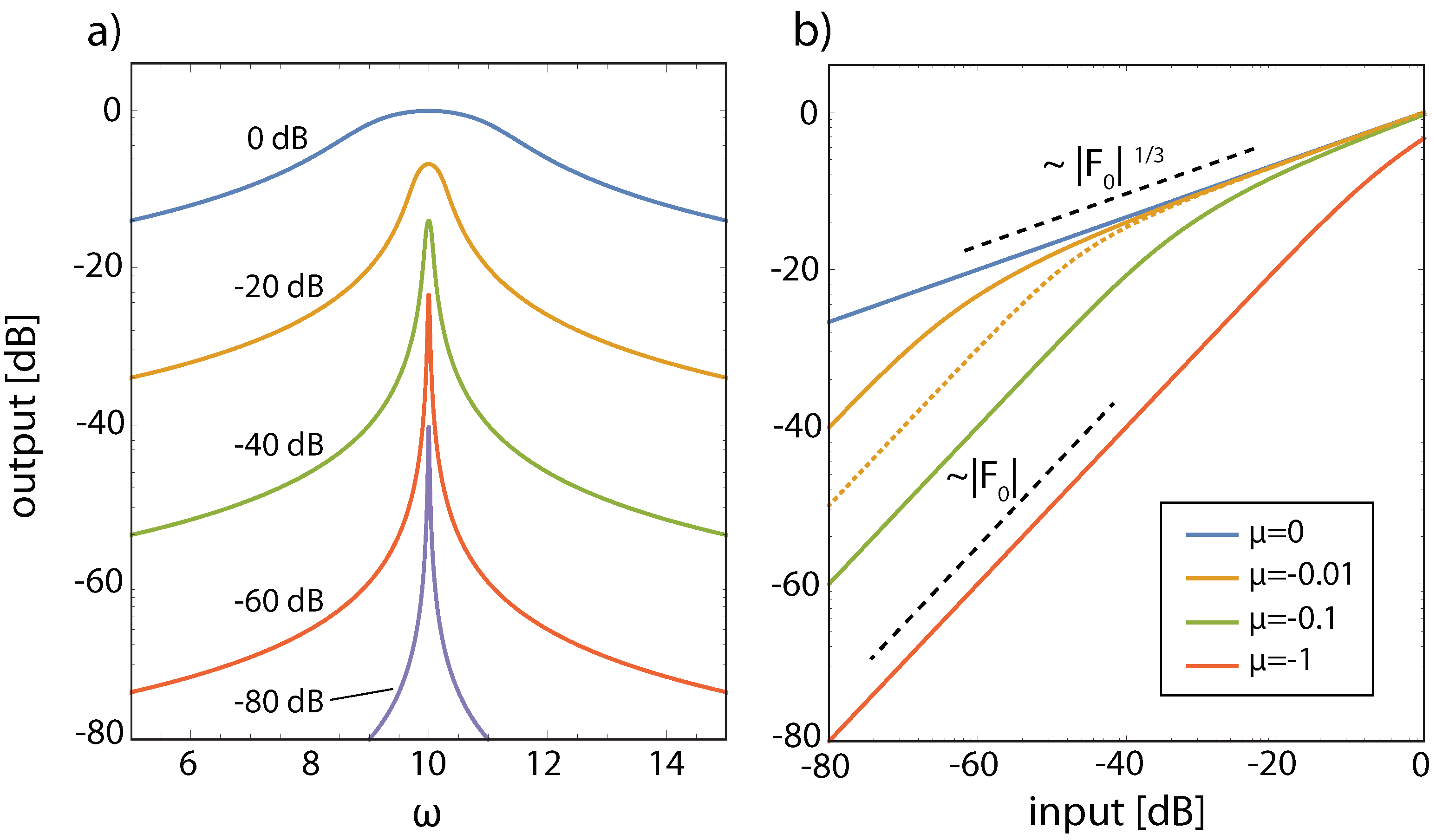
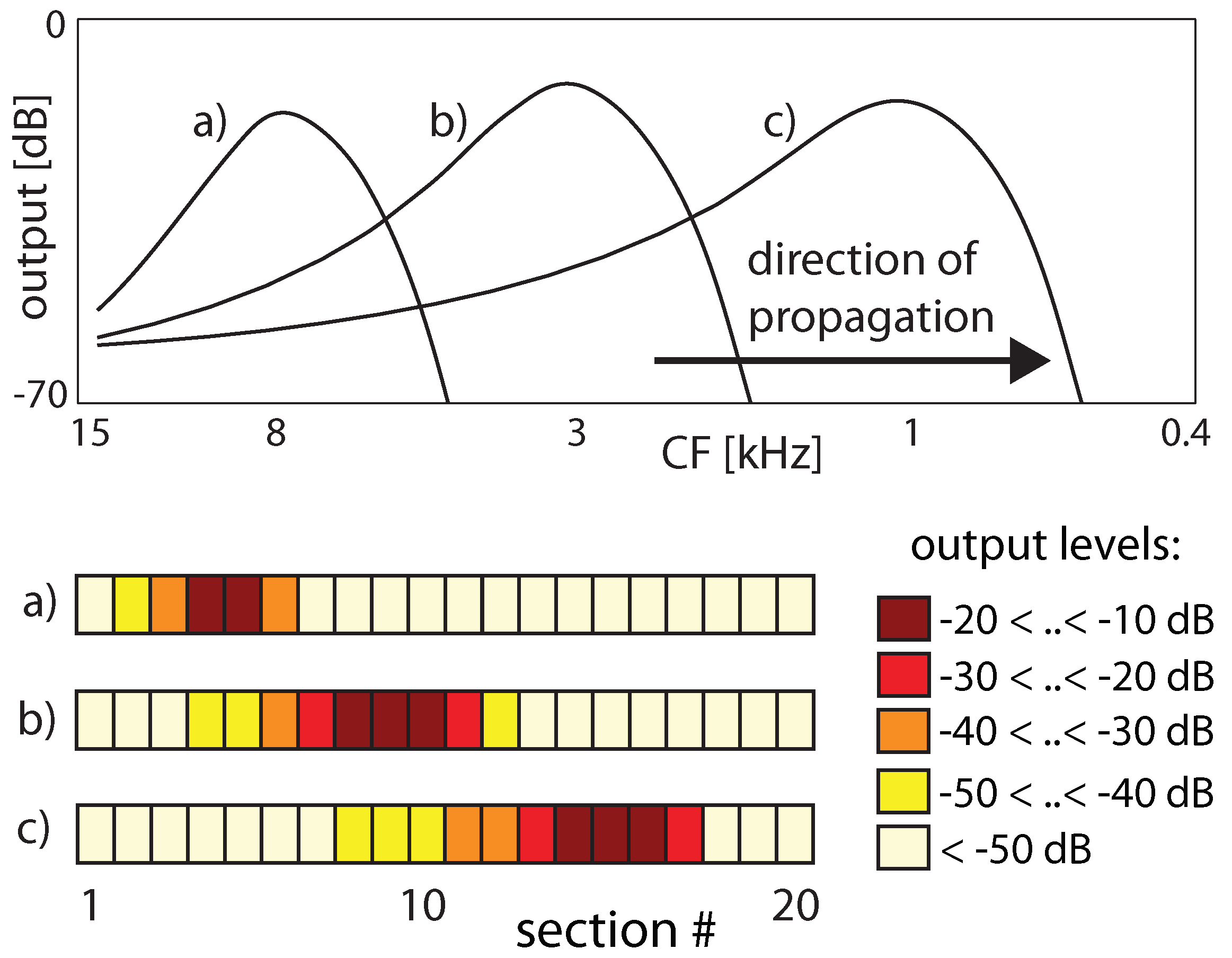
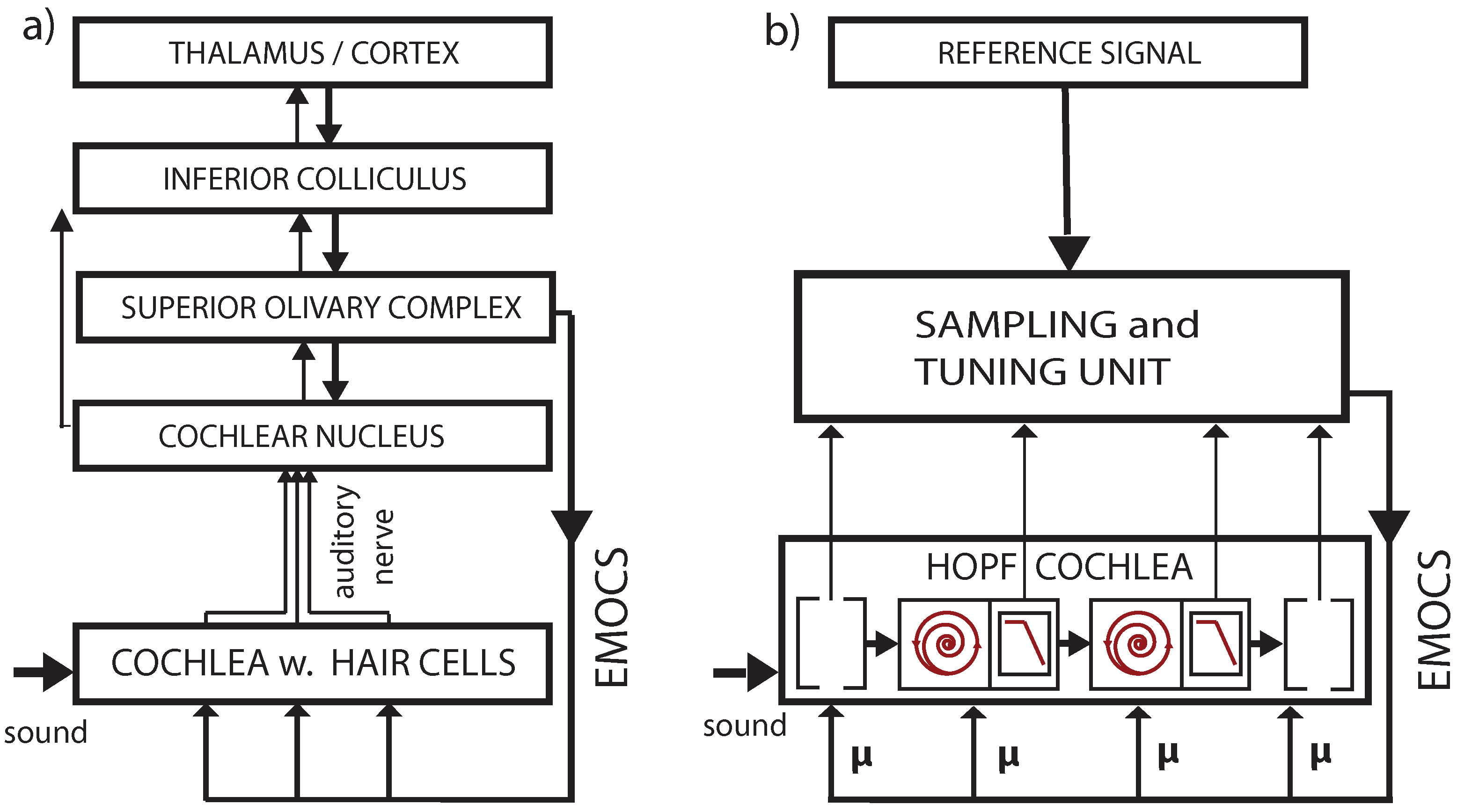
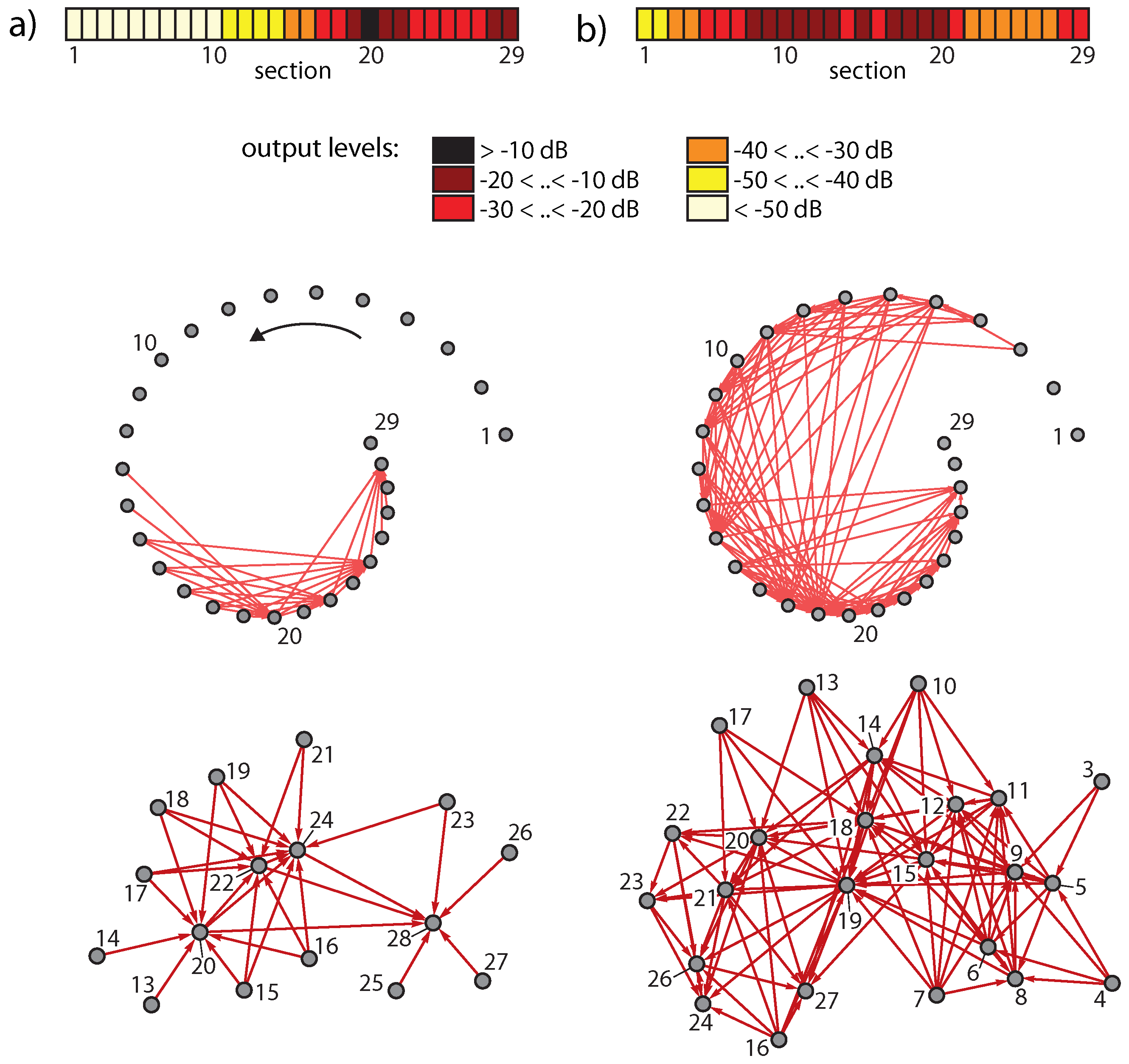
3.2. Cochlear Prototype of Neural Circuits
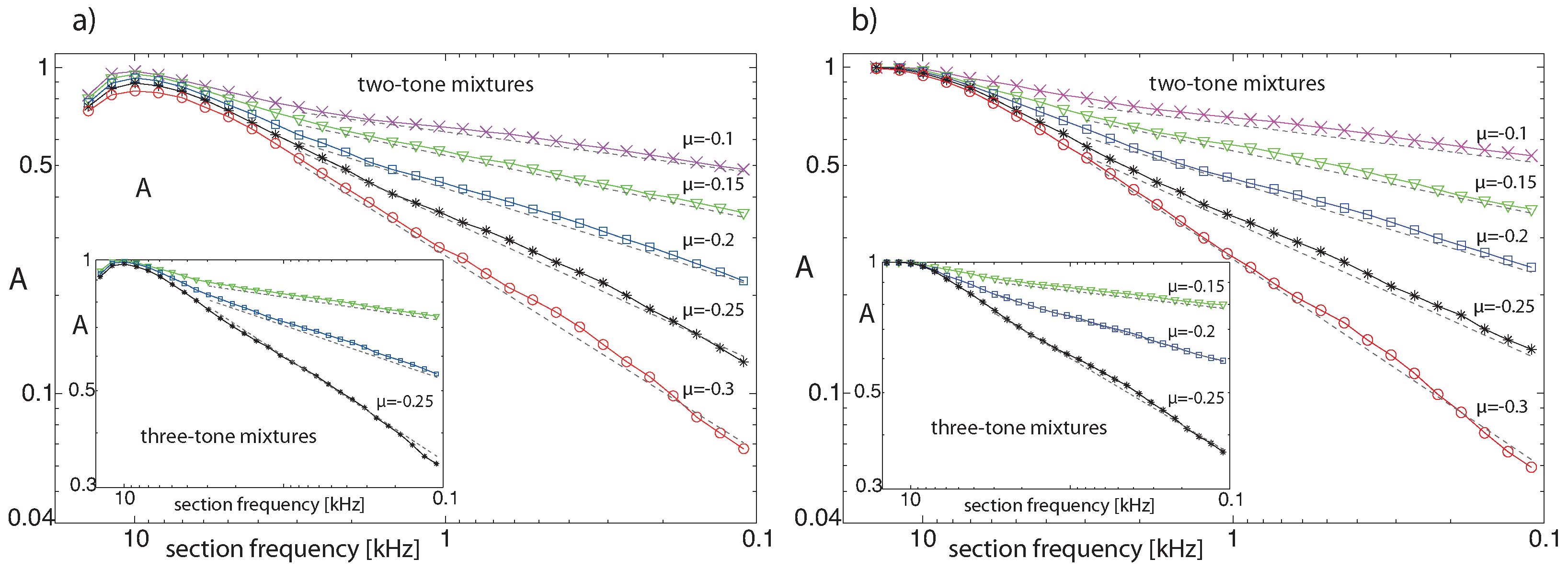
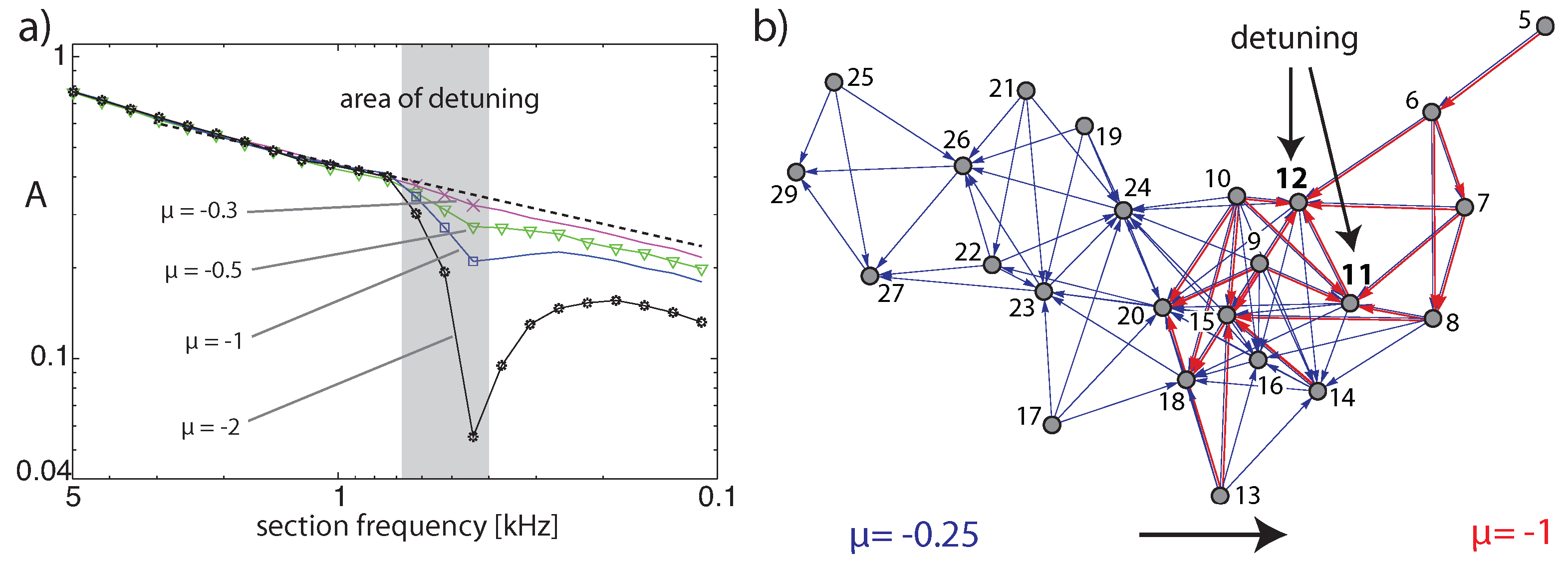
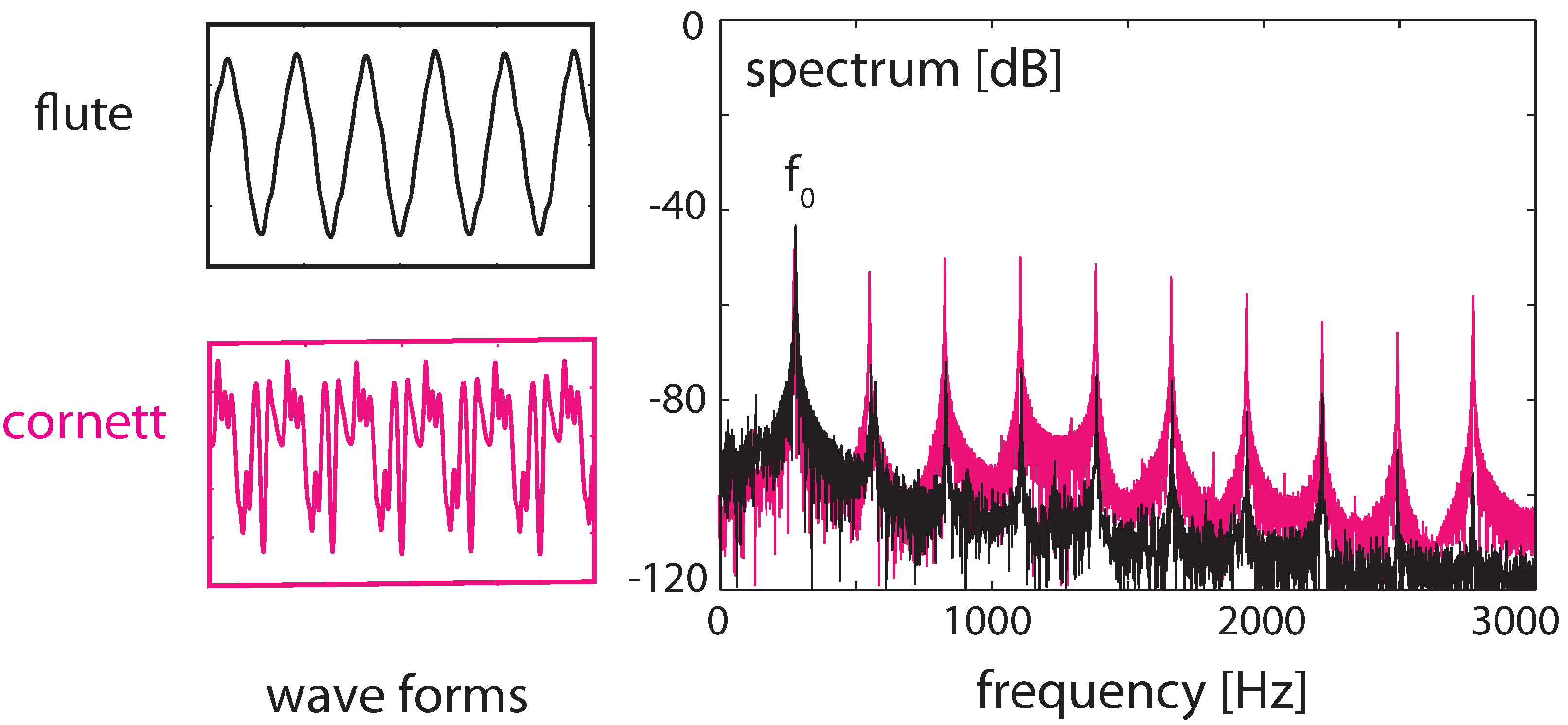
3.3. Effects of Computation
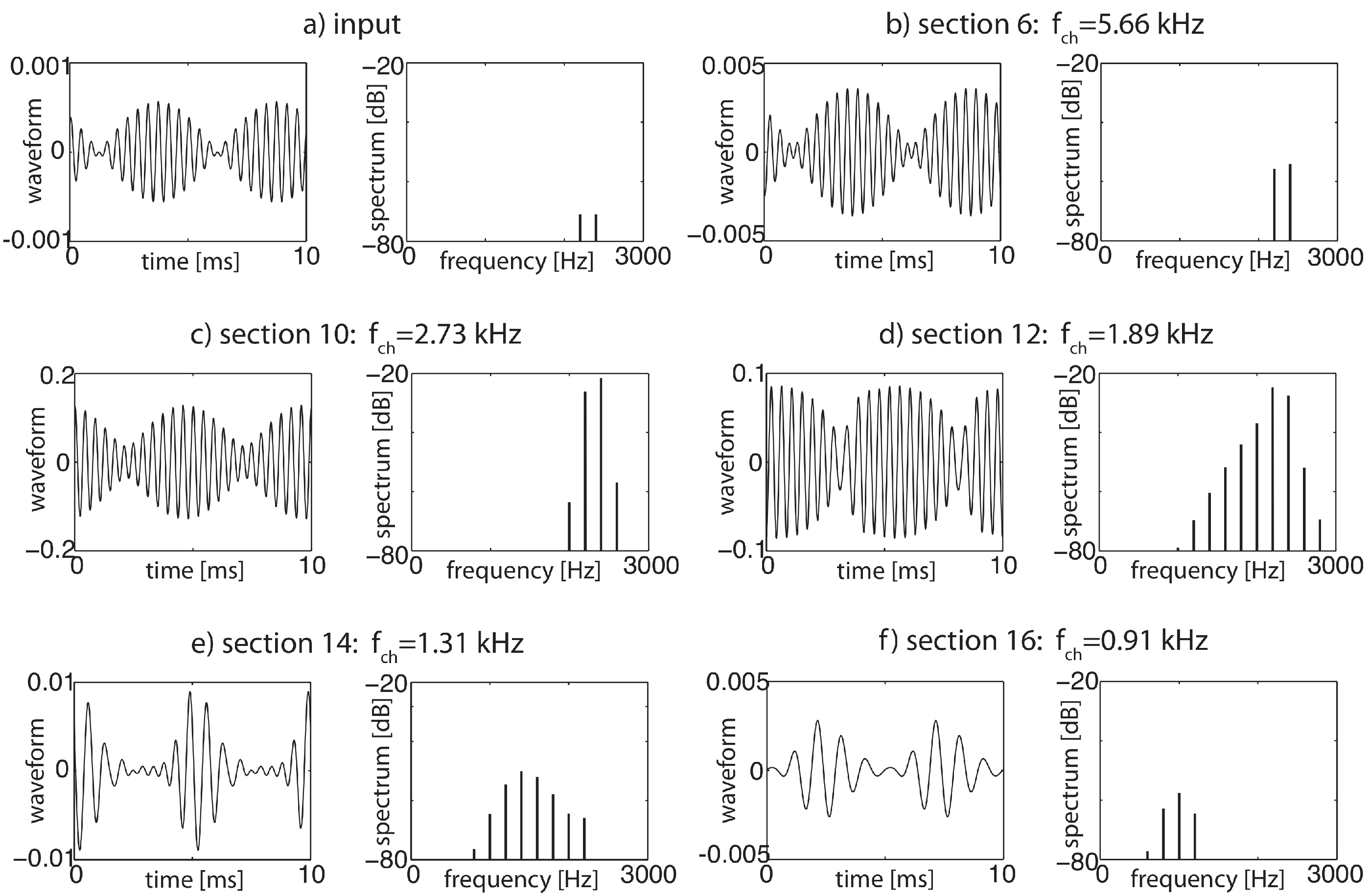
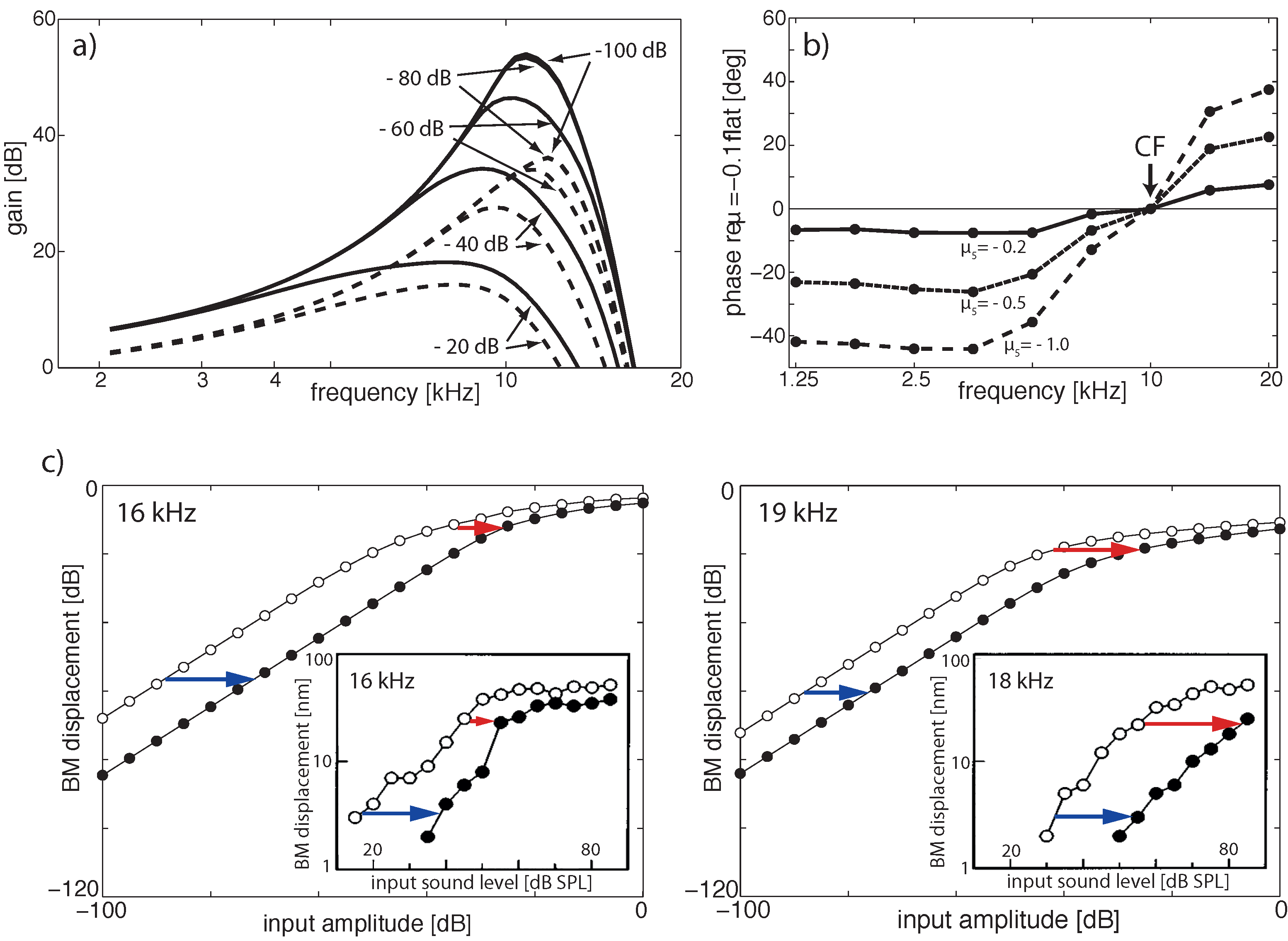
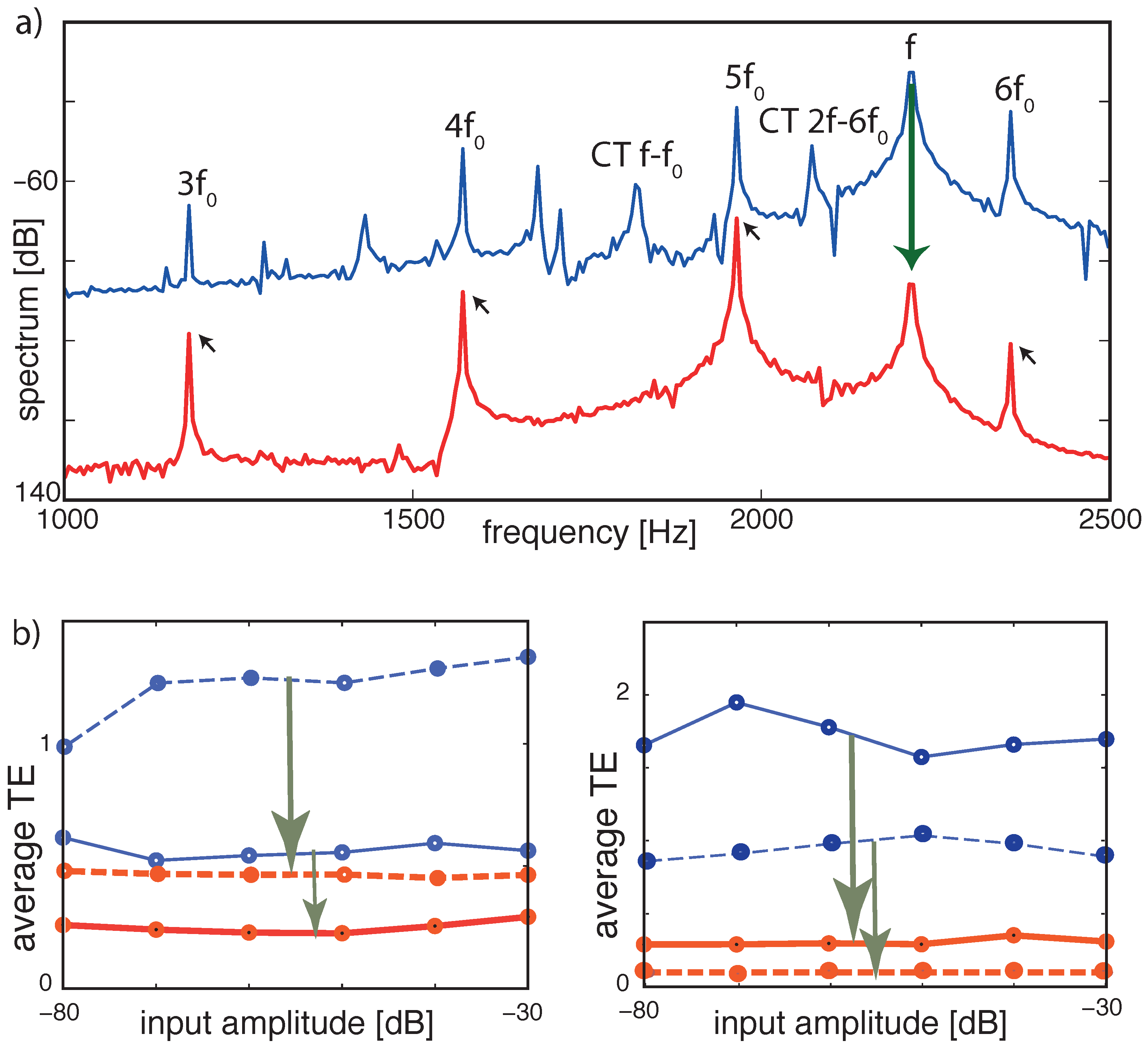
3.4. Real-World Example of EMOCS-Guided Computation
3.5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vogels, T.P.; Rajan, K.; Abbott, L.F. Neural network dynamics. Annu. Rev. Neurosci. 2005, 28, 357–376. [Google Scholar] [CrossRef] [PubMed]
- Ringach, D.L. Spontaneous and driven cortical activity: Implications for computation. Curr. Opin. Neurobiol. 2009, 19, 439–444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sussillo, D. Neural circuits as computational dynamical systems. Curr. Opin. Neurobiol. 2014, 25, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Kanders, K.; Lorimer, T.; Stoop, R. Avalanche and edge-of-chaos criticality do not necessarily co-occur in neural networks. Chaos 2017, 27, 047408. [Google Scholar] [CrossRef] [PubMed]
- Kanders, K.; Lee, H.; Hong, N.; Nam, Y.; Stoop, R. Fingerprints of a second order critical line in developing neural networks. Commun. Phys. 2020, 3, 13. [Google Scholar] [CrossRef] [Green Version]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [CrossRef] [Green Version]
- Mazzoni, A.; Broccard, F.D.; Garcia-Perez, E.; Bonifazi, P.; Ruaro, M.E.; Torre, V. On the dynamics of the spontaneous activity in neuronal networks. PLoS ONE 2007, 2, e439. [Google Scholar] [CrossRef] [Green Version]
- Pasquale, V.; Massobrio, P.; Bologna, L.L.; Chiappalone, M.; Martinoia, S. Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neurosciences 2008, 153, 1354–1369. [Google Scholar] [CrossRef]
- Petermann, T.; Thiagarajana, T.C.; Lebedev, M.A.; Nicolelis, M.A.L.; Chialvo, D.R.; Plenz, D. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl. Acad. Sci. USA 2009, 106, 15921–15926. [Google Scholar] [CrossRef] [Green Version]
- Hahn, G.; Petermann, T.; Havenith, M.N.; Yu, S.; Singer, W.; Plenz, D.; Nikolić, D. Neuronal avalanches in spontaneous activity in vivo. J. Neurophysiol. 2010, 104, 3312–3322. [Google Scholar] [CrossRef]
- Allegrini, P.; Paradisi, P.; Menicucci, D.; Gemignani, A. Fractal complexity in spontaneous EEG metastable-state transitions: New vistas on integrated neural dynamics. Front. Physiol. 2010, 1, 128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palva, J.M.; Zhigalov, A.; Hirvonen, J.; Korhonen, O.; Linkenkaer-Hansen, K.; Palva, S. Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws. Proc. Natl. Acad. Sci. USA 2013, 110, 3585–3590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tagliazucchi, E.; Balenzuela, P.; Fraiman, D.; Chialvo, D.R. Criticality in large-scale brain FMRI dynamics unveiled by a novel point process analysis. Front. Physiol. 2012, 3, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Mora, T.; Bialek, W. Are biological systems poised at criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef] [Green Version]
- Beggs, J.M. The criticality hypothesis: How local cortical networks might optimize information processing. Philos. Trans. R. Soc. A 2008, 366, 329–343. [Google Scholar] [CrossRef]
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef] [Green Version]
- Hesse, J.; Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci. 2014, 8, 166. [Google Scholar] [CrossRef] [Green Version]
- Priesemann, V.; Wibral, M.; Valderrama, M.; Pröpper, R.; Le Van Quyen, M.; Geisel, T.; Triesch, J.; Nikolic, D.; Munk, M.H. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 2014, 8, 108. [Google Scholar] [CrossRef] [Green Version]
- Shew, W.L.; Plenz, D. The functional benefits of criticality in the cortex. Neuroscientist 2013, 19, 88–100. [Google Scholar] [CrossRef]
- Shew, W.L.; Yang, H.; Petermann, T.; Roy, R.; Plenz, D. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci. 2009, 29, 15595–15600. [Google Scholar] [CrossRef]
- Haldeman, C.; Beggs, J.M. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys. Rev. Lett. 2005, 94, 058101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoop, R.; Gomez, F. Auditory power-law activation avalanches exhibit a fundamental computational ground state. Phys. Rev. Lett. 2016, 117, 038102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Touboul, J.; Destexhe, A. Power-law statistics and universal scaling in the absence of criticality. Phys. Rev. E 2017, 95, 012413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martinello, M.; Hidalgo, J.; Maritan, A.; di Santo, S.; Plenz, D.; Muñoz, M.A. Neural theory and scale-free neural dynamics. Phys. Rev. X 2017, 7, 041071. [Google Scholar] [CrossRef] [Green Version]
- Beggs, J.M.; Timme, N. Being critical of criticality in the brain. Front. Physiol. 2012, 3, 163. [Google Scholar] [CrossRef] [Green Version]
- Gomez, F.; Saase, V.; Buchheim, N.; Stoop, R. How the ear tunes in to sounds: A physics approach. Phys. Rev. Appl. 2014, 1, 014003. [Google Scholar] [CrossRef]
- Gomez, F.; Stoop, R. Mammalian pitch sensation shaped by the cochlear fluid. Nat. Phys. 2014, 10, 530–536. [Google Scholar] [CrossRef] [Green Version]
- Kadanoff, L.P. Scaling laws for Ising models near Tc. Phys. Phys. Fiz. 1966, 6, 263–272. [Google Scholar] [CrossRef] [Green Version]
- Tong, D. Statistical Field Theory; Lecture Notes; University of Cambridge: Cambridge, UK, 2017. [Google Scholar]
- Täuber, U.C. Critical Dynamics: A Field Theory Approach to Equilibrium and Non-Equilibrium Scaling Behavior; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Zarzycki, J. Glasses and the Vitreous State; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Feigenbaum, M.J. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 1978, 19, 158. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Universality in Complex Discrete Dynamics; Report 1975–1976; LA-6816-PR, 98-102; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1976. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Wechsler, D.; Stoop, R. Complex structures and behavior from elementary adaptive network automata. In Emergent Complexity from Nonlinearity, in Physics, Engineering and the Life Sciences; Springer: Cham, Switzerland, 2017; Volume 191, pp. 105–126. [Google Scholar]
- Amaral, L.A.N.; Scala, A.; Barthélémy, M.; Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad. Sci. USA 2000, 97, 11149. [Google Scholar] [CrossRef] [Green Version]
- Mossa, S.; Barthélémy, M.; Stanley, H.E.; Amaral, L.A.N. Truncation of power law behavior in ‘scale-free’ network models due to information filtering. Phys. Rev. Lett. 2002, 88, 138701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dorogovtsev, S.N.; Mendes, J.F.F. Language as an evolving word web. Proc. R. Soc. Lond. B 2001, 268, 2603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Assenza, S.; Gutiérrez, R.; Gómez-Gardeñes, J.; Latora, V.; Boccaletti, S. Emergence of structural patterns out of synchronization in networks with competitive interactions. Sci. Rep. 2011, 1, 99. [Google Scholar] [CrossRef] [PubMed]
- Eurich, C.W.; Herrmann, J.M.; Ernst, U.A. Finite-size effects of avalanche dynamics. Phys. Rev. E 2002, 66, 066137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levina, A.; Herrmann, J.M.; Geisel, T. Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys. 2007, 3, 857. [Google Scholar] [CrossRef]
- de Arcangelis, L.; Lombardi, F.; Herrmann, H.J. Criticality in the brain. J. Stat. Mech. 2014, 3, P03026. [Google Scholar] [CrossRef]
- Lorimer, T.; Gomez, F.; Stoop, R. Two universal physical principles shape the power-law statistics of real-world networks. Sci. Rep. 2015, 5, 12353. [Google Scholar] [CrossRef] [Green Version]
- Stoop, R.; Stoop, N.; Bunimovich, L.A. Complexity of Dynamics as Variability of Predictability. J. Stat. Phys. 2004, 114, 1127–1137. [Google Scholar] [CrossRef]
- van der Waals, J.D. Over de Continuiteit van den gas—En Vloeistoftoestand; Sijthoff: Leiden, The Netherlands, 1873. [Google Scholar]
- Held, J.; Lorimer, T.; Pomati, F.; Stoop, R.; Albert, C. Second-order phase transition in phytoplankton trait dynamics. Chaos 2020, 30, 053109. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J.Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- Olami, Z.; Feder, H.J.S.; Christensen, K. Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes. Phys. Rev. Lett. 1992, 68, 1244–1247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drossel, B.; Schwabl, F. Self-organized critical forest-fire model. Phys. Rev. Lett. 1992, 69, 1629–1632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in a simple model of evolution. Phys. Rev. Lett. 1993, 71, 4083–4086. [Google Scholar] [CrossRef] [PubMed]
- Langton, C. Studying artificial life with cellular automata. Physica D 1986, 22, 120–149. [Google Scholar] [CrossRef] [Green Version]
- Packard, N. Adaptation Toward the Edge of Chaos. In Dynamic Patterns in Complex Systems; World Scientific: Singapore, 1988. [Google Scholar]
- Crutchfield, J.P.; Young, K. Computation at the Onset of Chaos. In Entropy, Complexity, and the Physics of Information; Zurek, W., Ed.; SFI Studies in the Sciences of Complexity, VIII; Addison-Wesley: Reading, MA, USA, 1990; pp. 223–269. [Google Scholar]
- Bak, P.; Tang, C. Earthquakes as a self-organized critical phenomenon. J. Geophys. Res. 1989, 94, 635–637. [Google Scholar] [CrossRef] [Green Version]
- Harris, T.E. The Theory of Branching Processes; Dover Publications: New York, NY, USA, 1989. [Google Scholar]
- Zapperi, S.; Lauritsen, K.B.; Stanley, H.E. Self-organized branching processes: Mean-field theory for avalanches. Phys. Rev. Lett. 1995, 75, 4071–4074. [Google Scholar] [CrossRef] [Green Version]
- Tetzlaff, C.; Okujeni, S.; Egert, U.; Wörgötter, F.; Butz, M. Self-organized criticality in developing neuronal networks. PLoS Comput. Bio. 2010, 6, e1001013. [Google Scholar] [CrossRef] [Green Version]
- Shew, W.L.; Clawson, W.P.; Pobst, J.; Karimipanah, Y.; Wright, N.C.; Wessel, R. Adaptation to sensory input tunes visual cortex to criticality. Nat. Phys. 2015, 11, 659–664. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, T.L.; Ribeiro, S.; Belchior, H.; Caixeta, F.; Copelli, M. Undersampled critical branching processes on small-world and random networks fail to reproduce the statistics of spike avalanches. PLoS ONE 2014, 9, e94992. [Google Scholar]
- Yaghoubi, M.; de Graaf, T.; Orlandi, J.G.; Girotto, F.; Colicos, M.A.; Davidsen, J. Neuronal avalanche dynamics indicates different universality classes in neuronal cultures. Sci. Rep. 2018, 8, 3417. [Google Scholar] [CrossRef] [PubMed]
- Sethna, J.P.; Dahmen, K.A.; Myers, C.R. Crackling noise. Nature 2001, 410, 242–250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sethna, J.P. Statistical Mechanics: Entropy, Order Parameters and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Stoop, R.; Stoop, N. Natural computation measured as a reduction of complexity. Chaos 2004, 14, 675–679. [Google Scholar] [CrossRef] [PubMed]
- Gomez, F.; Lorimer, T.; Stoop, R. Signal-coupled subthreshold Hopf-type systems show a sharpened collective response. Phys. Rev. Lett. 2016, 116, 108101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kern, A.; Stoop, R. Essential role of couplings between hearing nonlinearities. Phys. Rev. Lett. 2003, 91, 128101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin, P.; Bozovic, D.; Choe, Y.; Hudspeth, A.J. Spontaneous oscillation by hair bundles of the bullfrog’s sacculus. J. Neurosci. 2003, 23, 4533–4548. [Google Scholar] [CrossRef] [Green Version]
- Martignoli, S.; Gomez, F.; Stoop, R. Pitch sensation involves stochastic resonance. Sci. Rep. 2013, 3, 2676. [Google Scholar] [CrossRef] [Green Version]
- Mountain, D.C.; Hubbard, A.E. Computational analysis of hair cell and auditory nerve processes. In Auditory Computation; Hawkins, H.L., McMullen, T.A., Popper, A.N., Fay, R.R., Eds.; Springer: New York, NY, USA, 1996; pp. 121–156. [Google Scholar]
- Lopez-Poveda, E.A.; Eustaquio-Martín, A. A biophysical model of the inner hair cell: The contribution of potassium current to peripheral compression. J Assoc. Res. Otolaryngol. 2006, 7, 218–235. [Google Scholar] [CrossRef] [Green Version]
- Meddis, R.; Popper, A.N.; Lopez-Poveda, E.; Fay, R.R. Computational Models of the Auditory System; Springer: New-York, NY, USA, 2010. [Google Scholar]
- Wiesenfeld, K.; McNamara, B. Period-doubling systems as small-signal amplifiers. Phys. Rev. Lett. 1985, 55, 13–16. [Google Scholar] [CrossRef]
- Wiesenfeld, K.; McNamara, B. Small-signal amplification in bifurcating dynamical systems. Phys. Rev. A 1986, 33, 629–642. [Google Scholar] [CrossRef]
- Eguíluz, V.M.; Ospeck, M.; Choe, Y.; Hudspeth, A.J.; Magnasco, M.O. Essential nonlinearities in hearing. Phys. Rev. Lett. 2000, 84, 5232–5235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camalet, S.; Duke, T.; Julicher, F.; Prost, J. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proc. Natl. Acad. Sci. USA 2000, 97, 3183–3188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guinan, J.J. Olivocochlear efferents: Anatomy, physiology, function, and the measurement of efferent effects in humans. Ear Hear. 2006, 27, 589–607. [Google Scholar] [CrossRef] [PubMed]
- Cooper, N.P.; Guinan, J.J. Efferent-mediated control of basilar membrane motion. J. Physiol. 2006, 576, 49–54. [Google Scholar] [CrossRef] [PubMed]
- Ruggero, M.A.; Rich, N.C.; Recio, A.; Narayan, S.S.; Robles, L. Basilar- membrane responses to tones at the base of the chinchilla cochlea. J. Acoust. Soc. Am. 1997, 101, 2151–2163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kern, A.; Stoop, R. Principles and typical computational limitations of sparse speaker separation based on deterministic speech features. Neural Comput. 2011, 23, 2358–2389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russell, I.J.; Murugasu, E. Medial efferent inhibition suppresses basilar membrane responses to near characteristic frequency tones of moderate to high intensities. J. Acoust. Soc. Am. 1997, 102, 1734–1738. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stoop, R.; Gomez, F. The Analysis of Mammalian Hearing Systems Supports the Hypothesis That Criticality Favors Neuronal Information Representation but Not Computation. Entropy 2022, 24, 540. https://doi.org/10.3390/e24040540
Stoop R, Gomez F. The Analysis of Mammalian Hearing Systems Supports the Hypothesis That Criticality Favors Neuronal Information Representation but Not Computation. Entropy. 2022; 24(4):540. https://doi.org/10.3390/e24040540
Chicago/Turabian StyleStoop, Ruedi, and Florian Gomez. 2022. "The Analysis of Mammalian Hearing Systems Supports the Hypothesis That Criticality Favors Neuronal Information Representation but Not Computation" Entropy 24, no. 4: 540. https://doi.org/10.3390/e24040540
APA StyleStoop, R., & Gomez, F. (2022). The Analysis of Mammalian Hearing Systems Supports the Hypothesis That Criticality Favors Neuronal Information Representation but Not Computation. Entropy, 24(4), 540. https://doi.org/10.3390/e24040540




