The Regulatory Capacity of Bivalent Genes—A Theoretical Approach

Abstract

Bivalent genes are frequently associated with developmental and lineage specification processes. Resolving their bivalency enables fast changes in their expression, which potentially can trigger cell fate decisions. Here, we provide a theoretical model of bivalency that allows for predictions on the occurrence, stability and regulatory capacity of this prominent modification state. We suggest that bivalency enables balanced gene expression heterogeneity that constitutes a prerequisite of robust lineage priming in somatic stem cells. Moreover, we demonstrate that interactions between the histone and DNA methylation machineries together with the proliferation activity control the stability of the bivalent state and can turn it into an unmodified state. We suggest that deregulation of these interactions underlies cell transformation processes as associated with acute myeloid leukemia (AML) and provide a model of AML blast formation following deregulation of the Ten-eleven Translocation (TET) pathway.

1. Introduction

In the last decade, different histone modifications have been implicated in transcriptional regulation of genes. In this regard, tri-methylation of lysine 4 and 27 at histone H3 are well studied modifications [1]. Tri-methylation of lysine 4 at histone H3 (H3K4me3), if present at nucleosomes that are associated with CpG-rich gene promoters, has been found to be positively correlated with the transcription of the respective gene. In contrast, tri-methylation of lysine 27 at histone H3 (H3K27me3), if present at these nucleosomes, is often associated with gene repression. Experimentally, a non-linear, approximately sigmoidal relationship between gene transcription and the modification level of the gene promoter has been observed for both the H3K4me3 and the H3K27me3 modification [2]. Thereby, the modification level of H3K4me3 at the promoter of a gene changes from low to high, when the transcription rate of the gene exceeds a particular threshold. The opposite holds true for the modification level of H3K27me3.

It has been shown that both the H3K4me3 and the H3K27me3 modification are set by specific methyltransferase complexes (tri-thorax and polycomb group complexes, respectively) that can not only write but also read the modification [1]. This capability results in a positive feedback on writing the modification. Such feedback enables bi-stability, i.e., the coexistence of two stable modification states. Accordingly, cells can either carry a modified or an unmodified gene under the same, defined conditions. We have predicted that the occurrence of bi-stable modification states depends, e.g., on the histone (de)-modification rates, the methylation of the associated DNA or the number of nucleosomes that are cooperatively modified [3].

Genes that carry both the H3K4me3 and the H3K27me3 modification at nucleosomes associated with their promoter region are called bivalent and typically show an intermediate gene expression. Initially, bivalency has been described as a “zonal” phenomenon only, in which a broad domain of H3K27me3 surrounds a narrower one of H3K4me3. However, it has been demonstrated recently that both modifications indeed can reside at the same nucleosome [4]. We here focus on such truly bivalent nucleosomes being often enriched in the vicinity of the transcription start site of a gene [5]. Bivalent genes have come into research focus because they often change their modification state from bivalent to monovalent during developmental processes [6]. These dynamic state changes are accompanied by alterations in the transcription of the affected gene. Loss of H3K27me3 is accompanied by transcriptional activation of the gene, while a loss of H3K4me3 is related to its transcriptional repression. Well known examples of bivalent genes are genes encoding transcription factors (TFs) involved in developmental and stem cell differentiation processes, such as GATA3 [7] and Achaete-scute complex homolog 2 (ASCL2) [8] being involved in hematopoietic and intestinal lineage specification, respectively, or ATOH1 controlling sensory hair cell differentiation [9]. Findings on such TFs suggest an instructive role of bivalent histone modifications regarding cell fate decisions by controlling heterogeneous gene expression. Nevertheless, a mechanistic understanding of this control process is still largely missing.

In the following, we introduce a theoretical model of bivalency to gain a mechanistic understanding of the link between histone modification and transcriptional regulation. In particular, we analyze the stability of the bivalent state depending on the properties of the histone modification and transcriptional machinery. By computational simulation, we demonstrate: (i) that the regulatory circuit can induce stable gene expression heterogeneity in proliferating cell populations by (reversible) transitions from the bivalent modification state into the monovalent states; and (ii) that these transitions are a consequence of a particular kind of asymmetric cell division randomly distributing modified histones from the mother onto the daughter cells. Subsequently, we investigate the role of DNA methylation in this process. We show: (i) that following DNA methylation the bivalent state becomes destabilized; and (ii) that under these conditions gene expression heterogeneity can be induced by active DNA demethylation. Our findings have implications for a better understanding the control and deregulation of cell population heterogeneity as observed, e.g., in the hematopoietic stem cell system and during tissue transformation, as e.g., blast formation in acute myeloid leukemia (AML).

2. Basic Model Assumptions

2.1. Epigenetic Regulation of Transcription: The Basic Regulatory Circuit

In the following, we built on an established theoretical model of histone methylation, which has been introduced by our group previously [3,10]. This model, which applies to histone modifications of CpG-rich gene promoters, considers dynamic histone modification states due to permanent histone de-modification processes. It quantifies modification levels as the fraction of modified nucleosomes associated with the promoter. The modification processes are described in dependence of binding properties of the histone methyltransferase (HMT) complexes to nucleosomes and the associated DNA, which change depending on their respective methylation state. Details on the basic model system can be found in [3].

In an extension of the model [11], we have recently introduced a positive feedback loop between the transcriptional activity of the gene (T) and the H3K4me3 modification level (m₄). Based on experimental findings, we assumed that transcriptional activity facilitates recruitment of H3K4me3 HMTs [12] and that H3K4me3 contributes in recruiting Pol II [13]. In the following, we assume a negative feedback loop between transcriptional activity (T) and the H3K27me3 level (m₂₇) in addition. We assume that transcriptional activity suppresses the recruitment of the H3K27me3 HMTs and that H3K27me3 impedes recruitment of Pol II. In fact, binding of activating TFs in the promoter region has been reported as a major factor suppressing H3K27me3 modification [14]. Moreover, polycomb group complexes, containing the HMTs of H3K27me3, have been suggested to suppress transcription by preventing the binding of acetyl-transferases to target genes [15].

In a first version of the model (MV1, Figure 1A), we neglect effects of DNA methylation at the gene promoter. We describe genes that are effectively protected from DNA methylation independent of the histone modification states of the associates nucleosomes; as genes that undergo permanent DNA demethylation, e.g., due to the activity of Ten-eleven Translocation (TET) proteins (reviewed in [16]). We do not consider explicit interdependencies between the two histone modifications.

This model constraint will be released in a second version of the model (MV2, Figure 1B) that includes interactions between histone and DNA methylation at the gene promoter. In order to describe the DNA methylation level of the gene promoter m_DNA, i.e., the fraction of methylated CpGs at the promoter, we basically use the same mathematical formulation of the DNA methylation machinery as described in [10]. Thus, we consider maintenance and de novo DNA methylation, controlled by the DNA methyltransferases 1 (DNMT1) and 3a,b (DNMT3a,b), respectively. Both processes are assumed to be active during cell division only. In accordance with experimental observations, we assume DNA methylation to be subject to regulatory feedback loops with both H3K4me3 and H3K27me3. We assume that H3K4me3 suppresses binding of de novo DNMTs [17] and that DNA methylation weakens the binding of H3K4me3 HMTs to DNA [18]. The latter is assumed also for H3K27me3 HMTs [14]. In contrast to H3K4me3, H3K27me3 is assumed to contribute in recruiting de novo DNMTs, and thus destabilizes itself. This is in agreement with experimental findings showing that the H3K27me3 HMT Enhancer of zeste homolog 2 (EZH2) recruits DNMTs, but the DNMTs subsequently do not induce de novo DNA methylation before H3K27me3 is removed [19].

DNA methylation is assumed to have no direct impact on transcription. This assumption is in agreement with experimental findings, which show that transcriptional silencing of promoters precedes their DNA methylation [20].

2.2. Simulations of Cell Populations

We analyze the dynamics of transcription, histone modifications and DNA methylation in a small cell population of 100 cells by stochastic simulations of the behavior of the bivalent circuit. One simulation consists of 10,000 simulation steps. We record the state of the cells every 100 simulation steps, here referred as one time step. Thereby, changes of the regulatory state of an individual cell originate in fluctuations of the histone methylation states that depend on the methylation state of the associated DNA and on gene transcription. We neglect all other types of permanent fluctuations, e.g., fluctuations in Pol II binding [21]. Fluctuations of histone modifications are simulated considering modification and de-modification of individual histones that are associated with the gene promoter with rate k_mod θ^K and k_de, respectively. Here, k_mod and k_de are constants and θ^K (K = 4, 27) is the binding affinity of the respective HMT [3]. Subsequent changes in DNA methylation and transcription are simulated according to differential equations given in the text below. The regulatory states are mapped on discrete cell fates (e.g., the bivalent state) that define subpopulations of cells.

It has been shown experimentally that during cell division the histones of the mother cell are randomly distributed onto the two daughters [22]. Accordingly, cell division results in a strong dilution of the modified histones in both daughter cells. We simulated these effects of cell division by performing a dilution of the modified histones after a (gamma-distributed) waiting time, i.e., after cell cycle time τ [23]. Whenever one daughter cell retains a fraction x of the modified nucleosomes present in the mother, the other daughter retains a fraction (1 − x). We consider that the cells compete for space within their niches. Accordingly, we keep the total number of cells fixed assuming that each increase due to a cell division event is exactly balanced by cell loss from the niche. Thereby, subpopulations might differ in their specific cell loss probability.

3. Results

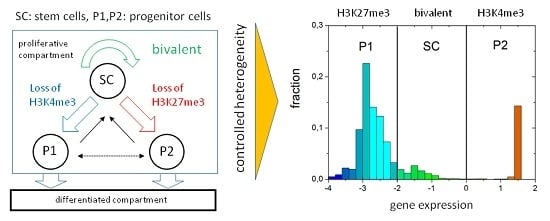
3.1. The Occurrence of the Bivalent Modification States

Our model is consistent with the experimental finding of a non-linear, approximately sigmoidal relationship between gene transcription and the modification level of the gene promoter; for both the H3K4me3 and the H3K27me3 modification [2]. The H3K4me3 (H3K27me3) modification level of a gene changes from low to high (high to low), when its transcription rate exceeds a particular threshold. Depending on the transcriptional level at which this change occurs for the individual modification, here referred as T_K (K = K4, K27), one can, in general, distinguish two cases (Figure 2A).

In the case T_K27 is smaller than T_K4 (System A1) one observes an “unmodified” state for transcription levels between T_K27 and T_K4. In this state the nucleosomes associated with the gene promoter are neither H3K4me3 nor H3K27me3 modified. Increasing the transcription in this case, the promoter modification state will change from “H3K27me3” to “unmodified” to “H3K4me3”. In the opposite case, where T_K27 is larger than T_K4 (System A2), one observes a “bivalent” state for transcriptional levels between T_K4 and T_K27. In this state, the nucleosomes associated with the gene promoter are H3K4me3 and H3K27me3 modified.

Which of these cases is actually realized for a particular gene depends, among others, on the promoter accessibility for HMTs. Thus, system A1 (Figure 2A, thin lines) can be changed to system A2 (Figure 2A, thick lines) just by assuming a more open chromatin state (see: Appendix A). Accordingly, our model predicts that cells with an open chromatin state, such as embryonic stem cells (ESC), will have more bivalent genes than cells with more condensed chromatin, in agreement with experimental observations [24]. Another way to induce bivalent states is increasing the cooperativity of HTM binding and thereby inducing bi-stable states of the both histone modifications (Figure 2B, regions I and III, [3]). In the System A1 (Figure 2A), such an increase of the cooperativity switches the unmodified state, seen for transcriptional levels between T_K27 and T_K4 into a bivalent state (Figure 2B, region II). Our further studies are focused on systems with high cooperativity of HTM binding.

3.2. Balance between Histone Modification States (the Histone Modification Machinery)

In our model each value of the H3K4me3 modification level (m₄) and the H3K27me3 modification level (m₂₇) is associated with a well-defined transcription level T₁(m₄) and T₂(m₂₇), respectively, via a self-consistent equation. In contrast, due to potential bi-stability of the modifications, a specific transcription level can be associated with either one or three different modification levels (compare: Figure 2). The explicit functions T₁(m₄) and T₂(m₂₇) used in our model are given in the Appendix A. All modification states, i.e., all pairs {m₄*, m₂₇*}, which can be realized given a particular organization of the histone modification machinery, need to solve the equation:

$$T_1\left({\mathrm{m}}_4*;\left\{\mathrm{X}\right\}\right)=T_2\left({\mathrm{m}}_{27}*;\left\{\mathrm{X}\right\}\right)$$

(1)

Thereby, the solutions depend on the parameter set {X}. Among these parameters are the binding energies of the HMTs, the histone (de-)modification rates and the number N_H of cooperative nucleosomes associated with the gene promoter. Examples of the set of possible modification states {m₄*, m₂₇*} are shown in Figure 3A for genes with different numbers of cooperative nucleosomes N_H. For N_H > 5, bi-stable regions for m₄ and m₂₇ are induced (compare: Figure 2B). Thus, for a limited range of m₄ (m₂₇) three possible pairs {m₄*, m₂₇*} exist for each value of m₄ (m₂₇). Under the same conditions, a range of bivalent states becomes manifest that extents with increasing N_H. The full parameter sets {X} applied in these examples are given in

Table A1. Parameter set {X} of the histone modification machinery. * scaled by the Boltzmann unit.

Parameter	Value	Description
ε04, ε027	9.0, 10.0	ground enthalpy per bound HMT *
εBS4, εBS27	−5.0, −5.0	free energy of CpG binding *
εHM4, εHM27	−0.5, −0.5	free energy of histone binding *
C4, C27	0.1, 0.1	de-modification constant
NH	4/12/20	number of cooperative nucleosomes

.

3.3. Transcription Controls Epigenetics (the Transcriptional Machinery)

According to the assumptions described above, the histone modification machinery defines all possible modification states that potentially can be realized. Which of them actually become realized is defined by the transcriptional machinery. The fix points of the modeled regulatory circuit {m₄^#, m₂₇^#, T^#} are the solutions of the equation:

$$\mathrm{dT}/\mathrm{dt}=f\left({\mathrm{m}}_4*,{\mathrm{m}}_{27}*,T;\left\{\mathrm{Y}\right\}\right)=0$$

(2)

Here, dT/dt is the time derivative of T and {Y} refers to the parameter set describing the transcriptional machinery. Among the parameters of {Y} are the maximum promoter activity of a gene and the effective transcript degradation rate. In case a gene encodes a TF that auto-activates itself—which is observed for several key developmental or differentiation regulators, such as the TFs PU.1 or ASCL2 [25,26]—the parameter set {Y} contains also the parameters describing this kind of feedback; as e.g., the number N_TF of TF binding sites contained in the gene promoter that are bound by the TF encoded by the gene itself.

As m₄ and m₂₇ depend on T, solving Equation (2) in general requires solving a self-consistent equation:

$$T^{\#}=g\left({{\mathrm{m}}_4}^{\#},{{\mathrm{m}}_{27}}^{\#},T^{\#};\left\{\mathrm{Y}\right\}\right)$$

(3)

Details about the functions g applied in our study are given in the Appendix B. Figure 3B shows typical solutions of Equations (1)–(3) for different degrees of auto-activation (N_TF = 0 and 3). The gene without auto-activation (N_TF = 0) possesses three transcriptional states; two of them being stable and one being unstable. The stable, low expression state is associated with an H3K27me3 state and the intermediate expression state with a bivalent one. Introducing auto-activation (N_TF = 3) enables a third stable state—a high expressing H3K4me3 state—and increases the expression level of the bivalent state. Figure 3C shows the localization of the obtained solutions and their transcriptional level in the {m₄, m₂₇} space. It can be seen that: (i) H3K27me3 states are always related to low gene expression; (ii) the H3K4me3 states are associated with high gene expression; and (iii) the bivalent states show a broad range of intermediate expression values. For the chosen parameter set {X}, there exists no stable unmodified state independent of the chosen parameter set {Y}. The set {Y} applied in these examples is given in

Table A2. Parameter set {Y} of the transcription machinery. Rates are given in events per simulation step. * scaled by the Boltzmann unit.

Parameter	Value	Description
Pmax	100	maximum transcription rate
δ	1.5	transcript degradation rate
εA	2	free energy of polymerase binding *
FTF	4/1/0.25	regulation factor of the TF-network
NTF	0/3	number of binding sites for auto-activation

.

The described circuit can control transitions between regulatory states characterized by different histone modification levels and, thus, transcriptional activities. Such transitions can be induced, e.g., by a TF network that is linked to the gene of interest [10]. The modification states and the transcriptional activity of such a “network-driven” genes are shown in Figure 3D–F. The gene that is solely activated by the TF network (N_TF = 0, F_TF = 4, Figure 3D) has only a single stable bivalent state. However, small changes of its transcriptional activity can induce state transitions. In particular, an increase (decrease) of less than 35% of the transcriptional activity through the background TF network enables the gene to switch into a monovalent H3K4me3 (H3K27me3) state. This option does not exist for the reference gene (F_TF = 1), which can only switch between a bivalent and a monovalent H3K27me3 state. The gene with auto-feedback that is repressed by the background TF network (N_TF = 3, F_TF = 1/4, Figure 3E) possesses a bivalent state with low transcriptional activity, while the reference system (F_TF = 1) shows a bivalent state with high activity. Thus, switches into H3K4me3 and H3K27me3 states will occur with different frequencies. Figure 3F shows the localization of the fix points following gene repression and their transcriptional level in the {m₄, m₂₇} space. Remarkably, for genes that are slightly less repressed, two stable bivalent states can be observed, i.e., multiple bivalent states can exist for a single gene that is embedded in a larger regulatory network structure.

Changes between the stable states require fluctuations of the histone modification level. Details on the stability of the fix points of the system under permanent histone (de-)modification are given in Appendix C. These results demonstrate that, for the applied parameter sets, the bivalent states are more or less long term stable. Hence, cell division-related fluctuation, i.e., cell division-related dilution of modified nucleosomes, are required to resolve the bivalent states. This effect was considered in the following stochastic simulations.

3.4. Histone Modification Can Instruct Gene Expression

Epigenetic lineage priming and specification have been described for different stem cell systems including the hematopoietic system [27]. Thereby, resolution of bivalent chromatin states of TFs has particularly been associated with T-cell specification. The maybe best analyzed example is GATA3 [7,27,28]. The promoter of this gene is bivalent modified in hematopoietic stem cells (HSCs), multipotent (MPPs) and common lymphoid progenitors (CLPs) as well as in B-cells and becomes activated, i.e., it loses H3K27me3, in T-cells. In contrast, GATA3 expression becomes repressed, i.e., its promoter loses H3K4me3, in common myeloid (CMPs), granulocyte-macrophage (GMPs), and megakaryocyte-erythroid Progenitors (MEPs). Moreover, GATA3 is auto-activated [29] and the promoter DNA of GATA3 remains unmethylated in all analyzed cell types [28]. Thus, resolving the bivalent mark at nucleosomes associated with the GATA3 promoter during proliferation can serve as an example of an instructive role of histone modifications regarding gene expression. If the promoter loses the H3K27me3 marks, GATA3 expression becomes up-regulated. Up-regulation of GATA3 increases the potential to specify into T-cell lineages [30]. If the promoter loses the H3K4me3 marks, GATA3 expression becomes down-regulated and the cell starts to specify more likely into the myeloid lineage [31].

In order to study the establishment and long-term maintenance of such a heterogeneous cell population, we translated the experimental findings on a GATA3-dependent lineage specification into a general model. As illustrated in Figure 4A, the model accounts for three different cell types that are defined by their histone modification state: bivalent stem cells (SC), H3K27me3-monovalent, pro-myeloid progenitors (P1), and H3K4me3-monovalent, pro-lymphoid progenitors (P2). Furthermore, we assumed that all cell types proliferate with an average cell cycle time τ₀ of 2.5 time steps (250 simulation steps). Subsequent to each cell division P1 or P2 cells leave the system providing space for the daughters.

Starting from a homogeneous cell population of bivalent SCs, over time a heterogeneous, albeit dynamically stabilized cell population is established. This heterogeneity inherently emerges due to a random loss of H3K4me3 or H3K27me3 modifications in individual cells after cell division, which leads to bimodal H3K4me3 and H3K27me3 distributions as shown in Figure 4C. As transitions from the bivalent to a monovalent histone modification state are directly linked to changes in gene expression, the different cell types can also be distinguished based on their transcriptional activity (Figure 4B). In the model, bivalent SCs are characterized by an intermediate transcription (0.01 < T < 1), while P1 cells express low levels (T < 0.01) and P2 cells high levels (T > 1) of GATA3 (Figure 4B) closely mimicking experimental results. In contrast to typical flow cytometry measurements, which can only provide a snapshot of the population heterogeneity, computer simulations allow monitoring the dynamic changes of transcriptional (Figure 4D) and epigenetic states (Figure 4E,F) over time. It can be seen that the heterogeneity of the cell population remains long-term stable.

Systematic imbalance of the expression states of GATA3 can lead to disease. For example, loss of GATA3 induces B cell lymphoma [32]. This can be due to changes in the histone modification machinery [33]. Examples of related simulations are given in the Appendix D (Figure A4).

3.5. DNA Methylation Destabilizes Bivalent States

Thus far, we have neglected DNA methylation. However, transcription of many genes has been demonstrated to be affected by DNA methylation. In particular, methylation of CpG-rich promoters is frequently accompanied by repression of the associated gene [16]. Moreover, age-related changes in DNA methylation can be predicted by histone modification states in young individuals [34]. Thus, we considered effects of promoter DNA methylation on bivalent histone modification in a second model version (MV2).

In this setting, we describe changes of the fraction m_DNA of methylated CpGs at the gene promoter, neglecting effects of stochastic methylation of individual CpGs [35]. As consequence of the interactions between histone modifications and DNA methylation (Figure 1B), all possible modification states of the gene, i.e., all triples {m₄*, m₂₇*, m_DNA*}, need to solve, beside Equations (1)–(3), the equation:

$${\mathsf{\tau }\mathrm{dm}}_{\mathrm{DNA}}/\mathrm{dt}=H\left({\mathrm{m}}_4*,{\mathrm{m}}_{27}*,{\mathrm{m}}_{\mathrm{DNA}}*;\left\{\mathrm{Z}\right\}\right)=0$$

(4)

where dm_DNA/dt is the time derivative of m_DNA and {Z} refers to the parameter set describing the DNA methylation machinery. This set includes the probability of de novo DNA methylation D_novo and the probability of maintaining DNA methylation D_main. The parameter set {Z} is given in

Table A3. Parameter set {Z} of the DNA methylation machinery. Rates are given in events per simulation step. * scaled by the Boltzmann unit.

Parameter	Value	Description
Dmain	0.8	probability of maintaining DNA methylation
Dnovo	0.0/0.1/0.3	probability of de novo DNA methylation
DCG4, DCG27	6, 4	interaction energy between HMTs and DNMTs *
DDE0	6/2	maximum rate of active DNA demethylation

. A general difference compared to the system without DNA methylation is that the two histone states are now linked not only via transcription but also via DNA methylation. Details can be found in Appendix E.

Figure 5A shows all possible pairs {m4*, m27*} for such a regulatory system, using the same parameter set as in the unmethylated system (Figure 3A–C) for a fixed number of cooperatively acting nucleosomes (N_H = 20). It can be seen that with increasing de novo DNA methylation activity unmodified states become possible, where the nucleosomes carry neither H3K4me3 nor H3K27me3. For the system with a de novo DNA methylation probability of 0.3, four stable states are observed (Figure 5B,C); among them, two intermediate expressing states that are distinguished by their DNA methylation level. The bivalent state shows low, while the unmodified state shows high methylation.

As discussed above, state fluctuations are required to switch between the stable modification states. In simulations, we observed that DNA methylation reduces the stability of the bivalent state against fluctuations. The basin of attraction of the bivalent state shrinks and the state becomes less frequent populated (see: Appendix C, Figure A2). Thus, in the model, DNA methylation has similar effects on bivalent states as chromatin compaction (compare: Figure 2A and Appendix A) but can occur independently. In cells these events are often linked [24].

3.6. A Model of Blast Formation during AML

Besides GATA3, PU.1 is a second gene encoding a major TF responsible for specification into either the myeloid or the lymphoid lineage. In HSCs and MPPs the PU.1 promoter is associated with H3K4me3 only and accordingly the gene is expressed [27]. In myeloid progenitors PU.1 expression becomes further up-regulated, while in T-cell progenitors the gene becomes down-regulated [36]. In T-cells, the promoter loses H3K4me3 [27] and becomes methylated [37]. PU.1 can become auto-activated because it encodes a TF that binds back to its promoter [25]. This binding was suggested to result in recruitment of TET2-proteins and subsequently in active demethylation of the promoter in all cells where PU.1 is activated [38]. Strikingly, in myeloma cells, PU.1 becomes down-regulated and methylation of the PU.1 promoter is found similar to T-cells [39]. Based on these observations, we suggest a mechanistic model of TET2 mutation associated AML.

Figure 6A shows a sketch of a model of undisturbed PU.1 regulation (SC: unmodified, multi-potent progenitors: 0.01 < T < 1, P1: H3K4me3-monovalent, pro-myeloid progenitors: T < 0.01, P2: H3K27me3-monovalent, pro-lymphoid progenitors: T > 1), which considers both DNA methylation and demethylation. Thereby, DNA demethylation occurs permanently and its rate is assumed to be proportional to the expression of the PU.1 gene as suggested by the experimental finding mentioned above (see also: Appendix E). As in the GATA3 model, we assume that all cell types proliferate and that subsequent to each cell division (if available) only P1 or P2 cells are transferred into a differentiated compartment, providing space for the daughters.

Simulation results of that model are shown in Figure 6B,C. In contrast to the GATA3 model, SCs are characterized by an unmodified and partially DNA methylated state. A bistable state is not observed because both H3K4me3 and H3K27me3 have been destabilized by DNA methylation. In committed cells, PU.1 becomes either up-regulated (P1) following gain of H3K4me3 or down-regulated (P2) following gain of H3K27me3 (Appendix F, Figure A5A,B). Thereby, gain of modification is enabled as a consequence of the ongoing active DNA demethylation between two cell division events. Thus, it depends on the cell cycle time τ. Increasing τ, such that DNA demethylation is effective even for slowly demethylating promoters of repressed genes (compare: Appendix E, Equation (A9)), the bivalent state becomes stabilized (Appendix F, Figure A5C,D). In contrast to the GATA3 system, an expansion of the SC state is observed, accelerating and not decelerating proliferation (Appendix F, Figure A6).

To model blast formation, we assume that active DNA demethylation is no longer functional, e.g., according to mutations in the gene encoding TET2 [40]. Consequently, the promoter of the PU.1 gene, as other promoters being under the control of active DNA demethylation by TET2-proteins, becomes methylated independent of the expression of PU.1. This results in complete de-modification of the PU.1 promoter also in cells where PU.1 is expressed under normal conditions. The affected cells express PU.1 at an intermediate level and thus are assumed to remain in the expansive niche (see cell type definition). This copes the phenotype known from so-called “blast cells” (SC′), which show PU.1 hypermethylation and are proliferative active [41]. Simulations of the system (Figure 6D,E and Appendix F, Figure A5E,F) actually show that nearly all cells become fixed in the unmodified and DNA methylated state immediately after the TET2 mutation is induced (t = 50).

The system can be re-transformed by external triggered DNA demethylation but will fall back into the blast system in case this trigger is taken away. In contrast to recruited DNA demethylation, external triggered DNA demethylation (e.g., applying DNMT1 inhibitors) will affect all expression states in the same way and thus induces the bivalent and not the unmodified state. Under such forced DNA demethylation the PU.1 expression might be similar to the un-mutated system, but the specification of P1 and P2 is enforced by higher and not by lower cell division frequency (see discussion).

4. Discussion

Transcriptional feedback loops that enable switches between gene expression states have been identified as basic motifs of gene regulatory networks [42]. Combination of feedback mechanism allows triggering decision processes between alternative gene expression programs. Histone modifications have been originally thought to stabilize the so achieved states [43]. Nevertheless, bivalent modifications have early been implicated also in decision making regarding developmental and stem cell differentiation processes [6]. Here, we provided a mechanistic model on how they might confer their regulatory capacity. In our model, both the activity of TFs as well as cell division events can change the state of bivalent modified promoters. Accordingly, circuits of bivalent genes can be considered as responsive or instructive, respectively. The latter because cell division can not only induce switches between histone modification states [3], but can also robustly trigger cell intrinsic decision processes. In contrast to extrinsically triggered decisions, these decisions do not require a heterogeneous or fluctuating environment. They only require random distribution of histones from the mother onto the daughter cells. Thereby, cell cycle time affects the proportions of decision making. Consequently, the model predicts proliferation activities to be essential for gene expression heterogeneity. Interestingly, a recent report on bivalent genes suggests that in fast proliferating cells, as ESCs, histone modification is under cell cycle control [44].

We focused on the case where the nucleosomes associated with the gene promoter carry both H3K4me3 and H3K27me3. ChIP-seq measurements alone do not provide this information and cannot distinguish this case from a case where a fraction of cells carries one and the complementary fraction the other modification. However, such kind of heterogeneity might be equally important for lineage specification and developmental processes as shown for H3K27me3 heterogeneity [45].

Our theoretical studies build on previous results of our group on the dynamics of histone modifications that are set by HMTs, being part of protein complexes that can read the modification. The gene promoters bound by these HMTs can assume bi-stable modification states capable of encoding a memory. Similar approaches have been published for the first time by Dodd et al. [46,47]. More complex models of cooperative pattern formation of histone modifications have been suggested by Anink-Groenen et al. [48]. Here, we studied a model combining histone modifications that can activate and repress gene transcription. Such a circuit has also been approached mathematically by Ku et al. but without a direct link between histone modification and transcription [49]. The regulation proposed by our model defines a set of histone modification states that can be realized in general, while the specific coupling of the gene’s transcription to the modifications specifies the states that are actually realized under given conditions. Thus, our approach allows separating the properties of the regulatory circuit that rely on the histone modification machinery from those relying on the TF-network. Thereby, existence of bivalency depends, among others, on the accessibility of the promoter.

In our model, DNA methylation de-stabilizes bivalent states reducing the effective binding energy of the HMTs to the promoter, i.e., reducing its accessibility. Such de-stabilization can induce an unmodified histone state. We have shown that introducing active DNA demethylation, gene expression heterogeneity can also result from this unmodified state as a consequence of successive DNA demethylation during the cell cycle; increasing the accessibility again. Assuming that the effectiveness of this process depends on the expression of the gene, first activated and at later times also repressed genes become DNA demethylated. Thus, also in this case, cell cycle time affects gene expression heterogeneity. Consequently, the response of gene expression heterogeneity on changing proliferation activities might dependent of the promoter methylation dynamics of the gene under consideration. Recent experimental findings suggest that they show large clonal differences [35].

We applied our circuits to explain gene expression heterogeneity in hematopoietic cells. The examples provided describe qualitative features of expression heterogeneity of two genes encoding basic TFs of hematopoietic lineage specification, GATA3 and PU.1. Activation of these genes is known to be associated with an increased potential to specify into lymphoid and myeloid lineages, respectively. These models may not qualify to explain the entire specification process into these two lineages, as e.g., [36], but they provide, for the first time, clear hypotheses on how histone modification might be involved. Thereby, the models are consistent with different experimental findings on histone modification profiles of HSCs and their progeny. Formally, they could be used to fit fluorescence-activated cell sorting (FACS) data on the decision process, but this would overstress their potential at the current state of the art.

The two examples (GATA3, PU.1) were chosen as closely related as possible, sharing all parameters of the histone and transcriptional machinery. This allows us to demonstrate that the introduction of DNA methylation can impair one regulatory principal while potentially introducing a “complementary” one. Thus, tight regulation of DNA methylation is an essential mechanism not only controlling bivalency but also a regulatory mechanism during lineage specification in general.

Our AML model bases on break down of an active lineage specification mechanism. Under normal conditions, self-renewal of the stem cells (SC) requires DNA methylation, in agreement with experimental findings on HSC self-renewal [50], and specification of P1 requires active DNA demethylation. Loss of demethylation, i.e., of the active lineage specification mechanism, induces hypermethylation of the PU.1 promoter and a differentiation block in agreement with experimental findings in AML [39] as well. Such loss of demethylation can be expected in about 28% of AML cases, where either the TET2 gene or the isocitrate dehydrogenase 1/2 (IDH1/2) genes are mutated [51]. Beside PU.1 many other demethylation targets are affected in these cases. However, a similar affect can be expected by down-regulation of PU.1 alone, as TET2 is recruited to PU.1 binding sites. Consistently, a moderate down-regulation of PU.1 indeed is sufficient to induce AML in mice [52]. Moreover, in about 26% of AML cases mutations of DNMT3a have been found [51]. Changes in DNMT3a function will affect the DNA methylation efficiency and thus also affect the outcome of our model. However, we have shown that lineage specification in the PU.1 system can be repressed simply by accelerating proliferation. This agrees with experimental findings that DNMT3a-mediated promoter hypermethylation is rather a consequence of AML progression, in particular of enforced proliferation, than the origin of AML [53].

We already mentioned that, analog to PU.1, also systematic imbalance of the expression states of GATA3 can lead to tissue transformation and that loss of GATA3 has been found to induce B cell lymphoma [32]. In the last years, it has been shown that PU.1 and GATA3 interact to control the myeloid-lymphoid switch [31]. Thus, the models introduced here can be considered as basic modules of a more complex model of this essential switch in hematopoietic lineage specification.

5. Conclusions

In agreement with experimental observations, our model suggests that bivalent states are fostered by open chromatin and a high degree of cooperative binding of H3K4me3 and H3K27me3 HMTs. Loss of bivalency due to promoter de-modification subsequent to cell division can instruct gene expression. Accordingly, major effectors of gene expression heterogeneity are the kinetics of histone modification reactions and the cell cycle time. Decreasing the cell cycle time de-stabilizes the bivalent state. This could be experimentally tested, e.g., for the GATA3 promoter.

Such destabilization can also be achieved by DNA methylation, which potentially replaces bivalent by unmodified states. In such a case, active DNA demethylation during the cell cycle can instruct gene expression similar to loss of bivalency after cell division. In addition, here, emerging gene expression heterogeneity depends on the time scale of histone modification reactions and on the cell cycle time. We suggest that this kind of regulation is impaired during AML blast formation following loss of function mutation of the TET pathway.

Computational models of epigenetic regulation of transcription enable testing hypotheses on the interactions between different (activating and repressive) epigenetic marks. Thus, they can support a mechanistic understanding of chromatin dynamics and its impact on decision processes during development and lineage specification.