Cantilever-Based Sensor Utilizing a Diffractive Optical Element with High Sensitivity to Relative Humidity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cantilever Deflection and Bragg Selectivity Curve Measurements
2.2. Preparation of Photopolymer Grating Sensing Layer
2.3. Assessment of Sensor Outputs
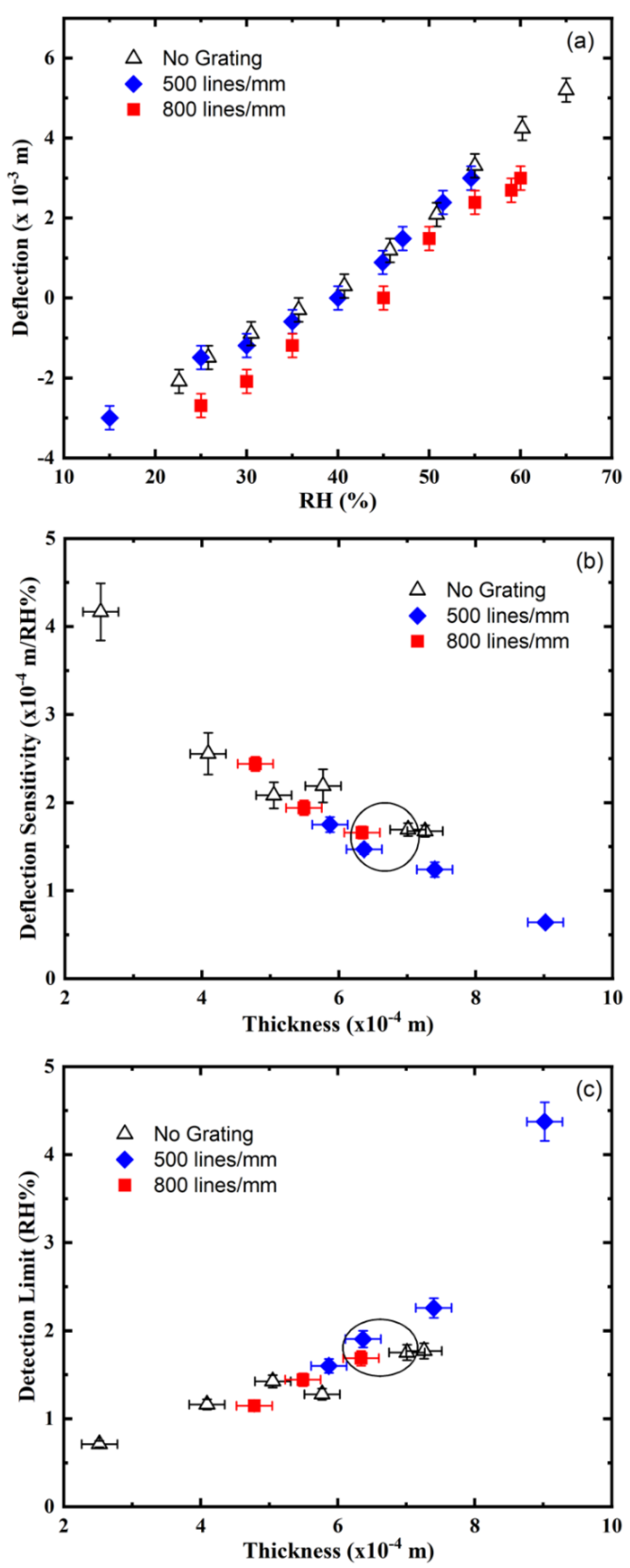
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thundat, T.; Warmack, R.J.; Chen, G.Y.; Allison, D.P. Thermal and ambient-induced deflections of scanning force microscope cantilevers. Appl. Phys. Lett. 1994, 64, 2894–2896. [Google Scholar] [CrossRef]
- Raiteri, R.; Grattarola, M.; Berger, R. Micromechanics senses biomolecules. Mater. Today 2002, 5, 22–29. [Google Scholar] [CrossRef]
- Grogan, C.; Raiteri, R.; O’Connor, G.; Glynn, T.; Cunningham, V.; Kane, M.; Charlton, M.; Leech, D.; O’Connor, G. Characterisation of an antibody coated microcantilever as a potential immuno-based biosensor. Biosens. Bioelectron. 2002, 17, 201–207. [Google Scholar] [CrossRef]
- Boisen, A.; Dohn, S.; Keller, S.S.; Schmid, S.; Tenje, M. Cantilever-like micromechanical sensors. Rep. Prog. Phys. 2011, 74, 36101. [Google Scholar] [CrossRef]
- Bai, X.; Hou, H.; Zhang, B.; Tang, J. Label-free detection of kanamycin using aptamer-based cantilever array sensor. Biosens. Bioelectron. 2014, 56, 112–116. [Google Scholar] [CrossRef]
- Jensen, J.; Maloney, N.; Hegner, M. A multi-mode platform for cantilever arrays operated in liquid. Sens. Actuators B Chem. 2013, 183, 388–394. [Google Scholar] [CrossRef]
- Zhang, J.; Lang, H.P.; Battiston, F.; Backmann, N.; Huber, F.; Gerber, C. Development of Robust and Standardized Cantilever Sensors Based on Biotin/Neutravidin Coupling for Antibody Detection. Sensors 2013, 13, 5273–5285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.; Nan, T.; Xue, C.; Cheng, T.; Liu, H.; Wang, B.; Zhang, Q.; Wu, X. Mechanism and enhancement of the surface stress caused by a small-molecule antigen and antibody binding. Biosens. Bioelectron. 2013, 48, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chen, X.; Zhang, Z.; Tang, J.; Zhang, B. Gold Nanoparticle-DNA conjugates enhanced determination of dopamine by aptamer-based microcantilever array sensor. Sens. Actuators B Chem. 2018, 275, 25–30. [Google Scholar] [CrossRef]
- Lang, H.P.; Hegner, M.; Gerber, C. Nanomechanical Cantilever Array Sensors. In Springer Handbook of Surface Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2010; pp. 427–452. [Google Scholar]
- Zhao, L.; Huang, L.; Luo, G.; Wang, J.; Wang, H.; Wu, Y.; Li, Z.; Zhou, X.; Jiang, Z. An immersive resonant sensor with microcantilever for pressure measurement. Sens. Actuators A Phys. 2020, 303, 111686. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, H.-K.; Lv, R.-Q.; Yang, Y. A practical FBG pressure sensor based on diaphragm-cantilever. Sens. Actuators A Phys. 2018, 279, 101–106. [Google Scholar] [CrossRef]
- Lang, H.P.; Hegner, M.; Gerber, C. Cantilever array sensors. Mater. Today 2005, 8, 30–36. [Google Scholar] [CrossRef]
- Alunda, B.O.; Lee, Y.J. Review: Cantilever-Based Sensors for High Speed Atomic Force Microscopy. Sensors 2020, 20, 4784. [Google Scholar] [CrossRef]
- Grogan, C.; Florea, L.; Koprivica, S.; Scarmagnani, S.; O’Neill, L.; Lyng, F.; Pedreschi, F.; Benito-Lopez, F.; Raiteri, R. Microcantilever arrays functionalised with spiropyran photoactive moieties as systems to measure photo-induced surface stress changes. Sens. Actuators B Chem. 2016, 237, 479–486. [Google Scholar] [CrossRef]
- Baller, M.K.; Lang, H.P.; Fritz, J.; Gerber, C.; Gimzewski, J.K.; Drechsler, U.; Rothuizen, H.; Despont, M.; Vettiger, P.; Battiston, F.M.; et al. A cantilever array-based artificial nose. Ultramicroscopy 2000, 82, 1–9. [Google Scholar] [CrossRef]
- Ceccacci, A.C.; Chen, C.-H.; Hwu, E.-T.; Morelli, L.; Bose-Goswami, S.; Bosco, F.G.; Schmid, S.; Boisen, A. Blu-Ray-based micromechanical characterization platform for biopolymer degradation assessment. Sens. Actuators B Chem. 2017, 241, 1303–1309. [Google Scholar] [CrossRef] [Green Version]
- Hegner, M.; Gerber, C.; Arntz, Y.; Zhang, J.; Bertoncini, P.; Husale, S.; Grange, W. Chapter 11—Biological Single Molecule Applications and Advanced Biosensing. J. Chromatogr. Libr. 2003, 68, 241–263. [Google Scholar]
- Rabenimanana, T.; Walter, V.; Kacem, N.; Le Moal, P.; Bourbon, G.; Lardiès, J. Mass sensor using mode localization in two weakly coupled MEMS cantilevers with different lengths: Design and experimental model validation. Sens. Actuators A Phys. 2019, 295, 643–652. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Peng, H.; Mao, T.; Liu, T.; Guo, M.; Lu, P.; Bai, Y.; Zhao, C.; Zhao, C. An airflow sensor array based on polyvinylidene fluoride cantilevers for synchronously measuring airflow direction and velocity. Flow Meas. Instrum. 2019, 67, 166–175. [Google Scholar] [CrossRef]
- Sang, S.; Zhao, Y.; Zhang, W.; Li, P.; Hu, J.; Li, G. Surface stress-based biosensors. Biosens. Bioelectron. 2014, 51, 124–135. [Google Scholar] [CrossRef]
- Wang, J.; Feng, B.; Wu, W.; Huang, Y. Chemisorption sensing and analysis using silicon cantilever sensor based on n-type metal–oxide–semiconductor transistor. Microelectron. Eng. 2011, 88, 1019–1023. [Google Scholar] [CrossRef]
- Abu-Lail, N.I.; Kaholek, M.; LaMattina, B.; Clark, R.L.; Zauscher, S. Micro-cantilevers with end-grafted stimulus-responsive polymer brushes for actuation and sensing. Sens. Actuators B Chem. 2006, 114, 371–378. [Google Scholar] [CrossRef]
- Bai, X.; Lu, B.; Chen, X.; Zhang, B.; Tang, J. Reversible detection of vancomycin using peptide-functionalized cantilever array sensor. Biosens. Bioelectron. 2014, 62, 145–150. [Google Scholar] [CrossRef]
- Johnson, B.N.; Mutharasan, R. Biosensing using dynamic-mode cantilever sensors: A review. Biosens. Bioelectron. 2012, 32, 1–18. [Google Scholar] [CrossRef]
- Bao, Y.; Xu, P.; Cai, S.; Yu, H.; Li, X. Detection of volatile-organic-compounds (VOCs) in solution using cantilever-based gas sensors. Talanta 2018, 182, 148–155. [Google Scholar] [CrossRef]
- Lee, D.; Shin, N.; Lee, K.-H.; Jeon, S. Microcantilevers with nanowells as moisture sensors. Sens. Actuators B Chem. 2009, 137, 561–565. [Google Scholar] [CrossRef]
- Lee, P.-S.; Lee, J.; Shin, N.; Lee, K.-H.; Lee, D.; Jeon, S.; Choi, D.; Hwang, W.; Park, H. Microcantilevers with Nanochannels. Adv. Mater. 2008, 20, 1732–1737. [Google Scholar] [CrossRef]
- Salerno, M.; Patra, N.; Diaspro, A. Anodization of aluminium coated atomic force microscopy microcantilevers for conversion of the coating into nanoporous alumina. Microelectron. Eng. 2011, 88, 2383–2385. [Google Scholar] [CrossRef]
- Xu, J.; Bertke, M.; Wasisto, H.S.; Peiner, E. Piezoresistive microcantilevers for humidity sensing. J. Micromech. Microeng. 2019, 29, 053003. [Google Scholar] [CrossRef]
- Dennis, J.-O.; Ahmed, A.-Y.; Khir, M.-H. Fabrication and Characterization of a CMOS-MEMS Humidity Sensor. Sensors 2015, 15, 16674–16687. [Google Scholar] [CrossRef] [Green Version]
- Trigona, C.; Al-Hamry, A.; Kanoun, O.; Baglio, S. Analysis of a Hybrid Micro-Electro-Mechanical Sensor Based on Graphene Oxide/Polyvinyl Alcohol for Humidity Measurements. Sensors 2019, 19, 1720. [Google Scholar] [CrossRef] [Green Version]
- Le, X.; Peng, L.; Pang, J.; Xu, Z.; Gao, C.; Xie, J. Humidity sensors based on AlN microcantilevers excited at high-order resonant modes and sensing layers of uniform graphene oxide. Sens. Actuators B Chem. 2019, 283, 198–206. [Google Scholar] [CrossRef]
- Fraiwan, A.; Lee, H.; Choi, S. A paper-based cantilever array sensor: Monitoring volatile organic compounds with naked eye. Talanta 2016, 158, 57–62. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-S.; Jeong, Y.-J.; Lee, B.-K.; Shanmugasundaram, A.; Lee, D.-W. Piezoresistive sensor-integrated PDMS cantilever: A new class of device for measuring the drug-induced changes in the mechanical activity of cardiomyocytes. Sens. Actuators B Chem. 2017, 240, 566–572. [Google Scholar] [CrossRef]
- Lowe, A.G.; Millington, C.R.; Blyth, R.B.; Mayes, J. Hologram used as a sensor. WO Patent Application 1995026499 A1, 5 October 1995. [Google Scholar]
- Zawadzka, M.; Mikulchyk, T.; Cody, D.; Martin, S.; Yetisen, A.K.; Martinez-Hurtado, J.L.; Butt, H.; Mihaylova, E.; Awala, H.; Mintova, S.; et al. Photonic Materials for Holographic Sensing. In Computational Materials, Chemistry, and Biochemistry: From Bold Initiatives to the Last Mile; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 315–359. [Google Scholar]
- Blanche, P.A. Optical Holography: Materials, Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Yetisen, A.K.; Naydenova, I.; Vasconcellos, F.D.C.; Blyth, J.; Lowe, C.R. Holographic Sensors: Three-Dimensional Analyte-Sensitive Nanostructures and Their Applications. Chem. Rev. 2014, 114, 10654–10696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moghaddam, G.K.; Margerison, H.; Suzuki, J.; Blyth, J.; Lowe, C.R. A transparent glucose-sensitive double polymerised holographic sensor. Sens. Actuators B Chem. 2018, 267, 1–4. [Google Scholar] [CrossRef]
- Yetisen, A.K.; Martinez-Hurtado, J.; Garcia-Melendrez, A.; Vasconcellos, F.D.C.; Lowe, C.R. A smartphone algorithm with inter-phone repeatability for the analysis of colorimetric tests. Sens. Actuators B Chem. 2014, 196, 156–160. [Google Scholar] [CrossRef]
- Zhou, K.; Geng, Y.; Liu, H.; Wang, S.; Mao, D.; Yu, D. Improvement of holographic sensing response in substrate-free acrylamide photopolymer. Appl. Opt. 2017, 56, 3714–3724. [Google Scholar] [CrossRef] [PubMed]
- Bajgrowicz-Cieslak, M.; AlQurashi, Y.; Elshereif, M.I.; Yetisen, A.K.; Hassan, M.U.; Butt, H. Optical glucose sensors based on hexagonally-packed 2.5-dimensional photonic concavities imprinted in phenylboronic acid functionalized hydrogel films. RSC Adv. 2017, 7, 53916–53924. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gul, S.-E.; Cody, D.; Kharchenko, A.; Martin, S.; Mintova, S.; Cassidy, J.; Naydenova, I. LTL type nanozeolites utilized in surface photonics structures for environmental sensors. Microporous Mesoporous Mater. 2018, 261, 268–274. [Google Scholar] [CrossRef] [Green Version]
- Cody, D.; Naydenova, I.; Naydenova, D.C.A.I. Theoretical modeling and design of photonic structures in zeolite nanocomposites for gas sensing Part I: Surface relief gratings. J. Opt. Soc. Am. A 2017, 34, 2110. [Google Scholar] [CrossRef]
- Cody, D.; Naydenova, I.; Naydenova, D.C.A.I. Theoretical modeling and design of photonic structures in zeolite nanocomposites for gas sensing Part II: Volume gratings. J. Opt. Soc. Am. A 2017, 35, 12. [Google Scholar] [CrossRef] [PubMed]
- Naydenova, I.; Jallapuram, R.; Toal, V.; Martin, S. Characterisation of the humidity and temperature responses of a reflection hologram recorded in acrylamide-based photopolymer. Sens. Actuators B Chem. 2009, 139, 35–38. [Google Scholar] [CrossRef] [Green Version]
- Naydenova, I.; Jallapuram, R.; Toal, V.; Martin, S. A visual indication of environmental humidity using a color changing hologram recorded in a self-developing photopolymer. Appl. Phys. Lett. 2008, 92, 31109. [Google Scholar] [CrossRef] [Green Version]
- Busch-Vishniac, I.J. Optomechanical Sensors. In Nanoindentation; Springer International Publishing: Berlin/Heidelberg, Germany, 1999; pp. 250–275. [Google Scholar]
- Cho, K.; Kim, S.T.; Park, Y.-H.; Cho, J.-R. Measurement of Mechanical and Thermal Strains by Optical FBG Sensors Embedded in CFRP Rod. J. Sens. 2019, 2019, 1–6. [Google Scholar] [CrossRef]
- Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V.M.N. Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef] [Green Version]
- Dubey, V.N.; Crowder, R.M. A dynamic tactile sensor on photoelastic effect. Sens. Actuators A Phys. 2006, 128, 217–224. [Google Scholar] [CrossRef] [Green Version]
- Hariharan, P. Optical Holography. Principles, Techniques and Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Havermeyer, F.; Liu, W.; Moser, C.; Psaltis, D.; Steckman, G.J. Volume holographic grating-based continuously tunable optical filter. Opt. Eng. 2004, 43, 2017. [Google Scholar] [CrossRef] [Green Version]
- Raiteri, R.; Grattarola, M.; Butt, H.-J.; Skládal, P. Micromechanical cantilever-based biosensors. Sens. Actuators B Chem. 2001, 79, 115–126. [Google Scholar] [CrossRef]
- Mallik, A.K.; Liu, D.; Kavungal, V.; Wu, Q.; Farrell, G.; Semenova, Y. Agarose coated spherical micro resonator for humidity measurements. Opt. Express 2016, 24, 21216–21227. [Google Scholar] [CrossRef] [Green Version]
- Grogan, C.; Amarandei, G.; Naydenova, I. Hybrid Optical Sensor. UK Patent Application No. 1917813.6., 5 December 2019. [Google Scholar]
- Madry, M.; Thomaso, C.; Beres-Pawlik, E. The compact FBG-based humidity sensor setup. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; Volume 168, pp. 1–4. [Google Scholar]
- Alwis, L.S.M.; Sun, T.; Grattan, K.T.V. Fibre Grating-based Sensor Design for Humidity Measurement in Chemically Harsh Environment. Procedia Eng. 2016, 168, 1317–1320. [Google Scholar] [CrossRef]
- Yang, J.; Xu, J.; Wu, W.; Bertke, M.; Wasisto, H.S.; Peiner, E. Piezoresistive Silicon Cantilever Covered by ZnO Nanorods for Humidity Sensing. Procedia Eng. 2016, 168, 1114–1117. [Google Scholar] [CrossRef]
- World Health Organisation Regional Office for Europe. WHO Guidelines for Indoor Air Quality: Selected Pollutants; World Health Organisation: Geneva, Switzerland, 2010. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grogan, C.; McGovern, F.R.; Staines, R.; Amarandei, G.; Naydenova, I. Cantilever-Based Sensor Utilizing a Diffractive Optical Element with High Sensitivity to Relative Humidity. Sensors 2021, 21, 1673. https://doi.org/10.3390/s21051673
Grogan C, McGovern FR, Staines R, Amarandei G, Naydenova I. Cantilever-Based Sensor Utilizing a Diffractive Optical Element with High Sensitivity to Relative Humidity. Sensors. 2021; 21(5):1673. https://doi.org/10.3390/s21051673
Chicago/Turabian StyleGrogan, Catherine, Faolan Radford McGovern, Rory Staines, George Amarandei, and Izabela Naydenova. 2021. "Cantilever-Based Sensor Utilizing a Diffractive Optical Element with High Sensitivity to Relative Humidity" Sensors 21, no. 5: 1673. https://doi.org/10.3390/s21051673
APA StyleGrogan, C., McGovern, F. R., Staines, R., Amarandei, G., & Naydenova, I. (2021). Cantilever-Based Sensor Utilizing a Diffractive Optical Element with High Sensitivity to Relative Humidity. Sensors, 21(5), 1673. https://doi.org/10.3390/s21051673







