Leveraging Metaheuristic Unequal Clustering for Hotspot Elimination in Energy-Aware Wireless Sensor Networks
Abstract
:1. Introduction
2. Literature Review
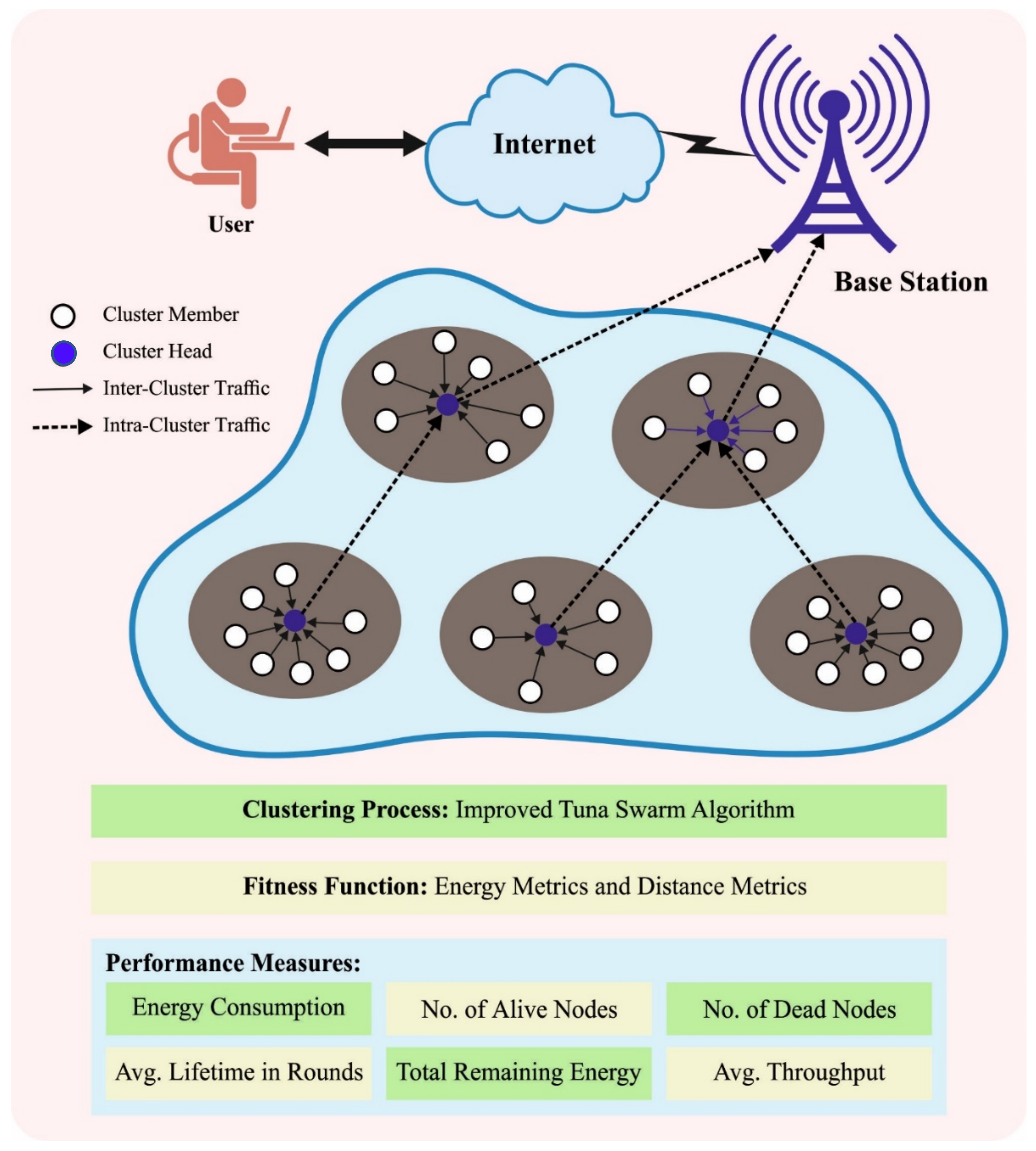
3. The Proposed Model
3.1. Energy Model
3.2. Design of ITSA
| Algorithm 1: Pseudocode for ITSA |
| Initializing the random population of individuals Allocate free parameters and While Compute the fitness values of individuals Upgrade For (each individual) do Update using Equations (3) and (4). If (and ) then Update the position Else if (r and ) then If (and ) then If r) then Update the position Else if r) then Update the position Else if (r and ) then Update the position End for End while Return the optimal individual and the optimal fitness value |
3.3. Process Involved in Unequal Clustering
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moussa, N.; Alaoui, A.E.B.E. An energy-efficient cluster-based routing protocol using unequal clustering and improved ACO techniques for WSNs. Peer-to-Peer Netw. Appl. 2021, 14, 1334–1347. [Google Scholar] [CrossRef]
- Arjunan, S.; Sujatha, P. Corrigendum to ‘A survey on unequal clustering protocols in Wireless Sensor Networks. J. King Saud Univ. Comput. Inf. Sci. 2021, 33, 304–317. [Google Scholar]
- Jasim, A.; Idris, M.; Bin Azzuhri, S.R.; Issa, N.; Rahman, M.; Khyasudeen, M. Energy-Efficient Wireless Sensor Network with an Unequal Clustering Protocol Based on a Balanced Energy Method (EEUCB). Sensors 2021, 21, 784. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H. A WSN Clustering Multi-Hop Routing Protocol Using Cellular Virtual Grid in IoT Environment. Math. Probl. Eng. 2020, 2020, 8886687. [Google Scholar] [CrossRef]
- Agrawal, D.; Pandey, S. Load balanced fuzzy-based unequal clustering for wireless sensor networks assisted Internet of Things. Eng. Rep. 2020, 2, e12130. [Google Scholar] [CrossRef] [Green Version]
- Vinodhini, R.; Gomathy, C. Fuzzy Based Unequal Clustering and Context-Aware Routing Based on Glow-Worm Swarm Optimization in Wireless Sensor Networks: Forest Fire Detection. Wirel. Pers. Commun. 2021, 118, 3501–3522. [Google Scholar] [CrossRef]
- Phoemphon, S.; So-In, C.; Aimtongkham, P.; Nguyen, T.G. An energy-efficient fuzzy-based scheme for unequal multihop clustering in wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 873–895. [Google Scholar] [CrossRef]
- Zhu, F.; Wei, J. An energy-efficient unequal clustering routing protocol for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719879384. [Google Scholar] [CrossRef] [Green Version]
- Shagari, N.M.; Idris, M.Y.I.; Bin Salleh, R.; Ahmedy, I.; Murtaza, G.; Sabri, A.Q.B.M. A hybridization strategy using equal and unequal clustering schemes to mitigate idle listening for lifetime maximization of wireless sensor network. Wirel. Netw. 2021, 27, 2641–2670. [Google Scholar] [CrossRef]
- Sahoo, B.M.; Amgoth, T. An Improved Bat Algorithm for Unequal Clustering in Heterogeneous Wireless Sensor Networks. SN Comput. Sci. 2021, 2, 290. [Google Scholar] [CrossRef]
- Arikumar, K.S.; Natarajan, V.; Satapathy, S.C. EELTM: An Energy Efficient LifeTime Maximization Approach for WSN by PSO and Fuzzy-Based Unequal Clustering. Arab. J. Sci. Eng. 2020, 45, 10245–10260. [Google Scholar] [CrossRef]
- Mehra, P.S. E-FUCA: Enhancement in fuzzy unequal clustering and routing for sustainable wireless sensor network. Complex Intell. Syst. 2021, 8, 393–412. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Pan, J.-S.; Dao, T.-K. A Compact Bat Algorithm for Unequal Clustering in Wireless Sensor Networks. Appl. Sci. 2019, 9, 1973. [Google Scholar] [CrossRef] [Green Version]
- Rao, P.C.S.; Lalwani, P.; Banka, H.; Rao, G.S.N. Competitive swarm optimization based unequal clustering and routing algorithms (CSO-UCRA) for wireless sensor networks. Multimed. Tools Appl. 2021, 80, 17. [Google Scholar] [CrossRef]
- Amutha, J.; Sharma, S.; Sharma, S.K. Hybrid based Optimization with Unequal Clustering and Mobile Sink for Wireless Sensor Networks. In Proceedings of the 6th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 25–27 May 2022; pp. 722–728. [Google Scholar]
- Agrawal, D.; Pandey, S.; Gupta, P.; Goyal, M.K. Optimization of cluster heads through harmony search algorithm in wireless sensor networks. J. Intell. Fuzzy Syst. 2020, 39, 8587–8597. [Google Scholar] [CrossRef]
- Maheswari, M.; Karthika, R.A. A Novel QoS Based Secure Unequal Clustering Protocol with Intrusion Detection System in Wireless Sensor Networks. Wirel. Pers. Commun. 2021, 118, 1535–1557. [Google Scholar] [CrossRef]
- Revanesh, M.; Acken, J.M.; Sridhar, V. DAG block: Trust aware load balanced routing and lightweight authentication encryption in WSN. Futur. Gener. Comput. Syst. 2022, 140, 402–421. [Google Scholar] [CrossRef]
- Arjunan, S.; Sujatha, P. Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol. Appl. Intell. 2017, 48, 2229–2246. [Google Scholar] [CrossRef]
- Agrawal, D.; Pandey, S. Optimization of the selection of cluster-head using fuzzy logic and harmony search in wireless sensor networks. Int. J. Commun. Syst. 2020, 34, e4391. [Google Scholar] [CrossRef]
- Yuen, K.-V.; Kuok, S.-C. Efficient Bayesian sensor placement algorithm for structural identification: A general approach for multi-type sensory systems. Earthq. Eng. Struct. Dyn. 2014, 44, 757–774. [Google Scholar] [CrossRef]
- Osamy, W.; Khedr, A.M.; Aziz, A.; El-Sawy, A.A. Cluster-Tree Routing Based Entropy Scheme for Data Gathering in Wireless Sensor Networks. IEEE Access 2018, 6, 77372–77387. [Google Scholar] [CrossRef]
- Wu, H.; Meng, Q.; Xian, J.; Mei, X.; Claramunt, C.; Cao, J. An Information Entropy Based Event Boundary Detection Algorithm in Wireless Sensor Networks. Symmetry 2019, 11, 537. [Google Scholar] [CrossRef] [Green Version]
- Anuradha, D.; Srinivasan, R.; Kumar, T.C.A.; Banu, J.F.; Pundir, A.K.S.; Babu, D.V. Energy Aware Seagull Optimization-Based Unequal Clustering Technique in WSN Communication. Intell. Autom. Soft Comput. 2022, 32, 1325–1341. [Google Scholar] [CrossRef]
- Sivakumar, D.; Devi, S.S.; Nalini, T. Energy Aware Metaheuristics Unequal Clustering Protocol for WSN. In Proceedings of the 2022 Second International Conference on Artificial Intelligence and Smart Energy (ICAIS), Coimbatore, India, 23–25 February 2022; IEEE: New York, NY, USA; pp. 1418–1424. [Google Scholar]
- Muthukkumar, R.; Garg, L.; Maharajan, K.; Jayalakshmi, M.; Jhanjhi, N.; Parthiban, S.; Saritha, G. A genetic algorithm-based energy-aware multi-hop clustering scheme for heterogeneous wireless sensor networks. PeerJ Comput. Sci. 2022, 8, e1029. [Google Scholar] [CrossRef]
- Chauhan, V.; Soni, S. Energy aware unequal clustering algorithm with multi-hop routing via low degree relay nodes for wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2469–2482. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, L.; Wu, B.; Ryspayev, A. Forestry Canopy Image Segmentation Based on Improved Tuna Swarm Optimization. Forests 2022, 13, 1746. [Google Scholar] [CrossRef]
- Li, Y.; Duan, P. Research on the Innovation of Protecting Intangible Cultural Heritage in the “Internet Plus” Era. Procedia Comput. Sci. 2019, 154, 20–25. [Google Scholar] [CrossRef]
- Prakash, P.S.; Kavitha, D.; Reddy, P.C. Delay-aware relay node selection for cluster-based wireless sensor networks. Meas. Sensors 2022, 24, 100403. [Google Scholar] [CrossRef]





| Energy Consumption (J) | ||||
|---|---|---|---|---|
| No. of Nodes | ITSA-UCHSE | HHDAP | Q-DAEER | IPSO |
| 50 | 0.6666 | 0.7294 | 0.7811 | 0.8439 |
| 100 | 0.8402 | 0.9621 | 1.0545 | 1.1690 |
| 200 | 0.9621 | 1.1616 | 1.4387 | 1.5753 |
| 300 | 1.1173 | 1.3094 | 1.6936 | 1.8303 |
| 400 | 1.1690 | 1.3611 | 1.7379 | 1.9337 |
| Number of Alive Nodes | ||||
|---|---|---|---|---|
| No. of Rounds | ITSA-UCHSE | HHDAP | Q-DAEER | IPSO |
| 0 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 200 | 100 | 100 | 100 | 100 |
| 300 | 100 | 100 | 100 | 100 |
| 400 | 100 | 100 | 100 | 95 |
| 500 | 100 | 95 | 92 | 93 |
| 600 | 100 | 90 | 74 | 91 |
| 700 | 97 | 63 | 19 | 65 |
| 800 | 93 | 40 | 12 | 0 |
| 900 | 77 | 27 | 0 | 0 |
| 1000 | 52 | 0 | 0 | 0 |
| 1100 | 31 | 0 | 0 | 0 |
| 1200 | 0 | 0 | 0 | 0 |
| Number of Dead Nodes | ||||
|---|---|---|---|---|
| No. of Rounds | ITSA-UCHSE | HHDAP | Q-DAEER | IPSO |
| 0 | 0 | 0 | 0 | 0 |
| 100 | 0 | 0 | 0 | 0 |
| 200 | 0 | 0 | 0 | 0 |
| 300 | 0 | 0 | 0 | 0 |
| 400 | 0 | 0 | 0 | 5 |
| 500 | 0 | 5 | 8 | 7 |
| 600 | 0 | 10 | 26 | 9 |
| 700 | 3 | 37 | 81 | 35 |
| 800 | 7 | 60 | 88 | 100 |
| 900 | 23 | 73 | 100 | 100 |
| 1000 | 48 | 100 | 100 | 100 |
| 1100 | 69 | 100 | 100 | 100 |
| 1200 | 100 | 100 | 100 | 100 |
| Avg. Lifetime in Rounds | ||||
|---|---|---|---|---|
| ITSA-UCHSE | HHDAP | Q-DAEER | IPSO | |
| FND | 668 | 472 | 448 | 359 |
| HND | 1041 | 768 | 639 | 712 |
| LND | 1200 | 100 | 900 | 800 |
| Avg. Throughput | ||||
|---|---|---|---|---|
| No. of Nodes | ITSA-UCHSE | HHDAP | Q-DAEER | IPSO |
| 50 | 34.66 | 33.99 | 32.56 | 31.04 |
| 100 | 31.54 | 27.25 | 23.29 | 21.27 |
| 200 | 26.41 | 23.20 | 20.26 | 18.40 |
| 300 | 21.27 | 17.81 | 14.78 | 13.35 |
| 400 | 14.86 | 10.06 | 8.46 | 6.36 |
| Total Remaining Energy (%) | ||||
|---|---|---|---|---|
| No. of Rounds | ITSA-UCHSE | HHDAP | Q-DAEER | IPSO |
| 0 | 100.00 | 100.00 | 100.00 | 100.00 |
| 100 | 98.14 | 97.09 | 89.96 | 87.59 |
| 200 | 97.61 | 95.50 | 79.67 | 76.25 |
| 300 | 90.75 | 84.42 | 70.18 | 63.85 |
| 400 | 81.52 | 76.51 | 63.32 | 59.89 |
| 500 | 70.18 | 64.90 | 58.04 | 53.03 |
| 600 | 67.80 | 59.89 | 53.56 | 48.81 |
| 700 | 63.85 | 54.61 | 48.02 | 43.01 |
| 800 | 61.21 | 52.77 | 41.42 | 34.30 |
| 900 | 58.04 | 49.07 | 31.66 | 27.44 |
| 1000 | 50.13 | 38.52 | 19.26 | 17.15 |
| 1100 | 43.27 | 28.76 | 15.04 | 10.03 |
| 1200 | 37.20 | 26.39 | 13.46 | 6.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsolai, H.; Maashi, M.; Saeed, M.K.; Mohamed, A.; Assiri, M.; Abdelbagi, S.; Drar, S.; Abdelmageed, A.A. Leveraging Metaheuristic Unequal Clustering for Hotspot Elimination in Energy-Aware Wireless Sensor Networks. Sensors 2023, 23, 2636. https://doi.org/10.3390/s23052636
Alsolai H, Maashi M, Saeed MK, Mohamed A, Assiri M, Abdelbagi S, Drar S, Abdelmageed AA. Leveraging Metaheuristic Unequal Clustering for Hotspot Elimination in Energy-Aware Wireless Sensor Networks. Sensors. 2023; 23(5):2636. https://doi.org/10.3390/s23052636
Chicago/Turabian StyleAlsolai, Hadeel, Mashael Maashi, Muhammad Kashif Saeed, Abdullah Mohamed, Mohammed Assiri, Sitelbanat Abdelbagi, Suhanda Drar, and Amgad Atta Abdelmageed. 2023. "Leveraging Metaheuristic Unequal Clustering for Hotspot Elimination in Energy-Aware Wireless Sensor Networks" Sensors 23, no. 5: 2636. https://doi.org/10.3390/s23052636
APA StyleAlsolai, H., Maashi, M., Saeed, M. K., Mohamed, A., Assiri, M., Abdelbagi, S., Drar, S., & Abdelmageed, A. A. (2023). Leveraging Metaheuristic Unequal Clustering for Hotspot Elimination in Energy-Aware Wireless Sensor Networks. Sensors, 23(5), 2636. https://doi.org/10.3390/s23052636







