Tesla Bladed Pump (Disc Bladed Pump) Preliminary Experimental Performance Analysis
Abstract
:1. Introduction
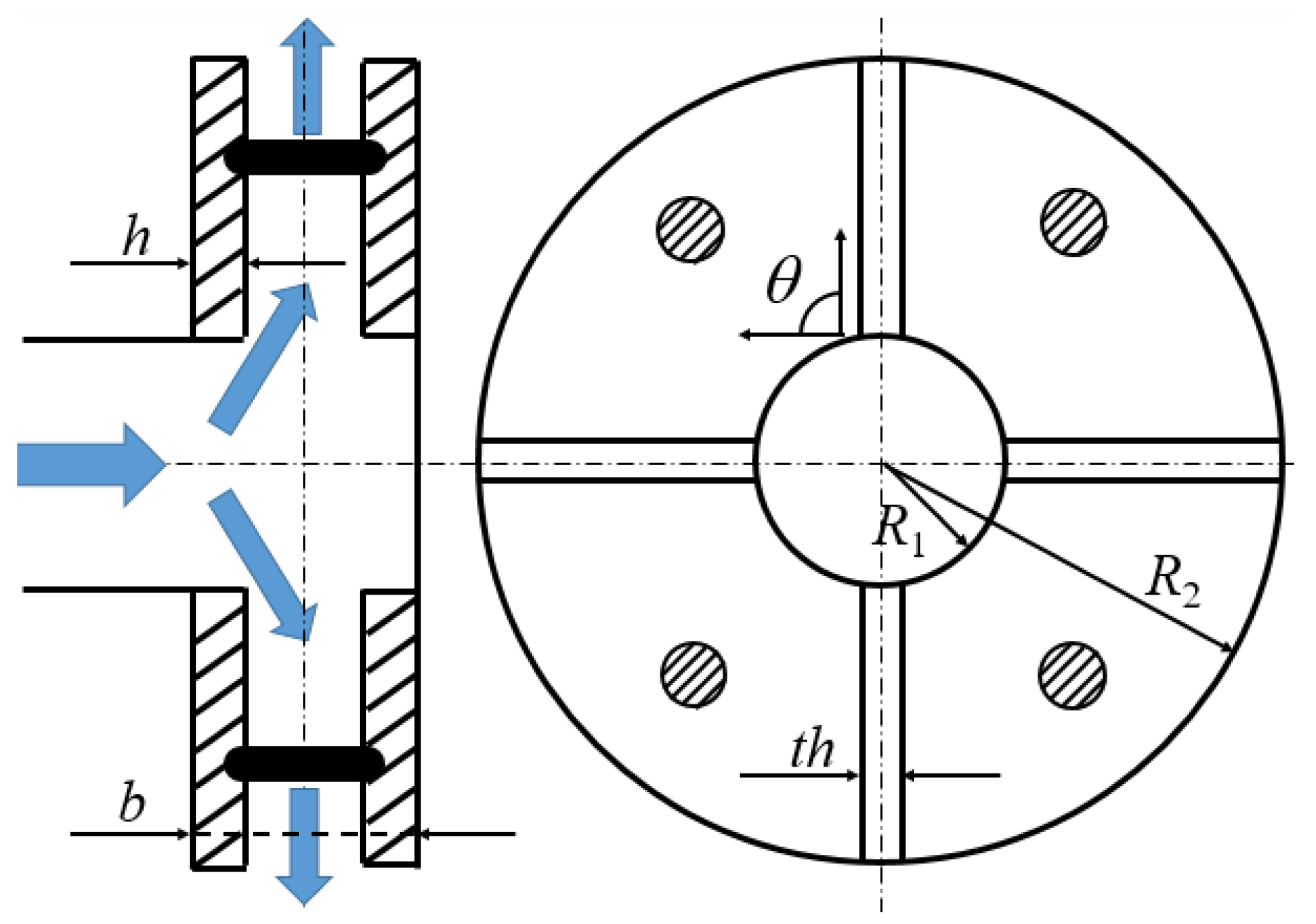
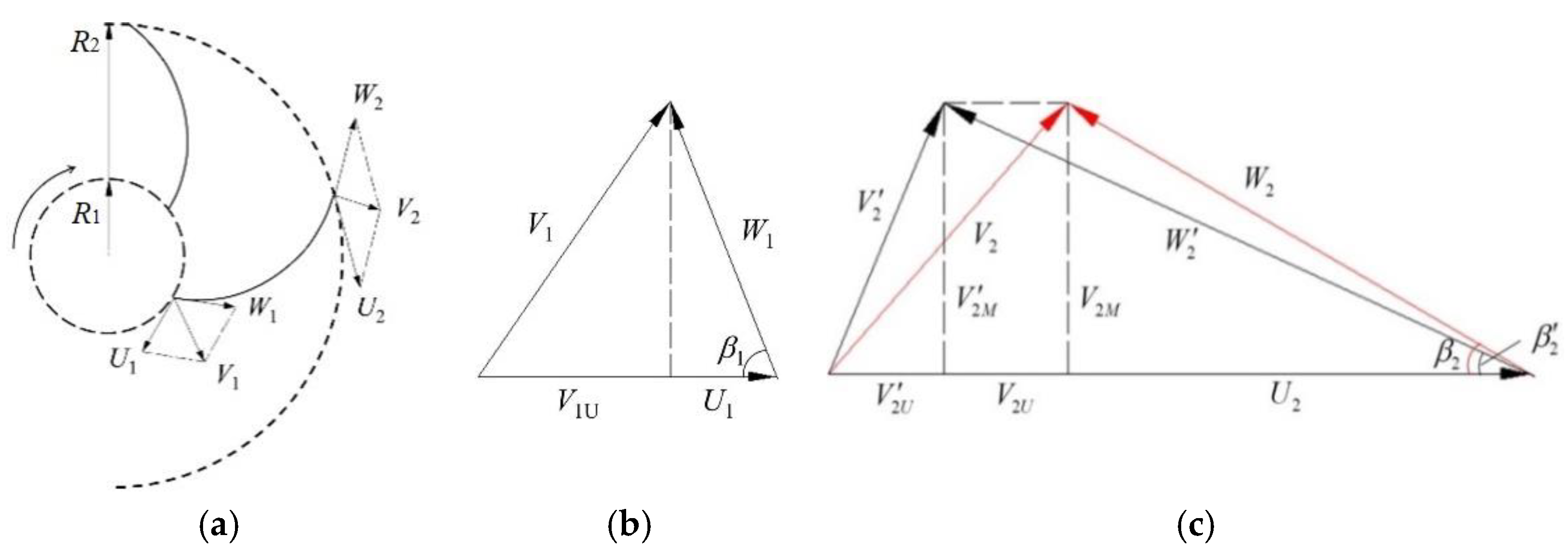
2. The Impeller Pump Model Main Parameters
| Inlet tip radius | R1 = 50 mm |
| Outlet radius | R2 = 100 mm |
| Number of blades | Z = 8 |
| Inter blade clearance gap | cl = 8 mm |
| Blade height | h = 4 mm |
| Blade angle | θ = 90°, radial blade |
| Impeller channel width | b = 16 mm |
3. Experimental Study
3.1. Experimental Set Up
- -
- Volume flow rate transducer precision: ±0.5%; range: 0–100 m3/h;
- -
- Volume flow rate measuring error due to uncertainty and fluctuation: ±2.5%;
- -
- Rotational speed transducer precision: ±0.1%; range: 0–3000 rpm;
- -
- Rotational speed error (speed regulation): ±0.5%;
- -
- Torque transducer precision: ±0.2%; Range: 0–1000 N·m;
- -
- Torque measuring error due to uncertainty and fluctuation: ±1%;
- -
- Pump inlet and outlet pressure measuring device precision: ±0.1 m; range: 0–50 m;
- -
- Pump head pressure precision: ±0.2 m, assuming pure axial velocity inside the inlet and outlet tube section in which static pressures are measured, and the corresponding error is ±0.4 m for full scale.
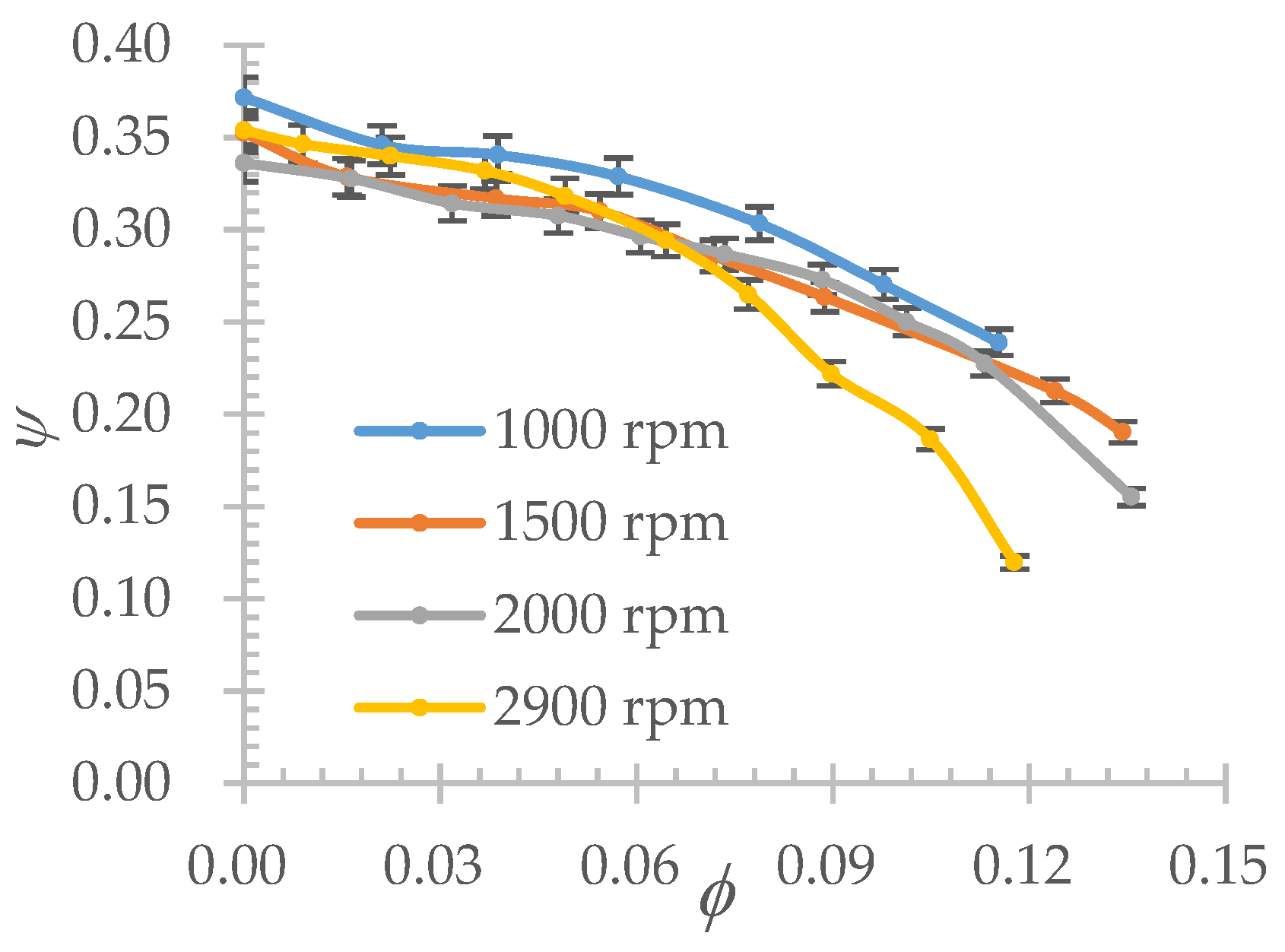
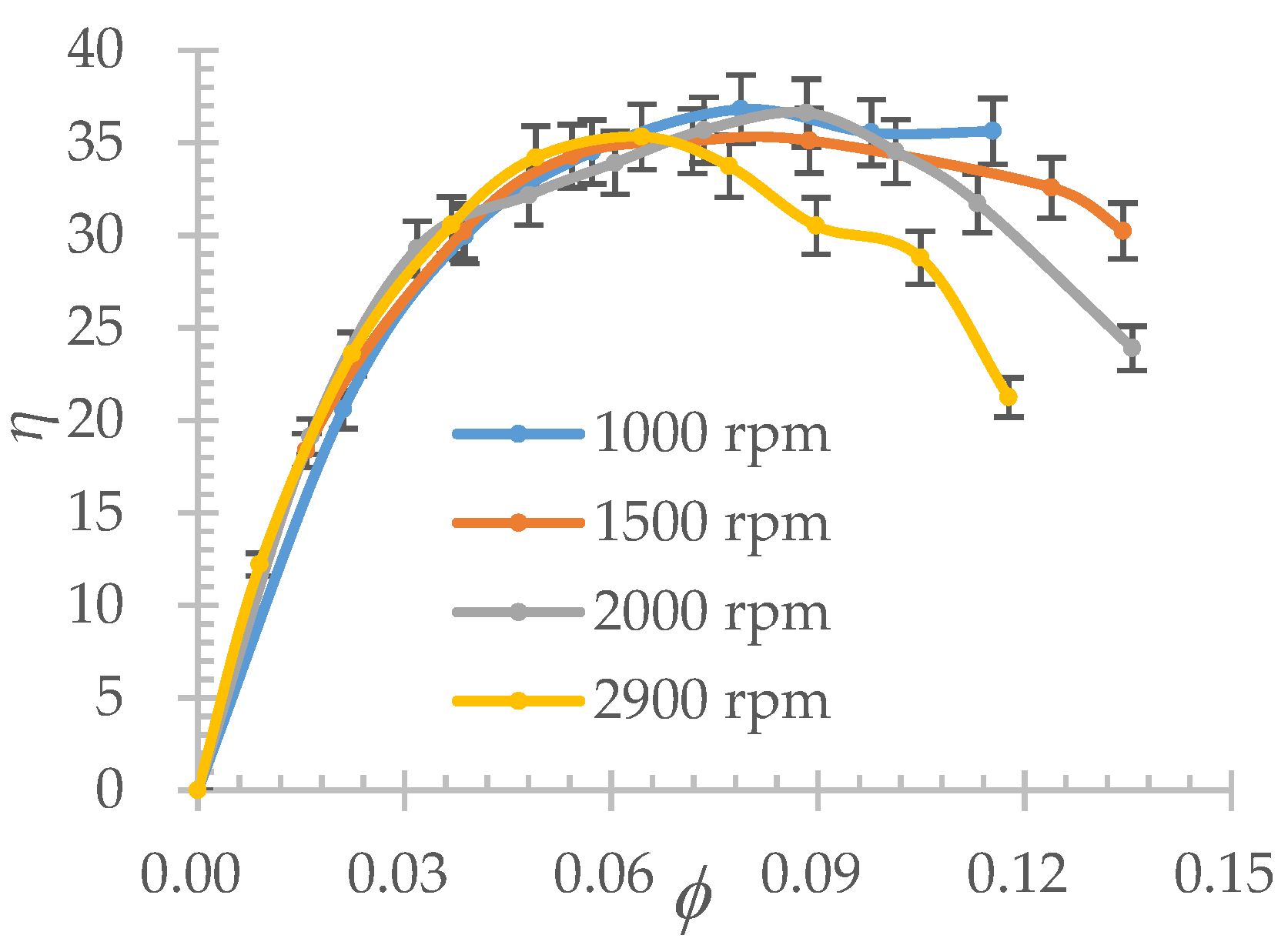
3.2. Head Coefficient and Efficiency Curves Versus Flow Coefficient
| Flow coefficient: | Φ = Q/(2πR2b2U2) |
| Head coefficient: | ψ = gH/(U2)2 |
| Efficiency: | η = ρgHQ/P |
- (a)
- The tested impeller design strongly differs from conventional design blade shape and blade arrangement including a large gap between each parallel disc. Thus, both pressure and viscous forces should have comparable relative effects compared with conventional designs for which pressure force work is generally much higher than viscous one.
- (b)
- Consequently, for the lowest rotational speed (1000 rpm), part of the work given to the fluid may be governed by Reynolds number effects specifically along the flat disc region that rotates inside the casing chambers. These parts act like the original tesla disc pump. It is well-known that these kinds of pumps give more pressure at low rotational speeds due to laminar flow regime but need higher relative shaft power.
- (c)
- For turbulent flow regimes, like the one that should be obtained at high rotational speeds, efficiency can more strongly depend on clearance flow mixing due to the increase of pressure difference between driving and driven impeller faces.
- (d)
- For 2900 rpm, cavitation noise has been detected for high flow rates. The last three experimental points maybe affected by this problem because of measured low inlet static pressure values and should be ignored.
- (e)
- Another effect cannot be neglected. It is related to leakage flows that occur inside both side chambers which are responsible to the so-called volumetric efficiency, this corresponds to the fact that the real flow rate that is driven by the impeller is bigger than the exhaust flow rate measured by the flow meter devices placed on the loop.
- (f)
- Maximum efficiency point is slightly shifted towards higher flow coefficients for decreasing rotational speeds. It reaches a maximum value of 0.37, for a flow coefficient value closed to 0.06 at 1000 rpm. Maximum efficiency values are relatively low, they are however quite comparable with the values obtained by Je and Kim [11] for the same relative blade height ratio h/b (See Table 2) at design conditions. Also note that such performance curves can also be found for conventional designs of open impeller pump with a relative blade height value h2/b2 = 0.9, which is even bigger than the present case (Choi et al. [12], see Table 2).
- (g)
- Flow coefficient values Φ given in [6] and [11] are quite low compared with the present case. This can be explained by the fact that efficiency curves are often flat ones and that maximum efficiency value have not been reached by these authors because of too much test loop losses that limit high flow rate experimental conditions.
3.3. Theoretical Head Coefficient Versus Flow Coefficient
4. Discussions
4.1. Euler Head Coefficient Curve Development
4.2. Comparison between Experimental Results and Simplified Euler Head Coefficent Relation
- -
- Nondimensional mean radial velocity: Vr2/U2 = 0.06
- -
- Nondimensional tangential velocity component (based on Euler relation): Vu2/U2 = 0.73
- -
- Mean absolute flow angle: α2 = 4.7°
- -
- Mean relative flow angle: β2 = 12.6°
- -
- Slip coefficient: μ = Vu2/U2 = 0.73
- (a)
- The value of this slip coefficient is identical to the one obtained by Choi et al. [12]. For the case of a semiopen fully radial blade impeller with low tip clearance value. The corresponding slip factor can be considerably affected by the impeller internal flow which is dominated by tip clearance ratio. The slip velocity of a semiopen impeller becomes higher than usual slip velocity correlations for increasing tip clearance ratio which is the case for present impeller design. This corresponds to the fact that the relative mean flow angle estimation (β2 = 12.6 degrees) is very low, because the relative flow cannot be correctly guided due to the significant interblade clearance gap that exists in between the two discs.
- (b)
- The impeller outlet absolute flow angle value is also small. Consequently, the present volute design cannot be adapted to this inlet angle condition. This means that losses may increase in the present volute, which has not being changed to be adapted to the present impeller outlet angle. If a modified volute design has been possible, the maximum efficiency of both impeller and pump would have been shifted to higher flow coefficient.
- (c)
- Compared with other published results on similar pump geometries (see first two lines in Table 2), one can observe that for the same outlet radius, same blade height h2 and same number of blades Z, the flow and head coefficients have bigger values probably because of the outlet impeller width b2 value is two times higher than present case study. In addition, the present geometrical outlet to inlet radius ratio R2/R1 is smaller compared with others and the impeller is followed by a classical volute design which is not adapted to the outlet flow angle, as explain just above.
4.3. Comparison between Experimental Results and Euler Head Coefficient Relation
- (a)
- High positive incidence angle values are present at the impeller’s leading edge and become greater and greater for deceasing values of flow coefficients. The slope modification can be explained by a change of the outlet relative angle value β2 which can be associated with local reverse flows at impeller outlet section.
- (b)
- Combined with the previous comment, the increase of the maximum head coefficient (for zero flow rate) can also be explained by the contribution of the last term of equation (3). If inlet local strong reverse flow is present, or if inlet tangential velocity component V1u is opposite to the rotational direction, the total head coefficient will increase by a fraction of the term: −. Applied to present case geometry, for which the tip inlet radius is 0.05 and outlet radius is 0.1, the last term of Equation (3) is equal to 0.25, assuming a maximum value of Vu1 = U1. It is so expected that inlet swirl velocity ratio Vu1/U1, may reach large positive values (because it is transported by local negative meridional velocity), when flow coefficient tends to zero.
- (c)
- The last part of the Euler curve, which belongs to low flow coefficients below 0.03, is related to additional phenomena that increase the power given to the pump shaft. One comes from strong leakage flow passing through impeller tip clearance from the blade pressure side to the blade suction side. Such leakages are known to generate strong secondary flow patterns in the impeller inlet section with an increase of losses and related strong local swirling flow. Additional effects are related to the increase of volumetric efficiency due to flow leakage inside the two side chambers between impeller discs and pump casing, associated with disc friction losses that are not negligible below nominal conditions.
- (d)
- Disc friction losses must be consequently taken into account; they depend on the rotational speed to the power of three, contrary to the head coefficient which varies with the rotational speed to the power of two.
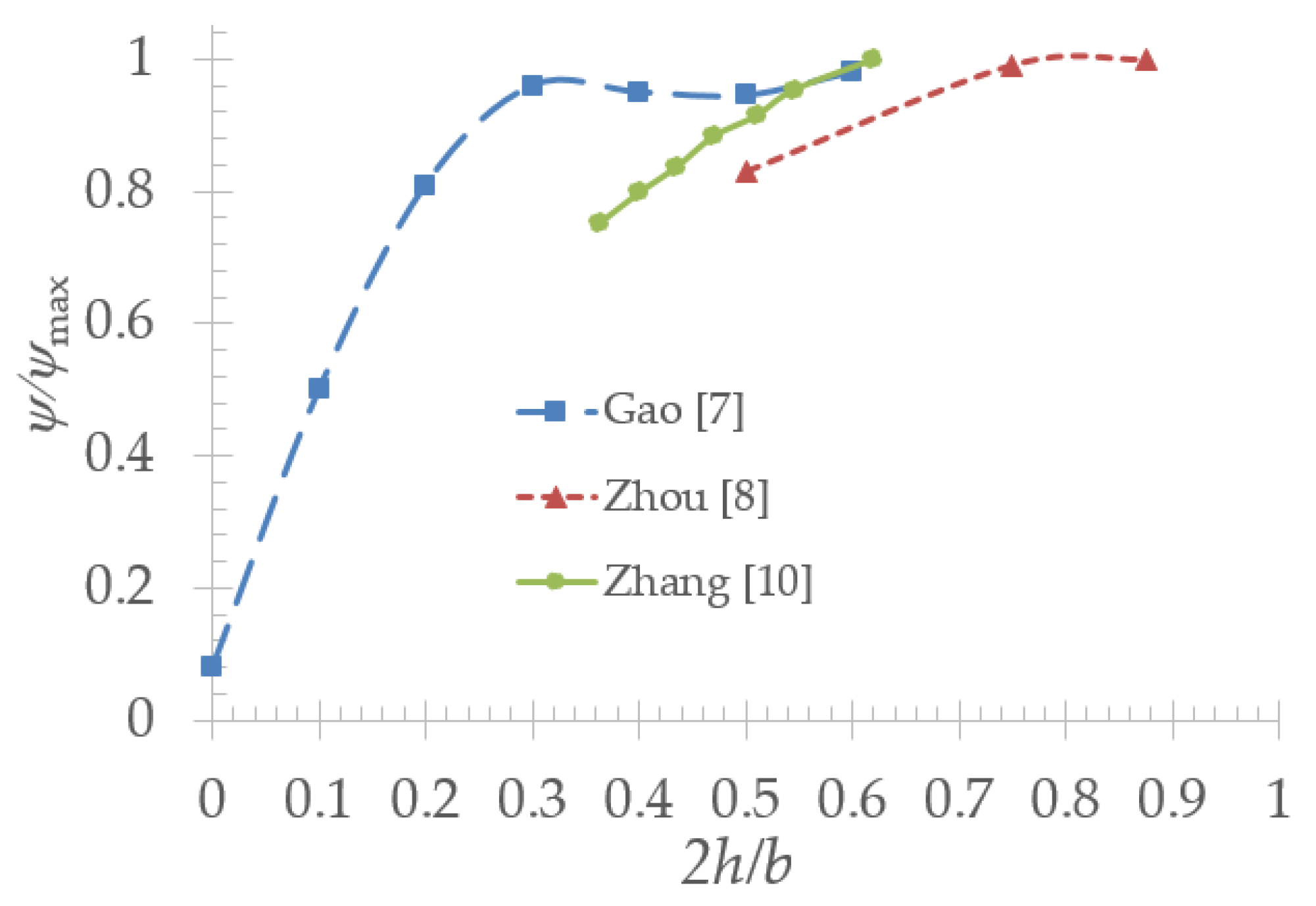
- (e)
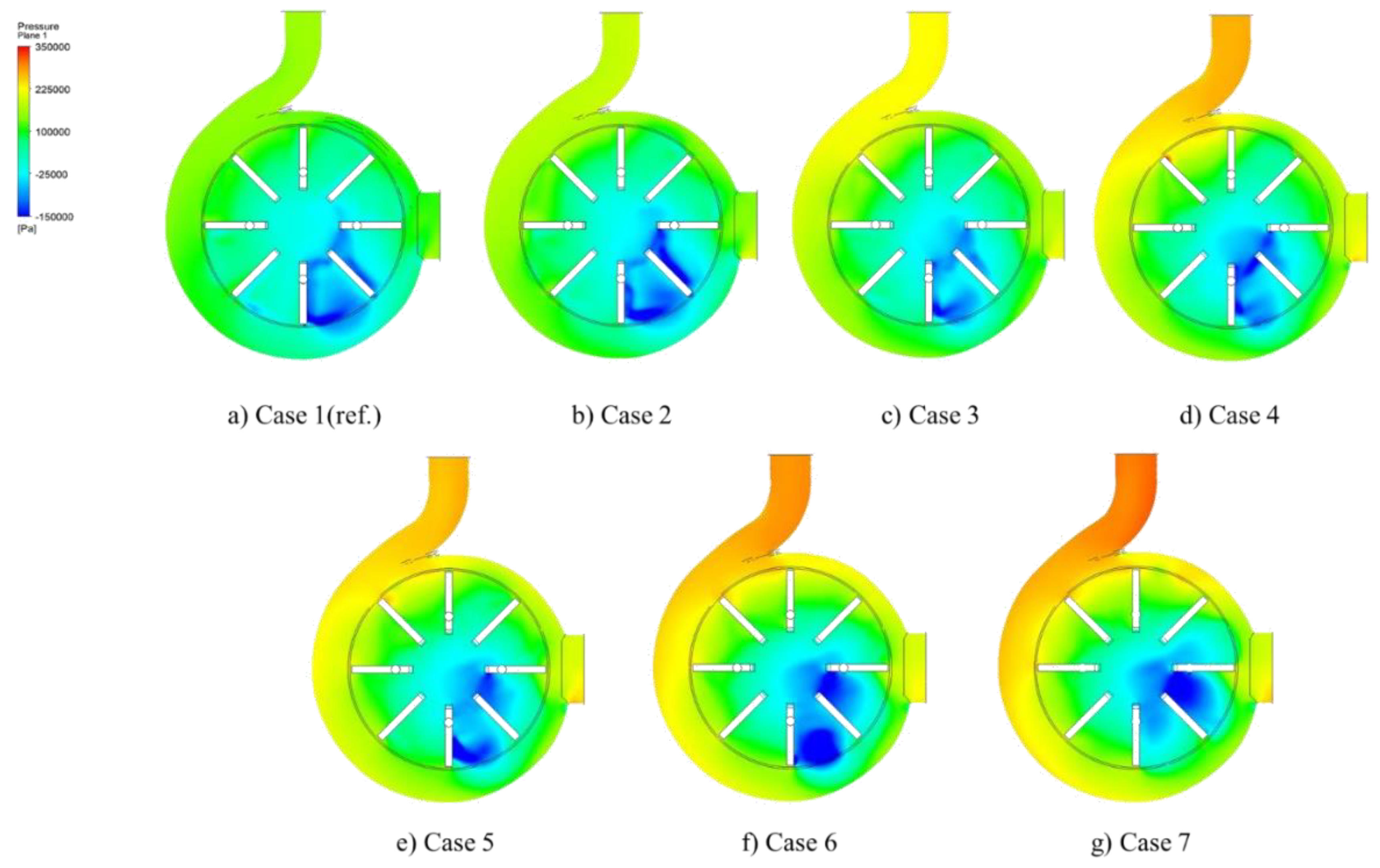
- Most existing numerical and experimental results that can be found in open literature are generally performed at low flow rate conditions and rather far from optimum efficiency condition due to the radial inlet blade angle. From existing CFD results and at nominal conditions, strong inlet swirl flows have been found at impeller inlet section and even upstream inside the inlet tube. Low values of inlet local static pressure have been also found by Je and Kim [11] for a similar design, as shown in Figure 11. Very low local pressure can be even reached in some blade passages. Each case corresponds to a different value of blade height h2. Results obtained in Case 3 are closed to the present impeller geometry looking at the blade height ratio 2h/b.
5. Recommendations and Conclusions
- (1)
- A preliminary experimental study has been performed on a centrifugal specific bladed disc pump design. These results show that acceptable performances can be achieved even in such a crude design approach with better head and flow coefficient values compared with bladeless tesla disc pump configuration.
- (2)
- The corresponding pump performance curve exhibit larger slope values of the head coefficient compared with conventional designs. Such cases should undergo additional analysis that are going to be performed by the present research team.
- (3)
- A simplified approach using complete Euler relation is attempted to explain the slope modifications that occur in the present geometry at low flow rate conditions. Part of the proposed results should undergo additional date reduction including disc friction effects.
- (4)
- Most experimental and numerical results that are available in open literature do not correspond to the real optimum conditions because of strong incidence angles for all flow rates and a lack of analysis concerning volute design adaptation. This may cause wrong interpretation on existing published results.
- (5)
- Most numerical results published in open literature are based on steady flow assumptions. This is physically nonvalid mainly because off-design conditions are always present due to the radial blade shape, strong fluid blockage at impeller inlet section and volute interactions.
- (6)
- Additional physical analysis using efficient CFD URANS (Unsteady Reynolds-averaged Navier-Stokes) approaches for several flow rates are necessary when aiming for a better understanding of local flow pattern, inlet flow rate distribution, swirl velocity value that may be transported by local reverse flow along impeller width inlet and outlet passages, and related losses levels.
- (7)
- More detailed experimental work must be performed at the impeller inlet plane, in between the blade open space and in the upstream tube section to check how far the swirling flow extends when flow rate decreases.
- (8)
- In case of low inlet pressure conditions, this impeller design will be quite sensitive to cavitation effects. However, the present design final purpose mainly concerns the pump’s ability to work under inlet gas-liquid mixtures preventing complete shut-off conditions excluding cavitation effects.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| b | impeller channel width (mm). b = 2h + cl |
| cl | inter blade clearance (mm) |
| th | inter blade thickness (mm) |
| g | acceleration (m2/s) |
| h | blade height (mm) |
| H | total head (m) |
| N | rotational speed (rev/min) |
| P | shaft power (W) |
| Q | volume flow rate (m3/s) |
| R | Radius (m) |
| U | impeller tip speed (m/s) |
| V | absolute velocity (m/s) |
| Z | number of impeller blades (-) |
| Greek symbols | |
| α | absolute flow angle (°), from tangential direction. |
| β | relative flow angle (°), from tangential direction. |
| θ | blade angle (°), from tangential direction. |
| η | global efficiency (%) |
| μ | slip coefficient, (-) μ = VU2/U2 |
| ω | angular velocity (rad/s) |
| Φ | flow coefficient (-) |
| Ψ | head coefficient (-) |
| Ψth | theoretical head coefficient, (-) Ψth = Ψ/η |
| Ωs | specific speed, |
| Subscripts | |
| 1 | impeller inlet section |
| 2 | impeller outlet section |
| E | Euler |
| th | theoretical |
| r | related to the radial component |
| u | related to the tangential component |
References
- Cappellino, C.A.; Roll, D.R.; Wilson, G. Design considerations and application guidelines for pumping liquids with entrained gas using open impeller centrifugal pumps. In Proceedings of the Ninth International Pumps User Symposium, College Station, TX, USA, 3–5 March 1992; pp. 51–60. [Google Scholar]
- Tesla, N. Fluid Propulsion. U.S. Patent No. 1061142, 6 May 1913. [Google Scholar]
- Max, I.G. Rotary Disc Slurry Pump. U.S. Patent No. 4773819, 27 September 1988. [Google Scholar]
- Max, I.G. Rotary Disc Pump. U.S. Patent No. 4940385, 10 July 1990. [Google Scholar]
- Max, I.G. Rotary Disc Pump. U.S. Patent No. 7097416B2, 29 August 2006. [Google Scholar]
- Yin, S.M. The Optimization of Subsea Mudlift Disc Pump and the Development of Its Multi-Stage Pump (In Chinese). Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2012. [Google Scholar]
- Gao, B. Flow Field Simulation and Performance Assessment for the Subsea Mudlift Disc Pump (In Chinese). Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2009. [Google Scholar]
- Zhou, C. Research on the Blade Disk Pump for Subsea Mudlift Drilling (In Chinese). Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2012. [Google Scholar]
- Chen, Y. Strength Analysis of Fluid-Solid Interaction and Performance Improvement of Disc Pump with Radial Straight Blade (In Chinese). Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2013. [Google Scholar]
- Zhang, Y. Study on Design Application Method for Subsea Mudlift Disc Pump (In Chinese). Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2015. [Google Scholar]
- Je, Y.W.; Kim, Y.J. Influence of impeller blade height on the performance of a slurry pump. In Proceedings of the 15th Asian International Conference on Fluid Machinery, Busan, Korea, 25–27 September 2019. AICFM15-PM7-2. [Google Scholar]
- Choi, Y.D.; Kurokawa, J.; Matsui, J. Performance and internal flow characteristics of a very low specific speed centrifugal pump. ASME J. Fluid Eng. 2006, 128, 341–349. [Google Scholar] [CrossRef]
- Gülich, J.F. Pumping highly viscous fluids with centrifugal pumps—Part 1. World Pumps 1999, 395, 30–34. [Google Scholar] [CrossRef]
- Gülich, J.F. Pumping highly viscous fluids with centrifugal pumps—Part 2. World Pumps 1999, 396, 39–42. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, H.Q. A Review of Experiments and Modeling of Gas-Liquid Flow in Electrical Submersible Pumps. Energies 2018, 11, 180. [Google Scholar] [CrossRef] [Green Version]





| Reference | R2/R1 | 2h/b | N | θ | th |
|---|---|---|---|---|---|
| Yin [6] | √ | ||||
| Gao [7] | √ | √ | √ | ||
| Zhou [8] | √ | √ | √ | ||
| Chen [9] | √ | √ | |||
| Zhang [10] | √ | √ | |||
| Je and Kim [11] | √ |
| Reference | R2 | R2/R1 | N | b2/R2 | h2/b2 | Z | θ2 | θ1 | Φ | Ψ | Ωs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Yin [6] | 0.16 | 2.7 | 2900 | 0.33 | 0.28 | 8 | 90 | 90 | 0.026 | 0.48 | 0.34 |
| Je and Kim [11] | 0.11 * | 2.7 | 1750 | 0.33 | 0.25 * | 8 * | 90 * | 90 * | 0.04 | 0.38 | 0.316 |
| Present study | 0.10 * | 2.0 | 1000/2900 | 0.16 | 0.25 * | 8 * | 90 * | 90 * | 0.08 | 0.28 | 0.74 |
| Choi et al. [12] | 0.06 | 4.0 | 700 | 0.15 | 0.888 | 6 | 90 | 90 | 0.04 | 0.4 | 0.20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heng, Y.; Han, Y.; Zhang, H.; Zhang, W.; Bois, G.; Jiang, Q.; Wang, Z.; Liu, X. Tesla Bladed Pump (Disc Bladed Pump) Preliminary Experimental Performance Analysis. Energies 2020, 13, 4873. https://doi.org/10.3390/en13184873
Heng Y, Han Y, Zhang H, Zhang W, Bois G, Jiang Q, Wang Z, Liu X. Tesla Bladed Pump (Disc Bladed Pump) Preliminary Experimental Performance Analysis. Energies. 2020; 13(18):4873. https://doi.org/10.3390/en13184873
Chicago/Turabian StyleHeng, Yaguang, Yuming Han, Huiyu Zhang, Weibin Zhang, Gérard Bois, Qifeng Jiang, Zhengwei Wang, and Xiaobing Liu. 2020. "Tesla Bladed Pump (Disc Bladed Pump) Preliminary Experimental Performance Analysis" Energies 13, no. 18: 4873. https://doi.org/10.3390/en13184873
APA StyleHeng, Y., Han, Y., Zhang, H., Zhang, W., Bois, G., Jiang, Q., Wang, Z., & Liu, X. (2020). Tesla Bladed Pump (Disc Bladed Pump) Preliminary Experimental Performance Analysis. Energies, 13(18), 4873. https://doi.org/10.3390/en13184873






