Fuel Consumption Dependence on a Share of Reduction Processes in Imperial Smelting Furnace
Abstract
:1. Introduction
- Launching of gas desulphurization installation from the sintering strand, enabling metallurgical waste processing;
- Extension by three rectification columns, which allowed an increase in the possibility of hazardous waste processing;
- Systems of sewage neutralization with thallium removal.
- The quality and method of preparing metal-bearing feed (sintering, briquetting);
- Coke quality;
- The hot blast temperature;
- The technical condition of the refractory lining and the cooling system and their effect on heat losses;
- The technological level of the measurement equipment;
- External conditions, which indirectly influence the continuity of a furnace operation, such as the market situation.
- The list presented above show that the fuel consumption depends on factors that the shaft blast furnace operator cannot affect online. However, the correctness in furnace operation as a crew experience may bring cost reduction resulting from the fuel saving.
- The use of modern modelling techniques can help to achieve these goals, as it took place in ironmaking. These techniques may help in the understanding of phenomena taking place in the working volume of shaft blast furnaces, such as:
2. Materials and Methods
2.1. ISF Process Description
2.2. Reduction Processes in ISF
2.3. Fuel Rate Minimization Model Construction
- QZn—zinc enthalpy, MJ/tZn;
- Qslag—slag enthalpy, MJ/tZn;
- QPb—lead enthalpy, MJ/tZn;
- Qtg—top gas enthalpy, MJ/tZn;
- QCL—cooling losses, MJ/tZn;
- QHB—hot blast enthalpy, MJ/tZn;
- QC700—coke enthalpy at 700 °C, MJ/tZn;
- QS200—sinter enthalpy at 200 °C, MJ/tZn;
- 240 × 10−3—enthalpy of endothermic reaction (IV), MJ/mol Zn;
- 65.4 × 10−6—molar mass of zinc, t/mol;
- 9.196—enthalpy of exothermic reaction (V), MJ/kg C.
- CR—coke rate, kg/tZn;
- 88—average carbon content in coke, mass %.
2.4. Calculation of ISF Output
- %Zn, %Pb, %SiO2—weight percent of element or substance, wt.%;
- M—a mass of stream per charge, kg;
3. Results of Model Implementation and Discussion
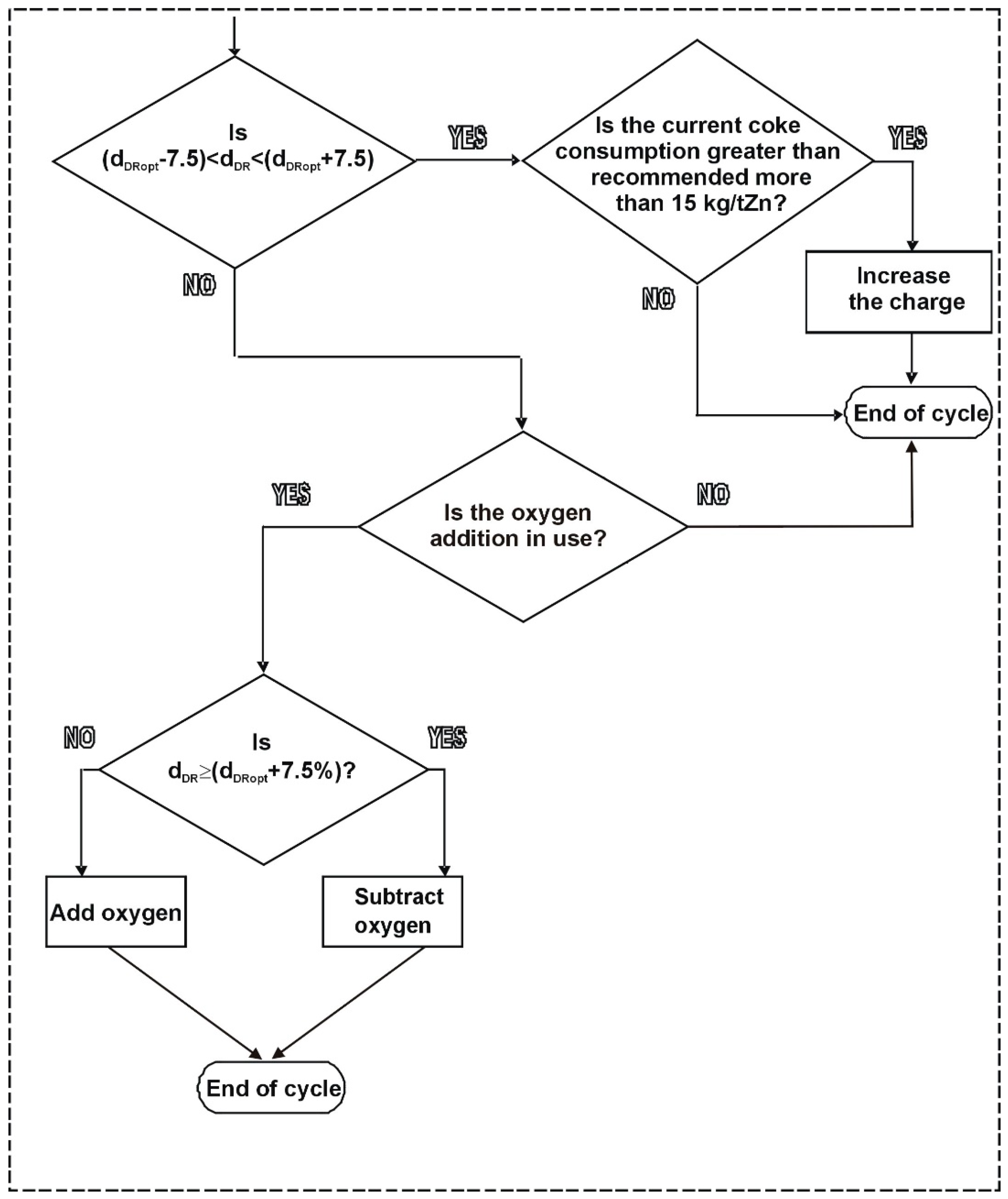
- The ISF operating point, which reflects current coke consumption at the actual direct reduction rate;
- Boundaries of optimal direct ZnO reduction rate; they are set as ±7.5% deviation from the optimal direct reduction rate (two vertical blue lines);
- Results of the fuel rate minimization model, as current coke rate at the current dDR, recommended coke rate, and also theoretical minimum coke rate at the optimal dDR.
- C/Znrecom—top charge recommended to use in next hour;
- C/Zncurrent—current top charge;
- Pch—charge production tZn/charge;
- Cch—coke input, kg/charge;
- CRrecom—recommended coke rate, kg/tZn;
- CRcurrent—current coke rate, kg/tZn.
4. Conclusions
- Thermochemical analysis of reduction processes necessary for the determination of boundary conditions to build the fuel rate minimization model;
- Construction of the model using A.N. Ramm’s principles of direct and indirect reduction share;
- Calculation of current zinc production in tonne per charge, what is necessary to unify material input and output streams;
- Development of regulatory recommendations that will affect the optimization of fuel consumption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Śmieszek, Z.; Czernecki, J.; Sak, T.; Madej, P. Metallurgy of non-ferrous metals in Poland. J. Chem. Technol. Metall. 2017, 52, 221–234. [Google Scholar]
- Patil, S.B.; Vyas, A.K.; Gupta, A.B.; Patil, R.S. Imperial smelting furnace slag as fine aggregate in cement concrete mixes. J. Solid Waste Technol. Manag. 2016, 42, 128–136. [Google Scholar] [CrossRef]
- Szweda, Z.; Ponikiewski, T.; Katzer, J. A study on replacement of sand by granulated ISP slag in SCC as a factor formatting its durability against chloride ions. J. Clean. Prod. 2017, 156, 569–576. [Google Scholar] [CrossRef]
- Patil, S.B.; Vyas, A.K.; Gupta, A.B. Utilization of an industrial waste in cement concrete mixes. J. Solid Waste Technol. Manag. 2014, 40, 79–85. [Google Scholar] [CrossRef]
- Banerjee, A.; Sen, P.K.; Roy, S.K. Novel approach to modeling of imperial smelting furnace behavior. Miner. Process. Extr. Metall. Rev. 2007, 28, 159–176. [Google Scholar] [CrossRef]
- Ebrahim, H.A.; Jamshidi, E. Kinetic study and mathematical modeling of the reduction of ZnO-PbO mixtures by methane. Ind. Eng. Chem. Res. 2005, 44, 495–504. [Google Scholar] [CrossRef]
- Hu, Z.K.; Yin, L.Z.; Chen, Z.W.; Gui, W.H.; Yang, C.H.; Peng, X.Q. An efficient multi-PCA based on-line monitoring scheme for multi-stages imperial smelting process. Int. J. Control Autom. Syst. 2013, 11, 317–324. [Google Scholar] [CrossRef]
- Straka, R.; Bernasowski, M.; Klimczyk, A.; Stachura, R.; Svyetlichnyy, D. Prediction of raceway shape in zinc blast furnace under the different blast parameters. Energy 2020, 207, 118153. [Google Scholar] [CrossRef]
- Małecki, S.; Gargul, K.; Warzecha, M.; Stradomski, G.; Hutny, A.; Madej, M.; Dobrzyński, M.; Prajsnar, R.; Krawiec, G. High-performance method of recovery of metals from eaf dust—Processing without solid waste. Materials 2021, 14, 6061. [Google Scholar] [CrossRef]
- Xue, Y.; Hao, X.; Liu, X.; Zhang, N. Recovery of Zinc and Iron from Steel Mill Dust—An Overview of Available Technologies. Materials 2022, 15, 4127. [Google Scholar] [CrossRef]
- Brunelli, K.; Dabalà, M. Ultrasound effects on zinc recovery from EAF dust by sulfuric acid leaching. Int. J. Miner. Metall. Mater. 2015, 22, 353–362. [Google Scholar] [CrossRef]
- Xin, C.; Xia, H.; Jiang, G.; Zhang, Q.; Zhang, L.; Xu, Y. Studies on Recovery of Valuable Metals by Leaching Lead–Zinc Smelting Waste with Sulfuric Acid. Minerals 2022, 12, 1200. [Google Scholar] [CrossRef]
- Yan, H.; Chai, L.; Peng, B.; Li, M.; Peng, N.; Hou, D. A novel method to recover zinc and iron from zinc leaching residue. Miner. Eng. 2014, 55, 103–110. [Google Scholar] [CrossRef]
- Li, H.; Saxén, H.; Liu, W.; Zou, Z.; Shao, L. Model-based analysis of factors affecting the burden layer structure in the blast furnace shaft. Metals 2019, 9, 1003. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Wu, S.; Kou, M.; Luo, Z.; He, W.; Zou, Z.; Shen, Y. Discrete particle simulation of solid flow in a large-scale reduction shaft furnace with center gas supply device. ISIJ Int. 2018, 58, 422–430. [Google Scholar] [CrossRef] [Green Version]
- Ariyama, T.; Natsui, S.; Kon, T.; Ueda, S.; Kikuchi, S.; Nogami, H. Recent progress on advanced blast furnace mathematical models based on discrete method. ISIJ Int. 2014, 54, 1457–1471. [Google Scholar] [CrossRef] [Green Version]
- Shatokha, V.; Velychko, O. Study of softening and melting behaviour of iron ore sinter and pellets. High Temp. Mater. Process. 2012, 31, 215–220. [Google Scholar] [CrossRef]
- Small, J.; Adema, A.; Andreev, K.; Zinngrebe, E. Petrological study of ferrous burden-crucible interaction in softening & melting experiments: Implications for the relevance of pressure drop measurements. Metals 2018, 8, 1082. [Google Scholar] [CrossRef] [Green Version]
- Bernasowski, M.; Klimczyk, A.; Stachura, R. Calculation of coke layers situation in the cohesive zone of blast furnace. Materials 2021, 14, 192. [Google Scholar] [CrossRef]
- Hou, Q.; Dianyu, E.; Kuang, S.; Yu, A. A Transient Discrete Element Method-Based Virtual Experimental Blast Furnace Model. Steel Res. Int. 2020, 91, 106369. [Google Scholar] [CrossRef]
- Guha, M. Revealing cohesive zone shape and location inside blast furnace. Ironmak. Steelmak. 2018, 45, 787–792. [Google Scholar] [CrossRef]
- Kuang, S.; Li, Z.; Yu, A. Review on Modeling and Simulation of Blast Furnace. Steel Res. Int. 2018, 89, 1700071. [Google Scholar] [CrossRef]
- Kexin, J.; Jianliang, Z.; Chunlin, C.; Senran, W.; Lisheng, L. Analysis of the deadman features in hearth based on blast furnace dissection by comprehensive image-processing technique. ISIJ Int. 2019, 59, 16–21. [Google Scholar] [CrossRef] [Green Version]
- Okosun, T.; Silaen, A.K.; Zhou, C.Q. Review on Computational Modeling and Visualization of the Ironmaking Blast Furnace at Purdue University Northwest. Steel Res. Int. 2019, 90, 1353–1362. [Google Scholar] [CrossRef]
- Zhou, C.; Tang, G.; Wang, J.; Fu, D.; Okosun, T.; Silaen, A.; Wu, B. Comprehensive Numerical Modeling of the Blast Furnace Ironmaking Process. JOM 2016, 68, 1353–1362. [Google Scholar] [CrossRef]
- Kardas, E.; Prusak, R. The assessment of efficiency of work of blast furnace. Metalurgija 2020, 59, 403–406. [Google Scholar]
- Hashimoto, Y.; Masuda, R.; Mulder, M.; van Paassen, M.M. (René) Automatic Control of Hot Metal Temperature. Metals 2022, 12, 1624. [Google Scholar] [CrossRef]
- Bernasowski, M.; Klimczyk, A.; Stachura, R. Support algorithm for blast furnace operation with optimal fuel consumption. J. Min. Metall. Sect. B Metall. 2019, 55, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Bernasowski, M.; Ledzki, A.; Stachura, R.; Klimczyk, A. Basic structure of the fuel rate optimization model and its practical use at the blast furnace technology. In Proceedings of the METAL 2014: 23rd International Conference on Metallurgy and Materials, Brno, Czech Republic, 21–23 May 2014; pp. 39–44. [Google Scholar]
- Brožová, S.; Jursová, S.; Pustejovská, P.; Bilík, J. Kinetics of reduction and oxidation reactions during pyrometallurgical metal extraction. Sci. Iran. 2017, 24, 2009–2018. [Google Scholar] [CrossRef]
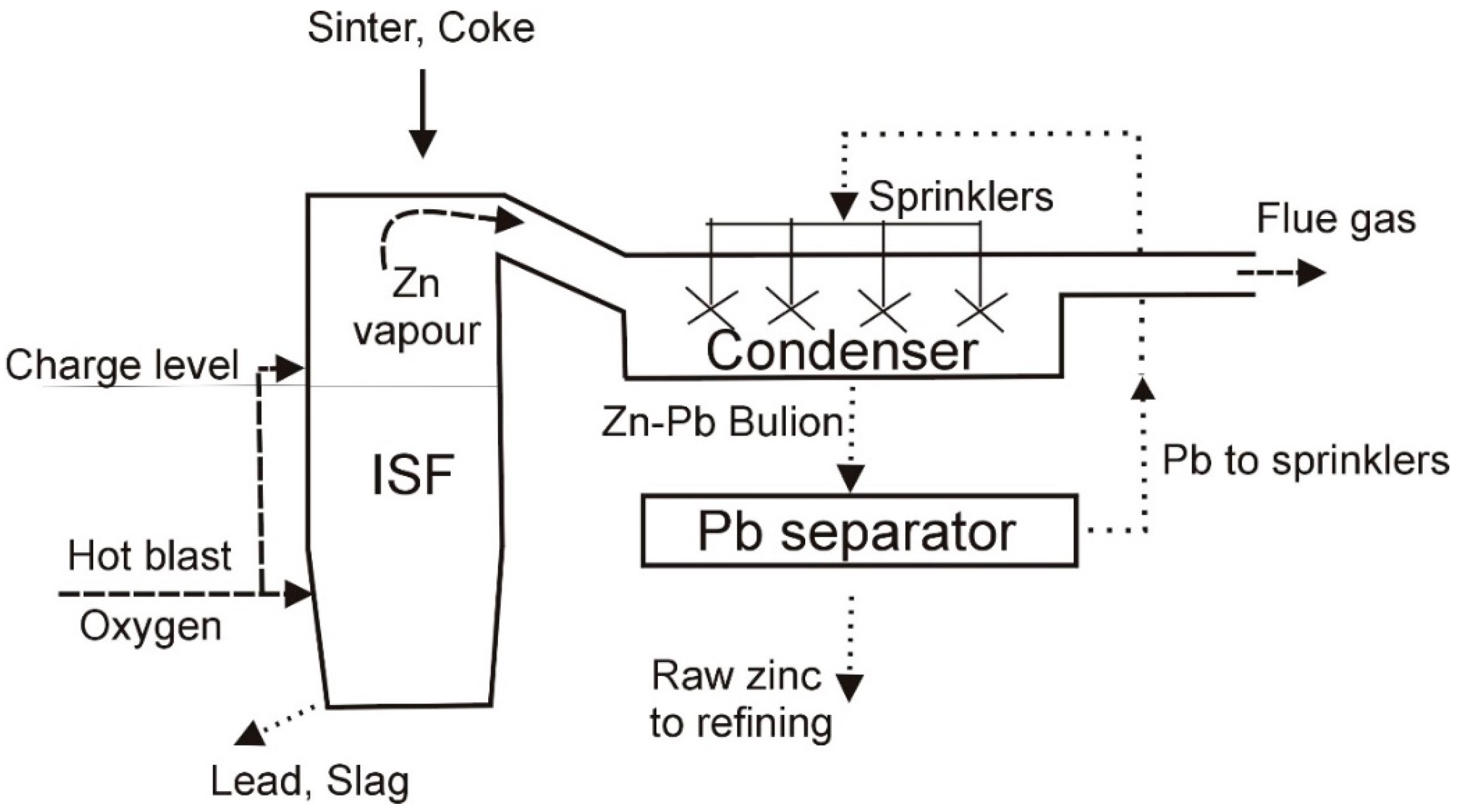
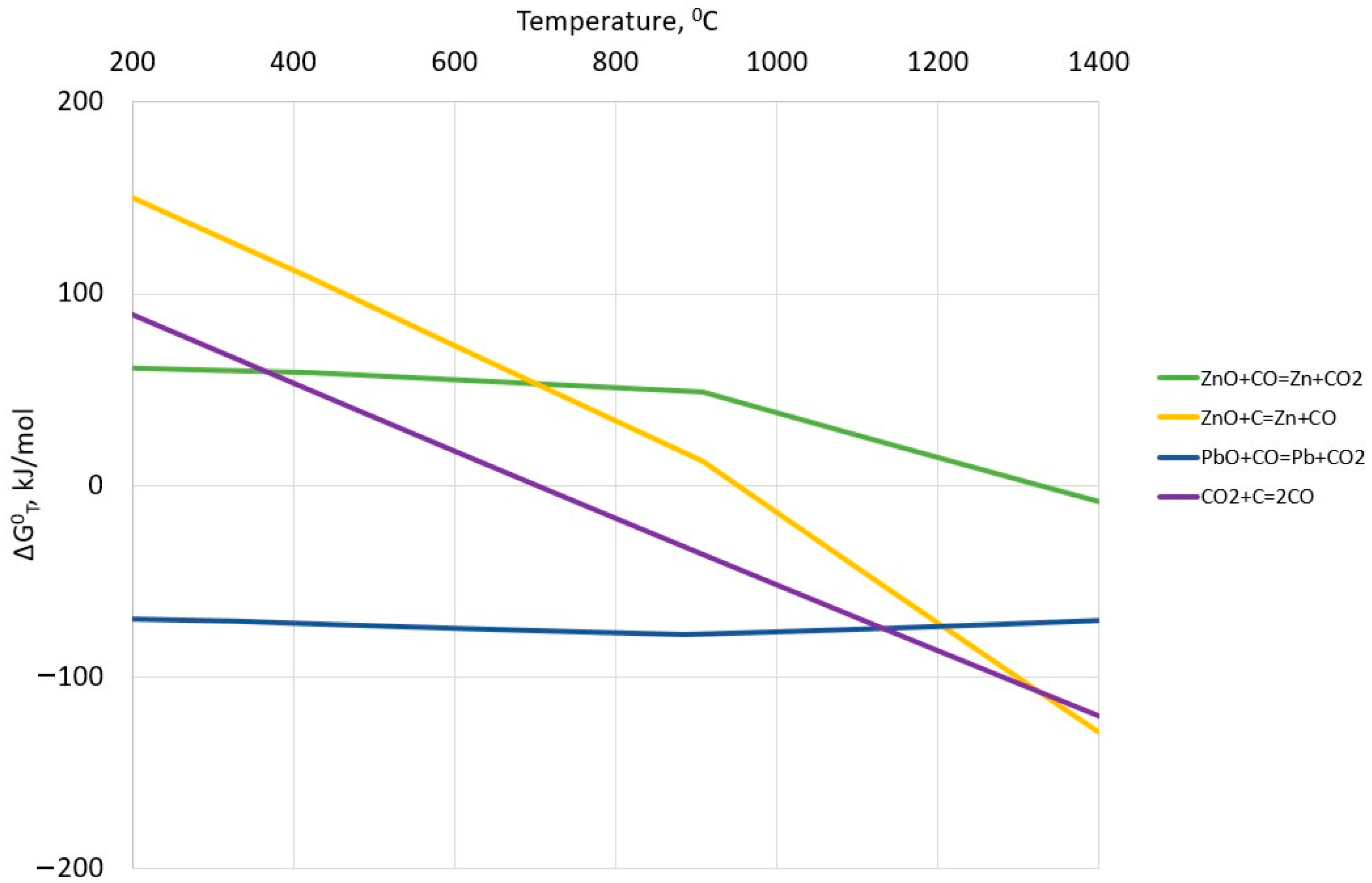
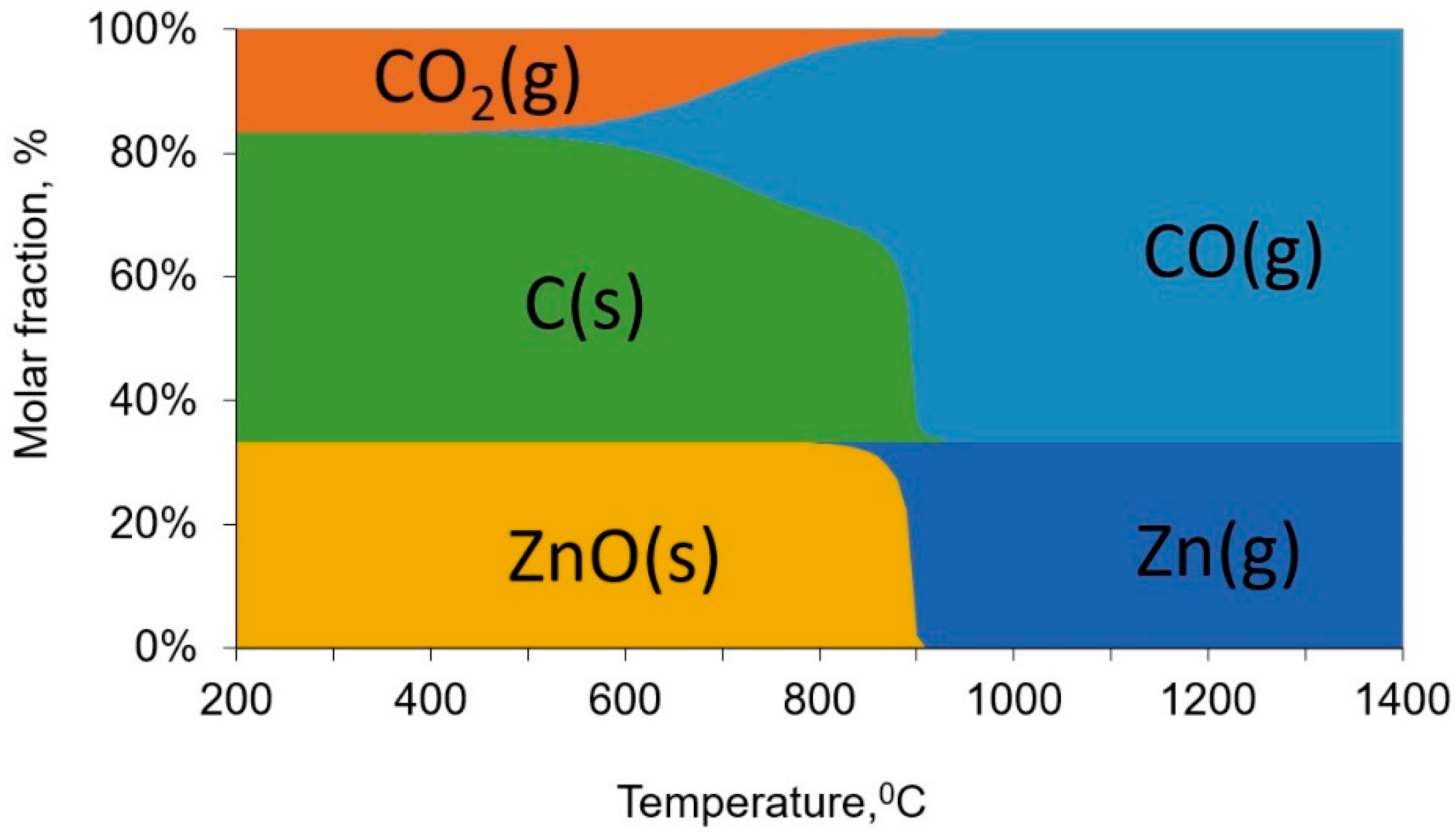
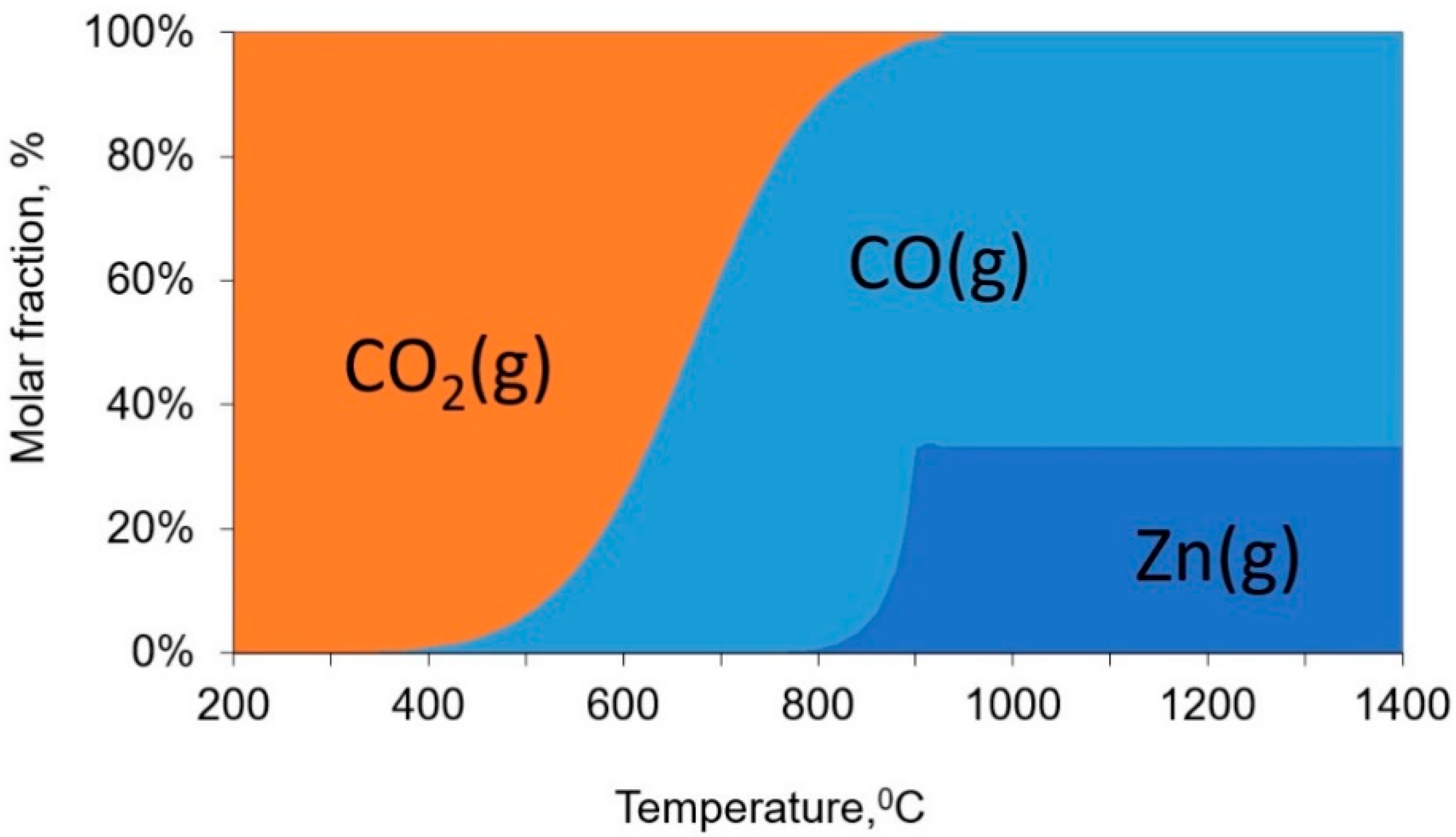
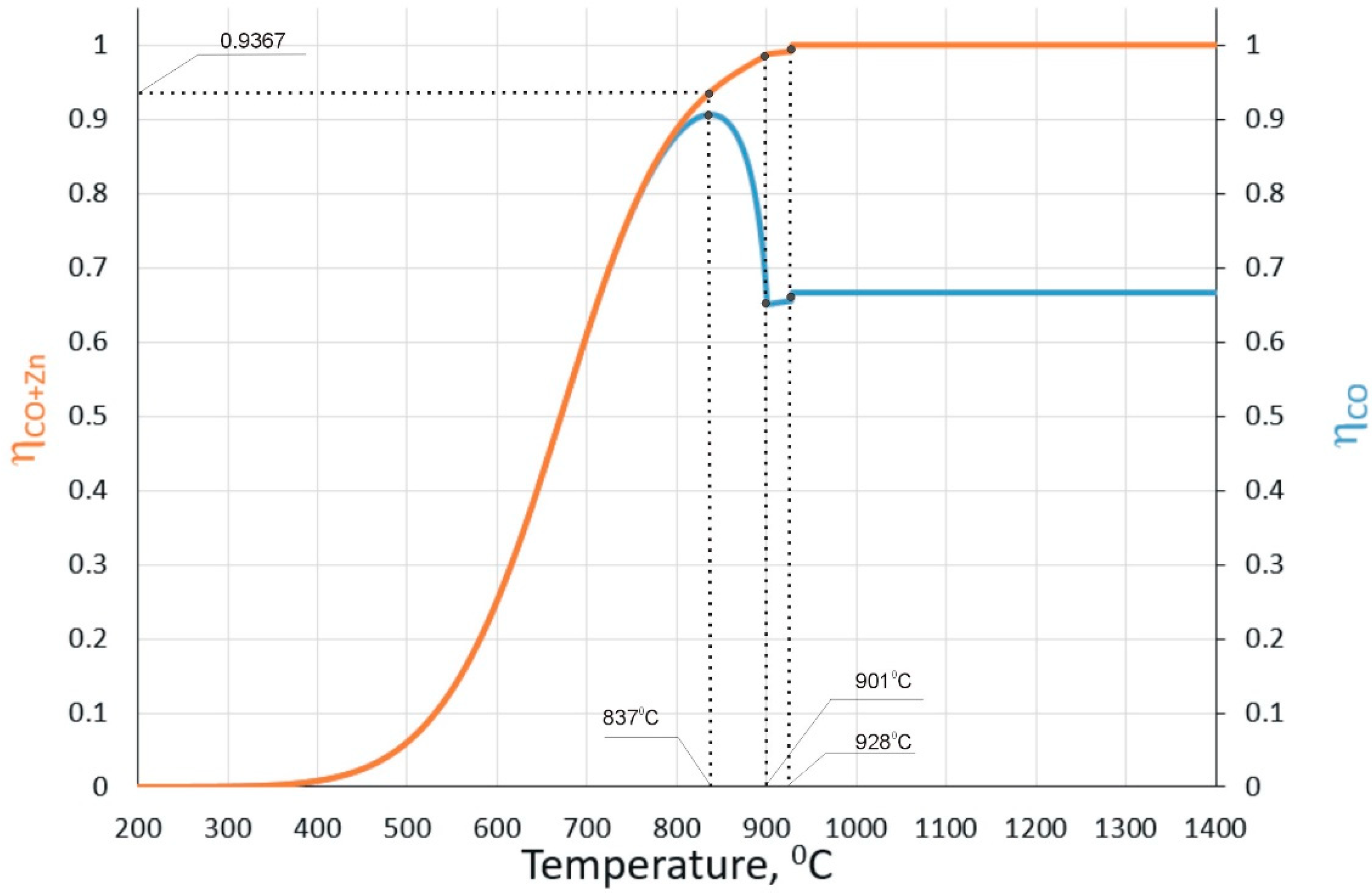
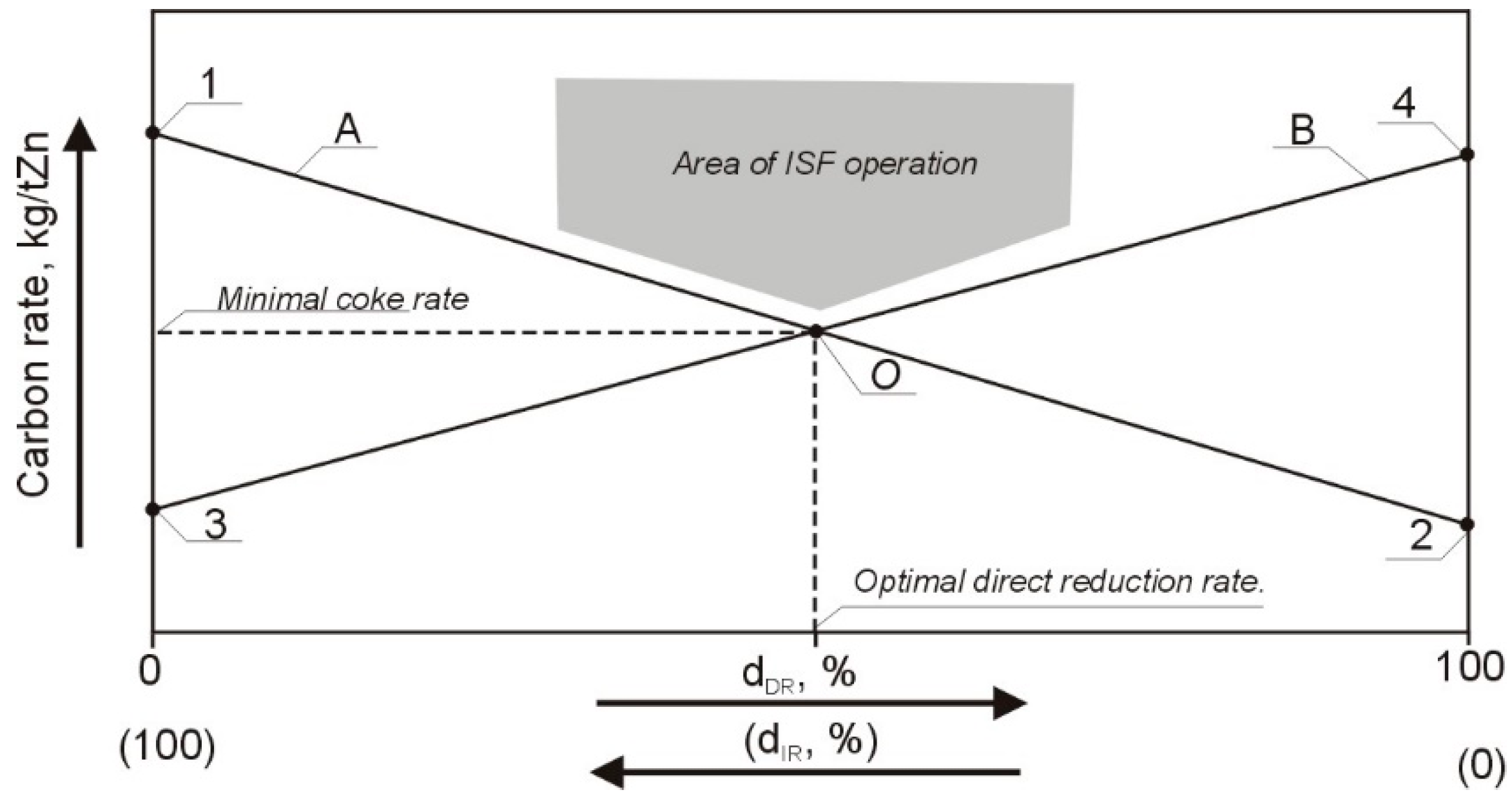
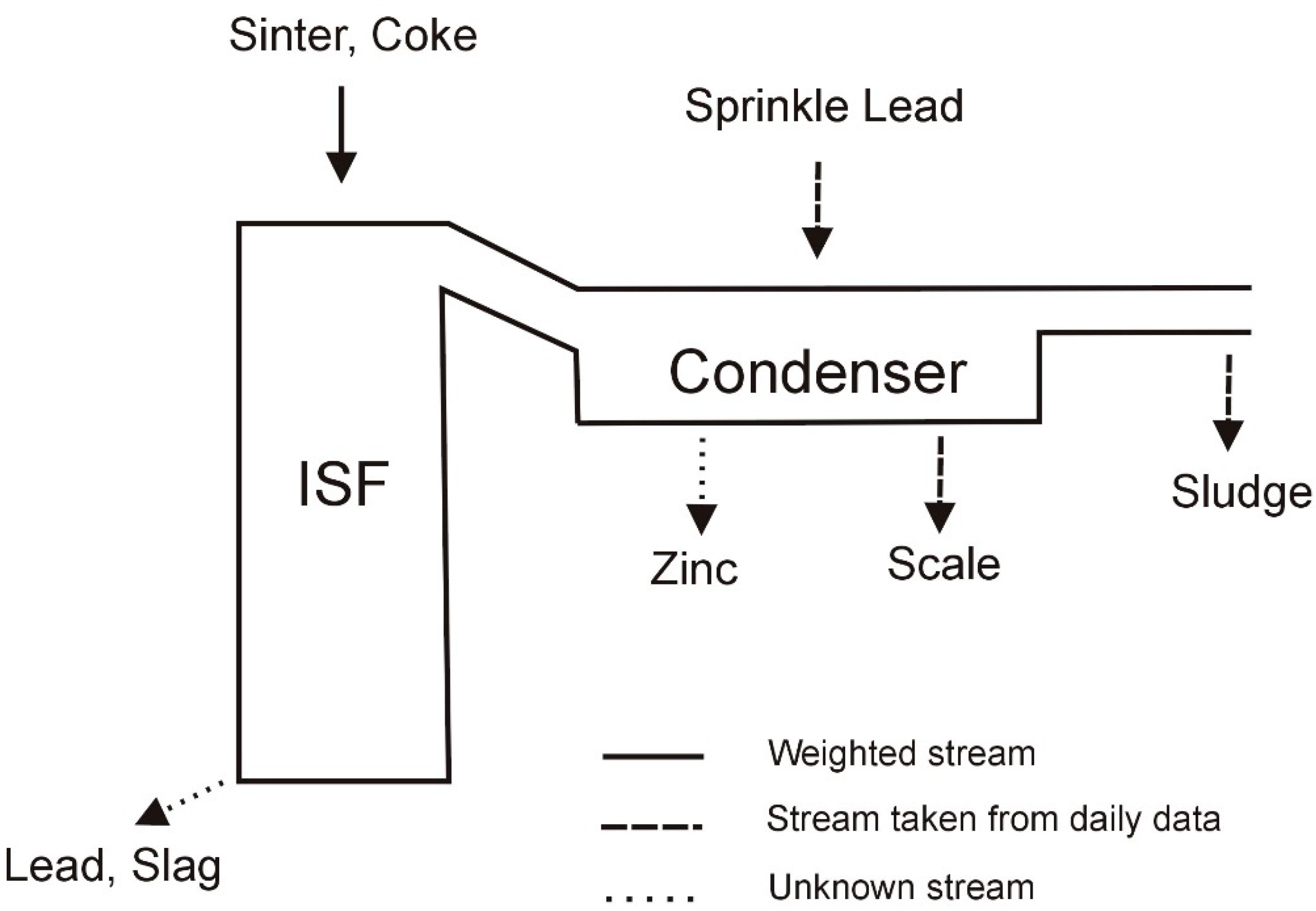
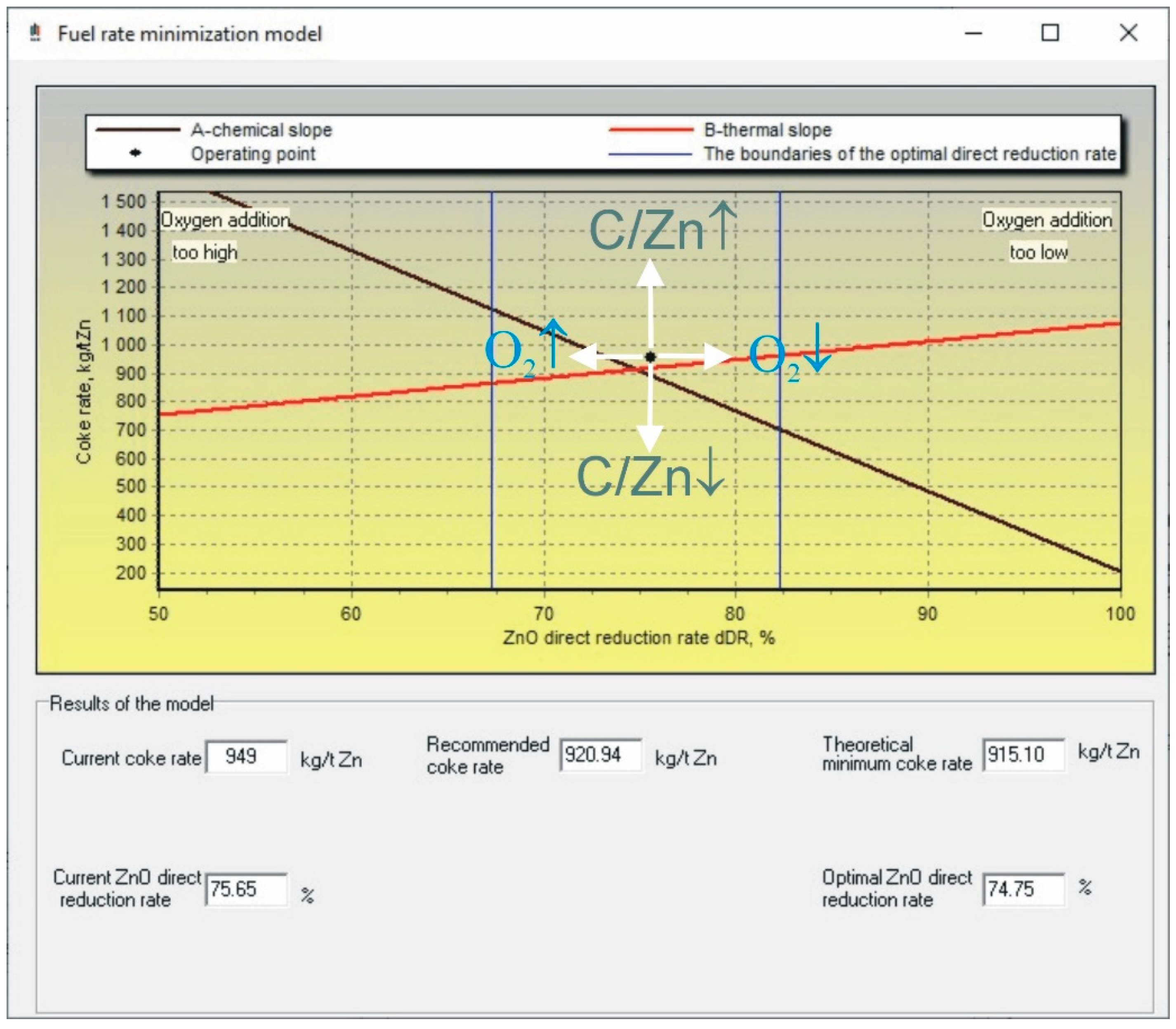
| Ingredient Input, mol | Possible Substances in Equilibrium |
|---|---|
| 1ZnO(s) * + 1CO(g) + 1C(s) | ZnO(s), ZnO(liq), Zn(s), Zn(liq), Zn(g), CO(g), CO2(g), C(s) |
| Group of Variables | Variable Name | Value | Unit |
|---|---|---|---|
| Measured characteristics | Sinter input Coke input Hot blast input Hot blast temperature CO in flue gas CO2 in flue gas Top gas temperature | 2932 1195 36,248 1053 28.42 7.16 918 | kg/charge kg/charge m3/h °C vol.% vol.% °C |
| Calculated characteristics of heat balance in Equation (8) | QZn Qslag QPb Qtg QCL QHB QC700 QS200 | 2281 606 −32 * 5030 1670 4355 1194 377 | MJ/tZn |
| Calculated characteristics of the fuel rate minimization model | Current direct reduction rate, dDR Charge production, Pch Current coke rate, CRcurrent Recommended coke rate, CRrecom Current top charge, C/Zncurrent Recommended top charge, C/Znrecom | 74.53 1.18 1013 980 0.863 0.848 | % tZn/charge kg/tZn kg/tZn - - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernasowski, M.; Stachura, R.; Klimczyk, A. Fuel Consumption Dependence on a Share of Reduction Processes in Imperial Smelting Furnace. Energies 2022, 15, 9259. https://doi.org/10.3390/en15239259
Bernasowski M, Stachura R, Klimczyk A. Fuel Consumption Dependence on a Share of Reduction Processes in Imperial Smelting Furnace. Energies. 2022; 15(23):9259. https://doi.org/10.3390/en15239259
Chicago/Turabian StyleBernasowski, Mikolaj, Ryszard Stachura, and Arkadiusz Klimczyk. 2022. "Fuel Consumption Dependence on a Share of Reduction Processes in Imperial Smelting Furnace" Energies 15, no. 23: 9259. https://doi.org/10.3390/en15239259
APA StyleBernasowski, M., Stachura, R., & Klimczyk, A. (2022). Fuel Consumption Dependence on a Share of Reduction Processes in Imperial Smelting Furnace. Energies, 15(23), 9259. https://doi.org/10.3390/en15239259







