A Compendium of Formulae for Natural Frequencies of Offshore Wind Turbine Structures
Abstract
:1. Introduction
2. Offshore Wind Turbine Structure and Vibration Characteristics
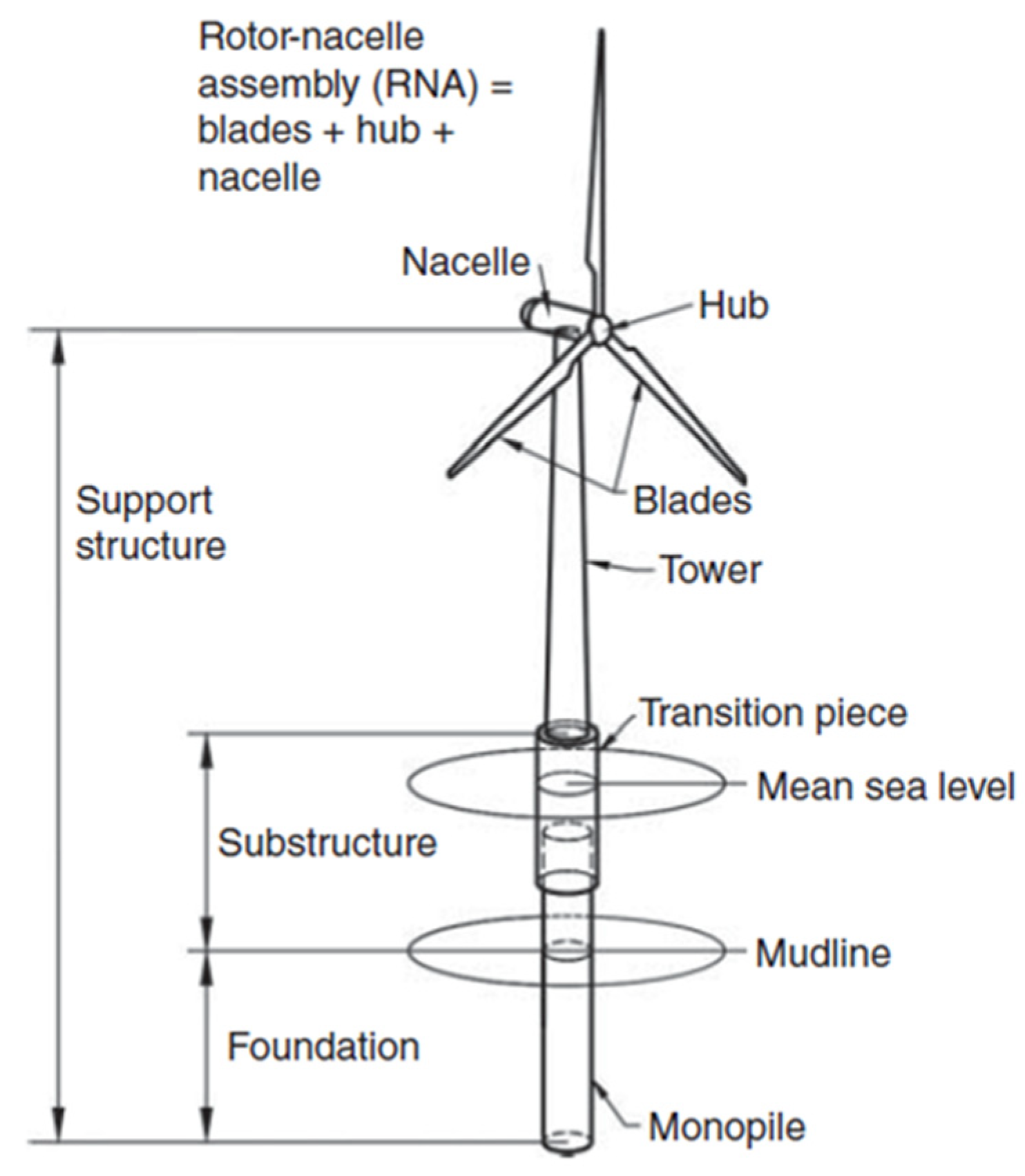
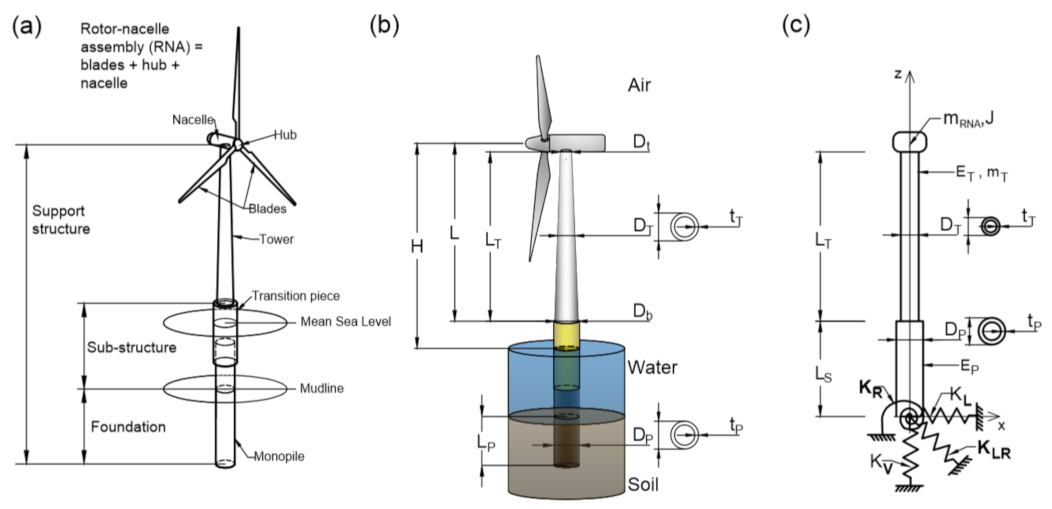
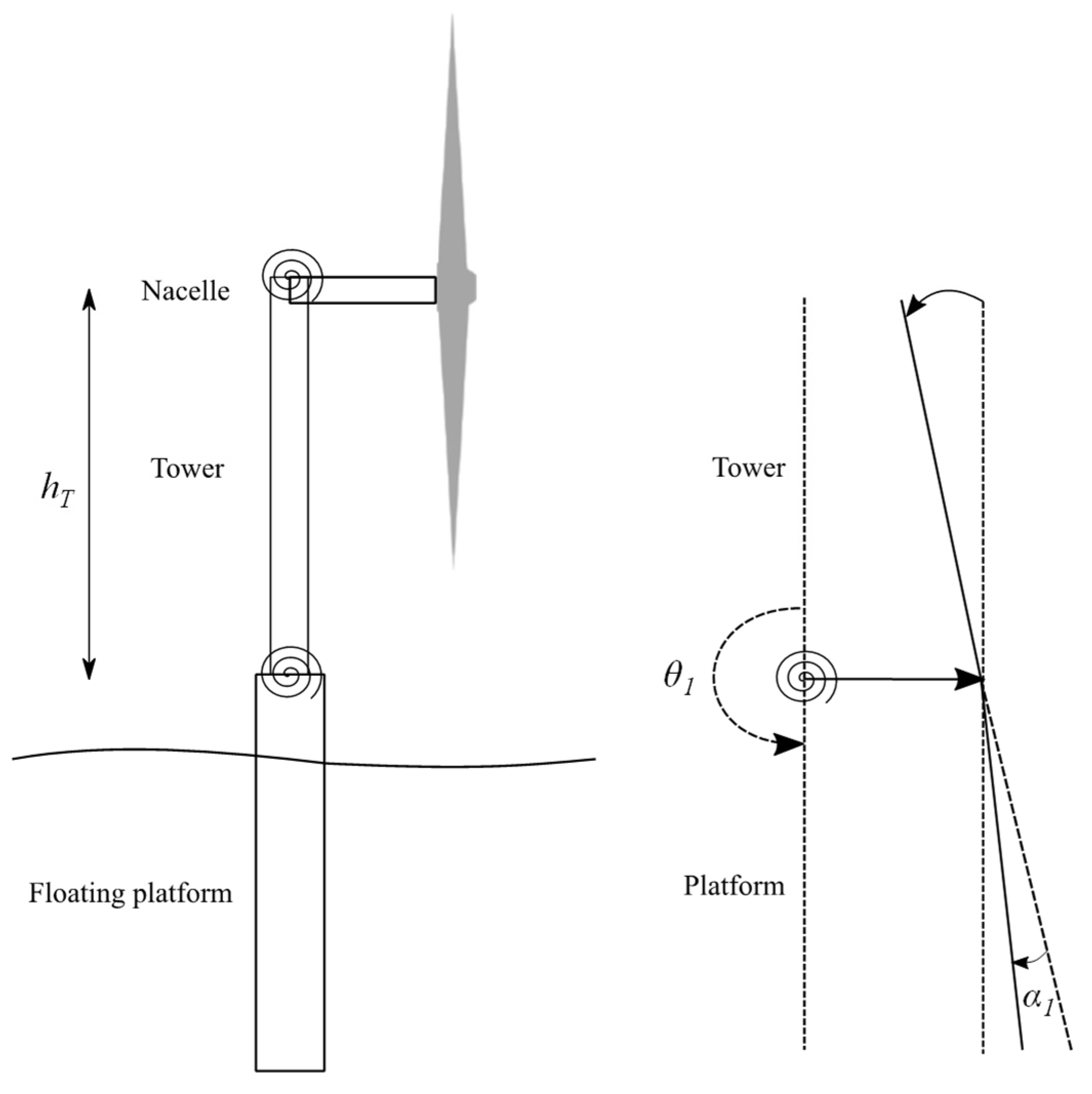
2.1. The Structure of an Offshore Wind Turbine
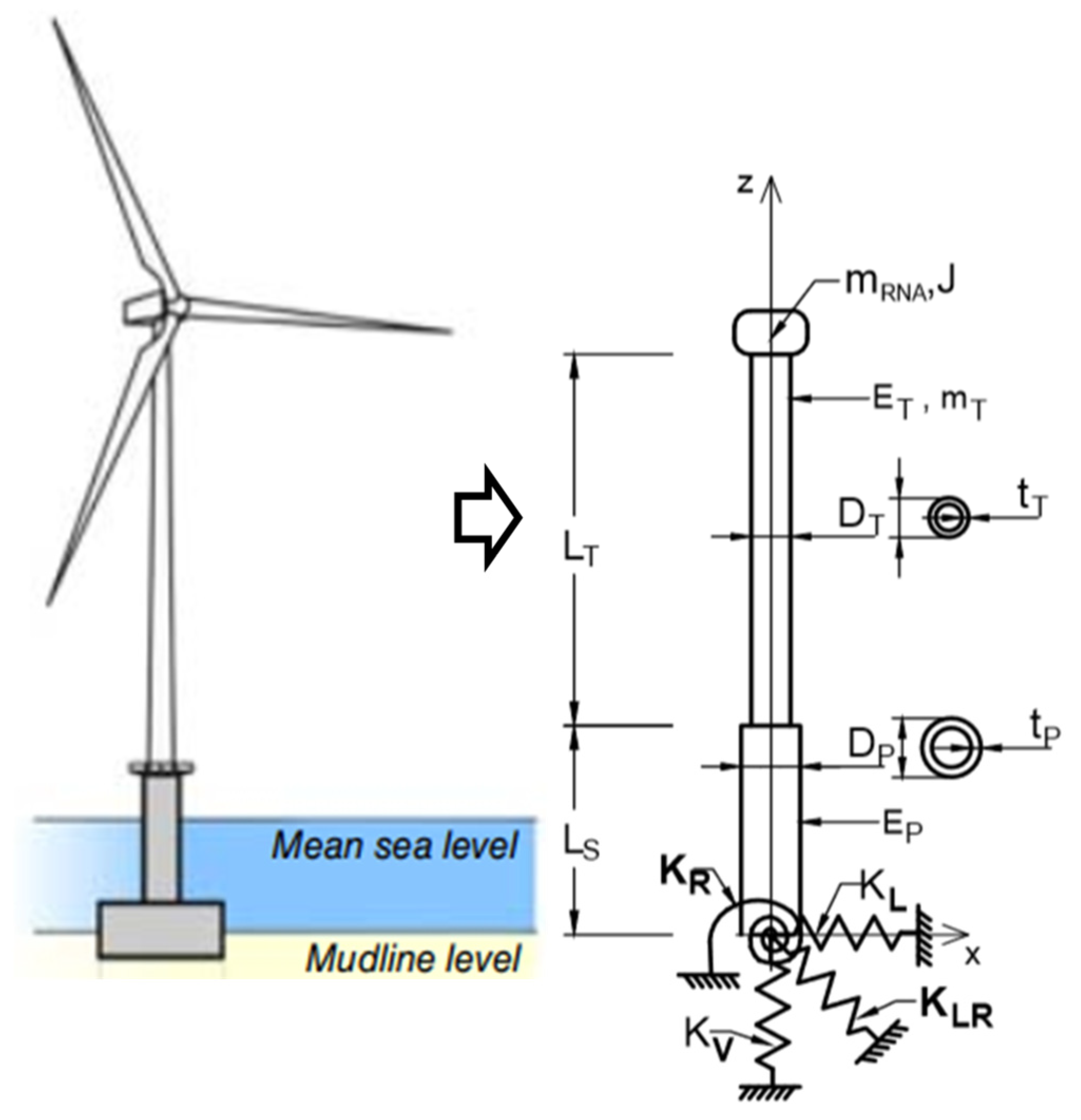
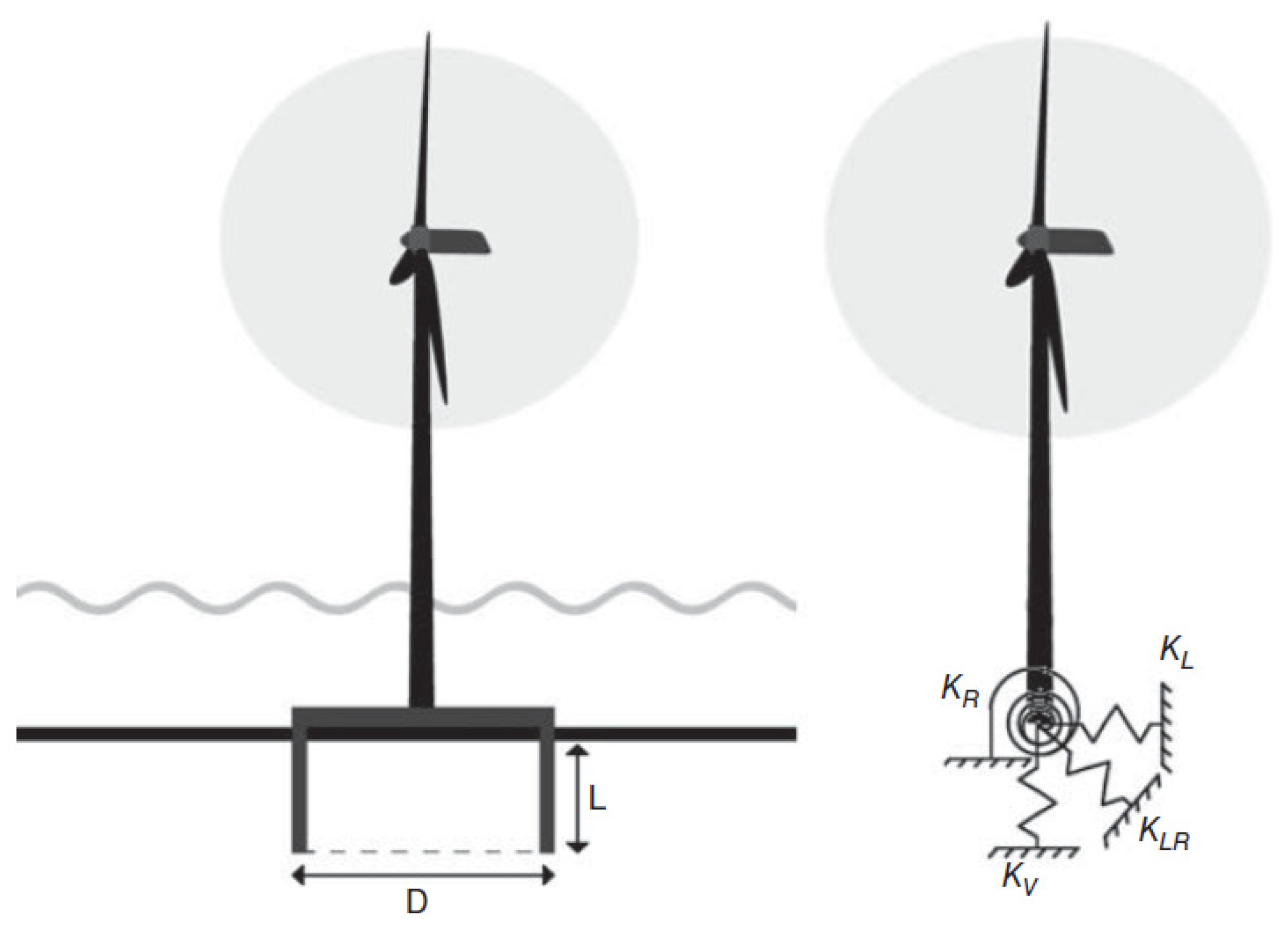
2.2. OWT As a Dynamical System
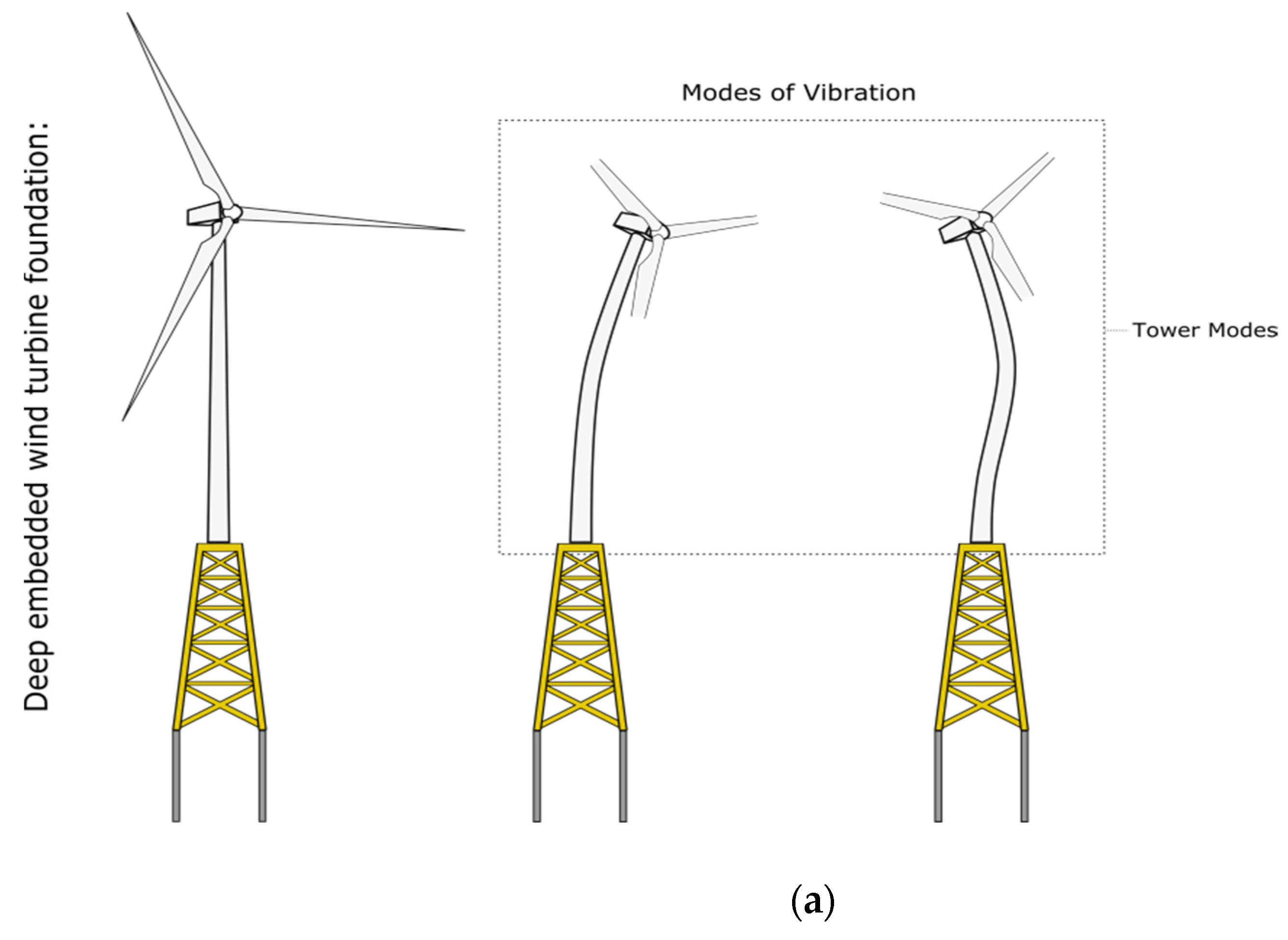
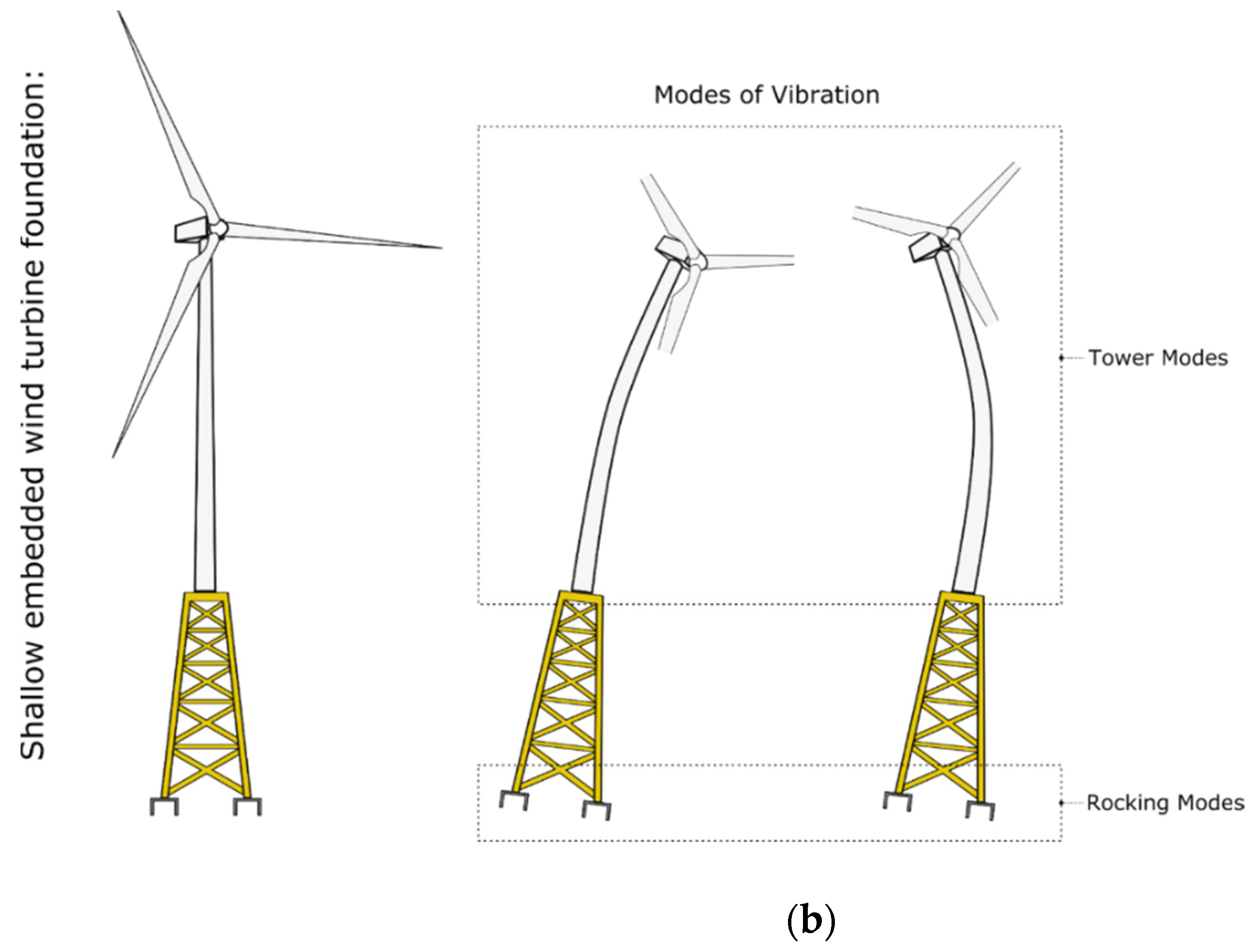
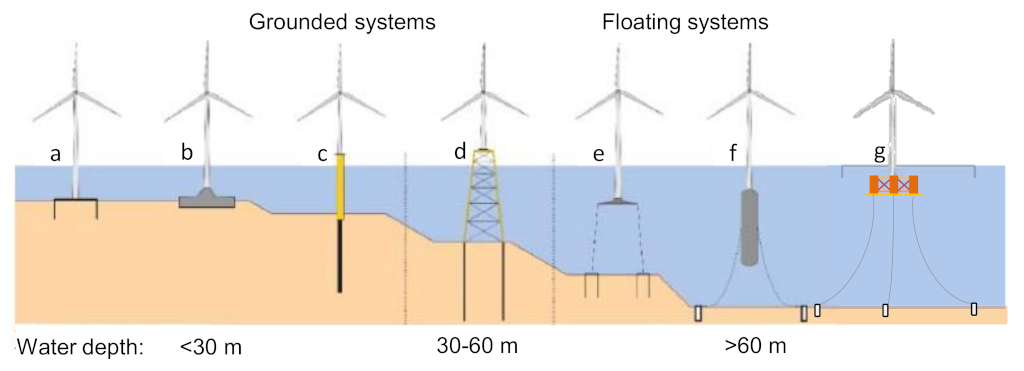
2.3. Classification of OWT Systems
3. Formulae for Stiffness and Natural Frequency
3.1. Wind Turbine Supported by Gravity Based Foundation
- Step 1. Calculate the average tower diameter, the average wall thickness, and the average tower diameter.
- Step 2. Calculate the non-dimensional foundation stiffness values:
- Identify and tabulate the shear modulus and Poisson’s ratio for a depth not less than 20 times the foundation diameter/width.
- Compute the weight distribution function as follows:where is the depth normalized with the foundation diameter, and a and b are parameters defined in Table 4.
- Evaluate the equivalent shear modulus using the expression:
- Compute the foundation stiffnesses using the expressions:
- Step 3. Compute the foundation flexibility factors.
- Step 4. Compute the fixed-base natural frequency.
- Step 5. Compute the flexible-base natural frequency.
3.2. Wind Turbine Supported by Single-Suction Caisson
3.3. Wind Turbine Supported by Monopile
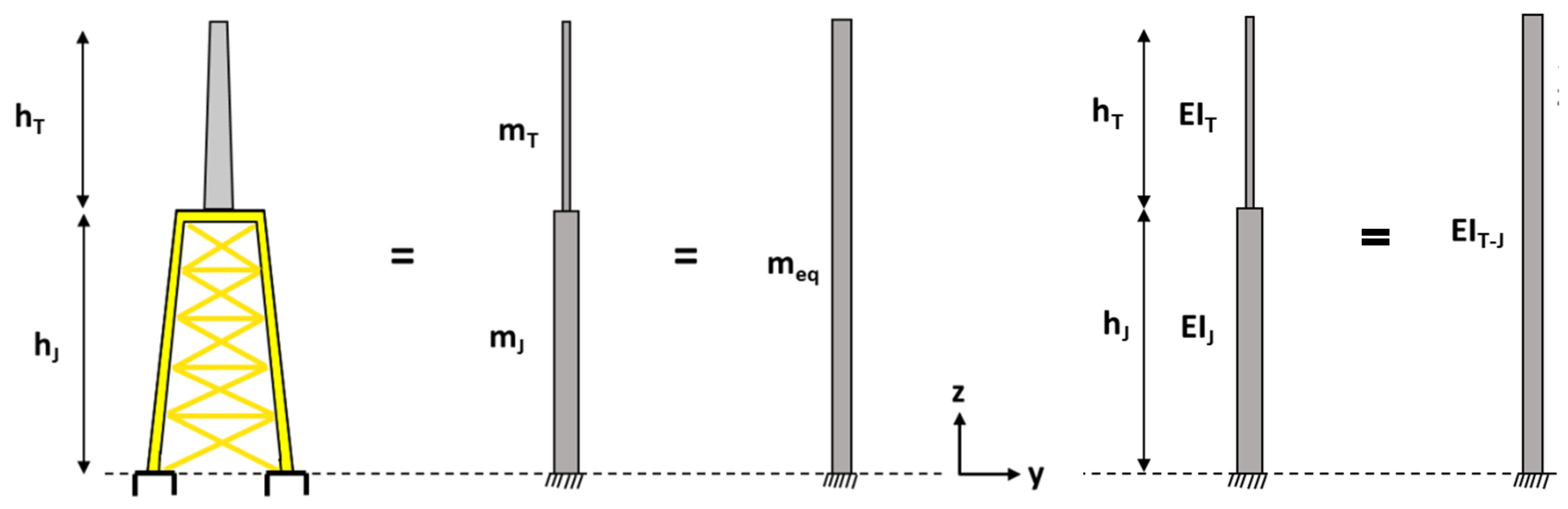
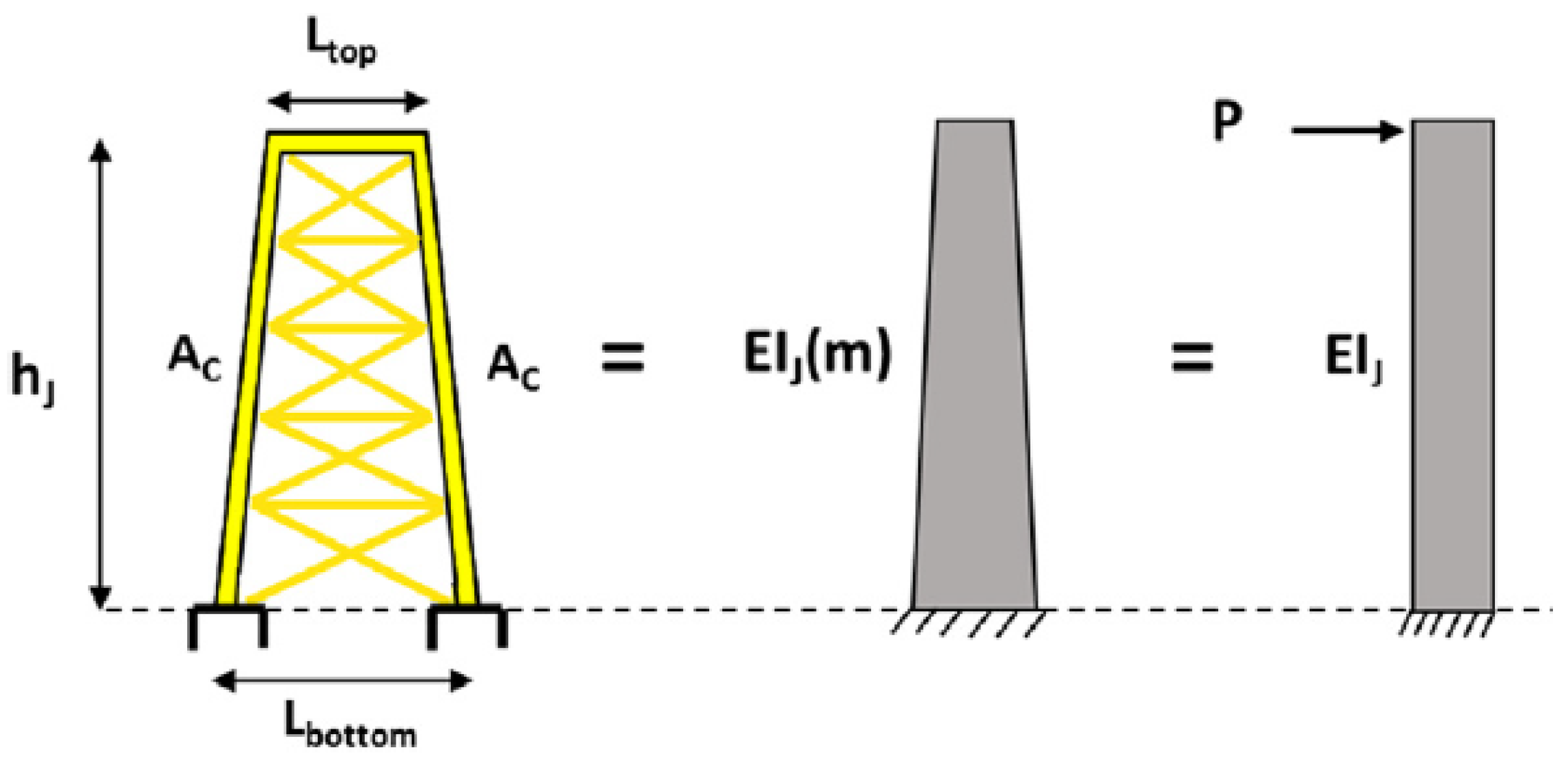
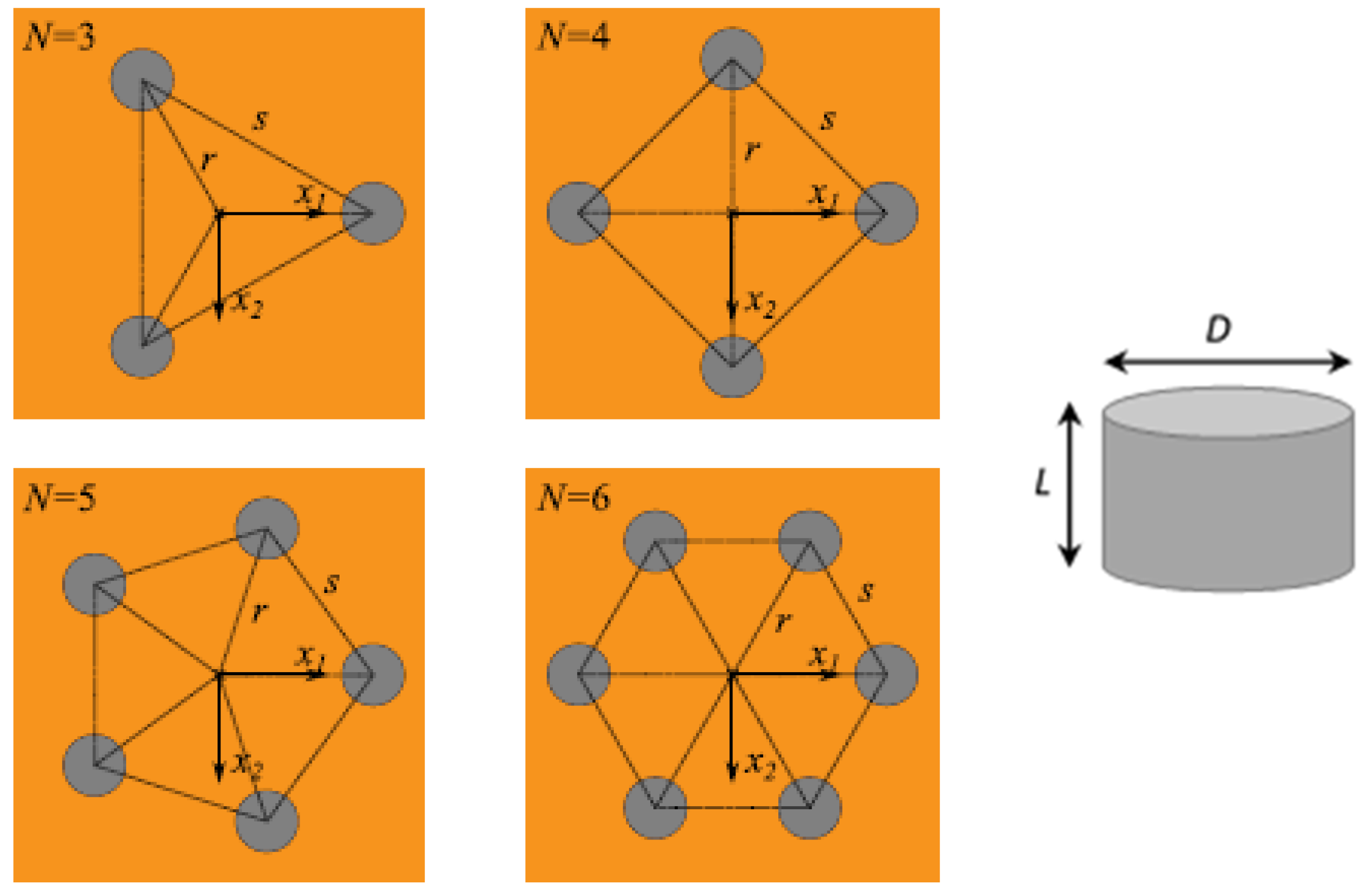
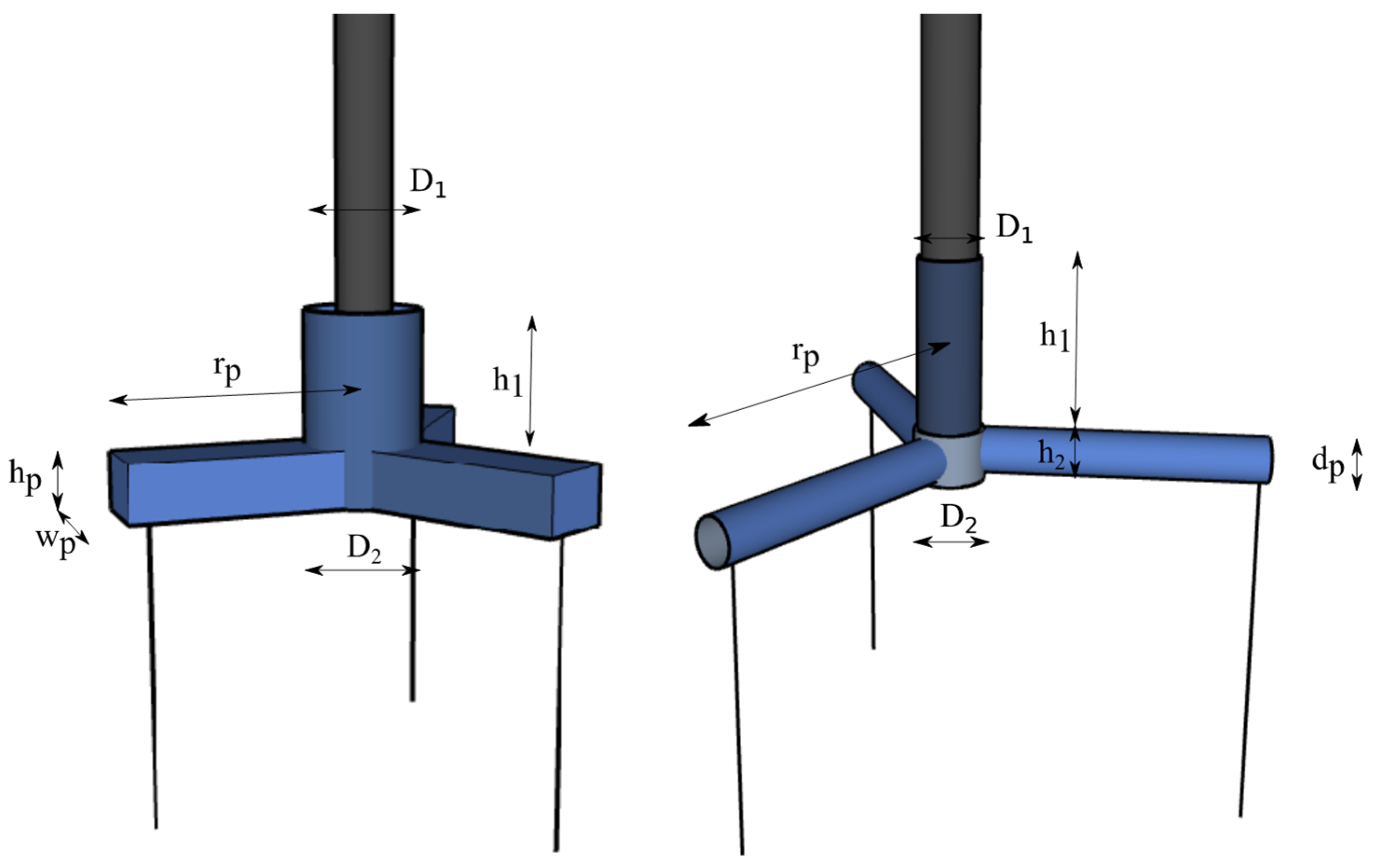
3.4. Wind Turbine Supported by Jackets on Suction Buckets
- Step 1. Calculate the equivalent stiffness of the jacket-truss and tower,
- Step 2. Calculate the equivalent bending stiffness of the tower–jacket system.
- Step 3. Calculate the equivalent mass of the tower–jacket system.
- Step 4. Calculate the fixed-base natural frequency:where
- Step 5. Calculate the rotational stiffness of the foundation group.
- Step 6. Calculate the flexibility factor .
- Step 7. Calculate the flexible-base natural frequency.
3.5. Wind Turbine Supported by Jacket on Piles
3.6. Wind Turbine Supported on Tension-Leg Platform
- Step 1. Calculate the mooring system stiffness factors.
- Step 2. Calculate the added-mass terms.
- Step 3. Calculate the hydrostatic stiffness terms.
- Step 4. Compute the natural frequencies.
3.7. Wind Turbine Supported by Floating Spar Buoy
- Step 1. Compute the matrix elements.
- Step 2. Solve the transcendental equation for .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
| Ground profile | |||
| Homogeneous | |||
| Parabolic | |||
| Linear |
| Ground profile | |||
| Homogeneous | |||
| Parabolic | |||
| Linear |
Appendix A.2
| Lateral stiffness | Cross-coupling stiffness | Rotational stiffness |
| Randolph (1981), slender piles, both for homogeneous and linear inhomogeneous soils | ||
| Pender (1993), slender piles, homogeneous soil | ||
| Pender (1993), slender piles, linear inhomogeneous soil | ||
| Pender (1993), slender piles, parabolic inhomogeneous soil | ||
| Poulos and Davis (1980) following Barber (1953), slender pile, homogeneous soil | ||
| Poulos and Davis (1980) following Barber (1953), slender pile, linear inhomogeneous soil | ||
| Gazetas (1984) and Eurocode 8 Part 5 (2003), slender pile, homogeneous soil | ||
| Gazetas (1984) and Eurocode 8 Part 5 (2003), slender pile, linear inhomogeneous soil | ||
| Gazetas (1984) and Eurocode 8 Part 5 (2003), slender pile, parabolic inhomogeneous soil | ||
| Shadlou and Bhattacharya (2016), slender pile, homogeneous soil | ||
| Shadlou and Bhattacharya (2016), slender pile, linear inhomogeneous soil | ||
| Shadlou and Bhattacharya (2016), slender pile, parabolic inhomogeneous soil | ||
| Parameter definitions: | ||
for Randolph (1981) and for Shadlou and Bhattacharya (2016) | ||
| Poulos and Davis (1980) following Barber (1953), rigid pile, homogeneous soil | ||
| Poulos and Davis (1980) following Barber (1953), rigid pile, linear inhomogeneous soil | ||
| Carter and Kulhawy (1992), rigid pile, rock | ||
| Shadlou and Bhattacharya (2016), rigid pile, homogeneous soil | ||
| Shadlou and Bhattacharya (2016), rigid pile, linear inhomogeneous soil | ||
| Shadlou and Bhattacharya (2016), rigid pile, parabolic inhomogeneous soil | ||
| Parameter definitions: | ||
Appendix B
Appendix B.1
| # | Input Parameter | Value | Unit |
|---|---|---|---|
| 1 | Mass of the rotor-nacelle assembly | 130 | |
| 2 | Tower height | 80 | |
| 3 | Tower top diameter | 2.8 | |
| 4 | Tower bottom diameter | 4.3 | |
| 5 | Average tower wall thickness | 0.035 | |
| 6 | Tower Young’s modulus | 210 | |
| 7 | Tower mass | 247 | |
| 10 | Foundation diameter | 30 |
| Soil Layer | Thickness (m) | Unit Weight (kN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 1 | 10 | 0.97 | 14.2 | 0.35 |
| 2 | 18 | 0.92 | 10.6 | 0.35 |
| 3 | 22 | 0.95 | 11.5 | 0.35 |
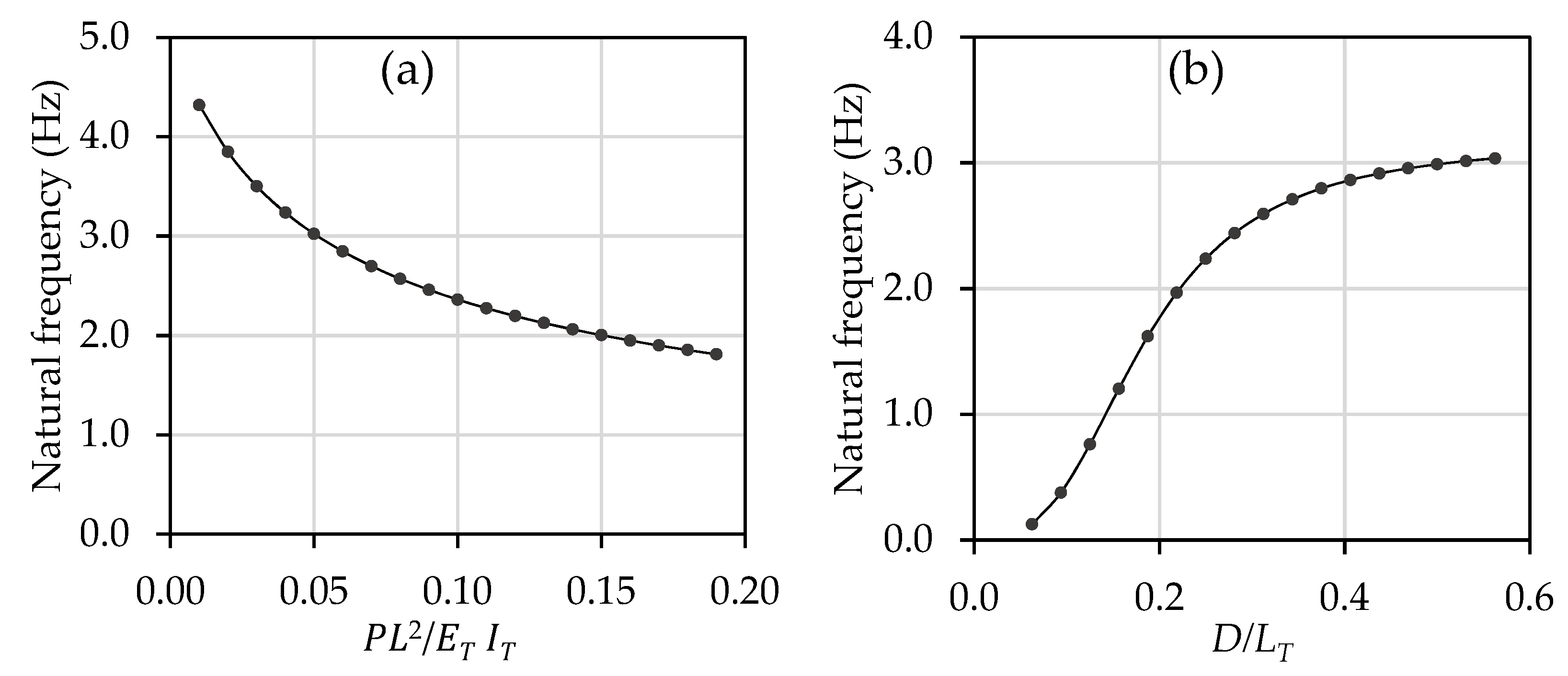
Appendix B.2
| # | Input Parameter | Value | Unit |
|---|---|---|---|
| 1 | Mass of the rotor-nacelle assembly | 100 | |
| 2 | Tower height | 70 | |
| 3 | Tower top diameter | 2.3 | |
| 4 | Tower bottom diameter | 4 | |
| 5 | Average tower wall thickness | 0.035 | |
| 6 | Tower Young’s modulus | 210 | |
| 7 | Tower mass | 130 | |
| 8 | Length of the substructure | 0 | |
| 9 | Monopile length | 21.9 | |
| 10 | Monopile diameter | 4 | |
| 11 | Monopile wall thickness | 0.05 | |
| 12 | Monopile Young’s modulus | 210 |
Appendix B.3
| # | Input Parameter | Value | Unit |
|---|---|---|---|
| 1 | Mass of the rotor-nacelle assembly | 350 | |
| 2 | Mass of tower | 347.5 | |
| 3 | Height of tower | 87.6 | |
| 4 | Platform height | 30 | |
| 5 | Tower bottom diameter | 3.87 | |
| 6 | Wall thickness of tower | 27 | |
| 7 | Diameter of caisson | 12 | |
| 8 | Height of caisson | 6 | |
| 9 | Elastic modulus of soil | 40 | |
| 10 | Poisson’s ratio of soil | 0.35 |
Appendix B.4
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| Tower | |||
| 1 | Mass of RNA | 350 | |
| 2 | Height of tower | 70 | |
| 3 | Top diameter | 4 | |
| 4 | Bottom diameter | 5.6 | |
| 5 | Distributed mass of tower | 3730 | |
| 6 | Density of material | 7850 | |
| 7 | Young’s modulus of material | 210 | |
| Jacket | |||
| 9 | Top width | 9.5 | |
| 10 | Bottom width | 12 | |
| 11 | Height of jacket | 70 | |
| 12 | Area of jacket leg chords | 0.1281 | |
| 13 | Distributed mass of jacket | 8150 | |
| Foundation | |||
| 15 | Number of footings | 4 | |
| 16 | Distance, s | 12 | |
| 17 | Distance, r | 8.48 | |
| 18 | Diameter of foundation | 4 | |
| 19 | Depth of foundation dpe | 4 | |
Appendix B.5
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Overall draft | 40 | |
| 2 | Number of tendons | 4 | |
| 3 | Pretension in each cable | 6868 | |
| 4 | Unstretched length of tendon | 140 | |
| 5 | Young’s modulus | 200 | |
| 6 | Outer diameter | 1.4 | |
| 7 | Thickness | 46.2 | |
| 8 | Number of pontoons | 4 | |
| 9 | Height of rectangular pontoon | 2.4 | |
| 10 | Width of rectangular pontoon | 2.4 | |
| 11 | Radius of pontoon from cylinder center | 27 | |
| 12 | Vertical location of pontoon | −43.8 | |
| 13 | Diameter of main cylinder of hull | 18 | |
| 14 | Diameter of base node of hull | 18 | |
| 15 | Height of main cylinder of hull | 52.6 | |
| 16 | Height of base node of hull | 2.4 | |
| 17 | Center of gravity (full system) | −32.7957 | |
| 18 | Center of buoyancy | −23.945 | |
| 19 | Total steel mass | 2322 |
Appendix B.6
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| Tower | |||
| 1 | Mass of nacelle + blades | 293.22 | |
| 2 | Height of tower | 90 | |
| 3 | Average diameter | 5 | |
| 4 | Thickness | 0.03 | |
| 5 | Location of CG of superstructure | 64 | |
| 6 | Angle between longitudinal axes of nacelle and tower | 90 | |
| 7 | Stiffness of torsion spring between nacelle and tower | ||
| 8 | Moment of inertia of the nacelle about the top end of the tower | 698720 | |
| Platform | |||
| 9 | Mass of platform | 7593 | |
| 10 | Location of CG of platform | −92.6 | |
| 11 | Height of jacket | 70 | |
| 12 | Angle between longitudinal axes of platform and tower | 180 | |
| 13 | Stiffness of torsion spring between platform and tower | ||
| 14 | Moment of inertia of the platform about the bottom end of the tower | 65108152680 | |
References
- Bhattacharya, S. Design of Foundations for Offshore Wind Turbines; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Bashetty, S.; Ozcelik, S. Review on Dynamics of Offshore Floating Wind Turbine Platforms. Energies 2021, 14, 6026. [Google Scholar] [CrossRef]
- Zania, V. Natural vibration frequency and damping of slender structures founded on monopiles. Soil Dyn. Earthq. Eng. 2014, 59, 8–20. [Google Scholar] [CrossRef]
- Andersen, L.; Vahdatirad, M.; Sichani, M.; Sørensen, J. Natural frequencies of wind turbines on monopile foundations in clayey soils—A probabilistic approach. Comput. Geotech. 2012, 43, 1–11. [Google Scholar] [CrossRef]
- Harte, M.; Basu, B.; Nielsen, S.R. Dynamic analysis of wind turbines including soil-structure interaction. Eng. Struct. 2012, 45, 509–518. [Google Scholar] [CrossRef]
- Lombardi, D.; Bhattacharya, S.; Wood, D.M. Dynamic soil–structure interaction of monopile supported wind turbines in cohesive soil. Soil Dyn. Earthq. Eng. 2013, 49, 165–180. [Google Scholar] [CrossRef]
- Bisoi, S.; Haldar, S. Dynamic analysis of offshore wind turbine in clay considering soil–monopile–tower interaction. Soil Dyn. Earthq. Eng. 2014, 63, 19–35. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Adhikari, S. Experimental validation of soil–structure interaction of offshore wind turbines. Soil Dyn. Earthq. Eng. 2011, 31, 805–816. [Google Scholar] [CrossRef]
- Adhikari, S.; Bhattacharya, S. Vibrations of wind-turbines considering soil-structure interaction. Wind Struct. 2011, 14, 85. [Google Scholar] [CrossRef] [Green Version]
- Dezvareh, R. Evaluation of turbulence on the dynamics of monopile offshore wind turbine under the wave and wind excitations. J. Appl. Comput. Mech. 2019, 5, 704–716. [Google Scholar]
- Arany, L.; Bhattacharya, S.; Adhikari, S.; Hogan, S.; Macdonald, J. An analytical model to predict the natural frequency of offshore wind turbines on three-spring flexible foundations using two different beam models. Soil Dyn. Earthq. Eng. 2015, 74, 40–45. [Google Scholar] [CrossRef] [Green Version]
- Arany, L.; Bhattacharya, S.; Macdonald, J.; Hogan, S.J. Design of monopiles for offshore wind turbines in 10 steps. Soil Dyn. Earthq. Eng. 2017, 92, 126–152. [Google Scholar] [CrossRef] [Green Version]
- Arany, L.; Bhattacharya, S.; Macdonald, J.; Hogan, S. Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef] [Green Version]
- Gazetas, G. Formulas and charts for impedances of surface and embedded foundations. J. Geotech. Eng. 1991, 117, 1363–1381. [Google Scholar] [CrossRef]
- Gazetas, G. Analysis of machine foundation vibrations: State of the art. Int. J. Soil Dyn. Earthq. Eng. 1983, 2, 2–42. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Verbič, B. Vibration of viscoelastic foundations. Earthq. Eng. Struct. Dyn. 1973, 2, 87–102. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Wei, Y.T. Lateral and rocking vibration of footings. J. Soil Mech. Found. Div. 1971, 97, 1227–1248. [Google Scholar] [CrossRef]
- Mayne, P.W.; Poulos, H.G. Approximate displacement influence factors for elastic shallow foundations. J. Geotech. Geoenviron. Eng. 1999, 125, 453–460. [Google Scholar] [CrossRef]
- Suryasentana, S.K.; Mayne, P.W. Simplified method for the lateral, rotational, and torsional static stiffness of circular footings on a nonhomogeneous elastic half-space based on a work-equivalent framework. J. Geotech. Geoenviron. Eng. 2022, 148, 04021182. [Google Scholar] [CrossRef]
- Jalbi, S.; Bhattacharya, S. Closed form solution for the first natural frequency of offshore wind turbine jackets supported on multiple foundations incorporating soil-structure interaction. Soil Dyn. Earthq. Eng. 2018, 113, 593–613. [Google Scholar] [CrossRef] [Green Version]
- Bordón, J.; Aznárez, J.J.; Padrón, L.; Maeso, O.; Bhattacharya, S. Closed-form stiffnesses of multi-bucket foundations for OWT including group effect correction factors. Mar. Struct. 2019, 65, 326–342. [Google Scholar] [CrossRef]
- Bordón, J.D.R.; Aznárez, J.J.; Maeso, O.; Bhattacharya, S. Simple approach for including foundation–soil–foundation interaction in the static stiffnesses of multi-element shallow foundations. Géotechnique 2021, 71, 686–699. [Google Scholar] [CrossRef]
- Ryu, M.-S.; Jung, M.-U.; Lee, J.-S.; Kim, D.-S. Closed Form Solutions for Predicting Lateral Response of Tripod Suction Pile for Offshore Wind Turbine Foundation. Energies 2020, 13, 6176. [Google Scholar] [CrossRef]
- Karimirad, M.; Moan, T. A simplified method for coupled analysis of floating offshore wind turbines. Mar. Struct. 2012, 27, 45–63. [Google Scholar] [CrossRef]
- Pegalajar-Jurado, A.; Bredmose, H.; Borg, M. Multi-level hydrodynamic modelling of a scaled 10 MW TLP wind turbine. Energy Procedia 2016, 94, 124–132. [Google Scholar] [CrossRef] [Green Version]
- Nematbakhsh, A.; Bachynski, E.E.; Gao, Z.; Moan, T. Comparison of wave load effects on a TLP wind turbine by using computational fluid dynamics and potential flow theory approaches. Appl. Ocean Res. 2015, 53, 142–154. [Google Scholar] [CrossRef] [Green Version]
- Oguz, E.; Clelland, D.; Day, A.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and numerical analysis of a TLP floating offshore wind turbine. Ocean Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef] [Green Version]
- Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tension Leg Platform with a Comparison to Other Floating Turbine Concepts: April 2009; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010.
- Jonkman, J.M.; Matha, D. Dynamics of offshore floating wind turbines—analysis of three concepts. Wind Energy 2011, 14, 557–569. [Google Scholar] [CrossRef]
- Lackner, M.A.; Rotea, M.A. Structural control of floating wind turbines. Mechatronics 2011, 21, 704–719. [Google Scholar] [CrossRef]
- Robertson, A.N.; Jonkman, J.M. Loads analysis of several offshore floating wind turbine concepts. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Si, Y.; Karimi, H.R.; Gao, H. Modelling and optimization of a passive structural control design for a spar-type floating wind turbine. Eng. Struct. 2014, 69, 168–182. [Google Scholar] [CrossRef]
- Cottura, L.; CaraDonna, R.; Ghigo, A.; Novo, R.; Bracco, G.; Mattiazzo, G. Dynamic Modeling of an Offshore Floating Wind Turbine for Application in the Mediterranean Sea. Energies 2021, 14, 248. [Google Scholar] [CrossRef]
- Liu, Y.; Ishihara, T. Numerical Study on Sectional Loads and Structural Optimization of an Elastic Semi-Submersible Floating Platform. Energies 2021, 14, 182. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Moan, T. Design considerations for tension leg platform wind turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J. Natural Frequency Analysis of a Spar-Type Offshore Wind Turbine Tower With End Mass Components. J. Offshore Mech. Arct. Eng. 2018, 140, 064501. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Z.; Wan, D.; Xiao, Q. Comparisons of the dynamical characteristics of a semi-submersible floating offshore wind turbine based on two different blade concepts. Ocean Eng. 2018, 153, 305–318. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in semi-submersible floating foundations supporting wind turbines: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 60, 433–449. [Google Scholar] [CrossRef]
- Galera-Calero, L.; Blanco, J.M.; Iglesias, G. Numerical Modelling of a Floating Wind Turbine Semi-Submersible Platform. Appl. Sci. 2021, 11, 11270. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Wang, W.; Shi, W.; Zhao, L.; Wang, S. Analysis of dynamic characteristics of an ultra-large semi-submersible floating wind turbine. J. Mar. Sci. Eng. 2019, 7, 169. [Google Scholar] [CrossRef] [Green Version]
- Katsanos, E.I.; Thöns, S.; Georgakis, C.Τ. Wind turbines and seismic hazard: A state-of-the-art review. Wind Energy 2016, 19, 2113–2133. [Google Scholar] [CrossRef] [Green Version]
- Veritas, D.N. DNV-OS-J101-Design of Offshore Wind Turbine Structures; DNV: Copenhagen, Denmark, 2014. [Google Scholar]
- Gelagoti, F.M.; Lekkakis, P.P.; Kourkoulis, R.S.; Gazetas, G. Estimation of elastic and non-linear stiffness coefficients for suction caisson foundations. In Geotechnical Engineering for Infrastructure and Development; ICE Publishing: London, UK, 2015; pp. 943–948. [Google Scholar]
- Jalbi, S.; Shadlou, M.; Bhattacharya, S. Impedance functions for rigid skirted caissons supporting offshore wind turbines. Ocean Eng. 2018, 150, 21–35. [Google Scholar] [CrossRef]
- Shadlou, M.; Bhattacharya, S. Dynamic stiffness of monopiles supporting offshore wind turbine generators. Soil Dyn. Earthq. Eng. 2016, 88, 15–32. [Google Scholar] [CrossRef]
- Poulos, H.G.; Davis, E.H. Pile Foundation Analysis and Design; Wiley: New York, NY, USA, 1980; Volume 397. [Google Scholar]
- Randolph, M.F. The response of flexible piles to lateral loading. Geotechnique 1981, 31, 247–259. [Google Scholar] [CrossRef]
- Carter, J.P.; Kulhawy, F.H. Analysis of laterally loaded shafts in rock. J. Geotech. Eng. 1992, 118, 839–855. [Google Scholar] [CrossRef]
- Abhinav, K.; Saha, N. Coupled hydrodynamic and geotechnical analysis of jacket offshore wind turbine. Soil Dyn. Earthq. Eng. 2015, 73, 66–79. [Google Scholar] [CrossRef]
- Blevins, R.D.; Plunkett, R. Formulas for natural frequency and mode shape. J. Appl. Mech. 1980, 47, 461. [Google Scholar] [CrossRef]
- Shama, A.; El Naggar, H. Bridge Foundations. Encycl. Earthq. Eng. 2015, 1, 298–317. [Google Scholar]
- Chakrabarti, S.; Hanna, S. Added mass and damping of a TLP column model. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 7–10 May 1990. [Google Scholar]
- Jain, A. Nonlinear coupled response of offshore tension leg platforms to regular wave forces. Ocean Eng. 1997, 24, 577–592. [Google Scholar] [CrossRef]
- O’Kelly-Lynch, P.; Long, C.; McAuliffe, F.D.; Murphy, J.; Pakrashi, V. Structural design implications of combining a point absorber with a wind turbine monopile for the east and west coast of Ireland. Renew. Sustain. Energy Rev. 2020, 119, 109583. [Google Scholar] [CrossRef]
- Buckley, T.; Watson, P.; Cahill, P.; Jaksic, V.; Pakrashi, V. Mitigating the structural vibrations of wind turbines using tuned liquid column damper considering soil-structure interaction. Renew. Energy 2018, 120, 322–341. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Lombardi, D.; Amani, S.; Aleem, M.; Prakhya, G.; Adhikari, S.; Aliyu, A.; Alexander, N.; Wang, Y.; Cui, L.; et al. Physical Modelling of Offshore Wind Turbine Foundations for TRL (Technology Readiness Level) Studies. J. Mar. Sci. Eng. 2021, 9, 589. [Google Scholar] [CrossRef]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2021. [Google Scholar] [CrossRef]
- Jaksic, V.; O’Shea, R.; Cahill, P.; Murphy, J.; Mandic, D.P.; Pakrashi, V. Dynamic response signatures of a scaled model platform for floating wind turbines in an ocean wave basin. Philos. Trans. A Math Phys. Eng. Sci. 2015, 373, 20140078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Leary, K.; Pakrashi, V.; Kelliher, D. Optimization of composite material tower for offshore wind turbine structures. Renew. Energy 2019, 140, 928–942. [Google Scholar] [CrossRef]
- Quilligan, A.; O’Connor, A.; Pakrashi, V. Fragility analysis of steel and concrete wind turbine towers. Eng. Struct. 2012, 36, 270–282. [Google Scholar] [CrossRef]
- Jaksic, V.; Wright, C.S.; Murphy, J.; Afeef, C.; Ali, S.F.; Mandic, D.P.; Pakrashi, V. Dynamic response mitigation of floating wind turbine platforms using tuned liquid column dampers. Philos. Trans. A Math Phys. Eng. Sci. 2015, 373, 20140079. [Google Scholar] [CrossRef]
- Arrigan, J.; Pakrashi, V.; Basu, B.; Nagarajaiah, S. Control of flapwise vibrations in wind turbine blades using semi-active tuned mass dampers. Struct. Control Health Monit. 2011, 18, 840–851. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Guo, Y.H.; Ding, H.Y.; Xiong, K.P.; Yang, Y.F. Study on vibration of offshore wind turbine supporting system under the wind-wave coupling effect. J. Vibroengineering 2015, 17, 2655–2668. [Google Scholar]
- Augustesen, A.H.; Brødbæk, K.T.; Møller, M.; Sørensen, S.P.H.; Ibsen, L.B.; Pedersen, T.S.; Andersen, L. Numerical Modelling of Large-Diameter Steel Piles at Horns Rev. In Proceedings of the 12th International Conference on Civil, Structural and Environmental Engineering Computing, Funchal, Madeira, 1–4 September 2009. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009.

| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Mass of the rotor-nacelle assembly | kg | |
| 2 | Tower height | m | |
| 3 | Tower top diameter | m | |
| 4 | Tower bottom diameter | m | |
| 5 | Average tower wall thickness | m | |
| 6 | Tower Young’s modulus | N/m2 | |
| 7 | Tower mass | kg |
| Turbine | NREL | LW | DTU | Haliade-X | Unit |
|---|---|---|---|---|---|
| Power rating | 5 | 8 | 10 | 12 | MW |
| Rotor diameter | 126 | 164 | 178.3 | 218.2 | m |
| Hub height | 90 | 110 | 119 | 135 | m |
| Rotor speed range | 6.9–12.1 | 6.3–10.5 | 6–9.6 | 7.81 | rpm |
| Cut-in, rated | 3, 11.4 | 4, 12.5 | 4, 11.4 | 3.5 | m/s |
| Cut-out wind speed | 25 | 25 | 25 | 28 | m/s |
| Nacelle mass | 296.78 | 375 | 551.56 | 600 | tonne |
| Blade mass | 17.74 | 35 | 41.72 | 55 | tonne |
| Tower mass | 347.46 | 558 | 605 | 2500 | tonne |
| Tower height | 87.6 | 106.3 | 115.6 | 129.1 | m |
| Tower top diameter | 3.87 | 5 | 5.5 | 5.5 | m |
| Tower bottom diameter | 6 | 7.7 | 8 | 8 | m |
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Foundation diameter | ||
| 2 | Total tower height | ||
| 3 | Substructure Young’s modulus | ||
| 4 | Substructure moment of inertia | ||
| 5 | Lateral stiffness of foundation | ||
| 6 | Rocking stiffness of foundation |
| Stiffness | a | b |
|---|---|---|
| Lateral | 1.27 | |
| Rotational | 1.35 |
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Platform height above mudline | ||
| 2 | Substructure Young’s modulus | ||
| 3 | Substructure moment of inertia | ||
| 4 | Caisson diameter | ||
| 5 | Caisson depth | ||
| 6 | Initial soil Young’s modulus at 1D depth | ||
| 7 | Soil Poisson’s ratio | ||
| 8 | Lateral stiffness of foundation | ||
| 9 | Cross-stiffness of foundation | ||
| 10 | Rocking stiffness of foundation |
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Platform height above mudline | ||
| 2 | Substructure Young’s modulus | ||
| 3 | Substructure moment of inertia | ||
| 4 | Pile diameter | ||
| 5 | Pile depth | ||
| 6 | Pile Young’s modulus | ||
| 7 | Pile moment of inertia | ||
| 8 | Initial soil Young’s modulus at 1D depth | ||
| 9 | Soil Poisson’s ratio | ||
| 10 | Lateral stiffness of foundation | ||
| 11 | Cross-stiffness of foundation | ||
| 12 | Rocking stiffness of foundation |
| Reference | Parameters Required | Criteria |
|---|---|---|
| Poulos and Davis [46] | If pile is slender If pile is rigid | |
| Randolph [47], Carter, and Kulhawy [48] | If pile is slender If pile is rigid |
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Tower Young’s modulus | ||
| 2 | Height of jacket | ||
| 3 | Top spacing of jacket leg chords | ||
| 4 | Bottom spacing of jacket leg chords | ||
| 5 | Area of jacket leg chords | ||
| 6 | Distributed mass of jacket | ||
| 7 | Equivalent distributed mass of tower–jacket system | ||
| 8 | Jacket bending stiffness | ||
| 9 | Tower bending stiffness | ||
| 10 | Tower–jacket system bending stiffness | ||
| 11 | Number of foundations | ||
| 12 | Vertical stiffness of individual foundation | ||
| 13 | Rocking stiffness of individual foundation | ||
| 14 | Rocking stiffness of foundation group |
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Overall draft | ||
| 2 | Number of tendons | ||
| 3 | Pretension in each cable | ||
| 4 | Unstretched length of tendon | ||
| 5 | Young’s modulus | ||
| 6 | Outer diameter of tendon | ||
| 7 | Thickness of tendon | ||
| 8 | Number of pontoons | ||
| 9 | Diameter of cylindrical pontoon | ||
| 11 | Height of rectangular pontoon | ||
| 12 | Width of rectangular pontoon | ||
| 13 | Radius of pontoon from cylinder center | ||
| 14 | Vertical location of pontoon | ||
| 15 | Diameter of main cylinder of hull | ||
| 16 | Diameter of base node of hull | ||
| 17 | Height of main cylinder of hull | ||
| 18 | Height of base node of hull | ||
| 19 | Total steel mass |
| # | Input Parameter | Symbol | Unit |
|---|---|---|---|
| 1 | Mass of the platform | ||
| 2 | Mass of the rotor-nacelle assembly | ||
| 3 | Tower height | ||
| 4 | Tower top diameter | ||
| Tower bottom diameter | |||
| 5 | Average tower diameter | m | |
| 6 | Average tower wall thickness | ||
| 7 | Tower Young’s modulus | ||
| 8 | Mass per unit length of tower | ||
| 9 | Location of CG of platform | G1 | |
| 10 | Location of CG of superstructure | g2 | |
| 11 | Angle between longitudinal axes of platform and tower | degrees | |
| 12 | Angle between longitudinal axes of nacelle and tower | degrees | |
| 13 | Radius of gyration of tower section | r | |
| 14 | Moment of inertia of the platform about the bottom end of the tower | ||
| 15 | Moment of inertia of the nacelle about the top end of the tower |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varghese, R.; Pakrashi, V.; Bhattacharya, S. A Compendium of Formulae for Natural Frequencies of Offshore Wind Turbine Structures. Energies 2022, 15, 2967. https://doi.org/10.3390/en15082967
Varghese R, Pakrashi V, Bhattacharya S. A Compendium of Formulae for Natural Frequencies of Offshore Wind Turbine Structures. Energies. 2022; 15(8):2967. https://doi.org/10.3390/en15082967
Chicago/Turabian StyleVarghese, Ramon, Vikram Pakrashi, and Subhamoy Bhattacharya. 2022. "A Compendium of Formulae for Natural Frequencies of Offshore Wind Turbine Structures" Energies 15, no. 8: 2967. https://doi.org/10.3390/en15082967
APA StyleVarghese, R., Pakrashi, V., & Bhattacharya, S. (2022). A Compendium of Formulae for Natural Frequencies of Offshore Wind Turbine Structures. Energies, 15(8), 2967. https://doi.org/10.3390/en15082967








