A Multi-Objective Collaborative Optimization Method for the Excavator Working Device to Support Energy Consumption Reduction

Abstract

To address the limitation of existing excavator optimization methods, which primarily focus on the force performance while neglecting energy consumption and fail to realize environmentally friendly and low-carbon designs, this paper proposes a new multi-objective collaborative optimization method for an excavator to reduce energy consumption during the working process while maintaining optimal performance. By formulating a mathematical model that quantifies the energy consumption during the working process, this paper optimizes the working conditions by analyzing the energy consumption characteristics under typical working conditions. To overcome the limitation of existing linear weighting methods in multi-objective optimization, such as imbalanced optimization quality among sub-objectives, this paper proposes a new modeling approach based on the loss degree of sub-objectives. A multi-objective collaborative optimization model for the excavator with reduced energy consumption is established, and a corresponding multi-objective collaborative optimization algorithm is developed and applied to achieve optimal solutions for sub-objectives. The optimization results demonstrate that applying the new multi-objective collaborative optimization method to the excavator achieves better optimization quality than traditional methods. It also provides a more balanced improvement in the optimization values of each sub-objective, resulting in a significant reduction in the energy consumption of the excavator during operation.

1. Introduction

Construction machinery plays a vital role in human production activities, with its working devices significantly influencing the longevity and efficiency of the machines [1]. In line with the growing emphasis on low-carbon practices, contemporary research on construction machinery should focus on enhancing its performance while reducing energy consumption [2,3,4].

Hydraulic excavators are applied as vital construction machinery in various construction fields, including construction, transportation, and water conservancy. The optimization design of excavator working devices has been studied by numerous scholars. Solazzi et al. utilized an innovative lightweight composite material in the design of an excavator [5,6]. Golami et al. researched a design method for the long-reach boom of excavators [7]. Sun et al. focused on designing the shape of an excavator bucket by considering the digging trajectory and limited digging force [8,9]. Additionally, Bender et al. developed a virtual prototype model of an excavator to simulate its movement process [10]. Janošević et al. conducted a study on the dynamic stability of excavators through mathematical modeling and experimental analysis methods [11]. Yu et al. performed finite element analysis and optimization on the structure of the excavator’s boom [12]. Xu et al. employed a multi-objective optimization algorithm to optimize the digging force, working range, and other objectives for a hydraulic shovel [13]. Yu et al. designed a lightweight bucket with enhanced structural strength based on uncertain loads [14]. Zou et al. established the relationship between hydraulic cylinder driving force and digging force through convex polygons. They also optimized the excavation trajectory by developing a resistance model for the interaction between the bucket and the soil [15,16]. Oh et al. employed VR technology and safety system algorithms to mitigate collision accidents between excavators and operators during the work process [17]. Dragoljub et al. conducted a dynamic characteristic analysis of wheel excavators by establishing a mathematical model [18]. Wu et al. utilized discrete element method (DEM) simulation to simulate the digging force and energy consumption of large mining excavators [19]. Yoshida et al. and Mitrev et al. developed mathematical models for the motion process of excavators and performed dynamic characteristic analysis [20,21]. Yu et al. proposed an energy-recovery system for hybrid excavators, which achieved high energy-recovery rates at low-speed operating conditions through variable displacement hydraulic motors and flow-control valves [22]. Kim et al. and Li et al. aimed to optimize various performance factors, including the bucket digging force, arm digging force, and boom lifting force in hydraulic excavator operations. They achieved this by converting multiple optimization objectives into a single objective function through linear weighting [23,24]. Wei utilized Adams 2013 software to perform the simulation analysis of excavator performance by establishing different hydraulic cylinder drive functions [25]. The sequential optimization of the excavator’s bucket, arm, and boom was conducted with the objectives of maximizing the working device’s maximum transmission ratio, average transmission ratio, and average hydraulic cylinder power. In this paper, the average power of the hydraulic cylinder was obtained by averaging the sampled values of the power curve throughout the entire excavation process. However, when the hydraulic cylinder is not moving and remains stationary, the sampled values of the power curve are still included in the calculation of the average power. As a result, the calculated average power may not accurately reflect the actual energy consumption.

Based on the above, the current optimization design methods for excavators mainly focus on the mechanical performance of the excavation process as the optimization objective without considering the reduction in energy consumption during the work process. This is not aligned with modern society’s requirements for green and low-carbon production of mechanical equipment. Additionally, existing multi-objective optimization modeling methods mainly employ linear weighting methods to transform multiple objectives into a single objective function. The weights assigned to different sub-objectives directly influence the optimization results of both individual sub-objectives and the overall objective. This method relies on empirical weight allocation and is only suitable for optimization problems with few objectives. When the number of optimization objectives exceeds five, the balance between various sub-objectives often becomes more challenging, making it difficult to achieve satisfactory results. Therefore, it is necessary to propose new multi-objective optimization methods that consider energy consumption during the working process as an optimization objective, explore more effective mathematical models to represent energy consumption, and investigate new approaches for multi-objective collaborative optimization modeling along with corresponding optimization algorithms.

This paper proposes a new method for optimizing excavator work devices to support energy consumption reduction and thus address the limitations of existing research. This method involves establishing a mathematical model for energy consumption during the excavator work process and analyzing the energy consumption under different working conditions. Based on this analysis, the objectives of excavator optimization, including energy consumption and force characteristics, are determined, which addresses the limitation whereby the existing research fails to consider energy consumption. Additionally, a new multi-objective collaborative optimization model is established to achieve balanced optimization quality for multiple objectives. In summary, the proposed method can improve the excavator’s performance and reduce the energy consumption in the work process, and the optimization quality of each objective can be more balanced.

2. Energy Consumption Calculation Model during the Working Process

The excavation operation of an excavator typically involves two forms: bucket digging and arm digging. It relies on the independent drive of the bucket and arm cylinders to perform the digging action. Once the digging is completed, the boom cylinder is responsible for lifting the excavated material. The energy consumption during the digging process can be characterized by the energy consumption of the bucket cylinder and the arm cylinder, while the energy consumption during the lifting process can be characterized by the energy consumption of the boom hydraulic cylinder. The hydraulic cylinders consume energy to overcome digging resistance, support the weight of loaded materials, and bear the weight of excavator components. These energy-consumption factors are influenced not only by the size of the working device but also by the digging technique and posture. Therefore, it is essential to establish a reasonable mathematical model to evaluate the energy consumption of the excavator’s operation.

2.1. Working Loads of Different Excavation Forms

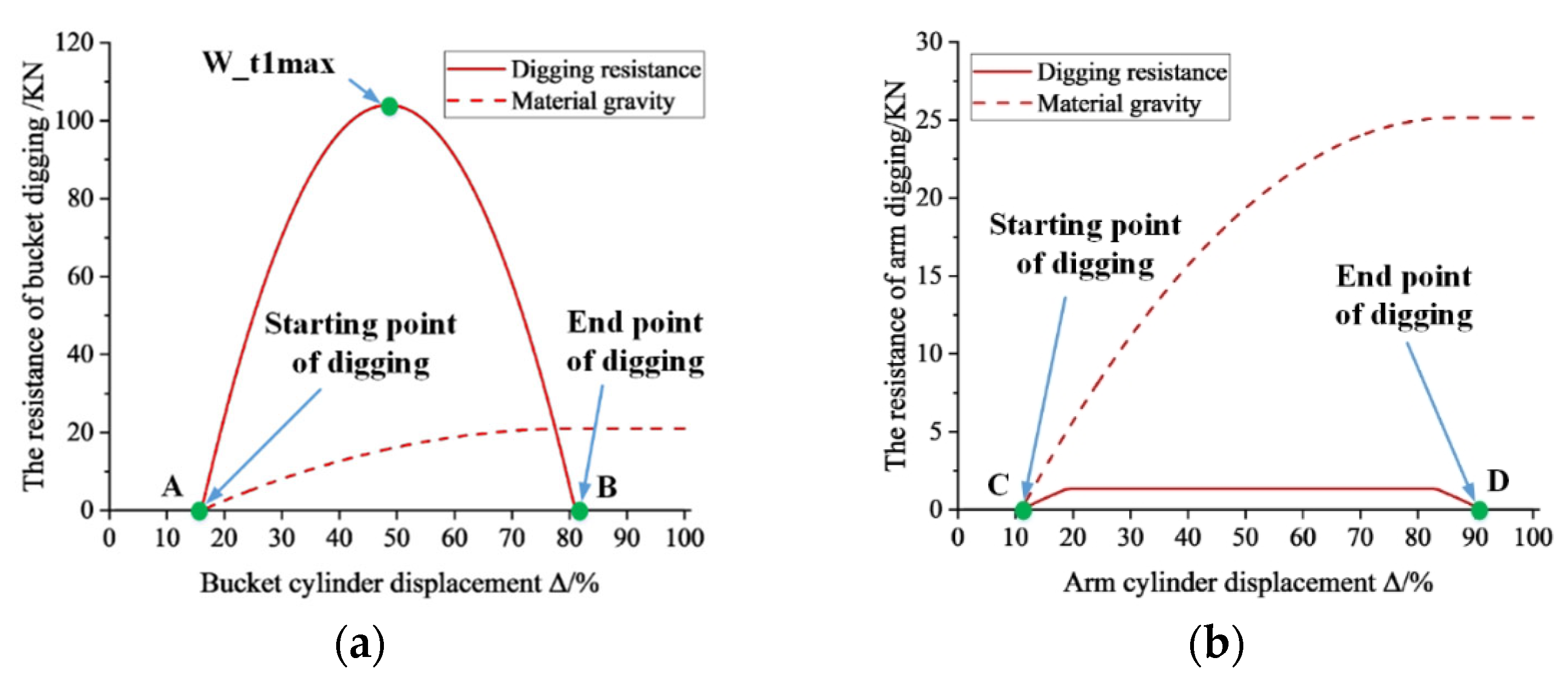
The tangential resistance encountered in soil excavation is affected by both the dimensions of the working device and the excavation form. In bucket digging, the bucket cylinder independently drives the digging operation while the arm and boom cylinders remain locked. Conversely, in arm digging, the arm cylinder independently performs the excavation action while the boom and bucket cylinders remain locked. Different excavation methods exhibit distinct curves of excavation resistance, as shown in Figure 1.

The excavation radius in bucket digging is smaller, leading to significant variations in cutting thickness. As the bucket moves, the excavation resistance changes significantly. The resistance can be approximated by a parabolic curve with lower points on both sides and a higher point in the middle, as shown in Figure 1a. Point A represents the starting point of excavation, and point B marks the endpoint. The maximum value of the resistance during bucket digging can be calculated using the following empirical formula [26]:

$$W_{t1max}=C{\left[R\left(1-\cos {\phi }_1\right)\right]}^{1.35}\cdot B\cdot A\cdot X\cdot Z+D$$

(1)

In this formula, W_t1max is the maximum resistance of bucket digging, C is the coefficient of soil hardness, R is the excavation radius of bucket digging, φ₁ is half of the total digging angle of the bucket, and B is the influence coefficient of the cutting edge width. A is the change coefficient of the cutting angle; Z is the influence coefficient of the bucket teeth; X is the influence coefficient of the side wall of the bucket; D is the force of the cutting edge pressing the soil. The above parameters can be determined by the size of the working device as well as the design specifications.

The excavation radius for arm digging is larger, leading to smaller variations in cutting thickness. As the arm moves, the excavation resistance shows minimal changes and is lower than those in bucket digging. It can be approximated as a constant value, as shown in Figure 1b. Point C indicates the starting point of arm digging, while point D represents the endpoint. The tangential resistance during arm digging can be calculated using an empirical formula [26]:

$$W_{t2}=\frac{K_0\cdot q}{0.01745r\cdot {\phi }_2\cdot K_s}$$

(2)

In this formula, Wt₂ is the resistance of arm digging, K₀ is the specific resistance of excavation, q is the bucket capacity, r is the digging radius of the bucket rod, φ₂ is the total digging angle of the arm, and K_s is the soil looseness.

The loaded material gravity is influenced by the bucket capacity and the excavation process. As the excavation progresses, the bucket gradually fills with soil, and the gravitational force of the material is increased. At the end of the excavation stage, the gravitational force reaches its maximum value. In Figure 1, the dashed red line represents the variation in loaded material gravity during the excavation process. The maximum value of the material gravity can be calculated based on the bucket capacity. The gravitational force exerted on each component of the working device is related to its size and remains constant throughout the excavation. During the lifting process, the working load primarily consists of the gravitational force of the fully loaded bucket and the self-weight of each component.

2.2. Mathematical Expression for Hydraulic Cylinders’ Energy Consumption

The structure and force distribution of the excavator working device are shown in Figure 2. The relationship between the working loads, including digging resistance, material gravity, component self-weight, and the force exerted by the hydraulic cylinder, can be expressed as follows:

Figure 2. The structure and force distribution of the excavator working device.

Figure 2. The structure and force distribution of the excavator working device.

$$P_1(\mathit{X})=\frac{W_{t1}\left(\mathit{X}\right)\cdot r_{w1}\left(\mathit{X}\right)+G_1\left(\mathit{X}\right)\cdot r_{G11}\left(\mathit{X}\right)}{r_1\left(\mathit{X}\right)}$$

(3)

$$P_2(\mathit{X})=\frac{W_{t2}\left(\mathit{X}\right)\cdot r_{w2}\left(\mathit{X}\right)+G_1\left(\mathit{X}\right)\cdot r_{G12}\left(\mathit{X}\right)+G_2\left(\mathit{X}\right)\cdot r_{G22}\left(\mathit{X}\right)}{r_2\left(\mathit{X}\right)}$$

(4)

$$P_3(\mathit{X})=\frac{G_1\left(\mathit{X}\right)\cdot r_{G13}\left(\mathit{X}\right)+G_2\left(\mathit{X}\right)\cdot r_{G23}\left(\mathit{X}\right)+G_3\left(\mathit{X}\right)\cdot r_{33}\left(\mathit{X}\right)}{r_3\left(\mathit{X}\right)}$$

(5)

In the equation, P₁(X), P₂(X), and P₃(X), respectively, represent the thrust of the bucket hydraulic cylinder, the arm hydraulic cylinder, and the boom hydraulic cylinder, measured in kN. W_t1(X) and W_t2(X) denote the tangential digging resistance, while G₁(X), G₂(X), and G₃(X) represent the weight of the bucket with material, the weight of the arm, and the weight of the boom, respectively, measured in kN. r₁(X), r₂(X), and r₃(X) are the force arms of the thrust exerted by the bucket cylinder at point Q, the arm cylinder at point F, and the boom cylinder at point C, respectively. r_w1(X) and r_w2(X) represent the force arms of the digging resistance at points Q and F, respectively. r_G11(X) and r_G12(X) indicate the force arms of the weight of the bucket with the material at points Q and F, respectively. r_G22(X) represents the force arm of the arm gravity at point F, while r_G33(X) denotes the force arm of the boom gravity at point C. X represents a vector composed of dimensional parameters of the excavator’s working device components and the extension length of the hydraulic cylinders. It is referred to as the main parameter of the excavator working devices, depicted by the solid bold line in Figure 2.

The energy consumption of the bucket cylinder, arm cylinder, and boom cylinder during the excavator’s operation can be calculated using the infinitesimal method [27]. It can be expressed by the following equation:

$$E_1\left(\mathit{X}\right)\approx \sum _{i=a_1}^{b_1}{N}_{1i}\left(\mathit{X}\right)\cdot {\mathsf{\Delta }t}_{1i}\left(\mathit{X},n\right)\approx \sum _{i=a_1}^{b_1}{P}_{1i}\left(\mathit{X}\right)\cdot {\mathsf{\Delta }s}_1\left(\mathit{X},n\right) (1\le a_1<b_1\le n)$$

(6)

$$E_2\left(\mathit{X}\right)\approx \sum _{i=a_2}^{b_2}{N}_{2i}\left(\mathit{X}\right)\cdot {\mathsf{\Delta }t}_{2i}\left(\mathit{X},n\right)\approx \sum _{i=a_2}^{b_2}{P}_{2i}\left(\mathit{X}\right)\cdot {\mathsf{\Delta }s}_2\left(\mathit{X},n\right) (1\le a_2<b_2\le n)$$

(7)

$$E_3\left(\mathit{X}\right)\approx \sum _{i=a_3}^{b_3}{N}_{3i}\left(\mathit{X}\right)\cdot {\mathsf{\Delta }t}_{3i}\left(\mathit{X},n\right)\approx \sum _{i=a_3}^{b_3}{P}_{3i}\left(\mathit{X}\right)\cdot {\mathsf{\Delta }s}_3\left(\mathit{X},n\right) (1\le a_3<b_3\le n)$$

(8)

In the equation, E₁(X), E₂(X), and E₃(X) represent the total energy consumption in kilojoules for completing working operations by the bucket cylinder, arm cylinder, and boom cylinder, respectively. a₁ and b₁ are the starting and ending positions for the bucket cylinder. a₂ and b₂ are the starting and ending positions for the arm cylinder, and a₃ and b₃ are the starting and ending positions for the boom cylinder. These positions can be determined based on specific working conditions. n represents the number of discrete steps during the cylinder stroke. N_1i(X), N_2i(X), and N_3i(X) represent the instantaneous power of the bucket cylinder, arm cylinder, and boom cylinder in the i-th segment of micro-displacement. Δt_1i(X, n), Δt_2i(X, n), and Δt_3i(X, n) are the operating times for the bucket cylinder, arm cylinder, and boom cylinder in that segment of micro-displacement. P_1i(X), P_2i(X), and P_3i(X) denote the instantaneous thrust of the bucket cylinder, arm cylinder, and boom cylinder in the i-th segment of micro-displacement. Δs₁(X, n), Δs₂(X, n), and Δs₃(X, n) represent the micro-displacements of the bucket cylinder, arm cylinder, and boom cylinder, which are divided into n equal parts of the total cylinder stroke.

3. Energy Consumption Analysis and Optimized Conditions Selection under Typical Working Conditions

In Equations (5) and (6) and Figure 1, it is observed that the profiles of excavation resistance and loaded material gravity curves vary not only with the size parameters of the working equipment but also with the digging angle and the starting and ending points of excavation. Additionally, due to the gravitational forces of the components and materials acting perpendicular to the ground, the load exerted on the hydraulic cylinder differs depending on the orientation of the excavator working device. This load difference leads to variations in the thrust and energy consumption of the hydraulic cylinder. Therefore, a detailed analysis of the energy consumption characteristics of the working device is necessary for different excavation forms and postures.

The working process of an excavator involves excavation, leveling, and lifting. However, statistics show that excavators consume significantly more energy during excavation and lifting than other operations [26]. Therefore, this paper aims to analyze the energy consumption during these processes to identify the optimal start and end positions for calculating excavator energy consumption. Additionally, specific optimization conditions for energy consumption are selected. Considering the various operating conditions in real excavation work, this paper analyzes the energy consumption characteristics of bucket digging, arm digging, and post-digging lifting. The analysis is conducted based on the four typical working conditions defined in the Chinese national standard GB9141-88 as the starting positions for excavation [28]. The starting positions for the four typical operating conditions are as follows:

In Condition 1, the boom cylinder is fully retracted, and the arm cylinder has the maximum force arm. The cutting edge of the bucket, the pivot point where the arm and bucket connect, and the pivot point where the boom and arm connect all aligned in a straight line. An offset load exists in this configuration.

In Condition 2, both the boom and arm cylinders have maximum force arms. The cutting edge of the bucket; the pivot point where the boom, arm, and bucket connect; and the pivot point where the boom and arm connect are aligned in a straight line. The digging resistance is symmetrical, and there is no offset load.

In Condition 3, the boom cylinder, arm cylinder, and bucket cylinder all have the maximum force arm. The digging resistance is symmetrical, and there is no offset load.

In Condition 4, the boom cylinder is fully retracted. The pivot point where the boom and arm connect, the pivot point where the arm and bucket connect, and the cutting edge of the bucket are all aligned vertically. An offset load exists in this configuration.

This paper analyzes the energy consumption characteristics of an excavator with a 1 m³ bucket capacity. The empirical formula for digging resistance includes parameters such as R = 150 cm, r = 3.8 m, C = 80, B = 2.8, A = 1.3, Z = 0.75, X = 1.03, D = 12,000 N, Ks = 1, and K₀ = 9. The total digging angles for various typical working conditions, determined based on real excavation scenarios and design specifications, are provided in

Table 1. The total digging angle φ1, φ2.

Digging Form	Condition 1	Condition 2	Condition 3	Condition 4
Bucket digging	120°	120°	90°	120°
Arm digging	60°	70°	70°	90°

. Before the working process, all hydraulic cylinders are fully retracted, and the starting positions required for each working condition are achieved through posture adjustment without resistance. Throughout the operation, the average extension speeds of the boom hydraulic cylinder, arm hydraulic cylinder, and bucket hydraulic cylinder are 120 mm/s, 180 mm/s, and 150 mm/s, respectively.

Based on the above parameters, the working load model is established. The energy consumption characteristics of different excavation processes in four typical working conditions are analyzed using the above energy consumption calculation model. The energy consumption and power characteristic curves for the excavation processes are shown in Figure 3, and the energy consumption and power characteristic curves for the lifting processes are shown in Figure 4. Solid lines represent the energy consumption of hydraulic cylinders (referred to as EC), while dashed lines represent the power of hydraulic cylinders (referred to as PW).

The energy consumption and power characteristic curve of the bucket-digging process is shown in Figure 4a, exhibiting a single peak in the power characteristic. The power remains close to zero when the extension length of the bucket cylinder is less than 15% of the maximum stroke. In Condition 4, the hydraulic cylinder power reaches its peak at approximately 60% extension, measuring around 72 kW. The second-highest power output is observed in Condition 1, at 70 kW. Regarding energy consumption during bucket digging, the highest consumption is recorded in Condition 4, reaching around 200 kJ, closely followed by Condition 1, which is slightly lower.

The energy consumption and power characteristic curve of the arm-digging process is shown in Figure 4b, exhibiting a single peak in the power characteristic. The power remains close to zero when the extension length of the arm cylinder is less than 10% of the maximum stroke. In Condition 1, the hydraulic cylinder power reaches its peak at approximately 75% extension, measuring around 25 kW. The second-highest power output is observed in Condition 4 at 24 kW. Regarding energy consumption during arm digging, the highest consumption is recorded in Condition 4, reaching around 100 kJ, closely followed by Condition 1, which is slightly lower.

The energy consumption and power characteristic curves during the lifting process are illustrated in Figure 5. The shape of the power characteristic curve for the boom cylinder remains consistent across different excavation forms during the boom lifting action. The power curves exhibit a single peak state in Conditions 1 and 4 and exhibit a dual-peak state in Conditions 2 and 3, corresponding to the two working stages of position adjustment and lifting action. During the position-adjustment stage, the peak power is relatively low, around 10 kW. During the lifting-action stage, the peak power is much higher with the bucket digging. In Condition 2, the power reaches its peak when the cylinder extends to approximately 70% of its maximum stroke, measuring around 60 kW, followed closely by Condition 3, with a power output of 58 kW. Regarding energy consumption during boom lifting, the highest consumption occurs in Condition 1 with bucket digging, approximately 312 kJ. Condition 4 follows closely behind, with slightly lower energy consumption.

In conclusion, the power peak and energy consumption of the bucket cylinder during the digging process are highest in Condition 4, slightly higher than in Condition 1, and significantly higher than in the other conditions. The arm cylinder also exhibits a relatively high power peak and energy consumption in Condition 4, with a power peak slightly lower than in Condition 1 but higher energy consumption than the other conditions. The boom cylinder has the highest power peak during the lifting process in Condition 2, while the highest energy consumption during the lifting process occurs in Condition 1. Analyzing the energy consumption and power characteristic curves under these typical conditions helps identify the working conditions for reducing energy consumption during the optimization process: Condition 4 for bucket digging and arm digging and Condition 1 for bucket digging lifting. Moreover, it is determined that the starting positions for calculating energy consumption for each hydraulic cylinder should be set at 15% of the maximum stroke for the bucket cylinder, 10% of the maximum stroke for the arm cylinder, and the minimum stroke for the boom cylinder. The ending positions for energy consumption calculations should be set at the respective maximum stroke for each hydraulic cylinder.

4. Mathematical Model of Multi-Objective Collaborative Optimization for Excavator Working Device

The working device of an excavator consists of the boom, arm, bucket, and three hydraulic cylinders. The positions of the hinge points, dimensions of the components, and stroke of the hydraulic cylinders all contribute to various performance objectives such as digging force, lifting force, and energy consumption. Analyzing the relationship between the hinge point positions (L_AC, L_CB, L_BF, L_CD, L_DF, L_EF, L_FG, L_FN, L_NQ, L_GN, L_MN, L_MK, L_KQ), dimensions of the components (L_CF, L_FQ, L_QV), and the maximum extension lengths (L_ABmax, L_DEmax, L_GMmax) and minimum extension lengths (L_ABmin, L_DEmin, L_GMmin) of the hydraulic cylinders, as shown in Figure 2, helps to determine the optimization variables for the excavator working device. These variables, collectively denoted as vector X, are represented by the solid bold lines in Figure 2.

4.1. Objective Function

4.1.1. Sub-Objective Functions for the Working Energy Consumption

To achieve the low-carbon working process for excavators, the energy consumption of hydraulic cylinders during the excavator’s operation has been identified as the target for optimization, including the energy consumption of bucket digging and arm digging under Condition 4, as well as the energy consumption of bucket digging lifting under Condition 1. By incorporating Equations (6)–(8), the expression of the objective function for optimizing the excavator’s energy consumption is determined as follows:

$$\min f_1\left(\mathit{X}\right)=E_1\left(\mathit{X}\right)$$

(9)

$$\min f_2\left(\mathit{X}\right)=E_2\left(\mathit{X}\right)$$

(10)

$$\min f_3\left(\mathit{X}\right)=E_3\left(\mathit{X}\right)$$

(11)

In the equation, X is the vector of optimization variables for the working device. E₁(X), E₂(X), and E₃(X) represent the energy consumption of hydraulic cylinders during bucket-digging, arm-digging, and boom-lifting processes, respectively, under the selected optimization conditions.

4.1.2. Sub-Objective Function for the Theoretical Digging Force

This paper aims to optimize the working device, with one of the sub-objectives being maximizing the theoretical digging force during bucket-digging and arm-digging processes. The relationship between the theoretical digging force at the bucket tooth tip and the component dimensions under different digging forms is expressed by the following equation:

$$P_{OD}({\mathit{X}}_1,t_1)=P_{01}\cdot \frac{r_1\left({\mathit{X}}_1,t_1\right)\times r_3({\mathit{X}}_1,t_1)}{r_2\left({\mathit{X}}_1,t_1\right)\times L_{QV}}$$

(12)

$$P_{OG}\left({\mathit{X}}_2,t_2\right)=P_{02}\cdot \frac{r_5\left({\mathit{X}}_2,t_2\right)}{r_6\left({\mathit{X}}_2,t_2\right)}$$

(13)

In the equation, P_OD represents the theoretical digging force of the bucket, and P_OG represents the theoretical digging force of the arm. P₀₁ is the maximum thrust of the bucket cylinder, and X₁ = [L_QV, L_KQ, L_FQ, L_FN, L_NQ, L_GN, L_MN, L_MK, L_GMmin, L_GMmax]. t₁ represents the position of the bucket tooth tip during bucket digging. L_QV represents the length of the bucket. r₁(X₁, t₁), r₂(X₁, t₁), and r₃(X₁, t₁) are the force arms of the bucket cylinder thrust on point N, the force arm of the connecting rod MK on point N, and the force arm of the connecting rod MK on point Q, respectively. P₀₂ is the maximum thrust of the arm cylinder, and X₂ = [L_QV, L_FQ, L_DF, L_EF, L_DEmin, L_DEmax]. t₂ represents the position of the bucket tooth tip during arm digging. r₅(X₂, t₂) and r₆(X₂, t₂) are the force arms of the arm cylinder thrust on point F and the force arm of the bucket tooth tip digging force on point F, respectively, as shown in Figure 2.

To optimize the theoretical digging force throughout the entire excavation process, this paper focuses on multiple objectives related to the digging force. These objectives include maximizing the theoretical digging force at the extreme positions of different excavation forms, as well as at 10% and 80% of the maximum stroke of the bucket cylinder, and at 70% of the maximum stroke of the boom cylinder. Therefore, the sub-objective functions for the digging force are as follows:

$$\min f_4\left({\mathit{X}}_1\right)={-P}_{OD}\left({\mathit{X}}_1,t_{11}\right)$$

(14)

$$\min f_5\left({\mathit{X}}_1\right)={-P}_{OD}\left({\mathit{X}}_1,t_{12}\right)$$

(15)

$$\min f_6\left({\mathit{X}}_1\right)={-P}_{OD}\left({\mathit{X}}_1,t_{13}\right)$$

(16)

$$\min f_7\left({\mathit{X}}_2\right)={-P}_{OG}\left({\mathit{X}}_2,t_{21}\right)$$

(17)

$$\min f_8\left({\mathit{X}}_2\right)={-P}_{OG}\left({\mathit{X}}_2,t_{22}\right)$$

(18)

4.1.3. Sub-Objective Functions for the Boom Lifting Force

Once the working device completes the digging process, it enters the lifting phase to transfer the loaded materials. The relationship between the boom lifting force P_ON and the component dimensions can be expressed as follows:

$$P_{ON}({\mathit{X}}_3,t_3)=P_{03}\cdot \frac{e_3({\mathit{X}}_3,t_3)}{r_C({\mathit{X}}_3,t_3)}$$

(19)

In the equation, P₀₃ represents the maximum thrust of the boom cylinder. X₃ = [L_CF, L_FQ, L_QV, L_AB1, L_AB2, L_DE2, L_GM1]. Meanwhile, t₃ is the position of the bucket’s center of gravity during the lifting action. Additionally, e₃(X₃, t₃) and r_C(X₃, t₃) correspond to the force arm of the boom cylinder thrust force on point C and the force arm of the boom lifting force on point C, respectively.

One of the optimization objectives for the excavator working device is to maximize the lifting force of the boom to enhance the capability of lifting materials. The lifting force at the extreme position is selected as a sub-objective, which can be expressed by the following objective function:

$$\min f_9\left({\mathit{X}}_3\right)={-P}_{ON}\left({\mathit{X}}_3,t_{31}\right)$$

(20)

4.2. Multi-Objective Collaborative Optimization Model Based on Sub-Objective Loss Degree

This paper aims to address the multi-objective optimization problem of the excavator’s working device with the goal of reducing energy consumption. It involves nine optimization sub-objectives. However, utilizing the existing linear weighting method to transform the multi-objective optimization problem into a single-objective one often results in an imbalance between the objectives, making it challenging to achieve the desired overall effect. Therefore, the concept of the sub-objective loss degree is proposed in this paper to overcome the above problems, which measures the satisfaction level of each sub-objective in the multi-objective optimization result. The expression of the sub-objective loss is as follows:

$$z_i(\mathit{X})=\frac{f_i\left(\mathit{X}\right)-f_i^{*}}{f_i^{*}}$$

(21)

In this equation, z_i(X) represents the loss degree of the i-th sub-objective, f_i(X) represents the value of the i-th sub-objective function during the multi-objective optimization process, and f_i^* represents the optimal solution of the i-th sub-objective when it is optimized individually. The individual optimization of each sub-objective can be performed during the pre-processing stage to obtain the optimal solution for each sub-objective.

Based on the mentioned sub-objective loss degree, it is possible to develop a new collaborative multi-objective optimization model with reduced energy consumption.

$$\begin{gathered} \min F(\mathit{X})=\sum {\left[z_i\left(\mathit{X}\right)\right]}^2=\sum _{i=1}^9{\left(\frac{f_i\left(\mathit{X}\right)-f_i^{*}}{f_i^{*}}\right)}^2 \\ s.t. z_i\left(\mathit{X}\right)=\left|\frac{f_i\left(\mathit{X}\right)-f_i^{*}}{f_i^{*}}\right|<{\delta }_i \end{gathered}$$

(22)

In this equation, δ_i represents the allowable loss degree for the i-th sub-objective. By imposing constraints on the sub-objective loss degrees, it is possible to effectively balance the collaborative effects of each sub-objective while ensuring that none of the sub-objective loss degrees exceeds the permissible values during the multi-objective optimization process.

4.3. Constraints

During the multi-objective optimization process of the excavator working device, it is essential to satisfy the geometric and motion relationships among its components, which ensures that the components maintain their intended shapes and prevents any interference during their movements. Therefore, it is necessary to impose constraint conditions throughout the optimization process. Based on the shapes and motion relationships of the components, the constraints for the optimization process include six constraints on the bucket linkage movements, four constraints on the bucket’s geometric dimensions, six constraints on the boom’s geometric dimensions, and three constraints on the shape relationship between the boom and the bucket. In total, 19 constraints are implemented within the optimization procedure.

5. Multi-Objective Collaborative Optimization Process and Algorithm for the Working Device

5.1. Multi-Objective Collaborative Optimization Process

This paper focuses on energy consumption, the digging force, and the boom lifting force during the excavator working process. Multiple objectives are considered in the optimization using the calculation model for energy consumption and the multi-objective optimization model. The optimization process, as illustrated in Figure 5, consists of the following steps:

(1)

Input basic parameters and design requirements such as bucket capacity and working pressure.

(2)

Conduct independent pre-optimization, including excavation energy consumption and digging force, to obtain the optimal solutions for each sub-objective.

(3)

Establish the multi-objective coordinated optimization model for the excavator working device based on Equation (22).

(4)

Perform knowledge-guided multi-objective collaborative optimization for the excavator working device.

(5)

Evaluate the optimization results. If the design requirements are met, output the optimization results; otherwise, the knowledge-guided variable adjustments are made, and a new optimization round is initiated.

5.2. Construction of the Multi-Objective Optimization Algorithm for the Working Device

The multi-objective collaborative optimization model for the excavator working device established in this paper involves 9 optimization sub-objectives, 22 optimization variables, and 19 constraints, making it a complex, real-world engineering optimization problem. Considering the superior performance of the differential evolution algorithm in solving such complex engineering problems [29], this paper proposes a new multi-objective evolutionary algorithm that integrates the differential evolution algorithm with the previously mentioned multi-objective coordinated optimization model. This algorithm is specifically designed to address the multi-objective optimization problem of the excavator working device.

This algorithm utilizes Equation (22) to establish an individual evaluation function and classify the individuals within the population. Individuals with low loss degrees are categorized as excellent individuals, while those with high loss degrees are categorized as poor individuals, and the remaining individuals are considered average. An external population is created to preserve the excellent individuals, and the initial set of excellent individuals can be obtained by extracting the pre-optimized results from the pre-processing stage. Differential evolution operations are performed on all individuals within the population by randomly selecting one individual from the population and one excellent individual from the external population as parent individuals, as illustrated in the following equation:

$${x_j}^{\prime }=\left\{\begin{array}{c}{x}_j+a_{de}\left|x_j^1-x_j^2\right| \left(\mathrm{u}\le P_{de}\right)\\ x_j \left(\mathrm{u}>P_{de}\right) \end{array}\right.$$

(23)

In the equation, x_j′, x_j, x_j1, and x_j2 represent the j-th variable of the newly generated individual, the original individual, the parent individual from the population, and the parent individual from the external population, respectively. a_de is the differential scaling factor, usually a constant between 1 and 2. u is a random number between 0 and 1. P_de is the differential probability, typically set to 0.9.

To further enhance the search range and improve the optimization quality of the population, an additional mutation operation is performed on the poor individuals within the population after applying the differential evolution operation. It can be expressed as follows:

$$\begin{array}{c}{x_j}^{\prime }=\left\{\begin{array}{c}{x}_j+F_m·({EH}_j-x_j), (u\le P_m)\cap (x_j>{EH}_j)\\ x_j+F_m·({EL}_j-x_j), (u\le P_m)\cap (x_j<{EL}_j)\\ x_j, \left(\mathrm{u}>P_m\right)\cup ({EL}_j\le x_j\le {EH}_j)\end{array}\right.\end{array}$$

(24)

In the equation, x_j′ and x_j represent the j-th variable of the newly generated individual through the mutation operation and the original individual, respectively. F_m is the mutation scaling factor, typically a constant between 0 and 1. EH_j and EL_j are the maximum and minimum values of the j-th variable among the excellent individuals in the external population. u is a random number between 0 and 1. P_m is the mutation probability, which can be calculated according to the following equation:

$$P_m=\frac{q}{\mu +b{G}_0}·P_{mL}$$

(25)

In the equation, μ, b, and q are parameters for the mutation operation, commonly chosen as constants between 0.5 and 1. G₀ represents the current generation during the evolutionary process. At the early stages of population evolution, when G₀ is small, the genetic loci of individuals have a higher probability of mutation, facilitating the expansion of the search space. However, to prevent excessive mutation operations and potential deviation from the optimal solution in later stages of evolution, G₀ increases as the evolution progresses, gradually decreasing the individual mutation probability. P_mL is the base probability of the mutation operation, typically set to 0.5.

Furthermore, this algorithm utilizes a neighborhood updating strategy to update the population [30]. During the population initialization stage, each individual is randomly assigned several neighboring individuals. After an individual completes the evolutionary operations and generates a new offspring, the evaluation function is computed using Equation (22). The offspring are then compared and updated with the original individual as well as its neighboring individuals. Once all individuals in the population have been updated and a new population is generated, the excellent individuals from the new population compete with those from the external population to update the external population.

6. Optimization Results and Analysis

To validate the effectiveness of the multi-objective collaborative optimization modeling and algorithm proposed in this paper for reducing energy consumption in excavator working devices, a medium-sized backhoe excavator with a weight of around 25 tons was taken as an example for multi-objective collaborative optimization. The initial parameters for optimization design are shown in

Table 2. The initial conditions for optimization design.

Symbols	Description	Value	Symbols	Description	Value
q	Bucket capacity	1 m3	d2	Arm cylinder rod diameter	75 mm
WS	Hydraulic pressure	37.8 MPa	D1	Bucket cylinder bore	140 mm
D3	Boom cylinder bore	140 mm	d1	Bucket cylinder rod diameter	70 mm
d3	Boom cylinder rod diameter	70 mm	H1	Maximum digging radius	9 m
D2	Arm cylinder bore	150 mm	H2	Maximum digging depth	4 m

.

Based on the design requirements, the mentioned modeling method was employed during the optimization pre-processing stage to establish the sub-objective models for optimizing the main parameters of the excavator working device. Each sub-objective was independently optimized to obtain the optimal solution. The independent optimization was performed with a standard genetic algorithm with a population size of 200, a maximum number of evolution generations set to 1000, a crossover probability of 90%, and a mutation probability of 1%. The results of the independent optimization for each sub-objective are presented in

Table 3. The optimal solution of each sub-objective.

Objective	Description	Value	Objective	Description	Value
f1	Energy consumption of bucket digging (kJ)	199	f6	Bucket digging force at ending point (kN)	142.1
f2	Energy consumption of arm digging (kJ)	78.4	f7	Arm digging force at extreme point (kN)	162.8
f3	Energy consumption of boom lifting (kJ)	267.1	f8	Arm digging force at ending point (kN)	146.9
f4	Bucket digging force at start point (kN)	155.9	f9	Boom lifting force at extreme point (kN)	190.9
f5	Bucket digging force at extreme point (kN)	165.2

.

After completing the independent pre-optimization for each sub-objective, the multi-objective collaborative optimization model for optimizing the excavator working device was established using Equations (21) and (22). This model aims to reduce energy consumption in the working process. The loss degrees of each sub-objective were calculated, and the objective function was obtained. The optimization process was conducted with the multi-objective evolutionary algorithm proposed in this paper. The algorithm employs a population size of 100, a maximum number of evolution generations set to 1000, and a neighborhood size of 20. The optimization process was performed 30 times. The results of the multi-objective collaborative optimization for each sub-objective are presented in

Table 4. The multi-objective optimization results of the excavator working device.

Objective	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$	${\mathit{f}}_6$	${\mathit{f}}_7$	${\mathit{f}}_8$	${\mathit{f}}_9$
Value	200 kJ	81 kJ	276 kJ	148 kN	163 kN	132 kN	155 kN	141 kN	175 kN
Loss degree	0.3%	3.9%	3.2%	5.1%	1.4%	7.0%	4.7%	3.7%	8.6%
Constrain (δ)	5%	5%	5%	10%	5%	10%	5%	10%	10%

.

To validate the superiority of the proposed optimization model in enhancing excavation performance and reducing energy consumption, two different optimization modeling approaches were employed under the same basic algorithm parameters. Approach A does not consider energy consumption as a sub-objective but focuses on traditional linear weighting modeling of force characteristics such as the digging force and lifting force during the excavation process. On the other hand, Approach B adopts the new multi-objective collaborative optimization modeling method proposed in this paper, incorporating energy consumption during the excavation process as a sub-objective. The comparison of optimization results is presented in

Table 5. Comparison of different optimization schemes.

Objective	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$	${\mathit{f}}_6$	${\mathit{f}}_7$	${\mathit{f}}_8$	${\mathit{f}}_9$
Approach A	216 kJ	104 kJ	311 kJ	134 kN	163 kN	135 kN	156 kN	123 kN	184 kN
Approach B	200 kJ	81 kJ	276 kJ	148 kN	163 kN	132 kN	155 kN	141 kN	175 kN

and Figure 6. In Figure 6, the red curve represents the power and energy consumption characteristics of the hydraulic cylinder optimized under Approach A, while the blue curve corresponds to the power and energy consumption characteristics of the hydraulic cylinder optimized under Approach B.

As shown in Table 5, each modeling approaches demonstrates different performances in terms of force characteristics during the excavation process. Compared to Approach A, the optimization in Approach B results in an average increase of 2.8% in the bucket digging force, an average increase of 7% in the arm digging force, and a 4.9% decrease in the boom lifting force.

As illustrated in Figure 6, when optimized using Approach B, there is a significant reduction in average power and energy consumption during different working processes compared to Approach A. Throughout the entire bucket-digging process, the average power increases by 0.7%, the power peak increases by 1.4%, and the energy consumption decreases from 216 kJ to 200 kJ, resulting in a 7.4% reduction. Throughout the entire arm-digging process, the average power decreases by 10.2%, the power peak decreases by 25%, and the excavation energy consumption decreases from 104 kJ to 81 kJ, resulting in a 22.1% reduction. Similarly, throughout the entire boom lifting process, the average power decreases by 4.1%, the power peak decreases by 4.9%, and the lifting energy consumption decreases from 311 kJ to 276 kJ, resulting in an 11.3% reduction.

To further validate the rationality of the selected optimization conditions in this paper, an analysis of the energy consumption during the working processes under the mentioned typical working conditions (TWC) was conducted on the optimized results of the two schemes. The energy consumption results are shown in

Table 6. The digging energy consumption under typical working conditions.

Bucket Digging	TWC 1	TWC 2	TWC 3	TWC 4	Arm Digging	TWC 1	TWC 2	TWC 3	TWC 4
Approach A	208 kJ	183 kJ	72 kJ	216 kJ	Approach A	100 kJ	64 kJ	58 kJ	104 kJ
Approach B	194 kJ	171 kJ	68 kJ	200 kJ	Approach B	78 kJ	47 kJ	43 kJ	81 kJ

and

Table 7. The lifting energy consumption under typical working conditions.

Bucket Digging Lifting	TWC 1	TWC 2	TWC 3	TWC 4	Arm Digging Lifting	TWC 1	TWC 2	TWC 3	TWC 4
Approach A	311 kJ	255 kJ	255 kJ	285 kJ	Approach A	252 kJ	207 kJ	207 kJ	261 kJ
Approach B	276 kJ	223 kJ	223 kJ	254 kJ	Approach B	224 kJ	182 kJ	182 kJ	232 kJ

, revealing that Approach B consistently outperforms Approach A in energy consumption across all four typical working conditions. Specifically, the average energy consumption during bucket digging is reduced by 6.8%, the average energy consumption during arm digging is reduced by 24%, and the average energy consumption during the lifting process is reduced by 11.8%. These findings demonstrate that the proposed optimization modeling method for the excavator’s working device, considering force characteristics and energy consumption during the working process, effectively enhances the digging force and decreases energy consumption under different working conditions. An efficient, environmentally friendly, and energy-efficient excavator operation is achieved.

To further validate the superiority of the proposed multi-objective collaborative optimization model, it was compared to the conventional linearly weighted (LW) model with the same optimization algorithm. Additionally, four weight-allocation schemes (as shown in

Table 8. The weight-allocation schemes for the linearly weighted model.

Objective	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$	${\mathit{f}}_6$	${\mathit{f}}_7$	${\mathit{f}}_8$	${\mathit{f}}_9$
Scheme A	1	1	1	1	1.5	1	1.5	1	1
Scheme B	1.5	1.5	1.5	1	1	1	1	1	1
Scheme C	1	1	1	1	1	1	1	1	1.5
Scheme D	1	1	1	1	1	1	1	1	1

) were employed to demonstrate the impact on the optimization results of the conventional linearly weighted method. The comparison between different models is presented in

Table 9. Comparison of optimized results between the new model and the linearly weighted model.

Model	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$	${\mathit{f}}_6$	${\mathit{f}}_7$	${\mathit{f}}_8$	${\mathit{f}}_9$
New model	200 kJ	81 kJ	276 kJ	148 kN	163 kN	132 kN	155 kN	141 kN	175 kN
LW model A	201 kJ	109 kJ	311 kJ	139 kN	161 kN	135 kN	160 kN	123 kN	188 kN
LW model B	234 kJ	81 kJ	297 kJ	142 kN	160 kN	120 kN	157 kN	142 kN	173 kN
LW model C	222 kJ	120 kJ	311 kJ	111 kN	158 kN	140 kN	156 kN	118 kN	184 kN
LW model D	203 kJ	86 kJ	298 kJ	119 kN	155 kN	140 kN	157 kN	145 kN	172 kN

, while the loss degrees for each sub-objective are shown in Figure 7. In the figure, the x-axis represents the objective number, and the y-axis represents the loss degree value. The black curve represents the new optimization model, while the red, blue, green, and purple curves represent linear weighting schemes A, B, C, and D, respectively.

The results in Table 9 and Figure 7 reveal significant differences in the optimization results and loss degrees for each sub-objective among the various weight-allocation schemes used in the linearly weighted model. It is evident that the weight allocation in the conventional linearly weighted method obviously influences the optimization results. The average loss degrees for the four allocation schemes are 10.52%, 8.43%, 16%, and 7.59%, respectively. The maximum loss degrees for each scheme are 39.13%, 15.46%, 53.31%, and 23.59%, respectively. The variances in loss degrees are 154.47, 28.69, 279.22, and 51.41, respectively. In contrast, by adopting the proposed multi-objective collaborative optimization model, the average loss degree for each sub-objective is reduced to 4.2%, with a maximum loss degree of 8.6%. Furthermore, the remaining sub-objectives loss degrees are below 7%, and their variance is 6.51. Compared to the average loss degrees achieved by the four different weight-allocation schemes in the conventional linearly weighted method, the new optimization model demonstrates decreases of 6.32%, 4.23%, 11.91%, and 3.39%, respectively.

To further validate the optimization results, this paper compared the new method with two representative optimization methods: Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) [31]. The excavator was optimized under the same basic parameters, and the results were compared. The optimization results are presented in

Table 10. Comparison of the different optimization methods.

Method	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$	${\mathit{f}}_6$	${\mathit{f}}_7$	${\mathit{f}}_8$	${\mathit{f}}_9$
New method	200 kJ	81 kJ	276 kJ	148 kN	163 kN	132 kN	155 kN	141 kN	175 kN
GA method	219 kJ	110 kJ	288 kJ	136 kN	164 kN	133 kN	148 kN	126 kN	158 kN
PSO method	218 kJ	93 kJ	301 kJ	152 kN	166 kN	125 kN	161 kN	143 kN	160 kN

, and the loss degrees of each sub-objective are depicted in Figure 8.

The results in Table 10 and Figure 8 reveal that the maximum loss degree of the GA method is 40.7%. Its average loss degree is 13.1%, and the variance in loss degrees is 128.8. The maximum loss degree of the PSO method is 19.2%. Its average loss degree is 8.3, and the variance in loss degrees is 49.7. Compared to the other methods, the new method exhibits an average improvement of 2.8% in digging force and an average reduction of 14.1% in energy consumption. Additionally, the optimization quality of each objective is more balanced.

7. Discussion

This paper proposes a multi-objective collaborative optimization method for excavator working devices to support a reduction in energy consumption. A mathematical model for energy consumption during the excavator’s work process is established. By analyzing energy consumption under different operating conditions, optimization objectives are determined. The excavator working devices are then optimized using a multi-objective collaborative optimization model based on the loss degree. In contrast to previous studies, this research takes into full consideration the energy consumption during excavator optimization and addresses the issue of imbalanced optimization quality among sub-objectives. The optimization results demonstrate that the proposed method can enhance the excavator’s working performance while reducing energy consumption when compared to conventional methods. Moreover, it achieves a balanced improvement in the optimization quality of each sub-objective. In the future, these methods can be further extended to facilitate multi-objective optimization designs for other complex mechanical systems.

8. Conclusions

(1)

Based on the mathematical model of energy consumption during the working process of the excavator and the analysis of energy-consumption patterns for four typical working conditions, this paper identifies the optimization conditions for the main parameters of the excavator working device. A multi-objective collaborative optimization model is developed to optimize the energy consumption during the excavator’s working process, and multi-objective collaborative optimization is conducted. The results demonstrate that the proposed optimization method for the overall energy consumption during the excavator’s working process effectively reduces energy consumption compared to the optimization solely focused on the mechanical performance of the excavator. Specifically, the energy consumption during bucket digging is reduced by 7.4%, the energy consumption during arm digging is reduced by 22.1%, and the energy consumption during boom lifting is reduced by 11.3%.

(2)

This paper establishes a multi-objective collaborative optimization model based on sub-objective loss degrees and develops a corresponding optimization algorithm. This approach overcomes the limitations of existing linearly weighted modeling methods, which often rely on empirical weight allocation and tend to result in suboptimal solutions that favor some objectives while neglecting others. The optimization results demonstrate that utilizing the proposed optimization model and algorithm for optimizing the excavator working device obtains superior overall optimization quality and ensures a more balanced improvement across all sub-objectives. The optimized results reveal average reductions of 5.2%, 23.7%, and 9.5% in energy consumption during bucket digging, arm digging, and boom lifting, respectively. Moreover, the average increases in bucket digging force, arm digging force, and boom lifting force are 3.72%, 2.5%, and 1.2%, respectively. The average sub-objective loss degrees, maximum sub-objective loss degrees, and loss degree variances are significantly reduced.

(3)

The analysis of the energy consumption characteristics of the optimized results under typical working conditions reveals that the multi-objective collaborative optimization of excavator working devices, performed within the determined optimization conditions presented in this paper, can effectively reduce the energy consumption of the excavator during the working process. Significant reductions in working energy consumption are observed across all four typical working conditions.

In conclusion, the proposed optimization method for excavator working devices, aimed at reducing energy consumption, exhibits significant superiority in optimizing the performance of excavator working devices. The new method enhances the working performance while achieving energy savings during the excavator working processes.