Design of an Integrated Optics Sensor Structure Based on Diamond Waveguide for Hemoglobin Property Detection
Abstract
:1. Introduction
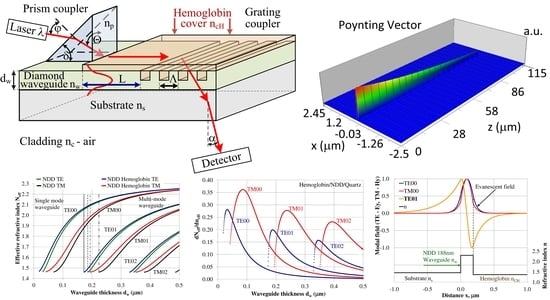
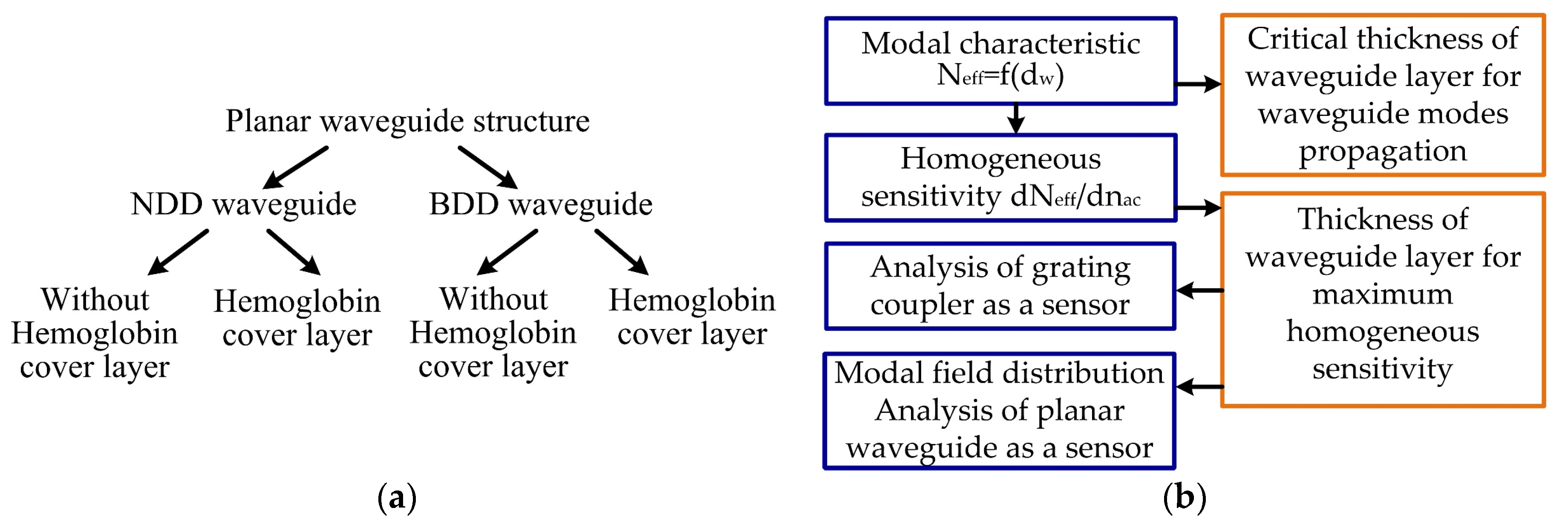
2. Methods
3. Calculation Results
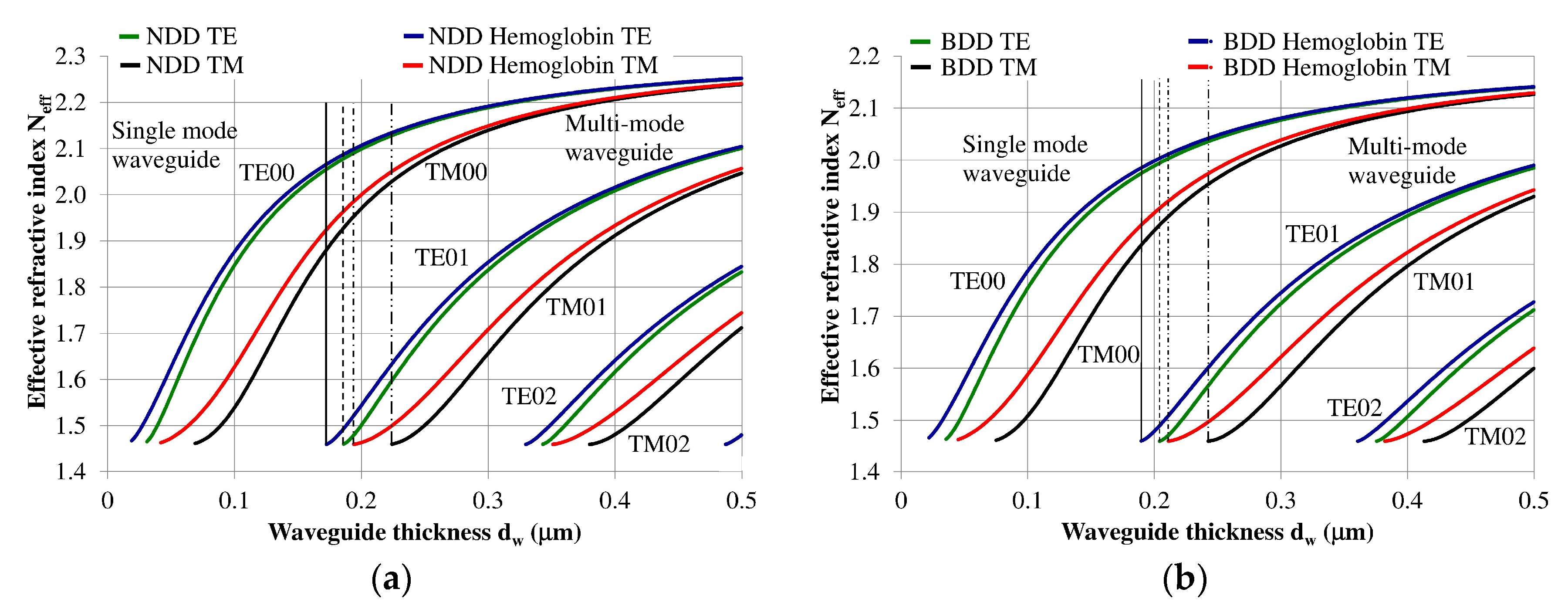
3.1. Modal Characteristics of the Planar Waveguide Structure
3.2. The Homogeneous Sensitivity dNeff/dncH
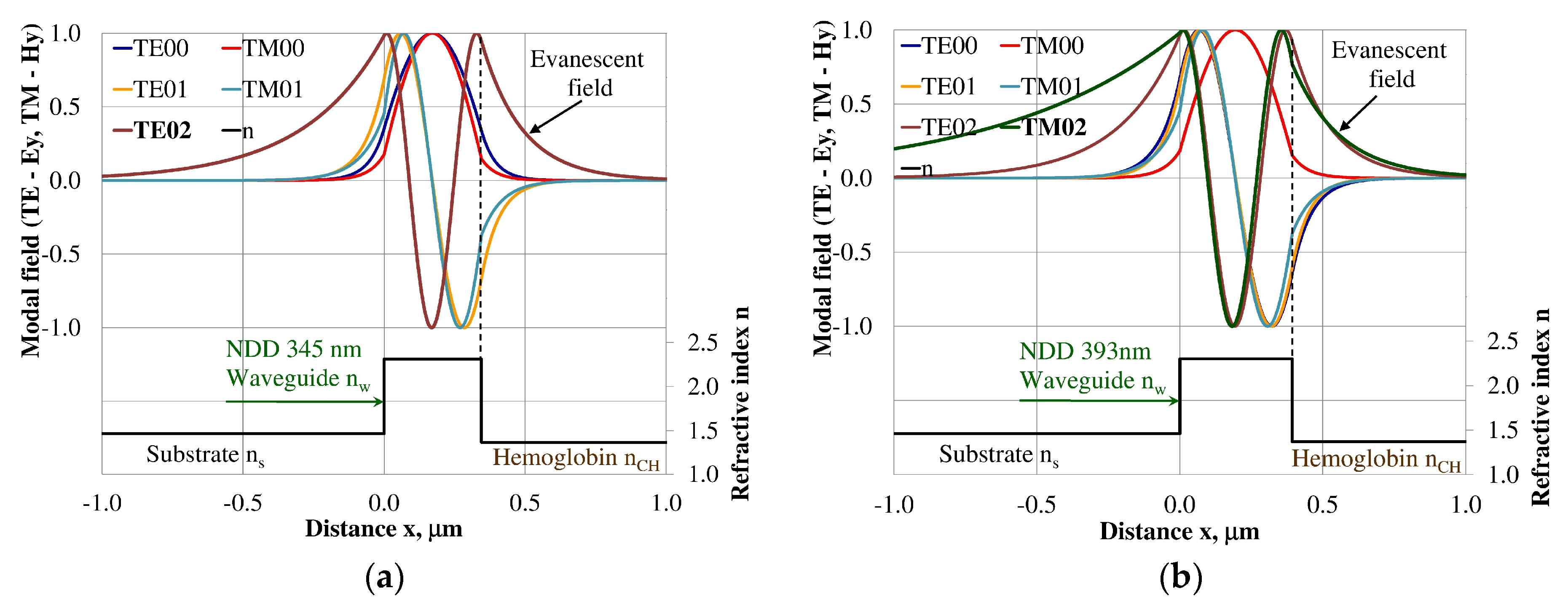
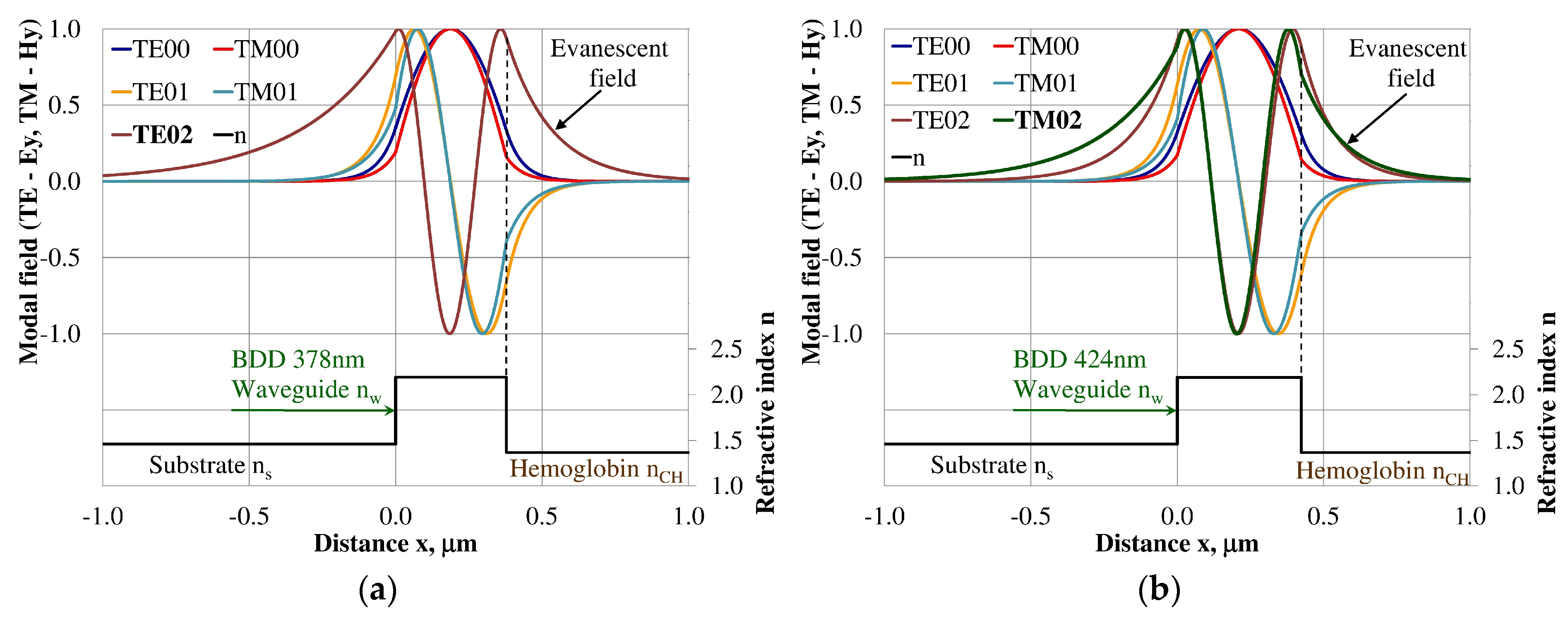
3.3. Modal Field Distribution
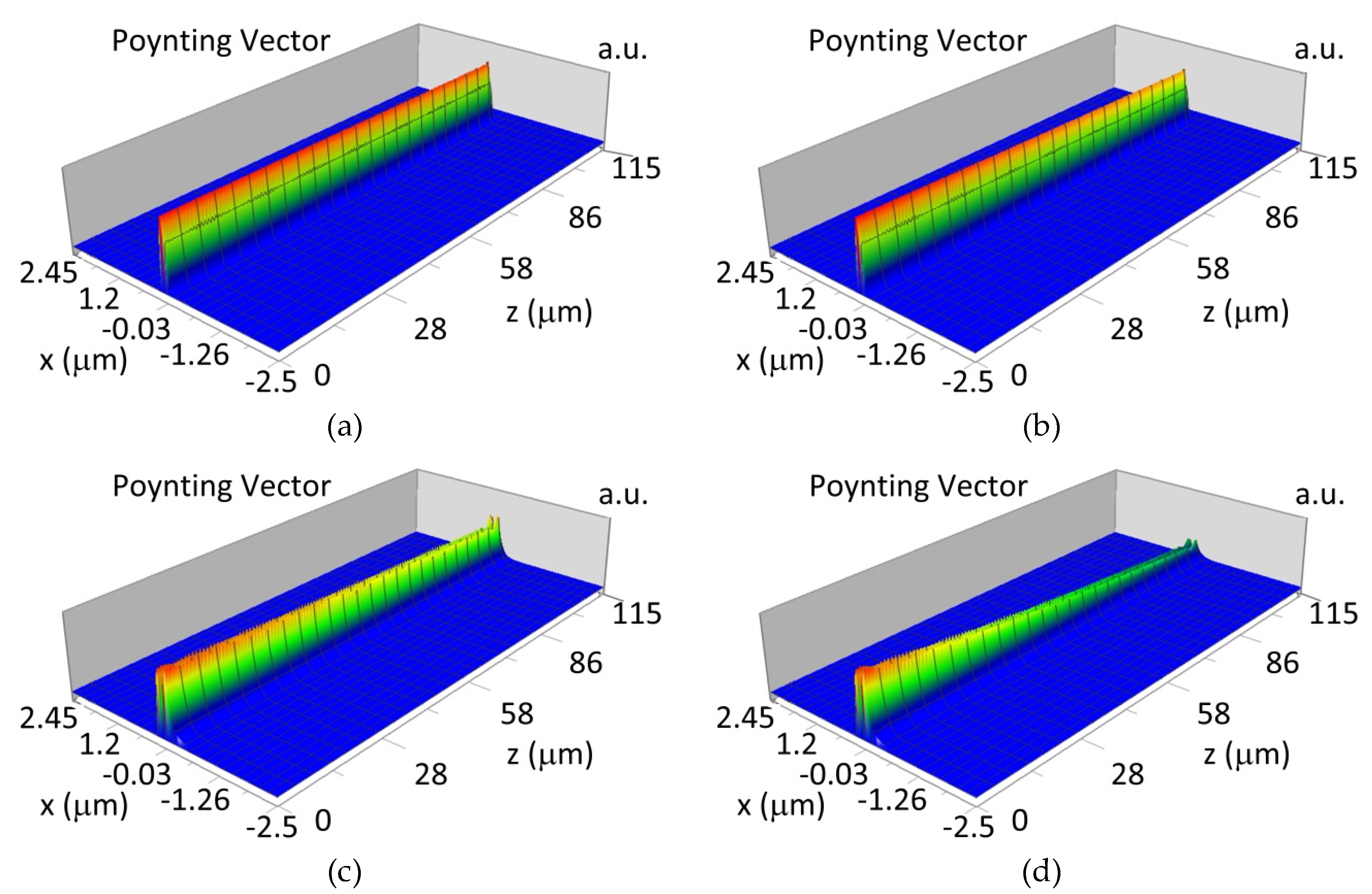
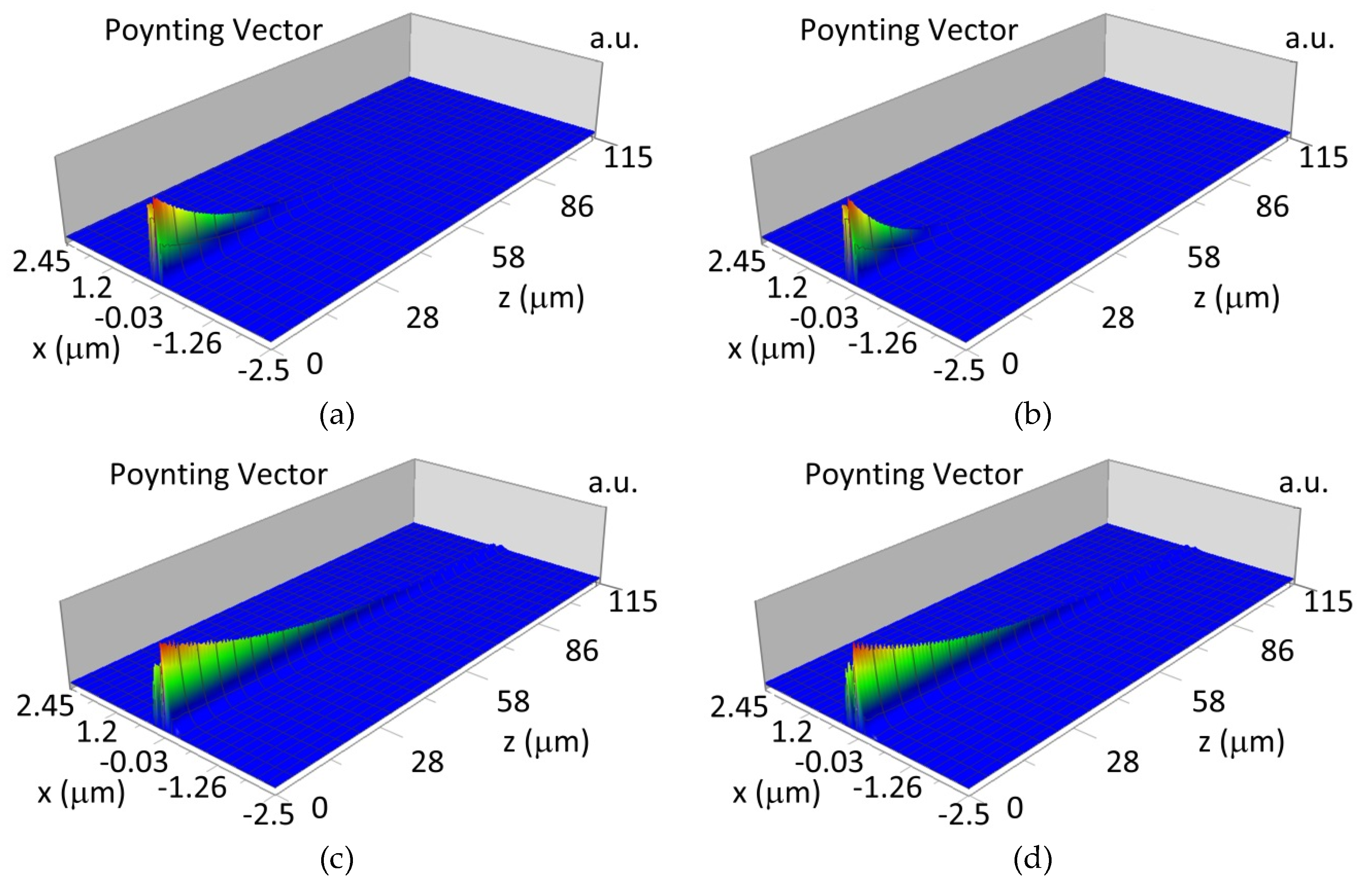
3.4. Propagation of Modes in Planar Waveguide Structure with Hemoglobin Cover Layer
4. Conclusions
Funding
Conflicts of Interest
References
- Singh, I.; Weston, A.; Kundur, A.; Dobie, G. Haematology Case Studies with Blood Cell Morphology and Pathophysiology; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Schechter, A.N. Hemoglobin research and the origins of molecular medicine. Blood 2008, 112, 3927–3938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gell, D.A. Structure and function of haemoglobins Blood Cells. Mol. Dis. 2018, 70, 13–42. [Google Scholar] [CrossRef]
- Majchrowicz, D.; Kosowska, M.; Sankaran, K.J.; Struk, P.; Wąsowicz, M.; Sobaszek, M.; Haenen, K.; Jędrzejewska-Szczerska, M. Nitrogen-Doped Diamond Film for Optical Investigation of Hemoglobin Concentration. Materials 2018, 11, 109. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Deka, B.; Partha, P.P. Planar Waveguide Optical Sensors: From Theory to Applications; Springer: Berlin, Germany, 2016. [Google Scholar]
- Kang, S.; Sasaki, K.; Minamitani, H. Determining the absorption coefficient of hemoglobin derivatives with integrated optic waveguide sensor. In Proceedings of the 14th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Paris, France, 29 October–1 November 1992; pp. 171–172. [Google Scholar] [CrossRef]
- Lukosz, W.; Tiefenthaler, K. Sensitivity of integrated optical grating and prism couplers as (bio)chemical sensors. Sens. Actuators 1988, 15, 273–284. [Google Scholar] [CrossRef]
- Lukosz, W. Integrated optical chemical and direct biochemical sensors. Sens. Actuators B Chem. 1995, 29, 37–50. [Google Scholar] [CrossRef]
- Lambeck, P.V. Integrated optical sensors for the chemical domain. Meas. Sci. Technol. 2006, 17, R93–R116. [Google Scholar] [CrossRef]
- Struk, P.; Pustelny, T.; Gołaszewska, K.; Kamińska, E.; Borysiewicz, M.A.; Ekielski, M.; Piotrowska, A. Hybrid photonics structures with grating and prism couplers based on ZnO waveguides. Opto-Electron. Rev. 2013, 21, 376–381. [Google Scholar] [CrossRef] [Green Version]
- Struk, P.; Pustelny, T.; Gołaszewska, K.; Kamińska, E.; Borysiewicz, M.A.; Ekielski, M.; Piotrowska, A. Photonic structures with grating couplers based on ZnO. Opto-Electron. Rev. 2011, 19, 76–81. [Google Scholar] [CrossRef]
- Jedrzejewska-Szczerska, M.; Majchrowicz, D.; Hirsch, M.; Struk, P.; Bogdanowicz, R.; Bechelany, M.; Tuchin, V.V. Chapter 14—Nanolayers in Fiber-Optic Biosensing. In Nanotechnology and Biosensors A volume in Advanced Nanomaterials; Nikolelis, D., Nikoleli, G.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 395–426. [Google Scholar]
- Karasinski, P.; Szponik, M.; Tyszkiewicz, C. Sensor properties of the input grating couplers. Proc. SPIE 2014, 9228, 92280G-1–92280G-6. [Google Scholar] [CrossRef]
- Struk, P. Numerical analysis of integrated optics structures based on wide band gap semiconductor materials for biosensors application. Proc. SPIE 2018, 10830, 1083004-1–1083004-6. [Google Scholar] [CrossRef]
- Mukundan, H.; Anderson, A.S.; Grace, W.K.; Grace, K.M.; Hartman, N.; Martinez, J.S.; Swanson, B.I. Waveguide-Based Biosensors for Pathogen Detection. Sensors 2009, 9, 5783–5809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grichko, V.P.; Shenderova, O.A. Nanodiamond: Designing and Bio-Platfrom. In Ultrananocrystalline Diamond: Synthesis, Properties, and Applications; Shenderova, O.A., Gruen, D.M., Eds.; Imprint William Andrew: Norwich, NY, USA, 2006; pp. 547–554. ISBN 978-0-8155-1524-1. [Google Scholar]
- Prajzler, V.; Varga, M.; Nekvindova, P.; Remes, Z.; Kromka, A. Design and investigation of properties of nanocrystalline diamond optical planar waveguides. Opt. Express 2013, 21, 8417–8425. [Google Scholar] [CrossRef] [PubMed]
- Hiscocks, M.P.; Ganesan, K.; Gibson, B.C.; Huntington, S.T.; Ladouceur, F.; Prawer, S. Diamond Waveguides Fabricated by Reactive ion Etching. Opt. Express 2008, 16, 19512–19519. [Google Scholar] [CrossRef] [PubMed]
- Sobaszek, M.; Skowronski, Ł.; Bogdanowicz, R.; Siuzdak, K.; Cirocka, A.; Zieba, P.; Gnyba, M.; Naparty, M.; Gołunski, Ł.; Płotka, P. Optical and electrical properties of ultrathin transparent nanocrystalline boron-doped diamond electrodes. Opt. Mater. 2015, 42, 24–34. [Google Scholar] [CrossRef]
- Ficek, M.; Sobaszek, M.; Gnyba, M.; Ryl, J.; Gołuński, Ł.; Smietana, J.J.; Caband, P.; Bogdanowicza, R. Optical and electrical properties of boron doped diamond thin conductive films deposited on fused silica glass substrates. Appl. Surf. Sci. 2016, 387, 846–856. [Google Scholar] [CrossRef]
- Sobaszek, M.; Siuzdak, K.; Skowroński, Ł.; Bogdanowicz, R.; Pluciński, J. Optically transparent boron-doped nanocrystalline diamond films for spectroelectrochemical measurements on different substrates. IOP Conf. Ser. Mater. Sci. Eng. 2015, 104, 1–10. [Google Scholar] [CrossRef]
- Tang, L.; Tsai, C.; Gerberich, W.W.; Kruckeberg, L.; Kania, D.R. Biocompatibility of chemical-vapour-deposited diamond. Biomaterials 1995, 16, 483–488. [Google Scholar] [CrossRef]
- Lazareva, E.N.; Tuchin, V.V. Measurement of refractive index of hemoglobin in the visible/NIR spectral range. J. Biomed. Opt. 2018, 23. [Google Scholar] [CrossRef] [PubMed]
- Prahl, S.A. Optical Absorption of Hemoglobin. Available online: http://omlc.ogi.edu/spectra/hemoglobin/index.html (accessed on 14 December 2018).
- Sydoruk, O.; Zhernovaya, O.; Tuchin, V.; Douplik, A. Refractive index of solutions of human hemoglobin from the near-infrared to the ultraviolet range: Kramers-Kronig analysis. J. Biomed. Opt. 2012, 17, 115002. [Google Scholar] [CrossRef] [PubMed]
- Gut, K. Chapter–Pomiar różnicy stałych propagacji ortogonalnych modów. In Laboratorium Optoelektroniki Światłowodowej; Opilski, A., Ed.; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2002; pp. 249–263. ISBN 83-7335-036-5. [Google Scholar]
- Tyszkiewicz, C. Homogeneous sensitivity of sol–gel derived planar waveguide Structures—Theoretical analysis. Opt. Appl. 2012, 42, 555–569. [Google Scholar] [CrossRef]
- Billett, H.H. Chapter 151 Hemoglobin and Hematocrit. In Clinical Methods: The History, Physical, and Laboratory Examinations; Walker, H.K., Hall, W.D., Hurst, J.W., 3rd, Eds.; Butterworths: Boston, MA, USA, 1990. [Google Scholar]













| Wavelength (nm) | Refractive Index | ||||
|---|---|---|---|---|---|
| Non-Doped Diamond nwNDD [21] | Boron-Doped Diamond nwBDD [21] | Quartz Substrate ns | Air | Biological liquid-Hemoglobin ncH [23] * 0/17.3/26.0 g/dL | |
| 560 | 2.30 | 2.19 | 1.4595 | 1.0003 | 1.3342/1.3681/1.3836 |
| Structure | Waveguide Layer Thickness dw, nm | |||||
|---|---|---|---|---|---|---|
| Single-Mode | Multi-Mode | |||||
| TE00 | TM00 | TE01 | TM01 | TE02 | TM03 | |
| NDD/Quartz | 31 | 69 | 186 | 224 | 343 | 380 |
| Hemoglobin/NDD/Quartz | 19 | 42 | 172 | 194 | 329 | 351 |
| BDD/Quartz | 35 | 75 | 204 | 242 | 375 | 413 |
| Hemoglobin/BDD/Quartz | 22 | 45 | 189 | 211 | 360 | 382 |
| Waveguide Layer Thickness dw (nm) for Maximum Homogeneous Sensitivity dNeff/dncH | |||||||||||
| Hemoglobin/NDD/Quartz | Hemoglobin/BDD/Quartz | ||||||||||
| Single-mode | Multi-Mode | Single-mode | Multi-Mode | ||||||||
| TE00 | TM00 | TE01 | TM01 | TE02 | TM02 | TE00 | TM00 | TE01 | TM01 | TE02 | TM02 |
| 32 | 85 | 188 | 237 | 345 | 393 | 37 | 89 | 207 | 255 | 378 | 424 |
| Expected changes of the angle ∆α(°) as a function of hemoglobin concentration 0–26 g/dL. | |||||||||||
| 0.95 | 1.28 | 0.65 | 0.94 | 0.51 | 0.77 | 0.91 | 1.19 | 0.62 | 0.87 | 0.48 | 0.71 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Struk, P. Design of an Integrated Optics Sensor Structure Based on Diamond Waveguide for Hemoglobin Property Detection. Materials 2019, 12, 175. https://doi.org/10.3390/ma12010175
Struk P. Design of an Integrated Optics Sensor Structure Based on Diamond Waveguide for Hemoglobin Property Detection. Materials. 2019; 12(1):175. https://doi.org/10.3390/ma12010175
Chicago/Turabian StyleStruk, Przemysław. 2019. "Design of an Integrated Optics Sensor Structure Based on Diamond Waveguide for Hemoglobin Property Detection" Materials 12, no. 1: 175. https://doi.org/10.3390/ma12010175
APA StyleStruk, P. (2019). Design of an Integrated Optics Sensor Structure Based on Diamond Waveguide for Hemoglobin Property Detection. Materials, 12(1), 175. https://doi.org/10.3390/ma12010175