Micromechanism of Cold Deformation of Two-Phase Polycrystalline Ti–Al Alloy with Void
Abstract
:1. Introduction
2. Molecular Dynamics Simulation
2.1. Atomic Potential
2.2. Modeling
2.3. Analysis Method
2.4. Model Verification
3. Results and Discussion
3.1. Deformation Mechanism of Two Phase Ti–Al Alloy
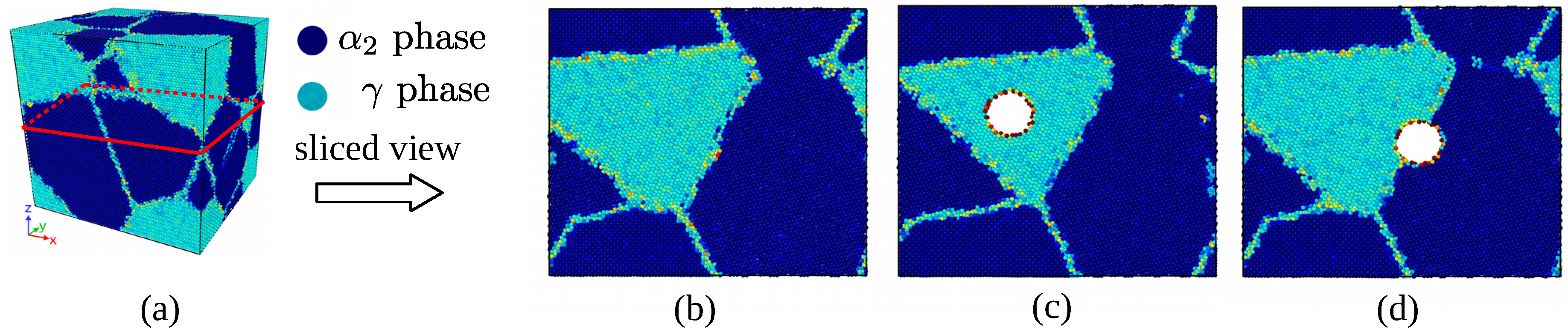
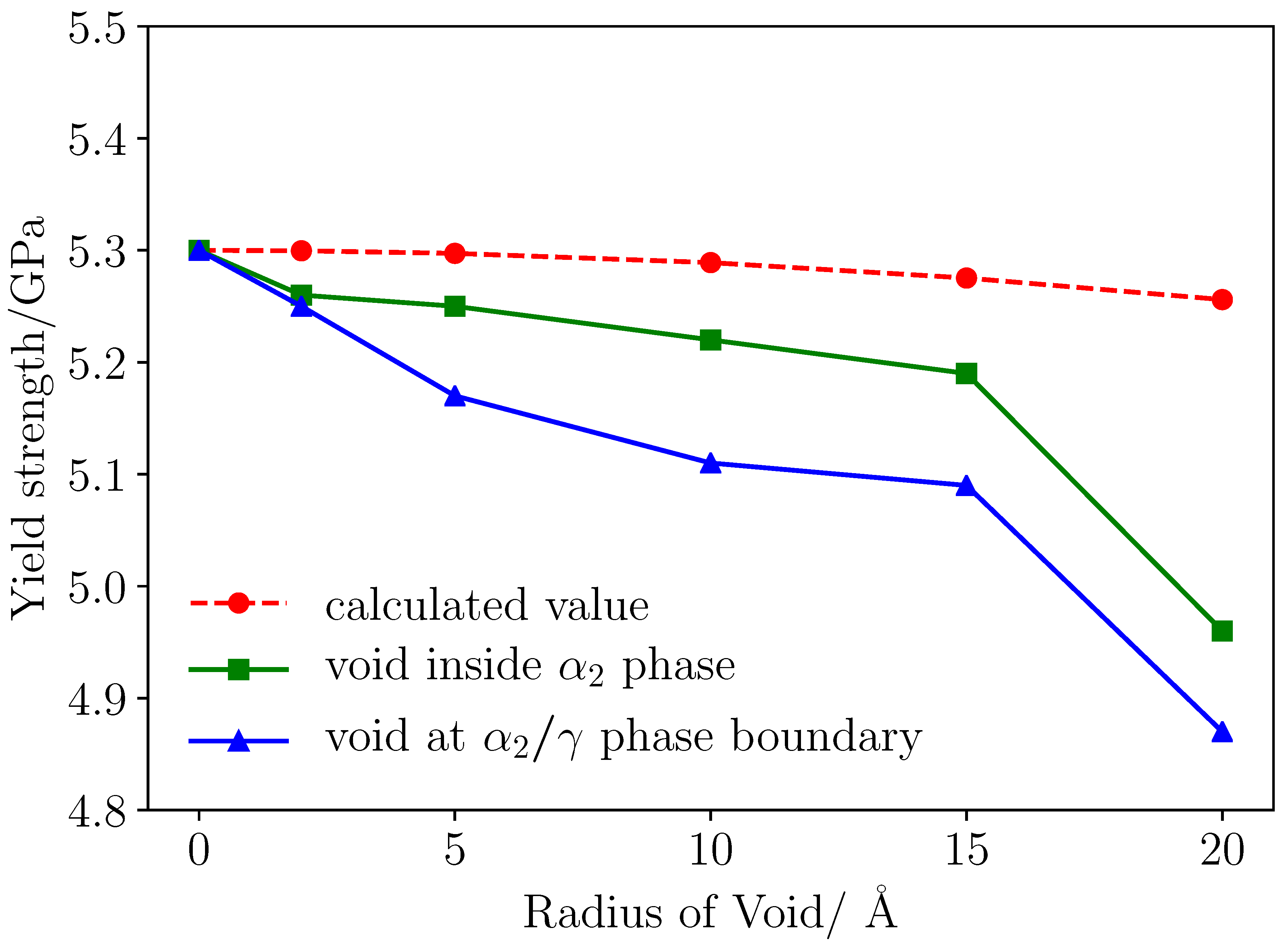
3.2. The Effect of Void on the Strength of Material
3.3. Evolution of Spherical Void
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clemens, H.; Mayer, S. Advanced Intermetallic TiAl Alloys. Mater. Sci. Forum 2016, 879, 113–118. [Google Scholar] [CrossRef]
- Bewlay, B.P.; Nag, S.; Suzuki, A.; Weimer, M.J. TiAl alloys in commercial aircraft engines. Mater. High Temp. 2016, 33, 549–559. [Google Scholar] [CrossRef]
- Martínková, N.; Nová, P.; Sablina, O.V.; Graphodatsky, A.S.; Zima, J. Karyotypic relationships of the Tatra vole (Microtus tatricus). Folia Zool. 2004, 53, 279–284. [Google Scholar] [CrossRef]
- Appel, F.; Clemens, H.; Fischer, F.D. Modeling concepts for intermetallic titanium aluminides. Prog. Mater. Sci. 2016, 81, 55–124. [Google Scholar] [CrossRef]
- Sastry, S.M.L.; Lipsitt, H.A. Plastic deformation of TiAl and Ti3Al. In Proceedings of the 4th International Conference on Titanium, Kyoto, Japan, 19–22 May 1980; pp. 1231–1243. [Google Scholar]
- Farenc, S.; Coujou, A.; Couret, A. An in situ study of twin propagation in TiAl. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 1993, 67, 127–142. [Google Scholar] [CrossRef]
- Appel, F. An electron microscope study of mechanical twinning and fracture in TiAl alloys. Philos. Mag. 2005, 85, 205–231. [Google Scholar] [CrossRef]
- Appel, F.; Wagner, R. Microstructure and deformation of two-phase γ-titanium aluminides. Mater. Sci. Eng. R Rep. 1998, 22, 187–268. [Google Scholar] [CrossRef]
- Tang, F.L.; Cai, H.M.; Bao, H.W.; Xue, H.T.; Lu, W.J.; Zhu, L.; Rui, Z.Y. Molecular dynamics simulations of void growth in γ-TiAl single crystal. Comput. Mater. Sci. 2014, 84, 232–237. [Google Scholar] [CrossRef]
- Kim, Y.W. Effects of microstructure on the deformation and fracture of γ-TiAl alloys. Mater. Sci. Eng. A 1995, 192–193, 519–533. [Google Scholar] [CrossRef]
- Singh, J.B.; Molénat, G.; Sundararaman, M.; Banerjee, S.; Saada, G.; Veyssière, P.; Couret, A. In situ straining investigation of slip transfer across α 2 lamellae at room temperature in a lamellar TiAl alloy. Philos. Mag. Lett. 2006, 86, 47–60. [Google Scholar] [CrossRef]
- Hempel, N.; Bunn, J.R.; Nitschke-Pagel, T.; Payzant, E.A.; Dilger, K. Study on the residual stress relaxation in girth-welded steel pipes under bending load using diffraction methods. Mater. Sci. Eng. A 2017, 688, 289–300. [Google Scholar] [CrossRef]
- Groh, S.; Marin, E.B.; Horstemeyer, M.F.; Zbib, H.M. Multiscale modeling of the plasticity in an aluminum single crystal. Int. J. Plast. 2009, 25, 1456–1473. [Google Scholar] [CrossRef]
- Trout, P.E. Plastic Contaminants: Bad News for the Paper Recycler. Tappi 1972, 55, 956–958. [Google Scholar] [CrossRef]
- Xu, S.Z.; Hao, Z.M.; Su, Y.Q.; Yu, Y.; Wan, Q.; Hu, W.J. An analysis on nanovoid growth in body-centered cubic single crystalline vanadium. Comput. Mater. Sci. 2011, 50, 2411–2421. [Google Scholar] [CrossRef]
- Jing, P.; Yuan, L.; Shivpuri, R.; Xu, C.; Zhang, Y.; Shan, D.; Guo, B. Evolution of spherical nanovoids within copper polycrystals during plastic straining: Atomistic investigation. Int. J. Plast. 2018, 100, 122–141. [Google Scholar] [CrossRef]
- Elkhateeb, M.G.; Shin, Y.C. Molecular dynamics-based cohesive zone representation of Ti6Al4V/TiC composite interface. Mater. Des. 2018, 155, 161–169. [Google Scholar] [CrossRef]
- Xiong, L.; Xu, S.; McDowell, D.L.; Chen, Y. Concurrent atomistic-continuum simulations of dislocation-void interactions in fcc crystals. Int. J. Plast. 2015, 65, 33–42. [Google Scholar] [CrossRef]
- Kiener, D.; Hosemann, P.; Maloy, S.A.; Minor, A.M. In situ nanocompression testing of irradiated copper. Nat. Mater. 2011, 10, 608–613. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Baker, I. The influence of vacancy concentration on the mechanical behavior of Fe-40Al. Intermetallics 1998, 6, 167–175. [Google Scholar] [CrossRef]
- Nazmy, M.; Staubli, M.; Onofrio, G.; Lupinc, V. Surface defect tolerance of a cast TiAl alloy in fatigue. Scr. Mater. 2001, 45, 787–792. [Google Scholar] [CrossRef]
- Brimmo, A.T.; Hassan, M.I.; Shatilla, Y. Transient heat transfer computational model for the stopped aluminium reduction pot—Cooling techniques evaluation. Appl. Therm. Eng. 2014, 73, 114–125. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schitz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef] [Green Version]
- Ko, W.S.; Grabowski, B.; Neugebauer, J. Development and application of a Ni-Ti interatomic potential with high predictive accuracy of the martensitic phase transition. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 92, 134107. [Google Scholar] [CrossRef]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bulatov, V.V. Probing the limits of metal plasticity with molecular dynamics simulations. Nature 2017, 550, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Zhu, Y.; El-Awady, J.A.; Raabe, D. Precipitation hardening effects on extension twinning in magnesium alloys. Int. J. Plast. 2018, 106, 186–202. [Google Scholar] [CrossRef]
- Zope, R.R.; Mishin, Y. Interatomic potentials for atomistic simulations of the Ti–Al system. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 68, 024102. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Samanta, A.; Leach, A.; Gall, K. Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 2008, 100, 025502. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Tang, T.; Kim, S.; Horstemeyer, M.F. Molecular dynamics simulations of void growth and coalescence in single crystal magnesium. Acta Mater. 2010, 58, 4742–4759. [Google Scholar] [CrossRef]
- Chen, J.H.; Cao, R. Chapter 9-Brittle Fracture of TiAl Alloys. In Micromechanism of Cleavage Fracture of Metals; Chen, J.H., Cao, R., Eds.; Butterworth-Heinemann: Boston, MA, USA, 2015. [Google Scholar]
- He, Y.; Schwarz, R.; Migliori, A.; Whang, S. Elastic constants of single crystal γ—TiAl. J. Mater. Res. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
- Tanaka, K.; Okamoto, K.; Inul, H.; Mlnonishl, Y.; Yamaguch, M.; Koiwa, M. Elastic constants and their temperature dependence for the intermetallic compound Ti3Al. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 1996, 73, 1475–1488. [Google Scholar] [CrossRef]
- Stein, D.F.; Low, J.R. Mobility of edge dislocations in silicon-iron crystals. J. Appl. Phys. 1960, 31, 362–369. [Google Scholar] [CrossRef]
- Escaig, B. L’activation thermique des déviations sous faibles contraintes dans les structures h.c. et c.c. Par. Phys. Status Solidi (B) 1968, 28, 463–474. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, L.M.; Wang, S.Q.; Ye, H.Q. First-principles study of shear deformation in TiAl alloys. J. Alloys Compd. 2007, 440, 287–294. [Google Scholar] [CrossRef]
- Rösner, H.; Markmann, J.; Weissmüller, J. Deformation twinning in nanocrystalline Pd. Philos. Mag. Lett. 2004, 84, 321–334. [Google Scholar] [CrossRef]
- Appel, F.; Paul, J.D.; Oehring, M. Deformation Behavior of Two-Phase α2(Ti3Al) + γ(TiAl) Alloys. Gamma Titan. Alum. Alloys 2011, 2, 125–248. [Google Scholar] [CrossRef]
- Zghal, S.; Menand, A.; Couret, A. Pinning points anchoring ordinary and shockley dislocations in TiAl alloys. Acta Mater. 1998, 46, 5899–5905. [Google Scholar] [CrossRef]










| Phase | Space Group | Designation | Parameters |
|---|---|---|---|
| - | a = 0.5765 | ||
| c = 0.46833 | |||
| - | a = 0.3997 | ||
| c = 0.4062 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Stage | I | I | II | II | II | II | III | III | III | III |
| Strain | 0.05 | 0.088 | 0.092 | 0.096 | 0.099 | 0.101 | 0.104 | 0.107 | 0.110 | 0.112 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, R.; Wang, M.; Li, H.; Qi, Y.; Wang, Q.; Rui, Z. Micromechanism of Cold Deformation of Two-Phase Polycrystalline Ti–Al Alloy with Void. Materials 2019, 12, 184. https://doi.org/10.3390/ma12010184
Feng R, Wang M, Li H, Qi Y, Wang Q, Rui Z. Micromechanism of Cold Deformation of Two-Phase Polycrystalline Ti–Al Alloy with Void. Materials. 2019; 12(1):184. https://doi.org/10.3390/ma12010184
Chicago/Turabian StyleFeng, Ruicheng, Maomao Wang, Haiyan Li, Yongnian Qi, Qi Wang, and Zhiyuan Rui. 2019. "Micromechanism of Cold Deformation of Two-Phase Polycrystalline Ti–Al Alloy with Void" Materials 12, no. 1: 184. https://doi.org/10.3390/ma12010184
APA StyleFeng, R., Wang, M., Li, H., Qi, Y., Wang, Q., & Rui, Z. (2019). Micromechanism of Cold Deformation of Two-Phase Polycrystalline Ti–Al Alloy with Void. Materials, 12(1), 184. https://doi.org/10.3390/ma12010184






