Fatigue Life Assessment of the Shell Structure of Purified Terephthalic Acid Filter Press
Abstract
:1. Introduction
2. Stress Fluctuation Measurement
3. Finite Element Analysis
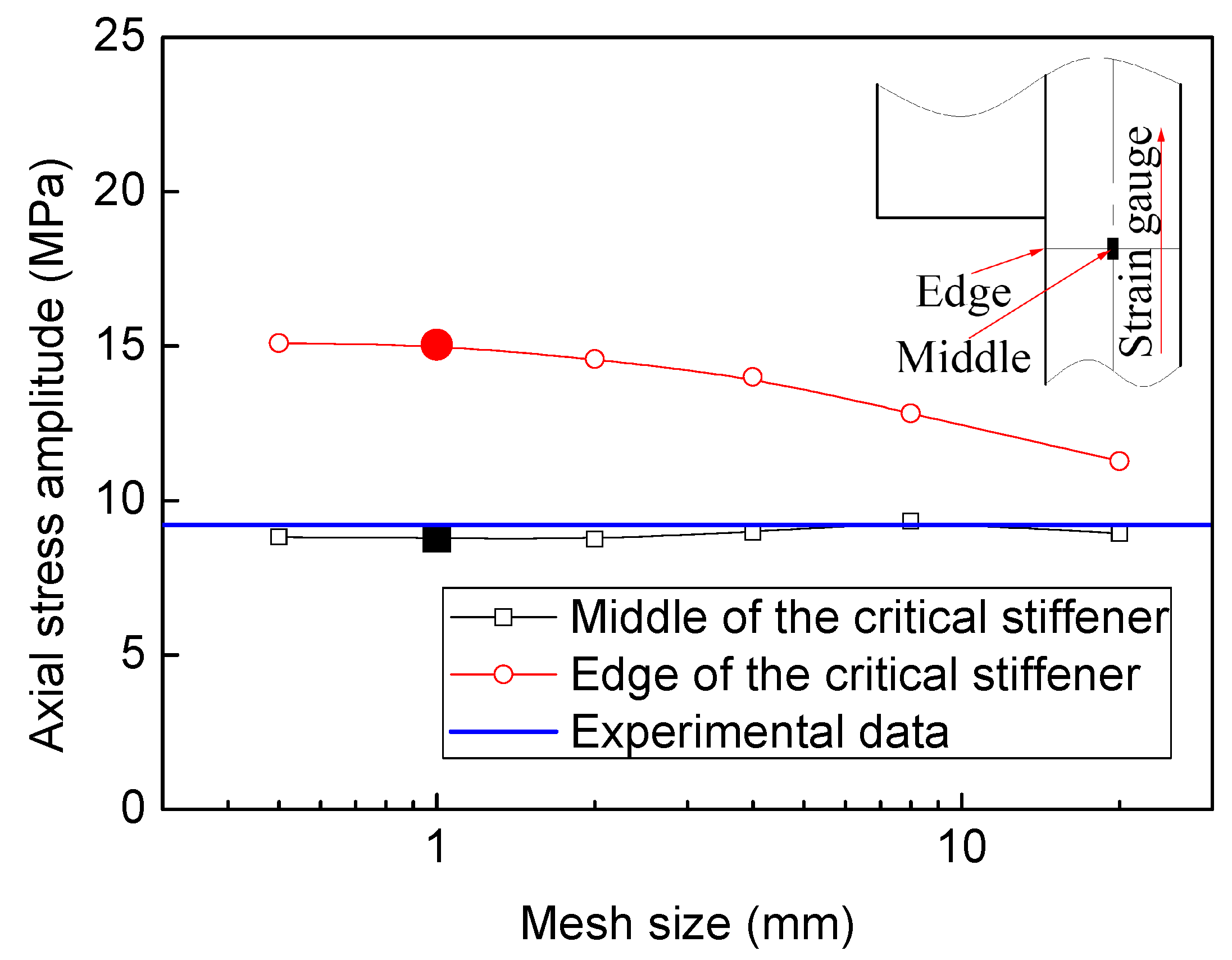
3.1. Finite Element Model
3.2. Thermomechanical Coupled Modeling
3.3. Criterions of Fatigue Life Evaluation
3.3.1. Fatigue Strength Reduction Method of ASME VIII 2
3.3.2. Hot Spot Stress Method of EN 13445-3
4. Results and Discussion
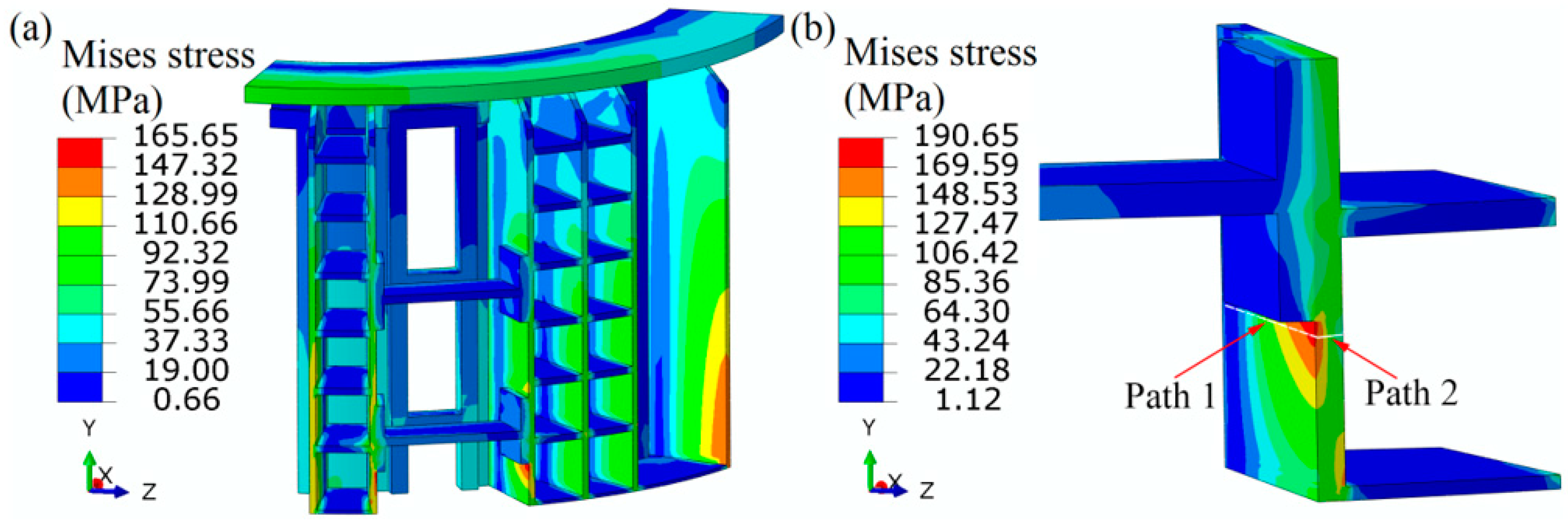
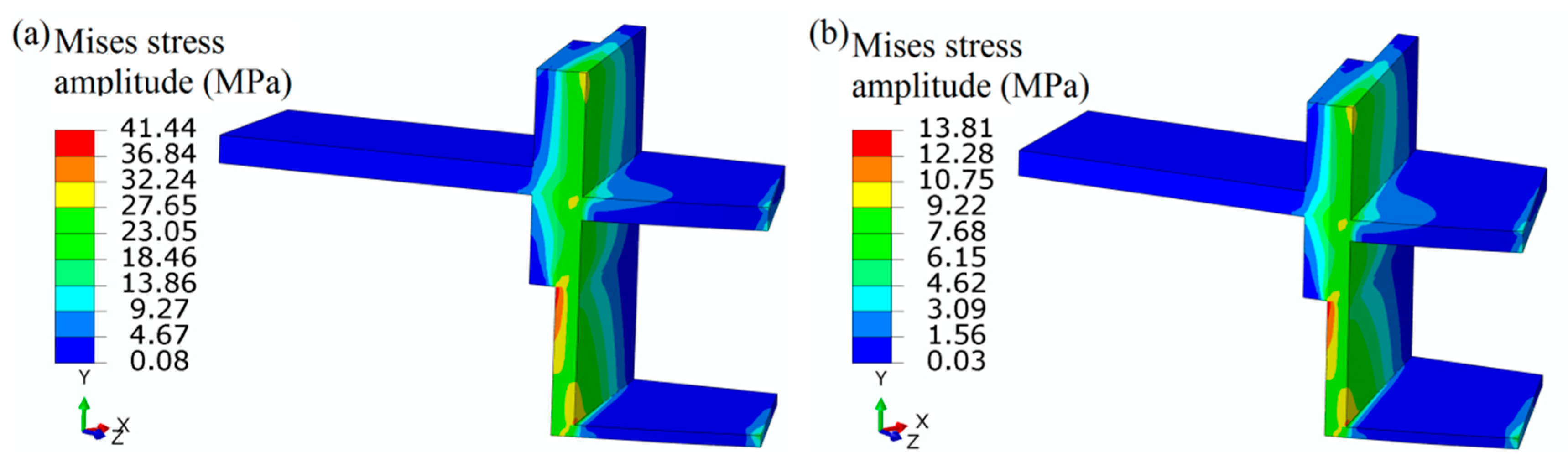
4.1. Thermomechanical Stress Evaluation
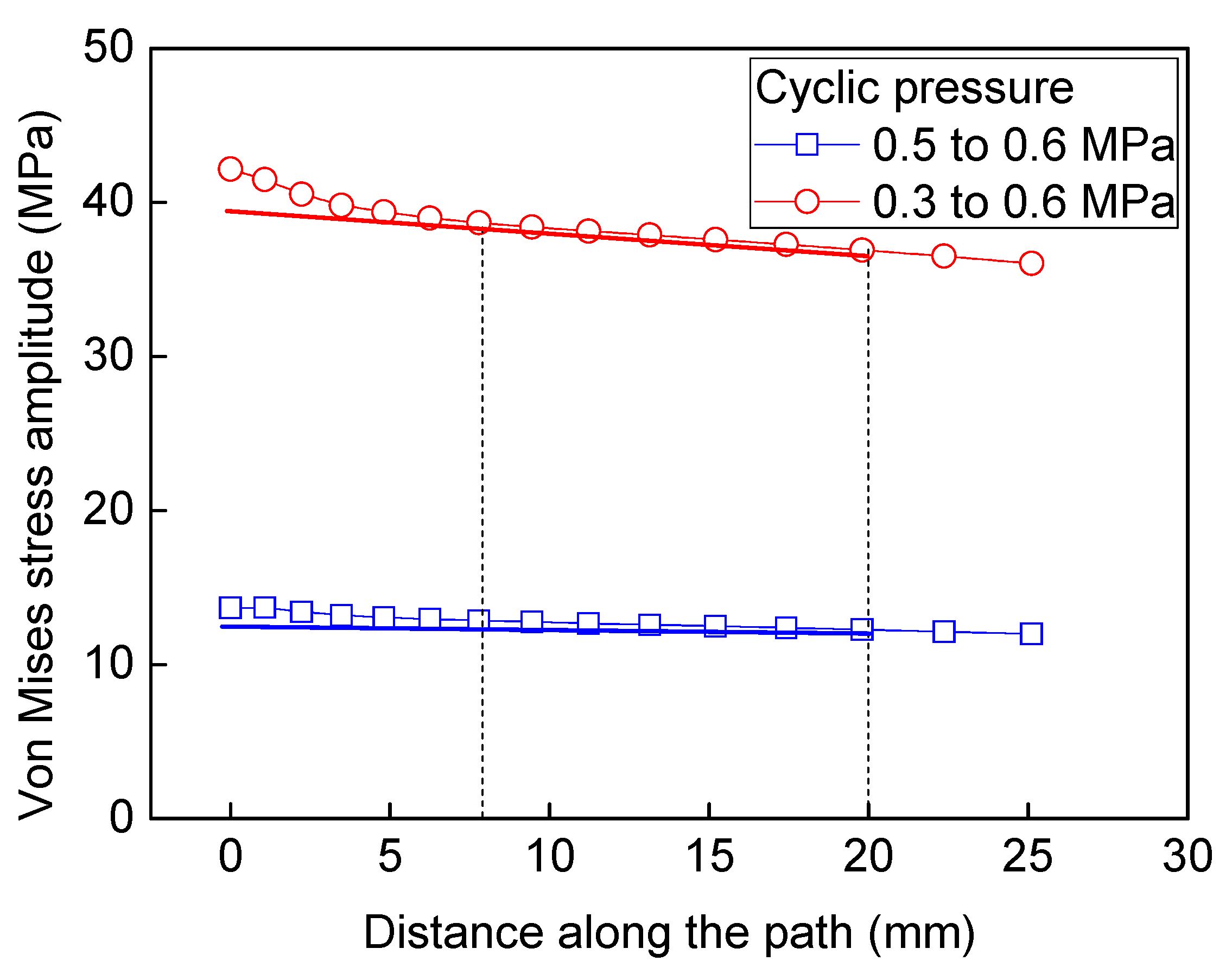
4.2. Fatigue Life Validation and Prediction
4.3. Discussion
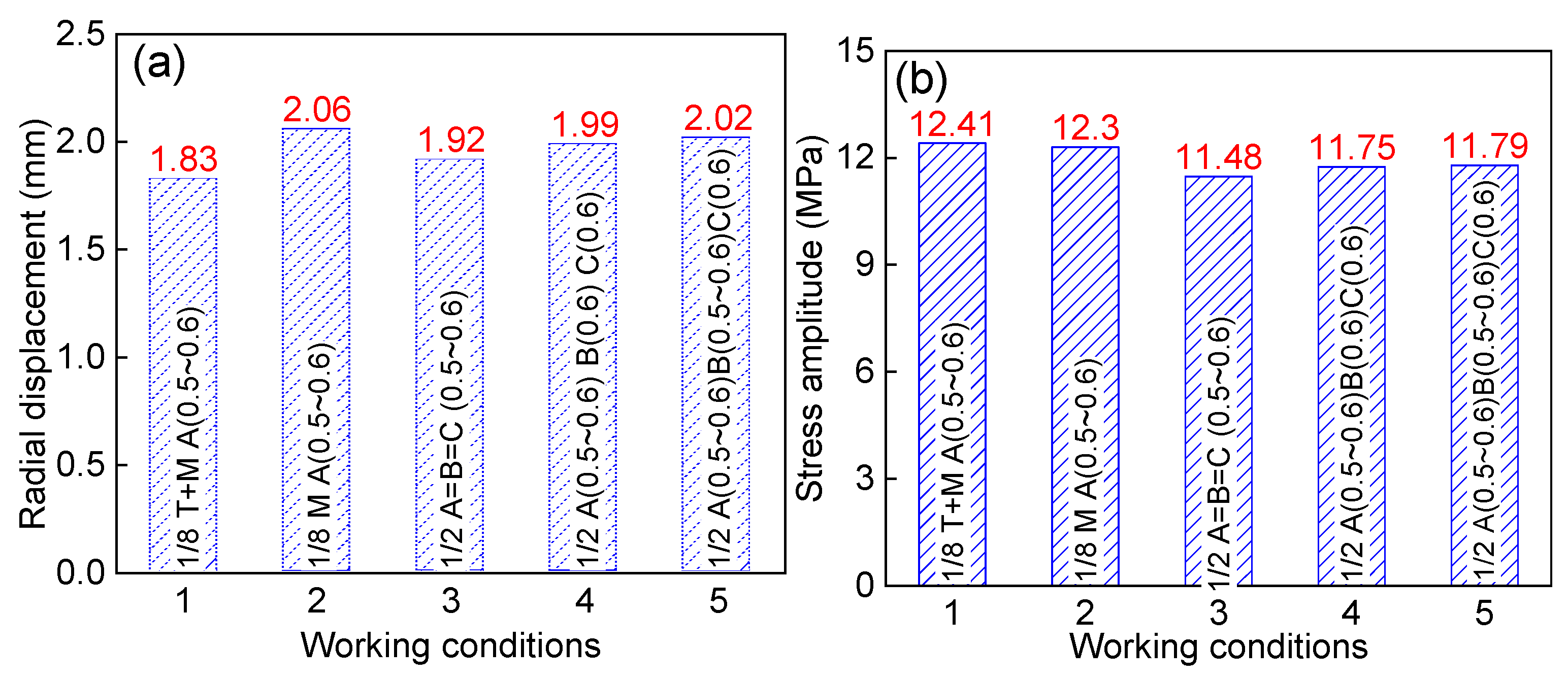
4.3.1. Working Condition on the Deformation and Stress Fluctuation
4.3.2. Comparison of the Fatigue Design Criterions
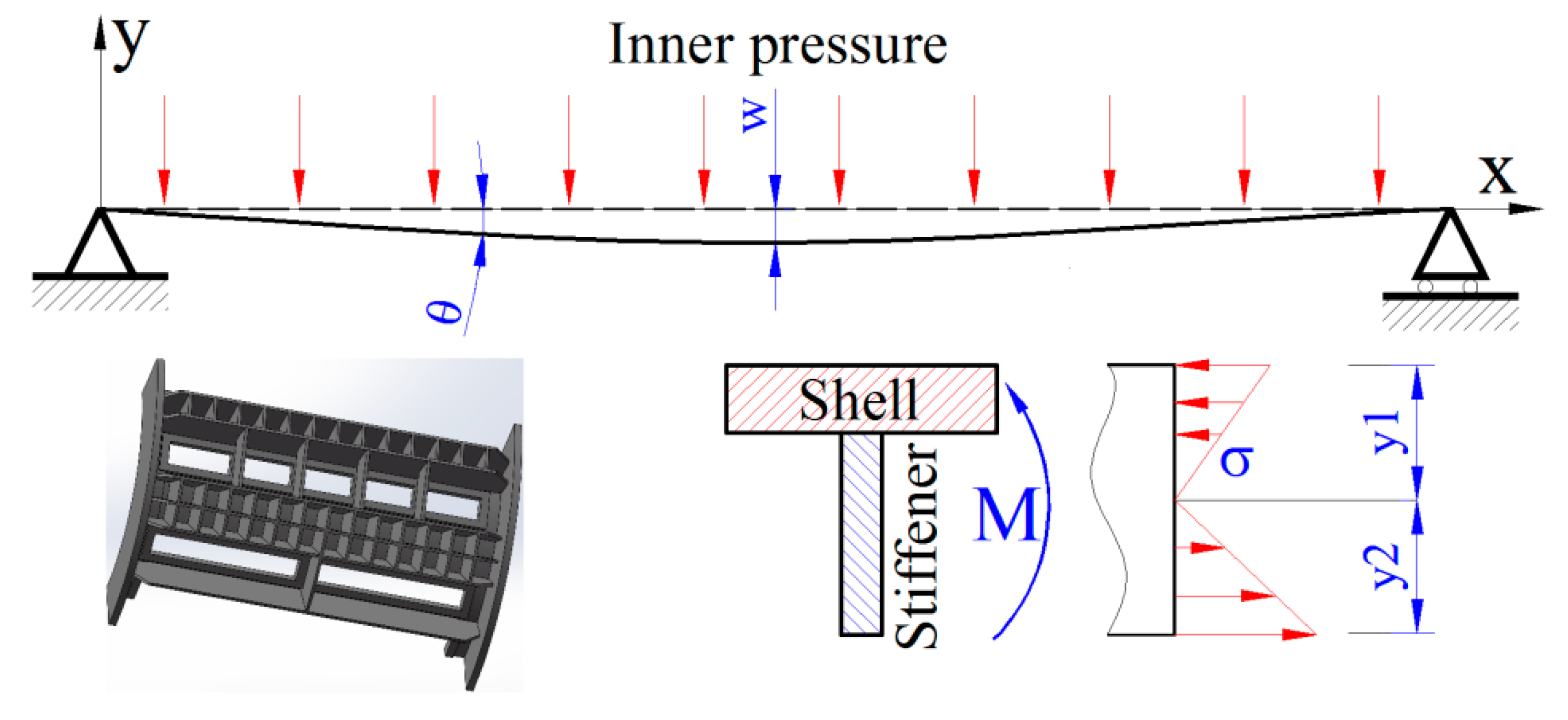
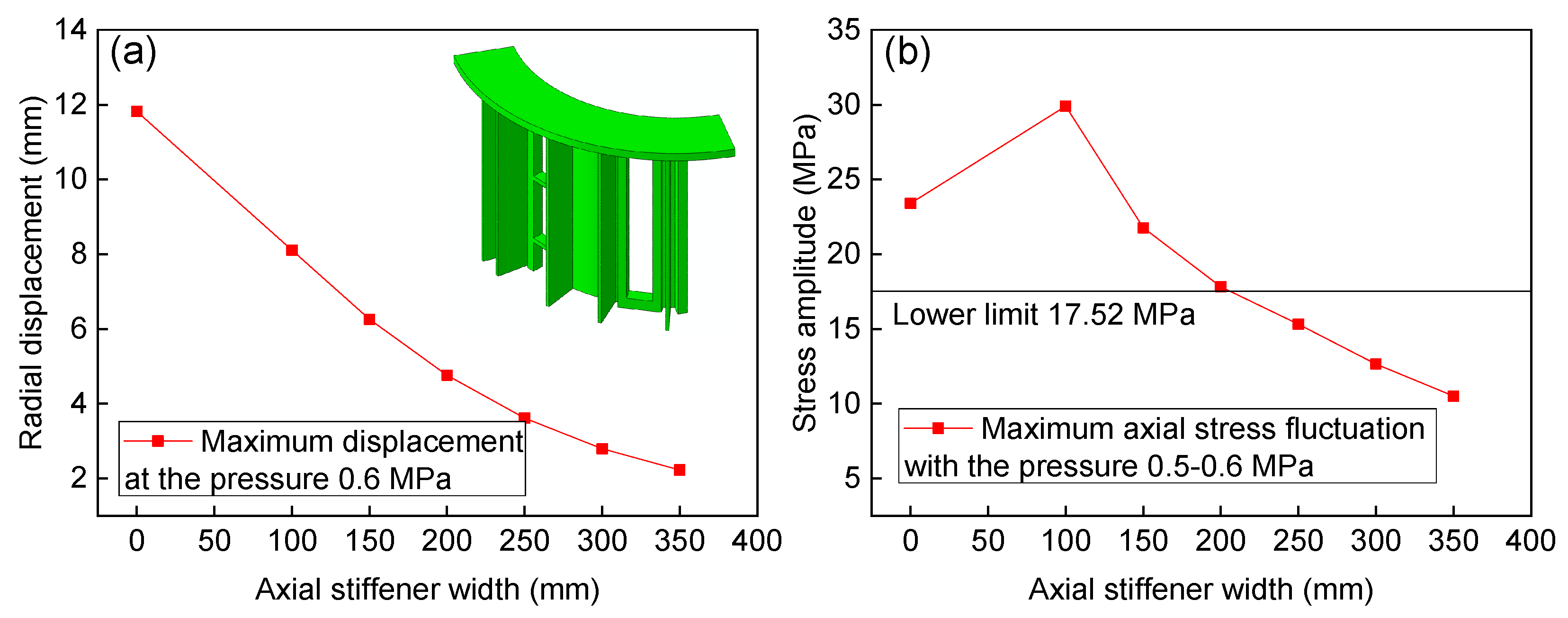
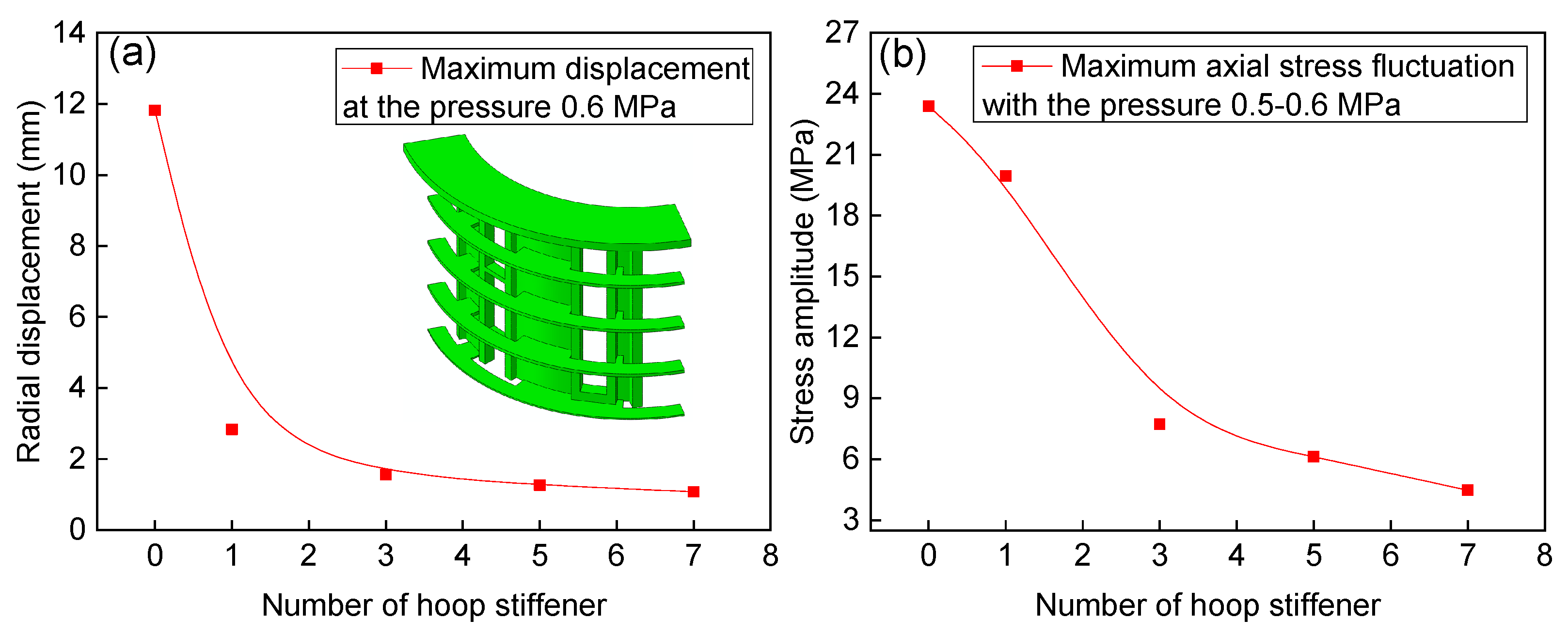
4.3.3. Mechanism of the Structure Deformation and Optimization
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geng, Z.; Yang, X.; Han, Y.; Zhu, Q. Energy optimization and analysis modeling based on extreme learning machine integrated index decomposition analysis: Application to complex chemical processes. Energy 2017, 120, 67–78. [Google Scholar] [CrossRef]
- Gong, H.-F.; Chen, Z.-S.; Zhu, Q.-X.; He, Y.-L. A Monte Carlo and PSO based virtual sample generation method for enhancing the energy prediction and energy optimization on small data problem: An empirical study of petrochemical industries. Appl. Energy 2017, 197, 405–415. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, W.; Sun, Z.; Zhang, M.; Tan, Y.; Zhai, X.; Wang, T.; Shen, T.; Wang, R.; Liang, Y.; et al. Method for Processing Acetic Acid Solvent in Oxidising Unit of PTA Industrial Apparatus. U.S. Patent 9902680, 27 February 2018. [Google Scholar]
- Carpinteri, A.; Boaretto, J.; Fortese, G.; Giordani, F.; Iturrioz, I.; Ronchei, C.; Scorza, D.; Vantadori, S. Fatigue life estimation of fillet-welded tubular T-joints subjected to multiaxial loading. Int. J. Fatigue 2017, 101, 263–270. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, W.; Zhao, X.; Tu, S.-T. Fatigue life of a dissimilar welded joint considering the weld residual stress: Experimental and finite element simulation. Int. J. Fatigue 2018, 109, 182–190. [Google Scholar] [CrossRef]
- Ngoula, D.T.; Beier, H.; Vormwald, M. Fatigue crack growth in cruciform welded joints: Influence of residual stresses and of the weld toe geometry. Int. J. Fatigue 2017, 101, 253–262. [Google Scholar] [CrossRef]
- Sepe, R.; Wiebesiek, J.; Sonsino, C.M. Numerical and experimental validation of residual stresses of laser-welded joints and their influence on the fatigue behavior. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1126–1141. [Google Scholar] [CrossRef]
- Rouse, J.; Zacharzewski, P.; Hyde, C.; Jefferson-Loveday, R.; Morris, A.; Kyaw, S. A case study investigation into the effects of spatially dependent convection coefficients on the fatigue response of a power plant header component. Int. J. Fatigue 2018, 113, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; An, G.; Lee, H. Effect of external load on angular distortion in fillet welding. Mater. Des. 2012, 42, 403–410. [Google Scholar] [CrossRef]
- Gao, F.; Li, P.; Jiang, P.; Liao, Z. The effect of constraint conditions on microstructure and properties of titanium alloy electron beam welding. Mater. Sci. Eng. A 2018, 721, 117–124. [Google Scholar] [CrossRef]
- Schork, B.; Kucharczyk, P.; Madia, M.; Zerbst, U.; Hensel, J.; Bernhard, J.; Tchuindjang, D.; Kaffenberger, M.; Oechsner, M. The effect of the local and global weld geometry as well as material defects on crack initiation and fatigue strength. Eng. Fract. Mech. 2018, 198, 103–122. [Google Scholar] [CrossRef]
- Rao, H.M.; Kang, J.; Shi, L.; Sigler, D.R.; Carlson, B.E. Effect of specimen configuration on fatigue properties of dissimilar aluminum to steel resistance spot welds. Int. J. Fatigue 2018, 116, 13–21. [Google Scholar] [CrossRef]
- Sant’Anna, H.M.; Leal, M.F. A practical procedure to assess critical defects in pressure vessels subjected to fatigue loads. Eng. Fract. Mech. 2011, 78, 1669–1683. [Google Scholar] [CrossRef]
- Alegre, J.M.; Bravo, P.; Cuesta, I. Fatigue design of wire-wound pressure vessels using ASME-API 579 procedure. Eng. Fail. Anal. 2010, 17, 748–759. [Google Scholar] [CrossRef]
- Joshi, S.; Price, J. A comparative study on application of design codes for prediction of fatigue life of a mining dragline cluster. Eng. Fail. Anal. 2009, 16, 1562–1569. [Google Scholar] [CrossRef]
- Yapıcı, A.; Saracoglu, G. Fatigue analysis of bolted flange joints of a rotary dryer. Eng. Fail. Anal. 2016, 63, 182–190. [Google Scholar] [CrossRef]
- Boiler, A.; Code, P.V. Section VIII, Division 2, Rules for Construction of Pressure Vessels; ASME: New York, NY, USA, 2013. [Google Scholar]
- British Standards Institution. EN, 13445–3: 2009, Unfired Pressure Vessels, Part 3: Design; British Standards Institution: London, UK, 2009. [Google Scholar]
- Kalnins, A.; Bergsten, V.; Rana, M.D. Fatigue Assessment of a Weld Joint of a Pressure Vessel. In Proceedings of the Volume 7: Operations, Applications, and Components; ASME International: New York, NY, USA, 2005; Volume 7, pp. 263–270. [Google Scholar]
- Kim, I.-T.; Yamada, K. Fatigue life evaluation of welded joints under combined normal and shear stress cycles. Int. J. Fatigue 2005, 27, 695–701. [Google Scholar] [CrossRef]
- Mei, J.; Dong, P. An equivalent stress parameter for multi-axial fatigue evaluation of welded components including non-proportional loading effects. Int. J. Fatigue 2017, 101, 297–311. [Google Scholar] [CrossRef]
- Zuo, J.; Wang, Z.; Han, E. Effect of microstructure on ultra-high cycle fatigue behavior of Ti–6Al–4V. Mater. Sci. Eng. A 2008, 473, 147–152. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, W.; Wang, P.; Liu, Y.; Li, J. Fatigue behavior and mechanism of FV520B-I welding seams in a very high cycle regime. Int. J. Fatigue 2016, 87, 22–37. [Google Scholar] [CrossRef]
- Deng, C.; Gao, R.; Gong, B.; Yin, T.; Liu, Y. Correlation between micro-mechanical property and very high cycle fatigue (VHCF) crack initiation in friction stir welds of 7050 aluminum alloy. Int. J. Fatigue 2017, 104, 283–292. [Google Scholar] [CrossRef]
- He, C.; Liu, Y.; Dong, J.; Wang, Q.; Wagner, D.; Bathias, C. Through thickness property variations in friction stir welded AA6061 joint fatigued in very high cycle fatigue regime. Int. J. Fatigue 2016, 82, 379–386. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H. Fatigue Life in Very High Cycle Range of 304 Stainless Steel. Mater. Mech. Eng. 2008, 1, 22. [Google Scholar]
- Effertz, P.; Infante, V.; Quintino, L.; Suhuddin, U.; Hanke, S.; Dos Santos, J. Fatigue life assessment of friction spot welded 7050-T76 aluminium alloy using Weibull distribution. Int. J. Fatigue 2016, 87, 381–390. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, H. Weibull modeling of the probabilistic S–N curves for rolling contact fatigue. Int. J. Fatigue 2014, 66, 47–54. [Google Scholar] [CrossRef]
- ISO 12107:2012. Metallic Materials-Fatigue Testing-Statistical Planning and Analysis of Data; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- Wan, Y.; Jiang, W.; Li, J.; Sun, G.; Kim, D.-K.; Woo, W.; Tu, S. Weld residual stresses in a thick plate considering back chipping: Neutron diffraction, contour method and finite element simulation study. Mater. Sci. Eng. A 2017, 699, 62–70. [Google Scholar] [CrossRef]
- Ulger, T.; Okeil, A.M. Analysis of thin-walled steel beams retrofitted by bonding GFRP stiffeners: Numerical model and investigation of design parameters. Eng. Struct. 2017, 153, 166–179. [Google Scholar] [CrossRef]
- Lee, K.C.; Kang, J.; Yoo, C.H. Stiffness requirements for transverse stiffeners of rectangular CFT compression panels. Int. J. Steel Struct. 2013, 13, 265–274. [Google Scholar] [CrossRef]
- Ghavami, P. Mechanics of Materials: An Introduction to Engineering Technology; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
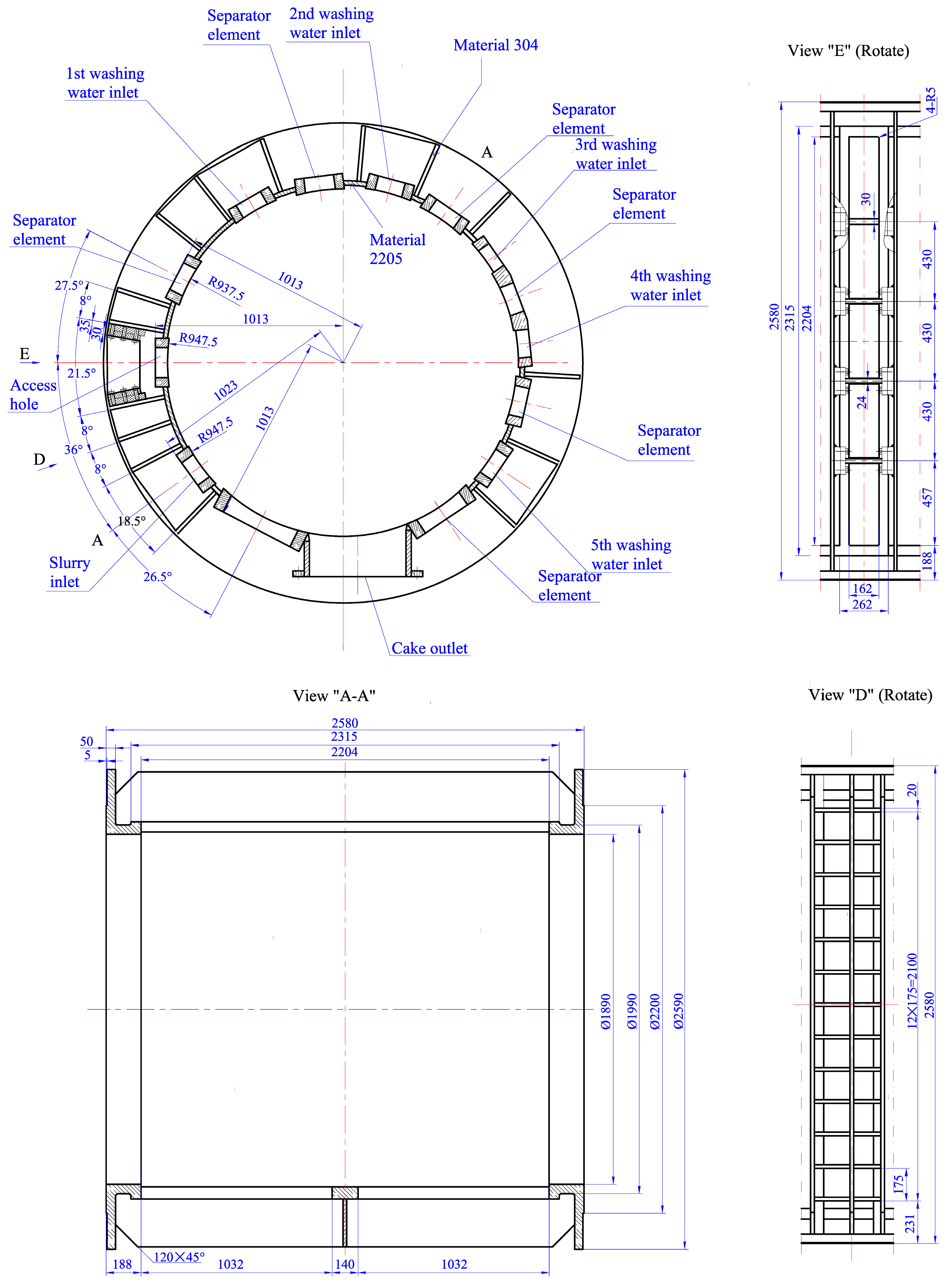


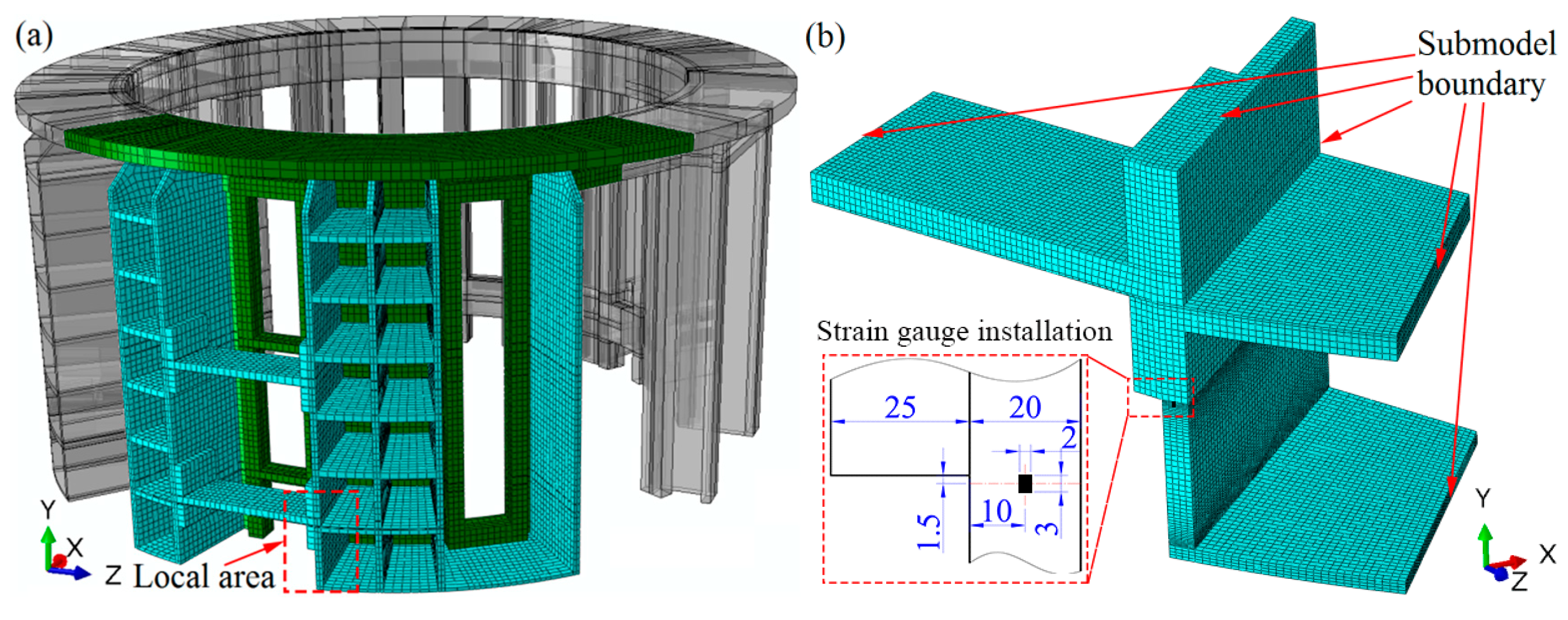
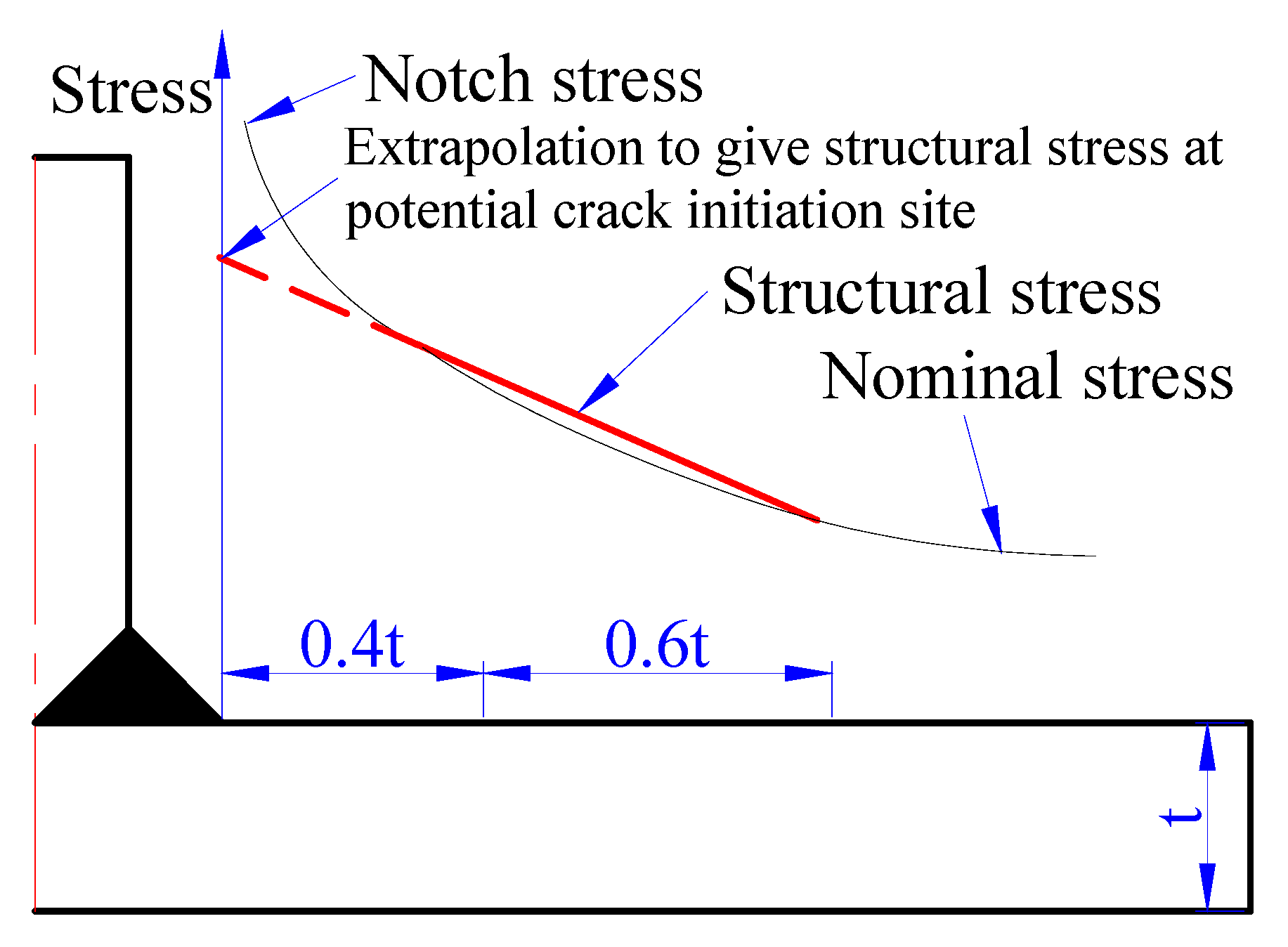
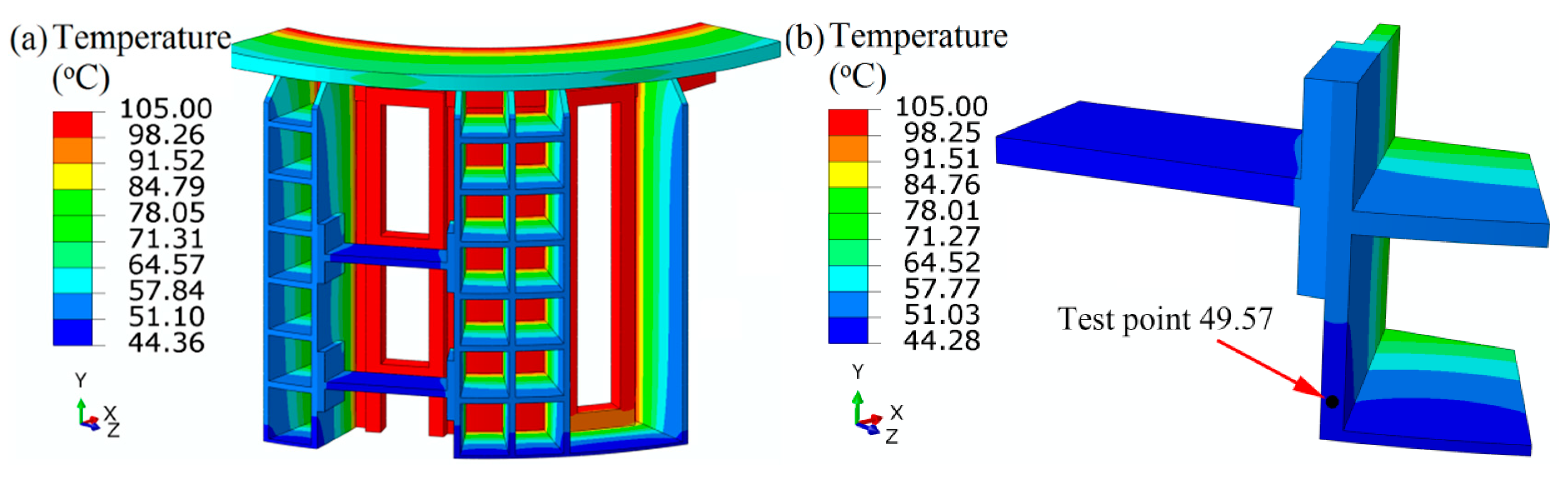


| Material | SAF 2205 | SS 304 | ||
|---|---|---|---|---|
| Temperature (°C) | 20 | 100 | 20 | 100 |
| Elastic Modulus (GPa) | 200 | 194 | 199 | 192 |
| Poisson Ratio | 0.30 | 0.30 | 0.28 | 0.28 |
| Density (kg/m3) | 7800 | 7800 | 8010 | 7930 |
| Thermal Conductivity (W/m/°C) | 15.00 | 15.00 | 15.26 | 16.30 |
| Specific Heat (J/kg/°C) | 500 | 500 | 504 | 523 |
| Coefficient of Thermal Expansion (×10−6) | 13.00 | 13.00 | 16.00 | 16.50 |
| Path | Pm (MPa) | 1.5 Sm (MPa) | Pm+ Pb (MPa) | 3 Sm (MPa) |
|---|---|---|---|---|
| 1 | 118.63 | 210 | 221.09 | 420 |
| 2 | 118.50 | 210 | 178.13 | 420 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; Zhang, W.; Jiang, W.; Wang, J.; Zhao, X.; Zhai, X. Fatigue Life Assessment of the Shell Structure of Purified Terephthalic Acid Filter Press. Materials 2020, 13, 3276. https://doi.org/10.3390/ma13153276
Song M, Zhang W, Jiang W, Wang J, Zhao X, Zhai X. Fatigue Life Assessment of the Shell Structure of Purified Terephthalic Acid Filter Press. Materials. 2020; 13(15):3276. https://doi.org/10.3390/ma13153276
Chicago/Turabian StyleSong, Ming, Weiya Zhang, Wenchun Jiang, Jinguang Wang, Xu Zhao, and Xiangnan Zhai. 2020. "Fatigue Life Assessment of the Shell Structure of Purified Terephthalic Acid Filter Press" Materials 13, no. 15: 3276. https://doi.org/10.3390/ma13153276
APA StyleSong, M., Zhang, W., Jiang, W., Wang, J., Zhao, X., & Zhai, X. (2020). Fatigue Life Assessment of the Shell Structure of Purified Terephthalic Acid Filter Press. Materials, 13(15), 3276. https://doi.org/10.3390/ma13153276





