Using Satellite Imagery to Improve Local Pollution Models for High-Voltage Transmission Lines and Insulators
Abstract
:1. Introduction
2. Potential Model Improvement Directions
- A significant increase in the number (spatial density) of stations for field measurements of pollution deposits, along with their long-term operation so as to obtain longer time series for a more detailed analysis;
- A change in approach: to shift from modeling the upper bound estimates of pollution deposits to modeling their individual six-week field-measured values, from which their upper bound estimates could be subsequently calculated by appropriate statistical methods;
- To add new types of relevant input attributes that are typically ignored by domain experts in the fields of electric power and meteorology, but which could still capture significant events affecting local pollution levels in the monitored locations;
- To develop new statistical models of true probability distributions underlying the input and output (target) variables. Analysis of these distributions, their deviations from the expected distribution, and their detailed examination could help in identifying useful properties for their successful modeling and perhaps also reveal the reasons why our previous models failed to achieve the desired accuracy.
2.1. Increasing the Number of Field Measurements
2.2. Modeling Field-Measured Values of Pollution Deposits Rather Than Their Upper Bounds
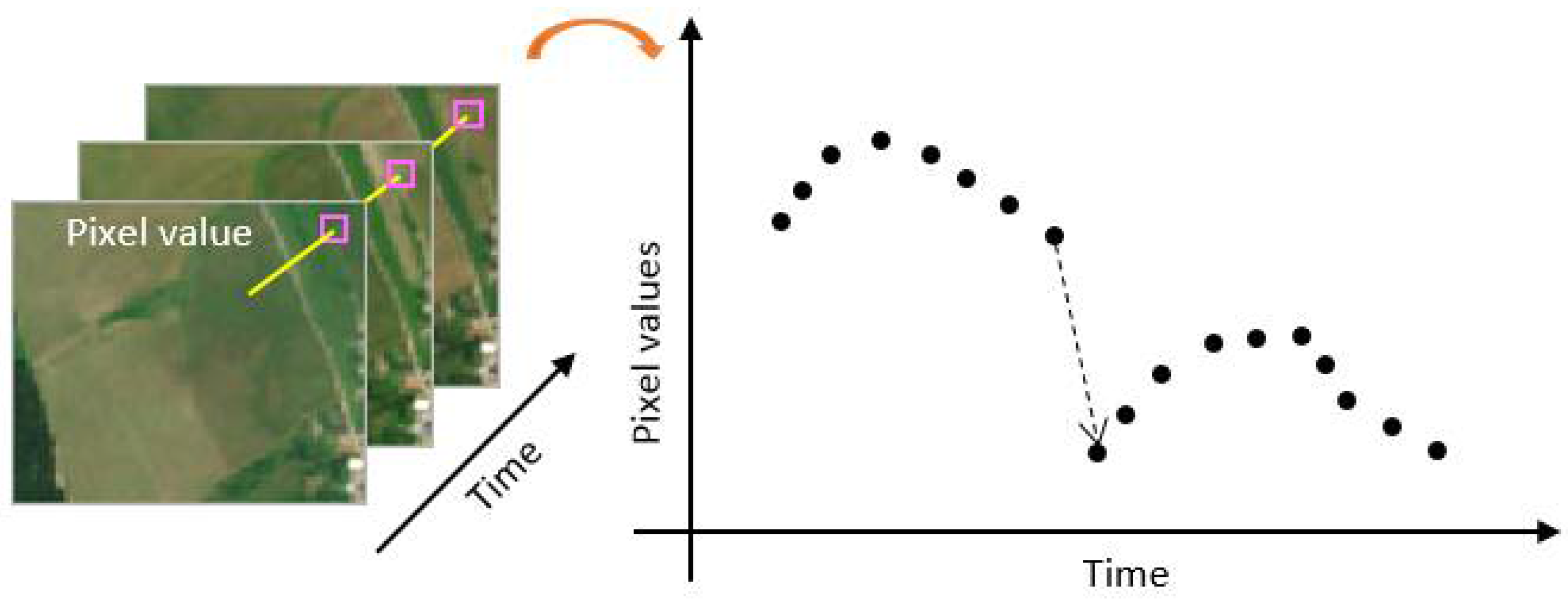
2.3. Define and Collect New Relevant Input Attributes
2.4. Determine True Probability Distributions of Our Input and Output (Target) Variables
3. Available Data
- S—total pollution deposit
- Sr—soluble fraction of pollution deposit
- g02—electrical conductivity of soluble fraction
- PM2.5—yearly average of concentrations of dust particles with a diameter less than 2.5 μm;
- PM10—yearly average of concentrations of dust particles with a diameter less than 10 μm;
- O3—yearly average of ozone concentrations;
- NO2—yearly average of nitrogen dioxide concentrations;
- SO2—yearly average of sulfur dioxide concentrations.
- An insufficient number of data records (i.e., insufficiently representative data set), which does not allow for generalizing the relationship between the inputs and the outputs;
- Missing input variables with dominant effect on target attributes, which makes the behavior of target variables appear to be random;
- Unknown confidence intervals for input and output attributes that reduced the accuracy of the used models;
- An insufficient spatial density of the measured input and output values;
- An inherent difficulty of learning to reliably estimate upper bounds of random variables.
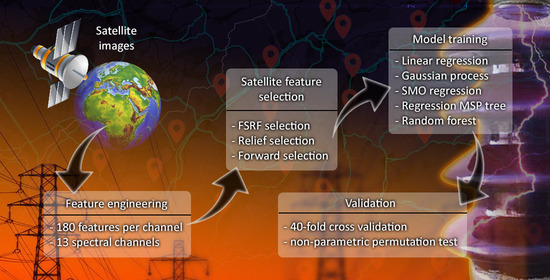
4. Brief Outline of Our Approach
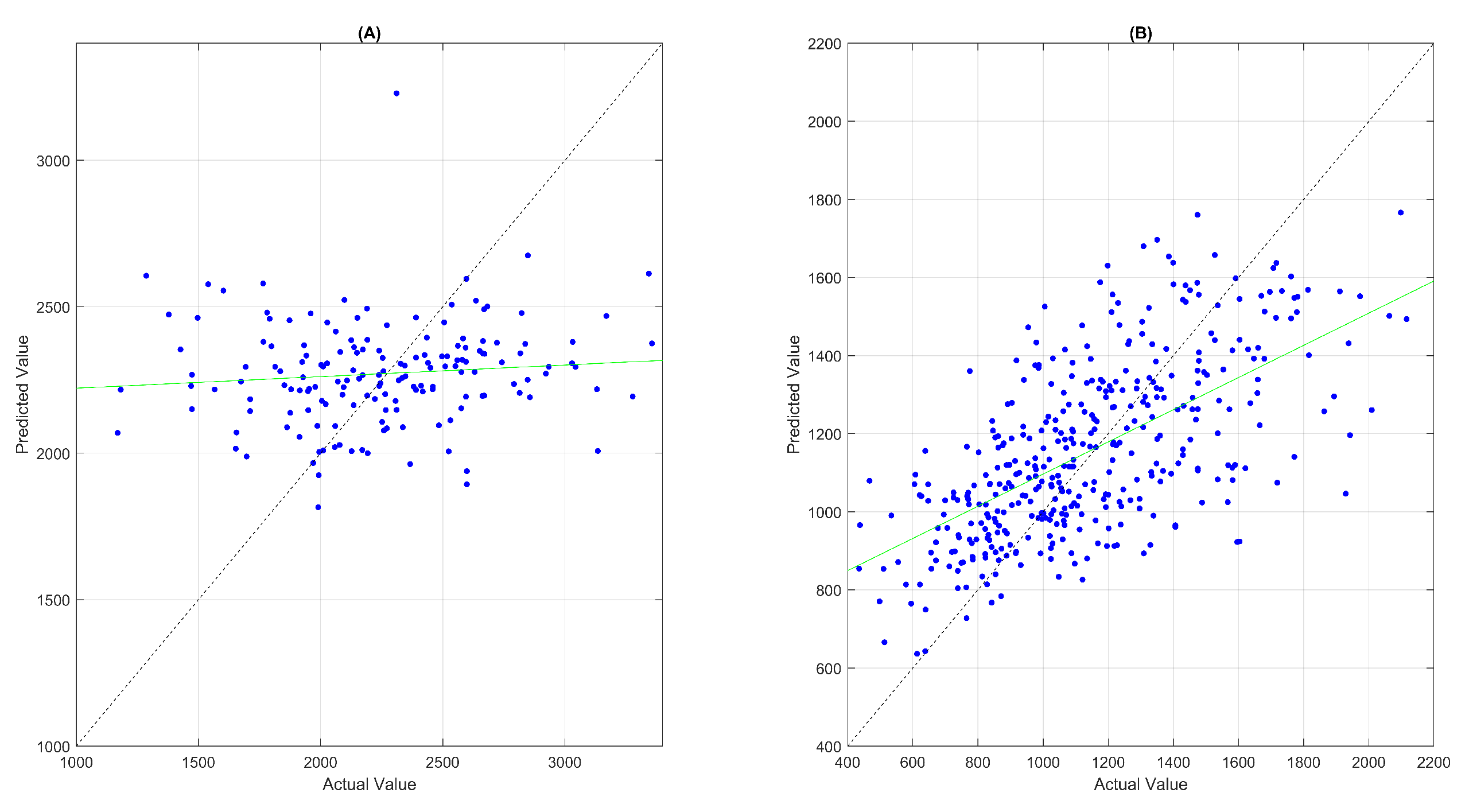
5. Selection of Attributes, Modeling, and Results
6. Discussion
Statistical Tests
- Test statistic: absolute difference of mean values (abs (mean (XA) − mean (XB)));
- Number of permutations in the statistical test = 1,000,000;
- Significance level alpha = 0.05;
- Null hypothesis: XA and XB have the same mean value;
- Alternative hypothesis: XA and XB do not have the same mean value.
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Outline of Slovak Technical Standard STN 33 0405 (Selection of Outdoor Insulators According to the Level of Environmental Pollution)
References
- Zhang, Z.; Qiao, X.; Zhang, Y.; Tian, L.; Zhang, D.; Jiang, X. AC flashover performance of different shed configurations of composite insulators under fanshaped non-uniform pollution. High Volt. 2018, 3, 199–206. [Google Scholar] [CrossRef]
- Savadkoohi, E.M.; Mirzaie, M.; Seyyedbarzegar, S.; Mohammadi, M.; Khodsuz, M.; Pashakolae, M.G.; Ghadikolaei, M.B. Experimental investigation on composite insulators AC flashover performance with fanshaped non-uniform pollution under electro-thermal stress. Int. J. Electron. Power Energy Syst. 2020, 121, 106142. [Google Scholar] [CrossRef]
- Mahdjoubi, A.; Zegnini, B.; Belkheiri, M.; Seghier, T. Fixed least squares support vector machines for flashover modelling of outdoor insulators. Electr. Power Syst. Res. 2019, 173, 29–37. [Google Scholar] [CrossRef]
- Palangar, M.F.; Mirzaie, M.; Mahmoudi, A. Improved flashover mathematical model of polluted insulators: A dynamic analysis of the electric arc parameters. Electr. Power Syst. Res. 2020, 179, 106083. [Google Scholar] [CrossRef]
- Velásquez, R. Insulation failure caused by special pollution around industrial environments. Eng. Fail. Anal. 2019, 102, 123–135. [Google Scholar] [CrossRef]
- Ferreira, T.V.; Germano, A.D.; da Costa, E.G. Ultrasound and artificial intelligence applied to the pollution estimation in insulations. IEEE Trans. Power Deliv. 2012, 27, 583–589. [Google Scholar] [CrossRef]
- Maraaba, L.; Alhamouz, Z.; Alduwaish, H. A neural network-based estimation of the level of contamination on high-voltage porcelain and glass insulators. Electr. Eng. 2018, 100, 1545–1554. [Google Scholar] [CrossRef]
- Wang, X.; Lu, S.; Wang, T.; Qin, X.; Wang, X.; Jia, Z. Analysis of Pollution in High Voltage Insulators via Laser-Induced Breakdown Spectroscopy. Molecules 2020, 25, 822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, L.; Ai, J.; Tian, Z.; Zhang, Y. Detection of polluted insulators using the information fusion of multispectral images. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3530–3538. [Google Scholar] [CrossRef]
- He, Z.; Gao, F.; Tu, Z.; Zhang, Y.; Chen, H. Analysis of natural contamination components and sources of insulators on ±800 kV DC lines. Electr. Power Syst. Res. 2019, 167, 192–198. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Z. Dynamic Pollution Prediction Model of Insulators Based on Atmospheric Environmental Parameters. Energies 2020, 13, 3066. [Google Scholar] [CrossRef]
- Qiao, X.; Zhang, Z.; Jiang, X.; He, Y.; Li, X. Application of grey theory in pollution prediction on insulator surface in power systems. Eng. Fail. Anal. 2019, 106, 104153. [Google Scholar] [CrossRef]
- Ferm, M.; Watt, J.; O’Hanlon, S.; De Santis, F.; Varotsos, C. Deposition measurement of particulate matter in connection with corrosion studies. Anal. Bioanal. Chem. 2006, 384, 1320–1330. [Google Scholar] [CrossRef] [PubMed]
- Slovak Hydrometeorological Institute. Available online: http://www.shmu.sk/en/?page=1 (accessed on 26 February 2022).
- Krammer, P.; Kvassay, M.; Forgac, R.; Ockay, M.; Skovajsova, L.; Hluchy, L.; Skurcak, L.; Pavlov, L. Regression Analysis and Modeling of Local Environment Pollution Levels for Electric Power Industry. CaI J. 2022. submitted. Available online: http://ssrn.com/abstract=4059473 (accessed on 16 March 2022).
- NEIS: Slovak National Emission Information System. Available online: http://www.air.sk/en/index.php (accessed on 26 February 2022).
- A ‘Toast’ to Copernicus Sentinel-2B as It Delivers Its First Images. Available online: https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-2/A_toast_to_Copernicus_Sentinel-2B_as_it_delivers_its_first_images (accessed on 16 March 2022).
- Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/COPERNICUS_S2_SR?hl=en#bands (accessed on 26 February 2022).
- Sentinelhub Playground. Available online: https://apps.sentinel-hub.com/sentinel-playground (accessed on 26 February 2022).
- Urbanowicz, R.J.; Meeker, M.; La Cava, W.; Olson, R.S.; Moore, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef] [PubMed]
- Feature Ranking for Regression Using F-Test. Available online: https://se.mathworks.com/help/stats/fsrftest.html (accessed on 26 February 2022).
- Gutlein, M.; Frank, E.; Hall, M.; Karwath, A. Large-scale attribute selection using wrappers. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 332–339. [Google Scholar]


| Name | Scale | Pixel Size | Wavelength | Description |
|---|---|---|---|---|
| AOT | 0.001 | 10 m | Aerosol optical thickness | |
| B1 | 0.0001 | 10 m | 443.9 nm | Aerosols |
| B2 | 0.0001 | 10 m | 496.6 nm | Blue |
| B3 | 0.0001 | 10 m | 560.0 nm | Green |
| B4 | 0.0001 | 10 m | 664.5 nm | Red |
| B6 | 0.0001 | 20 m | 740.2 nm | Red Edge 2 |
| B8 | 0.0001 | 10 m | 835.1 nm | NIR |
| L1 B10 cir | 0.0010 | 60 m | 1373.5 nm | Cirrus |
| B11 | 0.0001 | 20 m | 1613.7 nm | SWIR 1 |
| NDVI (normalized difference vegetation index) | 0.0001 | 10 m | NDVI = (B8 − B4)/(B8 + B4) | |
| NDWI (normalized difference water index) | 0.0001 | 10 m | NDWI = (B3 − B8)/(B3 + B8) | |
| NDSI (normalized difference soil index) | 0.0001 | 20 m | NDSI = (B3 − B11)/(B3 + B11) | |
| Moisture index | 0.0001 | 20 m | moisture index = (B8 − B11)/(B8 + B11) |
| Linear Model | Gaussian Process | SMO Regression | M5P Tree | Random Forest | |
|---|---|---|---|---|---|
| Models using attributes SHMU, without Day of Year and without Satellites | |||||
| Correlation coefficient | 0.2195 | 0.2289 | 0.2377 | 0.1921 | 0.2243 |
| Relative absolute error | 0.960381 | 0.958122 | 0.838752 | 0.963788 | 0.996284 |
| Root relative sq. error | 0.975826 | 0.971225 | 1.013767 | 0.983825 | 1.007389 |
| Models using attributes SHMU and Day of Year, without Satellites | |||||
| Correlation coefficient | 0.3044 | 0.3228 | 0.3221 | 0.3655 | 0.3810 |
| Relative absolute error | 0.953682 | 0.931039 | 0.81304 | 0.873916 | 0.867675 |
| Root relative sq. error | 0.952256 | 0.944247 | 0.990007 | 0.933188 | 0.960127 |
| Models using attributes SHMU, Satellites (FSRF-TEST 20 attr), without Day of Year | |||||
| Correlation coefficient | 0.3962 | 0.3962 | 0.3936 | 0.4011 | 0.5015 |
| Relative absolute error | 0.929776 | 0.91984 | 0.776143 | 0.913888 | 0.834525 |
| Root relative sq. error | 0.918874 | 0.916169 | 0.971942 | 0.928474 | 0.863463 |
| Model using attributes SHMU, Satellites (Relief 20 attr), without Day of Year | |||||
| Correlation coefficient | 0.2934 | 0.3322 | 0.2697 | 0.3291 | 0.3574 |
| Relative absolute error | 0.998795 | 0.958923 | 0.827651 | 0.952494 | 0.930419 |
| Root relative sq. error | 0.969389 | 0.945013 | 1.009543 | 0.972802 | 0.936803 |
| Models using attributes SHMU, Satellites (Forward selection 20 attr), without Day of Year | |||||
| Correlation coefficient | 0.3754 | 0.3691 | 0.2771 | 0.2891 | 0.4214 |
| Relative absolute error | 0.977038 | 0.942754 | 0.808266 | 1.005264 | 0.851436 |
| Root relative sq. error | 0.934184 | 0.928854 | 0.999298 | 1.010215 | 0.905755 |
| Models using attributes SHMU, Satellites (Forward selection 10 attr), Day of Year | |||||
| Correlation coefficient | 0.4288 | 0.4475 | 0.4104 | 0.4263 | 0.3976 |
| Relative absolute error | 0.948856 | 0.89844 | 0.778747 | 0.922759 | 0.861133 |
| Root relative sq. error | 0.911549 | 0.892596 | 0.962801 | 0.916577 | 0.921097 |
| Models using attributes SHMU, Satellites (Forward selection 5 attr), Day of Year | |||||
| Correlation coefficient | 0.4635 | 0.4508 | 0.4506 | 0.3769 | 0.4381 |
| Relative absolute error | 0.923401 | 0.896762 | 0.762388 | 0.924544 | 0.843924 |
| Root relative sq. error | 0.886452 | 0.890677 | 0.952388 | 0.948177 | 0.898847 |
| Models using attributes SHMU, Satellites (FSRF-TEST 10 attr), Day of Year | |||||
| Correlation coefficient | 0.4363 | 0.4339 | 0.4242 | 0.4686 | 0.5400 |
| Relative absolute error | 0.900255 | 0.892416 | 0.761173 | 0.868294 | 0.806506 |
| Root relative sq. error | 0.899348 | 0.899034 | 0.956712 | 0.885832 | 0.84258 |
| Models using attributes SHMU, Satellites (FSRF-TEST 5 attr), Day of Year | |||||
| Correlation coefficient | 0.3956 | 0.3884 | 0.3983 | 0.4255 | 0.5183 |
| Relative absolute error | 0.925902 | 0.911766 | 0.768899 | 0.885788 | 0.805674 |
| Root relative sq. error | 0.918372 | 0.919311 | 0.969704 | 0.905563 | 0.853435 |
| Models using attributes SHMU, Satellites (Relief 10 attr), Day of Year | |||||
| Correlation coefficient | 0.4016 | 0.4063 | 0.3959 | 0.4021 | 0.3987 |
| Relative absolute error | 0.934508 | 0.910194 | 0.781673 | 0.908593 | 0.863821 |
| Root relative sq. error | 0.921802 | 0.913254 | 0.960806 | 0.921916 | 0.916560 |
| Models using attributes SHMU, Satellites (Relief 5 attr), Day of Year | |||||
| Correlation coefficient | 0.3533 | 0.3364 | 0.3490 | 0.3028 | 0.3347 |
| Relative absolute error | 0.922774 | 0.915231 | 0.784270 | 0.912179 | 0.904339 |
| Root relative sq. error | 0.938938 | 0.941382 | 0.975032 | 0.972598 | 0.956348 |
| Linear model | Gaussian process | SMO Regression | M5P Tree | Random forest | |
| Linear Model | Gaussian Process | SMO Regression | M5P Tree | Random Forest | |
|---|---|---|---|---|---|
| Models using attributes SHMU, without Day of Year, and without Satellites | |||||
| Correlation coefficient | 0.2302 | 0.1822 | 0.1934 | 0.2314 | 0.1898 |
| Relative absolute error | 0.961795 | 0.974067 | 0.855066 | 0.960243 | 1.006067 |
| Root relative sq. error | 0.971534 | 0.981626 | 1.014425 | 0.971155 | 1.016997 |
| Models using attributes SHMU, Day of Year without Satellites | |||||
| Correlation coefficient | 0.2582 | 0.2236 | 0.2305 | 0.2053 | 0.2643 |
| Relative absolute error | 0.952205 | 0.962065 | 0.857284 | 0.962442 | 0.913962 |
| Root relative sq. error | 0.964646 | 0.973101 | 1.006680 | 0.988054 | 1.005748 |
| Models using attributes SHMU, Satellites (FSRF-TEST 20 attr) without Day of Year | |||||
| Correlation coefficient | 0.1428 | 0.1786 | 0.1742 | 0.065 | 0.3264 |
| Relative absolute error | 0.991643 | 0.970063 | 0.859727 | 1.034066 | 0.920992 |
| Root relative sq. error | 0.998483 | 0.984765 | 1.012168 | 1.097823 | 0.945923 |
| Models using attributes SHMU, Satellites (Relief 20 attr) without Day of Year | |||||
| Correlation coefficient | 0.0927 | 0.0648 | 0.1264 | 0.0789 | 0.1826 |
| Relative absolute error | 1.016839 | 1.016156 | 0.877836 | 1.064591 | 0.967896 |
| Root relative sq. error | 1.014047 | 1.007755 | 1.023097 | 1.049356 | 1.005119 |
| Models using attributes SHMU, Satellites (Forward selection 20 attr) without Day of Year | |||||
| Correlation coefficient | 0.1883 | 0.1210 | 0.233 | 0.1469 | 0.1377 |
| Relative absolute error | 1.005077 | 0.986239 | 0.835902 | 1.031335 | 0.953701 |
| Root relative sq. error | 0.995576 | 1.000356 | 0.992946 | 1.015140 | 1.007062 |
| Models using attributes SHMU, Satellites (Forward selection 10 attr), Day of Year | |||||
| Correlation coefficient | 0.2398 | 0.3101 | 0.3535 | 0.1445 | 0.2839 |
| Relative absolute error | 1.022736 | 0.948921 | 0.815373 | 1.054828 | 0.870082 |
| Root relative sq. error | 0.995421 | 0.951980 | 0.966335 | 1.135082 | 0.961922 |
| Models using attributes SHMU, Satellites (Forward selection 15 attr), Day of Year | |||||
| Correlation coefficient | 0.2611 | 0.3029 | 0.3283 | 0.2056 | 0.2714 |
| Relative absolute error | 1.007581 | 0.959974 | 0.805193 | 0.998895 | 0.878738 |
| Root relative sq. error | 0.982944 | 0.955482 | 0.972581 | 1.021172 | 0.962601 |
| Models using attributes SHMU, Satellites (FSRF-TEST 10 attr), Day of Year | |||||
| Correlation coefficient | 0.2888 | 0.323 | 0.3305 | 0.3005 | 0.3698 |
| Relative absolute error | 0.947149 | 0.919711 | 0.804691 | 0.937511 | 0.866946 |
| Root relative sq. error | 0.964184 | 0.945773 | 0.969808 | 0.960605 | 0.928711 |
| Models using attributes SHMU, Satellites (FSRF-TEST 5 attr), Day of Year | |||||
| Correlation coefficient | 0.3299 | 0.3438 | 0.36 | 0.3284 | 0.3999 |
| Relative absolute error | 0.936913 | 0.913589 | 0.793238 | 0.938661 | 0.866407 |
| Root relative sq. error | 0.945296 | 0.937339 | 0.965524 | 0.945354 | 0.921331 |
| Models using attributes SHMU, Satellites (Relief 10 attr), Day of Year | |||||
| Correlation coefficient | 0.2194 | 0.2357 | 0.2848 | 0.2272 | 0.3102 |
| Relative absolute error | 0.964405 | 0.956218 | 0.846194 | 0.963997 | 0.869070 |
| Root relative sq. error | 0.986047 | 0.975347 | 0.987452 | 0.988660 | 0.949752 |
| Models using attributes SHMU, Satellites (Relief 5 attr), Day of Year | |||||
| Correlation coefficient | 0.2587 | 0.2837 | 0.309 | 0.2601 | 0.2705 |
| Relative absolute error | 0.957589 | 0.94709 | 0.826091 | 0.961476 | 0.897960 |
| Root relative sq. error | 0.970585 | 0.958345 | 0.981613 | 0.971070 | 0.971982 |
| Linear model | Gaussian process | SMO Regression | M5P Tree | Random forest | |
| Linear Model | Gaussian Process | SMO Regression | M5P Tree | Random Forest | |
|---|---|---|---|---|---|
| Models using attributes SHMU, without Day of Year, and without Satellites | |||||
| Correlation coefficient | −0.0888 | 0.006 | −0.0239 | 0.076 | 0.1191 |
| Relative absolute error | 1.013206 | 1.011356 | 0.996436 | 1.000262 | 1.041810 |
| Root relative sq. error | 1.014285 | 1.005392 | 1.018875 | 1.000869 | 1.044912 |
| Models using attributes SHMU, Day of Year without Satellites | |||||
| Correlation coefficient | 0.4113 | 0.4373 | 0.4342 | 0.6206 | 0.6339 |
| Relative absolute error | 0.903762 | 0.894292 | 0.886614 | 0.755594 | 0.756144 |
| Root relative sq. error | 0.911274 | 0.897203 | 0.905929 | 0.782397 | 0.778181 |
| Modeling using attributes SHMU, Satellites (FSRF-TEST 20 attr), without Day of Year | |||||
| Correlation coefficient | 0.4195 | 0.4314 | 0.405 | 0.3931 | 0.4062 |
| Relative absolute error | 0.904127 | 0.892004 | 0.914068 | 0.91234 | 0.910343 |
| Root relative sq. error | 0.908831 | 0.899933 | 0.919583 | 0.925257 | 0.924097 |
| Models using attributes SHMU, Satellites (Relief 20 attr), without Day of Year | |||||
| Correlation coefficient | 0.4135 | 0.3942 | 0.3798 | 0.3853 | 0.4601 |
| Relative absolute error | 0.903282 | 0.905045 | 0.910703 | 0.912017 | 0.881088 |
| Root relative sq. error | 0.912632 | 0.918536 | 0.935326 | 0.929368 | 0.889698 |
| Models using attributes SHMU, Satellites (Forward selection 20 attr), without Day of Year | |||||
| Correlation coefficient | 0.3155 | 0.3276 | 0.3257 | 0.3426 | 0.4708 |
| Relative absolute error | 0.942383 | 0.931576 | 0.946136 | 0.910879 | 0.873131 |
| Root relative sq. error | 0.953646 | 0.946278 | 0.955216 | 0.951316 | 0.883867 |
| Models using attributes SHMU, Satellites (Manual selection 3 attr), Day of Year | |||||
| Correlation coefficient | 0.5163 | 0.5245 | 0.5092 | 0.6275 | 0.6004 |
| Relative absolute error | 0.855031 | 0.848659 | 0.849584 | 0.76101 | 0.78007 |
| Root relative sq. error | 0.855314 | 0.849386 | 0.863360 | 0.77716 | 0.800759 |
| Models using attributes SHMU, Satellites (Forward selection 5 attr), Day of Year | |||||
| Correlation coefficient | 0.5562 | 0.5565 | 0.5305 | 0.6058 | 0.6434 |
| Relative absolute error | 0.827117 | 0.82688 | 0.835880 | 0.788339 | 0.761934 |
| Root relative sq. error | 0.830543 | 0.829219 | 0.852279 | 0.795252 | 0.764349 |
| Models using attributes SHMU, Satellites (FSRF-TEST 5 attr), Day of Year | |||||
| Correlation coefficient | 0.5635 | 0.5661 | 0.5354 | 0.5608 | 0.626 |
| Relative absolute error | 0.822849 | 0.82399 | 0.850483 | 0.825195 | 0.762599 |
| Root relative sq. error | 0.825459 | 0.822494 | 0.849352 | 0.830468 | 0.779014 |
| Models using attributes SHMU, Satellites (Relief 5 attr), Day of Year | |||||
| Correlation coefficient | 0.4891 | 0.5099 | 0.4858 | 0.5494 | 0.6368 |
| Relative absolute error | 0.87403 | 0.861349 | 0.869334 | 0.822957 | 0.759978 |
| Root relative sq. error | 0.872218 | 0.858429 | 0.881012 | 0.837942 | 0.769692 |
| Linear model | Gaussian process | SMO Regression | M5P Tree | Random forest | |
| Target attribute S: | ||
| Used attributes for XA | Used attributes for XB | p-value |
| SHMU | SHMU + Day of Year | 0.000238 |
| SHMU | SHMU + Satellites | 0.000179 |
| SHMU + Day of Year | SHMU + Day of Year + Satellites | 0.000617 |
| SHMU + Satellites | SHMU + Day of Year + Satellites | 0.000698 |
| Target Attribute Sr: | ||
| Used attributes for XA | Used attributes for XB | p-value |
| SHMU | SHMU + Day of Year | 0.000297 |
| SHMU | SHMU + Satellites | 0.000119 |
| SHMU + Day of Year | SHMU + Day of Year + Satellites | 0.000917 |
| SHMU + Satellites | SHMU + Day of Year + Satellites | 0.002740 |
| Target Attribute g02: | ||
| Used attributes for XA | Used attributes for XB | p-value |
| SHMU | SHMU + Day of Year | 0.000249 |
| SHMU | SHMU + Satellites | 0.000314 |
| SHMU + Day of Year | SHMU + Day of Year + Satellites | 0.012501 |
| SHMU + Satellites | SHMU + Day of Year + Satellites | 0.006714 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krammer, P.; Kvassay, M.; Mojžiš, J.; Kenyeres, M.; Očkay, M.; Hluchý, L.; Pavlov, Ľ.; Skurčák, Ľ. Using Satellite Imagery to Improve Local Pollution Models for High-Voltage Transmission Lines and Insulators. Future Internet 2022, 14, 99. https://doi.org/10.3390/fi14040099
Krammer P, Kvassay M, Mojžiš J, Kenyeres M, Očkay M, Hluchý L, Pavlov Ľ, Skurčák Ľ. Using Satellite Imagery to Improve Local Pollution Models for High-Voltage Transmission Lines and Insulators. Future Internet. 2022; 14(4):99. https://doi.org/10.3390/fi14040099
Chicago/Turabian StyleKrammer, Peter, Marcel Kvassay, Ján Mojžiš, Martin Kenyeres, Miloš Očkay, Ladislav Hluchý, Ľuboš Pavlov, and Ľuboš Skurčák. 2022. "Using Satellite Imagery to Improve Local Pollution Models for High-Voltage Transmission Lines and Insulators" Future Internet 14, no. 4: 99. https://doi.org/10.3390/fi14040099
APA StyleKrammer, P., Kvassay, M., Mojžiš, J., Kenyeres, M., Očkay, M., Hluchý, L., Pavlov, Ľ., & Skurčák, Ľ. (2022). Using Satellite Imagery to Improve Local Pollution Models for High-Voltage Transmission Lines and Insulators. Future Internet, 14(4), 99. https://doi.org/10.3390/fi14040099