Evaluation of Optimal Occasional Tilt on Photovoltaic Power Plant Energy Efficiency and Land Use Requirements, Iran
Abstract
:1. Introduction
- Looking into the spatial effects of annual radiation intensity that reaches the panel surface concerning the optimum angle at optimum time intervals compared to the optimum constant angle installation.
- Assessing the effect of the optimum time intervals (OTIs) of each optimum angle on the choice of the angle at the equal time intervals (ETIs). However, in both cases, the number of angular changes is the same, and the optimum angle is selected at each time interval, whereas in the first case, the time intervals can be different from each other.
- Studying the capacity of the power plant for the movable and fixed structure in two cases of the equal time intervals and the variable time intervals.
2. Materials and Methods
3. Discussion
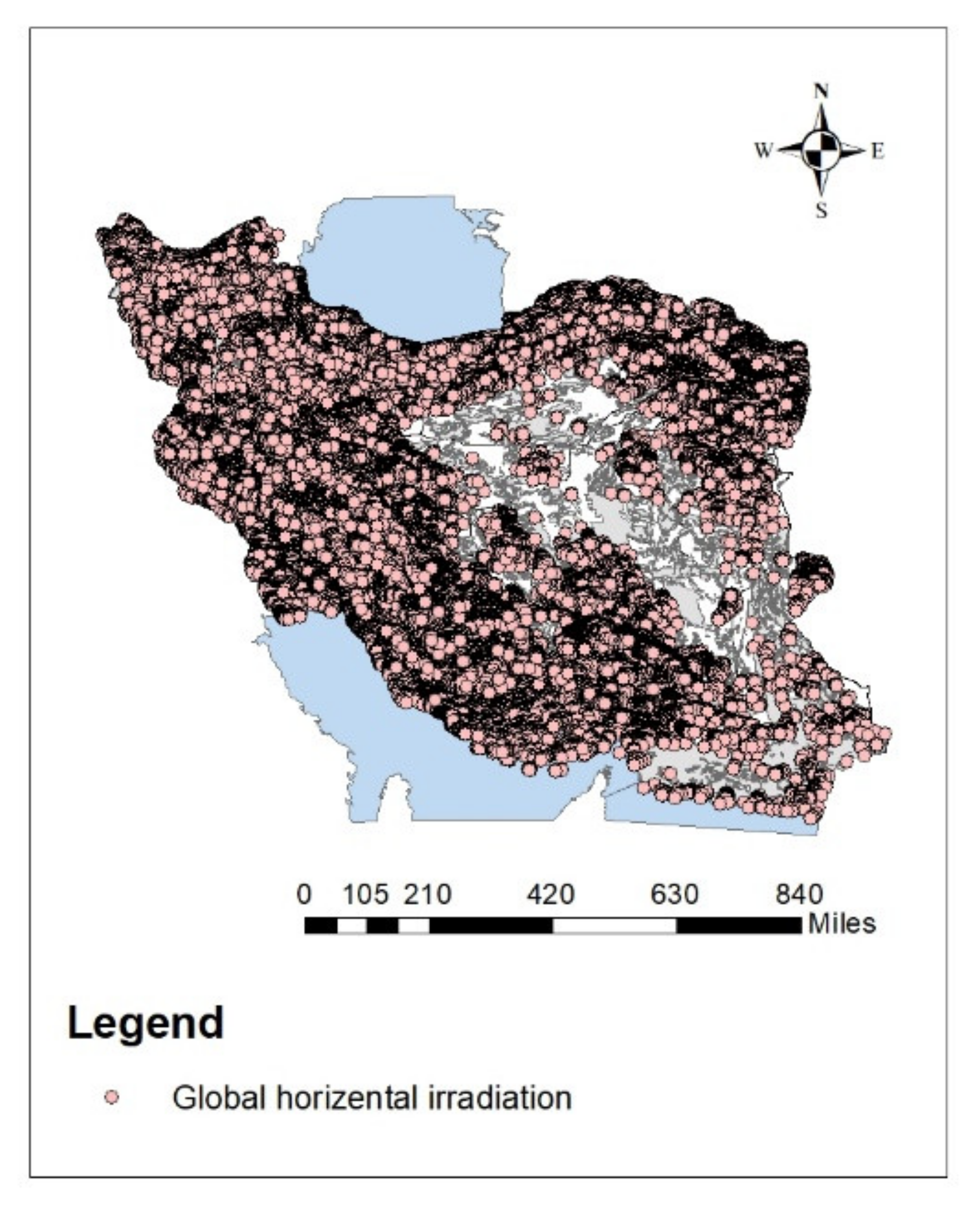
3.1. Solar Energy Atlas in Iran
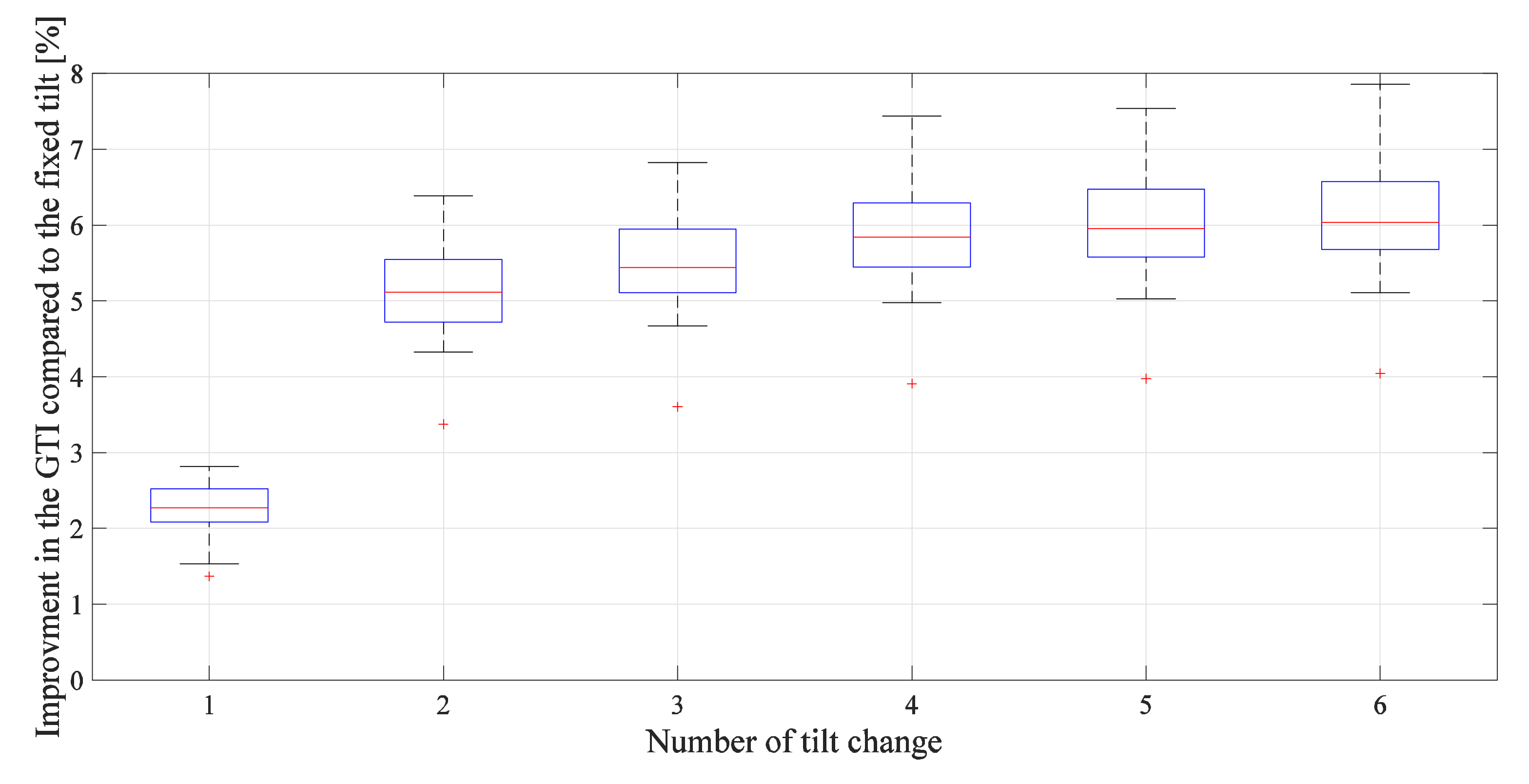
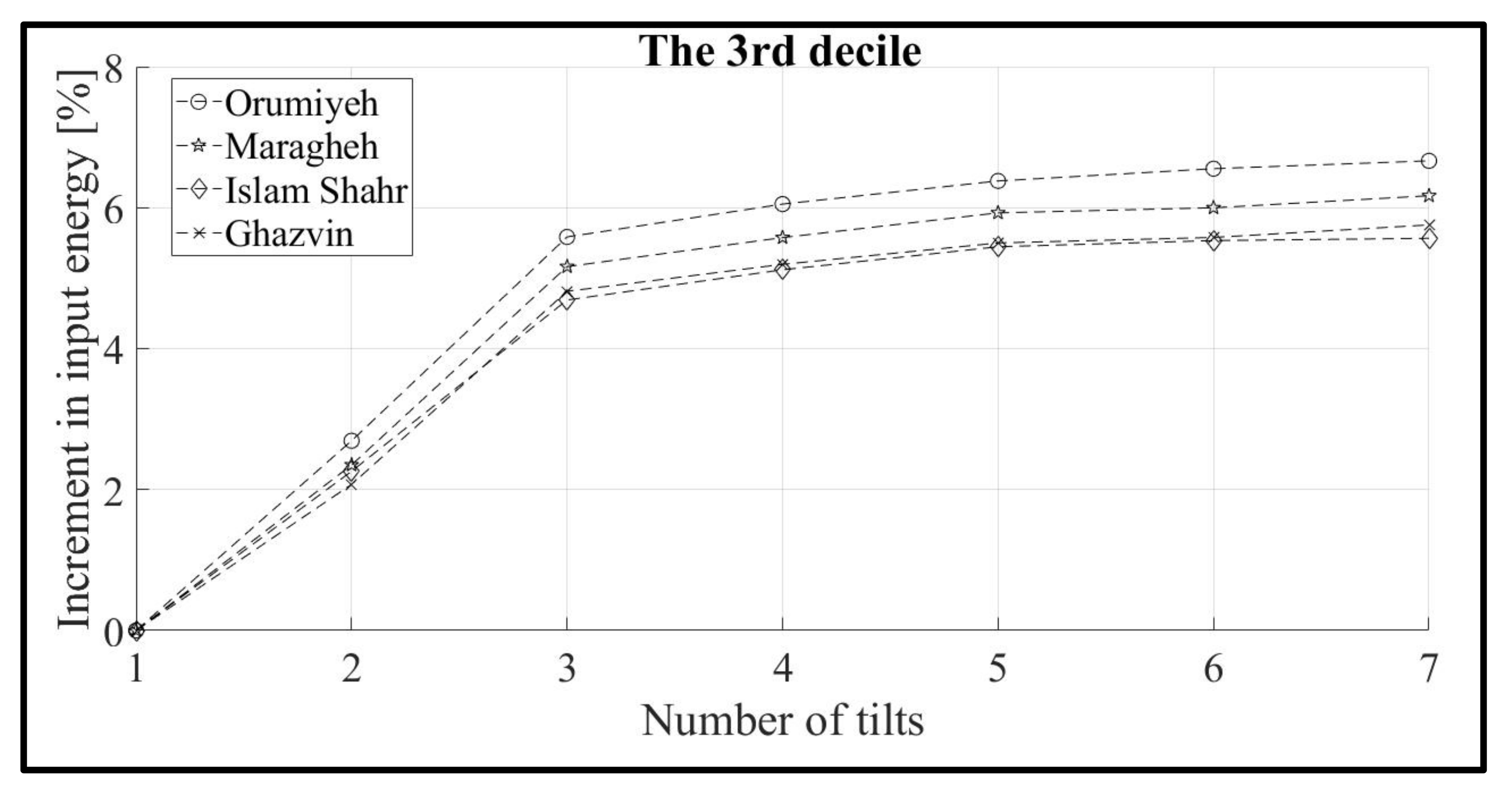
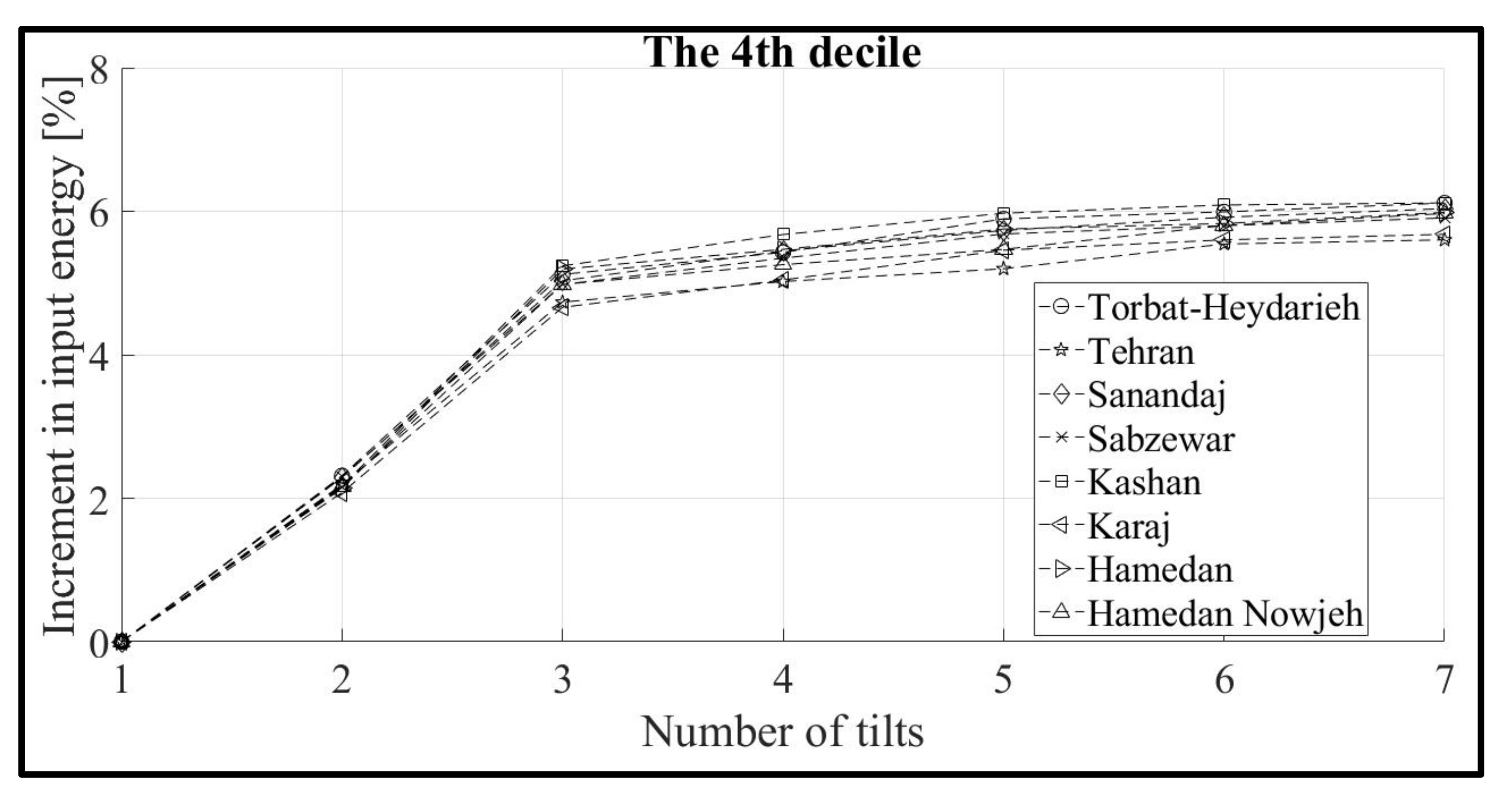
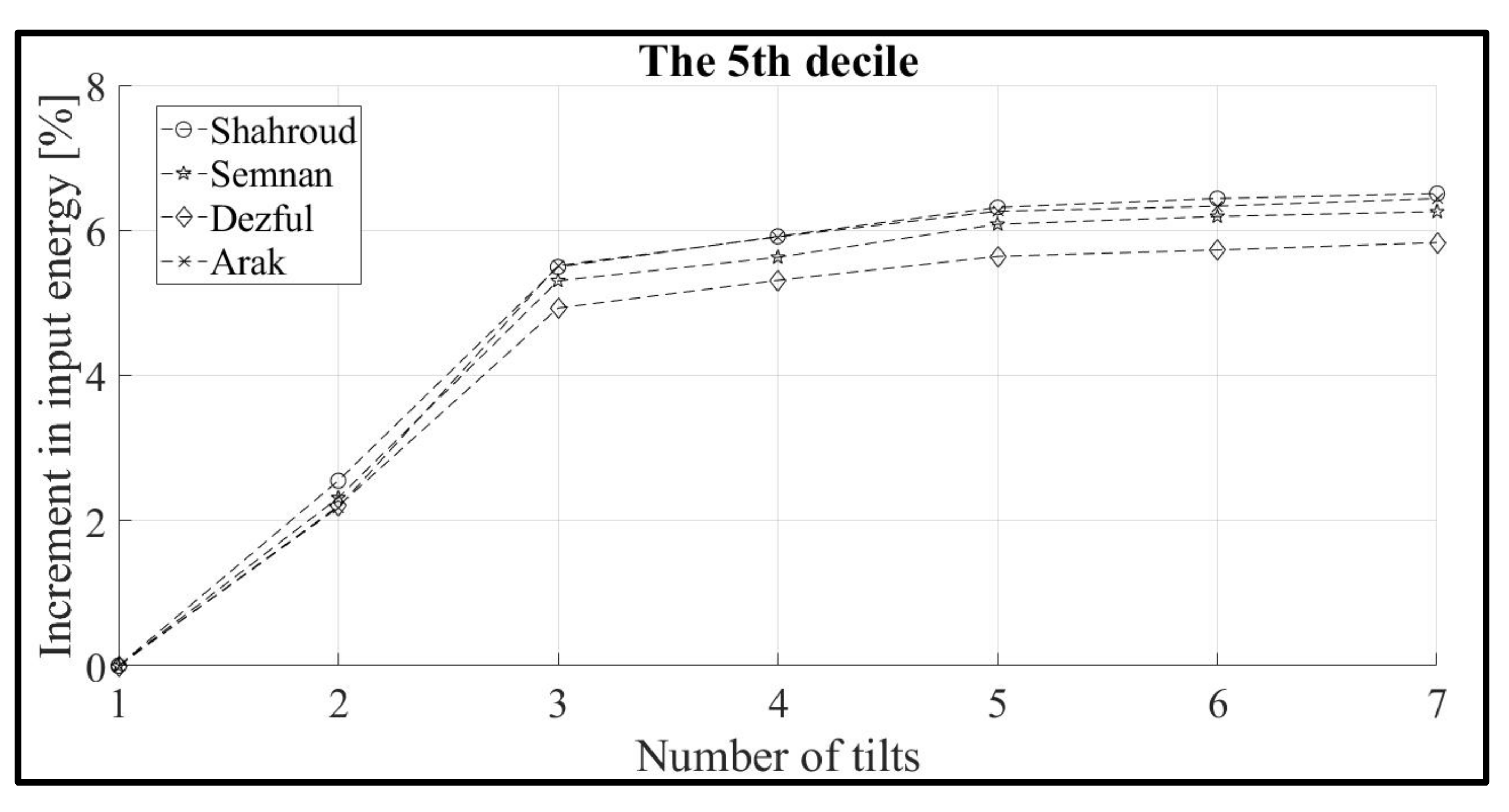
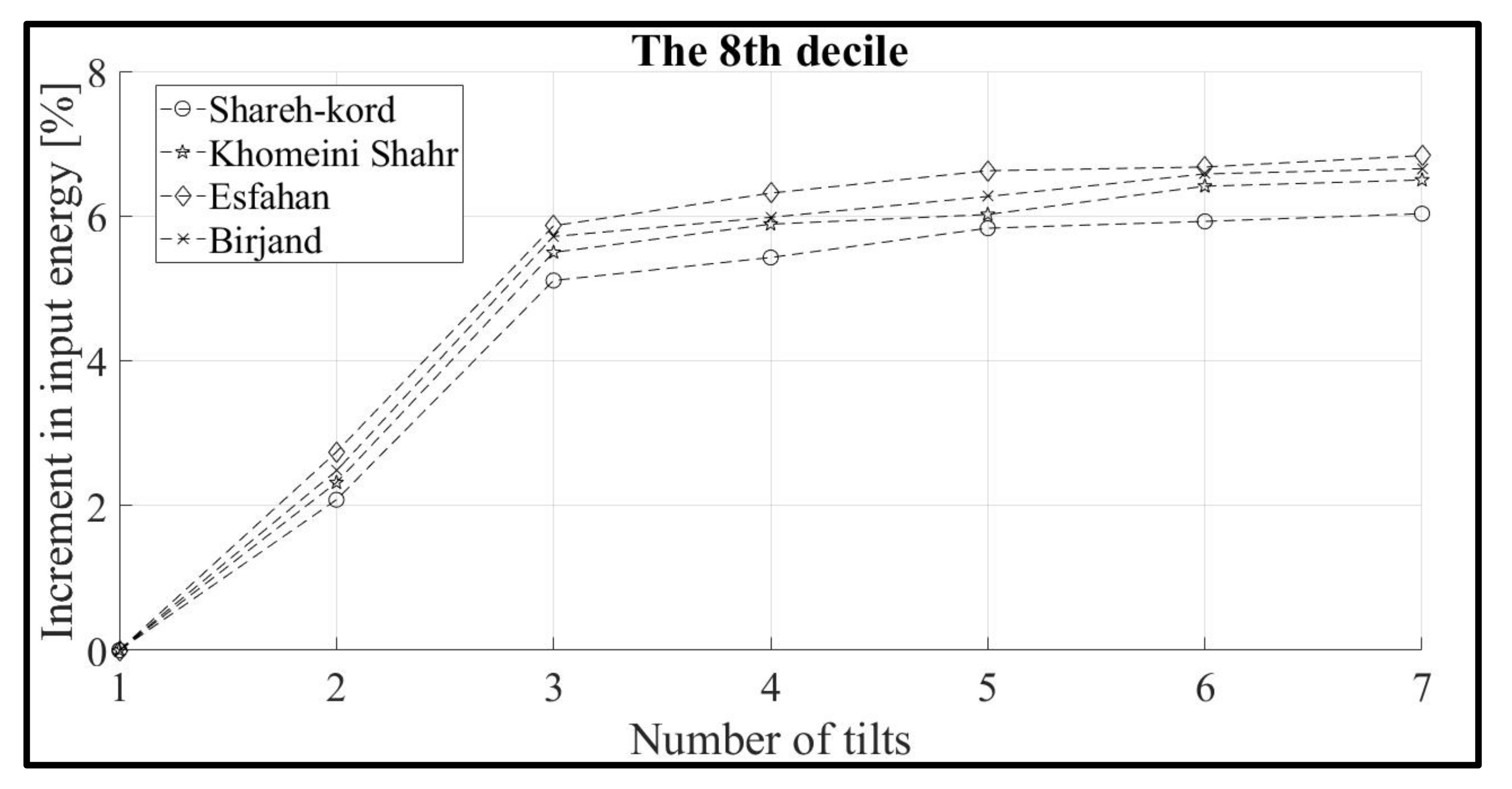
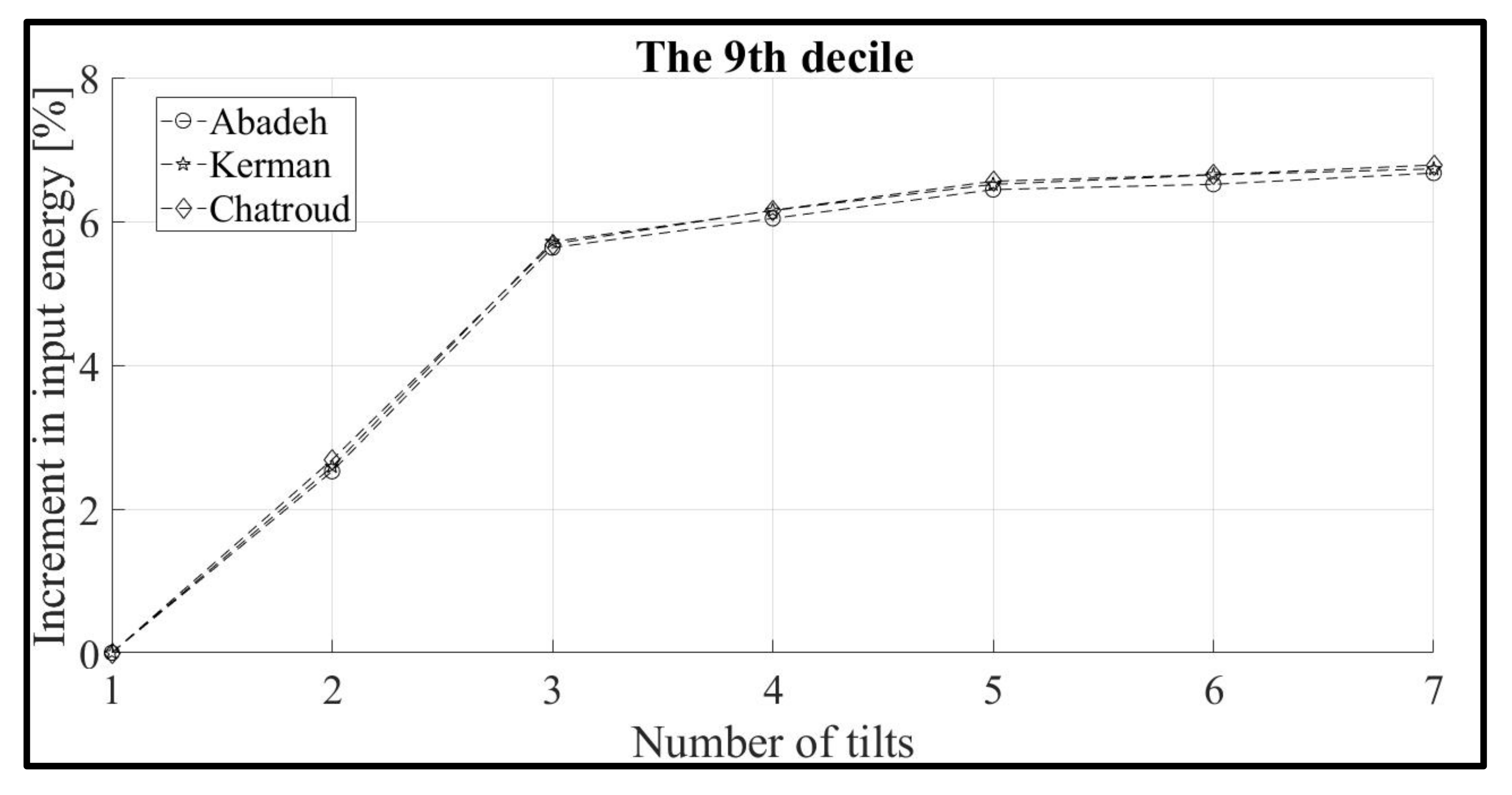
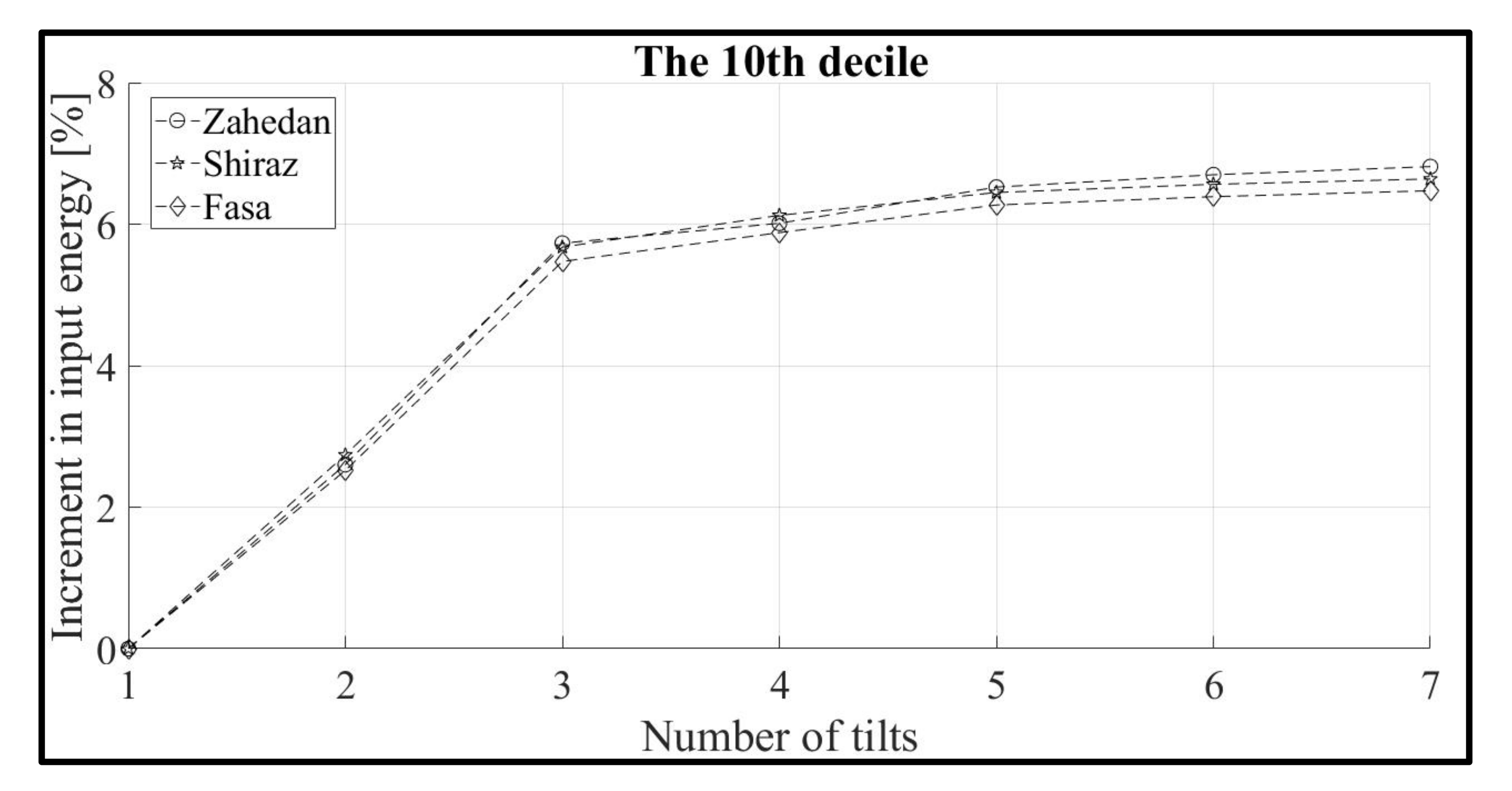
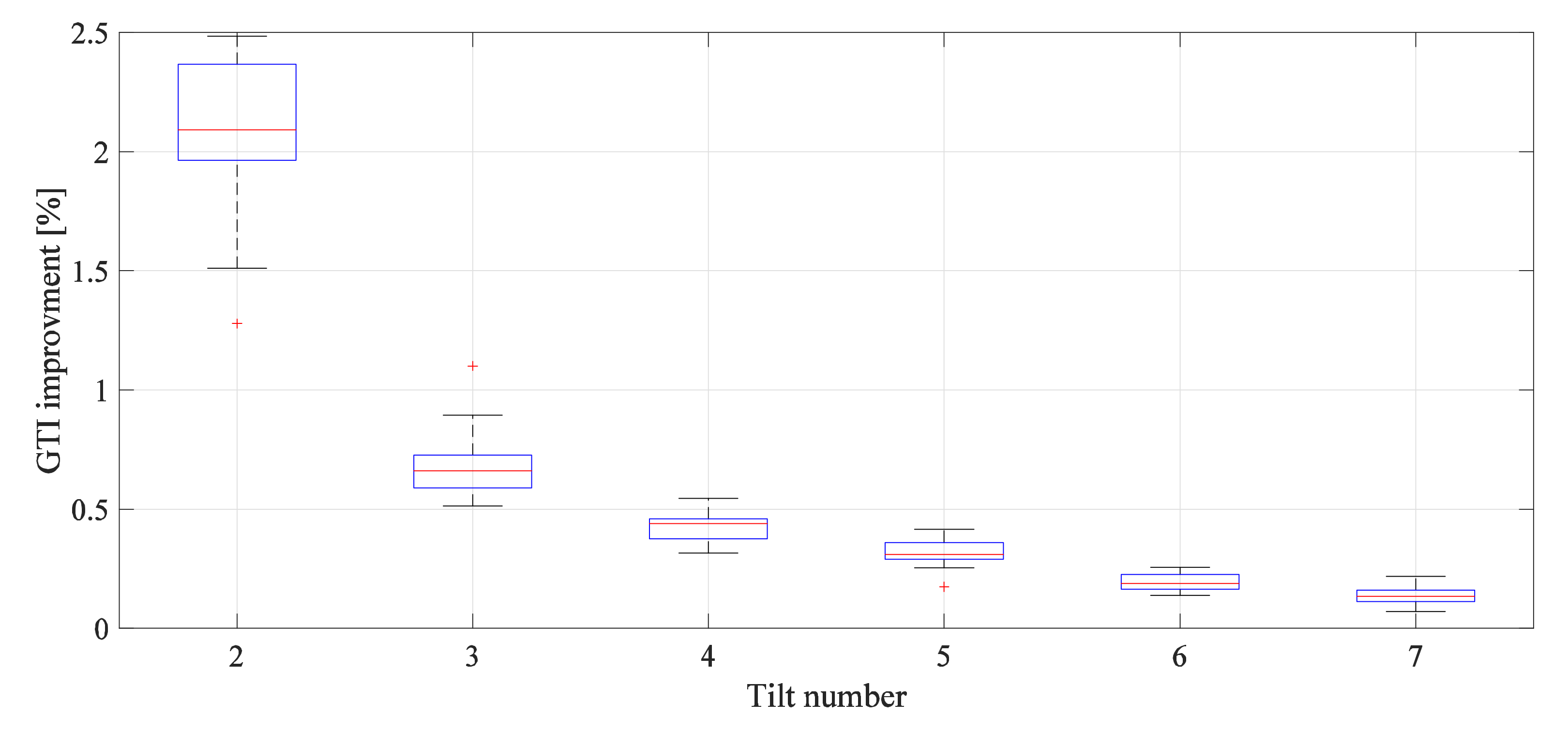
3.2. Effect of the Angle Variation and Solar Radiation Decile on the Amount of Input Energy Increment
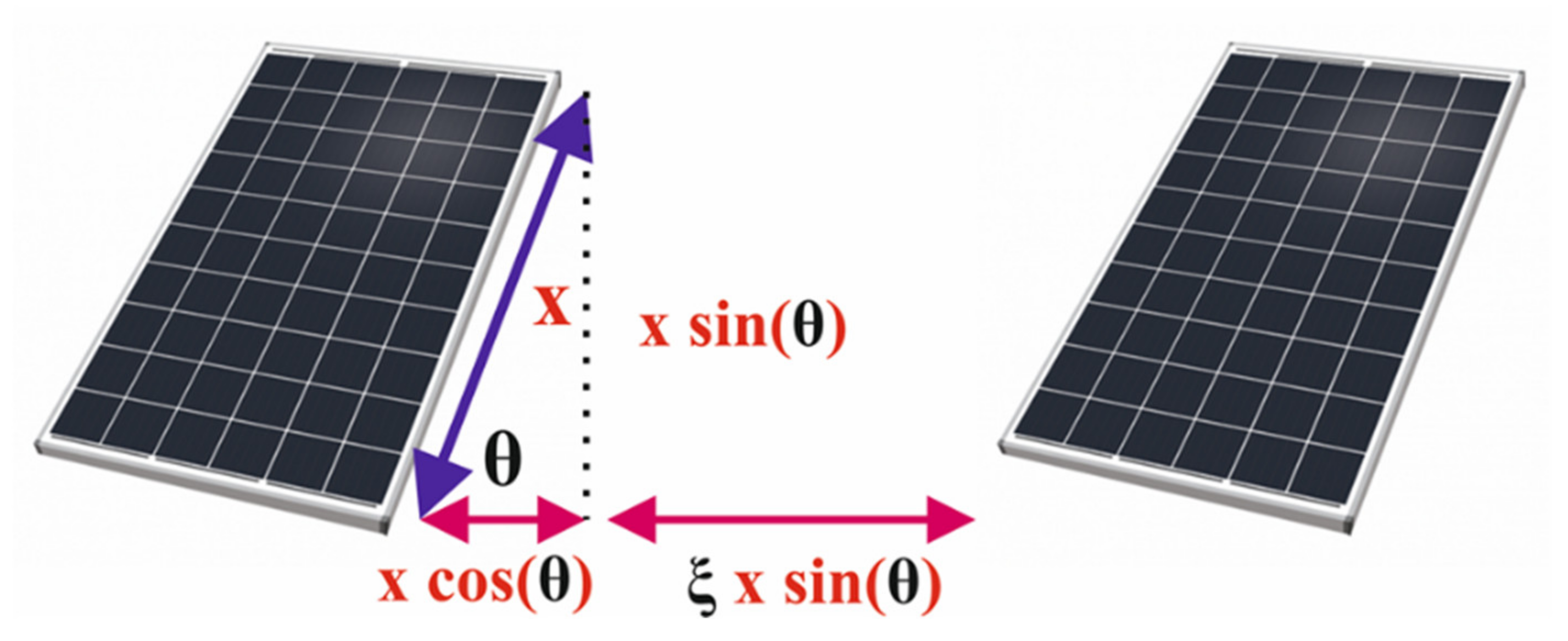
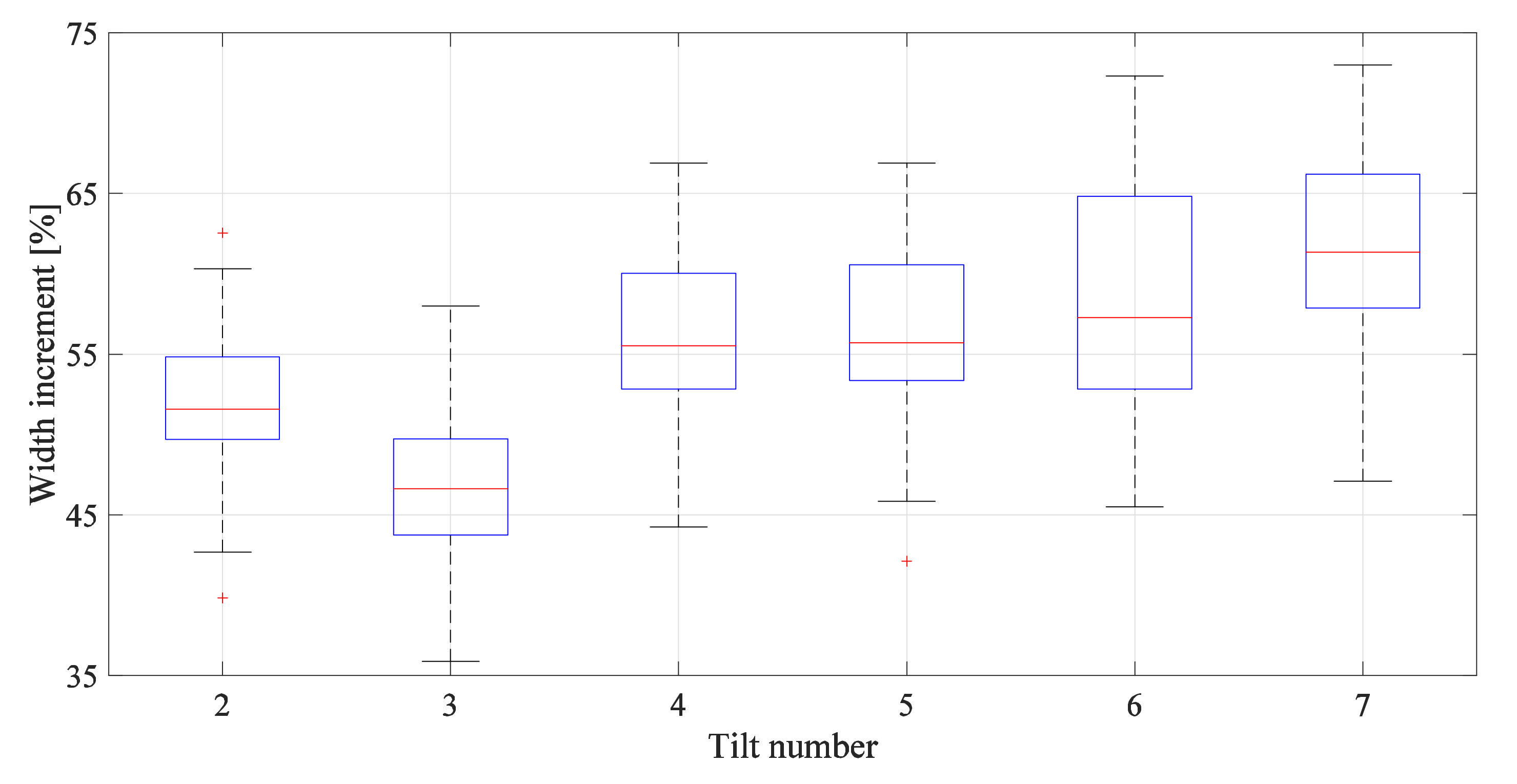
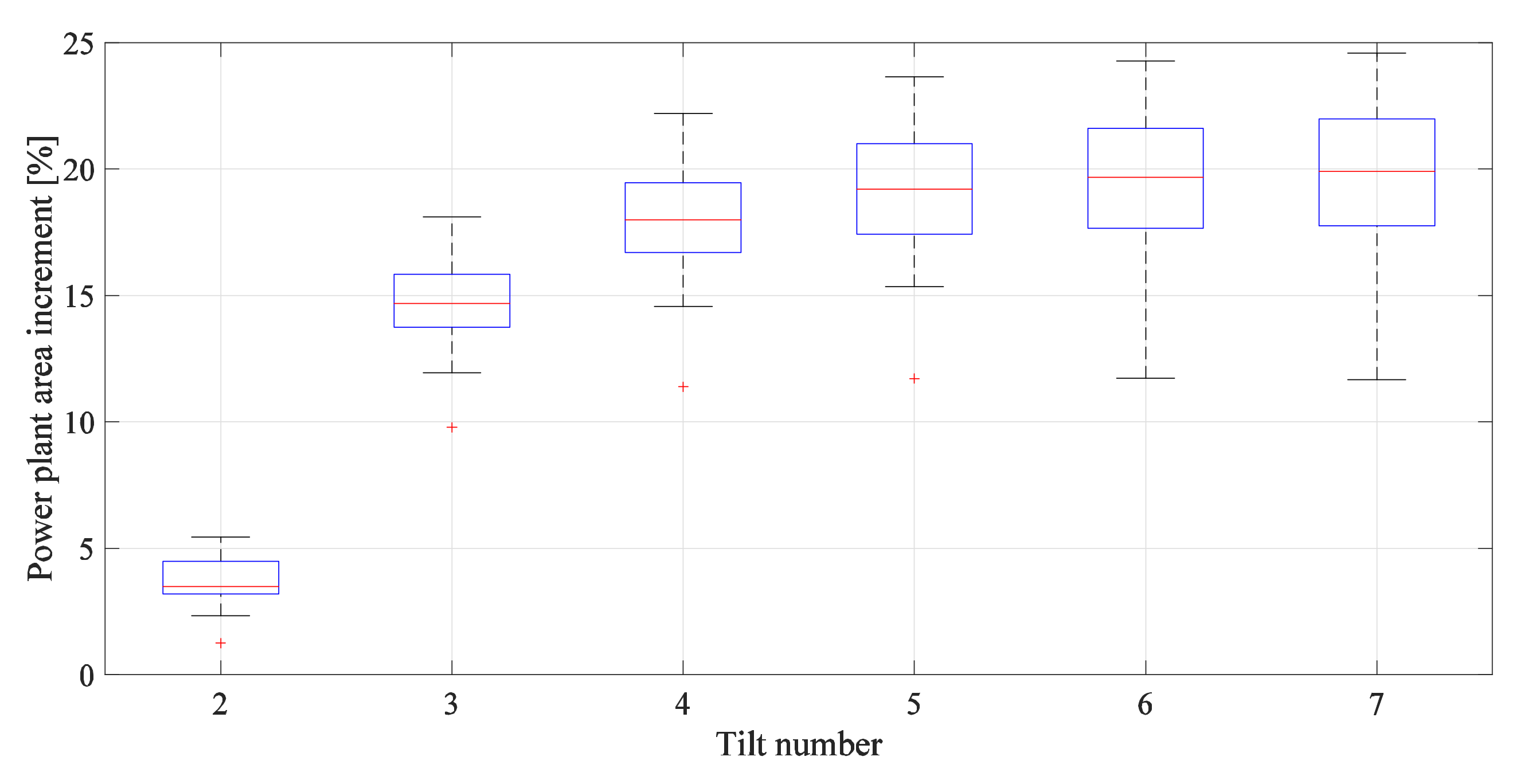
3.3. Effect of Changing the Tilt Angle on the Land-Use Requirement
4. Conclusions
- One of the problems of widespread use of the proposed structure is the design of the structure for different geographical locations. Therefore, by modifying the introduced structural model, it is possible to deploy a solar energy conversion technology on several pre-defined angles; however, it is possible to use this structure for a wide range. Only for each geographical point, the time and interval of deployment at each angle are different. Therefore, there is a possibility of industrial production of structures.
- The effect of increasing the input energy to the level of energy conversion technology on the change of efficiency and effectiveness has been studied
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Valancius, R.; Mutiari, A.; Singh, A.; Alexander, C.; De La Cruz, D.A.; del Pozo, F.E., Jr. Solar Photovoltaic Systems in the Built Environment: Today Trends and Future Challenges. J. Sustain. Arch. Civ. Eng. 2018, 23, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Kusch-Brandt, S. Urban Renewable Energy on the Upswing: A Spotlight on Renewable Energy in Cities in REN21’s “Renewables 2019 Global Status Report”. Resources 2019, 8, 139. [Google Scholar] [CrossRef] [Green Version]
- Nsengiyumva, W.; Chen, S.G.; Hu, L.; Chen, X. Recent advancements and challenges in Solar Tracking Systems (STS): A review. Renew. Sustain. Energy Rev. 2018, 81, 250–279. [Google Scholar] [CrossRef]
- Zandi, Z.; Mazinan, A.H. Maximum power point tracking of the solar power plants in shadow mode through artificial neural network. Complex Intell. Syst. 2019, 5, 315–330. [Google Scholar] [CrossRef] [Green Version]
- Perpiñán, O. Cost of energy and mutual shadows in a two-axis tracking PV system. Renew. Energy 2012, 43, 331–342. [Google Scholar] [CrossRef] [Green Version]
- Pillot, B.; Muselli, M.; Poggi, P.; Haurant, P.; Hared, I. The first disaggregated solar atlas of Djibouti: A decision-making tool for solar systems integration in the energy scheme. Renew. Energy 2013, 57, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists. Aust. Geol. Surv. Organ. 2008, 68, 154. Available online: http://www.ga.gov.au/image_cache/GA12526.pdf (accessed on 1 July 2021).
- Ghahreman, N.; Bakhtiari, B. Solar Radiation Estimation from Rainfall and Temperature Data in Arid and Semi-arid Climates of Iran. Desert 2009, 14, 141–150. [Google Scholar] [CrossRef]
- Ramedani, Z.; Omid, M.; Keyhani, A. Modeling solar energy potential in a tehran province using artificial neural networks. Int. J. Green Energy 2013, 10, 427–441. [Google Scholar] [CrossRef]
- Benghanem, M.; Mellit, A.; Alamri, S.N. ANN-based modelling and estimation of daily global solar radiation data: A case study. Energy Convers. Manag. 2009, 50, 1644–1655. [Google Scholar] [CrossRef]
- Jimenez, V.A.; Barrionuevo, A.; Will, A.; Rodríguez, S. Neural Network for Estimating Daily Global Solar Radiation Using Temperature, Humidity and Pressure as Unique Climatic Input Variables. Smart Grid Renew. Energy 2016, 7, 94–103. [Google Scholar] [CrossRef] [Green Version]
- Mensour, O.N.; El Ghazzani, B.; Hlimi, B.; Ihlal, A. Modeling of solar energy potential in Souss-Massa area-Morocco, using intelligence Artificial Neural Networks (ANNs). Energy Procedia 2017, 139, 778–784. [Google Scholar] [CrossRef]
- Olalekan, S.; Abdullahi, M.I.; Olabisi, A. Modeling of solar radiation using artificial neural network for renewable energy application Modeling of Solar Radiation Using Artificial Neural Network for Renewable Energy Application. IOSR J. Appl. Phys. 2018, 10, 6–12. [Google Scholar] [CrossRef]
- Adly, M. An Optimized Fuzzy Maximum Power Point Tracker for Stand Alone Photovoltaic Systems: Ant Colony Approach. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 113–119. [Google Scholar]
- Conceição, R.; Silva, H.G.; Fialho, L.; Lopes, F.M.; Collares-Pereira, M. PV system design with the effect of soiling on the optimum tilt angle. Renew. Energy 2019, 133, 787–796. [Google Scholar] [CrossRef]
- Lalouni, S.; Rekioua, D.; Rekioua, T.; Matagne, E. Fuzzy logic control of stand-alone photovoltaic system with battery storage. J. Power Sources 2009, 193, 899–907. [Google Scholar] [CrossRef]
- Taherbaneh, M.; Faez, K. Maximum power point estimation for photovoltaic systems using neural networks. In Proceedings of the 2007 IEEE International Conference on Control and Automation (ICCA), Guangzhou, China, 30 May–1 June 2007; pp. 1614–1619. [Google Scholar] [CrossRef]
- Algazar, M.M.; Al-Monier, H.; El-Halim, H.A.; Salem, M.E.E.K. Maximum power point tracking using fuzzy logic control. Int. J. Electr. Power Energy Syst. 2012, 39, 21–28. [Google Scholar] [CrossRef]
- Huang, B.J.; Sun, F.S. Feasibility study of one axis three positions tracking solar PV with low concentration ratio reflector. Energy Convers. Manag. 2007, 48, 1273–1280. [Google Scholar] [CrossRef]
- Alexandru, C.; Irina Tatu, N. Optimal design of the solar tracker used for a photovoltaic string. J. Renew. Sustain. Energy 2013, 5, 023133. [Google Scholar] [CrossRef]
- Dakkak, M.; Babelli, A. Design and performance study of a PV tracking system (100W-24Vdc/220Vac). Energy Procedia 2012, 19, 91–95. [Google Scholar] [CrossRef] [Green Version]
- Mattei, M.; Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation of the polycrystalline PV module temperature using a simple method of energy balance. Renew. Energy 2006, 31, 553–567. [Google Scholar] [CrossRef]
- Fu, R.; Feldman, D.; Margolis, R. U.S. Solar Photovoltaic System Cost Benchmark: Q1 2018; Technical Report NREL/TP-6A20-72399; National Renewable Energy Laboratory: Golden, CO, USA, 2018. Available online: https://www.nrel.gov/docs/fy19osti/72399.pdf (accessed on 1 July 2021).
- International Renewable Energy Agency—IRENA. Future of Solar Photovoltaic; IRENA: Abu Dhabi, United Arab Emirates, 2019; ISBN 9789292601553. Available online: https://www.irena.org/publications/2019/Nov/Future-of-Solar-Photovoltaic (accessed on 1 July 2021).
- Fakouriyan, S.; Saboohi, Y.; Fathi, A. Experimental analysis of a cooling system effect on photovoltaic panels’ efficiency and its preheating water production. Renew. Energy 2019, 134, 1362–1368. [Google Scholar] [CrossRef]
- Kumar, B.S.; Sudhakar, K. Performance evaluation of 10 MW grid connected solar photovoltaic power plant in India. Energy Rep. 2015, 1, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Kumar, S.; Gehlot, A.; Pachauri, R. An imperative role of sun trackers in photovoltaic technology: A review. Renew. Sustain. Energy Rev. 2018, 82, 3263–3278. [Google Scholar] [CrossRef]
- Sadeghi, S.; Mehranfar, S.; Ghandehariun, S. Analysis and Optimization of a Hybrid Solar-Ocean Powered Trigeneration System for Kish Island. In Proceedings of the 28th Annual International Conference of the Iranian Association of Mechanical Engineers, Tehran, Iran, 27 May 2020. [Google Scholar]
- Wang, H.X.; Muñoz-García, M.A.; Moreda, G.P.; Alonso-García, M.C. Optimum inverter sizing of grid-connected photovoltaic systems based on energetic and economic considerations. Renew. Energy 2018, 118, 709–717. [Google Scholar] [CrossRef]
- Awasthi, A.; Shukla, A.K.; Manohar, S.R.M.; Dondariya, C.; Shukla, K.N.; Porwal, D.; Richhariya, G. Review on sun tracking technology in solar PV system. Energy Rep. 2020, 6, 392–405. [Google Scholar] [CrossRef]
- Besarati, S.M.; Padilla, R.V.; Goswami, D.Y.; Stefanakos, E. The potential of harnessing solar radiation in Iran: Generating solar maps and viability study of PV power plants. Renew. Energy 2013, 53, 193–199. [Google Scholar] [CrossRef]
- Gueymard, C. Prediction and performance assessment of mean hourly global radiation. Sol. Energy 2000, 68, 285–303. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Haghparast-Kashani, A.; Saleh-Izadkhast, P.; Lari, H.R. Development of optimum solar irradiation energy model for Iran. Int. J. Glob. Energy Issues 2009, 31, 132–149. [Google Scholar] [CrossRef]
- Daneshyar, M. Solar radiation statistics for Iran. Sol. Energy 1978, 21, 345–349. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems; Academic Press: Amsterdam, The Netherlands, 2013. [Google Scholar]











| Tensile | City Name |
|---|---|
| 1 | Ramsar, Kandelous, Bandar anzali |
| 2 | Tabriz, Khoy, Bojnourd, Ardebil |
| 3 | Orumiyeh, Maragheh, Islam shahr, Ghazvin |
| 4 | Torbat heydarieh, Tehran, Sanandaj, Sabzvar, Kashan, Karaj, Hamedan, Hamedan nowjeh |
| 5 | Shahroud, Semnan, Dezful, Arak |
| 6 | Khoram abad, Kermanshah |
| 7 | Yazd, Ilam, Bushehr, Bandar lengeh, Bandar abas |
| 8 | Shahre-kord, Khoeini shahr, Esfahan, Birjand |
| 9 | Kerman, Chatroud, Abadeh |
| 10 | Zahedan, Shiraz, Fasa |
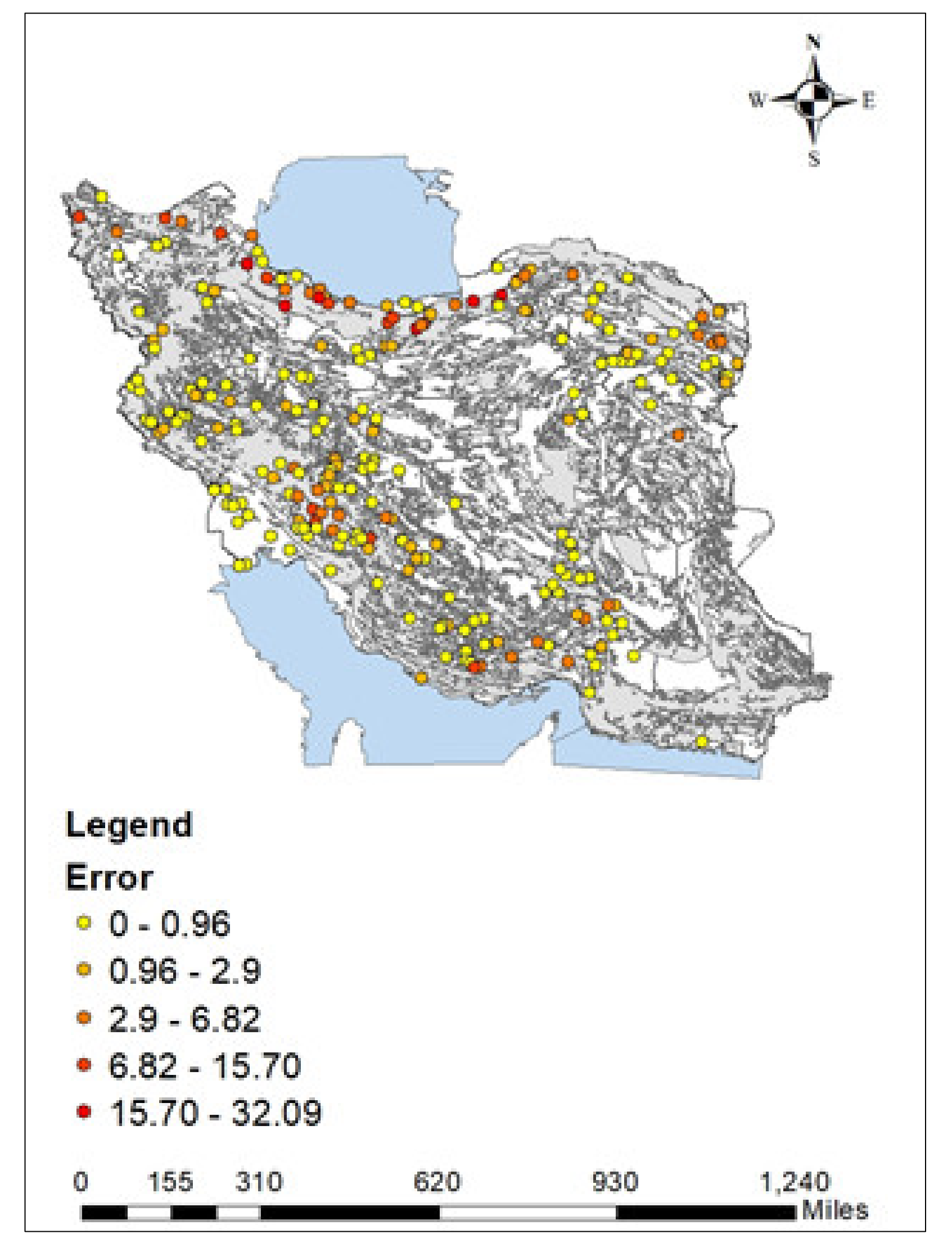
| The Error | City | The Non-Zero Optimum Tilt Angle Difference |
|---|---|---|
| 0–1% | Zahedan, Yazd, Kerman, Esfahan, Ardabil, Chatroud | |
| 1–2% | Shahroud, Semnanm Abadeh, Orumiyeh, Khomeini shahr, Fasa, Bandar lengeh | Shahroud: −1 |
| 2–3% | Tehran, Sanandaj, Kashan, Ilam, Bushehr, Bandar abbas | Ilam: −4, Bushehr: −3 |
| 3–4% | Torbat-Heydarieh, Shiraz, Ghazvin, Birjand | |
| 4–5% | Ramsar, Khoy, Karaj, Kandelous, Islam shahr, Bojnourd, Bandar anzali | |
| 5–6% | Maragheh, Khoram Abad, Kermanshah | |
| 6–7% | Share-kord, Sabzevar, Hamedan, Hamedan nowjeh, Arak | |
| 7–8% | Tabriz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathi, A.; Bararzadeh Ledari, M.; Saboohi, Y. Evaluation of Optimal Occasional Tilt on Photovoltaic Power Plant Energy Efficiency and Land Use Requirements, Iran. Sustainability 2021, 13, 10213. https://doi.org/10.3390/su131810213
Fathi A, Bararzadeh Ledari M, Saboohi Y. Evaluation of Optimal Occasional Tilt on Photovoltaic Power Plant Energy Efficiency and Land Use Requirements, Iran. Sustainability. 2021; 13(18):10213. https://doi.org/10.3390/su131810213
Chicago/Turabian StyleFathi, Amirhossein, Masoomeh Bararzadeh Ledari, and Yadollah Saboohi. 2021. "Evaluation of Optimal Occasional Tilt on Photovoltaic Power Plant Energy Efficiency and Land Use Requirements, Iran" Sustainability 13, no. 18: 10213. https://doi.org/10.3390/su131810213
APA StyleFathi, A., Bararzadeh Ledari, M., & Saboohi, Y. (2021). Evaluation of Optimal Occasional Tilt on Photovoltaic Power Plant Energy Efficiency and Land Use Requirements, Iran. Sustainability, 13(18), 10213. https://doi.org/10.3390/su131810213







