Next Article in Journal
Evaluation of Post-Tunneling Aging Buildings Using the InSAR Nonuniform Settlement Index
Next Article in Special Issue
Machine Learning Model-Based Retrieval of Temperature and Relative Humidity Profiles Measured by Microwave Radiometer
Previous Article in Journal
An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data
Previous Article in Special Issue
Enhancing Spatial Variability Representation of Radar Nowcasting with Generative Adversarial Networks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 14
10.3390/rs15143466
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

Multiscale Representation of Radar Echo Data Retrieved through Deep Learning from Numerical Model Simulations and Satellite Images

by
Mingming Zhu
1,2,
Qi Liao
3,
Lin Wu
1,4,*,
Si Zhang
1,2,
Zifa Wang
1,2,5,
Xiaole Pan
1,
Qizhong Wu
6,
Yangang Wang
7 and
Debin Su
3
1
State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
2
College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
3
College of Electronic Engineering, Chengdu University of Information Technology, Chengdu 610225, China
4
Carbon Neutrality Research Center, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
5
Center for Excellence in Urban Atmospheric Environment, Institute of Urban Environment, Chinese Academy of Sciences, Xiamen 361021, China
6
College of Global Change and Earth System Science, Beijing Normal University, Beijing 100875, China
7
Computer Network Information Center, Chinese Academy of Sciences, Beijing 100083, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(14), 3466; https://doi.org/10.3390/rs15143466
Submission received: 3 June 2023 / Revised: 26 June 2023 / Accepted: 5 July 2023 / Published: 9 July 2023
(This article belongs to the Special Issue Processing and Application of Weather Radar Data)
Browse Figures
Versions Notes

Abstract

:
Radar reflectivity data snapshot fine-grained atmospheric variations that cannot be represented well by numerical weather prediction models or satellites, which poses a limit for nowcasts based on model–data fusion techniques. Here, we reveal a multiscale representation (MSR) of the atmosphere by reconstructing the radar echoes from the Weather Research and Forecasting (WRF) model simulations and the Himawari-8 satellite products using U-Net deep networks. Our reconstructions generated the echoes well in terms of patterns, locations, and intensities with a root mean square error (RMSE) of 5.38 dBZ. We find stratified features in this MSR, with small-scale patterns such as echo intensities sensitive to the WRF-simulated dynamic and thermodynamic variables and with larger-scale information about shapes and locations mainly captured from satellite images. Such MSRs with physical interpretations may inspire innovative model–data fusion methods that could overcome the conventional limits of nowcasting.

1. Introduction

Meteorological forecasts at the convective scale are crucial to mitigate environmental hazards such as storms and floods that cause huge socioeconomic damages, but face fundamental challenges in representing the convective weather regime in numerical weather prediction (NWP) models, which is a less-known “gray zone” compared to the relatively well-resolved synoptic-scale systems [1,2]. Radar is an invaluable instrument to scan the convective atmosphere in nearly real time. The extrapolations of these sequential radar echo data can provide state-of-the-art nowcasts of precipitation patterns and severe weather events within a few hours based on the persistence principle [3,4,5]. However, these radar echo data are snapshots of the complex atmosphere with fine-grained details but not readily related to the dynamics of the atmosphere and the information from remote sensing satellites. This lack of representation of the dynamical and global atmospheric information poses a limit for convective nowcasting. For instance, when combining extrapolation-based methods with the dynamical information from NWP model simulations [6,7], the forecast skill in general decreases rapidly in the first forecast hour and remains low beyond a few forecast hours [8,9], despite advances in convective-permitting modeling [10], radar and satellite data assimilation [9,11,12] and high-resolution observations [13].
The representation gap, particularly when model–data fusion is to be conducted, is difficult to bridge [14,15]. Representing processes related to turbulence, convection, and topography is challenging for numerical models in gray zones [16]. Parameterizing and resolving the atmospheric motions in grid spacing for deep convection (1–10 km) and turbulence (0.1–1 km) requires ponderation and in-depth explorations [17,18,19]. The precipitation and storms observed using radar and satellites are among the most difficult to simulate, which is a consequence of the intertwined consecutive physical processes of NWPs with multiplicative error propagations [20]. Convective-scale NWPs also have fundamental theoretical challenges such as the mathematical characteristics of the underlying partial differential equations as well as the predictability and probability issues related to the nonlinear dynamics of the convective systems with effective dimensions much higher than those of the balanced synoptic systems [1]. It has long been recognized that the convective atmospheric motions are of multiscale interactions [19,21,22,23]. Currently, the first-principle multiscale formulation is beyond the traditional NWP modeling paradigm. In addition, a representation gap exists between satellite images and radar data. Geostationary satellites observe cloud evolution from a global perspective [24], but they are limited to detecting cloud tops and hardly probe the internal structure of clouds.
Deep learning (DL) has recently emerged as a general data-driven technology to represent the spatiotemporal features that cross multiple scales and are not captured well by geophysical models [25]. DL techniques can explore the rich patterns in radar data with deep networks of neurons and improve the precipitation nowcasting skill [26]. Numerous DL applications for the convective atmosphere have been proposed, ranging from radar- or satellite-based nowcasting [27,28,29,30] to reconstructions of radar data from satellites [31,32,33]. However, there are few applications aiming at bridging the representation gap for the fusion between radar data, satellite images, and NWP simulations. Accordingly, it remains largely unexplored how the deep networks represent the convective atmosphere. In addition, these deep networks are usually considered black boxes with limited physical interpretations. Here, we attempt to retrieve the deep network representations by reconstructing the radar reflectivity data from NWP simulations and satellite observations and then probe the structure of the obtained representations by diagnosing their relations with physical quantities such as NWP variables and satellite images. This attempt aims to reveal the potential of data-driven DL models to bridge the representation gaps between multiscale multi-source data. Hopefully, this potential of multiscale representation with investigations of physical interpretations could make the DL models more transparent and inspire innovative model–data fusion methods that could overcome the conventional limits of nowcasting.

2. Data and Methods

The study area is the Beijing–Tianjin–Hebei (BTH) region ([36°N, 113°E] × [43°N, 120°E]), which is vulnerable to floods caused by heavy summer precipitation. The study period is from June to September for the years 2015 and 2016, when precipitation is more frequent over this region.

2.1. Radar Echo Data

Radar reflectivity data are collected from six Doppler radars that sufficiently cover the BTH region from the Chinese new generation weather radar network (ChIna New generation doppler weather RADar, CINRAD), with four radars of type CINRAD/SA located in Beijing, Tanggu, Shijiazhuang, Qinhuangdao, and two radars of type CINRAD/CB located in Zhangjiakou and Chengde, respectively (Figure S1a). The SA and CB Doppler radars are S-band radars and C-band radars, respectively. The collected radar echo data are interpolated from plan position indicators (PPIs) to constant altitude PPIs (CAPPIs) with a vertical linear interpolation method [34,35]. Then, the radar data in the polar coordinate are mapped onto 0.01° × 0.01° Cartesian grids using the nearest neighbor interpolation method. After that, the data from different radars around the same time (e.g., within 3 min) are combined, and maximum values are preserved for overlapped grid cells. The resulting radar echo data have a temporal resolution of 6 min. The combined radar data are then smoothed and filtered using a convolution threshold method [36,37]. We calculate the maximum radar data based on CAPPIs at 1500 m, 2000 m, 2500 m, 3000 m, and 3500 m above sea level, a typical range of elevations around the level of free convection where convection develops actively.

2.2. Numerical Model Simulations

The Weather Research and Forecasting (WRF) model [38] is used as a convection-permitting modeling system over the BTH region with three nested domains at horizontal resolutions of 9, 3, and 1 km, respectively (Figure S1b). By switching off the cumulus parameterization of the inner two nested domains, convections are explicitly resolved in this setting. Detailed configuration is listed in Table 1. We run a 36 h simulation at a temporal resolution of 30 min, beginning at 12:00 UTC each day with the first 12 h of simulations as spin-ups. The remaining 24 h of simulations of the innermost domain are used to provide the meteorological input for deep networks. The initial and boundary conditions for the simulations are provided by the NCAR/NCEP 1 ° × 1 ° reanalysis data. We compare the simulations with weather station observations (Table S1) and verify that the performance on most selected meteorological factors is close to those in other state-of-the-art WRF studies [39,40]. We select 14 daily simulated variables commonly used in convective nowcasting from three categories (i.e., dynamic variables, thermodynamic variables, and moisture-related variables) to build the dataset for learning, such as the three components of wind velocity (U, V, W), K index (K), water vapor mixing ratio (WVMR), and relative humidity (RH). Five of the fourteen variables are three-dimensional and extracted from the pressure levels of 850 hPa, 700 hPa, and 500 hPa, generally around the elevations of the radar echo data. The other nine variables are two-dimensional. Therefore, the input data from WRF simulations have 24 channels (5 × 3 + 9 = 24). Detailed information about all the selected variables can be found in Table S2. These variables are mapped onto the same grid of radar data using a linear interpolation method.

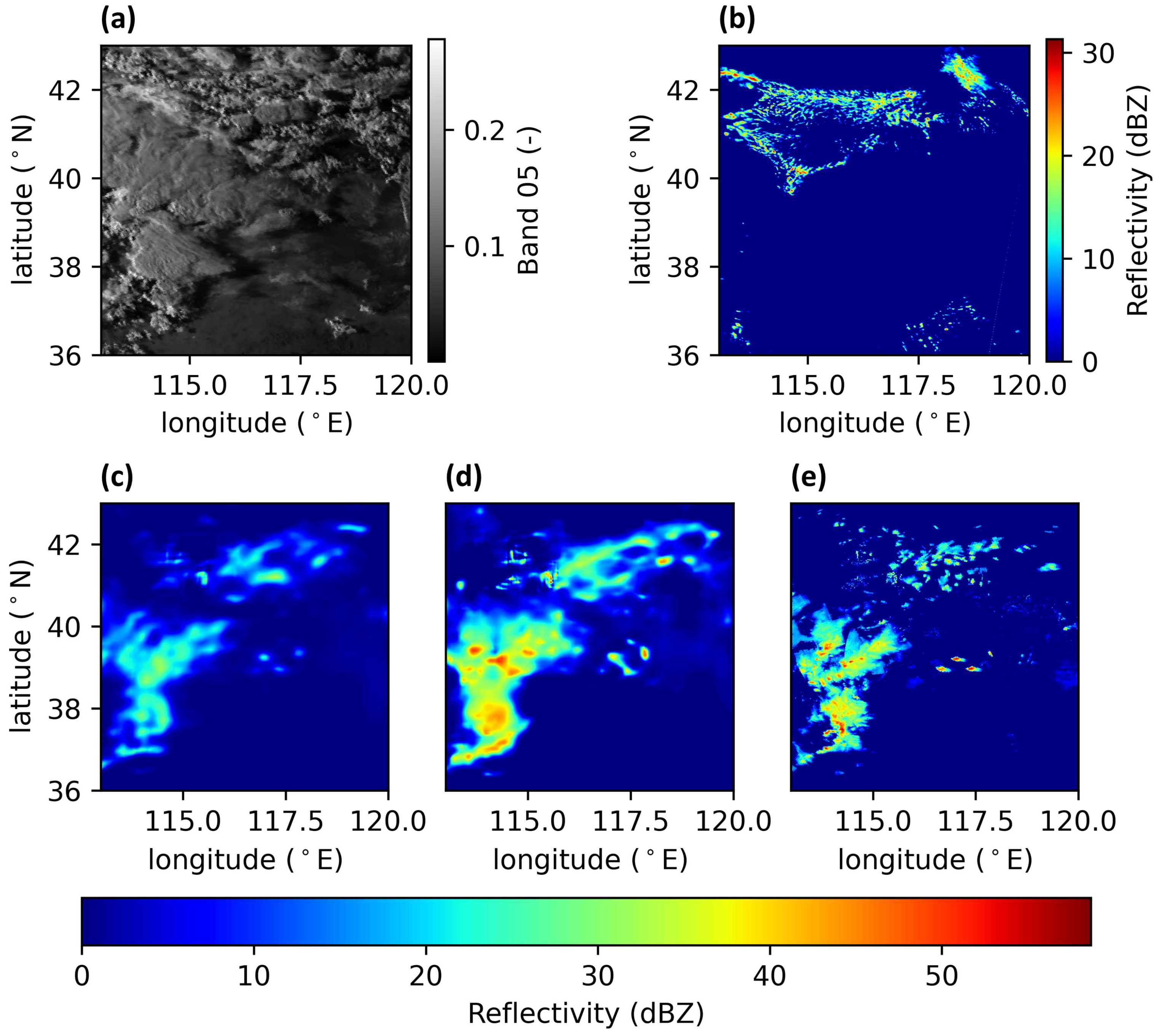
2.3. Geostationary Satellite Images

Five infrared bands (5th, 8th, 13th, 15th, and 16th) of data are collected from the Himawari-8 geostationary satellite products. These satellite images can provide global information on cloud properties such as phases and heights (Table 2) with high spatiotemporal resolution (2 km and 10 min) [48]. We also extract the deep convective cloud classification (CCC) data from the Himawari-8 cloud type products by assigning 1 to the grids of the deep convective cloud and 0 to the grids of other cloud types. Therefore, we obtain 6-channel input data from the Himawari-8 satellite products. All the satellite products are remapped in a way similar to the mapping of the WRF variables.

2.4. Data Preprocessing

We have obtained 30-channel input data from the WRF simulations and the Himawari-8 satellite products, and 1-channel labels from the radar echo data on the common grid of 0.01° × 0.01° over the BTH region (i.e., 700 × 700 horizontally). We first match the input data with labels for the same time and form a dataset of 2647 samples. We then use the min–max normalization to scale each channel of data in the dataset to be in the range of [0, 1], where the maximum value for the radar echo data is set at 70 dBZ, so that the effect of outliers can be suppressed. Moreover, we fill in missing or invalid values with 0 for the normalized dataset.

2.5. Deep Network Model

We adopt a U-Net for the representation learning of the radar echo data (Figure 1). The U-Net deep network is a convolutional neural network (CNN) variant originating from biomedical image segmentation [49] and is here repurposed for a regression task as in many previous studies [31,33,50,51]. It preserves the hierarchical convolutional structure of a CNN in its left contracting path, and uses upsampling operations in successive layers to form a right expansive path. Consequently, the network has a ‘U’ shape, hence its name. The U-Net is an encoder–decoder network architecture that allows the end-to-end learning of multiscale features and outputs with desired dimensions (i.e., 700 × 700 in this study). In general, early layers in the contrasting path learn small-scale features such as textures and edges, whereas deep layers learn large-scale features such as semantic information. The U-Net is equipped with so-called skip connections that perform identity mappings of low-level features from the contrasting path (encoder) to the expansive path (decoder) at corresponding levels. The U-Net combines large-scale information with small-scale information brought by the skip connections for reconstructing the data from the learnt multiscale features. Such a network architecture and reconstruction process are appealing for our study on how radar data are represented by deep networks.
Concretely, the U-Net depicted in Figure 1 has eight blocks (Block-As in gray) in the encoder and eight blocks (Block-Bs in blue) in the decoder, followed by an individual convolutional block (Block-C in orange). Each Block-A consists of a convolutional layer followed by a batch normalization layer [52] and a LeakyReLU activation layer. The 1st, 2nd, 4th, 6th, and 7th Block-As convolve the data with 4 × 4 convolution filters with 2 × 2 strides to reduce resolutions, enabling the subsequent layers to detect patterns in expanded areas. The 3rd Block-A employs 3 × 3 convolution filters with 2 × 2 strides to produce the output of a certain dimension (i.e., 88 × 88 horizontally). The remaining Block-As contain 3 × 3 convolution filters with 1 × 1 strides. All convolutional operations are carried out with a zero padding of size 1. The respective numbers of convolution filters in the eight Block-As are 36, 72, 144, 288, 288, 288, 288, and 288. Each Block-B in the decoder section consists of a bilinear upsampling layer, a 3 × 3 convolutional layer, a batch normalization layer, and a LeakyReLU activation layer, except for the 8th Block-B, which does not have the LeakyReLU activation layer. The respective numbers of convolution filters in eight Block-Bs are 288, 288, 288, 288, 144, 72, 36, and 1. Finally, an individual Block-C is added, which is composed of a 1 × 1 convolutional layer, a 3 × 3 convolutional layer, a 1 × 1 convolutional layer, and a ReLU-6 activation layer, which is considered to facilitate the learning of sparse features [53]. Therefore, the 30-channel input data are mapped into one-channel radar echo data reconstructions.

2.6. Training

Since we do not optimize the hyperparameters of the U-Net, we divide the dataset (2647 samples) in time order only into a training set (the first ~90%, 2387 samples) and a test set (the remaining 260 samples). We employ two types of loss functions for training (that is, the objective function penalizing the discrepancy between the radar echo observations and the reconstructions generated by the U-Net). The first type is the mean square error (MSE), and we denote the resulting network of this type as UNet-MSE. The second type of loss function is the echo-weighted mean square error (EWMSE), with larger weights assigned to grid cells of higher echo intensity [28]. The resulting network of this type is denoted as UNet-EW. The calculations of the MSE and the EWMSE can be found in Text S1. The U-Net models are trained using the stochastic gradient descent (SGD) with the momentum algorithm [54] (momentum = 0.9) with batch size 8. The initial learning rate is set as 1 × 10−5. The U-Net model is trained until the loss function shows no reduction on the test set for 100 subsequent epochs. We stop the trainings of the UNet-MSE and the UNet-EW at the 96th and the 92nd epoch, respectively. Since we obtain satisfactory trained models and the reconstruction accuracy is not our ultimate goal, we do not use data augmentation for potential improvement.

2.7. Evaluations and Interpretations

The performance of the U-Net reconstructions is evaluated by five indices, namely the root mean square error (RMSE), the mean error (ME), the critical success index (CSI), the probability of detection (POD), and the false alarm rate (FAR). RMSE and ME account for the difference between the reconstructed and observed echo data. CSI and POD measure the precision of reconstructions, whereas FAR measures the degree of overestimation. All indices range from 0% to 100%. Ideal CSI and POD values are supposed to approach 100%, whereas ideal FAR values are the opposite. Moreover, structural similarity (SSIM) is calculated in the following analysis, which quantifies the similarity between the visible structures of two images. SSIM is a value between −1 (perfect anti-correlation) and +1 (perfect similarity) and a value of 0 indicates no similarity. The calculations of these indices are detailed in Text S2.
To investigate the physical interpretations of the learnt deep network models, we propose a sensitivity analysis method inspired by Ankenbrand et al. [55]. We intentionally perturb the input data and then diagnose the relationships between the multiscale features and the input physical quantities by checking the consequences of perturbations on the reconstructions. Two types of perturbations are considered. First, we flip the input data from left to right and scale them by multiplying a coefficient. We denote this sensitivity analysis experiment as SA-a. Second, we evaluate the role of each input quantity by nullifying it while keeping other input quantities unchanged. This sensitivity analysis experiment is denoted as SA-b.

3. Results

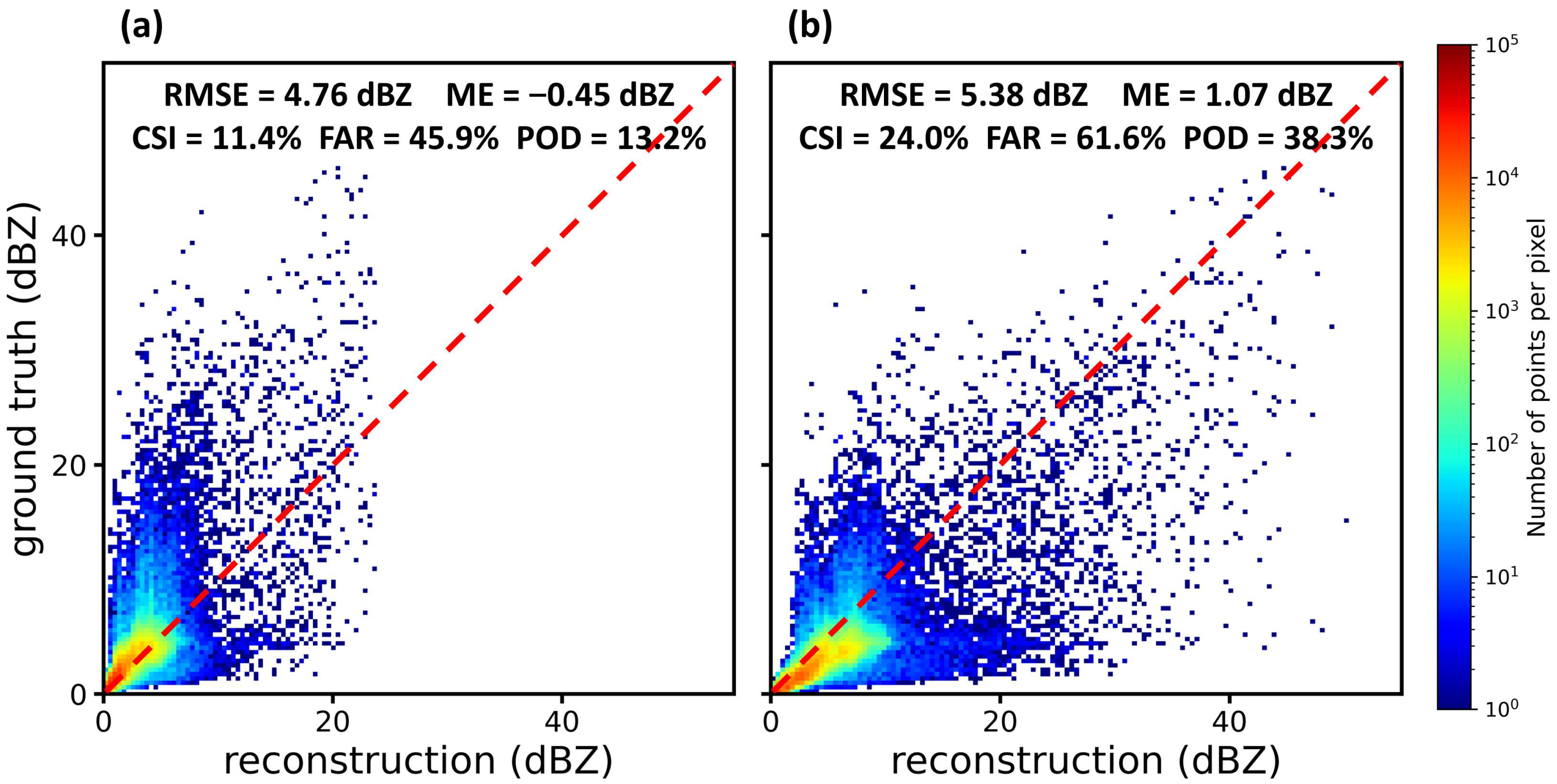
3.1. Echo Reconstructions

Figure 2 shows the performance of reflectivity data reconstructions with the deep networks. The UNet-MSE and UNet-EW networks reconstruct the echoes well, with RMSEs of 4.76 and 5.38 dBZ, respectively. Because most radar echoes are of low intensity, training with unweighted MSE loss functions will bias towards echoes of low intensity. The UNet-MSE networks systematically underestimate the echoes, especially those with high intensity. However, echoes of higher intensity are the most valuable radar signals that directly observe the precipitation and convective processes. Adding more weights on intense echoes for training is beneficial for reconstructing richer sparse high intensity patterns. The reconstructions in this case thus either overestimate or underestimate the intense echoes, which explains the slight increases in the RMSE and FAR values of the UNet-EW networks over the UNet-MSE networks. The richer patterns reconstructed by the UNet-EW networks have better CSI and POD scores, and we will further diagnose their network structures.
Figure 3 details a case of reconstruction at 09:30 UTC on 10 September 2016 from the test set. The spatial distribution of clouds from satellite images (Figure 3a) outlines the overall shape and location of echoes (Figure 3e). By contrast, the WRF-simulated reflectivity data (Figure 3b) miss a majority of the observed echo distribution. Indeed, the precipitation and convective processes are among the most difficult to simulate with NWPs. Nevertheless, our simulations are qualified to represent the general atmospheric conditions (Table S1), so they can provide dynamic and thermodynamic information for echo reconstruction. Note that we do not include the WRF-simulated reflectivity data in the input data of the U-Net deep networks. Based on the multi-source information, the reconstructions by deep networks well produce echo patterns, locations, and intensities (Figure 3c,d). Compared with the UNet-MSE network, the UNet-EW network (Figure 3d) exhibits more precise details such as clearer edges and high values. Data-driven deep learning techniques effectively reduce the gap of representation from the NWP simulations and satellite images to the radar echoes and tend to encode the missing physics in their network weights. Other cases of reconstructions show similar performances (Figures S3–S9).

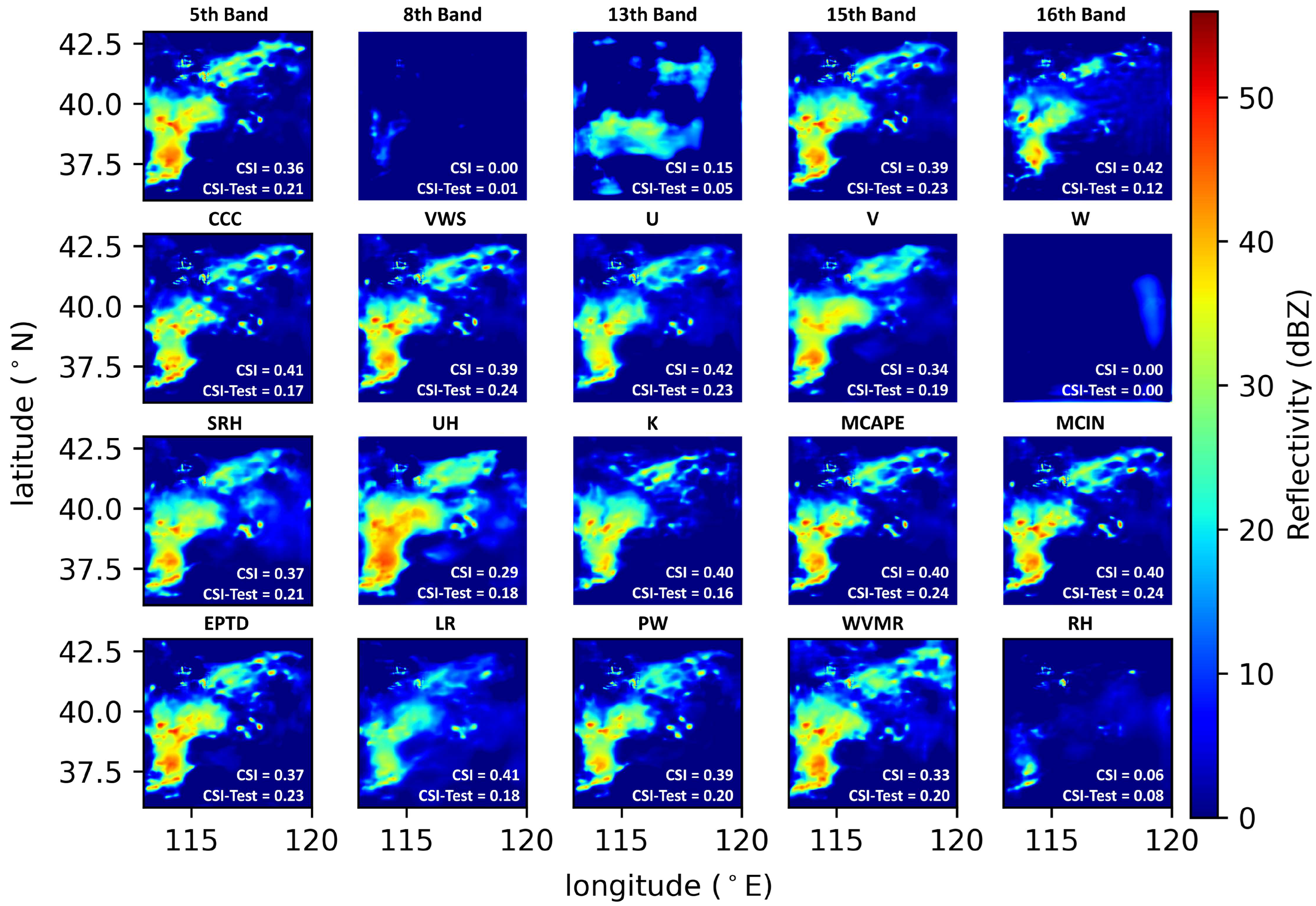
3.2. Multiscale Representation

The multiple layers of features encoded in the contracting path of U-Net are visualized in a naïve way [57]. In this way, a multiscale representation (MSR) of the radar data can be revealed and analyzed. Figure 4 exemplifies such an MSR for the reconstruction case in Figure 3. The multiscale features of the radar echo data appear to be automatically stratified in the multi-layer hierarchical structure of the U-Net, and are especially manifested in the deeper part, indicating the greater capacity of deep networks than shallow networks to represent multiscale high-dimensional relationships among multi-source data (e.g., [58,59]). Apart from the first layer with mostly texture-like information, the locations of echo signals (upper left triangles in Figure 4) are recognized in all subsequent layers and largely correspond to the cloud locations from satellite images. The location-aware ability of U-Net is one of the key factors for its success in image segmentation. The small-scale features in the shallow layers (first–third) still demonstrate no clear echo patterns. These small-scale features such as the echo intensities (hexagons in Figure 4) as well as larger-scale features like the echo shapes (ellipses in Figure 4) emerge in the middle layers (fourth–sixth). The shapes are more visibly related to the satellite images, whereas the sources of intensities need further investigation (see Section 3.3). The features in the deepest layers (seventh and eighth) are rather global descriptions of echoes and may have some semantic meanings. MSRs for other reconstruction cases manifest similar stratifications (see Figures S10–S16 for more examples).

3.3. Physical Interpretations of the MSR

We further investigate the physical interpretations of the MSR through sensitivity analysis. The SA-a experiments assess the overall contributions of the WRF simulations and satellite images to reconstructions by flipping or attenuating these different sets of input data. Figure 5 shows the resulting diverse reconstructions, where the CSI and SSIM of reconstructions of this case and over the test set are calculated. When all input data are flipped, the reconstruction flips accordingly (Figure 5a), but does not yield a perfect flipping of the original reconstruction (Figure 5i). This indicates that factors other than the input data (e.g., the topographic conditions) may also play a role in the spatial distribution of the reconstructions. The echo shapes and locations are much more influenced by the satellite images (Figure 5b, SSIM = −0.07) than by the WRF simulations (Figure 5c,g,h with higher SSIM). Moreover, this influence is mainly related to the spatial distribution of the satellite images rather than changes in magnitude (Figure 5e,f). Concerning the echo intensities, the representation is much more sensitive to the WRF simulations (Figure 5g,h, especially in Figure 5h CSI = 0.26 and CSI-Test = 0.17) than to the satellite images (Figure 5e,f). This sensitivity appears to depend more on the value than on the spatial distribution of the simulations (Figure 5c). Other cases of reconstructions have similar interpretations (Figures S17–S23).
Figure 6 shows the reconstructions with CSI for the SA-b experiment (see Figures S24–S30 for more examples). The MSR here is predominantly sensitive to the satellite images from the 8th and 13th bands of Himawari-8 as well as the WRF-simulated W, K, and RH. These bands of satellite images provide information on middle and upper tropospheric humidity and cloud-top properties, respectively. The three dominant WRF variables describe the vertical motion of the air, the atmospheric instability, and the water vapor content in the atmosphere. They correspond well with the three key ingredients for deep convection initiation and evolution, namely lift, instability, and moisture [60]. Therefore, for the current study, the MSR may encapsulate these complex atmospheric physics in their learnt multiscale features.

4. Summary and Discussions

We have addressed the difficulty of model–data fusion for convective nowcasting with a representation problem. Deep learning techniques were applied to represent the fine-grained radar reflectivity data by reconstructing them from the WRF model simulations and the Himawari-8 satellite products. We learnt a multiscale representation (MSR) of the radar data using the U-Net deep networks. The MSR manifested a stratification, and the richest features were in the middle layers. Sensitivity analyses on the retrieved representation showed that small-scale patterns like echo intensities were more sensitive to the magnitude of numerical model simulations, whereas larger-scale information about the shapes and locations was mainly from the spatial distribution of satellite images.
The retrieved multiscale representation takes advantage of the ability of deep learning techniques [61] to find complex relationships in data, which are otherwise difficult to model or formulate in traditional approaches, especially when the underlying physics is complex and multiscale or even unknown. The deep network representation can organize the learnt features at increasing levels of abstraction from local fine-grained details to global semantic information [62,63,64]. Such multiscale representation could inspire innovative methods that make use of the features in the mapping from numerical model simulations to radar data as well as in convective nowcasting, where machine learning has been demonstrated to be a useful tool [65]. Note that multiscale representations can also be obtained using traditional methods such as wavelets in a more compact manner [64,66]. However, in general, these traditional methods require domain expertise for feature extraction and should be combined with deep learning techniques for automatic end-to-end feature extractions [67,68].
This study has a number of limitations. First, although radar data provide routine verifications for convection-permitting models [10,69], they are not perfect and can suffer from various errors [70,71]. Hence, the retrieved multiscale representation may occasionally fit noise rather than signals. Second, our WRF simulations were configured at a convection-permitting resolution, but we did not tailor and optimize the WRF configurations and examine in-depth model–radar comparisons (e.g., [69]), which is not the main objective of this representation study. Third, we did not test other deep learning techniques such as CNN variants other than U-Nets or generative deep networks. These deep networks, once successfully trained, are known to have similar performances [72]. Finally, convective processes can vary by regions, so the learnt multiscale representation needs evaluation across regions, such as considering the role of terrain during training or applying the obtained representation to different regions. Hence, there is still room for qualitative and quantitative improvement in the accuracy of the reconstructed echo reflectivity. Despite these limitations, our finding on the functioning and potential of the deep network representation for convective atmosphere should not be affected.
For now, the proposed representation of radar echo data may not meet the requirements of practical convective nowcasting. We consider our attempt as a step towards a deep network framework of multiscale representation with physical interpretations that relate the features in hidden network layers with the convective atmosphere. Our sensitivity analyses for physical interpretations have been experimental. It is possible to apply more formal methods—notably explainable artificial intelligence techniques [62,73,74,75]—to analyze the cause-and-effect relationships among radar data, satellite images, and convective dynamics. The multiscale features with physical interpretations are seldom investigated in radar data assimilation practices [9,12]. Data assimilation based on multiscale features should merge with artificial intelligence techniques [76,77] and should be inevitably “deep” in some sense, either in models [78,79], in data (this study), or in assimilation algorithms [80]. Such deep assimilating techniques may be essential to overcome the conventional limits of convective nowcasting.

Supplementary Materials

The supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15143466/s1, Figure S1: (a): The selected six radar stations in the Beijing-Tianjin-Hebei region. (b): WRF simulation area with three nested domains; Figure S2: Visualizations of input data of the reconstruction sample at 09:30 UTC on 10 September 2016; Figure S3: A case of reconstruction at 00:30 UTC on 4 September 2016 from the test set; Figure S4: A case of reconstruction at 05:30 UTC on 4 September 2016 from the test set; Figure S5: A case of reconstruction at 08:30 UTC on 4 September 2016 from the test set; Figure S6: A case of reconstruction at 08:00 UTC on 10 September 2016 from the test set; Figure S7: A case of reconstruction at 03:30 UTC on 11 September 2016 from the test set; Figure S8: A case of reconstruction at 06:30 UTC on 13 September 2016 from the test set; Figure S9: A case of reconstruction at 07:30 UTC on 23 September 2016 from the test set; Figure S10: A multiscale representation of the radar echo data at 00:30 UTC on 4 September 2016; Figure S11: A multiscale representation of the radar echo data at 05:30 UTC on 4 September 2016; Figure S12: A multiscale representation of the radar echo data at 08:30 UTC on 4 September 2016; Figure S13: A multiscale representation of the radar echo data at 08:00 UTC on 10 September 2016; Figure S14: A multiscale representation of the radar echo data at 03:30 UTC on 11 September 2016; Figure S15: A multiscale representation of the radar echo data at 06:30 UTC on 13 September 2016; Figure S16: A multiscale representation of the radar echo data at 07:30 UTC on 23 September 2016; Figure S17: Reconstructions of the radar echo data at 00:30 UTC on 4 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S18: Reconstructions of the radar echo data at 05:30 UTC on 4 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S19: Reconstructions of the radar echo data at 08:30 UTC on 4 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S20: Reconstructions of the radar echo data at 08:00 UTC on 10 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S21: Reconstructions of the radar echo data at 03:30 UTC on 11 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S22: Reconstructions of the radar echo data at 03:30 UTC on 11 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S23: Reconstructions of the radar echo data at 07:30 UTC on 23 September 2016 by the UNet-EW deep network for the SA-a experiments; Figure S24: Reconstructions of the radar echo data at 00:30 UTC on 4 September 2016 by the UNet-EW deep network for the SA-b experiments; Figure S25: Reconstructions of the radar echo data at 05:30 UTC on 4 September 2016 by the UNet-EW deep network for the SA-b experiments; Figure S26: Reconstructions of the radar echo data at 08:30 UTC on 4 September 2016 by the UNet-EW deep network for the SA-b experiments; Figure S27: Reconstructions of the radar echo data at 08:00 UTC on 10 September 2016 by the UNet-EW deep network for the SA-b experiments; Figure S28: Reconstructions of the radar echo data at 03:30 UTC on 11 September 2016 by the UNet-EW deep network for the SA-b experiments; Figure S29: Reconstructions of the radar echo data at 06:30 UTC on 13 September 2016 by the UNet-EW deep network for the SA-b experiments; Figure S30: Reconstructions of the radar echo data at 07:30 UTC on 23 September 2016 by the UNet-EW deep network for the SA-b experiments; Table S1: Average evaluation indices comparing hourly WRF simulations and observations; Table S2: Descriptions of the selected and computed physical quantities from WRF simulations; Text S1: The calculations of the MSE and the EWMSE; Text S2: The calculations of the evaluation indices.

Author Contributions

Conceptualization, L.W. and M.Z.; methodology, M.Z. and Q.L.; software, Q.W. and Y.W.; validation, M.Z., Q.L. and S.Z.; formal analysis, M.Z.; investigation, M.Z. and L.W.; resources, L.W. and Q.W.; data curation, D.S.; writing—original draft preparation, M.Z. and L.W.; writing—review and editing, M.Z., L.W. and S.Z.; visualization, M.Z.; supervision, L.W., Z.W. and X.P.; project administration, L.W. and Z.W.; funding acquisition, L.W. and Z.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Informatization Plan of Chinese Academy of Sciences (Grant No. CAS-WX2021SF-0107), the National Key Basic Research Program of China (Grant No. 2014CB441401), the major science and technology project of Inner Mongolia Autonomous Region (Grand No. 2020ZD0013), and the Pioneer Hundred Talents Program of the Chinese Academy of Sciences.

Data Availability Statement

The test dataset (processed Himawari-8 satellite images, WRF simulations, and radar echo data), the codes supporting the analysis, and the trained U-Net model parameter files are available in a Zenodo archive (https://doi.org/10.5281/zenodo.7798803, accessed on 1 June 2023).

Acknowledgments

The authors thank the editors and reviewers for their valuable contributions and support throughout this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yano, J.-I.; Ziemianski, M.Z.; Cullen, M.; Termonia, P.; Onvlee, J.; Bengtsson, L.; Carrassi, A.; Davy, R.; Deluca, A.; Gray, S.L.; et al. Scientific challenges of convective-scale numerical weather prediction. Bull. Am. Meteorol. Soc. 2018, 99, 699–710. [Google Scholar] [CrossRef]
  2. Wyngaard, J.C. Toward numerical modeling in the “terra incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
  3. Dixon, M.; Wiener, G. TITAN: Thunderstorm identification, tracking, analysis, and nowcasting—A radar-based methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
  4. Pulkkinen, S.; Nerini, D.; Hortal, A.A.P.; Velasco-Forero, C.; Seed, A.; Germann, U.; Foresti, L. Pysteps: An open-source Python library for probabilistic precipitation nowcasting (v1.0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef] [Green Version]
  5. James, P.M.; Reichert, B.K.; Heizenreder, D. NowCastMIX: Automatic integrated warnings for severe convection on nowcasting time scales at the German weather service. Weather Forecast. 2018, 33, 1413–1433. [Google Scholar] [CrossRef]
  6. Foresti, L.; Sideris, I.V.; Panziera, L.; Nerini, D.; Germann, U. A 10-year radar-based analysis of orographic precipitation growth and decay patterns over the Swiss Alpine region. Q. J. R. Meteorol. Soc. 2018, 144, 2277–2301. [Google Scholar] [CrossRef]
  7. Sideris, I.V.; Foresti, L.; Nerini, D.; Germann, U. NowPrecip: Localized precipitation nowcasting in the complex terrain of Switzerland. Q. J. R. Meteorol. Soc. 2020, 146, 1768–1800. [Google Scholar] [CrossRef]
  8. Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.-W.; Golding, B.; et al. Use of NWP for nowcasting convective precipitation. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef] [Green Version]
  9. Fabry, F.; Meunier, V. Why are radar data so difficult to assimilate skillfully? Mon. Weather Rev. 2020, 148, 2819–2836. [Google Scholar] [CrossRef]
  10. Clark, P.; Roberts, N.; Lean, H.; Ballard, S.P.; Charlton-Perez, C. Convection-permitting models: A step-change in rainfall forecasting. Meteorol. Appl. 2016, 23, 165–181. [Google Scholar] [CrossRef] [Green Version]
  11. Gustafsson, N.; Janjic, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bucanek, A.; et al. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Q. J. R. Meteorol. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef] [Green Version]
  12. Bannister, R.N.; Chipilski, H.G.; Martinez-Alvarado, O. Techniques and challenges in the assimilation of atmospheric water observations for numerical weather prediction towards convective scales. Q. J. R. Meteorol. Soc. 2020, 146, 1–48. [Google Scholar] [CrossRef]
  13. Bluestein, H.B.; Carr, F.H.; Goodman, S.J. Atmospheric observations of weather and climate. Atmosphere-Ocean 2022, 60, 149–187. [Google Scholar] [CrossRef]
  14. Vignon, E.; Besic, N.; Jullien, N.; Gehring, J.; Berne, A. Microphysics of snowfall over coastal east Antarctica simulated by Polar WRF and observed by radar. J. Geophys. Res.-Atmos. 2019, 124, 11452–11476. [Google Scholar] [CrossRef]
  15. Troemel, S.; Simmer, C.; Blahak, U.; Blanke, A.; Doktorowski, S.; Ewald, F.; Frech, M.; Gergely, M.; Hagen, M.; Janjic, T.; et al. Overview: Fusion of radar polarimetry and numerical atmospheric modelling towards an improved understanding of cloud and precipitation processes. Atmos. Chem. Phys. 2021, 21, 17291–17314. [Google Scholar] [CrossRef]
  16. Chow, F.K.; Schar, C.; Ban, N.; Lundquist, K.A.; Schlemmer, L.; Shi, X. Crossing multiple gray zones in the transition from mesoscale to microscale simulation over complex terrain. Atmosphere 2019, 10, 274. [Google Scholar] [CrossRef] [Green Version]
  17. Jeworrek, J.; West, G.; Stull, R. Evaluation of cumulus and microphysics parameterizations in WRF across the convective gray zone. Weather Forecast. 2019, 34, 1097–1115. [Google Scholar] [CrossRef]
  18. Kirshbaum, D.J. Numerical simulations of orographic convection across multiple gray zones. J. Atmos. Sci. 2020, 77, 3301–3320. [Google Scholar] [CrossRef]
  19. Honnert, R.; Efstathiou, G.A.; Beare, R.J.; Ito, J.; Lock, A.; Neggers, R.; Plant, R.S.; Shin, H.H.; Tomassini, L.; Zhou, B. The atmospheric boundary layer and the “gray zone” of turbulence: A critical review. J. Geophys. Res.-Atmos. 2020, 125, e2019JD030317. [Google Scholar] [CrossRef]
  20. Tapiador, F.J.; Roca, R.; Del Genio, A.; Dewitte, B.; Petersen, W.; Zhang, F. Is precipitation a good metric for model performance? Bull. Am. Meteorol. Soc. 2019, 100, 223–234. [Google Scholar] [CrossRef]
  21. Koo, C.C. Similarity analysis of some meso-and micro-scale atmospheric motions. Acta Meteorol. Sin. 1964, 4, 519–522. [Google Scholar] [CrossRef]
  22. Tao, S.Y.; Ding, Y.H.; Sun, S.Q.; Cai, Z.Y.; Zhang, M.L.; Fang, Z.Y.; Li, M.T.; Zhou, X.P.; ZHao, S.X.; Dian, S.T.; et al. The Heavy Rainfalls in China; Science Press: Beijing, China, 1980; p. 225. [Google Scholar]
  23. Surcel, M.; Zawadzki, I.; Yau, M.K. A study on the scale dependence of the predictability of precipitation patterns. J. Atmos. Sci. 2015, 72, 216–235. [Google Scholar] [CrossRef]
  24. Mecikalski, J.R.; Bedka, K.M. Forecasting convective initiation by monitoring the evolution of moving cumulus in daytime GOES imagery. Mon. Weather Rev. 2006, 134, 49–78. [Google Scholar] [CrossRef] [Green Version]
  25. Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
  26. Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
  27. Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Advances in Neural Information Processing Systems; Neural Information Processing Systems: La Jolla, CA, USA, 2015; Volume 28. [Google Scholar]
  28. Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Deep learning for precipitation nowcasting: A benchmark and a new model. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Advances in Neural Information Processing Systems; Neural Information Processing Systems: La Jolla, CA, USA, 2017; Volume 30. [Google Scholar]
  29. Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
  30. Lebedev, V.; Ivashkin, V.; Rudenko, I.; Ganshin, A.; Molchanov, A.; Ovcharenko, S.; Grokhovetskiy, R.; Bushmarinov, I.; Solomentsev, D. Precipitation nowcasting with satellite imagery. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2680–2688. [Google Scholar]
  31. Hilburn, K.A.; Ebert-Uphoff, I.; Miller, S.D. Development and interpretation of a neural-network-based synthetic radar reflectivity estimator using GOES-R satellite observations. J. Appl. Meteorol. Climatol. 2021, 60, 3–21. [Google Scholar] [CrossRef]
  32. Veillette, M.S.; Hassey, E.P.; Mattioli, C.J.; Iskenderian, H.; Lamey, P.M. Creating synthetic radar imagery using convolutional neural networks. J. Atmos. Ocean. Technol. 2018, 35, 2323–2338. [Google Scholar] [CrossRef]
  33. Duan, M.; Xia, J.; Yan, Z.; Han, L.; Zhang, L.; Xia, H.; Yu, S. Reconstruction of the radar reflectivity of convective storms based on deep learning and Himawari-8 observations. Remote Sens. 2021, 13, 3330. [Google Scholar] [CrossRef]
  34. Mohr, C.G.; Vaughan, R.L. Economical procedure for Cartesian interpolation and display of reflectivity factor data in 3-dimensional space. J. Appl. Meteorol. 1979, 18, 661–670. [Google Scholar] [CrossRef]
  35. Zhang, J.; Howard, K.; Xia, W.W.; Gourley, J.J. Comparison of objective analysis schemes for the WSR-88D radar data. In Proceedings of the 31st Conference on Radar Meteorology, Seattle, WA, USA, 6–12 August 2003. [Google Scholar]
  36. Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef] [Green Version]
  37. Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part II: Application to convective rain systems. Mon. Weather Rev. 2006, 134, 1785–1795. [Google Scholar] [CrossRef] [Green Version]
  38. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A description of the Advanced Research WRF version 3. NCAR Tech. Note 2008, 475, 113. [Google Scholar] [CrossRef]
  39. Blanco-Ward, D.; Rocha, A.; Viceto, C.; Ribeiro, A.C.; Feliciano, M.; Paoletti, E.; Miranda, A.I. Validation of meteorological and ground-level ozone WRF-CHIMERE simulations in a mountainous grapevine growing area for phytotoxic risk assessment. Atmos. Environ. 2021, 259, 118507. [Google Scholar] [CrossRef]
  40. Giordano, C.; Vernin, J.; Ramio, H.V.; Munoz-Tunon, C.; Varela, A.M.; Trinquet, H. Atmospheric and seeing forecast: WRF model validation with in situ measurements at ORM. Mon. Not. R. Astron. Soc. 2013, 430, 3102–3111. [Google Scholar] [CrossRef] [Green Version]
  41. Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
  42. Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res.-Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
  43. Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
  44. Jimenez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef] [Green Version]
  45. Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
  46. Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
  47. Zhang, C.; Wang, Y.; Hamilton, K. Improved representation of boundary layer clouds over the southeast Pacific in ARW-WRF using a modified Tiedtke cumulus parameterization scheme. Mon. Weather Rev. 2011, 139, 3489–3513. [Google Scholar] [CrossRef] [Green Version]
  48. Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Japan. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
  49. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention, Pt Iii; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9351, pp. 234–241. [Google Scholar]
  50. Trebing, K.; Stanczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
  51. Li, Y.; Liu, Y.; Sun, R.; Guo, F.; Xu, X.; Xu, H. Convective storm VIL and lightning nowcasting using satellite and weather radar measurements based on multi-task learning models. Adv. Atmos. Sci. 2023, 40, 887–899. [Google Scholar] [CrossRef]
  52. Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
  53. Krizhevsky, A.; Hinton, G. Convolutional Deep Belief Networks on cifar-10. 2010. Available online: http://www.cs.toronto.edu/~kriz/conv-cifar10-aug2010.pdf. (accessed on 26 May 2023).
  54. Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
  55. Ankenbrand, M.J.; Shainberg, L.; Hock, M.; Lohr, D.; Schreiber, L.M. Sensitivity analysis for interpretation of machine learning based segmentation models in cardiac MRI. Bmc Med. Imaging 2021, 21, 27. [Google Scholar] [CrossRef] [PubMed]
  56. Ladwig, W. Wrf-Python, Version 1.2.3; Github: San Francisco, CA, USA, 2017. [CrossRef]
  57. Toda, Y.; Okura, F. How convolutional neural networks diagnose plant disease. Plant Phenomics 2019, 2019, 9237136. [Google Scholar] [CrossRef]
  58. Poggio, T.; Mhaskar, H.; Rosasco, L.; Miranda, B.; Liao, Q. Why and when can deep-but not shallow-networks avoid the curse of dimensionality: A review. Int. J. Autom. Comput. 2017, 14, 503–519. [Google Scholar] [CrossRef] [Green Version]
  59. Mhaskar, H.; Liao, Q.; Poggio, T. When and why Are deep networks better than shallow ones? In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
  60. Doswell, C.A.; Brooks, H.E.; Maddox, R.A. Flash flood forecasting: An ingredients-based methodology. Weather Forecast. 1996, 11, 560–581. [Google Scholar] [CrossRef]
  61. Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [Green Version]
  62. McGovern, A.; Lagerquist, R.; Gagne, D.J., II; Jergensen, G.E.; Elmore, K.L.; Homeyer, C.R.; Smith, T. Making the black box more transparent: Understanding the physical implications of machine learning. Bull. Am. Meteorol. Soc. 2019, 100, 2175–2199. [Google Scholar] [CrossRef]
  63. Bai, J.; Gong, B.; Zhao, Y.; Lei, F.; Yan, C.; Gao, Y. Multi-scale representation learning on hypergraph for 3d shape retrieval and recognition. IEEE Trans. Image Process. 2021, 30, 5327–5338. [Google Scholar] [CrossRef]
  64. Jiao, L.; Gao, J.; Liu, X.; Liu, F.; Yang, S.; Hou, B. Multi-scale representation learning for image classification: A survey. IEEE Trans. Artif. Intell. 2021, 4, 23–43. [Google Scholar] [CrossRef]
  65. Foresti, L.; Sideris, I.V.; Nerini, D.; Beusch, L.; Germann, U. Using a 10-year radar archive for nowcasting precipitation growth and decay: A probabilistic machine learning approach. Weather Forecast. 2019, 34, 1547–1569. [Google Scholar] [CrossRef]
  66. Mallat, S. Group invariant scattering. Commun. Pure Appl. Math. 2012, 65, 1331–1398. [Google Scholar] [CrossRef] [Green Version]
  67. Michau, G.; Frusque, G.; Fink, O. Fully learnable deep wavelet transform for unsupervised monitoring of high-frequency time series. Proc. Natl. Acad. Sci. USA 2022, 119, e2106598119. [Google Scholar] [CrossRef]
  68. Ramzi, Z.; Michalewicz, K.; Starck, J.-L.; Moreau, T.; Ciuciu, P. Wavelets in the deep learning era. J. Math. Imaging Vis. 2023, 65, 240–251. [Google Scholar] [CrossRef]
  69. Wilson, J.; Megenhardt, D.; Pinto, J. NWP and radar extrapolation: Comparisons and explanation of errors. Mon. Weather Rev. 2020, 148, 4783–4798. [Google Scholar] [CrossRef]
  70. Fabry, F. Radar Meteorology: Principles and Practice; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
  71. Sokol, Z.; Szturc, J.; Orellana-Alvear, J.; Popova, J.; Jurczyk, A.; Celleri, R. The role of weather radar in rainfall estimation and its application in meteorological and hydrological modelling-a review. Remote Sens. 2021, 13, 351. [Google Scholar] [CrossRef]
  72. Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [Green Version]
  73. Gagne, D.J., II; Haupt, S.E.; Nychka, D.W.; Thompson, G. Interpretable deep learning for spatial analysis of severe hailstorms. Mon. Weather Rev. 2019, 147, 2827–2845. [Google Scholar] [CrossRef]
  74. Toms, B.A.; Barnes, E.A.; Ebert-Uphoff, I. Physically interpretable neural networks for the geosciences: Applications to Earth system variability. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002002. [Google Scholar] [CrossRef]
  75. Davenport, F.V.; Diffenbaugh, N.S. Using machine learning to analyze physical causes of climate change: A case study of U.S. midwest extreme precipitation. Geophys. Res. Lett. 2021, 48, e2021GL093787. [Google Scholar] [CrossRef]
  76. Bocquet, M.; Brajard, J.; Carrassi, A.; Bertino, L. Bayesian inference of chaotic dynamics by merging data assimilation, machine learning and expectation-maximization. Found. Data Sci. 2020, 2, 55–80. [Google Scholar] [CrossRef] [Green Version]
  77. Geer, A.J. Learning earth system models from observations: Machine learning or data assimilation? Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2021, 379. [Google Scholar] [CrossRef]
  78. Penny, S.G.; Smith, T.A.; Chen, T.C.; Platt, J.A.; Lin, H.Y.; Goodliff, M.; Abarbanel, H.D.I. Integrating recurrent neural networks with data assimilation for scalable data-driven state estimation. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002843. [Google Scholar] [CrossRef]
  79. Bocquet, M.; Farchi, A.; Malartic, Q. Online learning of both state and dynamics using ensemble Kalman filters. Found. Data Sci. 2021, 3, 305–330. [Google Scholar] [CrossRef]
  80. Arcucci, R.; Zhu, J.; Hu, S.; Guo, Y.-K. Deep data assimilation: Integrating deep learning with data assimilation. Appl. Sci. 2021, 11, 1114. [Google Scholar] [CrossRef]
Remotesensing 15 03466 g001 550
Figure 1. The U-Net model architecture.
Figure 1. The U-Net model architecture.
Remotesensing 15 03466 g001
Remotesensing 15 03466 g002 550
Figure 2. Performance of reflectivity data reconstructions with the (a) UNet-MSE and (b) UNet-EW networks. The observed and reconstructed echoes are averaged on a 700 × 700 grid over the BTH region for the test set.
Figure 2. Performance of reflectivity data reconstructions with the (a) UNet-MSE and (b) UNet-EW networks. The observed and reconstructed echoes are averaged on a 700 × 700 grid over the BTH region for the test set.
Remotesensing 15 03466 g002
Remotesensing 15 03466 g003 550
Figure 3. A case of reconstruction at 09:30 UTC on 10 September 2016 from the test set. (a) The satellite image of the 5th band. (b) The WRF-simulated reflectivity data calculated according to [56]. (c) The echo reconstruction by the UNet-MSE network. (d) The echo reconstruction by the UNet-EW network. (e) The observed radar reflectivity data. The rest of the input data can be found in Figure S2.
Figure 3. A case of reconstruction at 09:30 UTC on 10 September 2016 from the test set. (a) The satellite image of the 5th band. (b) The WRF-simulated reflectivity data calculated according to [56]. (c) The echo reconstruction by the UNet-MSE network. (d) The echo reconstruction by the UNet-EW network. (e) The observed radar reflectivity data. The rest of the input data can be found in Figure S2.
Remotesensing 15 03466 g003
Remotesensing 15 03466 g004 550
Figure 4. A multiscale representation of the radar echo data at 09:30 UTC on 10 September 2016. The UNet-EW deep network is used for the reconstruction of echo data. Only parts of the input data for this reconstruction are presented. Hidden features at each hidden layer are averaged along the channel dimension.
Figure 4. A multiscale representation of the radar echo data at 09:30 UTC on 10 September 2016. The UNet-EW deep network is used for the reconstruction of echo data. Only parts of the input data for this reconstruction are presented. Hidden features at each hidden layer are averaged along the channel dimension.
Remotesensing 15 03466 g004
Remotesensing 15 03466 g005 550
Figure 5. Reconstructions of the radar echo data at 09:30 UTC on 10 September 2016 by the UNet-EW deep network for the SA-a experiments. The perturbations are conducted by (a) flipping all the input data, (b) flipping only the satellite images, (c) flipping only the WRF simulations, (d) multiplying all the input data (except for the binary CCC data) by 0.9, (e) multiplying only the satellite images (except for the binary CCC data) by 0.9 and (f) 0.8, and (g) multiplying only the WRF simulations by 0.9 and (h) 0.8. Also shown is the (i) original reconstruction without perturbation. CSI/SSIM and CSI-/SSIM-Test are CSI/SSIM of reconstructions of this case and over the test set, respectively, compared with radar echo observations.
Figure 5. Reconstructions of the radar echo data at 09:30 UTC on 10 September 2016 by the UNet-EW deep network for the SA-a experiments. The perturbations are conducted by (a) flipping all the input data, (b) flipping only the satellite images, (c) flipping only the WRF simulations, (d) multiplying all the input data (except for the binary CCC data) by 0.9, (e) multiplying only the satellite images (except for the binary CCC data) by 0.9 and (f) 0.8, and (g) multiplying only the WRF simulations by 0.9 and (h) 0.8. Also shown is the (i) original reconstruction without perturbation. CSI/SSIM and CSI-/SSIM-Test are CSI/SSIM of reconstructions of this case and over the test set, respectively, compared with radar echo observations.
Remotesensing 15 03466 g005
Remotesensing 15 03466 g006 550
Figure 6. Reconstructions of the radar echo data at 09:30 UTC on 10 September 2016 by the UNet-EW deep network for the SA-b experiments. Each reconstruction is obtained by setting the listed physical quantity to zero while keeping other quantities unchanged. CSI and CSI-Test are CSI of reconstructions of this case and over the test set, respectively, compared with radar echo observations.
Figure 6. Reconstructions of the radar echo data at 09:30 UTC on 10 September 2016 by the UNet-EW deep network for the SA-b experiments. Each reconstruction is obtained by setting the listed physical quantity to zero while keeping other quantities unchanged. CSI and CSI-Test are CSI of reconstructions of this case and over the test set, respectively, compared with radar echo observations.
Remotesensing 15 03466 g006
Table
Table 1. Parameterization schemes used in WRF simulations.
Table 1. Parameterization schemes used in WRF simulations.
ProcessParameterization Scheme
MicrophysicsWSM3 [41]
Longwave radiationRRTM [42]
Shortwave radiationDudhia [43]
Surface layerRevised MM5 Monin–Obukhov [44]
Surface physicsUnified Noah land surface [45]
Planetary boundary layerYSU [46]
CumulusModified Tiedtke [47] (only for the outermost domain)
Table
Table 2. Descriptions of the selected Himawari-8 satellite images.
Table 2. Descriptions of the selected Himawari-8 satellite images.
Band NumberCentral Wavelength (µm)Concerned Physical Properties
51.6Cloud phases
86.2Middle and upper tropospheric humidity
1310.4Clouds and cloud top
1512.4Clouds and total water
1613.3Cloud heights
Note. Himawari-8 satellite images listed above were supplied by the P-Tree System, Japan Aerospace Exploration Agency (JAXA).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhu, M.; Liao, Q.; Wu, L.; Zhang, S.; Wang, Z.; Pan, X.; Wu, Q.; Wang, Y.; Su, D. Multiscale Representation of Radar Echo Data Retrieved through Deep Learning from Numerical Model Simulations and Satellite Images. Remote Sens. 2023, 15, 3466. https://doi.org/10.3390/rs15143466

AMA Style

Zhu M, Liao Q, Wu L, Zhang S, Wang Z, Pan X, Wu Q, Wang Y, Su D. Multiscale Representation of Radar Echo Data Retrieved through Deep Learning from Numerical Model Simulations and Satellite Images. Remote Sensing. 2023; 15(14):3466. https://doi.org/10.3390/rs15143466

Chicago/Turabian Style

Zhu, Mingming, Qi Liao, Lin Wu, Si Zhang, Zifa Wang, Xiaole Pan, Qizhong Wu, Yangang Wang, and Debin Su. 2023. "Multiscale Representation of Radar Echo Data Retrieved through Deep Learning from Numerical Model Simulations and Satellite Images" Remote Sensing 15, no. 14: 3466. https://doi.org/10.3390/rs15143466

APA Style

Zhu, M., Liao, Q., Wu, L., Zhang, S., Wang, Z., Pan, X., Wu, Q., Wang, Y., & Su, D. (2023). Multiscale Representation of Radar Echo Data Retrieved through Deep Learning from Numerical Model Simulations and Satellite Images. Remote Sensing, 15(14), 3466. https://doi.org/10.3390/rs15143466

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop