Multi-View Data Integration Methods for Radiotherapy Structure Name Standardization
Abstract
:Simple Summary
Abstract
1. Introduction
- We demonstrate that the combination of the textual features (physician-given structure names) and image features (geometric information structures) helps in improving the structure name standardization process.
- We show that even the PTV structure can be identified along with the OARs with the physician-given names.
- We demonstrate that it is still challenging to predict the standard name with only geometric information in real-world clinical datasets.
- We demonstrate that late integration (combining at the prediction level) reduces the false positives and intermediate integration (combining at the feature level) performs better overall on metrics than single-view models on multi-center radiotherapy datasets.
2. Related Work
3. Materials and Methods
3.1. Dataset
3.2. Creation of the Structure Set
3.3. Data Preprocessing
3.3.1. Textual Data Preparation
3.3.2. Geometric Data Preparation
3.4. Multi-View Data Integration Methods
- Early integration: In this method, data from different views were concatenated to form a single feature space. Our dataset was heterogeneous (text and image) in nature, and hence, simple concatenation was not a feasible solution. Each structure was 442,368 features long (considering the imaging features) when it was converted to a single-dimensional binary vector. Simple concatenation of the image feature vector to other features was not feasible here because an increase in dimensionality negatively affected the model training and performance. For that reason, we decided to not implement this approach of integrating the features.
- Intermediate integration: This method converted all the data sources into a common or reduced feature space. This is also known as the transformation-based integration method. Next, the reduced feature vectors were concatenated to construct the final feature vector. The final vector was used to train and optimize the final model.
- Late integration: This method used data from each view to be separately analyzed, and then, the results from each view were integrated. This method has two main advantages over other integration types for heterogeneous data. First, the best suitable algorithm can be chosen depending on each data type. Second, each model is independent of each other and has the opportunity to be executed individually.
3.5. Model Selection
3.5.1. Single View
- Text data (physician-given structure names): We built the structure name standardization models using the combination of different feature extraction techniques, feature weighting, and ML algorithms. We tested NGram(unigram, bi-gram, and tri-grams), character n-grams, and word embedding techniques for feature extraction. For feature weighting, we evaluated the term presence (tp), term count (tc), term frequency (tf), and term frequency-inverse document frequency (tf-idf) techniques. Finally, we compared the following six ML-based classification methods to select the initial model: k-Nearest Neighbors (KNN) [11], SVM-linear [12], SVM-RBF [13], Random Forest (RF) [14], Logistic Regression (LR) [15], and fastText [16]. The scikit-learn library for machine learning [17] was used to build the models. Finally, we selected the fastText algorithm for automatically identifying the standard structure names using the physician-given names based on the performance comparison with other algorithms.
- Image data (3D geometric information of structures): In our initial work, we investigated the radiotherapy structure name standardization using geometric information. In order to extract geometric information, we converted the geometric information into binary vectors and selected the top 100 components with a truncated SVD algorithm. Having thoroughly tested different algorithms, we used the random forest classification algorithm to build our final model [8].
3.5.2. Intermediate Integration
- Image data transformation: We used the image data transformation explained in Section 3.3.2. However, we used the first 50 principal components in this method, which produced better results.
- Text data transformation: We used the fastText algorithm to generate the word embeddings of physician-given names (numerical representation) of size 200.
3.5.3. Late Integration
- Average (AVG): We created the final prediction probability vector by adding element-wise from each view and dividing it by the number of views. The final class was selected whose AVG probability was the highest.
- Maximum (MAX): We selected the maximum from each view, and the resulting vector contained the maximum for each class from all the views. The final class was predicted by selecting the class from this resultant vector with the highest probability.
3.6. Model Evaluation
- K-fold cross-validation: We split the VA-ROQS data into K-folds so that the individual folds were stratified by their corresponding standard names. Next, K-1 folds were used for the training phase, while the other fold for validation. We continued this process in order to validate all of the folds. Here, K indicated the number of folds in which the data were divided, and we used 5 folds.
- VA center-based cross-validation: In this technique, the data from each center were validated separately. Data from 30 centers were further divided such that 2 (n − 1) centers were utilized for the training phase, while the other center’s data were used for validation; this was repeated till each of the centers were validated.
Model Testing
- VA center-based test: We randomly selected 10 VA centers’ data used for testing. With this dataset, we were able to test the model’s ability to generalize on data from multiple VA centers.
- VCU test: We used the data from the VCU to test the model’s ability to generalize over the data coming from outside of the VA centers.
3.7. Performance Measures or Evaluation Metrics
4. Results
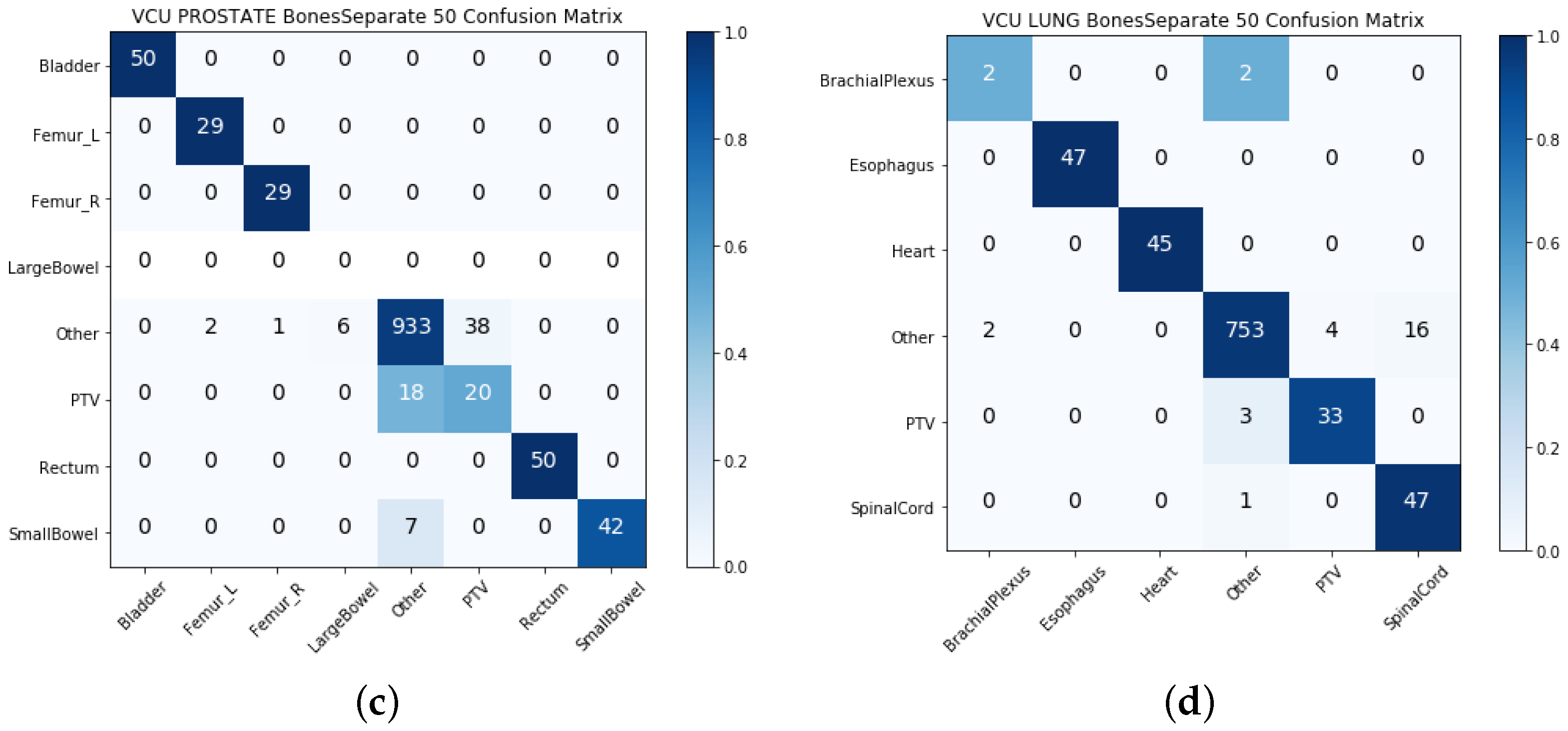
4.1. Single-View Results
4.2. Intermediate Integration Test Results
4.3. Late Integration Test Results
5. Discussion
5.1. Strengths and Limitations
5.1.1. Clinical Limitations
- So far, we were able to identify only OARs and PTV structures. Although these are critical structures, radiotherapy treatment involves other types of structures, such as GTV, CTV, and other derived structures. To fully standardize the data, we need to standardize all structures, not just the OARs and PTV.
- The OARs were originally selected based on the requirements of the VA-ROQS project, whose primary focus was treatment quality assessment based on specific quality metrics [9]. However, radiation oncologists may also delineate many other OAR structures, such as the kidney and liver. To truly build a generalized system to identify all possible structures, the dataset needs to identify all correctly labeled OAR structures, not just the significant OAR structures.
5.1.2. Methodological Limitations
- Extraction of 3D volumes of structures requires selecting the bounding box size to make sure it covers the biggest possible structure in any given disease. Although it only needs to be done once per dataset, it adds to the overhead of the standardization pipeline.
- It is difficult to capture the image semantics by turning images into a single vector and taking the 50 or 100 top components from it.
- We extracted the structures fitted with bounding boxes. Using just structures and discarding the other surrounding structures and anatomical information may negatively affect the model performance.
- In late integration, we tested only AVG and MAX for combining the data, which gives equal importance to both the text and geometric data. As we saw that the single-view results on the geometric information model were performing poorly when compared to the text-based single-view model, a weighted average technique may produce better results.
5.2. Comparison With Previous Work
5.3. Future Work
- In this work, we focused on identifying only the standard structure names of some OARs and PTV structures. In the future, we would like to define the hierarchy of structures representing the logical groupings such as OARs, targets (PTV, CTV, and GTV), implants, derived OARs, and derived targets.
- Here, we used only the prostate and lung disease sites. We started with these sites because they cover the majority of the patients treated across the 40 different VA radiation therapy treatment centers. Moving forward, we would like to investigate the efficacy of our approach on other disease sites such as brain, head and neck, and abdomen, which make up smaller datasets compared to the prostate and lung disease sites.
- The current dataset was comprised of only CT images, whereas in practice, both CT and MRI image datasets are used for treatment planning. We will investigate the efficacy of our approach on both the CT and MRI datasets in the future.
- In the late integration approach, we used the top 100 SVD features with a random forest classification algorithm. However, there are more suitable algorithms for image data such as 2D CNN algorithm, ResNet [20], VoxNet, and a 3D CNN supervised classification algorithm [21]. The radiotherapy structure set is 3D in nature, making it more suitable to solve using 3D algorithms.
- The current list of OARs identified for both lung and prostate datasets is per the VA-ROQS project requirement, which selected these OARs in consensus with a team of experts. Radiation oncologists also delineate other types of OARs for each patient, such as kidney (left and right) and liver. Although these are not critical OARs in prostate cancer treatment, we believe building a system to identify and standardize all structures delineated according to the TG-263 guideline would provide the radiation therapy healthcare institutes with an opportunity to produce a robust dataset for downstream analysis projects. In this regard, an interesting future direction is to define hierarchy such as targets, OARs, implants, sub-target volumes (e.g. PTVminusCTV), sub-target OARs (e.g., rectum sub CTV), isodose structures, “ghost” structures for optimization, etc., and assess the efficiency of such ML models considering each of these different categories.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AAPM | American Association of Physicists in Medicine |
| ASTRO | American Society for Radiation Oncology |
| TG-263 | Task Group-263 |
| RT | Radiotherapy |
| ROQS | Radiation Oncology Quality Surveillance Program |
| VCU | Virginia Commonwealth University |
| VA | Veterans Health Administration |
| OARs | Organs-At-Risk |
| Non_OARs | Non Organs-At-Risk |
| CT | Computed Tomography |
| MRI | Magnetic Resonance Imaging |
| HU | Hounsfield Unit |
| PRV | Planning Organs-At-Risk Volume |
| PTV | Planning Target Volume |
| GTV | Gross Target Volume |
| CTV | Clinical Target Volume |
| DVH | Dose Volume Histogram |
| DICOM | Digital Imaging and Communication in Medicine |
| QA | Quality Assurance |
| NLP | Natural Language Processing |
| ML | Machine Learning |
| SVD | Singular-Value Decomposition |
| TPS | Treatment Planning System |
| SVM | Support Vector Machine |
| KNN | k-Nearest Neighbors |
| RF | Random Forest |
| PCA | Principal Component Analysis |
References
- Wright, J.L.; Yom, S.S.; Awan, M.J.; Dawes, S.; Fischer-Valuck, B.; Kudner, R.; Mailhot Vega, R.; Rodrigues, G. Standardizing Normal Tissue Contouring for Radiation Therapy Treatment Planning: An ASTRO Consensus Paper. Pract. Radiat. Oncol. 2019, 9, 65–72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benedict, S.H.; Hoffman, K.; Martel, M.K.; Abernethy, A.P.; Asher, A.L.; Capala, J.; Chen, R.C.; Chera, B.; Couch, J.; Deye, J.; et al. Overview of the American Society for Radiation Oncology–National Institutes of Health–American Association of Physicists in Medicine Workshop 2015: Exploring opportunities for radiation oncology in the era of big data. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 873–879. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Syed, K.; Ivey, K.; Hagan, M.; Palta, J.; Kapoor, R.; Ghosh, P. Integrated Natural Language Processing and Machine Learning Models for Standardizing Radiotherapy Structure Names. Healthcare 2020, 8, 120. [Google Scholar] [CrossRef] [PubMed]
- Schuler, T.; Kipritidis, J.; Eade, T.; Hruby, G.; Kneebone, A.; Perez, M.; Grimberg, K.; Richardson, K.; Evill, S.; Evans, B.; et al. Big Data Readiness in Radiation Oncology: An Efficient Approach for Relabeling Radiation Therapy Structures With Their TG-263 Standard Name in Real-World Data Sets. Adv. Radiat. Oncol. 2019, 4, 191–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruan, D.; Shao, W.; Wong, J.; Veruttipong, D.; Steinberg, M.; Low, D.; Kupelian, P. SU-F-T-102: Automatic Curation for a Scalable Registry Using Machine Learning. Med Phys. 2016, 43, 3485. [Google Scholar] [CrossRef]
- Rhee, D.; Nguyen, C.; Netherton, T.; Owens, C.; Court, L.; Cardenas, C. TG263-Net: A Deep Learning Model for Organs-At-Risk Nomenclature Standardization. In Medical Physics; Wiley: Hoboken, NJ, USA, 2019; Volume 46, p. E263. [Google Scholar]
- Yang, Q.; Chao, H.; Nguyen, D.; Jiang, S. A Novel Deep Learning Framework for Standardizing the Label of OARs in CT. In Artificial Intelligence in Radiation Therapy, Proceedings of the Workshop on Artificial Intelligence in Radiation Therapy, Shenzhen, China, 17 October 2019; Springer: Berlin, Germany, 2019; pp. 52–60. [Google Scholar]
- Sleeman, W.C., IV; Nalluri, J.; Syed, K.; Ghosh, P.; Krawczyk, B.; Hagan, M.; Palta, J.; Kapoor, R. A Machine Learning method for relabeling arbitrary DICOM structure sets to TG-263 defined labels. J. Biomed. Inform. 2020, 109, 103527. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.; Kapoor, R.; Michalski, J.; Sandler, H.; Movsas, B.; Chetty, I.; Lally, B.; Rengan, R.; Robinson, C.; Rimner, A.; et al. VA-Radiation Oncology Quality Surveillance Program. Int. J. Radiat. Oncol. Biol. Phys. 2020, 106, 639–647. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R.; Corporation, R.; Collection, K.M.R. Dynamic Programming; Rand Corporation Research Study; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; ACM: New York, NY, USA, 1992; pp. 144–152. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Kleinbaum, D.G.; Dietz, K.; Gail, M.; Klein, M.; Klein, M. Logistic Regression; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Joulin, A.; Grave, E.; Bojanowski, P.; Mikolov, T. Bag of Tricks for Efficient Text Classification. arXiv 2016, arXiv:1607.01759. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed; Pearson: Essex, UK, 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3D convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 922–928. [Google Scholar]








| Structure Type | Standard Name | Patient 1 | Patient 1 | Patient 1 |
|---|---|---|---|---|
| OAR | Large Bowel | bowel_lg | colon | bowel |
| OAR | Femur_L | LtFemoral Head | Left Fem | Fem hdneck Lt |
| OAR | Femur_R | Fem Rt | Rt_Fem | Femoral_Rt |
| OAR | Bladder | bldr | bladder-KS | BLADDER |
| OAR | Small Bowel | bowel | SM_bowel | |
| OAR | Rectum | Rectum | Rect | rectum |
| Target | PTV | PTV_Prost | CTV | PTV |
| Other | Rectum subptv | Dose 107.1[%] | RFH | |
| Other | Prostate | PTV79.2 | Balloon | |
| Other | PTV45 | CTV45_OPT | CouchSurface | |
| Other | CTV45 | ProxSV | Pelvic Nodes | |
| Other | Rec50 | CTV vessels | Marker1 | |
| Other | POST | BLDSPARE | PROS+SV’S | |
| Other | out | 70opti | Blad_NO_ptv | |
| Other | External | ROI_1 | dosavoid2 | |
| Other | calcification | ROI_3 | Marker3 | |
| Other | FIDUCIALS | bulb | External | |
| Other | PTV_NDS | CouchInterior | Seeds |
| VA-ROQS | VCU | |||
|---|---|---|---|---|
| Non-Standard Name | Non-Standard Name | |||
| Standard Name | Structure Count | Unique Count | Structure Count | Unique Count |
| Brachial_Plexus | 108 | 44 | 4 | 4 |
| Esophagus | 613 | 26 | 47 | 3 |
| Heart | 670 | 20 | 45 | 2 |
| Other (Lung) | 10,292 | 3,639 | 775 | 317 |
| SpinalCord | 681 | 37 | 48 | 6 |
| PTV (Lung) | 680 | 286 | 36 | 4 |
| Lung Total | 13,044 | 4052 | 955 | 336 |
| Bladder | 609 | 10 | 50 | 3 |
| Femur_R | 700 | 62 | 29 | 14 |
| Femur_L | 694 | 59 | 29 | 13 |
| Rectum | 719 | 14 | 50 | 3 |
| SmallBowel | 250 | 40 | 49 | 10 |
| LargeBowel | 341 | 34 | 0 | 0 |
| Other (Prostate) | 11,038 | 2799 | 980 | 434 |
| PTV (Prostate) | 714 | 236 | 38 | 16 |
| Prostate Total | 15,065 | 3254 | 1225 | 493 |
| Grand Totals | 28,109 | 7306 | 2180 | 829 |
| Dataset | Disease | Data Type | Precision | Recall | F-Score | Acc |
|---|---|---|---|---|---|---|
| Test (VA-ROQS) | Prostate | MLB | 0.090 | 0.120 | 0.110 | 0.730 |
| Text | 0.890 | 0.866 | 0.872 | 0.930 | ||
| Image | 0.758 | 0.579 | 0.619 | 0.856 | ||
| Combined | 0.874 | 0.895 | 0.879 | 0.936 | ||
| Lung | MLB | 0.130 | 0.170 | 0.150 | 0.780 | |
| Text | 0.921 | 0.874 | 0.893 | 0.950 | ||
| Image | 0.825 | 0.694 | 0.708 | 0.916 | ||
| Combined | 0.896 | 0.873 | 0.882 | 0.946 | ||
| Text (VCU) | Prostate | MLB | 0.110 | 0.140 | 0.130 | 0.800 |
| Text | 0.778 | 0.730 | 0.740 | 0.927 | ||
| Image | 0.710 | 0.476 | 0.519 | 0.870 | ||
| Combined | 0.781 | 0.747 | 0.754 | 0.930 | ||
| Lung | MLB | 0.140 | 0.170 | 0.150 | 0.810 | |
| Text | 0.830 | 0.981 | 0.873 | 0.969 | ||
| Image | 0.610 | 0.565 | 0.585 | 0.918 | ||
| Combined | 0.821 | 0.976 | 0.860 | 0.964 |
| Dataset | Disease | Data Type | Precision | Recall | F-Score | Acc |
|---|---|---|---|---|---|---|
| Test (VCU) | Prostate | MLB | 0.110 | 0.140 | 0.130 | 0.800 |
| Text | 0.778 | 0.730 | 0.740 | 0.927 | ||
| Image | 0.710 | 0.476 | 0.519 | 0.870 | ||
| Avg | 0.802 | 0.685 | 0.719 | 0.929 | ||
| Max | 0.801 | 0.708 | 0.739 | 0.936 | ||
| Lung | MLB | 0.140 | 0.170 | 0.150 | 0.810 | |
| Text | 0.830 | 0.981 | 0.873 | 0.969 | ||
| Image | 0.610 | 0.565 | 0.585 | 0.918 | ||
| Avg | 0.858 | 0.807 | 0.811 | 0.964 | ||
| Max | 0.849 | 0.810 | 0.806 | 0.963 | ||
| Test (VA-ROQS) | Prostate | MLB | 0.090 | 0.120 | 0.110 | 0.730 |
| Text | 0.890 | 0.866 | 0.872 | 0.930 | ||
| Image | 0.758 | 0.579 | 0.619 | 0.856 | ||
| Avg | 0.897 | 0.836 | 0.857 | 0.930 | ||
| Max | 0.897 | 0.848 | 0.864 | 0.930 | ||
| Lung | MLB | 0.130 | 0.170 | 0.150 | 0.780 | |
| Text | 0.921 | 0.874 | 0.893 | 0.950 | ||
| Image | 0.825 | 0.694 | 0.708 | 0.916 | ||
| Avg | 0.918 | 0.840 | 0.868 | 0.964 | ||
| Max | 0.916 | 0.840 | 0.867 | 0.945 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syed, K.; Sleeman, W.C., IV; Hagan, M.; Palta, J.; Kapoor, R.; Ghosh, P. Multi-View Data Integration Methods for Radiotherapy Structure Name Standardization. Cancers 2021, 13, 1796. https://doi.org/10.3390/cancers13081796
Syed K, Sleeman WC IV, Hagan M, Palta J, Kapoor R, Ghosh P. Multi-View Data Integration Methods for Radiotherapy Structure Name Standardization. Cancers. 2021; 13(8):1796. https://doi.org/10.3390/cancers13081796
Chicago/Turabian StyleSyed, Khajamoinuddin, William C. Sleeman, IV, Michael Hagan, Jatinder Palta, Rishabh Kapoor, and Preetam Ghosh. 2021. "Multi-View Data Integration Methods for Radiotherapy Structure Name Standardization" Cancers 13, no. 8: 1796. https://doi.org/10.3390/cancers13081796
APA StyleSyed, K., Sleeman, W. C., IV, Hagan, M., Palta, J., Kapoor, R., & Ghosh, P. (2021). Multi-View Data Integration Methods for Radiotherapy Structure Name Standardization. Cancers, 13(8), 1796. https://doi.org/10.3390/cancers13081796






