Theoretical Investigations of the Structural, Dynamical, Electronic, Magnetic, and Thermoelectric Properties of CoMRhSi (M = Cr, Mn) Quaternary Heusler Alloys
Abstract
:1. Introduction
2. Computational Methodology
3. Results and Discussions
3.1. Structural Properties
3.2. Phonon Calculation
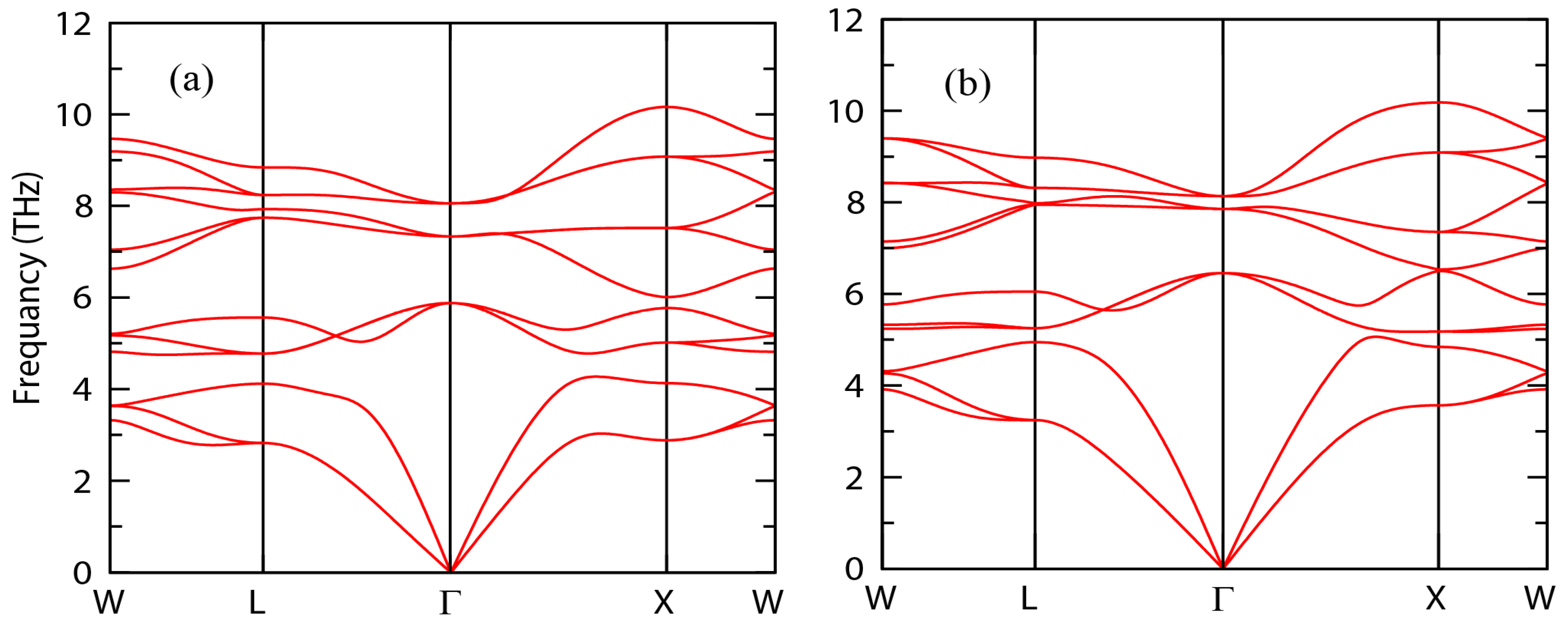
3.3. Mechanical Properties
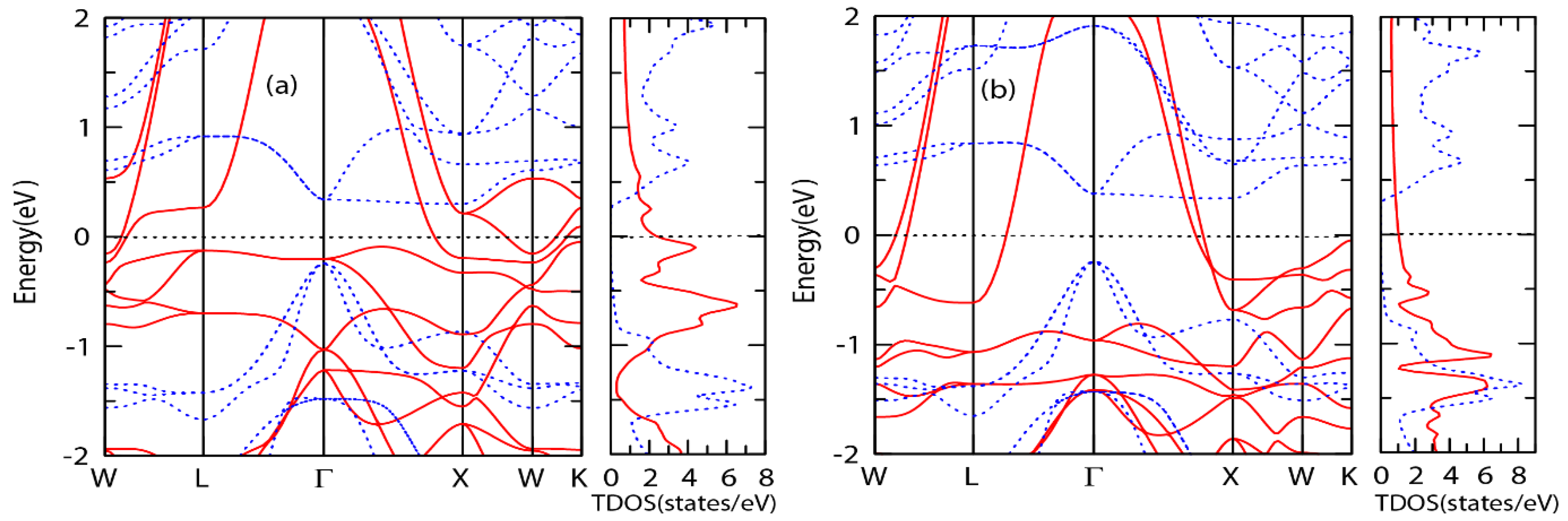
3.4. Electronic and Magnetic Properties
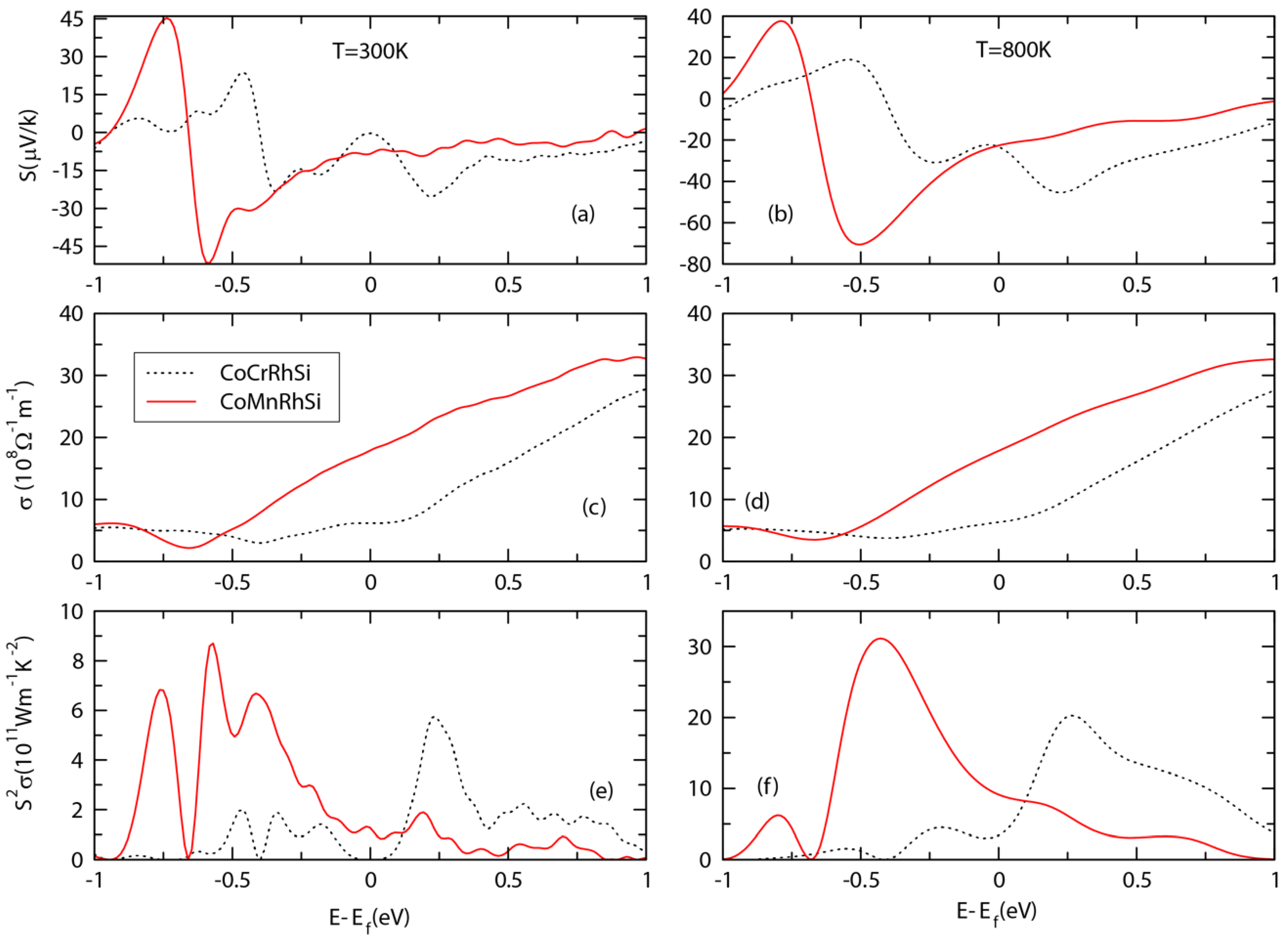
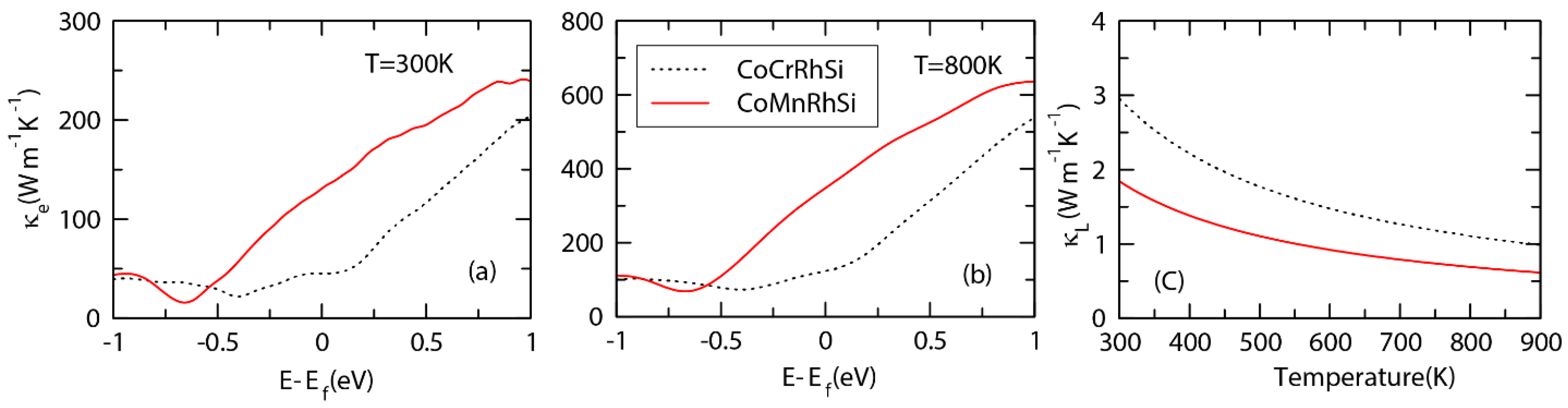
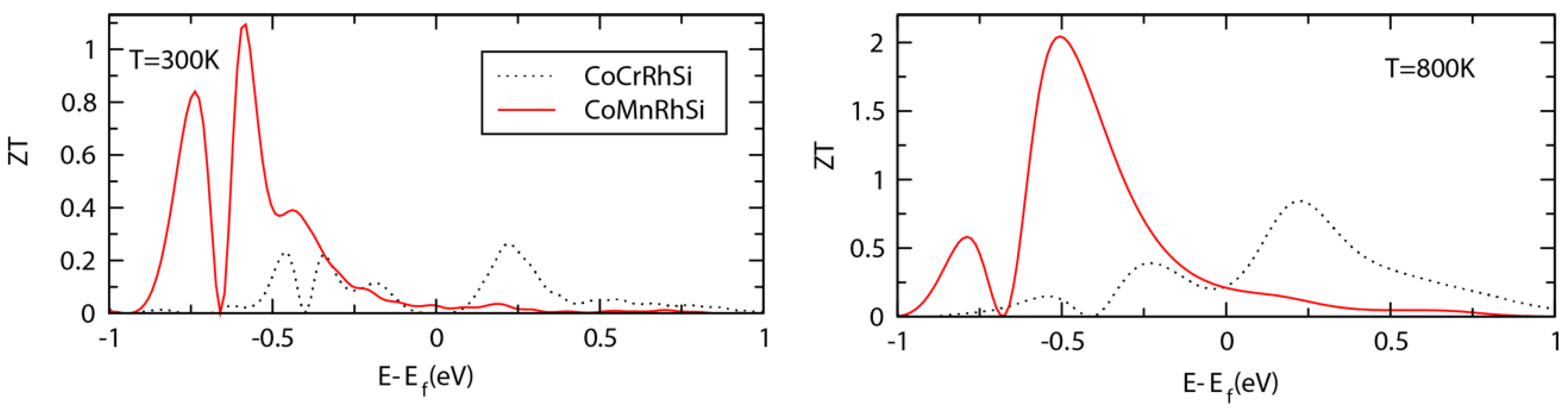
3.5. Transport Properties and ZT
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zoui, M.A.; Bentouba, S.; Stocholm, J.G.; Bourouis, M. A Review on Thermoelectric Generators: Progress and Applications. Energies 2020, 13, 3606. [Google Scholar] [CrossRef]
- Quinn, R.J.; Bos, J.-W.G. Advances in half-Heusler alloys for thermoelectric power generation. Mater. Adv. 2021, 2, 6246–6266. [Google Scholar] [CrossRef]
- Peng, S.Z.; Zhang, Y.; Wang, M.X.; Zhang, Y.G.; Zhao, W. Magnetic Tunnel Junctions for Spintronics: Principles and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; Wiley: Hoboken, NJ, USA, 2014; pp. 1–16. [Google Scholar] [CrossRef]
- Oogane, M.; Sakuraba, Y.; Nakata, J.; Kubota, H.; Ando, Y.; Sakuma, A.; Miyazaki, T. Large tunnel magnetoresistance in magnetic tunnel junctions using Co 2MnX (X ≤ Al, Si) Heusler alloys. J. Phys. D Appl. Phys. 2006, 39, 834–841. [Google Scholar] [CrossRef]
- Xie, W.-H.; Liu, B.-G.; Pettifor, D.G. Half-metallic ferromagnetism in transition metal pnictides and chalcogenides with wurtzite structure. Phys. Rev. B 2003, 68, 134407. [Google Scholar] [CrossRef]
- Khandy, S.A.; Gupta, D.C. Investigation of the transport, structural and mechanical properties of half-metallic REMnO3 (RE = Ce and Pr) ferromagnets. RSC Adv. 2016, 6, 97641–97649. [Google Scholar] [CrossRef]
- Mir, S.A.; Gupta, D.C. Understanding the origin of half-metallicity and thermophysical properties of ductile La2CuMnO6 double perovskite. Int. J. Energy Res. 2019, 43, 4783–4796. [Google Scholar] [CrossRef]
- Şaşioglu, E.; Galanakis, I.; Sandratskii, L.M.; Bruno, P. Stability of ferromagnetism in the half-metallic pnictides and similar compounds: A first-principles study. J. Phys. Condens. Matter 2005, 17, 3915–3930. [Google Scholar] [CrossRef] [PubMed]
- Graf, T.; Felser, C.; Parkin, S.S. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Wurmehl, S.; Fecher, G.H.; Kandpal, H.C.; Ksenofontov, V.; Felser, C.; Lin, H.J.; Morais, J. Geometric, electronic, and magnetic structure of Co2FeSi: Curie temperature and magnetic moment measurements and calculations. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 184434. [Google Scholar] [CrossRef]
- Alsayegh, S.; Alqurashi, H.; Andharih, E.; Hamad, B.; Manasreh, M. First-principal investigations of the electronic, magnetic, and thermoelectric properties of CrTiRhAl quaternary Heusler alloy. J. Magn. Magn. Mater. 2023, 568, 170421. [Google Scholar] [CrossRef]
- Ishida, S.; Masaki, T.; Fujii, S.; Asano, S. Theoretical search for half-metallic films of Co2MnZ (Z = Si, Ge). Phys. B Condens. Matter 1998, 245, 1–8. [Google Scholar] [CrossRef]
- Sakuraba, Y.; Nakata, J.; Oogane, M.; Kubota, H.; Ando, Y.; Sakuma, A.; Miyazaki, T. Huge spin-polarization of L21-ordered Co2MnSi epitaxial heusler alloy film. Jpn. J. Appl. Phys. Part 2 Lett. 2005, 44, L1100. [Google Scholar] [CrossRef]
- Seh, A.Q.; Gupta, D.C. Exploration of highly correlated Co-based quaternary Heusler alloys for spintronics and thermoelectric applications. Int. J. Energy Res. 2019, 43, 8864–8877. [Google Scholar] [CrossRef]
- Haleoot, R.; Hamad, B. Ab Initio Investigations of the Structural, Electronic, Magnetic, and Thermoelectric Properties of CoFeCuZ (Z = Al, As, Ga, In, Pb, Sb, Si, Sn) Quaternary Heusler Alloys. J. Electron. Mater. 2019, 48, 1164–1173. [Google Scholar] [CrossRef]
- Bainsla, L.; Suresh, K.G. Equiatomic quaternary Heusler alloys: A material perspective for spintronic applications. Appl. Phys. Rev. 2016, 3, 031101. [Google Scholar] [CrossRef]
- Andharia, E.; Alqurashi, H.; Hamad, B. Lattice Dynamics, Mechanical Properties, Electronic Structure and Magnetic Properties of Equiatomic Quaternary Heusler Alloys CrTiCoZ (Z = Al, Si) Using First Principles Calculations. Materials 2022, 15, 3128. [Google Scholar] [CrossRef] [PubMed]
- Yousuf, S.; Gupta, D.C. Thermoelectric and mechanical properties of gapless Zr2MnAl compound. Indian J. Phys. 2017, 91, 33–41. [Google Scholar] [CrossRef]
- Takahashi, Y.K.; Kasai, S.; Hirayama, S.; Mitani, S.; Hono, K. All-metallic lateral spin valves using Co2Fe(Ge0.5Ga0.5) Heusler alloy with a large spin signal. Appl. Phys. Lett. 2012, 100, 052405. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, Z.X.; Wang, X.T.; Khenata, R.; Rozale, H. First-Principles Investigation of Equiatomic Quaternary Heusler Alloys NbVMnAl and NbFeCrAl and a Discussion of the Generalized Electron-Filling Rule. J. Supercond. Nov. Magn. 2018, 31, 189–196. [Google Scholar] [CrossRef]
- Eliassen, S.N.H.; Katre, A.; Madsen, G.K.H.; Persson, C.; Løvvik, O.M.; Berland, K. Lattice thermal conductivity of TixZryHf1–x–yNiSn half-Heusler alloys calculated from first principles: Key role of nature of phonon modes. Phys. Rev. B 2017, 95, 045202. [Google Scholar] [CrossRef]
- Lue, C.S.; Chen, C.F.; Lin, J.Y.; Yu, Y.T.; Kuo, Y.K. Thermoelectric properties of quaternary Heusler alloys Fe2VAl1–xSix. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 75, 064204. [Google Scholar] [CrossRef]
- Yabuuchi, S.; Okamoto, M.; Nishide, A.; Kurosaki, Y.; Hayakawa, J. Large Seebeck Coefficients of Fe2TiSn and Fe2TiSi: First-Principles Study. Appl. Phys. Express 2013, 6, 025504. [Google Scholar] [CrossRef]
- Alqurashi, H.; Hamad, B. Magnetic structure, mechanical stability and thermoelectric properties of VTiRhZ (Z = Si, Ge, Sn) quaternary Heusler alloys: First-principles calculations. Appl. Phys. A Mater. Sci. Process. 2021, 127, 1–11. [Google Scholar] [CrossRef]
- Alqurashi, H.; Haleoot, R.; Pandit, A.; Hamad, B. Investigations of the electronic, dynamical, and thermoelectric properties of Cd1–xZnxO alloys: First-principles calculations. Mater. Today Commun. 2021, 28, 102511. [Google Scholar] [CrossRef]
- Kraemer, D.; Poudel, B.; Feng, H.-P.; Caylor, J.C.; Yu, B.; Yan, X.; Ma, Y.; Wang, X.; Wang, D.; Muto, A.; et al. High-performance flat-panel solar thermoelectric generators with high thermal concentration. Nat. Mater. 2011, 10, 532–538. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Gupta, D.C. Lanthanum based quaternary Heusler alloys LaCoCrX (X = Al, Ga): Hunt for half-metallicity and high thermoelectric efficiency. Results Phys. 2019, 13, 102300. [Google Scholar] [CrossRef]
- Haleoot, R.; Hamad, B. Thermodynamic and thermoelectric properties of CoFeYGe (Y = Ti, Cr) quaternary Heusler alloys: First principle calculations. J. Phys. Condens. Matter 2019, 32, 075402. [Google Scholar] [CrossRef] [PubMed]
- Ilkhani, M.; Boochani, A.; Amiri, M.; Asshabi, M.; Rai, D.P. Mechanical stability and thermoelectric properties of the PdZrTiAl quaternary Heusler: A DFT study. Solid State Commun. 2020, 308, 113838. [Google Scholar] [CrossRef]
- Alqurashi, H.; Haleoot, R.; Hamad, B. First-principles investigations of the electronic, magnetic and thermoelectric properties of VTiRhZ (Z = Al, Ga, In) Quaternary Heusler alloys. Mater. Chem. Phys. 2021, 278, 125685. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S. Full-potential, linearized augmented plane wave programs for crystalline systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Probert, M.I.J.; Hasnip, P.J.; Lejaeghere, K.; Bihlmayer, G.; Bjorkman, T.; Blaha, P.; Blum, V.; Caliste, D.; Castelli, I.E.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, 1415. [Google Scholar] [CrossRef]
- Kishore, M.R.A.; Okamoto, H.; Patra, L.; Vidya, R.; Sjåstad, A.O.; Fjellvåg, H.; Ravindran, P. Theoretical and experimental investigation on structural, electronic and magnetic properties of layered Mn5O8. Phys. Chem. Chem. Phys. 2016, 18, 27885–27896. [Google Scholar] [CrossRef] [PubMed]
- Madsen, G.K.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Lin, T.; Gao, Q.; Liu, G.; Dai, X.; Zhang, X.; Zhang, H. Dynamical stability, electronic and thermoelectric properties of quaternary ZnFeTiSi Heusler compound. Curr. Appl. Phys. 2019, 19, 721–727. [Google Scholar] [CrossRef]
- Khandy, S.A.; Chai, J.-D. Thermoelectric properties, phonon, and mechanical stability of new half-metallic quaternary Heusler alloys: FeRhCrZ (Z = Si and Ge). J. Appl. Phys. 2020, 127, 165102. [Google Scholar] [CrossRef]
- Hong, A.J.; Li, L.; He, R.; Gong, J.J.; Yan, Z.B.; Wang, K.F.; Liu, J.M.; Ren, Z.F. Full-scale computation for all the thermoelectric property parameters of half-Heusler compounds. Sci. Rep. 2016, 6, 22778. [Google Scholar] [CrossRef]
- Ma, H.; Yang, C.-L.; Wang, M.-S.; Ma, X.-G.; Yi, Y.-G. Effect of M elements (M = Ti, Zr, and Hf) on thermoelectric performance of the half-Heusler compounds MCoBi. J. Phys. D Appl. Phys. 2019, 52, 25550. [Google Scholar] [CrossRef]
- Slack, G. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 1973, 34, 321–335. [Google Scholar] [CrossRef]
- Chen, Q.; Sundman, B. Calculation of debye temperature for crystalline structures—A case study on Ti, Zr, and Hf. Acta Mater. 2001, 49, 947–961. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Horner, H. Lattice dynamics of quantum crystals. Z. Phys. 1967, 205, 72–89. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Xiong, X.; Wan, R.; Zhang, Z.; Lei, Y.; Tian, G. First-principle investigation on the thermoelectric properties of XCoGe (X = V, Nb, and Ta) half-Heusler compounds. Mater. Sci. Semicond. Process. 2022, 140, 106387. [Google Scholar] [CrossRef]
- Hoat, D.; Hoang, D.-Q.; Binh, N.T.; Naseri, M.; Rivas-Silva, J.; Kartamyshev, A.; Cocoletzi, G.H. First principles analysis of the half-metallic ferromagnetism, elastic and thermodynamic properties of equiatomic quaternary Heusler compound CoCrRhSi. Mater. Chem. Phys. 2021, 257, 123695. [Google Scholar] [CrossRef]
- Kundu, A.; Ghosh, S.; Banerjee, R.; Ghosh, S.; Sanyal, B. New quaternary half-metallic ferromagnets with large Curie temperatures. Sci. Rep. 2017, 7, 1803. [Google Scholar] [CrossRef]
- Zhao, J.-S.; Gao, Q.; Li, L.; Xie, H.-H.; Hu, X.-R.; Xu, C.-L.; Deng, J.-B. First-principles study of the structure, electronic, magnetic and elastic properties of half-Heusler compounds LiXGe (X = Ca, Sr and Ba). Intermetallics 2017, 89, 65–73. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Wang, J.; Liu, G. A full spectrum of spintronic properties demonstrated by a C1b-type Heusler compound Mn2Sn subjected to strain engineering. J. Mater. Chem. C 2016, 4, 8535–8544. [Google Scholar] [CrossRef]
- Berri, S. Computational Study of Structural, Electronic, Elastic, Half-Metallic and Thermoelectric Properties of CoCrScZ (Z = Al, Si, Ge, and Ga) Quaternary Heusler Alloys. J. Supercond. Nov. Magn. 2020, 33, 3809–3818. [Google Scholar] [CrossRef]
- Chen, X.-R.; Zhong, M.-M.; Feng, Y.; Zhou, Y.; Yuan, H.-K.; Chen, H. Structural, electronic, elastic, and thermodynamic properties of the spin-gapless semiconducting Mn2 CoAl inverse Heusler alloy under pressure. Phys. Status Solidi (b) 2015, 252, 2830–2839. [Google Scholar] [CrossRef]
- Semari, F.; Boulechfar, R.; Dahmane, F.; Abdiche, A.; Ahmed, R.; Naqib, S.; Bouhemadou, A.; Khenata, R.; Wang, X. Phase stability, mechanical, electronic and thermodynamic properties of the Ga3Sc compound: An ab-initio study. Inorg. Chem. Commun. 2020, 122, 108304. [Google Scholar] [CrossRef]
- Alqurashi, H.; Haleoot, R.; Hamad, B. First-principles investigations of Zr-based quaternary Heusler alloys for spintronic and thermoelectric applications. Comput. Mater. Sci. 2022, 210, 111477. [Google Scholar] [CrossRef]
- Rached, H. Prediction of a new quaternary Heusler alloy within a good electrical response at high temperature for spintronics applications: DFT calculations. Int. J. Quantum Chem. 2021, 121, e26647. [Google Scholar] [CrossRef]
- Benkabou, M.; Rached, H.; Abdellaoui, A.; Rached, D.; Khenata, R.; Elahmar, M.; Abidri, B.; Benkhettou, N.; Bin-Omran, S. Electronic structure and magnetic properties of quaternary Heusler alloys CoRhMnZ (Z = Al, Ga, Ge and Si) via first-principle calculations. J. Alloys Compd. 2015, 647, 276–286. [Google Scholar] [CrossRef]
- Dag, T.S.; Gencer, A.; Ciftci, Y.; Surucu, G. Equiatomic quaternary CoXCrAl (X = V, Nb, and Ta) Heusler compounds: Insights from DFT calculations. J. Magn. Magn. Mater. 2022, 560, 169620. [Google Scholar] [CrossRef]
- Elahmar, M.; Rached, H.; Rached, D.; Benalia, S.; Khenata, R.; Biskri, Z.; Bin Omran, S. Structural stability, electronic structure and magnetic properties of the new hypothetical half-metallic ferromagnetic full-Heusler alloy CoNiMnSi. Mater. Sci. 2016, 34, 85–93. [Google Scholar] [CrossRef]
- Gencer, A.; Surucu, O.; Usanmaz, D.; Khenata, R.; Candan, A.; Surucu, G. Equiatomic quaternary Heusler compounds TiVFeZ (Z = Al, Si, Ge): Half-metallic ferromagnetic materials. J. Alloys Compd. 2021, 883, 160869. [Google Scholar] [CrossRef]
- Rached, H.; Rached, D.; Khenata, R.; Abidri, B.; Rabah, M.; Benkhettou, N.; Omran, S.B. A first principle study of phase stability, electronic structure and magnetic properties for Co2-xCrxMnAl Heusler alloys. J. Mag. Mag. Mater. 2015, 379, 84. [Google Scholar] [CrossRef]
- Bourachid, I.; Rached, D.; Rached, H.; Bentouaf, A.; Rached, Y.; Caid, M.; Abidri, B. Magneto-electronic and thermoelectric properties of V-based Heusler in ferrimagnetic phase. Appl. Phys. A 2022, 128, 493. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S. Site dependent substitution and half-metallic behaviour in Heusler compounds: A case study for Mn2RhSi, Co2RhSi and CoRhMnSi. Comput. Condens. Matter. 2019, 21, e00423. [Google Scholar] [CrossRef]
- Candan, A.; Uğur, G.; Charifi, Z.; Baaziz, H.; Ellialtıoğlu, M. Electronic structure and vibrational properties in cobalt-based full-Heusler compounds: A first principle study of Co2MnX (X = Si, Ge, Al, Ga). J. Alloys Compd. 2013, 560, 215–222. [Google Scholar] [CrossRef]
- Elahmar, M.; Rached, H.; Rached, D.; Khenata, R.; Murtaza, G.; Bin Omran, S.; Ahmed, W. Structural, mechanical, electronic and magnetic properties of a new series of quaternary Heusler alloys CoFeMnZ (Z = Si, As, Sb): A first-principle study. J. Magn. Magn. Mater. 2015, 393, 165–174. [Google Scholar] [CrossRef]
- Jain, R.; Jain, V.K.; Chandra, A.R.; Jain, V.; Lakshmi, N. Study of the Electronic Structure, Magnetic and Elastic Properties and Half-Metallic Stability on Variation of Lattice Constants for CoFeCrZ (Z = P, As, Sb) Heusler Alloys. J. Supercond. Nov. Magn. 2018, 31, 2399–2409. [Google Scholar] [CrossRef]

| Y | 4a (0,0,0) | 4b (1/2, 1/2, 1/2) | 4c (1/4, 1/4, 1/4) | 4d (3/4, 3/4, 3/4) |
|---|---|---|---|---|
| Type-I | Co | Rh | Y | Z |
| Type-II | Co | Y | Rh | Z |
| Type-III | Rh | Co | Y | Z |
| Alloys | Type-I | Type-II | Type-III |
|---|---|---|---|
| CoCrRhSi | −29.719 | −30.633 | −30.145 |
| CoMnRhSi | −29.187 | −30.749 | −29.918 |
| Physical Parameter | CoCrRhSi | CoMnRhSi |
|---|---|---|
| −1.32 | −1.91 | |
| a | 5.78 | 5.83 |
| C11 | 335.89 | 334.40 |
| C12 | 145.23 | 141.94 |
| C44 | 58.91 | 72.14 |
| B | 216.88 | 211.45 |
| 238.85 a) | ||
| E | 185.23 | 216.13 |
| G | 68.35 | 81.29 |
| B/G | 3.17 | 2.60 |
| 3.39 a) | ||
| Cp | 86.31 | 69.05 |
| A | 0.61 | 0.74 |
| Tmelt | 2624 | 2574 |
| Compound | Eg (eV) | P (%) | |||||
|---|---|---|---|---|---|---|---|
| CoCrRhSi | 0.54 (minority) | 100 | 1.15 | 0.36 | 2.41 | −0.02 | 4.00 |
| 4.00 a) | |||||||
| CoMnRhSi | 0.57 (minority) | 100 | 1.25 | 0.44 | 3.31 | −0.02 | 5.00 |
| Alloys | ||||||
|---|---|---|---|---|---|---|
| CoCrRhSi | 420.78 | 3274.84 | 2909.84 | 6176.90 | 8186.08 | 2.19 |
| CoMnRhSi | 454.28 | 3533.46 | 3151.32 | 6250.75 | 8073.10 | 1.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hzzazi, A.; Alqurashi, H.; Andharia, E.; Hamad, B.; Manasreh, M.O. Theoretical Investigations of the Structural, Dynamical, Electronic, Magnetic, and Thermoelectric Properties of CoMRhSi (M = Cr, Mn) Quaternary Heusler Alloys. Crystals 2024, 14, 33. https://doi.org/10.3390/cryst14010033
Hzzazi A, Alqurashi H, Andharia E, Hamad B, Manasreh MO. Theoretical Investigations of the Structural, Dynamical, Electronic, Magnetic, and Thermoelectric Properties of CoMRhSi (M = Cr, Mn) Quaternary Heusler Alloys. Crystals. 2024; 14(1):33. https://doi.org/10.3390/cryst14010033
Chicago/Turabian StyleHzzazi, Abdullah, Hind Alqurashi, Eesha Andharia, Bothina Hamad, and M. O. Manasreh. 2024. "Theoretical Investigations of the Structural, Dynamical, Electronic, Magnetic, and Thermoelectric Properties of CoMRhSi (M = Cr, Mn) Quaternary Heusler Alloys" Crystals 14, no. 1: 33. https://doi.org/10.3390/cryst14010033
APA StyleHzzazi, A., Alqurashi, H., Andharia, E., Hamad, B., & Manasreh, M. O. (2024). Theoretical Investigations of the Structural, Dynamical, Electronic, Magnetic, and Thermoelectric Properties of CoMRhSi (M = Cr, Mn) Quaternary Heusler Alloys. Crystals, 14(1), 33. https://doi.org/10.3390/cryst14010033






