On the Binding Energy of Atoms in Crystals of Noble Gases and Metals and the Speed of Sound

Abstract

The speed of sound depends on the structure and material properties of the crystal, such as density and Young’s modulus. On the other hand, from atomistic arguments it is possible to associate Young’s modulus with other material properties. These observations lead to a relationship between binding energy of atoms in a crystal (which is one of the parameters appearing in Mie-Lennard-Jones potential), speed of sound in the longitudinal direction and mass of one atom in the lattice. This subject was addressed by several authors, providing different implementations of this relation. A literature review on this topic is made and the mathematical derivation of the relation is carried out. Applications of this relationship to rare gases, some metals and some rare earths are presented and the results compared to others taken from literature.

1. Introduction

Many interatomic potentials were developed to describe the interaction between atoms or molecules in condensed matter [1]. Among them, parametric two-body potentials, expressed by analytical relationships, allow the description of the intra-particle potential energy as a function of position, with the minimum value being the interatomic binding energy. Within this framework, potentials such as Morse, Mie and Lennard-Jones were successfully used to describe the bonding of atoms in crystal structures. Variations of these potentials have been proposed. For example, for the Lennard-Jones potential a variation has been implemented with truncation and shifting in order to mitigate performance issues and increase accuracy [2,3]. In solids, the binding energy, which appears as a parameter in the above mentioned potentials, can be evaluated from experiment via measurements of certain properties such as sublimation energy [4] or from simulation via molecular dynamics associated with ab initio calculations such as density functional theory (DFT) with periodic boundary conditions for crystalline structure optimisation [2,5,6,7]. Interatomic binding energy can be associated with physical phenomena in condensed matter; for example: a binding energy relationship can describe cohesion and other properties of metals [8]; a periodic binding energy dependence on atomic mass can be observed within the table of elements [4]; in nuclear reactor physics, the inter-nuclei binding energy can be associated with the neutron-nucleus interaction, expressed by the reaction’s cross sections [9]; and the binding energy of a crystal can be related to its melting temperature: the smaller the binding energy, the lower the melting temperature [10]. The aim of the present work is to explore the relationship between binding energy and sound velocity in crystals. This topic was previously addressed by several authors. Trachenko et al. [11] and Erokhin and Kalashnikov [12] proposed a proportionality between the speed of sound and the square root of the ratio between binding energy and the mass of the atom. Vos et al. [13] reported the square of the speed of sound as proportional to the ratio between the second derivative of the potential and the mass of the atom. Khrapak [14] related the product of the mass of the atom multiplied by the square of the speed of sound to an expression involving the first and second derivatives of the Lennard-Jones potential, making therefore appear the binding energy. The above kind of relationships is addressed in this work.

2. Theory

2.1. Preliminary Observations

The speed of sound in solids depends on the structure and on the material properties of the crystal. When the medium is a bar, the square of the speed of sound $c_s$, in the longitudinal direction, which is the constant appearing in the one-dimensional wave equation, can be expressed in terms of the ratio between the Young’s modulus E and the density $\rho$ [15]:

$$\begin{array}{c}\hfill c_s^2=E/\rho .\end{array}$$

(1)

In the theoretical derivation we consider a simple cubic crystal with Poisson’s ratio equal to zero, in order to prevent elastic deformation in the longitudinal direction from causing transverse deformation. Under this assumption, the Young’s modulus and the $c_{11}$ elastic constant coincide. This behavior can be transposed to fcc but not to bcc crystals. For symmetry reasons (cf. Appendix A) any of the axes of the referential perpendicular to the sides of the cubic structure can be chosen as direction of the sound wave. The chosen direction is perpendicular to the 100 face. The Young’s modulus, defined as the ratio between the strain and the stress, can be derived from atomistic arguments [16,17] based on the Mie-Lennard-Jones potential [18,19]. Combining the two expressions it is possible to obtain a relationship between the binding energy and the speed of sound in the crystal, in the longitudinal direction. Its derivation is presented in Section 2.2 and Section 2.3. Applications are presented in Section 3.

2.2. Young’s Modulus from Mie and Lennard-Jones Potential

The Mie potential is a simple particle-pair potential composed of two terms representing the repulsive and attractive forces between particles, such as the atoms in the crystal. Following the approach proposed in refs. [16,17], it is used here to represent the forces acting between the atoms in the crystal. Its formulation is as follows [20,21,22]

$$\begin{array}{c}\hfill U\left(r\right)={\displaystyle \frac{\epsilon }{m-n}}\left(n{\left({\displaystyle \frac{r_0}{r}}\right)}^m-m{\left({\displaystyle \frac{r_0}{r}}\right)}^n\right),\end{array}$$

(2)

where $\epsilon$ is the binding energy of the interacting particles (the energy required to separate them), r is the distance between the particles, and $r_0$ is their equilibrium distance. The exponents depend on the material.

A most used form, with $n=6$ and $m=12$, is the 12-6 Lennard-Jones potential [23]:

$$\begin{array}{c}\hfill U\left(r\right)=\epsilon \left({\left({\displaystyle \frac{r_0}{r}}\right)}^{12}-2{\left({\displaystyle \frac{r_0}{r}}\right)}^6\right).\end{array}$$

(3)

As shown in Figure 1, which plots function $U\left(r\right)$, parameters $\epsilon$ and $r_0$ are the depth of the potential $U\left(r\right)$ and its position, respectively.

The Young’s modulus can be obtained from the definition of the Mie potential, knowing that it is the curvature of the potential with regard to the distance between atoms, i.e., the second derivative [16]. More in details, taking the derivative of the potential provides the force between the particles:

$$\begin{array}{c}\hfill F\left(r\right)=-{\displaystyle \frac{mn}{(m-n)}}{\displaystyle \frac{\epsilon }{r}}\left({\left({\displaystyle \frac{r_0}{r}}\right)}^m-{\left({\displaystyle \frac{r_0}{r}}\right)}^n\right).\end{array}$$

(4)

From Equation (4), it can be seen that $F\left(r_0\right)=0$, which proves that for $r=r_0$ the potential $U\left(r\right)$ has a minimum. In the framework of our approach, $r_0$, which is the equilibrium distance, is also the size a of the crystal cell as illustrated by the simple cube (sc) lattice in Figure 2, representative of the internal structure of the bar.

Let us apply a force F to the ends of the bar. The distance between the atoms will change from a to r. Young’s modulus E is defined as the ratio between stress (force per unit surface, $F\left(r\right)/a^2$) and strain (relative deformation, $(r-a)/a$) in the limit as the strain goes to 0. Therefore, in mathematical terms, Young’s modulus can be written as:

$$\begin{array}{c}\hfill E=\underset{r\to a}{lim}{\displaystyle \frac{F\left(r\right)/a^2}{(r-a)/a}}.\end{array}$$

(5)

Taking into account that $F\left(r\right)$ vanishes for $r\to a$, Equation (5) can be written as:

$$\begin{array}{c}\hfill E={\displaystyle \frac{1}{a}}\underset{r\to a}{lim}{\displaystyle \frac{\left(F\right(r)-F(a\left)\right)}{(r-a)}},\end{array}$$

(6)

which, in virtue of the derivative definition, is equivalent to:

$$\begin{array}{c}\hfill E={\displaystyle \frac{1}{a}}{\displaystyle \frac{\mathrm{d}F\left(r\right)}{\mathrm{d}r}}{|}_{r=a}.\end{array}$$

(7)

Computing the derivative of $F\left(r\right)$ at the point $r=a$ from Equation (4), after some manipulations, the relationship between Young’s modulus and binding energy is obtained:

$$\begin{array}{c}\hfill E=mn{\displaystyle \frac{\epsilon }{a^3}}.\end{array}$$

(8)

Equation (8) is similar to the relationship between molar volume, bulk modulus and total energy in diamond proposed by Aleksandrov et al. [24]. In the above form, this relationship was proposed by Erokhin and Kalashnikov [12].

2.3. Relationship between Binding Energy and Speed of Sound

Substituting Equation (8) into Equation (1) we obtain:

$$\begin{array}{c}\hfill c_s^2=mn{\displaystyle \frac{\epsilon }{\rho a^3}}.\end{array}$$

(9)

The term at denominator, $\rho a^3$, i.e., the density multiplied by the atom-cell volume, is the mass M of a single atom-cell in a cubic lattice, where a simple cubic structure was assumed, which allows to write:

$$\begin{array}{c}\hfill \rho =M/a^3.\end{array}$$

(10)

Parameters $r_0$ and a and therefore the density $\rho$, are assumed to be at room temperature and atmospheric pressure, consistently with the conditions related to the sound velocity. The combination of Equation (10) and Equation (9) provides the relationship between binding energy and speed of sound in the longitudinal direction:

$$\begin{array}{c}\hfill \epsilon ={\displaystyle \frac{M{c}_s^2}{mn}}.\end{array}$$

(11)

Even if it was assumed a simple cubic structure, this relationship is valid for face centered cubic (fcc) structure (see Figure 2) as well (cf. Appendix B). Erokhin and Kalashnikov [12] proposed the above relation with another proportionality constant, because their work was based on another interatomic potential. A similar relationship was proposed by Trachenko et al. [11] who pointed out that elastic constants are governed by the density of electromagnetic energy in condensed matter phases. As a consequence a relation between the bulk modulus and the binding energy was provided, resulting in a proportionality relation between the binding energy, the square of the sound velocity and the mass of the atom.

2.4. Binding Energy in a Crystal and the Associated Mass Defect

An observation from a relativistic point of view can be made about the crystal binding energy. If we want to separate an atom from the crystal structure, the amount of energy that binds the atom to its neighbors must be supplied on the form of latent heat of sublimation. Inversely, if a crystal is formed from these free atoms, the same amount of energy is released and a mass defect appears. For each atom the amount of energy is the value $\epsilon$ expressed by Equation (11) multiplied by a factor Z/2, where Z is the number of neighbors a given atom interacts with, which differs between sc, bcc and fcc crystals. According to the mass-energy equivalence, the associated mass defect $\delta M$ responds to the relationship:

$$\begin{array}{c}\hfill {\displaystyle \frac{Z}{2}}\epsilon =\delta M{c}^2,\end{array}$$

(12)

where c is the speed of light. Substituting Equation (12) into Equation (11) after some algebra we obtain:

$$\begin{array}{c}\hfill {\displaystyle \frac{\delta M}{M}}={\displaystyle \frac{Z}{2nm}}{\left({\displaystyle \frac{c_s}{c}}\right)}^2.\end{array}$$

(13)

Equation (13) shows that the relative mass defect associated with the crystal binding energy (i.e., the ratio between this mass defect and the mass of the atom) is proportional to the square of the ratio between speed of sound and speed of light.

3. Values of Binding Energy for Several Elements

Equation (11) was used to compute the binding energy $\epsilon$ for several elements having cubic structure, where the mass of the atom M is defined as the ratio between atomic weight A and Avogadro number $N_{\mathrm{Av}}$:

$$\begin{array}{c}\hfill M=A/N_{\mathrm{Av}}.\end{array}$$

(14)

The elements studied are: 4 rare gases, Ne, Ar, Kr and Xe, which at solid state have fcc crystal structure [25], 7 metals with fcc, 3 metals with bcc and 3 rare earth metals with fcc structure (Ce, Yb, Th). Both the 12-6 Lennard-Jones and Mie potentials were used. The data used in the formula expressed by Equation (11), taken from references [26,27,28,29,30,31], is presented in

Table 1. Data used in the evaluation of the binding energy for the elements studied.

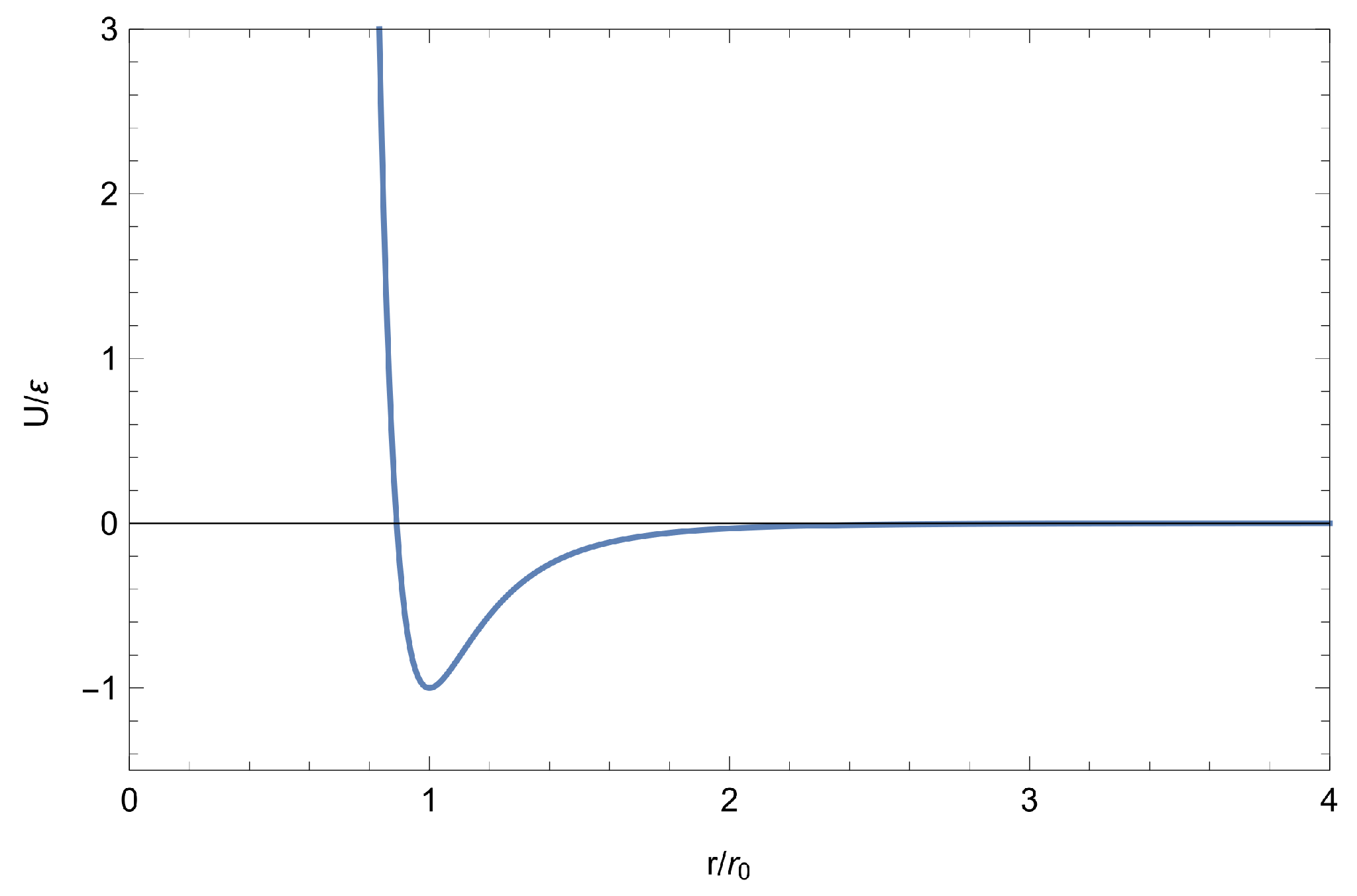
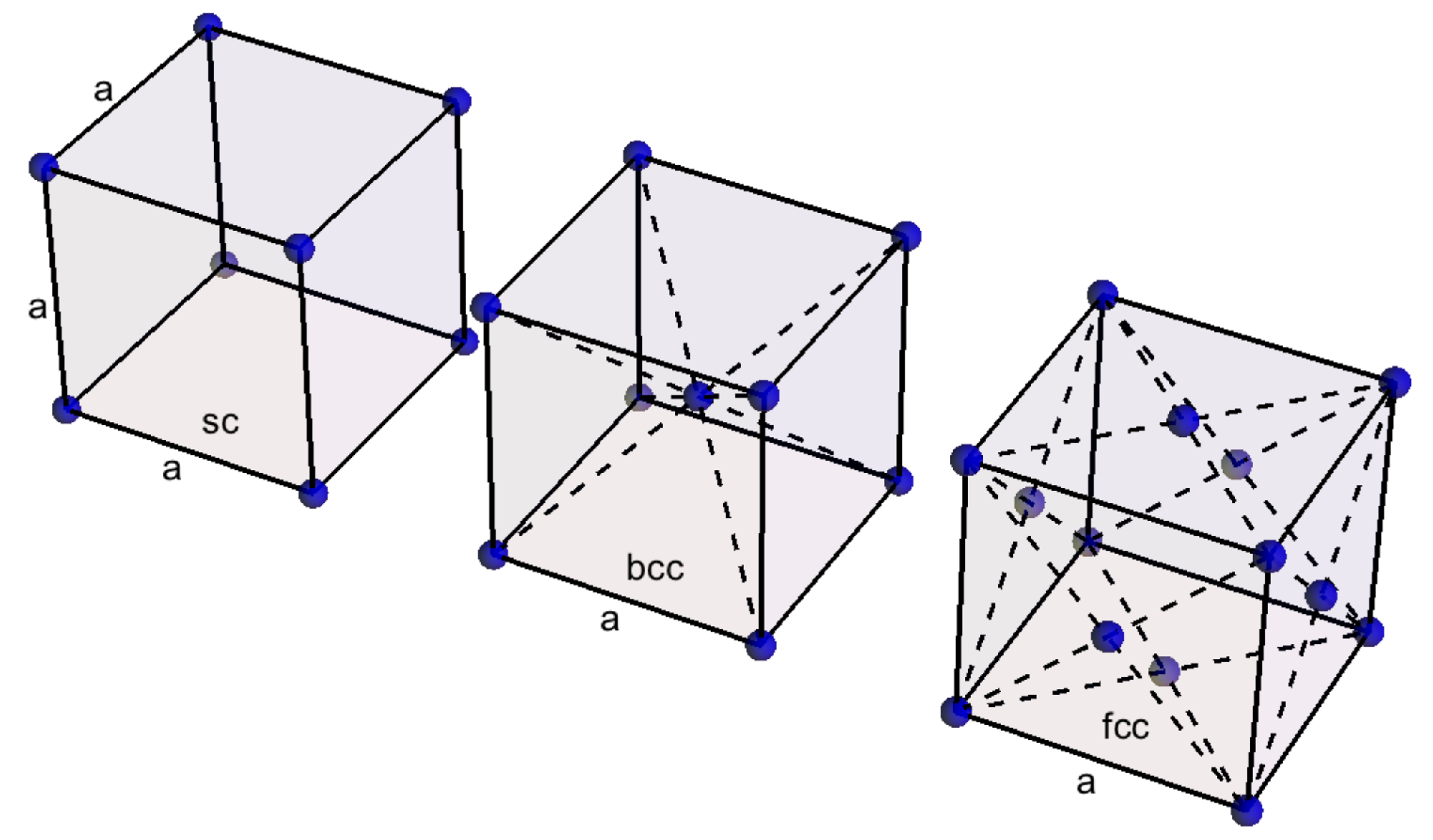
	Atomic Weight	Crystal Structure	Speed of Sound (m/s)	Reference
Ne	20.149	fcc	1290	[26]
Ar	39.948	fcc	1630	[27]
Kr	83.798	fcc	1335	[28]
Xe	131.29	fcc	1150	[29]
A1	26.981	fcc	6420	[30]
Au	196.97	fcc	3240	[30]
Pb	207.20	fcc	2160	[30]
Ni	58.693	fcc	6040	[30]
Pt	195.08	fcc	3260	[30]
Ag	107.87	fcc	3650	[30]
Cu	63.546	fcc	4760	[30]
Fe	55.845	bcc	5950	[30]
Mo	95.940	bcc	6250	[30]
W	183.84	bcc	5220	[30]
Ce	140.12	fcc	2100	[31]
Yb	173.04	fcc	1590	[31]
Th	232.04	fcc	2490	[31]

. It is pointed out that certain metals have more than one crystalline structure in nature. For example for iron, we have $\alpha$Fe which is bcc and $\gamma$Fe which is fcc. Within our approach it is assumed that the different forms have the same behavior with respect to atom-pair binding energy.

3.1. Values of Binding Energy Using the 12-6 Lennard-Jones Potential

For this formulation Equation (11) was used with the values $n=6$ and $m=12$. The results for 4 rare gases are presented in

Table 2. Binding energy (eV) for rare gases using the 12-6 Lennard-Jones potential and comparison with Horton’s results.

	This Work	Horton [21]
Ne	0.00483	0.00450
Ar	0.01528	0.01473
Kr	0.02150	0.02028
Xe	0.02500	0.02859

and compared to the ones obtained by Horton [21] solving a two-equation system set by fit of two crystal properties: the sublimation energy and the 0 °K lattice size. The results for 8 metals are presented in

Table 3. Binding energy (eV) for 10 metals using the 12-6 Lennard-Jones potential and comparison with Heinz’s, Kanhaiya’s (*) and Jacobson and Thompson’s results.

	This Work	Heinz et al. [23]	Jacobson and Thompson [33]
Al	0.1601	0.1743	0.1983
Au	0.2977	0.2294	0.2231
Pb	0.1392	0.1270	0.1188
Ni	0.3083	0.2450	0.2608
Pt	0.2985	0.3382	0.3427
Ag	0.2069	0.1977	0.1722
Cu	0.2073	0.2046	0.2050
Fe	0.2846	0.2601 *	0.2625
Mo	0.5395	-	-
W	0.7211	-	0.5377

and compared to the ones obtained by: Heinz et al. [23] and Kanhaiya et al. [32], who employed an isothermal–isobaric (NPT) molecular dynamics simulation with the Parrinello-Rahman method using a cubic $6\times 6\times 6$ supercell; Jacobson and Thompson [33] who determined the values of $\epsilon$ by calculating the total energy that binds an atom to the others in the crystal, without limiting the sum to the nearest neighbors, and imposing that the result be equal to the cohesion energy. The results for molybdenum are also provided but no comparison is available.

Table 4. Binding energy (eV) for 3 fcc rare earth metals using the 12-6 Lennard-Jones potential and comparison with Kanhaiya’s results.

	This Work	Kanhaiya et al. [32]
Ce	0.0890	0.2766
Yb	0.0630	0.1175
Th	0.2071	0.3672

presents the results obtained for 3 fcc rare earth metals, which are compared to the ones obtained by Kanhaiya et al. [32].

3.2. Values of Binding Energy Using the Mie Potential

For this formulation Equation (11) was used with the values of n and m taken from the works of Magomedov [20] and Fürth [22]. The results for 4 rare gases, 10 metals and 3 fcc rare earth metals are presented in

Table 5. Binding energy (eV) for rare gases using the Mie potential and comparison with Magomedov’s results.

	This Work	Magomedov [20]	n	m
Ne	0.0028	0.0045	5.83	21.39
Ar	0.0100	0.0150	6.62	16.69
Kr	0.0148	0.0205	6.56	15.92
Xe	0.0173	0.0285	6.73	15.42

,

Table 6. Binding energy (eV) for 10 metals using the Mie potential and comparison with Magomedov’s results.

	This Work	Magomedov [20]	n	m
Al	0.4239	0.5714	2.49	10.92
Au	0.7027	0.6387	1.96	15.56
Pb	0.3100	0.3399	2.27	14.24
Ni	0.8149	0.7506	3.56	7.65
Pt	0.6372	0.9795	2.53	13.33
Ag	0.4673	0.4944	3.08	10.35
Cu	0.5884	0.5895	3.03	8.37
Fe	0.8975	1.0838	3.54	6.45
Mo	2.3635	1.7042	2.14	7.68
W	1.7695	2.2068	3.42	8.58

and

Table 7. Binding energy (eV) for 3 fcc rare earth metals using the Mie potential and comparison with Magomedov’s results.

	This Work	Magomedov [20]	n	m
Ce	0.5390	0.7334	2.45	4.85
Yb	0.2374	0.2682	3.61	5.29
Th	0.8161	0.9970	3.02	6.05

, respectively, and compared to the ones obtained by Magomedov [20], who used an approach based on the preservation of measured quantities such as sublimation energy and thermal expansion coefficient.

Table 8. Binding energy (eV) for 10 metals using the Mie potential and comparison with Fürth’s results.

	This Work	Fürth [22]	n	m
Al	0.4117	0.4886	4	7
Au	0.4871	0.6556	5.5	8
Pb	0.2783	0.3397	3	12
Ni	0.7926	0.7083	4	7
Pt	0.4884	0.9013	5.5	8
Ag	0.4729	0.5016	4.5	7
Cu	0.5330	0.5905	4	7
Fe	0.7319	1.0462	4	7
Mo	1.1099	1.6913	5	7
W	1.4835	2.2107	5	7

shows the comparison with Fürth’s results for 10 metals [22]. The approximation of interaction of only nearest-neighbor atoms was adopted by both authors.

4. Conclusions

A relationship between the binding energy of atoms in crystals and the speed of sound was derived on the basis of the Mie and Lennard-Jones potentials. Comparing with other results taken from literature, its application to the 12-6 Lennard-Jones potential shows a quite good agreement in the case of rare gases. As far as metals are concerned, the deviations are higher but in the case of fcc structure they are consistent with the uncertainties inherent in the methods used by their authors to compute them [23]. However, results for rare earth metals show higher differences. Consistence is also observed in the case of the Mie potential, even though a difference of about 40% is observed for platinum. In both cases of Lennard-Jones and Mie potential, the comparison related to bcc metals shows higher differences. This is because the theory was derived for sc crystals and the behavior can be extended to fcc structures, as shown in Appendix B, but for bcc metals the extension is not justified. It is emphasized that this relationship, expressed by Equation (11), was obtained with a theoretical approach, while the models that were used to compute the binding energy values we compared with belong to force field classes that provide deeper insight into the physics of crystals. They use more complex algorithms to perform detailed calculations of interatomic interactions in crystals. These force fields are applicable to all types of crystals and other forms of condensed matter, while our approach is limited to cubic crystals of pure elements. Extension of this work to hpc crystals and salt crystals is ongoing.

The values of the binding energy computed for various elements depend on the form of the potential. Values associated with the 12-6 Lennard-Jones potential cannot be compared with the ones associated with the Mie potential. This is due to the fact that the values of the binding energy $\epsilon$, the exponents n and m, the $r_0$ distance, have to be seen as part of an inseparable whole.