Influence of Different Filler Systems on the Thermal Conductivity and Mechanical Properties of Thermosets
Abstract
:1. Introduction
1.1. Application Fields and Possible Extensions
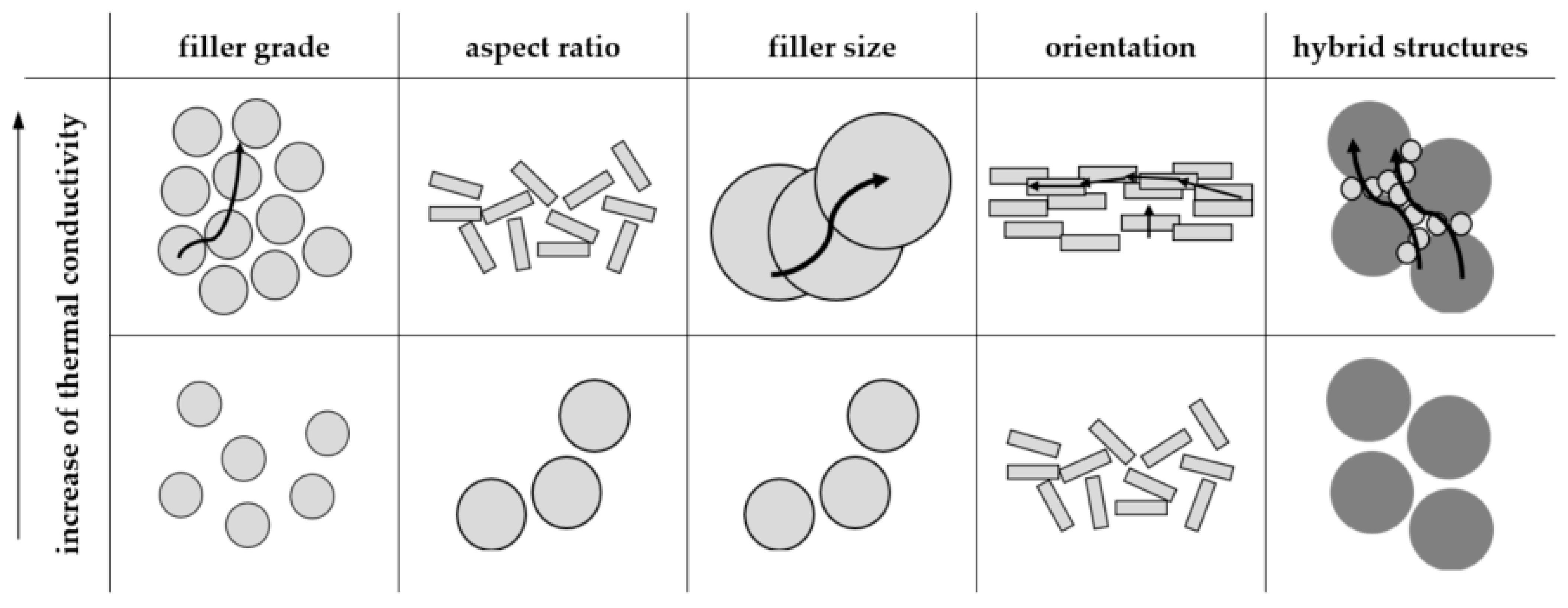
1.2. Thermal Conductivity of Thermoset-Based Compounds
1.3. Aim of This Paper
2. Materials and Methods
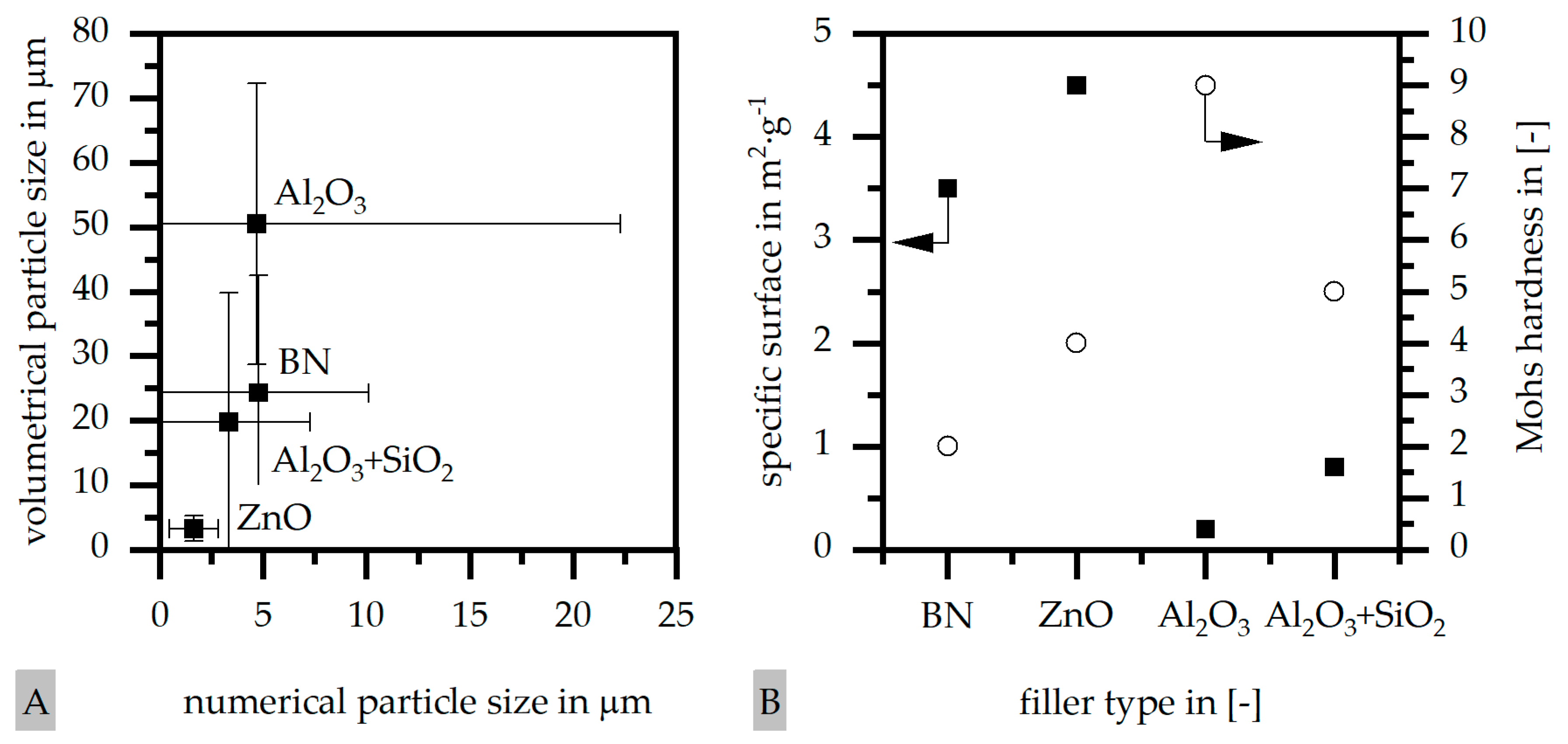
2.1. Materials
2.2. Fabrication of the Test Specimens
2.3. Characterization
2.3.1. Differential Scanning Calorimetry (DSC) According to DIN EN ISO 11357
2.3.2. Density ρ
2.3.3. Specific Heat Capacity c
2.3.4. Thermal Diffusivity a According to DIN EN ISO 22007
2.3.5. Thermal Conductivity λ According to DIN EN ISO 22007
2.3.6. Mechanical Properties According to DIN EN ISO 527
2.3.7. Filler Distribution and Linkage to Matrix Material
3. Results and Discussion
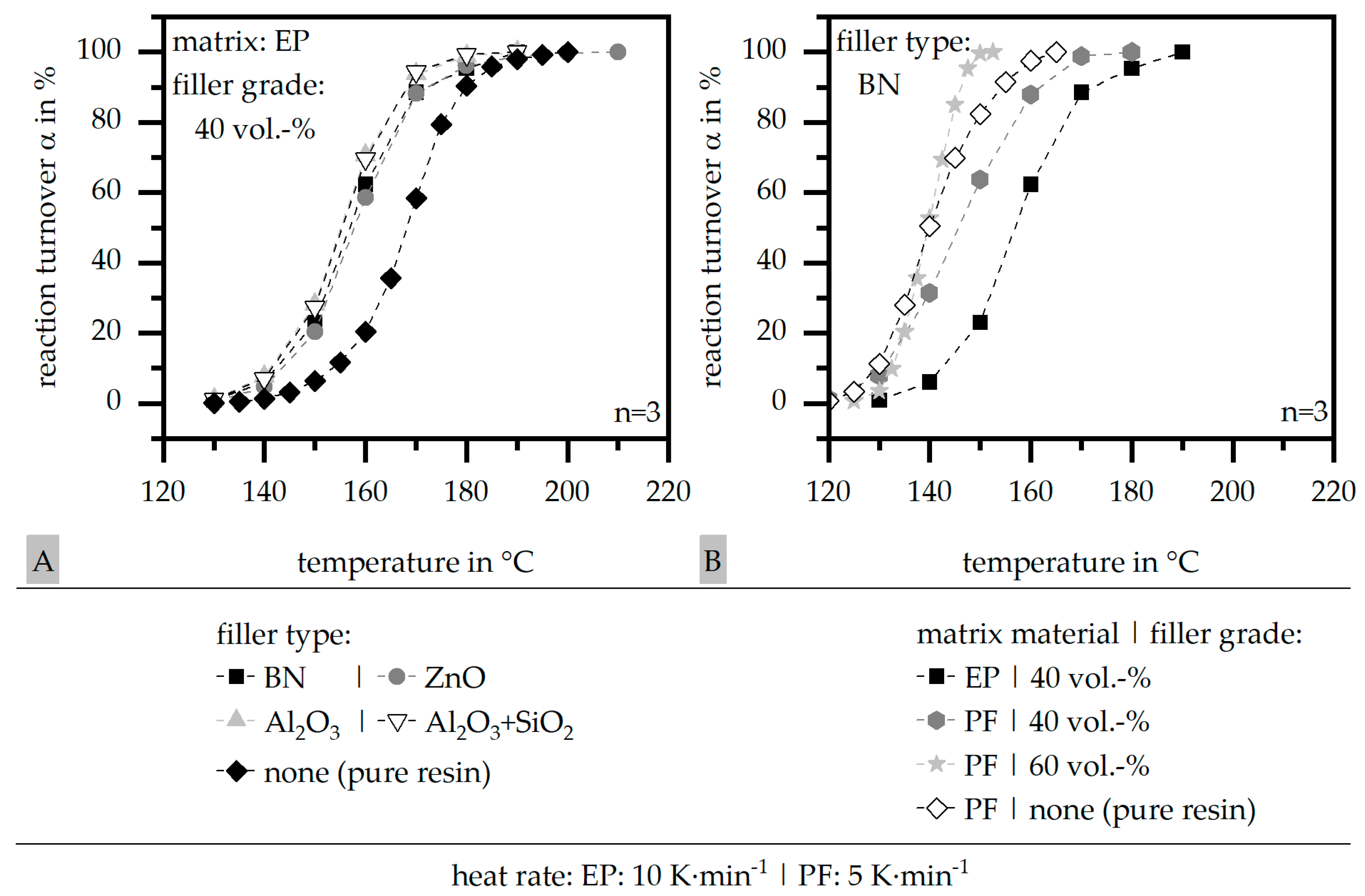
3.1. Differential Scanning Calorimetry (DSC) According to DIN EN ISO 11357
3.2. Density ρ
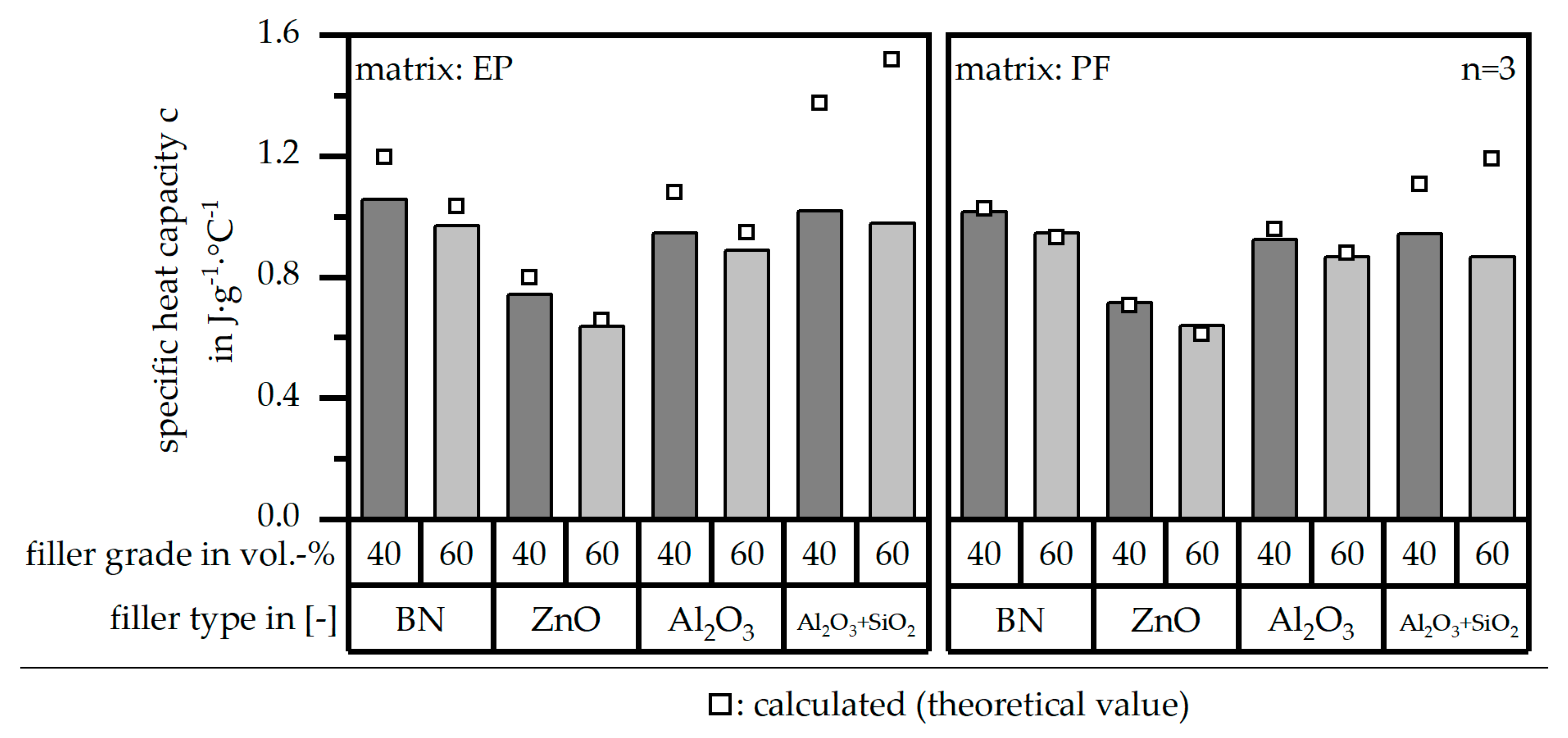
3.3. Specific Heat Capacity c
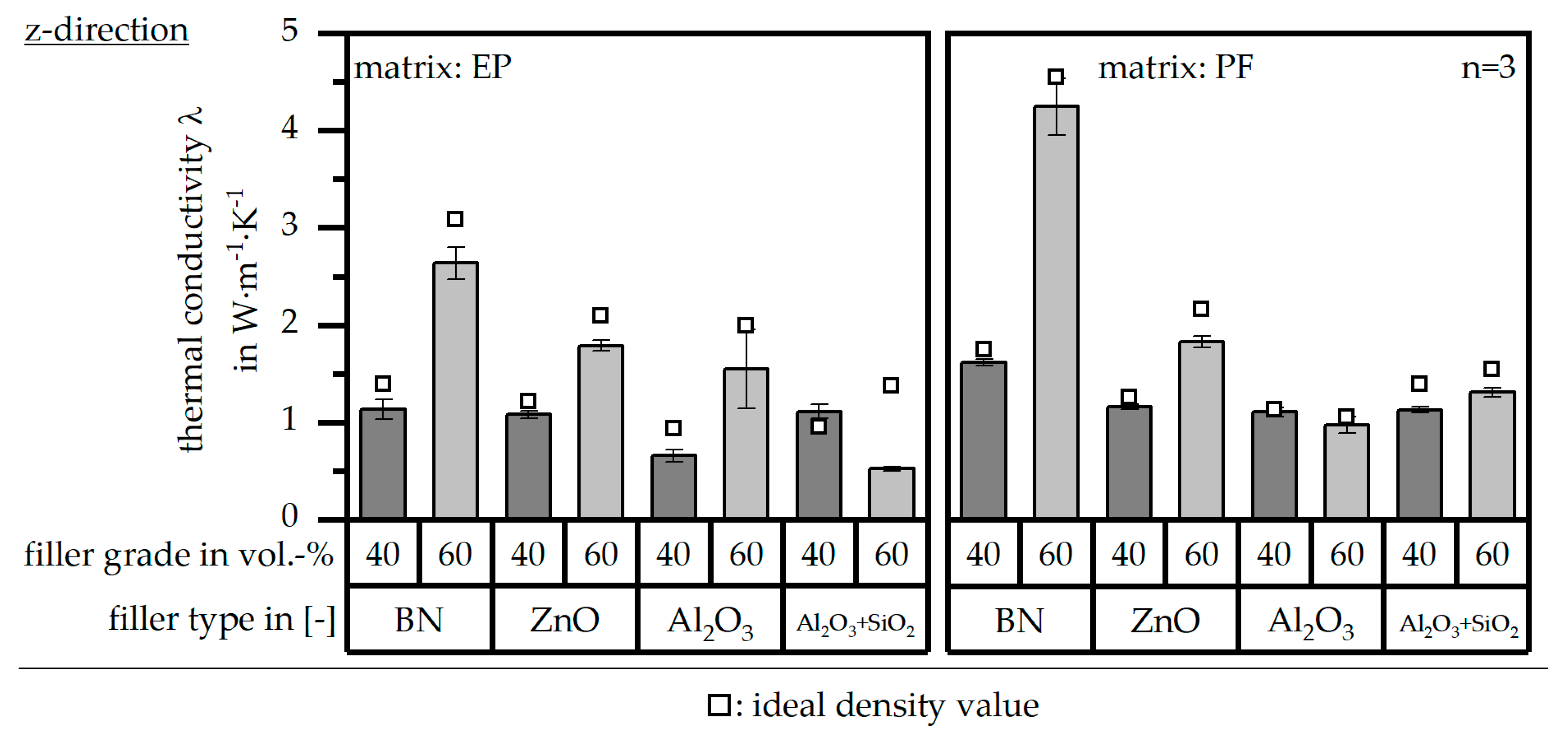
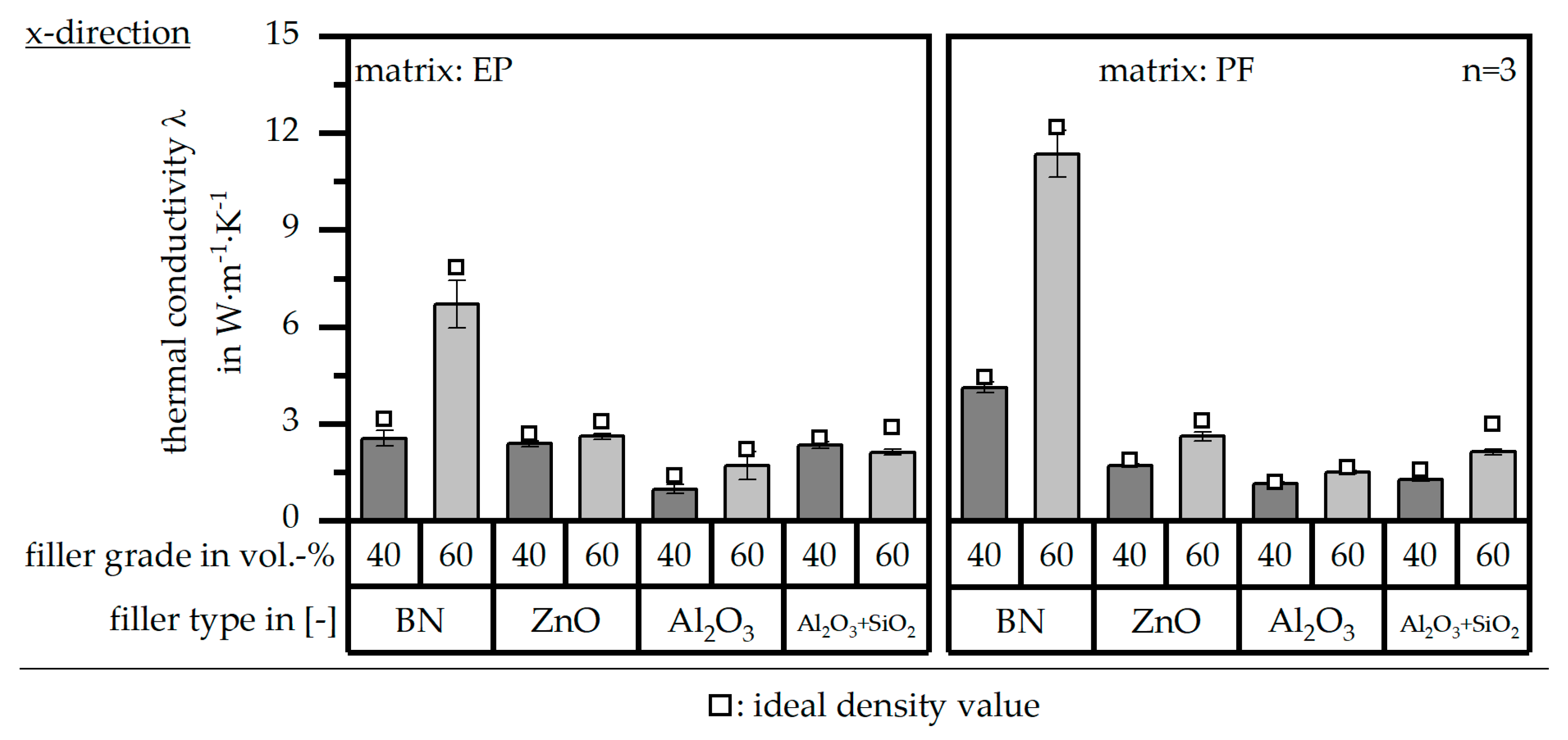
3.4. Thermal Conductivity λ According to DIN EN ISO 22007
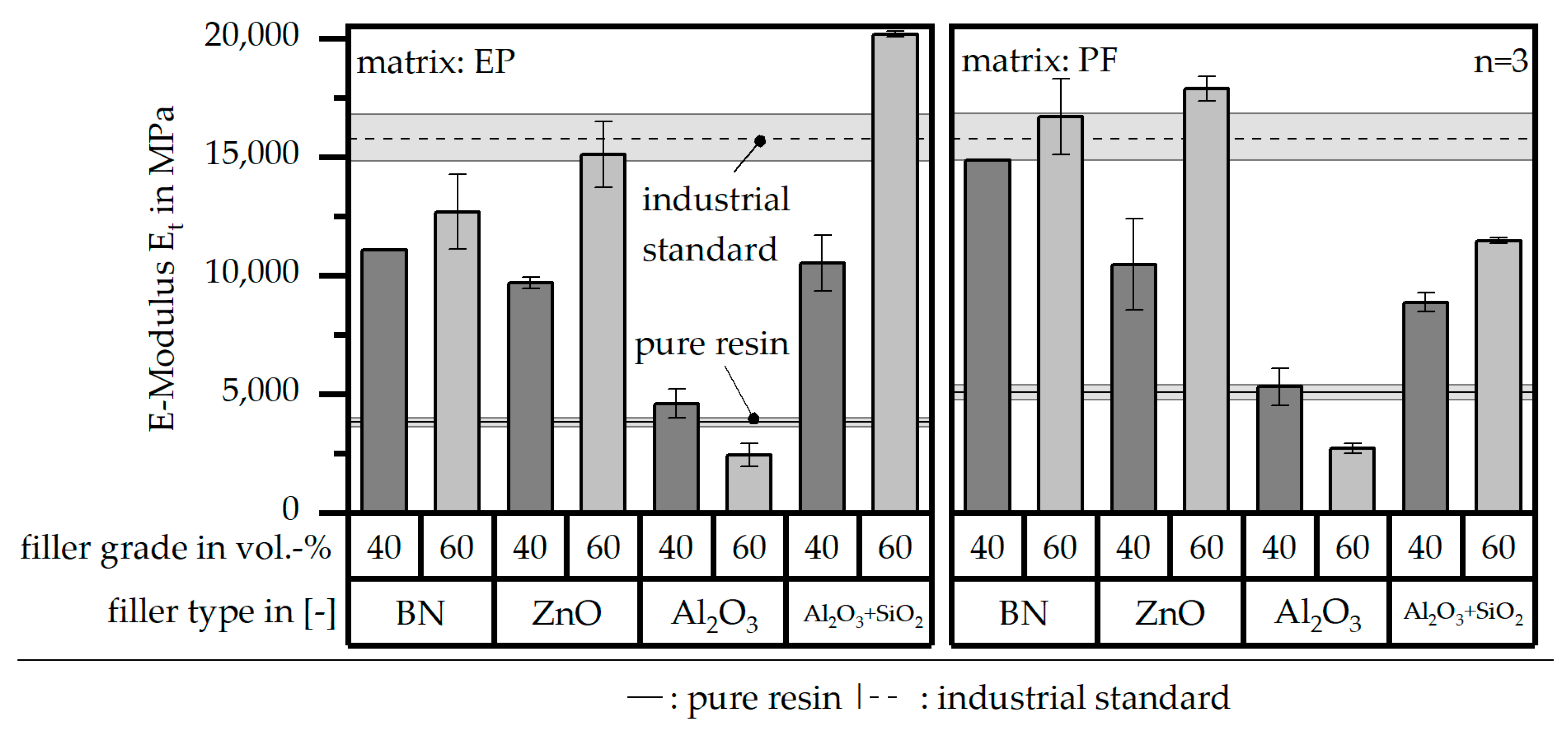
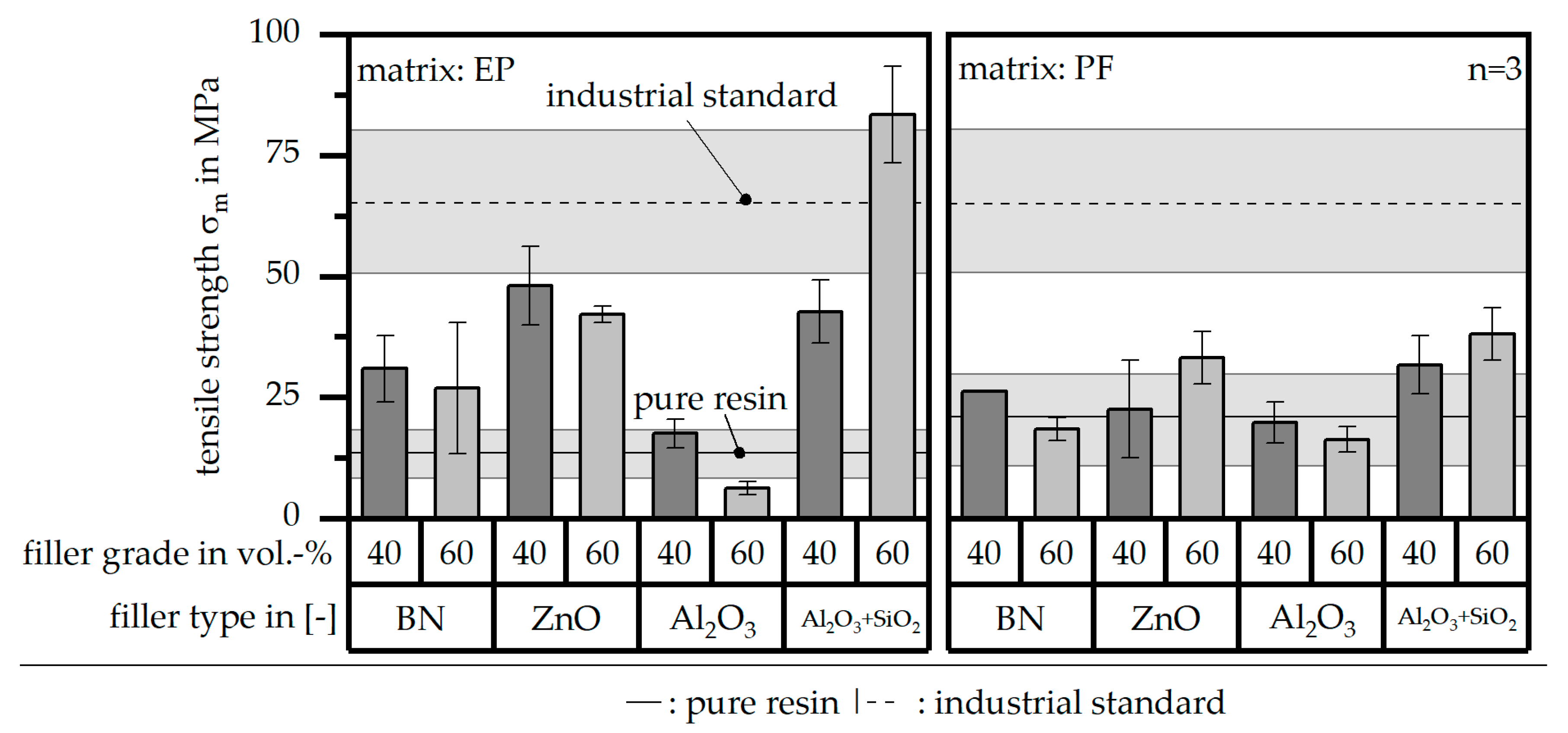
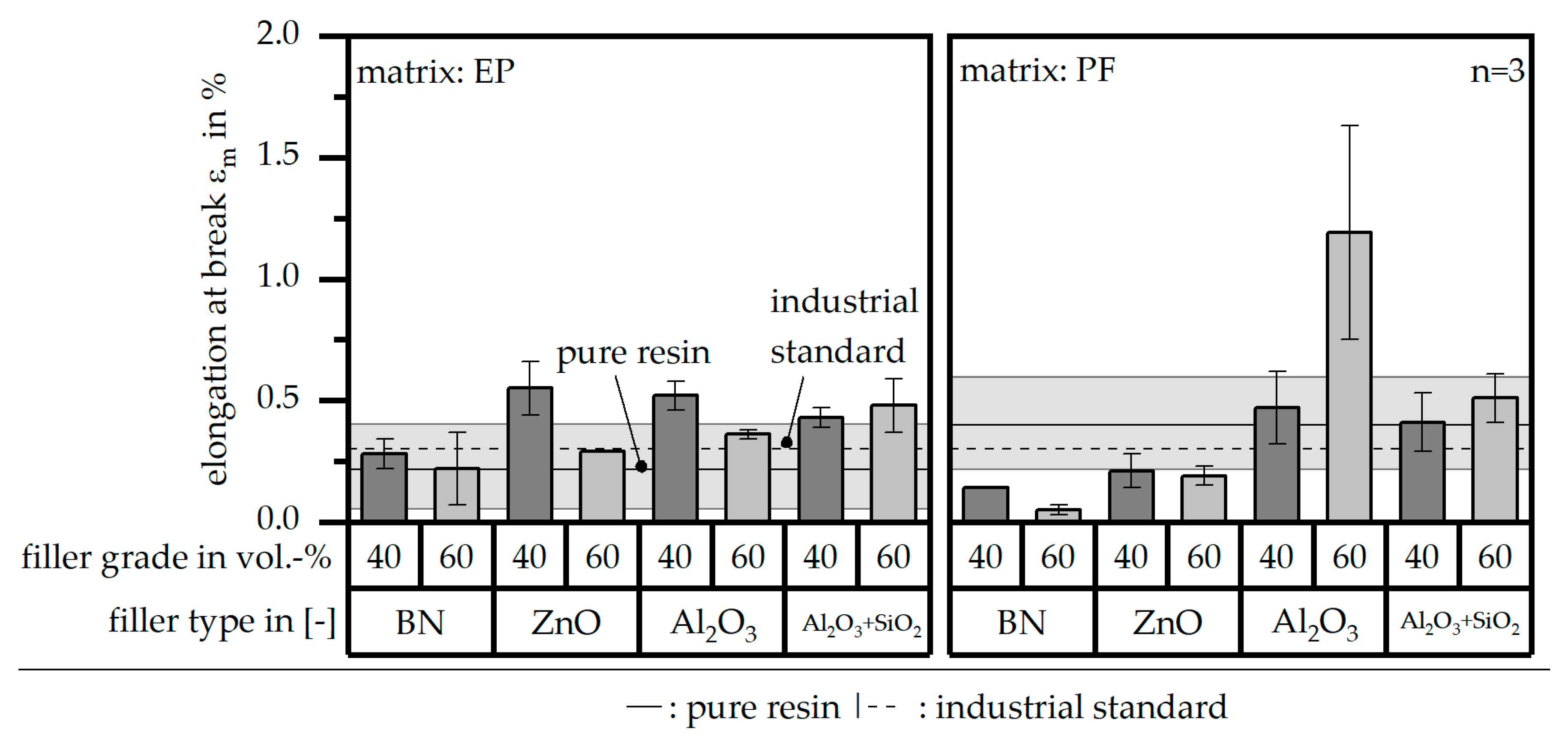
3.5. Mechanical Properties According to DIN EN ISO 527
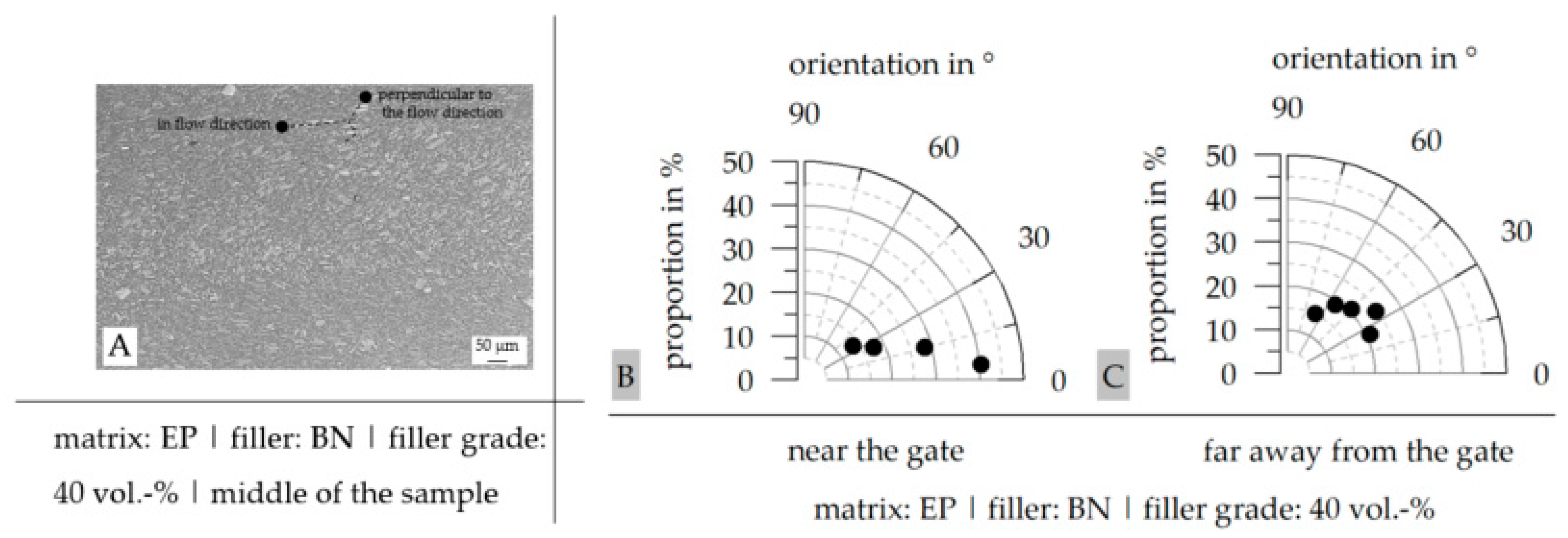
3.6. Filler Distribution and Linkage to Matrix Material
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koch, I. Vergleich Si und SiC Halbleiter; Jahresbericht: Brauchschweig, Germany, 2007. [Google Scholar]
- SiC-Halbleiter: Schlüsseltechnologie zur Effizienten und Nachhlatigen Elektronik. 2024. Available online: https://www.siconnex.com/de/siconnex/news/sic-halbleiter-technologie (accessed on 24 July 2024).
- Baur, E.; Brinkmann, S.; Osswald, T.; Rudolph, N.; Schmachtenberg, E. Saechtling Kunststoff Taschenbuch, 31st ed.; Carl Hanser Verlag: München, Germany, 2013. [Google Scholar]
- Ehrenstein, G.W.; Drummer, D. (Eds.) Hochgefüllte Kunststoffe mit Definierten Magnetischen, Thermischen und Elektrischen Eigenschaften; Springer VDI Verlag: Düsseldorf, Germany, 2002. [Google Scholar]
- Übler, W. Erhöhung der Thermischen Leitfähigkeit Elektrisch Isolierender Polymerwerkstoffe. Doctoral Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2004. [Google Scholar]
- Beyer, M. Epoxidharze in der Elektrotechnik: Grundlagen, Verabeitunsganlagen Anwendungen und neue Erkenntnisse; Grafenau/Württ. Expert-Verlag: Renningen, Germany, 1983. [Google Scholar]
- Johannaber, F.; Michaeli, W. Handbuch Spritzgießen, 2nd ed.; Carl Hanser Verlag: München, Germany, 2004. [Google Scholar]
- Zhao, Y.; Zhai, Z.; Drummer, D. Thermal conductivity of Aluminosilicate- and Aluminum Oxide-filled thermosets for injection molding: Effect of filler content, filler size and filer geometry. Polymers 2018, 10, 457. [Google Scholar] [CrossRef]
- Cassing, W.; Kuntze, K.; Ross, G. Dauermagnete: Mess- und Magnetisierungstechnik, 3rd ed.; Expert-Verlag: Renningen, Germany, 2018. [Google Scholar]
- Xu, Y.; Chung, D.; Mroz, C. Thermally conducting aluminum nitride polymer-matrix composites. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1749–1757. [Google Scholar] [CrossRef]
- Yung, K.C.; Liem, H. Enhanced thermal conductiity of boron nitride epoxy-matrix composite through multi-modal particle size mixing. J. Appl. Polym. Sci. 2007, 106, 3587–3591. [Google Scholar] [CrossRef]
- Wang, J.; Dai, G. Configuration-induced directional nonlinearity enhancement in Composite thermal media. Front. Phys. 2022, 10, 924890. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung e. V. Kunststoffe—Dynamische Differenz Thermoanalyse (DSC): Teil 1: Allgemeine Grundlagen; Beuth Verlag GmbH: Berlin, Germany, 2017; Available online: https://www.nautos.de/U3L/search/item-detail/DE30091378 (accessed on 21 February 2023).
- Deutsches Institut für Normung e. V. Kunststoffe—Bestimmung der Wärmeleitfähigkeit und der Temperaturleitfähigkeit: Teil 1: Allgemeine Grundlagen; Beuth Verlag GmbH: Berlin, Germany, 2018; Available online: https://www.nautos.de/U3L/search/item-detail/GB30486384 (accessed on 21 February 2023).
- Deutsches Institut für Normung e. V. Kunststoffe—Bestimmung der Zugeigenschaften: Teil 1: Allgemeine Grundsätze; Beuth Verlag GmbH: Berlin, Germany, 2019; Available online: https://www.nautos.de/U3L/search/item-detail/IX88984914 (accessed on 21 February 2023).



| Matrix Material | Density δ in g∙cm−3 | Heat Capacity c in J∙g−1∙°C−1 | Thermal Conductivity λ in W∙m−1∙K−1 | Molding Shrinkage (Longwise) in % |
|---|---|---|---|---|
| epoxy resin (EP) | 1.2250 | 1.616 | 0.4–0.6 | 0.4–0.6 |
| phenolic resin (PF) | 1.2915 | 1.294 | 0.4–0.6 | 0.3–0.5 |
| Filler System | Density δ in g∙cm−3 | Heat Capacity c in J∙g−1∙°C−1 | Thermal Conductivity λ in W∙m−1∙K−1 |
|---|---|---|---|
| boron nitride (BN) | 2.27 | 0.794 | 15⊥; 400 ∥ |
| zinc oxide (ZnO) | 5.65 | 0.505 | 30 |
| aluminum oxide (Al2O3) | 3.81 | 0.785 | 30 |
| aluminum silicate (Al2O3 + SiO2) | 3.56 | 0.765 | 14 |
| Filler System | BN | ZnO | Al2O3 | Al2O3 + SiO2 |
|---|---|---|---|---|
| particle geometry |  |  |  |  |
| platelet | star | sphere | platelet |
| matrix material | EP | EP | PF | PF | EP | EP | PF | PF | EP | EP | PF | PF | EP | EP | PF | PF | ||||
| filler system | BN | BN | BN | BN | ZnO | ZnO | ZnO | ZnO | Al2O3 | Al2O3 | Al2O3 | Al2O3 | Al2O3 + SiO3 | Al2O3 + SiO3 | Al2O3 + SiO3 | Al2O3 + SiO3 | ||||
| filler grade | 40 | 60 | 40 | 60 | 40 | 60 | 40 | 60 | 40 | 60 | 40 | 60 | 40 | 60 | 40 | 60 | ||||
| sample type | p | t | p | t | p | t | p | t | ||||||||||||
| process parameter | ||||||||||||||||||||
| mass temperature Tm in °C [feeding|noozle] | 55|95 | 75|110 | 55|95 | 75|110 | 55|95 | 55|105 | 65|85 | 65|85 | 65|85 | 65|95 | 65|95 | 65|100 | 65|85 | 65|105 | 65|85 | 55|110 | 55|85 | 55|85 | 65|85 | 75|115 |
| mould temperature TWZ in °C | 160 | 180 | 160 | 180 | 160 | 160 | 180 | 180 | 180 | 180 | 180 | 180 | 180 | 180 | 180 | 160 | 160 | 160 | 160 | 160 |
| heating time th in s | 85 | 85 | 85 | 85 | 75 | 75 | 75 | 75 | 40 | 40 | 85 | 85 | 30 | 30 | 30 | 75 | 75 | 30 | 30 | 30 |
| injection speed Vm in mm s−1 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 25 | 25 | 15 | 15 |
| BN | ZnO | Al2O3 | Al2O3 + SiO2 | |
|---|---|---|---|---|
| EP |  |  |  |  |
| PF |  |  | 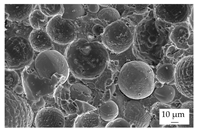 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rösel, U.; Drummer, D. Influence of Different Filler Systems on the Thermal Conductivity and Mechanical Properties of Thermosets. Polymers 2024, 16, 2917. https://doi.org/10.3390/polym16202917
Rösel U, Drummer D. Influence of Different Filler Systems on the Thermal Conductivity and Mechanical Properties of Thermosets. Polymers. 2024; 16(20):2917. https://doi.org/10.3390/polym16202917
Chicago/Turabian StyleRösel, Uta, and Dietmar Drummer. 2024. "Influence of Different Filler Systems on the Thermal Conductivity and Mechanical Properties of Thermosets" Polymers 16, no. 20: 2917. https://doi.org/10.3390/polym16202917
APA StyleRösel, U., & Drummer, D. (2024). Influence of Different Filler Systems on the Thermal Conductivity and Mechanical Properties of Thermosets. Polymers, 16(20), 2917. https://doi.org/10.3390/polym16202917






