Scaling Properties and Persistence of Long-Term Solar Activity
Abstract
:1. Introduction
2. Data and Methods
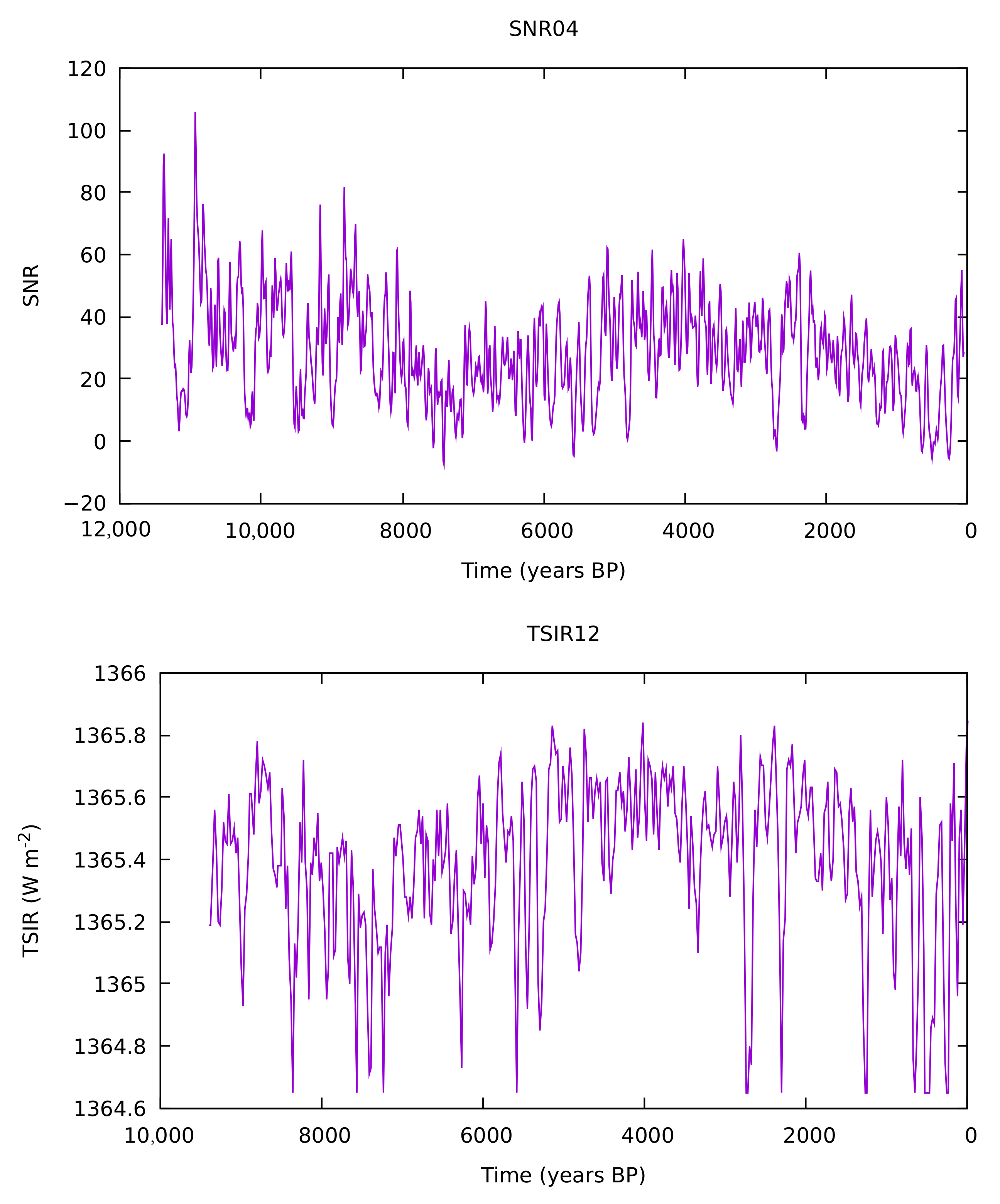
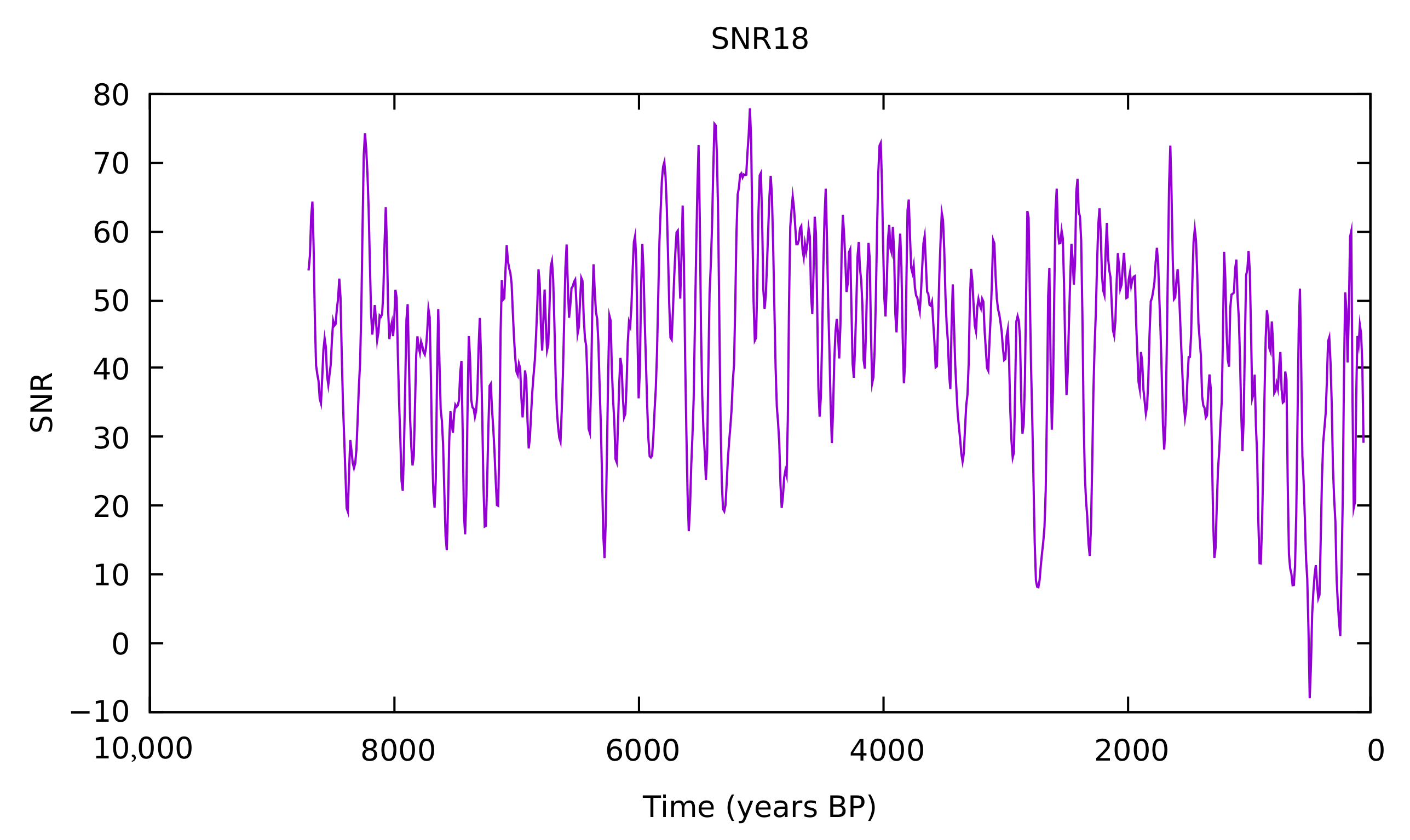
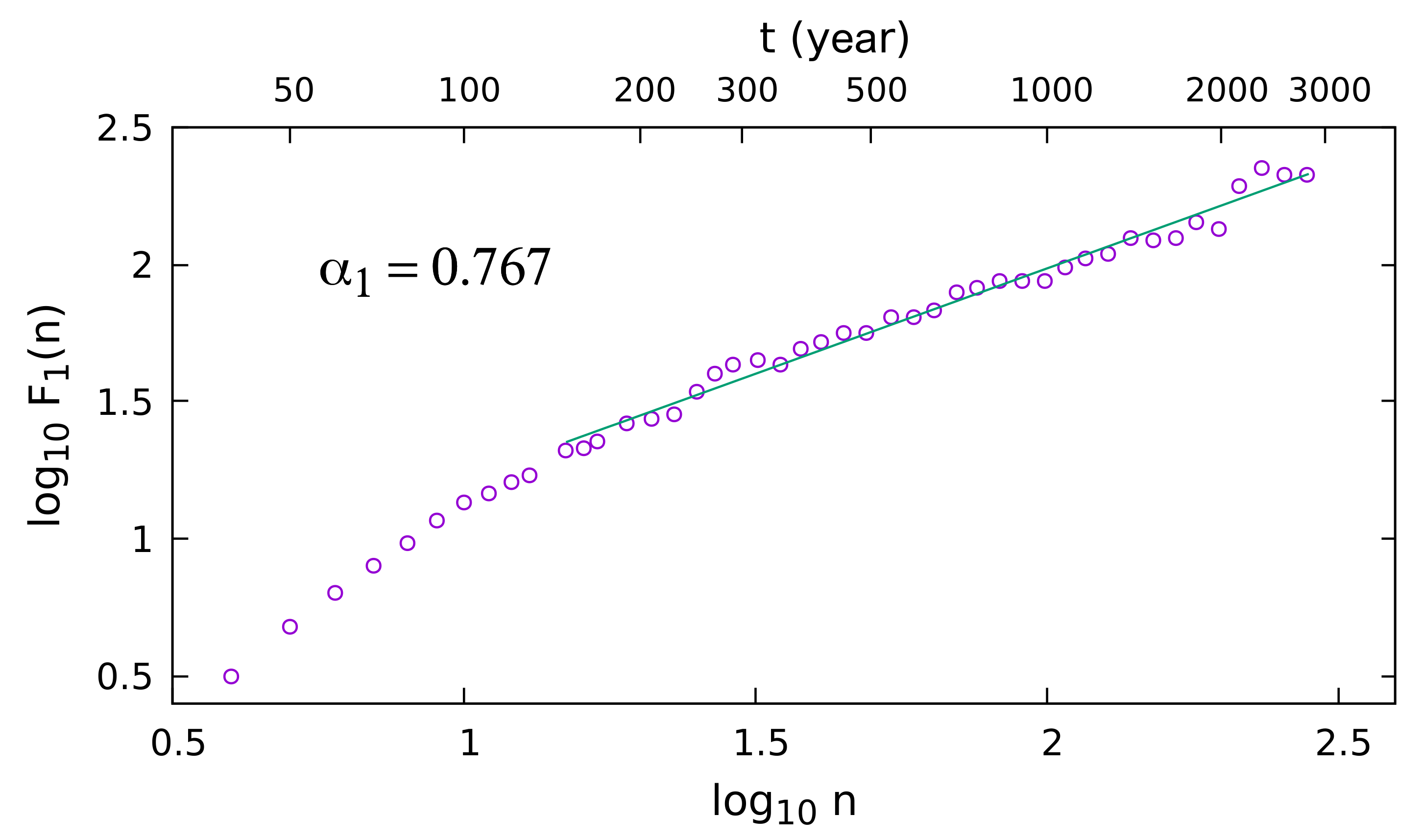
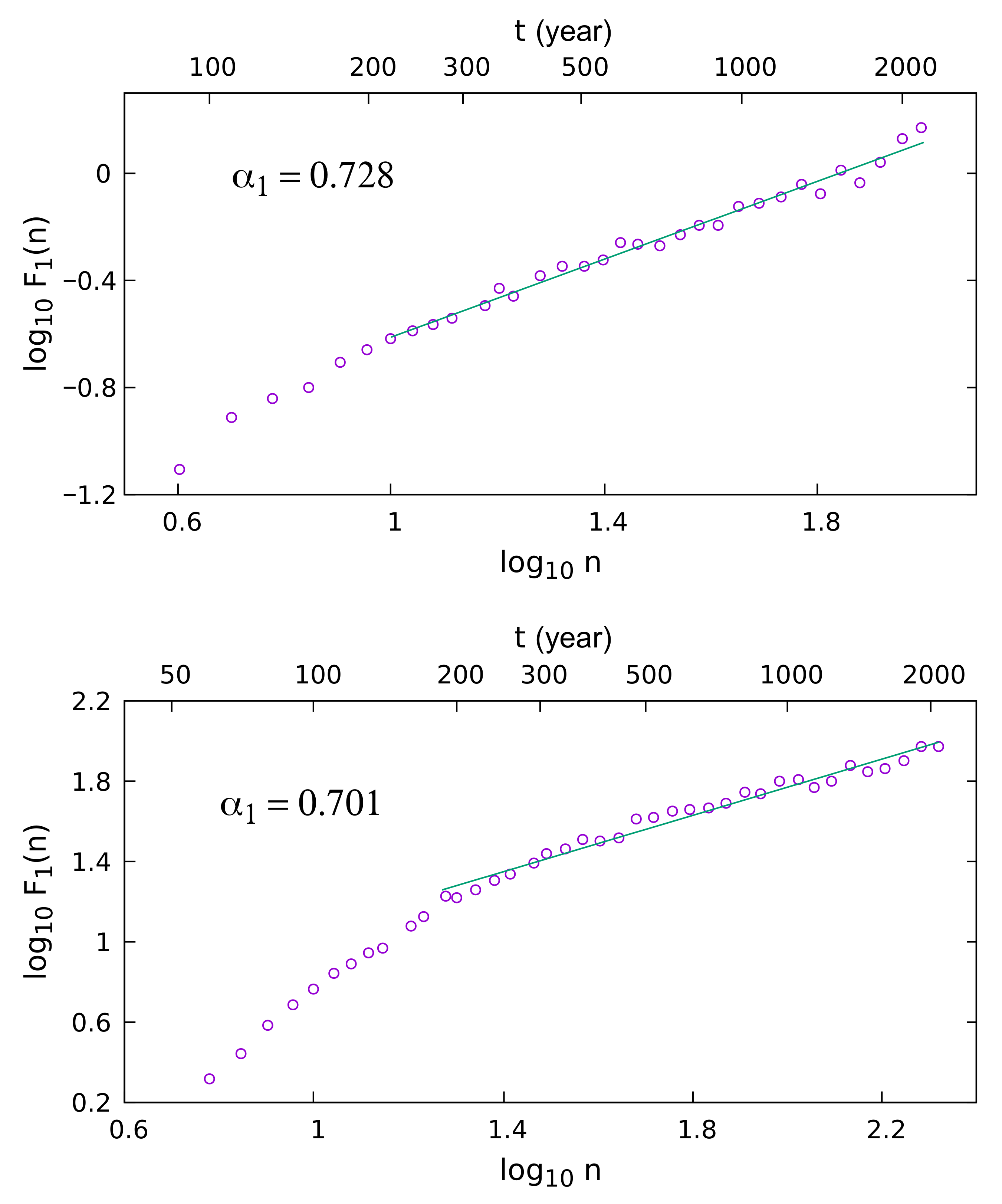
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFA | Detrended fluctuation analysis |
| SNR | Sunspot number reconstruction |
| TSIR | Total solar irradiance reconstruction |
References
- Hathaway, D.H. The Solar Cycle. Living Rev. Sol. Phys. 2015, 12, 4. [Google Scholar] [CrossRef] [PubMed]
- Hoyt, D.V.; Schatten, K.H. Group Sunspot Numbers: A New Solar Activity Reconstruction. Sol. Phys. 1998, 181, 491–512. [Google Scholar] [CrossRef]
- Clette, F.; Svalgaard, L.; Vaquero, J.M.; Cliver, E.W. Revisiting the Sunspot Number. A 400-Year Perspective on the Solar Cycle. Space Sci. Rev. 2014, 186, 35–103. [Google Scholar] [CrossRef] [Green Version]
- Petrovay, K. Solar cycle prediction. Living Rev. Sol. Phys. 2020, 17, 2. [Google Scholar] [CrossRef] [Green Version]
- Schwabe, H. Sonnenbeobachtungen im Jahre 1843. Von Herrn Hofrath Schwabe in Dessau. Astron. Nachr. 1844, 21, 233. [Google Scholar] [CrossRef]
- Gleissberg, W. Über die scheinbare Verteilung der Sonnenflecke. Astron. Nachr. 1939, 268, 81. [Google Scholar] [CrossRef]
- Gleissberg, W. The eighty-year sunspot cycle. J. Br. Astron. Assoc. 1958, 68, 148–152. [Google Scholar]
- Schove, D.J. The Sunspot Cycle, 649 BC to AD. 2000. J. Geophys. Res. 1955, 60, 127–146. [Google Scholar] [CrossRef] [Green Version]
- Link, F. Variations á longues périodes de l’activité solaire avant le 17ème siècle. Bull. Astron. Inst. Czechoslov. 1963, 14, 226. [Google Scholar]
- Feynman, J.; Fougere, P.F. Eighty-eight year periodicity in solar-terrestrial phenomena confirmed. J. Geophys. Res. 1984, 89, 3023–3027. [Google Scholar] [CrossRef] [Green Version]
- Attolini, M.R.; Cecchini, S.; Nanni, T.; Galli, M. On the persistence of the 22 Y solar cycle. Sol. Phys. 1990, 125, 389–398. [Google Scholar] [CrossRef]
- Frick, P.; Galyagin, D.; Hoyt, D.V.; Nesme-Ribes, E.; Schatten, K.H.; Sokoloff, D.; Zakharov, V. Wavelet analysis of solar activity recorded by sunspot groups. Astron. Astrophys. 1997, 328, 670–681. [Google Scholar]
- Ogurtsov, M.G.; Nagovitsyn, Y.A.; Kocharov, G.E.; Jungner, H. Long-Period Cycles of the Sun’s Activity Recorded in Direct Solar Data and Proxies. Sol. Phys. 2002, 211, 371–394. [Google Scholar] [CrossRef]
- Peristykh, A.N.; Damon, P.E. Persistence of the Gleissberg 88-year solar cycle over the last 12,000 years: Evidence from cosmogenic isotopes. J. Geophys. Res. Space Phys. 2003, 108, 1003. [Google Scholar] [CrossRef] [Green Version]
- Vecchio, A.; Lepreti, F.; Laurenza, M.; Alberti, T.; Carbone, V. Connection between solar activity cycles and grand minima generation. Astron. Astrophys. 2017, 599, A58. [Google Scholar] [CrossRef] [Green Version]
- Suess, H.E. The Radiocarbon Record in Tree Rings of the Last 8000 Years. Radiocarbon 1980, 22, 200–209. [Google Scholar] [CrossRef] [Green Version]
- Sonett, C.P. Very long solar periods and the radiocarbon record. Rev. Geophys. Space Phys. 1984, 22, 239–254. [Google Scholar] [CrossRef]
- Sonett, C.P.; Finney, S.A. The Spectrum of Radiocarbon. Philos. Trans. R. Soc. Lond. Ser. A 1990, 330, 413–425. [Google Scholar] [CrossRef]
- Stuiver, M.; Braziunas, T. Sun, ocean, climate and atmospheric 14CO2: An evaluation of casual and spectral relationships. Holocene 1993, 3, 289–305. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Mursula, K.; Solanki, S.; Schüssler, M.; Alanko, K. Reconstruction of solar activity for the last millennium using 10Be data. Astron. Astrophys 2004, 413, 745–751. [Google Scholar] [CrossRef] [Green Version]
- Damon, P.E.; Sonett, C.P. Solar and terrestrial components of the atmospheric C-14 variation spectrum. In The Sun in Time; Sonett, C.P., Giampapa, M.S., Matthews, M.S., Eds.; University of Arizona Press: Tucson, AZ, USA, 1991; pp. 360–388. [Google Scholar]
- Vasiliev, S.S.; Dergachev, V.A. The ~2400-year cycle in atmospheric radiocarbon concentration: Bispectrum of 14C data over the last 8000 years. Ann. Geophys. 2002, 20, 115–120. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B.; Wallis, J.R. Some Long-Run Properties of Geophysical Records. Water Resour. Res. 1969, 5, 321–340. [Google Scholar] [CrossRef] [Green Version]
- Ruzmaikin, A.; Feynman, J.; Robinson, P. Long-term persistence of solar activity. Sol. Phys. 1994, 149, 395–403. [Google Scholar] [CrossRef] [Green Version]
- Komm, R.W. Hurst Analysis of Mt. Wilson Rotation Measurements. Sol. Phys. 1995, 156, 17–28. [Google Scholar] [CrossRef]
- Lepreti, F.; Fanello, P.C.; Zaccaro, F.; Carbone, V. Persistence of solar activity on small scales: Hurst analysis of time series coming from Hα flares. Sol. Phys. 2000, 197, 149–156. [Google Scholar] [CrossRef]
- Oliver, R.; Ballester, J.L. Is there memory in solar activity? Phys. Rev. E 1998, 58, 5650–5654. [Google Scholar] [CrossRef]
- Ogurtsov, M.G. New Evidence for Long-Term Persistence in the Sun’s Activity. Sol. Phys. 2004, 220, 93–105. [Google Scholar] [CrossRef]
- Weron, R. Estimating long-range dependence: Finite sample properties and confidence intervals. Phys. A Stat. Mech. Appl. 2002, 312, 285–299. [Google Scholar] [CrossRef] [Green Version]
- Solanki, S.K.; Usoskin, I.G.; Kromer, B.; Schüssler, M.; Beer, J. Unusual activity of the Sun during recent decades compared to the previous 11,000 years. Nature 2004, 431, 1084–1087. [Google Scholar] [CrossRef] [Green Version]
- Steinhilber, F.; Abreu, J.A.; Beer, J.; Brunner, I.; Christl, M.; Fischer, H.; Heikkila, U.; Kubik, P.W.; Mann, M.; McCracken, K.G.; et al. 9,400 years of cosmic radiation and solar activity from ice cores and tree rings. Proc. Natl. Acad. Sci. USA 2012, 109, 5967–5971. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.J.; Usoskin, I.G.; Krivova, N.; Kovaltsov, G.A.; Baroni, M.; Bard, E.; Solanki, S.K. Solar activity over nine millennia: A consistent multi-proxy reconstruction. Astron. Astrophys. 2018, 615, A93. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Kristoufek, L. Rescaled Range Analysis and Detrended Fluctuation Analysis: Finite Sample Properties and Confidence Intervals. Czech Econ. Rev. 2010, 4, 236–250. [Google Scholar]
- Pontieri, A.; Lepreti, F.; Sorriso-Valvo, L.; Vecchio, A.; Carbone, V. A Simple Model for the Solar Cycle. Sol. Phys. 2003, 213, 195–201. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lepreti, F.; Carbone, V.; Vecchio, A. Scaling Properties and Persistence of Long-Term Solar Activity. Atmosphere 2021, 12, 733. https://doi.org/10.3390/atmos12060733
Lepreti F, Carbone V, Vecchio A. Scaling Properties and Persistence of Long-Term Solar Activity. Atmosphere. 2021; 12(6):733. https://doi.org/10.3390/atmos12060733
Chicago/Turabian StyleLepreti, Fabio, Vincenzo Carbone, and Antonio Vecchio. 2021. "Scaling Properties and Persistence of Long-Term Solar Activity" Atmosphere 12, no. 6: 733. https://doi.org/10.3390/atmos12060733
APA StyleLepreti, F., Carbone, V., & Vecchio, A. (2021). Scaling Properties and Persistence of Long-Term Solar Activity. Atmosphere, 12(6), 733. https://doi.org/10.3390/atmos12060733






