Decision-Tree-Based Classification of Lifetime Maximum Intensity of Tropical Cyclones in the Tropical Western North Pacific

Abstract

The National Typhoon Center of the Korea Meteorological Administration developed a statistical–dynamical typhoon intensity prediction model for the western North Pacific, the CSTIPS-DAT, using a track-pattern clustering technique. The model led to significant improvements in the prediction of the intensity of tropical cyclones (TCs). However, relatively large errors have been found in a cluster located in the tropical western North Pacific (TWNP), mainly because of the large predictand variance. In this study, a decision-tree algorithm was employed to reduce the predictand variance for TCs in the TWNP. The tree predicts the likelihood of a TC reaching a maximum lifetime intensity greater than 70 knots at its genesis. The developed four rules suggest that the pre-existing ocean thermal structures along the track and the latitude of a TC’s position play significant roles in the determination of its intensity. The developed decision-tree classification exhibited 90.0% and 80.5% accuracy in the training and test periods, respectively. These results suggest that intensity prediction with the CSTIPS-DAT can be further improved by developing independent statistical models for TC groups classified by the present algorithm.

1. Introduction

The accurate prediction of tropical cyclone (TC) intensity is a major task in operational forecasting. Regarding intensity prediction, the capabilities of the widely used traditional statistical approaches have improved considerably more than those of the dynamical models [1]. A new statistical–dynamical model, the CSTIPS-DAT [2], which uses a clustering technique and depth-averaged ocean temperature (DAT)-based predictors, has facilitated significant improvements in intensity prediction in the western North Pacific (WNP). However, the CSTIPS-DAT shows relatively large errors for specific clusters, particularly those with a large predictand variance [2].

The tropical western North Pacific (TWNP) TCs, which belong to Cluster 2 in the CSTIPS-DAT model, spend most of their lifetimes over the tropics, where the environmental factors are favorable for their development (Figure 1a). Therefore, Cluster 2 is characterized by the strongest mean TC intensity in the WNP, and many TCs in the said cluster are distinguished by noticeable intensification. However, a considerable number of TCs in the said cluster still do not intensify even under favorable conditions, which produces a large breadth of intensity distribution (Figure 2a) and a large predictand variance. The distribution of the lifetime maximum intensity (LMI) in the TWNP is bimodal, characterized by a local minimum (at about 70 knots LMI) that separates the two groups between weakly (1st mode) and strongly developing TCs (2nd mode). Because the CSTIPS-DAT is a multiple-linear-regression-based model, the TWNP cluster was trained to fit well with strong TCs with a high-density distribution; thus, major errors can occur in the prediction of weak TCs. For example, the intense Typhoon Phanfone in 2014, with an LMI of 95 kt, was well predicted by the CSTIPS-DAT. However, the relatively weak Typhoon Faxai (2014) was not accurately predicted, mostly because of overestimation (Figure 1b,c). These results suggest that with prior knowledge of the LMI type at the genesis of a TC, intensity prediction in the TWNP could be improved through the development of independent statistical models for each classified group.

The LMI, which is an integrated metric of TC intensification, can be used to present basic TC climatology characteristics [3,4,5]. Several studies have noted that the global distribution of the LMI is bimodal [6,7,8]. However, there is no consensus on why this bimodal LMI distribution occurs. Torn and Snyder [9] argued that the bimodality is the result of an artificially low number of Category 3 hurricanes in the Atlantic, and that this may be linked to the low resolution of the Dvorak technique which has been used to estimate their intensity. Soloviev et al. [10] attempted to explain the bimodal distribution of the LMI by using the ratio of surface exchange coefficients as a function of wind speed. They suggested that a local maximum of the ratio is favorable for rapid intensification (RI), and thereby increases the number of TCs in the second high-intensity peak. Lee et al. [8] reported that RI is be a key factor in the bimodality in the LMI distribution of two types of TCs: those that undergo RI during their lifetimes (RI TCs) and those that do not (non-RI TCs). They found that the LMI had a normal distribution with a unimodal peak for each TC type, at approximately 120 kt and 45 kt for RI TCs and non-RI TCs, respectively. The establishment of classification criteria to determine the types of TCs (weakly or strongly developing TCs) in the early developing stages of the TWNP TCs will contribute to a better understanding of the global bimodal LMI distribution.

The analysis of climate information on TCs has socioeconomic implications and scientific significance because it leads to a better understanding of TC activity and the related mechanisms [11,12,13]. However, the large volume of varied data on TCs has continued to increase significantly, at a pace that has seemed to outstrip the capabilities of traditional analytical methods [14,15]. The decision tree, as a data-mining technique, is a process of finding useful rules, patterns, and knowledge in large, diverse archived databases to facilitate decision making [16].

Recently, the decision tree, as a useful tool for schematic classification, has been widely employed to investigate the mechanisms of TC development and impact in the WNP [14,17,18,19,20,21,22,23] and the North Atlantic [24,25,26,27]. Li et al. [17] employed a decision-tree algorithm to investigate the collective contributions to Atlantic hurricanes from sea surface temperature (SST), water vapor, vertical wind shear, and zonal stretching deformation. Zhang et al. [14] applied a decision tree to the binary classification of TCs as intensifying or weakening within 24 h. The decision tree, which used only three variables, exhibited remarkable prediction accuracy: 90.2%. Zhang et al. [18] used a decision tree to investigate the classification of tropical disturbances that did or did not develop into tropical storms in the WNP. The classification accuracies of the developed model were 81.7% for training and 84.6% for validation. Gao et al. [19] used a decision-tree algorithm to develop an RI prediction model that classified intensity changes as RI and non-RI events. They showed that the prestorm ocean coupling potential intensity index, which uses DATs instead of SST to calculate the maximum potential intensity (MPI), improved the RI classification accuracy by approximately 6% during the test period. Park et al. [20] developed a decision-tree-based WNP TC genesis detection algorithm using satellite observation-based predictors. They found that circulation symmetry and intensity were the most critical parameters for characterizing the development of tropical disturbances. Lee et al. [21] developed a scheme for TC formation using machine learning in the WNP and applied it for operational prediction of TC formation. Kim et al. [22] compared the prediction performance of three machine-learning algorithms (decision tree, random forest, support vector machines) and a linear-discriminant-analysis-based model in WNP TC genesis detection. They showed that machine-learning-based models were more capable than conventional linear approaches at detecting TC formation. Yang et al. [24] showed that using the association rule algorithm, the RI prediction performance of the model using only three predictors was better than that of the model consisting of five predictors proposed by Kaplan and DeMaria [28]. Yang [25] performed RI prediction using various classifiers based on the Statistical Hurricane Intensity Prediction Scheme (SHIPS) database. Su et al. [26], using satellite-observation-based storm internal structure and the predictors of the National Hurricane Center probabilistic forecast guidance, developed an RI prediction model for Atlantic hurricanes based on a machine-learning method. Wei and Yang [27] built an artificial intelligence system based on the SHIPS database, significantly improving the RI prediction performance for Atlantic hurricanes. These studies have shown that decision trees are useful for binary classification related to TC genesis and intensification, which further suggests that a decision tree could be a useful tool to split the components in the bimodal distribution of the LMI.

The bimodal distribution results in a large variance of TC intensity, which makes accurate intensity predictions difficult. Therefore, if we can successfully classify the type of LMI at the point when a TC occurs, the statistical TC intensity prediction can be improved by reducing the variance of the predictand. To check such a possibility, this study aimed to build a decision-tree classifier that can predict the intensification type when a target TC occurs. Section 2 describes the dataset and the classification method. In Section 3, the potential predictors are examined, and the classification and model verification results are discussed. A summary and conclusion are provided in Section 4.

2. Data and Methodology

2.1. Data

A decision tree was trained using the 2004–2013 TWNP TCs, which belong to Cluster 2 as classified by the TC track pattern clustering method [2]. Meanwhile, the tree was validated using the 2014–2016 TCs. The TC information was obtained from the Regional Specialized Meteorological Center’s best track data. The environmental data were derived from two dynamical models’ analysis data. The atmospheric variables were obtained from the National Centers for Environmental Prediction Global Forecast System analysis data, with a 1 × 1 degree of horizontal resolution at 6 h intervals. The oceanic variables were calculated with three-dimensional ocean data derived from the Hybrid Coordinate Ocean Model (HYCOM) + Navy Coupled Ocean Data Assimilation Global Analysis (GLBa0.08) provided by the U.S. Naval Research Laboratory.

2.2. Methodology

2.2.1. Static and Synoptic Potential Predictors

A total of 38 variables were used to build the decision tree, and are listed in

Table 1. Potential variables in the present model and their correlation coefficients (r) with the lifetime maximum intensity for the 2004–2013 TWNP TCs (Cluster 2 in CTIPS-DAT). All the variables were averaged along the TC track from the genesis to 3.25 days.

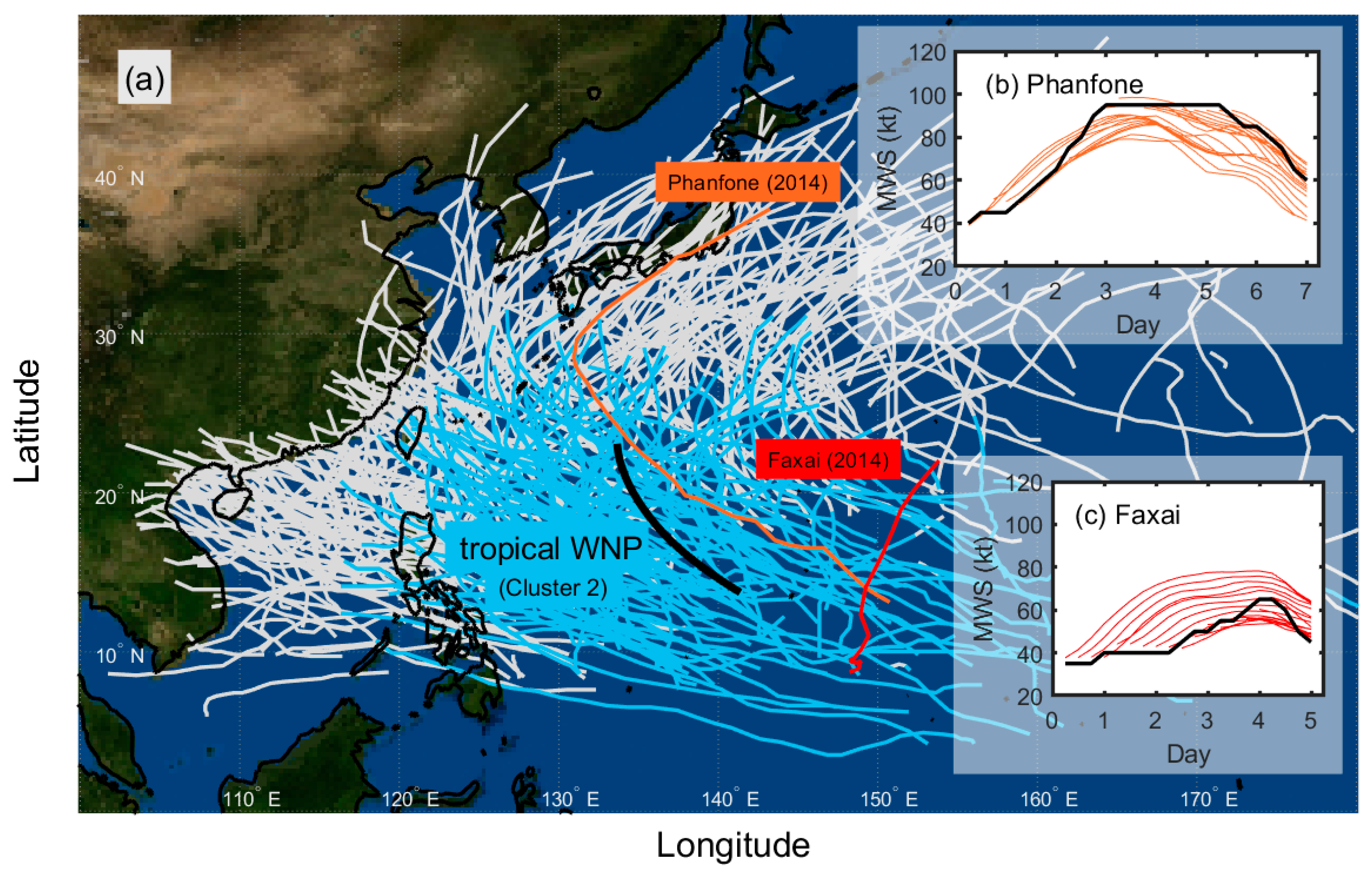
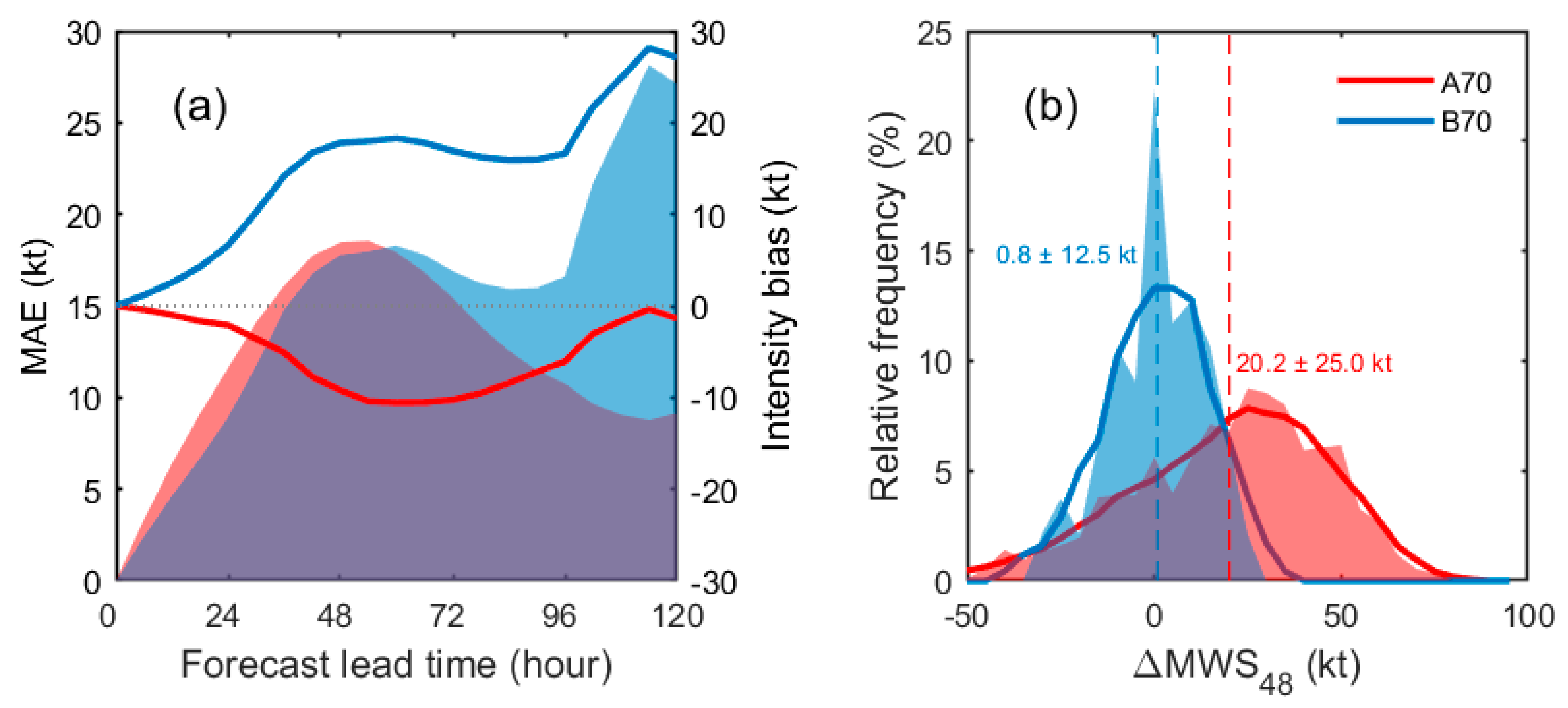
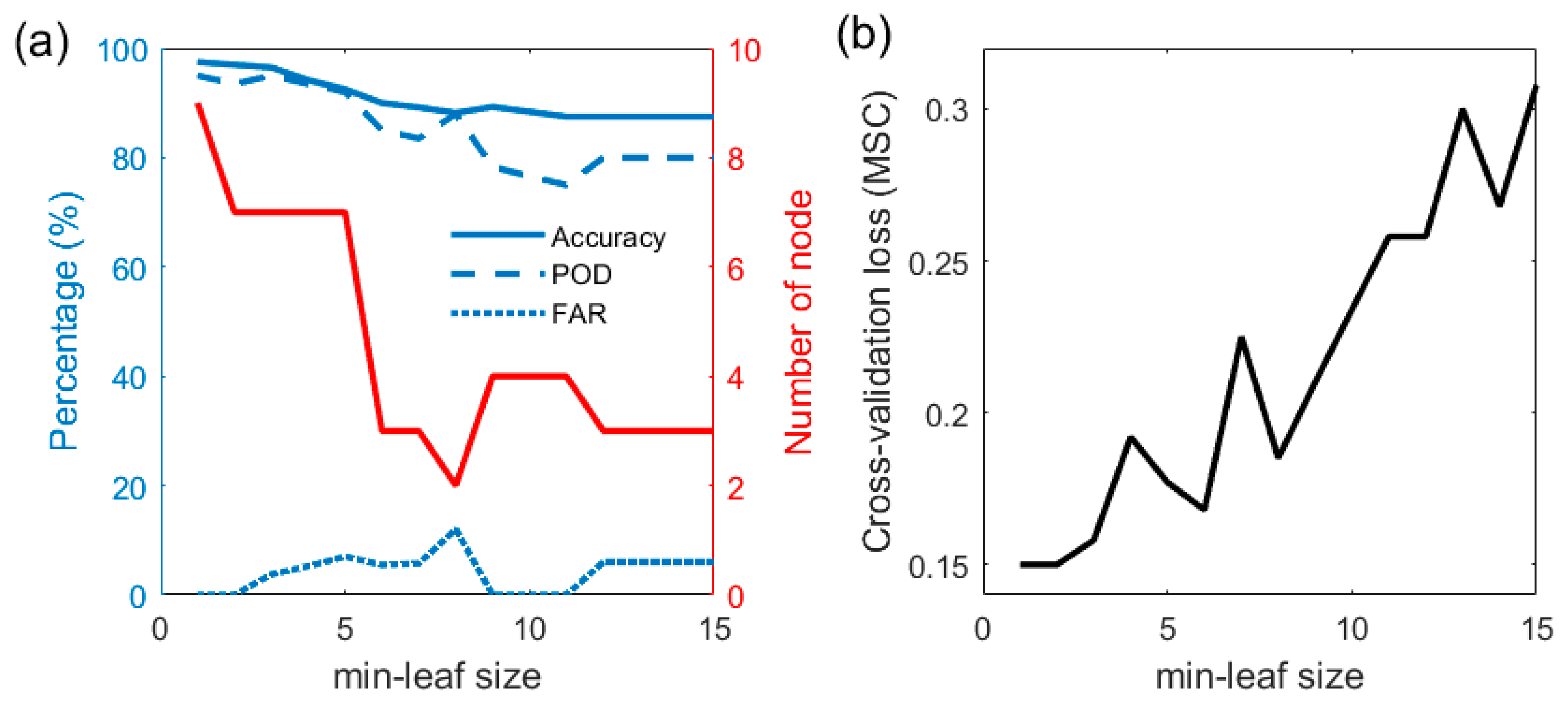
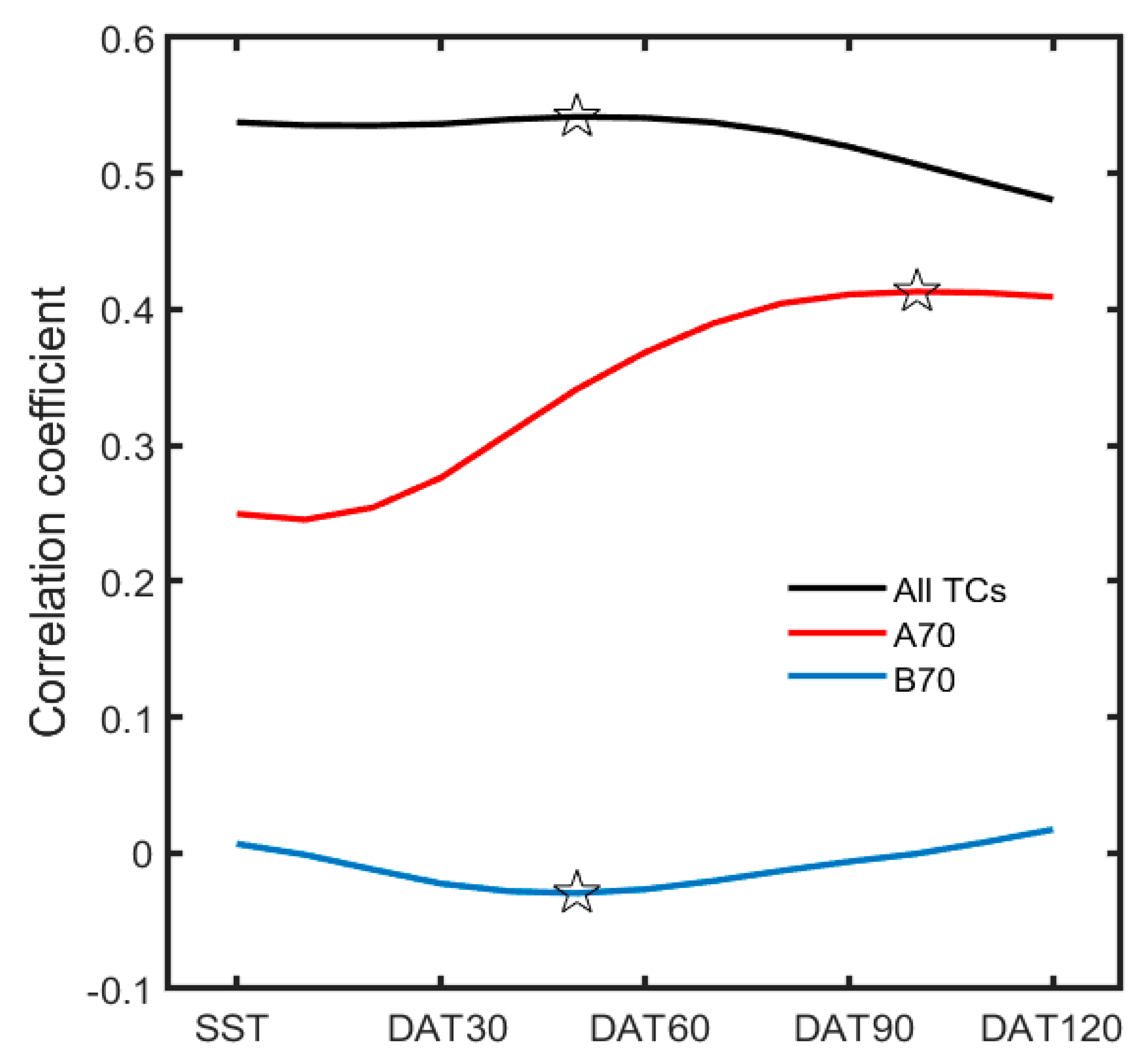
Variable	Description	r
JDAY	The absolute value of Julian day—248	−0.27
LAT	Latitude of typhoon location	−0.33
LON	Longitude of typhoon location	0.07
SPD	Storm moving speed	−0.23
D200	Area-averaged (0 km to 1000 km) divergence at 200 hPa	0.05
RV500	Area-averaged (0 km to 1000 km) relative vorticity at 500 hPa	0.16
RV850	Area-averaged (0 km to 1000 km) relative vorticity at 850 hPa	0.04
U200	Area-averaged (200 km to 800 km) zonal wind at 200 hPa	−0.28
T200	Area-averaged (200 km to 800 km) air temperature at 200 hPa	−0.39
RHHI	Area-averaged (200 km to 800 km) relative humidity 500–300 hPa	0.32
RHLO	Area-averaged (200 km to 800 km) relative humidity 850–700 hPa	0.29
SH200	Area-averaged (200 km to 800 km) 200 hPa to 850 hPa vertical wind shear	−0.17
SH500	Area-averaged (200 km to 800 km) 500 hPa to 850 hPa vertical wind shear	−0.32
OHC	Area-averaged (0 km to 200 km) ocean heat contents	0.52
DAT10—DAT120	Ocean temperatures averaged from the near-surface down to the various depth (10 to 120 m, 10-m interval)	0.48–0.54
DMPI10—DMPI120	Maximum potential intensity using DAT10—DAT120	0.47–0.56

with their correlations with LMI. The potential variables considered in this study are factors known to be related to TC intensity [2], and are similar to those considered for the development of the CSTIPS-DAT. Four static variables were included: the absolute Julian day number, TC latitude (LAT) and longitude, and TC translation speed. There were 34 synoptic variables: divergence at 200 hPa (D200), the relative vorticity at 500 hPa (RV500) and 850 hPa (RV850), 200 hPa zonal wind (U200) and air temperature (T200), 500–300 hPa layer mean relative humidity (RHHI), 850–700 hPa layer mean relative humidity (RHLO), 200–850 hPa vertical wind shear (SH200), 500–850 hPa vertical wind shear (SH500), ocean heat content (OHC), depth-averaged temperature at various depths (DAT; [29,30]), and DAT-based MPI (DMPI; [31,32]). Lin et al. [31] suggested DMPI using DAT instead of prestorm sea surface temperature to consider negative feedback by TC-induced sea surface cooling on existing SST-based MPI. DMPI has significantly reduced the overestimation of maximum intensity of the existing SST-based MPI and has frequently been used to predict TC intensity and RI [2,19,32,33]. The variables based on intensification potential (POT; MPI − initial intensity) were the essential factors in the CSTIPS-DAT model. However, in this study, TC genesis was defined as the first moment of at least 35 kt intensity; thus, the POT and DMPI had the same correlation coefficient. Because the current study focused on classifying the LMI of TCs at their genesis, the POT and DAT-based POT were excluded from the pool of potential variables. DATs and DMPIs had the highest correlation among all variables, reaching 0.54 and 0.56, respectively. OHC, a widely used index for upper-ocean thermal conditions, also had a high correlation coefficient (r = 0.52). Price [29] showed that OHC and DAT are well correlated in the high OHC range and deep water, but they are poorly correlated in low OHC and shallow continental shelves. Since the TWNP is mostly deep and has high OHC, the correlation coefficients of OHC and DAT are not very different there. All the variables were averaged from the genesis to 3.25 days along the TC track—the sum of the average time (1.7 days) and standard deviation (1.55 days) to reach LMI after TWNP TCs’ occurrence.

2.2.2. Classification and Regression Tree

The classification and regression tree (CART) is one of the decision-tree algorithms that are used for categorical and continuous variables [34]. The rules generated by the CART are easy to interpret, and overfitting can be avoided by postpruning a fully grown tree. The CART is a binary partitioning algorithm with only two child nodes from the parent node. The Gini index, the sum of the misclassification probabilities, can be used as an impurity or diversity measure in each node. It is expressed as follows:

$$\mathrm{G}=1-{\displaystyle \sum }_{j=1}^c{(\frac{n_j}{n})}^2$$

(1)

where n is the number of observations in the node, c is the number of categories of target variables, and n_j is the number of observations belonging to the jth category of the target variable. The CART algorithm selects the best predictor to minimize the Gini index for each split and finds the optimal separation of each node, and this division process is repeated for each node to construct a decision tree. For example, in order to classify TC intensity using environmental variables, it is necessary to perform the classification by repeatedly changing the classification reference value (e.g., the sea surface temperature, 26 °C), to calculate the Gini index of the classified group, and to determine the optimal reference value which has a minimum Gini index. The above process is repeatedly performed as many times as the specified number of nodes. In this study, a classifier was developed based on the “fitctree” function included in Matlab’s “statistics and machine learning toolbox”.

2.2.3. The k-Fold Cross-Validation

The k-fold cross-validation is one of the most popular resampling techniques for increasing the statistical reliability of model performance measurements [35]. The procedure is as follows. First, the entire sample is divided into k equally sized subsamples in which one subsample is reserved as validation data. Second, the model is trained with k − 1 subsample, tested (or validated) with the retained subsample, and cross-validated k times until each subsample has been used for validation only once. Finally, the results of each step of the process are averaged to form an evaluation index, which can be used to perform forecast verification. The advantage of cross-validation is that all the cases are used for both training and validation, and each case is used for validation once. In this study, 10-fold cross-validation was used.

2.2.4. Synthetic Minority Oversampling Technique

When the binary classification model is trained with inequality data, a classifier will be biased toward the more frequently occurring class. The accuracy of the majority class is likely to be inflated in training, thus resulting in inappropriate predictive accuracy in testing. In the present study, the synthetic minority oversampling technique (SMOTE; [36]), one of the most commonly used oversampling techniques, was used to avoid the inequality sample problem. It randomly extracts samples from the minority class and increases the number of samples by generating synthetic samples with the ambient values of the extracted samples. In this study, the number of nearest neighbors to consider was set to five.

3. Results

The 2004–2016 distribution of LMI in the TWNP had two local maxima at approximately 50 kt and 100 kt, and a local minimum at 70 kt (Figure 2a). A bimodal distribution of the relative frequency of the LMI was also found in the WNP (Figure 2b). However, unlike the TWNP, the first peak in the WNP was higher than the second. The TWNP is a sub-basin in which the strongest TCs in the WNP occur, so the relative frequency of the strong TCs (2nd peak) was higher than that of the weak TCs (1st peak). In this study, the TWNP TCs were classified into two types: those with LMI above 70 kt (strongly developing TCs; A70) and those with LMI below 70 kt (weak TCs; B70).

Intensity prediction using the CSTIPS-DAT [2] revealed large mean absolute error (MAE) values and bias for the two classified groups, A70 and B70 (Figure 3a). As predicted, this was because the model was trained with the entire TWNP TCs that contain both weakly and strongly developing TCs, resulting in a negative bias (underestimation; see the red solid line in Figure 3a) for A70 and a positive bias (overestimation; see the blue solid line in Figure 3a) for B70. Indeed, most of the MAE values in the TWNP were related to the large biases, suggesting that the bias correction using individual models for A70 and B70 reduced the intensity prediction error. Overall, the MAE and bias were greater in B70 than in A70. This was related to the fact that during training, the model fit A70 better than B70 because A70 had about four times more samples than B70. In fact, the numbers of samples of the A70 and B70 groups were 60 and 17 TCs, respectively, during the training period, and 26 and 10 TCs, respectively, during the test periods (

Table 2. Number of A70 and B70 tropical cyclones in 2004–2013, 2014–2016, and 2004–2016.

Period	A70	B70	Total
2004–2013	60	17	77
2014–2016	26	10	36
2004–2016	86	27	113

). To resolve the inequality in the training data set, SMOTE was used to increase the number of samples for B70 to 60, as in A70.

Figure 3b compares the relative frequencies of the intensity change for A70 and B70. The mean intensity change within 48 h was 20.2 ± 25.0 kt for A70 and 0.8 ± 12.5 kt for B70. The two-tailed Student’s t-test revealed that the difference between the means of the two groups was statistically significant at the 5% test level. Therefore, it was expected that an LMI-based classification could reduce the variance of the intensity change in Cluster 2 and that the intensity prediction would be improved by the development of specific prediction models for each intensity type.

A confusion matrix [37] was used to calculate verification measures, namely the probability of detection (POD), false alarm rate (FAR), and accuracy. The POD is the ratio of the number of times a correct warning is issued for a target event to the total number of target events. The FAR is the number of times a warning is issued but an event does not occur divided by the number of times the warning is issued. The POD, FAR, and accuracy were calculated as follows:

$$\mathrm{POD}=\frac{TP}{TP+FN}$$

(2)

$$\mathrm{FAR}=\frac{FP}{FP+TP}$$

(3)

$$\mathrm{Accuracy}=\frac{TP+TN}{TP+FP+TN+FN}$$

(4)

where TP is the true positive, TN is the true negative, FP is the false positive, and FN is the false negative. In this study, A70 was defined as the target class.

A decision tree generates the rule until the number of samples in a leaf drops below a specified size, i.e., the minimum leaf (min-leaf) size. The min-leaf size determines when splitting should be stopped; therefore, it is an important parameter that needs to be carefully tuned. Figure 4a presents the classification performance of the decision tree during the training period with various min-leaf sizes. The skill scores can be used to set the parameters. Naturally, the highest accuracy and POD were achieved at the min-leaf size of 1, and the performance score decreased with increased min-leaf sizes. The FAR varied by 0–12% with the min-leaf size; however, no significant trend was associated with the min-leaf size.

A decision tree with a smaller min-leaf size usually has better performance. However, a small min-leaf size generates a complicated tree with many nodes, making a physical interpretation difficult. In addition, complicated trees can cause overfitting problems in classifications with insufficient sample sizes. A model should be trained to make reliable predictions for the test data. Overfitting is the result of modeling with noise instead of the underlying relationship. An excessively overfitted model performs poorly in real-time predictions because it is tuned to overreact to minor fluctuations in the training data. To avoid the prediction instability of overfitting, we determined the optimal min-leaf size using comparisons of the cross-validation (CV) loss. In this study, k-fold cross-validation was used to obtain the CV loss by averaging the misclassification rate (MSC), as shown below:

$$\mathrm{CV}=\frac{1}{k}{\displaystyle \sum }_{i=1}^{k}MS{C}_i$$

(5)

$$MS{C}_i=\frac{n_{miss, i}}{n_i}$$

(6)

where k is the number of fold (here is set to be 10), n_miss,i is the number of misclassification samples in ith test set, and n_i is the total number of samples in ith test set.

Figure 4b shows the change of the CV loss with min-leaf sizes. The CV loss tended to increase as the min-leaf size increased. The CV was the smallest at min-leaf sizes of 1 and 2, followed by local minima at 6 and 8. Min-leaf sizes of 1 and 2 required nine and seven nodes (fairly complex structure), respectively, and min-leaf sizes of 6 and 8 required three and two nodes, respectively (red line in Figure 4a). In this study, the min-leaf size was set to 6 to make the decision tree structure relatively simple with a small CV loss.

The trained decision tree included three nodes with four decision rules.

Table 3. Description and the confidence of the rule of the developed decision tree. Note that all variables here were averaged along the TC track from genesis to 3.25 days.

Rule NO.	Decision Rules	The Confidence of the Rule
1	If DMPI20 < 114 kt, then TC will not develop above 70 kt.	45/51 = 88.2%
2	If DMPI20 ≥ 114 kt and LAT ≥ 22.1° N, then TC will not develop above 70 kt.	8/9 = 88.9%
3	If DMPI20 ≥ 114 kt, LAT < 22.1° N and DAT100 < 26.3 °C, TC will not develop above 70 kt.	4/6 = 66.7%
4	If DMPI20 ≥ 114 kt, LAT < 22.1° N and DAT100 ≥ 26.3 °C, TC will develop above 70 kt.	51/54 = 94.4%

lists the decision rules governing the decision tree. Rule 1 shows that it is difficult for a TC in a low DMPI20 environment to intensify as it develops. MPI has been the most critical predictor in previous statistical intensity prediction models [38,39,40,41,42]. In Rule 1, shallow (i.e., 20 m deep) DMPI was selected as a classification factor, and this informed the classification of many weak TCs. Weak TCs cannot interact with the deep ocean; thus, the shallow-depth ocean-temperature-based MPI can be a good criterion for categorizing weak TCs.

Rule 2 states the following: If DMPI20 ≥ 114 kt and LAT ≥ 22.1° N, TCs are less likely to intensify to more than 70 kt. This suggests that it is difficult for a TC that stays at high latitudes on average during development to be classified as A70. This is because TCs with higher LAT tend to move northward and thus their tracks become closer to the polar westerlies, resulting in increased vertical wind shear that suppress TC intensification. The selection of LAT explains why vertical wind shear (SH200 and SH500), a well-known dynamic index related to TC intensity, was not singled out in the rule.

Rule 3 states the following: If DMPI20 ≥ 114 kt, LAT < 22.1° N, and DAT100 < 26.3 °C, a TC cannot intensify to more than 70 kt. This suggests that a high DMPI20 and a low LAT are favorable for intensity; however, TCs are less likely to develop with strong intensity if DAT100 is less than 26.3 °C. Price [21] suggested that 100 m is the typical vertical mixing depth that major TCs induce; thus, DAT100 is the realistic temperature that represents the sea surface thermal conditions under intense TCs. If DAT100 is less than 26.3 °C, which is close to the 2 m dew point temperature of the tropics [43], the ocean can no longer supply heat to the TC, thus reducing the likelihood of strong intensification.

Rule 4 states the following: If DMPI20 ≥ 114 kt, LAT < 22.1° N, and DAT100 ≥ 26.3 °C, a TC can intensify to more than 70 kt. This rule suggests that the development of intense TCs generally occurs when all three conditions are satisfied. The confidence of this rule was 94.4%.

To evaluate the capability of the decision tree to classify intensity, we analyzed the accuracy during the training and test period. The results showed a classification accuracy of 90.0% for training (

Table 4. Confusion matrix for the training period.

		Model
		A70	B70
Observed	A70	51	9
	B70	3	57

) and 80.5% for testing (

Table 5. Confusion matrix for the test period.

		Model
		A70	B70
Observed	A70	24	2
	B70	5	5

). According to the confusion matrix for the test period (Table 5), 24 of 26 TCs were correctly classified as A70, and 5 of 29 that were classified as A70 were B70. Thus, the POD had 92.3%, and the FAR had only 17.2%. These results exhibited high enough accuracy to build an independent statistical model for the TC groups classified on the basis of this algorithm.

4. Discussion

Kim et al. [2] classified TCs on the basis of their track patterns, by which the intensity characteristics could be classified. They showed that the prediction performance could be improved by reducing the variance of the predictand through the development of an individual model for each cluster. This study attempted to further reduce the predictand variance on the basis of the LMI classification, especially for Cluster 2 (TWNP TCs) of CSTIPS-DAT. The TWNP TCs show a bimodal LMI distribution, which can be classified as weakly (B70) and strongly developing TCs (A70). Because of this bimodality, the intensity prediction estimated using the CSTIPS-DAT showed large MAEs for the two groups. The large MAEs are mostly attributed to significant positive and negative biases for B70 and A70, respectively. This implies that correcting the biases through binary classification and developing independent prediction models for the classified groups can reduce the predictand variance and ultimately improve TC intensity prediction.

To improve the performance of the CSTIPS-DAT and to increase the understanding of LMI bimodality, this study developed a CART-algorithm-based decision tree which classifies the TC type at the time of genesis, based on whether or not it will reach an intensity of 70 kt or more during its lifetime. Among the 38 potential predictors, CART selected three variables that reached an accuracy of 90.0% in the training period (2004–2013) and 80.5% in the testing period (2014–2016). The selected variables were DMPI20, LAT, and DAT100. The splitting values were 114 kt for DMPI20, 22.1° N for LAT, and 26.3 °C for DAT100. The four developed rules indicate that the prestorm ocean thermal conditions (DMPI20 and DAT100) and latitude play a key role in determining the LMI in the TWNP.

It should be noted that DAT100 played an essential role in the decision tree developed for binary classification. For the unclassified TWNP TCs (black line in Figure 5), the correlation coefficients between various DATs and LMI were highest at DAT50. However, for strongly developing TCs (red line in Figure 5), the correlation was highest in DAT100. Price [21] proposed DAT100 as an oceanic index reflecting the sea surface cooling induced by Saffir–Simpson Category 3 TCs (96–113 kts). Interestingly, the Category 3 intensity belonged to the second peak of the LMI distribution (Figure 2a) and accounted for about 40% of the TWNP TCs. In contrast, for weak TCs (blue line in Figure 5) the correlation was very low at all DATs. This suggests that the pre-existing ocean thermal structures along the track are not essential in determining the LMI for weak TCs. Again, this highlights the need to develop individual models that consider key environmental factors differently depending on the classified groups.

5. Conclusions

Understanding the bimodal LMI distribution is important for improving TC intensity prediction. Previously known causes of this bimodality are the reduction of air–sea roughness at a particular wind speed range [10] and the presence or absence of rapid intensification events [8]. However, due to the lack of observational data in extreme winds, it is still difficult to fully understand the cause of the bimodal distribution. This study cannot directly explain the mechanism of the bimodality with the rules discovered, but it does present environmental parameters and their thresholds that can distinguish the two modes. This will make some contribution to a better understanding of the causes of the bimodal LMI distribution.

In this study, the CART algorithm, a machine-learning algorithm, was used for classification. Although the CART algorithm is widely used for binary classification, it cannot be affirmed that it is the optimal classification algorithm for classification of intensification types. Therefore, as in previous studies [22,25] that compared and evaluated several machine-learning algorithms for binary classification, research to find the optimal classification method by applying new classification tools must be conducted.