Projection of Droughts as Multivariate Phenomenon in the Rhine River
Abstract
:1. Introduction
2. Methods
2.1. Study Area and Input Data
2.2. Hydrological Model
2.3. Estimation of Drought Characteristics
2.4. Bivariate and Probabilistic Model
3. Results and Discussion
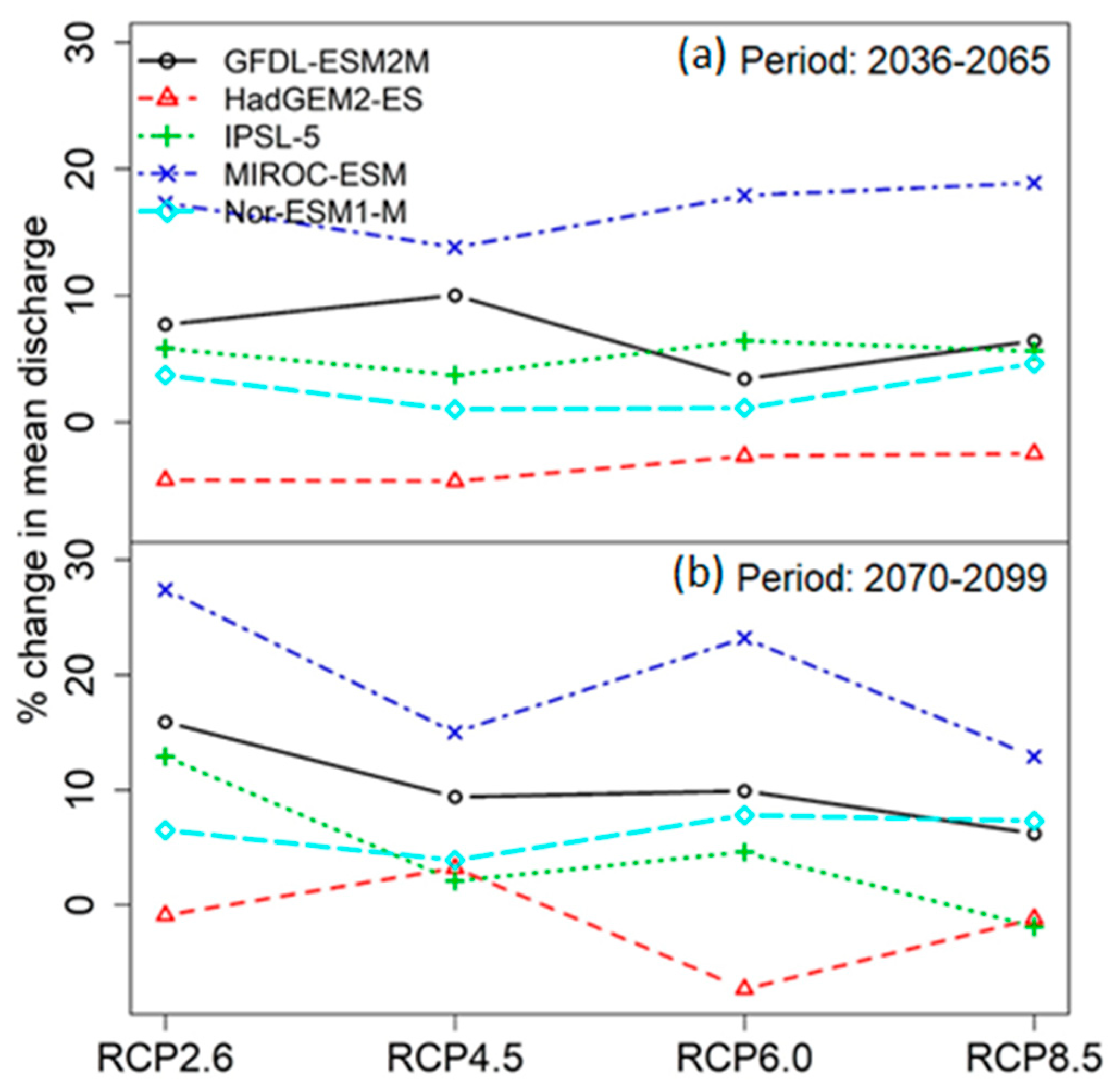
3.1. Hydrological Modelling and Projected Changes in Water Availability
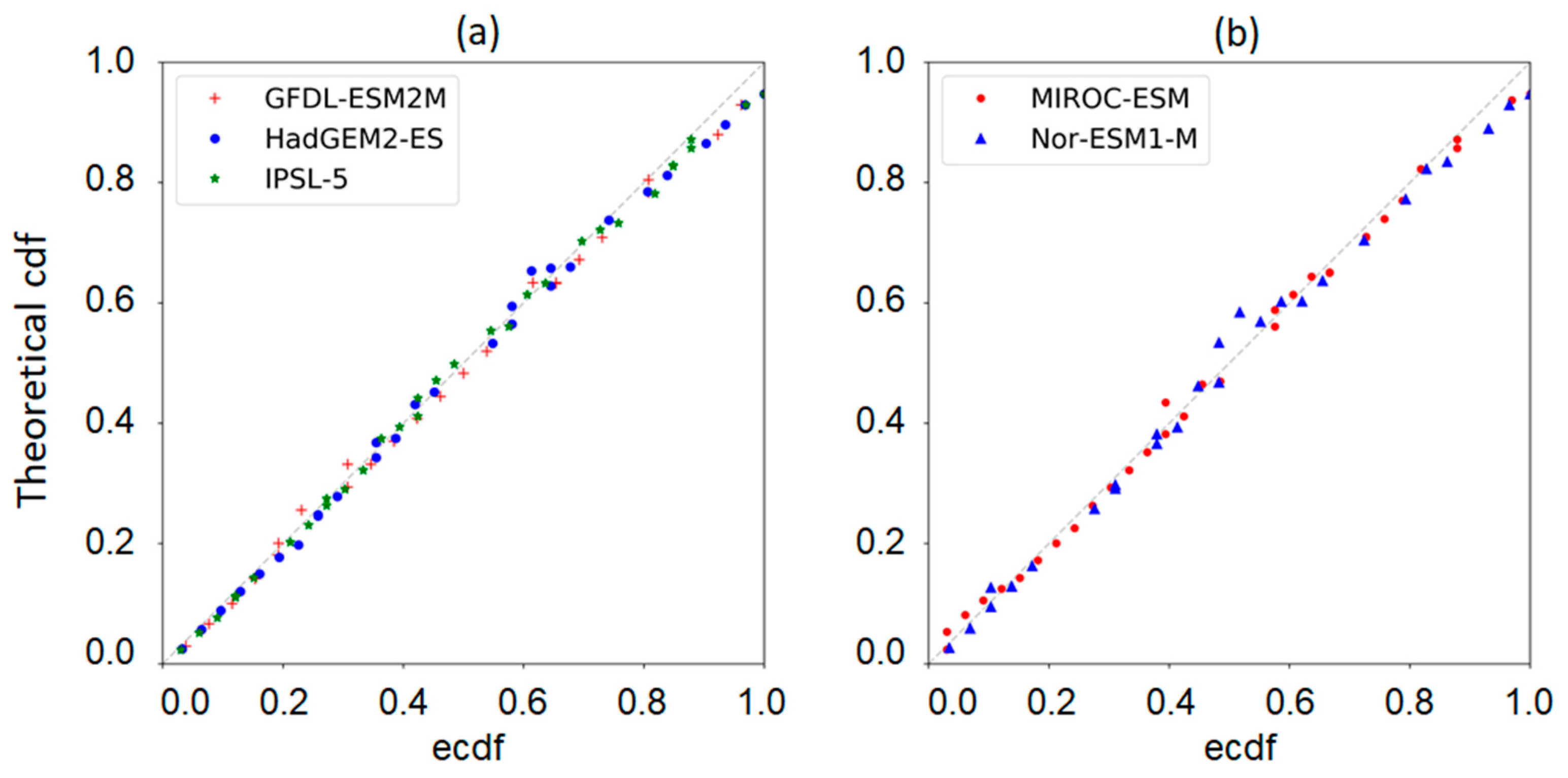
3.2. Drought Characteristics and Copula Selection
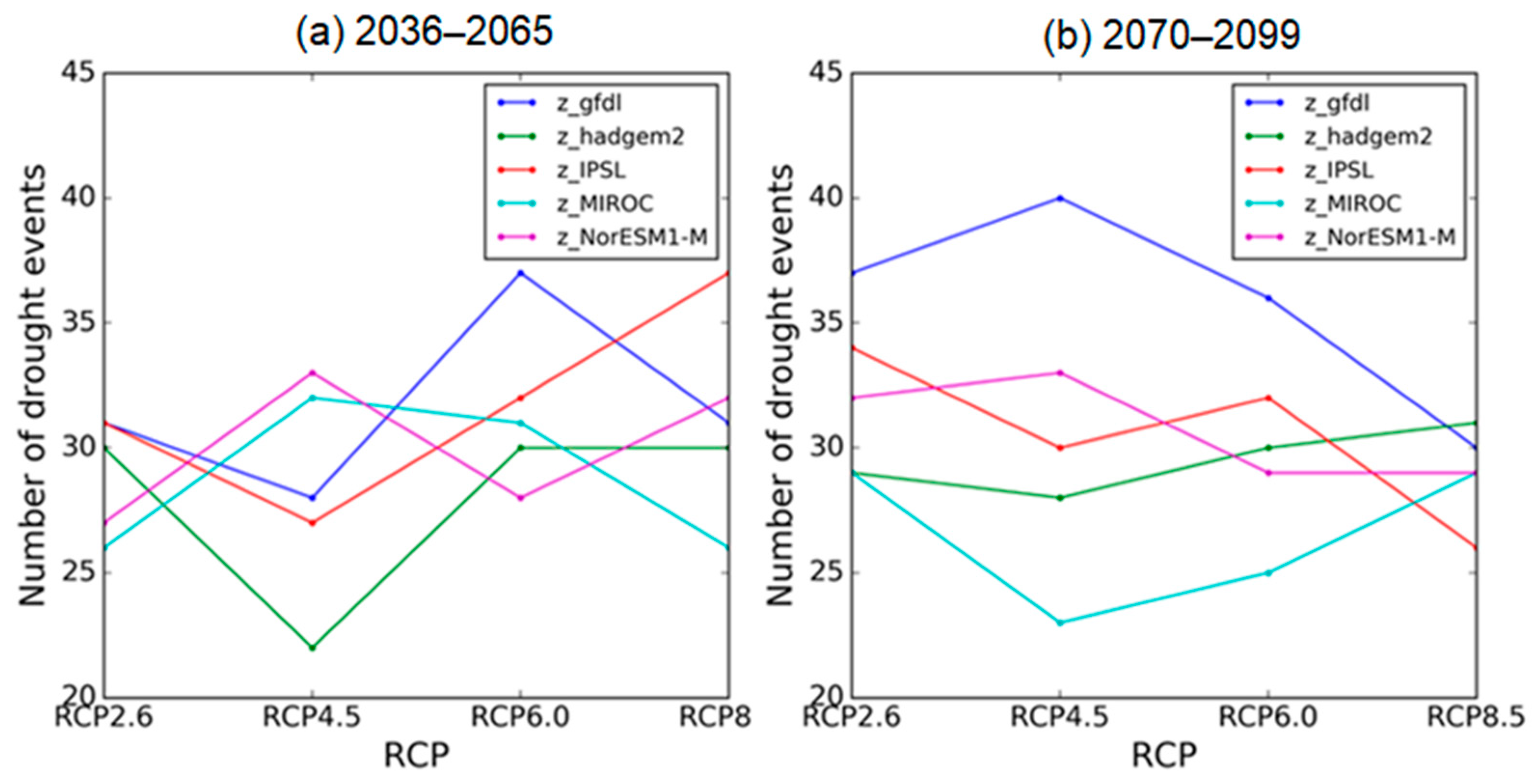
3.3. Drought Events
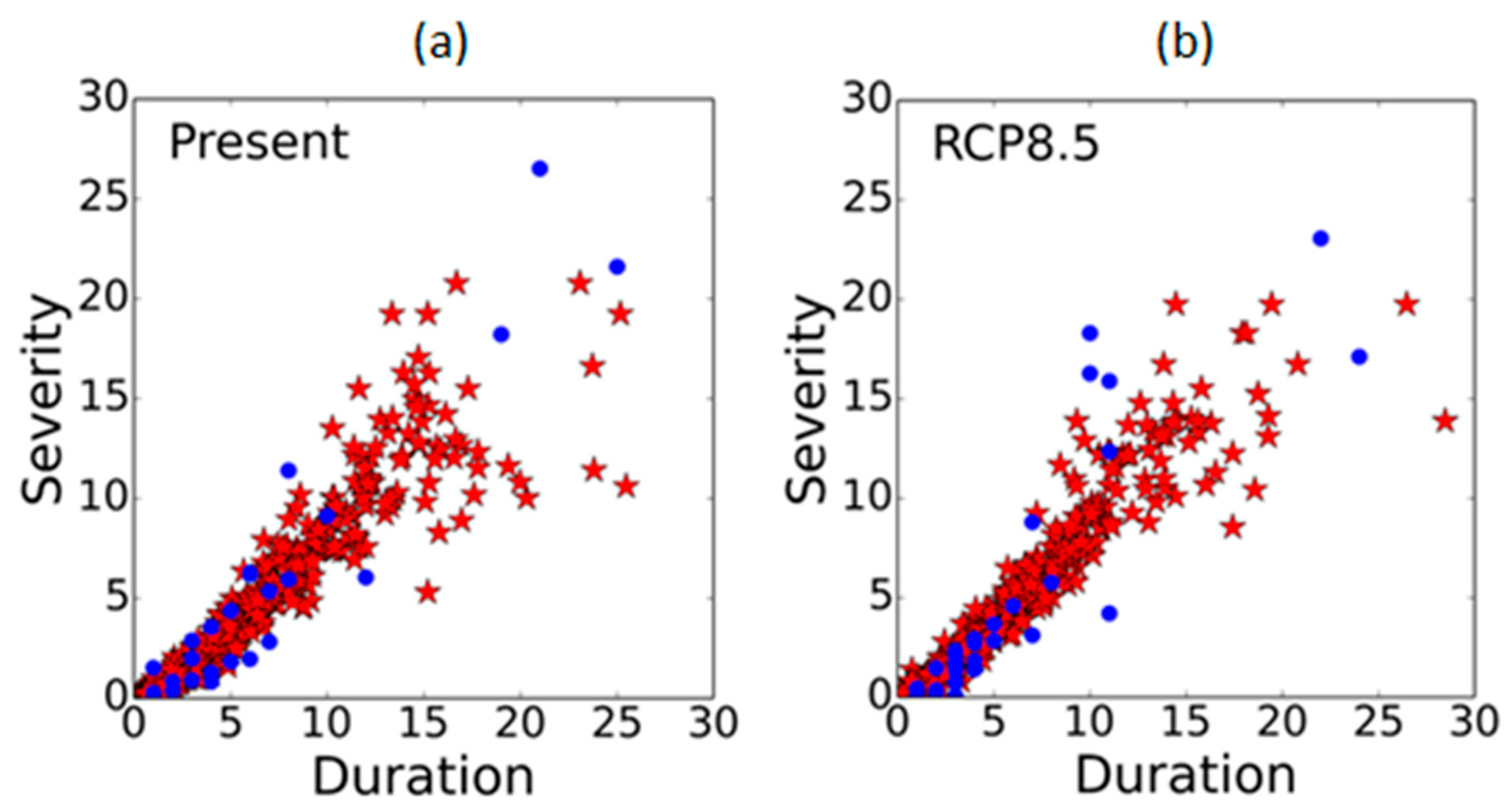
3.4. Duration–Severity Drought Patterns and Return Periods
3.5. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2012, 3, 52–58. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim. Dyn. 2007, 31, 79–105. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Breuer, L.; Chamorro, A.; Flörke, M.; Pechlivanidis, I.G.; Schäfer, D.; Shah, H.L.; Vetter, T.; Wortmann, M.; et al. Propagation of forcing and model uncertainties on to hydrological drought characteristics in a multi-model century-long experiment in large river basins. Clim. Chang. 2016, 141, 435–449. [Google Scholar] [CrossRef]
- Kiem, A.S.; Johnson, F.; Westra, S.; Van Dijk, A.I.J.M.; Evans, J.P.; O’Donnell, A.; Rouillard, A.; Barr, C.; Tyler, J.J.; Thyer, M.; et al. Natural hazards in Australia: Droughts. Clim. Chang. 2016, 139, 37–54. [Google Scholar] [CrossRef]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrão, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Clim. 2013, 34, 2792–2804. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Yoo, J.; Kwon, H.-H.; Kim, T.; Ahn, J.-H. Drought frequency analysis using cluster analysis and bivariate probability distribution. J. Hydrol. 2012, 420, 102–111. [Google Scholar] [CrossRef]
- Van Loon, A. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2010, 2, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Clim. 2013, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Heim, R.R. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef] [Green Version]
- Keyantash, J.A.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Thilakarathne, M.; Sridhar, V. Characterization of future drought conditions in the Lower Mekong River Basin. Weather. Clim. Extrem. 2017, 17, 47–58. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Zwolsman, J.J.G.; Van Bokhoven, A. Impact of summer droughts on water quality of the Rhine River—A preview of climate change? Water Sci. Technol. 2007, 56, 45–55. [Google Scholar] [CrossRef]
- Görgen, K.; Beersma, J.; Brahmer, G.; Buiteveld, H.; Carambia, M.; de Keizer, O.; Krahe, P.; Nilson, E.; Lammersen, R.; Perrin, C.; et al. Assessment of Climate Change Impacts on Discharge in the Rhine River Basin: Results of the RheinBlick2050 Project. Internationale Kommission für die Hydrologie des Rheingebietes, Report No. I–23 of the CHR. 2010. Available online: https://hal.inrae.fr/hal-02594596/document (accessed on 9 June 2020).
- Kwadijk, J.; Rotmans, J. The impact of climate change on the river rhine: A scenario study. Clim. Chang. 1995, 30, 397–425. [Google Scholar] [CrossRef]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A trend-preserving bias correction – the ISI-MIP approach. Earth Syst. Dyn. 2013, 4, 219–236. [Google Scholar] [CrossRef] [Green Version]
- Krysanova, V.; Hattermann, F.F. Intercomparison of climate change impacts in 12 large river basins: Overview of methods and summary of results. Clim. Chang. 2017, 141, 363–379. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kållberg, P.W.; Simmons, A.J.; Andrae, U.; Bechtold, V.D.C.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Weedon, G.P.; Gomes, S.; Viterbo, P.; Shuttleworth, W.J.; Blyth, E.; Österle, H.; Adam, J.C.; Bellouin, N.; Boucher, O.; Best, M. Creation of the WATCH Forcing Data and Its Use to Assess Global and Regional Reference Crop Evaporation over Land during the Twentieth Century. J. Hydrometeorol. 2011, 12, 823–848. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, M.; Smith, S.J.; Calvin, K.V.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K.; et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 2011, 109, 213–241. [Google Scholar] [CrossRef] [Green Version]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S.K. Robust estimation of hydrological model parameters. Hydrol. Earth Syst. Sci. 2008, 12, 1273–1283. [Google Scholar] [CrossRef] [Green Version]
- Hundecha, Y.; Bárdossy, A. Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model. J. Hydrol. 2004, 292, 281–295. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Halwatura, D.; Lechner, A.M.; Arnold, S. Drought severity–duration–frequency curves: A foundation for risk assessment and planning tool for ecosystem establishment in post-mining landscapes. Hydrol. Earth Syst. Sci. 2015, 19, 1069–1091. [Google Scholar] [CrossRef] [Green Version]
- Genest, C.; Favre, A.-C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef] [Green Version]
- Bárdossy, A. Copula-based geostatistical models for groundwater quality parameters. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Ganguli, P.; Ganguly, A.R. Space-time trends in U.S. meteorological droughts. J. Hydrol. Reg. Stud. 2016, 8, 235–259. [Google Scholar] [CrossRef] [Green Version]
- Vandenberghe, S.; Verhoest, N.E.C.; De Baets, B. Fitting bivariate copulas to the dependence structure between storm characteristics: A detailed analysis based on 105 year 10 min rainfall. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Shiau, J.-T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Linde, A.H.T.; Aerts, J.C.J.H.; Hurkmans, R.; Eberle, M. Comparing model performance of two rainfall-runoff models in the Rhine basin using different atmospheric forcing data sets. Hydrol. Earth Syst. Sci. 2008, 12, 943–957. [Google Scholar] [CrossRef] [Green Version]
- Eisner, S.; Flörke, M.; Chamorro, A.; Daggupati, P.; Donnelly, C.; Huang, J.; Hundecha, Y.; Koch, H.; Kalugin, A.; Krylenko, I.; et al. An ensemble analysis of climate change impacts on streamflow seasonality across 11 large river basins. Clim. Chang. 2017, 141, 401–417. [Google Scholar] [CrossRef]
- Photiadou, C.; Hurk, B.V.D.; Van Delden, A.; Weerts, A. Incorporating circulation statistics in bias correction of GCM ensembles: Hydrological application for the Rhine basin. Clim. Dyn. 2015, 46, 187–203. [Google Scholar] [CrossRef] [Green Version]
- Roudier, P.; Andersson, J.C.M.; Donnelly, C.; Feyen, L.; Greuell, W.; Ludwig, F. Projections of future floods and hydrological droughts in Europe under a +2 °C global warming. Clim. Chang. 2015, 135, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Villarini, G.; Scoccimarro, E.; White, K.D.; Arnold, J.R.; Schilling, K.; Ghosh, J. Projected Changes in Discharge in an Agricultural Watershed in Iowa. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 1361–1371. [Google Scholar] [CrossRef]
- Yan, D.; Werners, S.E.; Ludwig, F.; Huang, H.Q. Hydrological response to climate change: The Pearl River, China under different RCP scenarios. J. Hydrol. Reg. Stud. 2015, 4, 228–245. [Google Scholar] [CrossRef] [Green Version]
- Prudhomme, C.; Giuntoli, I.; Robinson, E.L.; Clark, D.B.; Arnell, N.W.; Dankers, R.; Fekete, B.M.; Franssen, W.; Gerten, D.; Gosling, S.N.; et al. Hydrological droughts in the 21st century, hotspots and uncertainties from a global multimodel ensemble experiment. Proc. Natl. Acad. Sci. USA 2013, 111, 3262–3267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orlowsky, B.; Seneviratne, S.I. Elusive drought: Uncertainty in observed trends and short- and long-term CMIP5 projections. Hydrol. Earth Syst. Sci. 2013, 17, 1765–1781. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, F.; Zhu, Y.; Fu, G.; Lü, H.; Zhang, A.; Yu, Z.; Chen, X. Impacts of climate change under CMIP5 RCP scenarios on streamflow in the Huangnizhuang catchment. Stoch. Environ. Res. Risk Assess. 2015, 29, 1781–1795. [Google Scholar] [CrossRef]
- Exbrayat, J.-F.; Buytaert, W.; Timbe, E.; Windhorst, D.; Breuer, L. Addressing sources of uncertainty in runoff projections for a data scarce catchment in the Ecuadorian Andes. Clim. Chang. 2014, 125, 221–235. [Google Scholar] [CrossRef]
- Teng, J.; Vaze, J.; Chiew, F.H.S.; Wang, B.; Perraud, J.-M. Estimating the Relative Uncertainties Sourced from GCMs and Hydrological Models in Modeling Climate Change Impact on Runoff. J. Hydrometeorol. 2012, 13, 122–139. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Thober, S.; Kumar, R.; Wanders, N.; Marx, A.; Pan, M.; Rakovec, O.; Samaniego, L.; Sheffield, J.; Wood, E.F.; Zink, M. Multi-model ensemble projections of European river floods and high flows at 1.5, 2, and 3 degrees global warming. Environ. Res. Lett. 2018, 13, 014003. [Google Scholar] [CrossRef]
- Marx, A.; Kumar, R.; Thober, S.; Zink, M.; Wanders, N.; Wood, E.; Ming, P.; Sheffield, J.; Samaniego, L. Climate change alters low flows in Europe under a 1.5, 2, and 3 degree global warming. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Christensen, J.H.; Christensen, O.B. A summary of the PRUDENCE model projections of changes in European climate by the end of this century. Clim. Chang. 2007, 81, 7–30. [Google Scholar] [CrossRef]
- Tölle, M.H.; Moseley, C.; Panferov, O.; Busch, G.; Knohl, A. Water supply patterns over Germany under climate change conditions. Biogeosciences 2013, 10, 2959–2972. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]

| Model/Copula | Clayton | Frank | FGM | Gumbel | AMH |
|---|---|---|---|---|---|
| GFDL-ESM2M | 0.056 | 0.017 | 0.018 | 0.114 | 0.092 |
| HadGEM2-ES | 0.058 | 0.020 | 0.017 | 0.113 | 0.101 |
| IPSL-5 | 0.053 | 0.016 | 0.014 | 0.117 | 0.102 |
| MIROC-ESM | 0.053 | 0.016 | 0.017 | 0.103 | 0.095 |
| Nor-ESM1-M | 0.055 | 0.023 | 0.024 | 0.120 | 0.092 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamorro, A.; Houska, T.; Singh, S.K.; Breuer, L. Projection of Droughts as Multivariate Phenomenon in the Rhine River. Water 2020, 12, 2288. https://doi.org/10.3390/w12082288
Chamorro A, Houska T, Singh SK, Breuer L. Projection of Droughts as Multivariate Phenomenon in the Rhine River. Water. 2020; 12(8):2288. https://doi.org/10.3390/w12082288
Chicago/Turabian StyleChamorro, Alejandro, Tobias Houska, Shailesh Kumar Singh, and Lutz Breuer. 2020. "Projection of Droughts as Multivariate Phenomenon in the Rhine River" Water 12, no. 8: 2288. https://doi.org/10.3390/w12082288
APA StyleChamorro, A., Houska, T., Singh, S. K., & Breuer, L. (2020). Projection of Droughts as Multivariate Phenomenon in the Rhine River. Water, 12(8), 2288. https://doi.org/10.3390/w12082288





