Vibration Localization and Anti-Localization of Nonlinear Multi-Support Beams with Support Periodicity Defect

Abstract

A response analysis method for nonlinear beams with spatial distribution parameters and non-periodic supports was developed. The proposed method is implemented in four steps: first, the nonlinear partial differential equation of the beams is transformed into linear partial differential equations with space-varying parameters by using a perturbation method; second, the space-varying parameters are separated into a periodic part and a non-periodic part describing the periodicity defect, and the linear partial differential equations are separated into equations for the periodic and non-periodic parts; third, the equations are converted into ordinary differential equations with multiple modes coupling by using the Galerkin method; fourth, the equations are solved by using a harmonic balance method to obtain vibration responses, which are used to discover dynamic characteristics including the amplitude–frequency relation and spatial mode. The proposed method considers multiple vibration modes in the response analysis of nonlinear non-periodic structures and accounts for mode-coupling effects resulting from structural nonlinearity and parametric non-periodicity. Thus, it can handle nonlinear non-periodic structures with a high parameter-varying wave in wide frequency vibration. In numerical studies, a nonlinear beam with non-periodic supports (resulting in non-periodic distribution parameters or periodicity defect) under harmonic excitations was explored using the proposed method, which revealed some new dynamic response characteristics of this kind of structure and the influences of non-periodic parameters. The characteristics include remarkable variation in frequency response and spatial mode, and in particular, vibration localization and anti-localization. The results have potential applications in vibration control and the support damage detection of nonlinear structures with non-periodic supports.

1. Introduction

Many engineering structures such as continuous girder viaducts and synchrotron radiation bridges can be simplified as a beam with multi-supports in dynamics analysis. The beam is usually symmetric and becomes asymmetric after a change in the stiffness of some supports, e.g., stiffness reduction due to damage. The changeability of dynamic characteristics such as frequency response and spatial mode (or mode component) is important for structural optimization design (or vibration control) and anomaly diagnosis (or damage detection). Periodic structures with spatial distribution parameters such as periodic geometric parameters, periodic physical parameters and periodic constraints have special dynamics which are different from those of common structures with uniform distribution parameters. Parametric periodicity has outstanding influence on structural dynamic responses because of the coupling of periodic time-varying (or harmonic) response and periodic distribution parameters. Numerous studies have reported characteristic frequencies [1,2,3,4], modal localization and buckling [5,6,7,8,9,10,11,12,13,14], quasi-periodic distribution parameter effects [15,16,17,18] and application [19,20,21,22,23,24,25,26,27] based on transfer matrix method, spatial (Bloch) harmonic expansion method, (Floquet–Bloch and Galerkin) double expansion method and finite element method, etc. Waves and vibration in beams with non-uniform distribution parameters have also been pursued using a fundamental solution, semi-analysis and finite element methods [28,29,30,31,32,33,34]. Perturbation and multiple scale methods were applied for weakly periodic parameter cases [35,36]. The periodic beam is an important engineering structure or structural component, and its dynamics including finite-size and boundary effects have been addressed [37,38,39,40]. Compared with periodic structures, quasi-periodic structures are likely to afford highly variable dynamic responses because period-structural dynamics have certain instability and are sensitive to periodicity perturbation (or defect). However, in the aforementioned investigations, only the dynamics of linear periodic and quasi-periodic structures and the corresponding linear dynamic characteristics were addressed.

Under certain large loads, engineering structures will produce nonlinear vibrations because of inherent geometric and physical nonlinearity. The nonlinear dynamic characteristics of periodic and non-periodic structures are a subject of research interest. Research on the wave propagation of periodic structures modeled by nonlinear single-degree-of-freedom systems has been pursued based on periodicity conditions, in which the multiple scales method, perturbation method, linearization method and harmonic balance method were adopted [41,42,43,44,45,46,47]. A nonlinear periodic structure with cycle symmetry was studied by converting it into independent nonlinear single-degree-of-freedom systems using nonlinear normal modes for frequency response analysis, and its mode localization under weak coupling was discovered by asymptotic approximation [48,49]. The nonlinear vibration of non-uniform beams and dynamic stability of sandwich beams on nonlinear elastic foundations have also been studied using the finite element and harmonic balance methods, Galerkin and iterative numerical methods, linearization and Chebyshev collocation methods, Bolotin method and Hamiltonian approach, respectively [50,51,52,53,54]. A differential quadrature method was applied to the nonlinear vibration analysis of sandwich beams where vibration modes were obtained using a numerical iterative algorithm [55,56]. Non-periodic dynamics of complex systems with fractional derivatives have been studied [57,58]. However, only a few studies have addressed the nonlinear dynamics of finite-size periodic beams. An asymptotic tolerance averaging technique was applied to the nonlinear vibration analysis of a beam with geometric nonlinearity and periodic distribution parameters, but this study was limited to low-frequency vibration and a high parameter-varying wave because of the averaging in a periodic unit [59,60]. Those analysis methods have limitations in the number of used vibration modes which can affect the accuracy and reliability of results as the nonlinearity and periodicity will induce the coupling of linear structural modes. Recently, a multimode perturbation method for the frequency response analysis of nonlinear beams with periodic distribution parameters has been proposed, and some novel dynamic response characteristics including remarkable variations of amplitude–frequency relation and spatial mode of nonlinear periodic beams were obtained [61]. However, the study only considered the dynamics of periodic beams. The dynamics of nonlinear non-periodic beams, e.g., with non-periodic supports (or support periodicity defect, that can be viewed as variation of periodicity), need to be further studied and to this end, the corresponding analysis method needs to be developed. Non-periodic or quasi-periodic beams are more realistic structures in engineering fields, and they would have dynamic responses which would greatly differ from those of periodic beams based on the results of linear periodic and quasi-periodic structures. This study of the dynamics of nonlinear non-periodic structures also has potential applications in vibration control and support damage detection [14,15,18,20,21,22,23,62,63,64,65,66].

In this paper, the vibrational amplitude–frequency characteristics of nonlinear multi-support beams with non-periodic supports (resulting in non-periodic distribution parameters or periodicity defect) under harmonic excitations was studied. A response analysis method for nonlinearly vibrational beams with spatial distribution parameters and non-periodic supports was developed by combining perturbation, periodic and non-periodic separation, Galerkin expansion and harmonic balance methods. First, a partial differential equation with space-varying parameters is elicited for a nonlinear non-periodic beam. The nonlinear equation is transformed into a set of linear partial differential equations by using a perturbation method. Second, the spatial distribution parameters are separated into periodic part and non-periodic part describing the periodicity defect. The linear partial differential equations are separated into a set of differential equations for the periodic beam with periodic part parameters and another set of differential equations for the non-periodic beam with the non-periodic part parameters. Third, the equations are converted into ordinary differential equations with coupling multiple modes by using the Galerkin method. Multiple vibration modes are considered and thus the equations are suited for the nonlinear vibration of non-periodic structures with high parameter-varying wave in a wide frequency band. Fourth, the ordinary differential equations are solved by using a harmonic balance method to obtain vibration responses of the beam with non-periodic parameters under harmonic excitations, which are used for characteristics analysis of amplitude–frequency relation and spatial mode. Finally, resulting graphs for a non-periodic beam with various support stiffness and damping are provided to illustrate effective application of the proposed method and to reveal frequency response characteristics. New response characteristics including remarkable variations in frequency response and spatial mode for the nonlinearly vibrational beam with different non-periodic supports, particularly vibration localization and vibration anti-localization, were discovered for the first time.

2. Nonlinear Vibration Equation of Beam with Non-Periodic Supports

Consider a horizontal elastic beam with spatial distribution parameters and non-periodic supports under vertical external excitation, as shown in Figure 1. Its material is isotropic, and normal stress in the z direction is small and neglected, where z denotes a vertical coordinate. Vertical displacement is assumed as unvarying with z and the cross-section is perpendicular to the central axis as the initial x, where x denotes the horizontal coordinate. Longitudinal and rotational inertias are small and neglected. For large excitation acting on a long beam, the vertical vibration in the (x,z) plane exhibits certain geometric nonlinearity, and the nonlinear longitudinal normal strain can be expressed as

$${\epsilon }_s=-z\frac{{\partial }^{2}w}{\partial x^2}+\frac{1}{2}{\left(\frac{\partial w}{\partial x}\right)}^2+\frac{1}{2}z\frac{{\partial }^{2}w}{\partial x^2}{\left(\frac{\partial w}{\partial x}\right)}^2$$

(1)

where w is vertical displacement. Longitudinal normal stress is σ_s = Eε_s, where E is Young’s modulus. Axial force F_N, shear force F_S and bending moment M of the beam can be calculated using the normal stress σ_s. For a long beam in low and middle frequency vibration, a mechanical model based on the Bernoulli–Euler theory can be applied. Considering the vertical middle support forces, vertical inertia force and damping force, the nonlinear vibration equation of the beam is obtained as

$$\begin{array}{l}\rho A_0\frac{{\partial }^{2}w}{\partial t^2}+c_d\frac{\partial w}{\partial t}+\frac{\partial }{\partial x}\left[F_S\cos \left(\frac{\partial w}{\partial x}\right)\right]\cos \left(\frac{\partial w}{\partial x}\right)\\ -\frac{\partial }{\partial x}\left[F_N\sin \left(\frac{\partial w}{\partial x}\right)\right]\cos \left(\frac{\partial w}{\partial x}\right)\\ +{\displaystyle \sum _{i=1}^{N_p}(c_{si}\frac{\partial w}{\partial t}+k_{si}w)\mathsf{\delta }(x-x_{si})}=f_e(x,t)\end{array}$$

(2)

where ρ is the mass density, A₀ is the cross-sectional area, c_d is the damping coefficient, k_si, c_si, x_si are, respectively, the stiffness, damping and coordinate of the ith support except two end constraints, δ(·) is the Dirac-delta function, N_p is the support number, f_e is the external force and t is the time variable. Equation (2) can be simplified by neglecting high-order nonlinear terms and using the condition that the beam height (h) is much smaller than beam length (L). The non-dimensional nonlinear vibration equation is [61]:

$$\begin{array}{l}{m}_b\frac{{\partial }^2\overline{w}}{\partial t^2}+c_b\frac{\partial \overline{w}}{\partial t}+\frac{{\partial }^2}{\partial {\overline{x}}^2}\left(E\overline{I}\frac{{\partial }^2\overline{w}}{\partial {\overline{x}}^2}\right)-\frac{\partial }{\partial \overline{x}}\left[E\overline{A}{\left(\frac{\partial \overline{w}}{\partial \overline{x}}\right)}^3\right]\\ +{\displaystyle \sum _{i=1}^{N_p}(c_{si}\frac{\partial \overline{w}}{\partial t}+k_{si}\overline{w})\mathsf{\delta }(\overline{x}-{\overline{x}}_{si})}=F(\overline{x},t)\end{array}$$

(3)

where:

$$\begin{gathered} \overline{x}=x/L,\overline{w}=w/W_a,m_b=\rho A_{0}L,c_b=c_{d}L,\overline{I}=I_0/L^3, \\ \overline{A}=A_0{W}_a^2/2L^3,F=f_{e}L/W_a \end{gathered}$$

(4)

in which I₀ is the cross-sectional second moment and W_a is a small displacement amplitude under unit excitation. For the beam with uniform distribution parameters, m_b, $E\overline{A}$ and $E\overline{I}$ are constants. For the case of non-periodic supports, there are supports whose coordinates ${\overline{x}}_{si}\ne i/(N_p+1)$ or the stiffness k_si and damping c_si differ from the others.

The partial differential Equation (3) describes the nonlinear vibration of the beam with spatial distribution parameters and non-periodic supports. Under W_a << 1, rewrite nonlinear coefficient as $E\overline{A}=-\epsilon B_{10}/3$, where ε is a small parameter. Equation (3) can be expressed in the following form to facilitate a common solution:

$$\begin{array}{l}{B}_1\frac{{\partial }^2\overline{w}}{\partial t^2}+B_2\frac{\partial \overline{w}}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}\overline{w}}{\partial {\overline{x}}^{(5-k)}}}\\ +\epsilon B_{10}\frac{{\partial }^2\overline{w}}{\partial {\overline{x}}^2}{\left(\frac{\partial \overline{w}}{\partial \overline{x}}\right)}^2+\epsilon B_{11}{\left(\frac{\partial \overline{w}}{\partial \overline{x}}\right)}^3\\ +{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial \overline{w}}{\partial t}+D_{2i}\overline{w})\mathsf{\delta }(\overline{x}-{\overline{x}}_i)}=F(\overline{x},t)\end{array}$$

(5)

where coefficients B_k and D_ji are determined by Equation (3), and ${\overline{x}}_i={\overline{x}}_{si}$. Consider two ends of the beam having simply supported constraints. The boundary conditions are:

$$\overline{w}(0,t)=\overline{w}(1,t)=0,\frac{{\partial }^2\overline{w}(0,t)}{\partial {\overline{x}}^2}=\frac{{\partial }^2\overline{w}(1,t)}{\partial {\overline{x}}^2}=0$$

(6)

Vibration responses can be obtained by solving Equation (5) with conditions (6). However, Equation (5) is a nonlinear partial differential equation with space-varying parameters. Conventional analysis methods can only consider a few modes and actually use several coupled nonlinear ordinary differential equations. The effect of limited modes on response accuracy increases with the wave number of varying parameters and supports and vibration frequency. Therefore, an improved analysis method [61] combined with periodic and non-periodic separation analysis method was developed herein. The analysis method can use multiple vibration modes and is suitable for the nonlinear vibration of non-periodic structures with a high parameter-varying wave in a wide frequency band, which is described in the following sections.

3. Perturbation and Separation Solutions to Nonlinear Vibration of Non-Periodically Supported Beam

A perturbation method was first applied to transform nonlinear partial differential Equation (5) into a set of linear partial differential equations. The dimensionless displacement $\overline{w}$, which depends on the small parameter ε, can be expanded as

$$\overline{w}(\overline{x},t)={\displaystyle \sum _{j=1}^{\infty }{\epsilon }^{j-1}{w}_j(\overline{x},t)}$$

(7)

where w_j is the jth-order approximation. Substituting Equation (7) into Equation (5) (see Appendix A as Equation (A1)) and balancing each power term of the small parameter yield the following linear differential equations:

$$\begin{array}{l}{B}_1\frac{{\partial }^2{w}_1}{\partial t^2}+B_2\frac{{\partial }^2{w}_1}{\partial t^2}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}{w}_1}{\partial {\overline{x}}^{(5-k)}}}\\ +{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial w_1}{\partial t}+D_{2i}{w}_1)\mathsf{\delta }(\overline{x}-{\overline{x}}_i)}=F\end{array}$$

(8)

$$\begin{array}{l}{B}_1\frac{{\partial }^2{w}_2}{\partial t^2}+B_2\frac{\partial w_2}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}{w}_2}{\partial {\overline{x}}^{(5-k)}}}+{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial w_2}{\partial t}}\\ +D_{2i}{w}_2)\mathsf{\delta }(\overline{x}-{\overline{x}}_i)=-B_{10}\frac{{\partial }^2{w}_1}{\partial {\overline{x}}^2}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^2-B_{11}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^3\end{array}$$

(9)

$$\begin{array}{c}{B}_1\frac{{\partial }^2{w}_3}{\partial t^2}+B_2\frac{\partial w_3}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}{w}_3}{\partial {\overline{x}}^{(5-k)}}}+{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial w_3}{\partial t}}\hfill \\ +D_{2i}{w}_3)\mathsf{\delta }(\overline{x}-{\overline{x}}_i)=-B_{10}[\frac{{\partial }^2{w}_2}{\partial {\overline{x}}^2}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^2\hfill \\ +2\frac{{\partial }^2{w}_1}{\partial {\overline{x}}^2}\frac{\partial w_1}{\partial \overline{x}}\frac{\partial w_2}{\partial \overline{x}}]-3B_{11}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^2\frac{\partial w_2}{\partial \overline{x}}\hfill \\ \dots \dots \end{array}$$

(10)

The above equations can be solved to obtain an asymptotic solution. The vibration displacement is generally determined by the first several approximate w_j. For the beam with spatial distribution parameters and non-periodic supports, B_k, D_ji, ${\overline{x}}_i$ and F can be regarded as periodicity defect parameters. The parameters are separated into a spatial periodic part and non-periodic part (which describes the periodicity defect) as

$$\begin{gathered} B_k=B_{pk}+\Delta B_k,D_{1i}=D_{p1}+\Delta D_{1i},D_{2i}=D_{p2}+\Delta D_{2i}, \\ {y}_i=y_{pi}+\Delta y_i,F=F_p+\Delta F \end{gathered}$$

(11)

where subscript “p” denotes the periodic part and “Δ” denotes the non-periodic part. The separation yields a periodic beam with the periodic part parameters and a non-periodic beam with non-periodic part parameters (or periodicity defect). The approximate displacement w_j can be separated accordingly into:

$$w_j=w_{pj}+\Delta w_j$$

(12)

Substituting expressions (11) and (12) into Equations (8)–(10) yields a set of differential equations for the periodic part displacement w_pj of the periodic beam and another set of differential equations for the non-periodic part displacement Δw_j of the non-periodic beam. The linear partial differential equations for the periodic part are:

$$\begin{array}{l}{B}_{p1}\frac{{\partial }^2{w}_{p1}}{\partial t^2}+B_{p2}\frac{{\partial }^2{w}_{p1}}{\partial t^2}+{\displaystyle \sum _{k=1}^3{B}_{p,k+2}\frac{{\partial }^{(5-k)}{w}_{p1}}{\partial {\overline{x}}^{(5-k)}}}\\ +{\displaystyle \sum _{i=1}^{N_p}(D_{p1}\frac{\partial w_{p1}}{\partial t}+D_{p2}{w}_{p1})\mathsf{\delta }(\overline{x}-{\overline{x}}_{pi})}=F_p\end{array}$$

(13)

$$\begin{array}{l}{B}_{p1}\frac{{\partial }^2{w}_{p2}}{\partial t^2}+B_{p2}\frac{\partial w_{p2}}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{p,k+2}\frac{{\partial }^{(5-k)}{w}_{p2}}{\partial {\overline{x}}^{(5-k)}}}\\ +{\displaystyle \sum _{i=1}^{N_p}(D_{p1}\frac{\partial w_{p2}}{\partial t}+D_{p2}{w}_{p2})\mathsf{\delta }(\overline{x}-{\overline{x}}_{pi})}\\ =-B_{p10}\frac{{\partial }^2{w}_{p1}}{\partial {\overline{x}}^2}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^2-B_{p11}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^3\end{array}$$

(14)

$$\begin{array}{c}{B}_{p1}\frac{{\partial }^2{w}_{p3}}{\partial t^2}+B_{p2}\frac{\partial w_{p3}}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{p,k+2}\frac{{\partial }^{(5-k)}{w}_{p3}}{\partial {\overline{x}}^{(5-k)}}}\hfill \\ +{\displaystyle \sum _{i=1}^{N_p}(D_{p1}\frac{\partial w_{p3}}{\partial t}+D_{p2}{w}_{p3})\mathsf{\delta }(\overline{x}-{\overline{x}}_{pi})}\hfill \\ =-B_{p10}\left[\frac{{\partial }^2{w}_{p2}}{\partial {\overline{x}}^2}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^2+2\frac{{\partial }^2{w}_{p1}}{\partial {\overline{x}}^2}\frac{\partial w_{p1}}{\partial \overline{x}}\frac{\partial w_{p2}}{\partial \overline{x}}\right]\hfill \\ -3B_{p11}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^2\frac{\partial w_{p2}}{\partial \overline{x}}\hfill \\ \dots \dots \end{array}$$

(15)

The linear partial differential equations for the non-periodic part (or periodicity defect) are:

$$\begin{array}{l}{B}_1\frac{{\partial }^2\Delta w_1}{\partial t^2}+B_2\frac{\partial \Delta w_1}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}\Delta w_1}{\partial {\overline{x}}^{(5-k)}}}\\ +{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial \Delta w_1}{\partial t}+D_{2i}\Delta w_1)\mathsf{\delta }(\overline{x}-{\overline{x}}_i)}\\ =\Delta F-\Delta B_1{B}_{p1}^{-1}{F}_p+(\Delta B_1{B}_{p1}^{-1}{B}_{p2}-\Delta B_2)\frac{\partial w_{p1}}{\partial t}\\ +{\displaystyle \sum _{k=1}^3(\Delta B_1{B}_{p1}^{-1}{B}_{p,k+2}-\Delta B_{k+2})\frac{{\partial }^{(5-k)}{w}_{p1}}{\partial {\overline{x}}^{(5-k)}}}\\ +{\displaystyle \sum _{i=1}^{N_p}[(1+\Delta B_1{B}_{p1}^{-1})(D_{p1}\frac{\partial w_{p1}}{\partial t}+D_{p2}{w}_{p1})\mathsf{\delta }(\overline{x}-{\overline{x}}_{pi})}\\ -(D_{1i}\frac{\partial w_{p1}}{\partial t}+D_{2i}{w}_{p1})\mathsf{\delta }(\overline{x}-{\overline{x}}_i)]\end{array}$$

(16)

$$\begin{array}{l}{B}_1\frac{{\partial }^2\Delta w_2}{\partial t^2}+B_2\frac{\partial \Delta w_2}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}\Delta w_2}{\partial {\overline{x}}^{(5-k)}}}+{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial \Delta w_2}{\partial t}}\\ +D_{2i}\Delta w_2)\mathsf{\delta }(\overline{x}-{\overline{x}}_i)=(\Delta B_1{B}_{p1}^{-1}{B}_{p2}-\Delta B_2)\frac{\partial w_{p2}}{\partial t}\\ +{\displaystyle \sum _{k=1}^3(\Delta B_1{B}_{p1}^{-1}{B}_{p,k+2}-\Delta B_{k+2})\frac{{\partial }^{(5-k)}{w}_{p2}}{\partial {\overline{x}}^{(5-k)}}}\\ +{\displaystyle \sum _{i=1}^{N_p}[(1+\Delta B_1{B}_{p1}^{-1})(D_{p1}\frac{\partial w_{p2}}{\partial t}+D_{p2}{w}_{p2})\mathsf{\delta }(\overline{x}-{\overline{x}}_{pi})}\\ -(D_{1i}\frac{\partial w_{p2}}{\partial t}+D_{2i}{w}_{p2})\mathsf{\delta }(\overline{x}-{\overline{x}}_i)]-[B_{10}\frac{{\partial }^2{w}_1}{\partial {\overline{x}}^2}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^2\\ -(1+\Delta B_1{B}_{p1}^{-1})B_{p10}\frac{{\partial }^2{w}_{p1}}{\partial {\overline{x}}^2}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^2]\\ -\left[B_{11}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^3-(1+\Delta B_1{B}_{p1}^{-1})B_{p11}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^3\right]\end{array}$$

(17)

$$\begin{array}{c}{B}_1\frac{{\partial }^2\Delta w_3}{\partial t^2}+B_2\frac{\partial \Delta w_3}{\partial t}+{\displaystyle \sum _{k=1}^3{B}_{k+2}\frac{{\partial }^{(5-k)}\Delta w_3}{\partial {\overline{x}}^{(5-k)}}}+{\displaystyle \sum _{i=1}^{N_p}(D_{1i}\frac{\partial \Delta w_3}{\partial t}}\hfill \\ +D_{2i}\Delta w_3)\mathsf{\delta }(\overline{x}-{\overline{x}}_i)=(\Delta B_1{B}_{p1}^{-1}{B}_{p2}-\Delta B_2)\frac{\partial w_{p3}}{\partial t}\hfill \\ +{\displaystyle \sum _{k=1}^3(\Delta B_1{B}_{p1}^{-1}{B}_{p,k+2}-\Delta B_{k+2})\frac{{\partial }^{(5-k)}{w}_{p3}}{\partial {\overline{x}}^{(5-k)}}}\hfill \\ +{\displaystyle \sum _{i=1}^{N_p}[(1+\Delta B_1{B}_{p1}^{-1})(D_{p1}\frac{\partial w_{p3}}{\partial t}+D_{p2}{w}_{p3})\mathsf{\delta }(\overline{x}-{\overline{x}}_{pi})}\hfill \\ -(D_{1i}\frac{\partial w_{p3}}{\partial t}+D_{2i}{w}_{p3})\mathsf{\delta }(\overline{x}-{\overline{x}}_i)]-B_{10}[\frac{{\partial }^2{w}_2}{\partial {\overline{x}}^2}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^2\hfill \\ +2\frac{{\partial }^2{w}_1}{\partial {\overline{x}}^2}\frac{\partial w_1}{\partial \overline{x}}\frac{\partial w_2}{\partial \overline{x}}]+(1+\Delta B_1{B}_{p1}^{-1})B_{p10}[\frac{{\partial }^2{w}_{p2}}{\partial {\overline{x}}^2}{\left(\frac{\partial w_{p1}}{\partial \overline{x}}\right)}^2\hfill \\ +2\frac{{\partial }^2{w}_{p1}}{\partial {\overline{x}}^2}\frac{\partial w_{p1}}{\partial \overline{x}}\frac{\partial w_{p2}}{\partial \overline{x}}]-3[B_{11}{\left(\frac{\partial w_1}{\partial \overline{x}}\right)}^2\frac{\partial w_2}{\partial \overline{x}}\hfill \\ -(1+\Delta B_1{B}_{p1}^{-1})B_{p11}{(\frac{\partial w_{p1}}{\partial \overline{x}})}^2\frac{\partial w_{p2}}{\partial \overline{x}}]\hfill \\ \dots \dots \end{array}$$

(18)

These equations can be solved to obtain the periodic part and non-periodic part of the asymptotic solution. The boundary conditions (6) can be expanded and separated, corresponding to displacements (7) and (12) for determining the linear vibration modes of the beam. The linear partial differential Equations (13)–(18) for the beam with partial distribution parameters and non-periodic supports can be further converted into linear ordinary differential equations by using the modes for obtaining modal displacement responses.

4. Mode Expansions of Asymptotic Solutions to Linear Partial Differential Equations for Periodic and Non-Periodic Beams

The Galerkin method was applied to convert the linear partial differential Equations (13)–(18) into a set of ordinary differential equations. Spatial distribution parameters and non-periodic supports of the beam result in the coupling of the differential equations, and multiple vibration modes need to be used in the transformation. The linear vibration modes of the beam can be determined based on boundary conditions (6). The dimensionless displacement $\overline{w}$ and then approximate displacement w_j can be expanded into series using the modes. The approximate displacement expansion is:

$$w_j(\overline{x},t)={\displaystyle \sum _{n=1}^{N_m}{\varphi }_n(\overline{x})q_{jn}(t)}=\mathbf{\Phi }(\overline{x}){\mathbf{Q}}_j(t)$$

(19)

where φ_n is the nth linear vibration mode, q_jn is the nth modal displacement of the jth-order approximation, Φ = [φ₁, φ₂, …, φ_Nm] is the mode vector, Q_j = [q_j1, q_j2, …, q_jNm]^T is the modal displacement vector and N_m is mode number. For the simply supported beam with boundary conditions (6), the mode function is ${\varphi }_n(\overline{x})=\sin n\pi \overline{x}$. The periodic part and non-periodic part of the displacement expansion (19) based on Equation (12) are:

$$w_{pj}(\overline{x},t)={\displaystyle \sum _{n=1}^{N_m}{\varphi }_n(\overline{x})q_{pjn}(t)}=\mathbf{\Phi }(\overline{x}){\mathbf{Q}}_{pj}(t)$$

(20)

$$\Delta w_j(\overline{x},t)={\displaystyle \sum _{n=1}^{N_m}{\varphi }_n(\overline{x})\Delta q_{jn}(t)}=\mathbf{\Phi }(\overline{x})\Delta {\mathbf{Q}}_j(t)$$

(21)

where q_pjn is the periodic part of the modal displacement q_jn corresponding to the periodic beam, Δq_jn is the non-periodic (or periodicity defect) part of the modal displacement q_jn corresponding to the non-periodic beam, Q_pj = [q_pj1, q_pj2, …, q_pjNm]^T and ΔQ_j = [Δq_j1, Δq_j2, …, Δq_jNm]^T are the periodic part and non-periodic part vectors of modal displacements, respectively.

According to the Galerkin method, substituting expression (20) into Equations (13)–(15), multiplying the equations by Φ^T and integrating them with respect to $\overline{x}$ yield the following linear ordinary differential equations in matrix form for the periodic part:

$${\mathbf{M}}_{p1}\frac{{\partial }^2{\mathbf{Q}}_{pj}}{\partial t^2}+{\mathbf{C}}_{p1}\frac{\partial {\mathbf{Q}}_{pj}}{\partial t}+{\mathbf{K}}_{p1}{\mathbf{Q}}_{pj}={\mathbf{F}}_{pj}(t)$$

(22)

where M_p1, C_p1, K_p1 are the modal mass, damping and stiffness matrices for the periodic part, respectively, and F_pj is the modal excitation vector for the periodic part. Their expressions are given in Appendix A as Equation (A2).

Similarly, substituting expressions (20) and (21) into Equations (16)–(18) yields the following linear ordinary differential equations in matrix form for the non-periodic part:

$${\mathbf{M}}_1\frac{{\partial }^2\Delta {\mathbf{Q}}_j}{\partial t^2}+{\mathbf{C}}_1\frac{\partial \Delta {\mathbf{Q}}_j}{\partial t}+{\mathbf{K}}_1\Delta {\mathbf{Q}}_j={\mathbf{F}}_j(t)$$

(23)

where M₁, C₁, K₁ are the modal mass, damping and stiffness matrices for the non-periodic part, respectively, and F_j is the modal excitation vector for the non-periodic part. Their expressions are given in Appendix A as Equation (A3).

The linear ordinary differential Equations (22) and (23) have coupling damping and stiffness, and can incorporate multiple vibration modes in accordance with Equations (A2) and (A3). The modal displacement Q_j (Q_pj with ΔQ_j) and then approximate displacement w_j (w_pj with Δw_j) can be obtained by solving these equations. Solution accuracy for the high parameter-varying wave and high frequency vibration will increase with the number of used modes. The effect of support periodicity defect on the vibration response of the beam can be explored based on the displacement solution with the periodicity defect part of the non-periodic beam.

5. Harmonic Balance Solutions to Ordinary Differential Equations for Multi-Mode Coupling Vibrations of Periodic and Non-Periodic Beams

To obtain amplitude–frequency characteristics, the beam is considered subjected to harmonic excitation F. Modal excitation F_p1 in Equation (22) is harmonic due to F or F_p based on Equation (A2). Let F_p1 be:

$${\mathbf{F}}_{p1}(t)={\mathbf{E}}_{p11s}\sin \omega t$$

(24)

where E_p11s = [E_p11s,1, E_p11s,2, …, E_p11s,Nm]^T is a constant vector and ω is the excitation frequency. According to the harmonic balance method, the stationary response of the modal displacement of the first-order approximation for the periodic beam is obtained by Equation (22) (j = 1) as

$${\mathbf{Q}}_{p1}={\mathbf{R}}_{p11s}\sin \omega t+{\mathbf{R}}_{p11c}\cos \omega t$$

(25)

where R_p11s = [R_p11s,1, R_p11s,2, …, R_p11s,Nm]^T, R_p11c = [R_p11c,1, R_p11c,2, …, R_p11c,Nm]^T and:

$${\mathbf{R}}_{p11}=\left[\begin{array}{c}{\mathbf{R}}_{p11s}\\ {\mathbf{R}}_{p11c}\end{array}\right]={\mathbf{\Delta }}_{p1}^{-1}\left[\begin{array}{c}{\mathbf{E}}_{p11s}\\ 0\end{array}\right],{\mathbf{\Delta }}_{p1}=\left[\begin{array}{cc}{\mathbf{K}}_{p1}-{\omega }^2{\mathbf{M}}_{p1}& -\omega {\mathbf{C}}_{p1}\\ \omega {\mathbf{C}}_{p1}& {\mathbf{K}}_{p1}-{\omega }^2{\mathbf{M}}_{p1}\end{array}\right]$$

(26)

By using Equations (A2) and (22) for j = 2, 3, …, modal excitations F_p2, F_p3, … can be determined and stationary responses of modal displacements of the high-order approximations Q_p2, Q_p3, … for the periodic beam can be obtained. They are:

$${\mathbf{F}}_{pj}={\displaystyle \sum _{l=1,3}^{2j-1}({\mathbf{E}}_{pjls}\sin l\omega t+{\mathbf{E}}_{pjlc}\cos l\omega t)}$$

(27)

$${\mathbf{Q}}_{pj}={\displaystyle \sum _{l=1,3}^{2j-1}({\mathbf{R}}_{pjls}\sin l\omega t+{\mathbf{R}}_{pjlc}\cos l\omega t)}$$

(28)

where E_pjls = [E_pjls,1, E_pjls,2, …, E_pjls,Nm]^T and E_pjlc = [E_pjlc,1, E_pjlc,2, …, E_pjlc,Nm]^T are constant vectors, R_pjls = [R_pjls,1, R_pjls,2, …, R_pjls,Nm]^T, R_pjlc = [R_pjlc,1, R_pjlc,2, …, R_pjlc,Nm]^T, and:

$${\mathbf{R}}_{pjl}=\left[\begin{array}{c}{\mathbf{R}}_{pjls}\\ {\mathbf{R}}_{pjlc}\end{array}\right]={\mathbf{\Delta }}_{pl}^{-1}\left[\begin{array}{c}{\mathbf{E}}_{pjls}\\ {\mathbf{E}}_{pjlc}\end{array}\right],{\mathbf{\Delta }}_{pl}=\left[\begin{array}{cc}{\mathbf{K}}_{p1}-l^2{\omega }^2{\mathbf{M}}_{p1}& -l\omega {\mathbf{C}}_{p1}\\ l\omega {\mathbf{C}}_{p1}& {\mathbf{K}}_{p1}-l^2{\omega }^2{\mathbf{M}}_{p1}\end{array}\right]$$

(29)

Similarly, for the non-periodic beam, modal excitations F_j (j = 1, 2, 3, …) can be determined and stationary responses of modal displacements of the approximations ΔQ_j (j = 1, 2, 3, …) for the non-periodic (or periodicity defect) part can be obtained by Equations (A3) and (23). They are:

$${\mathbf{F}}_j={\displaystyle \sum _{l=1,3}^{2j-1}({\mathbf{E}}_{jls}\sin l\omega t+{\mathbf{E}}_{jlc}\cos l\omega t)}$$

(30)

$$\Delta {\mathbf{Q}}_j={\displaystyle \sum _{l=1,3}^{2j-1}({\mathbf{R}}_{jls}\sin l\omega t+{\mathbf{R}}_{jlc}\cos l\omega t)}$$

(31)

where E_jls = [E_jls,1, E_jls,2, …, E_jls,Nm]^T and E_jlc = [E_jlc,1, E_jlc,2, …, E_jlc,Nm]^T are constant vectors, R_jls = [R_jls,1, R_jls,2, …, R_jls,Nm]^T, R_jlc = [R_jlc,1, R_jlc,2, …, R_jlc,Nm]^T, and:

$${\mathbf{R}}_{jl}=\left[\begin{array}{c}{\mathbf{R}}_{jls}\\ {\mathbf{R}}_{jlc}\end{array}\right]={\mathbf{\Delta }}_l^{-1}\left[\begin{array}{c}{\mathbf{E}}_{jls}\\ {\mathbf{E}}_{jlc}\end{array}\right],{\mathbf{\Delta }}_l=\left[\begin{array}{cc}{\mathbf{K}}_1-l^2{\omega }^2{\mathbf{M}}_1& -l\omega {\mathbf{C}}_1\\ l\omega {\mathbf{C}}_1& {\mathbf{K}}_1-l^2{\omega }^2{\mathbf{M}}_1\end{array}\right]$$

(32)

By using Equations (19)–(21), (28) and (31), frequency responses of the approximate displacement w_j in multi-mode coupling vibration can be obtained as a function of ω and $\overline{x}$, which is used to reveal amplitude–frequency characteristics and spatial mode. The response includes periodic part w_pj (for the beam with periodic parameters and supports) and non-periodic part Δw_j (for the beam with periodicity defect or non-periodic parameters and supports). Then, the dimensionless displacement response $\overline{w}$ of the nonlinearly vibrational beam with spatial distribution parameters and non-periodic supports is obtained by Equation (7) as

$$\overline{w}(\overline{x},t)={\displaystyle \sum _{j=1}^{\infty }{\epsilon }^{j-1}\mathbf{\Phi }(\overline{x}){\mathbf{Q}}_j(t)}$$

(33)

From Equation (12), the periodic part and non-periodic part of the displacement response are obtained as

$${\overline{w}}_p(\overline{x},t)={\displaystyle \sum _{j=1}^{\infty }{\epsilon }^{j-1}\mathbf{\Phi }(\overline{x}){\mathbf{Q}}_{pj}(t)}$$

(34)

$$\Delta \overline{w}(\overline{x},t)={\displaystyle \sum _{j=1}^{\infty }{\epsilon }^{j-1}\mathbf{\Phi }(\overline{x})\Delta {\mathbf{Q}}_j(t)}$$

(35)

For certain large nonlinear vibrations, principal harmonic response is dominant and the response amplitude is determined by constant vectors R_pj1s, R_pj1c, R_j1s and R_j1c (j = 1, 2, …) with the mode vector Φ. The above analysis method for the nonlinear vibration responses of non-periodic beams has no limit on the number of modes and is thus suitable for accurate numerical computation. The proposed method is particularly applicable to the nonlinear vibration of non-periodic structures with a high parameter-varying wave in wide frequency vibration. The nonlinear vibration of non-periodic structures under harmonic excitation has the coupling of multiple modes, and its dynamic stability is related to the parametrically excited stability of a multi-degree-of-freedom system with periodic time-varying parameters. The stability problem can be solved by using a direct eigenvalue analysis approach [61].

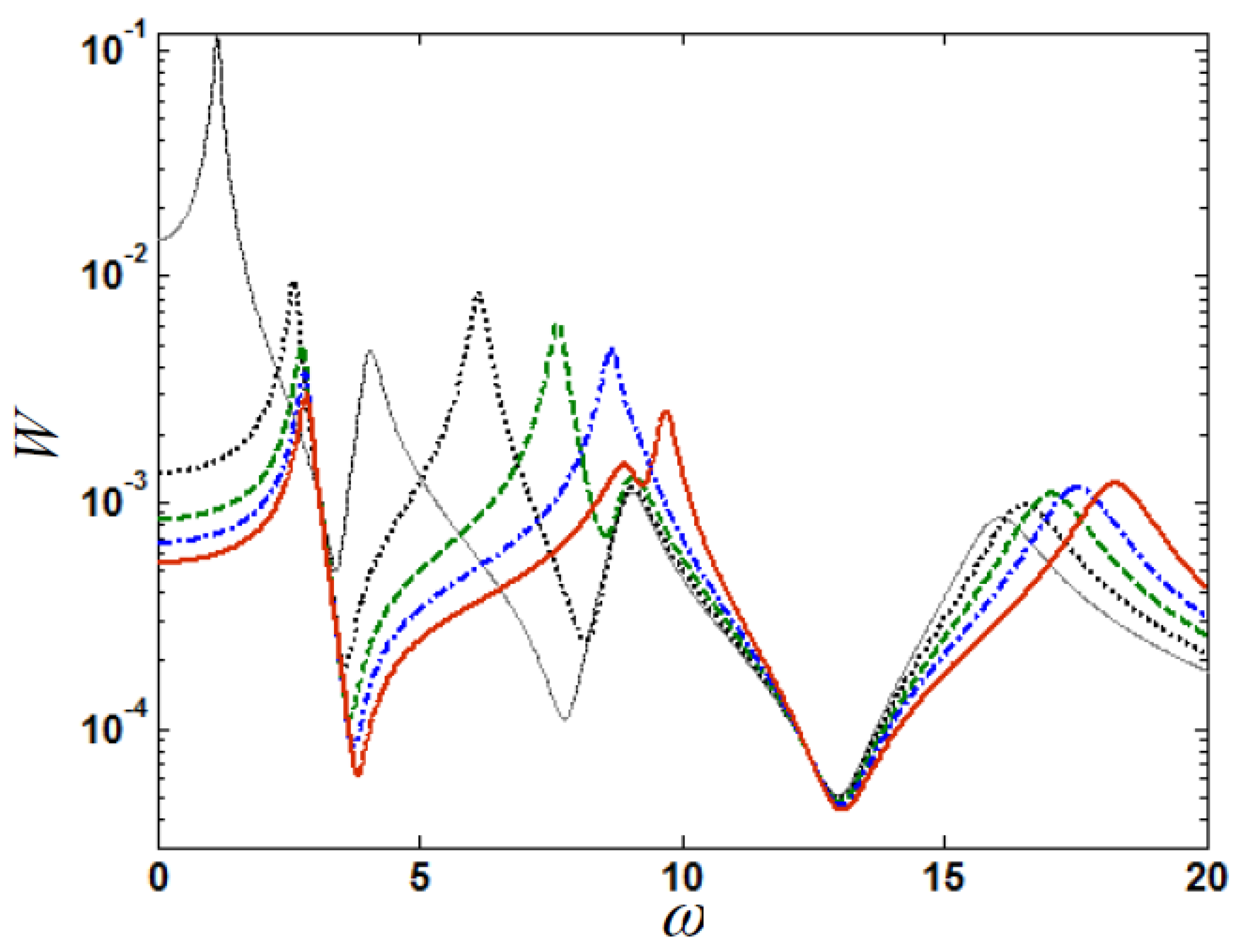
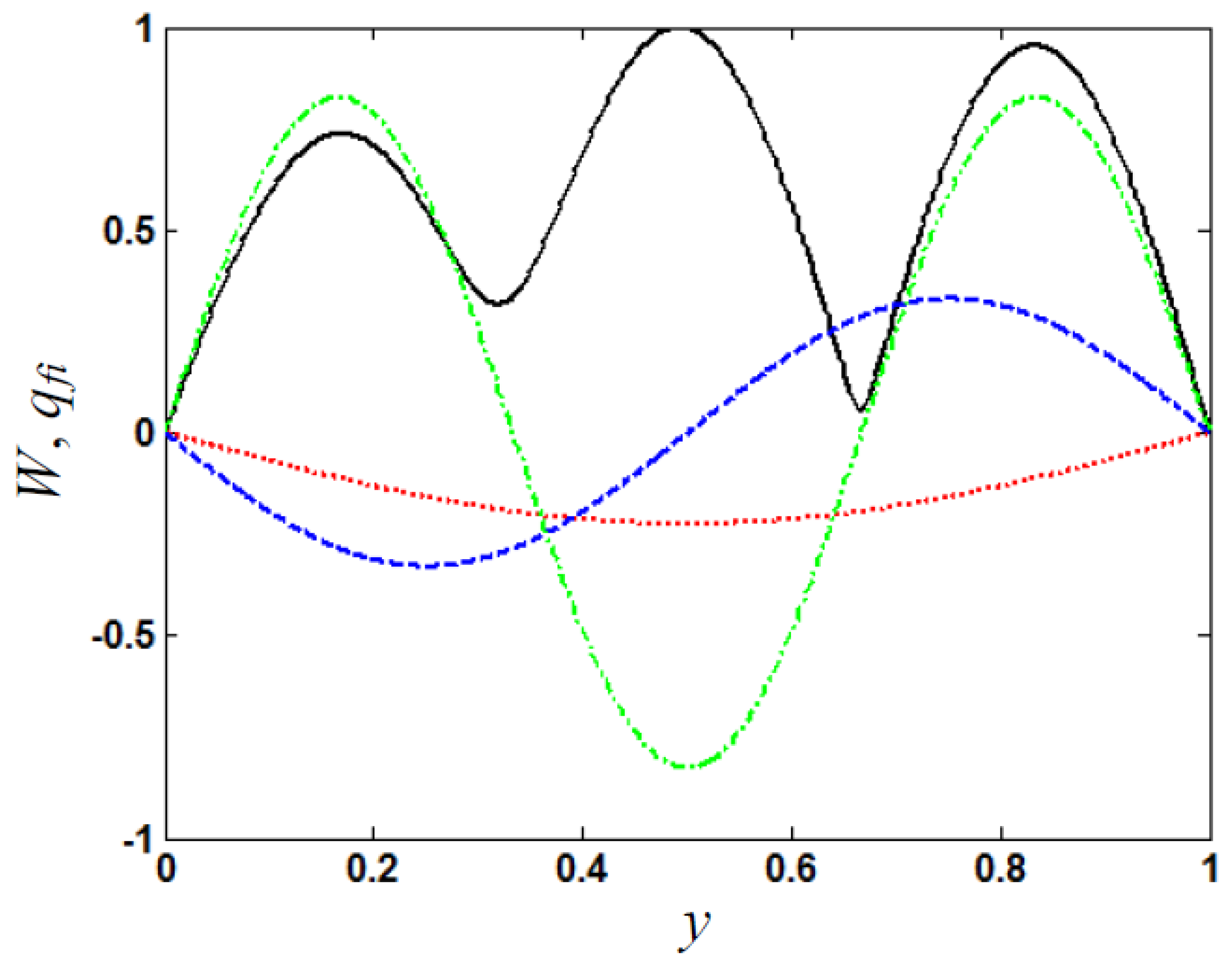
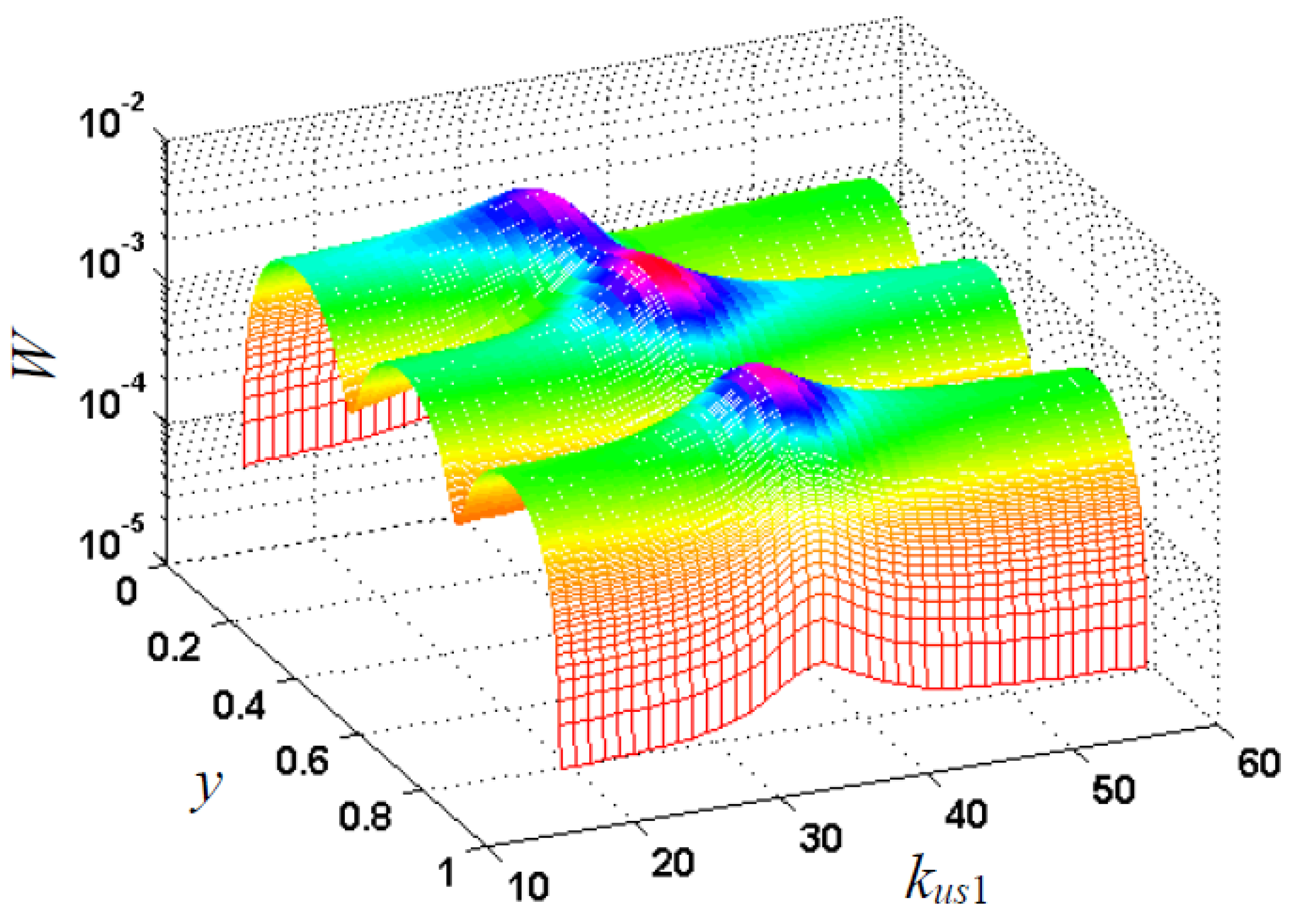
6. Results on Response Amplitude–Frequency Characteristics of Nonlinear Multi-Support Beam with Support Periodicity Defect

To illustrate the application of the proposed method and the response characteristics of non-periodic structures, consider a simply supported beam with a uniform distribution parameters and periodicity defect supports under harmonic excitation which models, e.g., a continuous girder viaduct. The nonlinear vibration of the beam is described by Equation (3) where m_b, $E\overline{A}$ and $E\overline{I}$ are constants. In the case of periodic supports, the dimensionless coordinate of the ith support is ${\overline{x}}_{si}=i/(N_p+1)$ (i = 1, 2, …, N_p). By using dimensionless time τ = t/ω₀, Equation (3) can be rewritten as

$$\begin{array}{l}\frac{{\partial }^2\overline{w}}{\partial {\tau }^2}+c_u\frac{\partial \overline{w}}{\partial \tau }+\frac{1}{{\mathsf{\pi }}^4}\frac{{\partial }^4\overline{w}}{\partial {\overline{x}}^4}-k_u\frac{{\partial }^2\overline{w}}{\partial {\overline{x}}^2}{\left(\frac{\partial \overline{w}}{\partial \overline{x}}\right)}^2\\ +{\displaystyle \sum _{i=1}^{N_p}(c_{usi}\frac{\partial \overline{w}}{\partial \tau }+k_{usi}\overline{w})\mathsf{\delta }(\overline{x}-{\overline{x}}_{si})}=F_u(\overline{x},\tau )\end{array}$$

(36)

where:

$$\begin{gathered} {\omega }_0={\mathsf{\pi }}^2\sqrt{\frac{E{I}_0}{\rho A_0{L}^4}},k_u=\frac{3W_a^2{A}_0}{2{\mathsf{\pi }}^4{I}_0},c_u=\frac{c_b}{m_b{\omega }_0},k_{usi}=\frac{k_{si}{L}^3}{{\mathsf{\pi }}^{4}E{I}_0}, \\ {c}_{usi}=\frac{c_{si}{\omega }_0{L}^3}{{\mathsf{\pi }}^{4}E{I}_0},F_u=\frac{F{L}^3}{{\mathsf{\pi }}^{4}EI} \end{gathered}$$

(37)

By comparing Equation (36) with Equation (5), there are B₁ = 1, B₂ = c_u, B₃ = 1/π⁴, B₄ = B₅ = 0, B₁₀ = −k_u/ε, B₁₁ = 0, D_1i = c_usi, D_2i = k_usi and F is replaced by F_u. Boundary conditions are as given by Equation (6). Equation (36) is a nonlinear partial differential equation with spatial varying parameters due to non-periodic supports. The proposed method was applied to obtain the dimensionless displacement responses of the non-periodic beam in nonlinear multi-mode coupling vibration. The response amplitude is a function of dimensionless frequency ω and coordinate $\overline{x}$, which is used to explore the characteristics of the amplitude–frequency relation and spatial mode.

Harmonic excitation on point y_e is considered as $F_u=F_0\mathsf{\delta }(\overline{x}-y_e)\sin \omega \tau$. For two middle supports, N_p = 2. Basic parameter values are k_u = 0.1, ε = 0.01, k_usi = 0.1, c_usi = 0.02, y_e = 0.4, F₀ = 0.01, and the modal damping coefficient is 0.04 [14]. Results obtained by the proposed method for linear vibration are verified by exact theoretical solution and those for nonlinear vibration are verified by direct numerical simulation. The first four dimensionless natural frequencies of the linearly vibrational beam without damping and middle supports are 1, 4, 9 and 16. For dimensionless frequency ω ∈ [0, 20], the corresponding dimensionless response covers the first four resonances, and its accurate results are obtained by using the proposed method with the mode number N_m = 10 which corresponds to the natural frequency with the upper limit ω = 100.

6.1. Effects of Support Periodicity Defect on Response Amplitude–Frequency Characteristics

Results on dimensionless response amplitude–frequency relations of the nonlinearly vibrational beam with periodic supports and with non-periodic supports are given for comparison. Figure 2 shows the amplitude–frequency relations on the point $\overline{x}$ = 0.4 of the beam with periodic supports and with non-periodic supports (i.e., the left support deviation to the right Δ$\overline{x}$_s1 = 0.1/3 and left support deviation to the left Δ$\overline{x}$_s1 = −0.1/3) under the harmonic excitation. It can be seen that the first response peak increases with local span due to the support deviation. Figure 3 illustrates the relative variation of the response amplitudes of the non-periodic beam with left support deviation to the right (Δ$\overline{x}$_s1 = 0.1/3) to the beam with periodic supports under harmonic excitation. The first response peak is reduced from 0.115 to 0.110 at the dimensionless frequency ω = 1.14 with a relative reduction of 4.52%, and the maximal relative reduction is 6.06% at ω = 1.10. Therefore, the small deviation of periodic supports has a slight effect on the response amplitudes of the nonlinearly vibrational beam.

Figure 4 shows the amplitude–frequency relations on the point $\overline{x}$ = 0.4 of the beam with periodic supports and with non-periodic supports (i.e., left support stiffness k_us1 = 0.6 and left support stiffness k_us1 = 1.1) under the harmonic excitation. It can be seen that the first response peak decreases with the increase in the support stiffness and the first resonant frequency increases with the support stiffness. As the left support stiffness increases from 0.1 to 1.1, the first response peak is reduced from 0.115 (at ω = 1.14) to 0.068 (at ω = 1.62) and the relative reduction is 41.0%. However, high-order resonant and anti-resonant responses have relatively small effects. Figure 5 shows the amplitude–frequency relations on the point $\overline{x}$ = 0.4 of the beam with periodic supports and with non-periodic supports (i.e., left support damping c_us1 = 0.12 and left support damping c_us1 = 0.22) under the harmonic excitation. It can be observed that the first and second response peaks decrease with the increase in the support damping and the resonant frequencies have small variation. As the left support damping increases from 0.02 to 0.12, the first response peak is reduced from 0.115 (at ω = 1.14) to 0.055 (at ω = 1.12) and the relative reduction is 52.1%. Therefore, increasing the stiffness and damping of several supports (as support periodicity defect) can especially reduce the first and second resonant responses of the nonlinearly vibrational beam, which has potential application to nonlinear structural vibration control.

Particularly, it can be observed that the third resonant response and resonant frequency remain unchanged against the increasing support stiffness. The dynamic characteristics of the frequency response of the beam with the support periodicity defect (i.e., several support stiffness variations) will determine the outstanding variation of vibration response distribution and jump or the alteration of mode component orders. The alteration of mode component orders caused by varying support stiffness has been demonstrated for beams with periodic supports [61]. It will be further demonstrated in the following subsections for the nonlinear beam with non-periodic supports (or support periodicity defect).

6.2. Effects of Non-Periodic Support Stiffness Increase on Amplitude–Frequency Characteristics and Vibration Anti-Localization

Special dimensionless amplitude–frequency characteristics and low-order mode component jump of the nonlinearly vibrational beam with non-periodic supports (i.e., a support stiffness larger than the others) are explored by increasing a support stiffness. Figure 6 shows the amplitude–frequency relations on the point $\overline{x}$ = 0.4 of the beam with non-periodic supports under the harmonic excitation for different left support stiffnesses (i.e., left support stiffness k_us1 = 10.1, k_us1 = 20.1, k_us1 = 30.1, k_us1 = 45.1, and k_us1 = 0.1 as periodic support for comparison). It is obtained that the second resonant frequency increases with the support stiffness and the increment is larger than that of the first resonant frequency. However, the third resonant frequency remains unchanged, and thus the second resonant frequency will reach the third resonant frequency as the support stiffness increases. The original third resonant response vanishes when the left support stiffness k_us1 > 30. However, the original third resonant response reappears when the left support stiffness k_us1 > 40, and the resonant response then becomes the second resonant response in accordance with the corresponding frequency order.

Figure 7 and Figure 8 show, in the case of the left support stiffness k_us1 = 10.1, the vibration response distributions (absolute amplitude values) and the corresponding mode components (first three components relevant to φ_n) of the beam with non-periodic supports (i.e., the left support stiffness is larger than the others) under the harmonic excitation with a dimensionless frequency close to the second and third resonant frequencies (ω = 5.0 and 9.0), respectively. The vibration response distributions of the beam without periodic support were also given for comparison. The second and third resonant responses have dominant components of the second and third modes, respectively. The second resonant response at the support ($\overline{x}$ = 1/3, 2/3) is large, but the third resonant response at the support ($\overline{x}$ = 1/3, 2/3) is close to zero, as shown in Figure 7 and Figure 8. Figure 9 shows, in the case of the left support stiffness k_us1 = 45.1, the vibration response distribution and the corresponding mode components of the beam with non-periodic supports under the harmonic excitation with a dimensionless frequency close to the second resonant frequency (ω = 8.9). The second resonant response has a dominant component of the third mode. Then, the original third mode component (for left support stiffness k_us1 = 10.1) becomes the second mode component (for left support stiffness k_us1 = 45.1), and the original second mode component becomes the third mode component. This is the mode component jump or alteration of mode component orders, which yields outstanding variation of the vibration response distribution due to the changing stiffness of a non-periodic support. The left support stiffness k_us1 = 40 is called critical stiffness for the mode alteration as the support periodicity defect. The current second resonant response at the support ($\overline{x}$ = 1/3, 2/3) is close to zero, which is called local weak coupling between adjacent spans.

By the comparison of the vibration response distributions in Figure 7 and Figure 9, the large variation of the spatial distribution of the second resonant response is obtained, particularly, at the supports as the non-periodic support stiffness increases to exceed the critical stiffness. The comparison of the amplitude–frequency relations in Figure 6 results in the large variation of the second resonant response versus frequency as the non-periodic support stiffness increases. Figure 10 shows the evolution of the vibration response distribution of the beam with increasing left support stiffness (k_us1) for ω = 8.9 near the original third resonant frequency. It is observed that the third mode component changes from dominance to puniness and returns dominance in the response. The remarkable variation of frequency response and the mode component jump or alteration of mode component orders for nonlinear beams with varying non-periodic supports (as non-periodic support stiffness increases) are revealed for the first time. The vibration response distribution (for the second resonant response) changes from the non-dominant third mode component (response at the support is large) to the dominant third mode component (response at the support is close to zero); this phenomenon is called vibration anti-localization. The anti-localization has potential application, e.g., in the vibration control of nonlinearly vibrational structures with non-periodic supports.

6.3. Effects of Non-Periodic Support Stiffness Reduction on Amplitude–Frequency Characteristics and Vibration Localization

Dimensionless amplitude–frequency characteristics and the low-order mode component jump of the nonlinearly vibrational beam with non-periodic supports (there is a support with its stiffness smaller than the others) are explored here by considering changes in large support stiffness. Figure 11 shows the amplitude–frequency relations at the point $\overline{x}$ = 0.4 of the beam with periodic supports under the harmonic excitation for different large support stiffnesses (k_us1 = k_us2) (the support stiffness is, respectively, k_us1 = 10, k_us1 = 23, k_us1 = 31, and k_us1 = 40). It can be seen that, as the support stiffness increases, the original second resonant response vanishes when the support stiffnesses k_us1 = k_us2 > 24, and the original second and third resonant responses vanish when the support stiffnesses k_us1 = k_us2 > 31. However, the original third resonant response reappears when the support stiffnesses k_us1 = k_us2 > 38, but the resonant response becomes the first resonant response and the original first resonant response then becomes the second resonant response in terms of the frequency order.

The beam with periodic supports of large support stiffnesses k_us1 = k_us2 = 45 has local weak coupling where the first resonant response at the support is close to zero. Now consider a support stiffness reduction for the periodic beam, e.g., due to damage, which is the support periodicity defect. Figure 12 illustrates the amplitude–frequency relations at the point $\overline{x}$ = 0.4 of the beam with non-periodic supports under the harmonic excitation for different left support stiffnesses (the left support stiffness is, respectively, k_us1 = 40, k_us1 = 38, k_us1 = 25, and k_us1 = 45 in the periodic support case for comparison). It can be seen that as the support stiffness decreases, the second resonant response reappears when the left support stiffness k_us1 < 40. The resonant response peak increases and the resonant frequency decreases with the left support stiffness. The original first resonant response (for the periodic beam) vanishes when the left support stiffness k_us1 < 38. However, the original first resonant response reappears when the left support stiffness k_us1 < 25, and the resonant response then becomes the second resonant response in terms of the frequency order.

Figure 13 shows, in the case of the periodic support stiffnesses k_us1 = k_us2 = 45, the vibration response distribution (absolute amplitude values) and the corresponding mode components (first three components relevant to φ_n) of the beam under the harmonic excitation with a dimensionless frequency close to the first resonant frequency (ω = 8.9). It is observed that the first resonant response has a dominant component of the third mode, and the resonant response at the support ($\overline{x}$ = 1/3, 2/3) is close to zero (local weak coupling). Figure 14 shows, in the case of the non-periodic supports with left support stiffness k_us1 = 25, the vibration response distribution and the corresponding mode components of the beam under the harmonic excitation with dimensionless frequency close to the first resonant frequency (ω = 8.0). It is observed that the first resonant response has dominant components of the first and second modes, and the resonant response at the left support ($\overline{x}$ = 1/3) is large. Therefore, the original second and third mode components (with support stiffness k_us1 = k_us2 = 45) then become the first and second mode components (with left support stiffness k_us1 = 25), and the original first mode component then becomes the third mode component. This is the mode component jump or alteration of mode component orders (support stiffness k_us1 = 25 is called critical stiffness), which yields outstanding variation of the vibration response distribution due to the stiffness reduction of a non-periodic support.

By the comparison of the vibration response distributions in Figure 13 and Figure 14, the large variation in the spatial distribution of the first resonant response (particularly at the support) is obtained, and the comparison of the amplitude–frequency relations in Figure 12 results in the large variation of the first resonant response versus frequency as the non-periodic support stiffness decreases below the critical stiffness. Figure 15 shows the evolution of the vibration response distribution of the beam with the reducing left support stiffness (k_us1) for ω = 8.9 near the original first resonant frequency. The observation similar to Figure 10 was obtained. The outstanding variation of the frequency response and the mode component jump or alteration of mode component orders for nonlinear beams with varying non-periodic supports (as non-periodic support stiffness decreases) are revealed for the first time. The vibration response distribution (for the first resonant response) changes from the dominant third mode component (response at the support is close to zero) to the non-dominant third mode component (response at the support is large); this is called vibration localization. The localization has a potential application, e.g., to support the damage detection of nonlinearly vibrational structures with non-periodic supports.

7. Conclusions

A response analysis method for nonlinearly vibrational beams with spatial distribution parameters and non-periodic supports (or support periodicity defect) was developed by combining perturbation, periodic and non-periodic separation, Galerkin expansion and harmonic balance methods, and applied to analyze the amplitude–frequency characteristics of non-periodic beams with multi-mode coupling vibration. The proposed method has the following main advantages: (i) it separates a non-periodic structure and its response into periodic and non-periodic (or periodicity defect) parts; (ii) it takes multiple vibration modes for the response analysis of nonlinear non-periodic structures; (iii) it considers the coupling effects of vibration modes owing to structural nonlinearity and parametric periodicity; (iv) it is applicable to nonlinear non-periodic structures with a high-parameter-varying wave in a wide frequency vibration; and (v) it is suitable for effective numerical computation. The proposed method can be extended for the dynamic response analysis of other nonlinear structures with periodic and non-periodic distribution parameters.

Nonlinear beams with non-periodic supports (resulting in non-periodic distribution parameters or periodicity defect) under harmonic excitation have been studied to demonstrate the application of the proposed method which has good convergence and accuracy with increasing expansion terms. Graphical results on the amplitude–frequency characteristics of a non-periodic beam with various support stiffness and damping demonstrate that: (i) a small deviation of periodic supports has a slight effect on the response, and the increasing stiffness and damping of several supports can remarkably reduce the first and second resonant responses which has a potential application to nonlinear structural vibration control; (ii) for the local strong coupling case, the second resonant frequency largely increases with non-periodic support stiffness, but the third resonant frequency with the response remains almost unchanged against increasing non-periodic support stiffness; (iii) for the local strong coupling case, the second resonant response and spatial distribution have remarkable variation as the non-periodic support stiffness increases to exceed the critical stiffness, and the mode component jump or alteration of mode component orders gives rise to the outstanding variation or vibration anti-localization, which has a potential application to nonlinear structural vibration control; (iv) for the local weak coupling case, the first resonant response increases and the resonant frequency largely decreases with non-periodic support stiffness when it is smaller than the critical stiffness, and there is the mode component jump or alteration of mode component orders; and (v) for the local weak coupling case, the first resonant response and spatial distribution have remarkable variation as the non-periodic support stiffness decreases below the critical stiffness, and the mode component jump yields the vibration localization, which has a potential application to support damage detection of nonlinear structures with non-periodic supports. Some salient dynamic characteristics including outstanding frequency response variation and the mode component jump for nonlinearly vibrational beams with non-periodic supports (or support periodicity defect) were discovered for the first time.