A Review of CP Violation Measurements in Charm at LHCb
Abstract
1. Introduction
2. Recent Results from LHCb
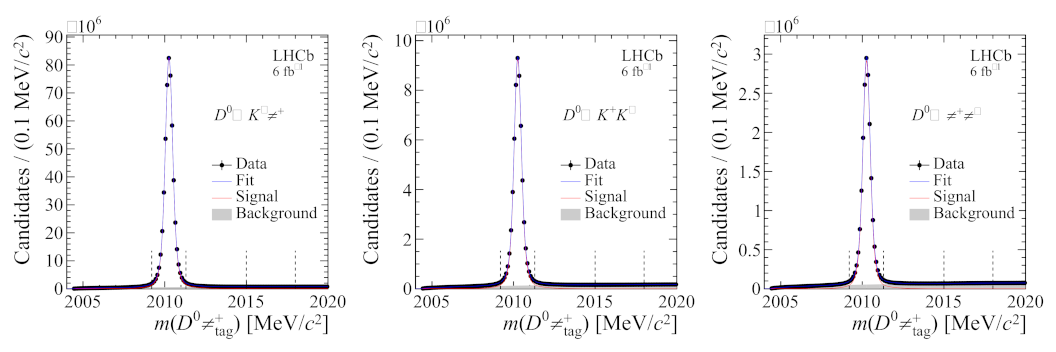
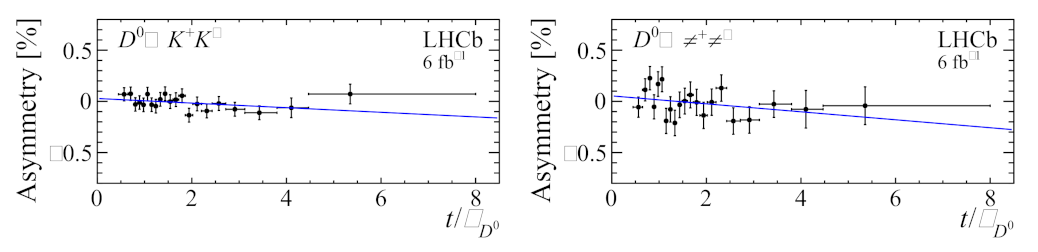
2.1. Measurement of Asymmetry in Decays
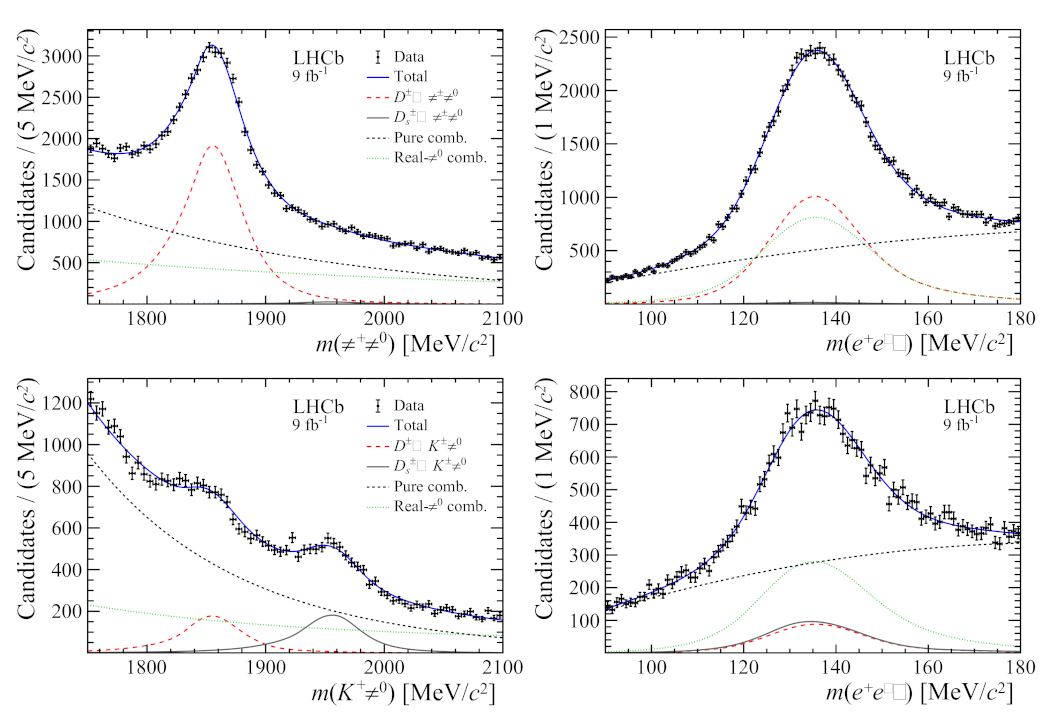
2.2. Search for Violation in and Decays
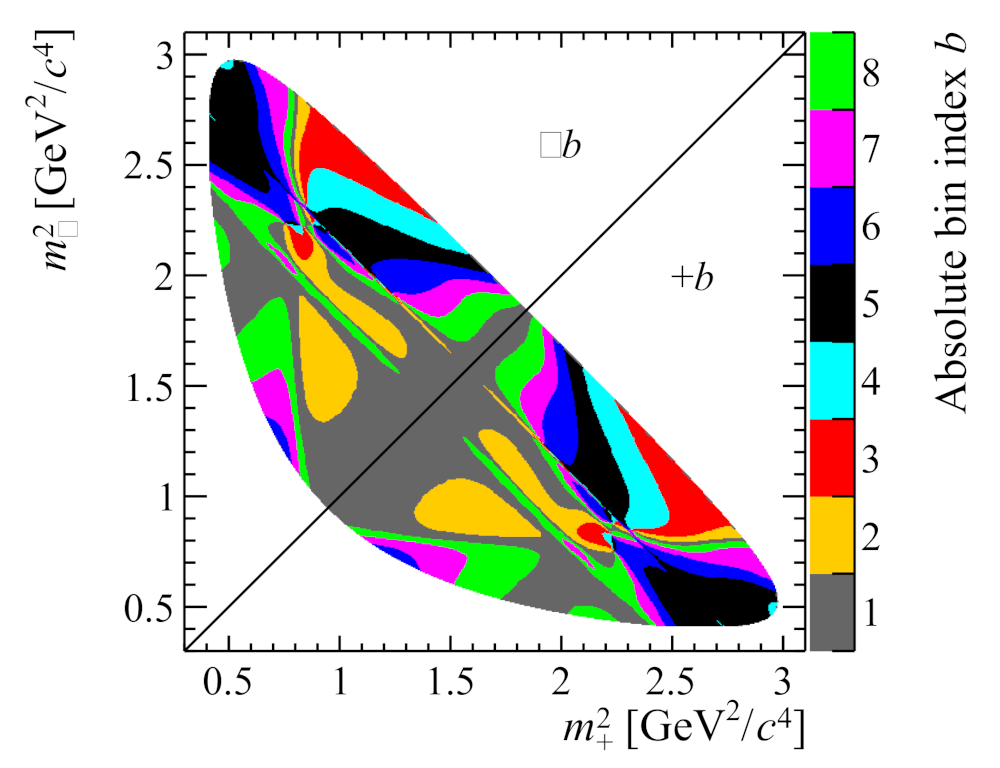
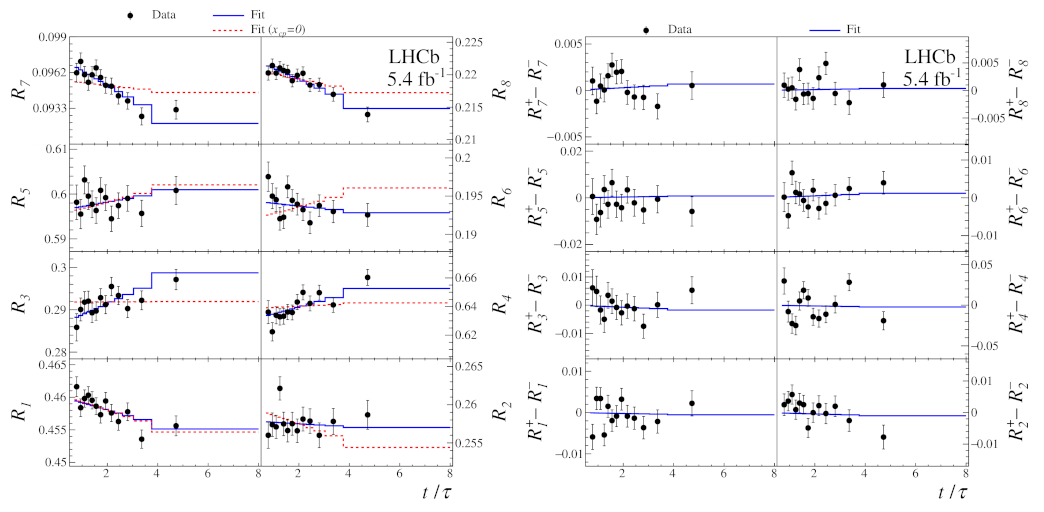
2.3. Search for Time-Dependent Violation in and Decays
2.4. Observation of the Mass Difference between Neutral Charm-Meson Eigenstates
3. Conclusions and Future Prospects
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grossman, Y.; Nir, Y.; Perez, G. Testing New Indirect CP Violation. Phys. Rev. Lett. 2009, 103, 071602. [Google Scholar] [CrossRef] [PubMed]
- Kagan, A.L.; Sokoloff, M.D. On Indirect CP Violation and Implications for D0 − D0 and B(s) − B(s) mixing. Phys. Rev. D 2009, 80, 076008. [Google Scholar] [CrossRef]
- Golden, M.; Grinstein, B. Enhanced CP Violations in Hadronic Charm Decays. Phys. Lett. B 1989, 222, 501–506. [Google Scholar] [CrossRef]
- Buccella, F.; Lusignoli, M.; Miele, G.; Pugliese, A.; Santorelli, P. Nonleptonic weak decays of charmed mesons. Phys. Rev. D 1995, 51, 3478–3486. [Google Scholar] [CrossRef]
- Bianco, S.; Fabbri, F.L.; Benson, D.; Bigi, I. A Cicerone for the physics of charm. Riv. Nuovo Cim. 2003, 26, 1–200. [Google Scholar] [CrossRef]
- Artuso, M.; Meadows, B.; Petrov, A.A. Charm Meson Decays. Ann. Rev. Nucl. Part. Sci. 2008, 58, 249–291. [Google Scholar] [CrossRef]
- Brod, J.; Kagan, A.L.; Zupan, J. Size of direct CP violation in singly Cabibbo-suppressed D decays. Phys. Rev. D 2012, 86, 014023. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Chiang, C.W. Direct CP violation in two-body hadronic charmed meson decays. Phys. Rev. D 2012, 85, 034036, Erratum in Phys. Rev. D 2012, 85, 079903. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Chiang, C.W. SU(3) symmetry breaking and CP violation in D → PP decays. Phys. Rev. D 2012, 86, 014014. [Google Scholar] [CrossRef]
- Li, H.N.; Lu, C.D.; Yu, F.S. Branching ratios and direct CP asymmetries in D → PP decays. Phys. Rev. D 2012, 86, 036012. [Google Scholar] [CrossRef]
- Franco, E.; Mishima, S.; Silvestrini, L. The Standard Model confronts CP violation in D0 → π+π− and D0 → K+K−. J. High Energy Phys. 2012, 5, 140. [Google Scholar] [CrossRef]
- Pirtskhalava, D.; Uttayarat, P. CP Violation and Flavor SU(3) Breaking in D-meson Decays. Phys. Lett. B 2012, 712, 81–86. [Google Scholar] [CrossRef]
- Feldmann, T.; Nandi, S.; Soni, A. Repercussions of Flavour Symmetry Breaking on CP Violation in D-Meson Decays. J. High Energy Phys. 2012, 6, 1–23. [Google Scholar] [CrossRef]
- Brod, J.; Grossman, Y.; Kagan, A.L.; Zupan, J. A Consistent Picture for Large Penguins in D → π+π−,K+K−. J. High Energy Phys. 2012, 10, 161. [Google Scholar] [CrossRef]
- Hiller, G.; Jung, M.; Schacht, S. SU(3)-flavor anatomy of nonleptonic charm decays. Phys. Rev. D 2013, 87, 014024. [Google Scholar] [CrossRef]
- Grossman, Y.; Robinson, D.J. SU(3) Sum Rules for Charm Decay. J. High Energy Phys. 2013, 04, 067. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Gronau, M.; Rosner, J.L. CP asymmetries in singly-Cabibbo-suppressed D decays to two pseudoscalar mesons. Phys. Rev. D 2012, 85, 054014. [Google Scholar] [CrossRef]
- Müller, S.; Nierste, U.; Schacht, S. Sum Rules of Charm CP Asymmetries beyond the SU(3)F Limit. Phys. Rev. Lett. 2015, 115, 251802. [Google Scholar] [CrossRef] [PubMed]
- Khodjamirian, A.; Petrov, A.A. Direct CP asymmetry in D → π−π+ and D → K−K+ in QCD-based approach. Phys. Lett. B 2017, 774, 235–242. [Google Scholar] [CrossRef]
- Buccella, F.; Paul, A.; Santorelli, P. SU(3)F breaking through final state interactions and CP asymmetries in D → PP decays. Phys. Rev. D 2019, 99, 113001. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Measurements of prompt charm production cross-sections in pp collisions at = 13 TeV. J. High Energy Phys. 2016, 3, 159, Erratum in J. High Energy Phys. 2016, 9, 013, Erratum in J. High Energy Phys. 2017, 5, 074. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Search for CP violation in and decays. J. High Energy Phys. 2014, 10, 025. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurement of CP asymmetries in and decays. Phys. Lett. B 2017, 771, 21–30. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; et al. Search for CP violation in , and decays. Phys. Rev. Lett. 2019, 122, 191803. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurement of indirect CP asymmetries in D0 → K−K+ and D0 → π−π+ decays using semileptonic B decays. J. High Energy Phys. 2015, 04, 043. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurement of the CP violation parameter AΓ in D0 → K+K− and D0 → π+π− decays. Phys. Rev. Lett. 2017, 118, 261803. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; et al. Measurement of the Charm-Mixing Parameter yCP. Phys. Rev. Lett. 2019, 122, 011802. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Updated measurement of decay-time-dependent CP asymmetries in D0 → K+K− and D0 → π+π− decays. Phys. Rev. D 2020, 101, 012005. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurement of CP asymmetry in D0 → K−K+ and D0 → π−π+ decays. J. High Energy Phys. 2014, 7, 041. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Measurement of the difference of time-integrated CP asymmetries in D0 → K−K+ and D0 → π−π+ decays. Phys. Rev. Lett. 2016, 116, 191601. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurement of CP asymmetry in D0 → K−K+ decays. Phys. Lett. B 2017, 767, 177–187. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurements of charm mixing and CP violation using D0 → K±π∓ decays. Phys. Rev. D 2017, 95, 052004, Erratum in Phys. Rev. D 2017, 96, 099907 . [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Alfonso Albero, A.; Ali, S.; et al. Updated determination of D0 − D0 mixing and CP violation parameters with D0 → K+π− decays. Phys. Rev. D 2018, 97, 031101. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Model-independent search for CP violation in D0 → K−K+π−π+ and D0 → π−π+π+π− decays. Phys. Lett. B 2013, 726, 623–633. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Search for CP violation in the decay D+ → π−π+π+. Phys. Lett. B 2014, 728, 585–595. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Search for CP violation using T-odd correlations in D0 → K+K−π+π− decays. J. High Energy Phys. 2014, 10, 005. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Search for CP violation in D0 → π−π+π0 decays with the energy test. Phys. Lett. B 2015, 740, 158–167. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Measurement of Angular and CP Asymmetries in D0 → π+π−μ+μ− and D0 → K+K−μ+μ− decays. Phys. Rev. Lett. 2018, 121, 091801. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; et al. Search for CP violation through an amplitude analysis of D0 → K+K−π+π− decays. J. High Energy Phys. 2019, 02, 126. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Measurement of the time-integrated CP asymmetry in decays. J. High Energy Phys. 2018, 11, 048. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; et al. Measurement of the mass difference between neutral charm-meson eigenstates. Phys. Rev. Lett. 2019, 122, 231802. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Alfonso Albero, A.; Ali, S.; et al. A measurement of the CP asymmetry difference in and pπ−π+ decays. J. High Energy Phys. 2018, 03, 182. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Search for CP violation in decays using model-independent techniques. Eur. Phys. J. C 2020, 80, 986. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessi, F.; et al. Observation of CP Violation in Charm Decays. Phys. Rev. Lett. 2019, 122, 211803. [Google Scholar] [CrossRef]
- Grossman, Y.; Kagan, A.L.; Nir, Y. New physics and CP violation in singly Cabibbo suppressed D decays. Phys. Rev. D 2007, 75, 036008. [Google Scholar] [CrossRef]
- Chala, M.; Lenz, A.; Rusov, A.V.; Scholtz, J. ΔACP within the Standard Model and beyond. J. High Energy Phys. 2019, 07, 161. [Google Scholar] [CrossRef]
- Grossman, Y.; Schacht, S. The emergence of the ΔU = 0 rule in charm physics. J. High Energy Phys. 2019, 07, 020. [Google Scholar] [CrossRef]
- Li, H.N.; Lu, C.D.; Yu, F.S. Implications on the first observation of charm CPV at LHCb. arXiv 2019, arXiv:hep-ph/1903.10638. [Google Scholar]
- Soni, A. Resonance enhancement of Charm CP. arXiv 2019, arXiv:hep-ph/1905.00907. [Google Scholar]
- Cheng, H.Y.; Chiang, C.W. Revisiting CP violation in D → PP and VP decays. Phys. Rev. D 2019, 100, 093002. [Google Scholar] [CrossRef]
- Dery, A.; Nir, Y. Implications of the LHCb discovery of CP violation in charm decays. J. High Energy Phys. 2019, 12, 104. [Google Scholar] [CrossRef]
- Wang, D.; Jia, C.P.; Yu, F.S. A self-consistent framework of topological amplitude and its SU(N) decomposition. arXiv 2020, arXiv:hep-ph/2001.09460. [Google Scholar]
- Bause, R.; Gisbert, H.; Golz, M.; Hiller, G. Exploiting CP-asymmetries in rare charm decays. Phys. Rev. D 2020, 101, 115006. [Google Scholar] [CrossRef]
- Dery, A.; Grossman, Y.; Schacht, S.; Soffer, A. Probing the ΔU = 0 rule in three body charm decays. J. High Energy Phys. 2021, 05, 179. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Chiang, C.W. CP violation in quasi-two-body D → VP decays and three-body D decays mediated by vector resonances. arXiv 2021, arXiv:hep-ph/2104.13548. [Google Scholar]
- Kagan, A.L.; Silvestrini, L. Dispersive and absorptive CP violation in D0 − D0 mixing. Phys. Rev. D 2021, 103, 053008. [Google Scholar] [CrossRef]
- Alves, A.A., Jr.; Andrade Filho, L.M.; Barbosa, A.F.; Bediaga, I.; Cernicchiaro, G.; Guerrer, G.; Lima, H.P., Jr.; Machado, A.A.; Magnin, J.; Marujo, F.; et al. The LHCb Detector at the LHC. J. Instrum. 2008, 3, S08005. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. LHCb Detector Performance. Int. J. Mod. Phys. A 2015, 30, 1530022. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurement of B0, , B+ and production asymmetries in 7 and 8 TeV proton-proton collisions. Phys. Lett. B 2017, 774, 139–158. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurement of the flavour-specific CP-violating asymmetry in decays. Phys. Lett. B 2014, 728, 607–615. [Google Scholar] [CrossRef]
- Aaij, R.; Abellan Beteta, C.; Adametz, A.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; et al. Measurement of the D± production asymmetry in 7 TeV pp collisions. Phys. Lett. B 2013, 718, 902–909. [Google Scholar] [CrossRef]
- Aaij, R.; Abellan Beteta, C.; Adametz, A.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; et al. Measurement of the production asymmetry in 7 TeV pp collisions. Phys. Lett. B 2012, 713, 186–195. [Google Scholar] [CrossRef]
- Nierste, U.; Schacht, S. CP Violation in D0 → KSKS. Phys. Rev. D 2015, 92, 054036. [Google Scholar] [CrossRef]
- Bonvicini, G.; Cinabro, D.; Dubrovin, M.; McGee, S.; Zhou, G.J.; Bornheim, A.; Lipeles, E.; Pappas, S.P.; Schmidtler, M.; Shapiro, A.; et al. Search for CP violation in and and decays. Phys. Rev. D 2001, 63, 071101. [Google Scholar] [CrossRef]
- Dash, N.; Bahinipati, S.; Bhardwaj, V.; Trabelsi, K.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.M.; Aulchenko, V.; Aushev, T.; et al. Search for CP Violation and Measurement of the Branching Fraction in the Decay . Phys. Rev. Lett. 2017, 119, 171801. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurement of the time-integrated CP asymmetry in decays. J. High Energy Phys. 2015, 10, 055. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Measurement of CP asymmetry in decays. arXiv 2021, arXiv:hep-ex/2105.01565. [Google Scholar]
- Babu, V.; Trabelsi, K.; Mohanty, G.B.; Aziz, T.; Greenwald, D.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; et al. Search for CP violation in the D+ → π+π0 decay at Belle. Phys. Rev. D 2018, 97, 011101. [Google Scholar] [CrossRef]
- Guan, Y.; Schwartz, A.J.; Kinoshita, K.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; Aulchenko, V.; Aushev, T.; et al. Measurement of branching fractions and CP asymmetries for → K+(η,π0) and → π+(η,π0) decays at Belle. Phys. Rev. D 2021, 103, 112005. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Search for CP violation in → h+π0 and → h+η decays. J. High Energy Phys. 2021, 06, 019. [Google Scholar] [CrossRef]
- Mendez, H.; Ge, J.Y.; Miller, D.H.; Shipsey, I.P.J.; Xin, B.; Adams, G.S.; Hu, D.; Moziak, B.; Napolitano, J.; Ecklund, K.M.; et al. Measurements of D Meson Decays to Two Pseudoscalar Mesons. Phys. Rev. D 2010, 81, 052013. [Google Scholar] [CrossRef]
- Li, H.N.; Umeeda, H.; Xu, F.; Yu, F.S. D meson mixing as an inverse problem. Phys. Lett. B 2020, 810, 135802. [Google Scholar] [CrossRef]
- Pajero, T.; Morello, M.J. Mixing and CP violation in D → K−π+ decays. arXiv 2021, arXiv:hep-ph/2106.02014. [Google Scholar]
- Pajero, T. Search for Time-Dependent CP Violation in D0 → K+K− and D0 → π+π− Decays. Ph.D. Thesis, Scuola Normale Superiore, Pisa, Italy, 2021. [Google Scholar]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Garra Tico, J.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; et al. Measurement of D0 − D0 Mixing and CP Violation in Two-Body D0 Decays. Phys. Rev. D 2013, 87, 012004. [Google Scholar] [CrossRef]
- Aaltonen, T.A.; Amerio, S.; Amidei, D.; Anastassov, A.; Annovi, A.; Antos, J.; Apollinari, G.; Appel, J.A.; Arisawa, T.; Artikov, A.; et al. Measurement of indirect CP-violating asymmetries in D0 → K+K− and D0 → π+π− decays at CDF. Phys. Rev. D 2014, 90, 111103. [Google Scholar] [CrossRef]
- Starič, M.; Abdesselam, A.; Adachi, I.; Aihara, H.; Arinstein, K.; Asner, D.M.; Aushev, T.; Ayad, R.; Aziz, T.; Babu, V.; et al. Measurement of D0 − D0 mixing and search for CP violation in D0 → K+K−,π+π− decays with the full Belle data set. Phys. Lett. B 2016, 753, 412–418. [Google Scholar] [CrossRef]
- Amhis, Y.S.; Banerjee, Sw.; Ben-Haim, E.; Bernlochner, F.U.; Bona, M.; Bozek, A.; Bozzi, C.; Brodzicka, J.; Chrzaszcz, M.; Dingfelder, J.; et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of 2018. Eur. Phys. J. C 2021, 81, 226. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Search for time-dependent CP violation in D0 → K+K− and D0 → π+π− decays. arXiv 2021, arXiv:hep-ex/2105.09889. [Google Scholar]
- Carrasco, N.; Ciuchini, M.; Dimopoulos, P.; Frezzotti, R.; Gimenez, V.; Lubicz, V.; Rossi, G.C.; Sanfilippo, F.; Silvestrini, L.; Simula, S.; et al. D0 − D0 mixing in the standard model and beyond from Nf = 2 twisted mass QCD. Phys. Rev. D 2014, 90, 014502. [Google Scholar] [CrossRef]
- Kirk, M.; Lenz, A.; Rauh, T. Dimension-six matrix elements for meson mixing and lifetimes from sum rules. J. High Energy Phys. 2020, 12, 068, Erratum in J. High Energy Phys. 2020, 06, 162. [Google Scholar] [CrossRef]
- Carrasco, N.; Dimopoulos, P.; Frezzotti, R.; Lubicz, V.; Rossi, G.C.; Simula, S.; Tarantino, C. ΔS = 2 and ΔC = 2 bag parameters in the standard model and beyond from Nf = 2 + 1 + 1 twisted-mass lattice QCD. Phys. Rev. D 2015, 92, 034516. [Google Scholar] [CrossRef]
- Bazavov, A.; Bernard, C.; Bouchard, C.M.; Chang, C.C.; DeTar, C.; Du, D.; El-Khadra, A.X.; Freeland, E.D.; Gámiz, E.; Gottlieb, S.; et al. Short-distance matrix elements for D0-meson mixing for Nf = 2 + 1 lattice QCD. Phys. Rev. D 2018, 97, 034513. [Google Scholar] [CrossRef]
- Lenz, A.; Piscopo, M.L.; Vlahos, C. Renormalization scale setting for D-meson mixing. Phys. Rev. D 2020, 102, 093002. [Google Scholar] [CrossRef]
- Jubb, T.; Kirk, M.; Lenz, A.; Tetlalmatzi-Xolocotzi, G. On the ultimate precision of meson mixing observables. Nucl. Phys. B 2017, 915, 431–453. [Google Scholar] [CrossRef]
- Georgi, H. D–anti-D mixing in heavy quark effective field theory. Phys. Lett. B 1992, 297, 353–357. [Google Scholar] [CrossRef]
- Ohl, T.; Ricciardi, G.; Simmons, E.H. D - anti-D mixing in heavy quark effective field theory: The Sequel. Nucl. Phys. B 1993, 403, 605–632. [Google Scholar] [CrossRef]
- Bigi, I.I.Y.; Uraltsev, N.G. D0 - anti-D0 oscillations as a probe of quark hadron duality. Nucl. Phys. B 2001, 592, 92–106. [Google Scholar] [CrossRef]
- Bobrowski, M.; Lenz, A.; Riedl, J.; Rohrwild, J. How Large Can the SM Contribution to CP Violation in D0 − D0 Mixing Be? J. High Energy Phys. 2010, 03, 009. [Google Scholar] [CrossRef]
- Bobrowski, M.; Lenz, A.; Rauh, T. Short distance D-Dbar mixing. In Proceedings of the 5th International Workshop on Charm Physics, Honolulu, HI, USA, 14–17 May 2012. [Google Scholar]
- Falk, A.F.; Grossman, Y.; Ligeti, Z.; Petrov, A.A. SU(3) breaking and D0–anti-D0 mixing. Phys. Rev. D 2002, 65, 054034. [Google Scholar] [CrossRef]
- Gronau, M.; Rosner, J.L. Revisiting D0-D0bar mixing using U-spin. Phys. Rev. D 2012, 86, 114029. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Chiang, C.W. Long-Distance Contributions to D0 − D0 Mixing Parameters. Phys. Rev. D 2010, 81, 114020. [Google Scholar] [CrossRef]
- Jiang, H.Y.; Yu, F.S.; Qin, Q.; Li, H.N.; Lü, C.D. D0 − D0 mixing parameter y in the factorization-assisted topological-amplitude approach. Chin. Phys. C 2018, 42, 063101. [Google Scholar] [CrossRef]
- Wolfenstein, L. D0 anti-D0 Mixing. Phys. Lett. B 1985, 164, 170–172. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Golowich, E.; Holstein, B.R.; Trampetic, J. Dispersive Effects in D0 anti-D0 Mixing. Phys. Rev. D 1986, 33, 179. [Google Scholar] [CrossRef] [PubMed]
- Asner, D.M.; Dytman, S.A.; Love, W.; Mehrabyan, S.; Mueller, J.A.; Savinov, V.; Li, Z.; Lopez, A.; Mendez, H.; Ramirez, J.; et al. Search for D0 − D0 mixing in the Dalitz plot analysis of D0 → π+π−. Phys. Rev. D 2005, 72, 012001. [Google Scholar] [CrossRef]
- del Amo Sanchez, P.; Lees, J.P.; Poireau, V.; Prencipe, E.; Tisserand, V.; Garra Tico, J.; Grauges, E.; Martinelli, M.; Palano, A.; Pappagallo, M.; et al. Measurement of D0 − D0 mixing parameters using D0 → π+π− and D0 → K+K− decays. Phys. Rev. Lett. 2010, 105, 081803. [Google Scholar] [CrossRef] [PubMed]
- Peng, T.; Zhang, Z.P.; Abdesselam, A.; Adachi, I.; Aihara, H.; Arinstein, K.; Asner, D.M.; Aulchenko, V.; Aushev, T.; Ayad, R.; et al. Measurement of D0 − D0 mixing and search for indirect CP violation using D0 → π+π− decays. Phys. Rev. D 2014, 89, 091103. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Model-independent measurement of mixing parameters in D0 → π+π− decays. J. High Energy Phys. 2016, 04, 033. [Google Scholar] [CrossRef]
- Di Canto, A.; Garra Ticó, J.; Gershon, T.; Jurik, N.; Martinelli, M.; Pilař, T.; Stahl, S.; Tonelli, D. Novel method for measuring charm-mixing parameters using multibody decays. Phys. Rev. D 2019, 99, 012007. [Google Scholar] [CrossRef]
- Libby, J.; Kornicer, M.; Mitchell, R.E.; Shepherd, M.R.; Tarbert, C.M.; Besson, D.; Pedlar, T.K.; Xavier, J.; Cronin-Hennessy, D.; Hietala, J.; et al. Model-independent determination of the strong-phase difference between D0 and D0 → h+h− (h = π,K) and its impact on the measurement of the CKM angle γ/ϕ3. Phys. Rev. D 2010, 82, 112006. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Ambrose, D.; Amoroso, A.; An, F.F.; An, Q.; et al. Model-independent determination of the relative strong-phase difference between D0 and D0 → π+π− and its impact on the measurement of the CKM angle γ/ϕ3. Phys. Rev. D 2020, 101, 112002. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Observation of the mass difference between neutral charm-meson eigenstates. arXiv 2021, arXiv:hep-ex/2106.03744. [Google Scholar]
- Aaij, R.; Abellan Beteta, C.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Measurement of the CKM angle γ from a combination of B± → Dh± analyses. Phys. Lett. B 2013, 726, 151–163. [Google Scholar] [CrossRef]
- Bediaga, I.; De Miranda, J.M.; Ferreira Rodrigues, F.; Magnin, J.; Massafferri, A.; Nasteva, I.; dos Reis, A.C.; Amato, S.; Carvalho Akiba, K.; De Paula, L.; et al. Framework TDR for the LHCb Upgrade: Technical Design Report. CERN-LHCC-2012-007. 2012. Available online: https://cds.cern.ch/record/1443882?ln=en (accessed on 26 April 2012).
- Bediaga, I.; De Miranda, J.M.; Ferreira Rodrigues, F.; Gomes, A.; Hicheur, A.; Massafferri, A.; dos Reis, A.C.; Rodrigues, A.B.; Amato, S.; Carvalho Akiba, K.; et al. LHCb Trigger and Online Upgrade Technical Design Report. CERN-LHCC-2014-016. 2014. Available online: https://cds.cern.ch/record/1701361?ln=en (accessed on 14 May 2014).
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Expression of Interest for a Phase-II LHCb Upgrade: Opportunities in Flavour Physics, and Beyond, in the HL-LHC Era. CERN-LHCC-2017-003. 2017. Available online: https://cds.cern.ch/record/2244311?ln=en (accessed on 8 February 2017).
- Aaij, R.; Bediaga, I.; Cruz Torres, M.; De Miranda, J.M.; Gomes, A.; Massafferri, A.; Molina Rodriguez, J.; dos Reis, A.C.; Soares Lavra, I.; Tourinho Jadallah Aoude, R.; et al. Physics case for an LHCb Upgrade II—Opportunities in flavour physics, and beyond, in the HL-LHC era. arXiv 2018, arXiv:hep-ex/1808.08865. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betti, F. A Review of CP Violation Measurements in Charm at LHCb. Symmetry 2021, 13, 1482. https://doi.org/10.3390/sym13081482
Betti F. A Review of CP Violation Measurements in Charm at LHCb. Symmetry. 2021; 13(8):1482. https://doi.org/10.3390/sym13081482
Chicago/Turabian StyleBetti, Federico. 2021. "A Review of CP Violation Measurements in Charm at LHCb" Symmetry 13, no. 8: 1482. https://doi.org/10.3390/sym13081482
APA StyleBetti, F. (2021). A Review of CP Violation Measurements in Charm at LHCb. Symmetry, 13(8), 1482. https://doi.org/10.3390/sym13081482





