On the τ Decomposition Method for the Stability and Bifurcation of the TCP/AQM Networks versus Time Delay
Abstract
:1. Introduction
2. Problems Statement and Preliminaries
3. Direction and Stability of Bifurcating Periodic Solutions
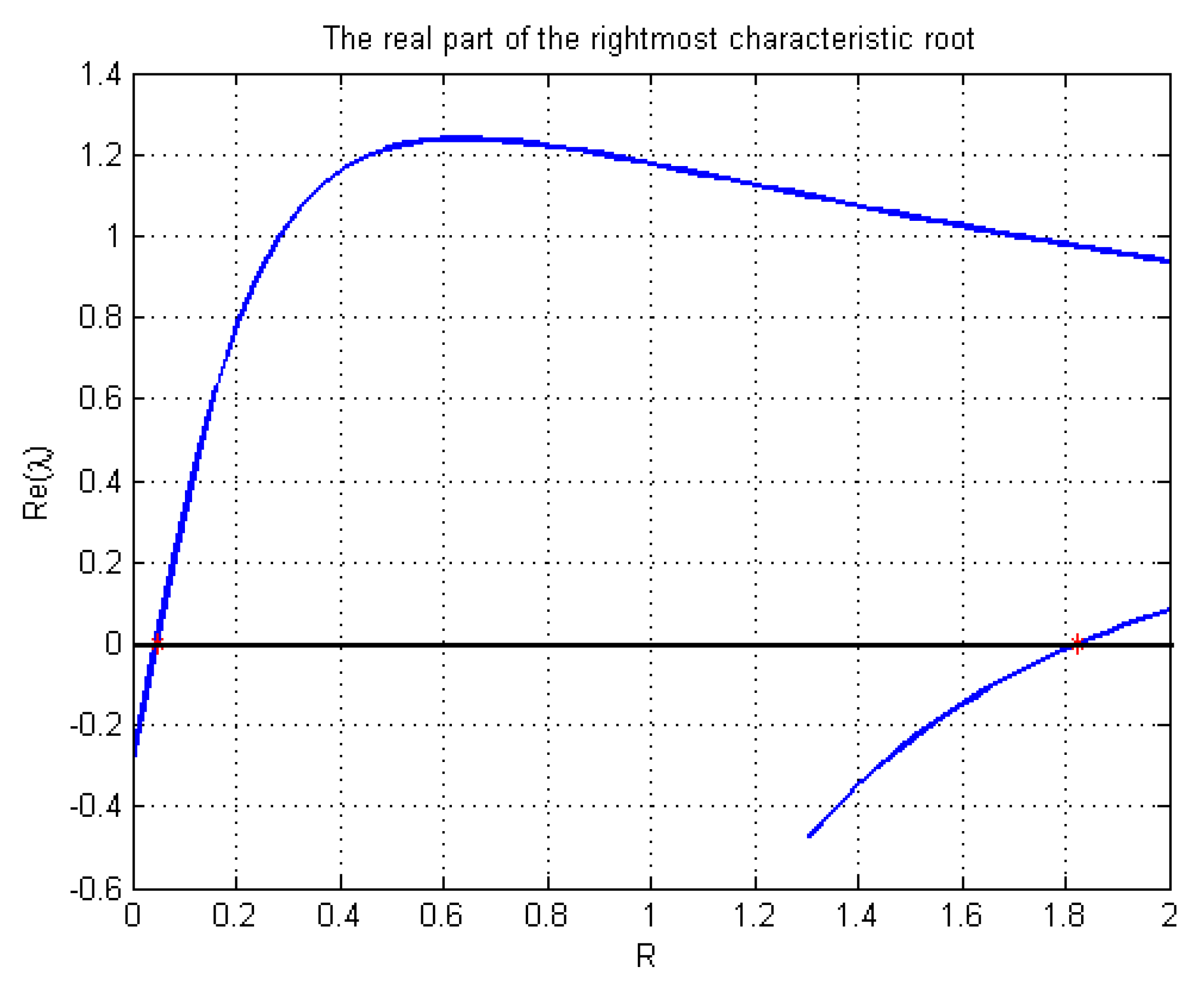
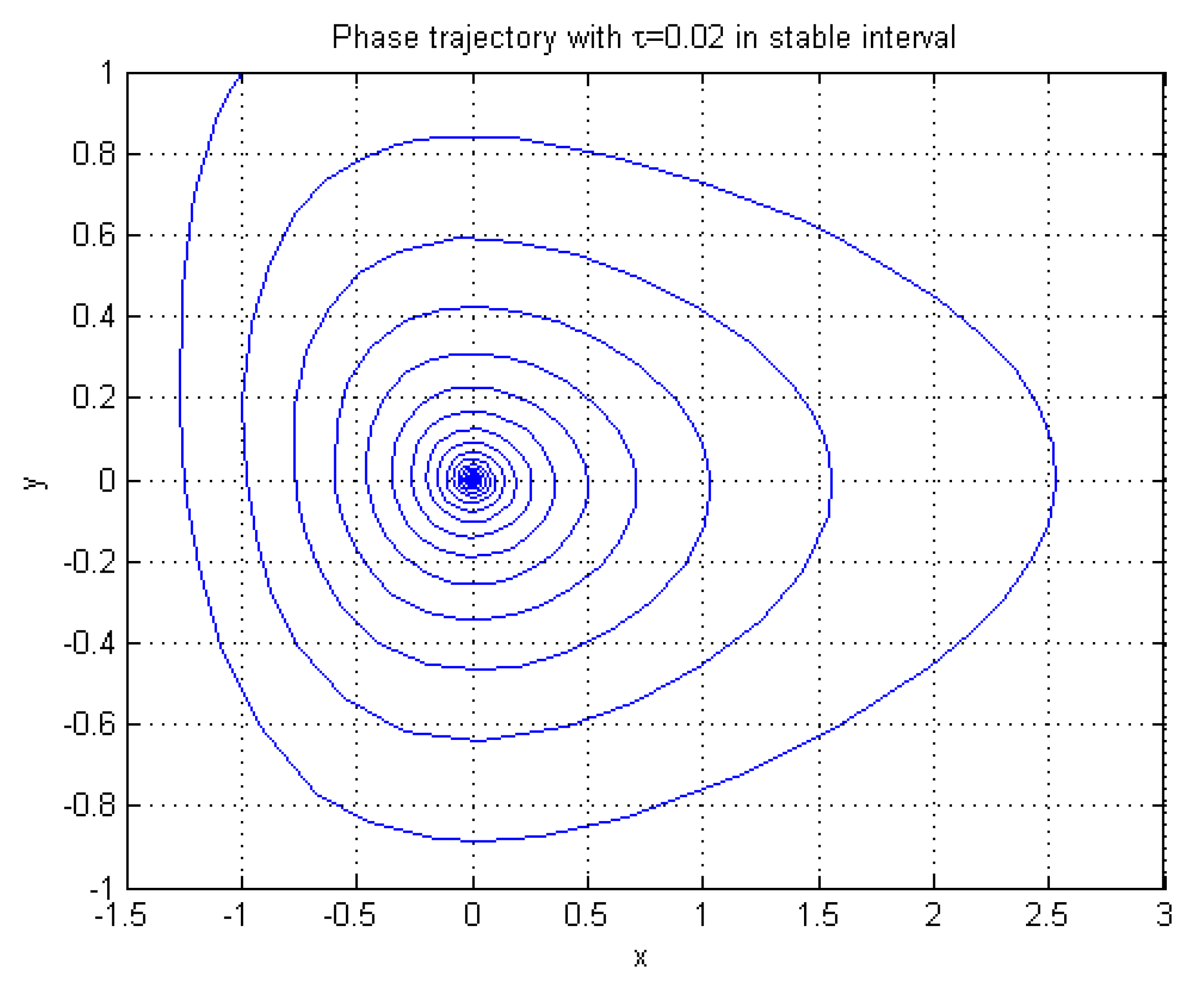
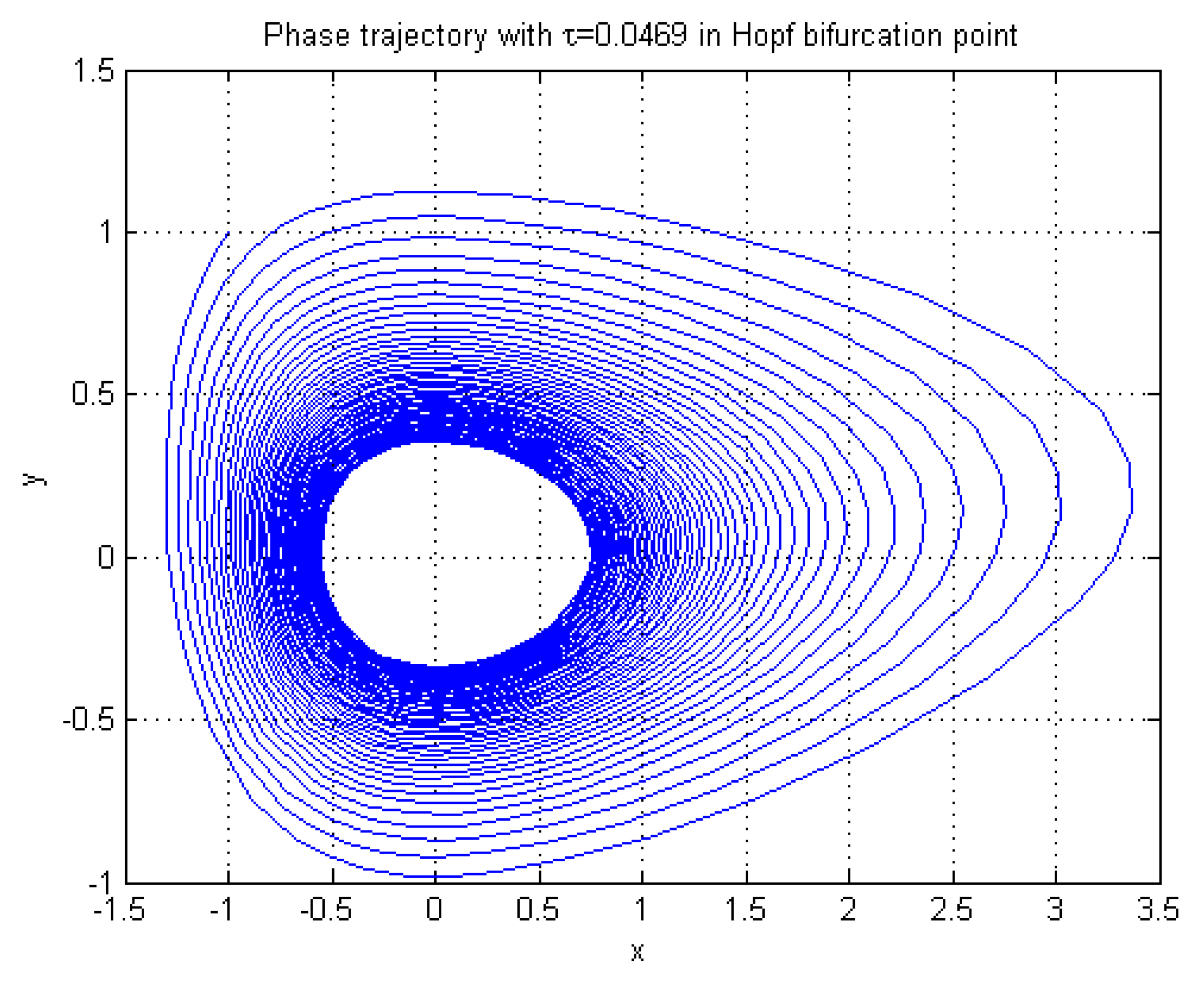
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Lemma 1
Appendix B. The Proof of Lemma 2
References
- Misra, V.; Gong, W.-B.; Towsley, D. Fluid based Analysis of a Network of AQM Routers Supporting TCP Flows with an Application to RED. In Proceedings of the Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication, Stockholm, Sweden, 28 August–1 September 2000. [Google Scholar]
- Hollot, C.V.; Chait, Y. Nonlinear stability analysis for a class of TCP/AQM networks. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No.01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 3, pp. 2309–2314. [Google Scholar]
- Hollot, C.V.; Misra, V.; Towsley, D.; Gong, W.B. Analysis and design of controllers for AQM routers supporting TCP flows. IEEE Trans. Autom. Control 2002, 47, 945–959. [Google Scholar] [CrossRef] [Green Version]
- Melchor Aguilar, D.; Niculescu, S.-I. Remarks on nonlinear stability analysis for a class of TCP/AQM networks. IFAC Proc. Vol. 2003, 36, 381–384. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Tian, Y.-P. Hopf bifurcation in REM algorithm with communication delay. Chaos Solitons Fractals 2005, 25, 1093–1105. [Google Scholar] [CrossRef]
- Michiels, W.; Niculescu, S.-I. Stability analysis of a fluid flow models for TCP like behaviour. J. Bifurc. Chaos 2005, 15, 2277–2282. [Google Scholar] [CrossRef]
- Guo, S.-T.; Liao, X.-F.; Li, C.-D. Stability and Hopf bifurcation analysis in a novel congestion control model with communication delay. Nonlinear Anal. Real World Appl. 2008, 9, 1292–1309. [Google Scholar] [CrossRef]
- Ding, D.W.; Zhu, J.; Luo, X.S. Hopf bifurcation analysis in a fluid flow model of Internet congestion control algorithm. Nonlinear Anal. Real World Appl. 2009, 10, 824–839. [Google Scholar] [CrossRef]
- Guo, S.-T.; Liao, X.-F.; Liu, Q.; Wu, H.-X. Linear stability and Hopf bifurcation analysis for exponential RED algorithm with heterogeneous delays. Nonlinear Anal. Real World Appl. 2009, 10, 2225–2245. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Wang, Z.H. Stability and Hopf bifurcation of a class of TCP/AQM networks. Nonlinear Anal. Real World Appl. 2010, 11, 1552–1559. [Google Scholar] [CrossRef]
- Liu, F.; Wang, H.-O.; Guan, Z.-H. Hopf bifurcation control in the XCP for the Internet congestion control system. Nonlinear Anal. Real World Appl. 2012, 13, 1466–1479. [Google Scholar] [CrossRef]
- Zhan, Z.-Q.; Zhu, J.; Li, W. Stability and bifurcation analysis in a FAST TCP model with feedback delay. Nonlinear Dyn. 2012, 70, 255–267. [Google Scholar] [CrossRef]
- Xu, Q.; Li, F.; Sun, J.-S.; Zukerman, M. A new TCP/AQM system analysis. J. Netw. Comput. Appl. 2015, 57, 43–60. [Google Scholar] [CrossRef] [Green Version]
- Khoshnevisan, L.; Liu, X.-Z.; Salmasi, F. Stability and Hopf bifurcation analysis of a TCP/RAQM network with ISMC procedure. Chaos Solitons Fractals 2019, 118, 255–273. [Google Scholar] [CrossRef]
- Raina, G.; Wischik, D. Buffer sizes for large multiplexers: TCP queuing theory and stability analysis. In Proceedings of the Next, Generation Internet Networks, Rome, Italy, 18–20 April 2005. [Google Scholar]
- Raina, G.; Manjunath, S.; Prasad, S.; Giridhar, K. Stability and performance analysis of compound TCP with REM and drop-tail queue management. IEEE/ACM Trans. Netw. 2016, 24, 1961–1974. [Google Scholar] [CrossRef]
- Nichols, K.; Jacobson, V.; McGregor, A.; Iyengar, J. Controlled delay active queue management. RFC 2018, 8298, 1–25. [Google Scholar]
- Lee, M.S.; Hsu, C.S. On the τ decomposition method of stability analysis for retarded dynamical systems. SIAM J. Control 1969, 7, 249–259. [Google Scholar] [CrossRef]
- Walton, K.; Marshall, J.E. Direct method for TDS stability analysis. IEEE Proc. D Control Theory Appl. 1987, 134, 101–107. [Google Scholar] [CrossRef]
- Cooke, K.; Driessche, P. On zeros of some transcendental equations. Funkc. Ekvacioj 1986, 29, 77–90. [Google Scholar]
- Hassard, B.D.; Kazarinoff, N.D.; Wan, Y.H. Theory and Applications of Hopf Bifurcation; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.-L.; Di, T.-L.; Yu, H.; Zhang, R.-R. On the τ Decomposition Method for the Stability and Bifurcation of the TCP/AQM Networks versus Time Delay. Symmetry 2022, 14, 463. https://doi.org/10.3390/sym14030463
Jin H-L, Di T-L, Yu H, Zhang R-R. On the τ Decomposition Method for the Stability and Bifurcation of the TCP/AQM Networks versus Time Delay. Symmetry. 2022; 14(3):463. https://doi.org/10.3390/sym14030463
Chicago/Turabian StyleJin, Hui-Long, Tian-Le Di, Hong Yu, and Ran-Ran Zhang. 2022. "On the τ Decomposition Method for the Stability and Bifurcation of the TCP/AQM Networks versus Time Delay" Symmetry 14, no. 3: 463. https://doi.org/10.3390/sym14030463




