Boolean-Based (k, n, m) Multi-Secret Image Sharing
Abstract
:1. Introduction
2. Review of Related Literature
2.1. Multiple Secret Images Sharing Scheme
- 1.
- Acquire the random image R with the secret images by Equation (1):
- 2.
- Shift the random image with different pixels to acquire a series of random images , as given in Equation (2):
- 3.
- Acquire shared images for participant i from Equation (3):
- 1.
- Collect all n shared images and perform XOR operation on all shared images, as defined by Equation (4):
- 2.
- Apply the result of Equation (4) to Equations (1) and (2) to obtain a series of random images .
- 3.
- Acquire the recovered secret images by applying and to Equation (5):
2.2. Boolean-Based (k, n) Secret Image Sharing Scheme
- Generate a series of n binary sharing matrices Mi(0 ≤ i ≤ n − 1) with size r × c, in which each matrix should satisfy the following two criteria:
- Gathering k sharing matrices leads to each entry containing at least a 1 among these sharing matrices.
- Gathering less than k sharing matrices leads to at least an entry without finding a 1 among these sharing matrices.
- Encrypt the secret image I to acquire a randomlike image R.
- For a sharing matrix Mi, each entry Mi(j,k)(0 ≤ j≤ r − 1,0 ≤ k ≤ c − 1) determines the corresponding shared image entry Si(j,k), as defined in Equation (6):
- Reconstruct the same series of n binary sharing matrices Mi(0 ≤ I ≤ n − 1) as applied in the sharing algorithm.
- Acquire the encrypted image R from and by applying Equation (7)
- 3.
- Decrypt the secret image from R to acquire the recovered secret image.
3. The Proposed Approach
3.1. Sharing Matrix Generation
- Each sharing matrix Pi has the same size with secret images.
- Each element in Pi are either 0 or 1.
- Selecting p matrices of Pi, for example, i = 1, 2, …, p, the following criteria should be satisfied.
- 3.1
- When p ≥ k, at least one matrix has the value of 1 in all entries among these p matrices.
- 3.2
- When p < k, at least one entry has the value of 0 in all p matrices.
- 1.
- Use Equation (8) to acquire an n × 1 binary vector M:
- 2.
- Acquire initial matrix N by permuting through M as Equation (9):
- 3.
- Extend one row vector of N, denoted by N(i,:), to acquire an extended matrix Ni with size r × t by using Equation (10):
- 4.
- Exchange rows of to acquire exchanged matrix :
- 5.
- Extend the matrix to fit the sizes of secret image for obtaining sharing matrix :
3.2. The Proposed (k, n, m) Source-Random-Mixed (SRM) Algorithm
- 1.
- Apply m secret images Ii (1 ≤ i ≤ m) to XOR operation for acquiring IXOR by Equation (13):
- 2.
- Generate a random image R by Equation (14):
- 3.
- Generate a series of randomlike images Ri (1 ≤ i ≤ m) from Equation (15):
- 4.
- A series of temporary images Ei (1 ≤ i ≤ m) are acquired from Ii and Ri by Equation (16):
- 5.
- Based on (k, n) thresholds, generate sharing matrix Pj (1 ≤ j ≤ n) from Equations (8)–(12).
- 6.
- Calculate initial shared images Sji by images Ei (1 ≤ i ≤ m) and Pj (1 ≤ j ≤ n), which is defined as:
- 7.
- Obtain shared images Sj (1 ≤ j ≤ n) by concatenating initial shared images Sji(1 ≤ I ≤ m), as shown in Equation (18):
- Collect k shared images and denote them by S1, S2, …, Sk.
- Separate all collected shared images Si(1 ≤ i ≤ k) to recovered shared images Sij(1 ≤ j ≤ m) with size r × c.
- Check all entries (k, l)(1 ≤ j ≤ k, 1 ≤ l ≤ c) among the images Sij(1 ≤ j ≤ k) to acquire the temporary image . For the entry (k, l) with one of the pixel , assign by the value of If all values in the entry (k, l) are 0, then assign by 0.
- Acquire the temporary image by Equation (19):
- 5.
- Apply to Equation (14) for acquiring the random image .
- 6.
- Apply to Equation (15) for acquiring randomlike images (1 ≤ i ≤ m).
- 7.
- Apply and to Equation (20) for obtaining recovered secret images :
3.3. The Proposed (k, n, m) Source-Random-Separate (SRS) Algorithm
- Apply m secret images Ii(1 ≤ i ≤ m) to XOR operation for acquiring IXOR by Equation (13).
- Generate a randomlike image Z with size r × c by the function image_synthesis(b,r,c) defined in Equation (14). The seed b is the same seed as used to generate the exchanged matrix in Equation (11).
- Apply the XOR operation between IXOR and Z to acquire the randomlike image by Equation (21):
- 4.
- Based on (k, n) thresholds, generate sharing matrix Pj(1 ≤ j ≤ n) by Equations (8)–(12).
- 5.
- Use Equation (22) to calculate images SRj(1 ≤ j ≤ n) by sharing matrix Pj.
- 6.
- Apply IXOR and Equation (14) to generate the random image R.
- 7.
- Generate a series of randomlike images Ri(1 ≤ i ≤ m) from the random image R by Equation (15).
- 8.
- Apply Ii and Ri by Equation (16) to obtain encrypted images Ei(1 ≤ i ≤ m).
- 9.
- Randomly select m columns from the initial matrix N in Equation (9) to acquire matrix Npart, i.e.,
- 10.
- Use Equation (24) to acquire share by the matrix value of Npart:
- 11.
- Concatenate SRj and (1 ≤ i ≤ m) to acquire shared images Sj, i.e.,

- Collect k shared images and denote them by Sj(1 ≤ j ≤ k).
- Extract each shared image with size r × c to acquire SRj(1 ≤ j ≤ k).
- Generate an initial matrix N and sharing matrix through Equations (8)–(12).
- Generate a randomlike image Z with size r × c by the function image_synthesis(b,r,c) defined in Equation (14), in which the seed b is the same seed as used to generate the exchanged matrix in sharing matrix generation step of Equation (11).
- Use Equation (26) to acquire :
- 6.
- Apply XOR operation between the and the randomlike image Z to acquire random image IXOR, i.e.,
- 7.
- Apply Equations (14) and (15) with IXOR to acquire h, R, and .
- 8.
- Apply the initial matrix N and coefficient h with Equation (23) to acquire the matrix Npart.
- 9.
- Split the remaining shared image in Step 2 to groups of r × c matrices and assign each r × c share to by Equation (28):
- 10.
- Replace by extracting the nonempty matrix to share . Moreover, two nonempty elements among r × c share should be identical.
- 11.
- Apply and to Equation (29) for covering the secret images , i.e.,
3.4. Examples of Sharing and Recovery of the Proposed SRS with Thresholds (2, 3, 2)
- Use Equation (8) to generate matrix by threshold k = 2, n = 3.
- Apply matrix to Equation (9) for acquiring matrix N, i.e.,
- 3.
- Acquire matrices N1, N2, and N3 by applying matrix N to Equation (10), i.e.,
- 4.
- Acquire exchanged matrix by applying matrices to Equation (11), i.e.,
- 5.
- Acquire sharing matrices P1, P2, and P3 by applying matrices to Equation (12):
- Apply secret images and to Equation (13) for obtaining .
- Generate randomlike image Z by Equation (14).
- Generate randomlike image by Equation (21).
- Generate the sharing matrices Pi(1 ≤ i ≤ 3) above by thresholds (2, 3, 2) with size 256 × 256 by Equations (8)–(12).
- Applying and to Equation (22) acquires .
- Apply and Equation (14) to generate the random image .
- Generate randomlike images and from the random image by Equation (15).
- Apply and by Equation (16) to obtain encrypted images , as shown in Figure 7c,d, respectively.
- Randomly select two columns of to acquire matrix .
- Apply and , to Equation (24) to generate , .
- Acquire shared images by , as shown in Figure 7e–g, respectively.
- Collect two shared images S1 and S2.
- Extract SR1, SR2 from S1, S2 with size of 256 × 256.
- Generate the initial matrix and sharing matrix P1, P2, P3 from Equations (8)–(12).
- Generate a randomlike image Z with size r × c by Equation (14).
- Use Equation (26) with P1, P2 and SR1, SR2 to recover .
- Use Equation (27) with SR0 and Z to acquire IXOR.
- Apply Equations (14) and (15) with IXOR to acquire R1 and R2.
- Acquire the matrix .
- Assign the remaining part of shared images S1 and S2 to E1 and E2, respectively.
- Apply Equation (29) with R1, R2 and E1, E2 to recover secret images I1, I2.
4. Experimental Results and Discussions
4.1. Experimental Results
4.2. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chanu, O.B.; Neelima, A. A survey paper on secret image sharing schemes. Int. J. Multimed. Inf. Retr. 2019, 8, 195–215. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Ulutas, M.; Ulutas, G.; Nabiyev, V.V. Invertible secret image sharing for gray level and dithered cover images. J. Syst. Softw. 2013, 86, 485–500. [Google Scholar] [CrossRef]
- Wu, X.; Ou, D.; Liang, Q.; Sun, W. A user-friendly secret image sharing scheme with reversible steganography based on cellular automata. J. Syst. Softw. 2012, 85, 1852–1863. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, L.; Ma, N.; Li, X. Two secret sharing schemes based on Boolean operations. Pattern Recognit. 2007, 40, 2776–2785. [Google Scholar] [CrossRef]
- Kabirirad, S.; Eslami, Z. Improvement of (n, n)-multi-secret image sharing schemes based on Boolean operations. J. Inf. Secur. Appl. 2019, 47, 16–27. [Google Scholar] [CrossRef]
- Dhara, B.C.; Chanda, B. A fast progressive image transmission scheme using block truncation coding by pattern fitting. J. Vis. Commun. Image Represent. 2012, 23, 313–322. [Google Scholar] [CrossRef]
- Fang, W.-P. Friendly progressive visual secret sharing. Pattern Recognit. 2008, 41, 1410–1414. [Google Scholar] [CrossRef]
- Huang, C.-P.; Hsieh, C.-H.; Huang, P.S. Progressive sharing for a secret image. J. Syst. Softw. 2009, 83, 517–527. [Google Scholar] [CrossRef]
- Lin, S.-J.; Lin, J.-C. VCPSS: A two-in-one two-decoding-options image sharing method combining visual cryptography (VC) and polynomial-style sharing (PSS) approaches. Pattern Recognit. 2007, 40, 3652–3666. [Google Scholar] [CrossRef]
- Chen, T.-H.; Wu, C.-S. Efficient multi-secret image sharing based on Boolean operations. Signal Process. 2011, 91, 90–97. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-J. A secure Boolean-based multi-secret image sharing scheme. J. Syst. Softw. 2014, 92, 107–114. [Google Scholar] [CrossRef]
- Wang, R.-Z.; Su, C.-H. Secret image sharing with smaller shadow images. Pattern Recognit. Lett. 2006, 27, 551–555. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.S.; Hsu, H.C.; Chen, H.W. New visual cryptography system based on circular shadow image and fixed angle segmentation. J. Electron. Imaging 2005, 14, 033018-1–033018-5. [Google Scholar] [CrossRef]
- Shyu, S.J.; Huang, S.-Y.; Lee, Y.-K.; Wang, R.-Z.; Chen, K. Sharing multiple secrets in visual cryptography. Pattern Recognit. 2007, 40, 3633–3651. [Google Scholar] [CrossRef]
- Lin, S.-J.; Chen, S.-K.; Lin, J.-C. Flip visual cryptography (FVC) with perfect security, conditionally-optimal contrast, and no expansion. J. Vis. Commun. Image Represent. 2010, 21, 900–916. [Google Scholar] [CrossRef]
- Wu, H.-C.; Chang, C.-C. Sharing visual multi-secrets using circle shares. Comput. Stand. Interfaces 2005, 28, 123–135. [Google Scholar] [CrossRef]
- Naor, M.; Shamir, A. Visual Cryptography. Proc. Int. Conf. Adv. Cryptol. 1995, 1–12. [Google Scholar]
- Bao, L.; Yi, S.; Zhou, Y. Combination of Sharing Matrix and Image Encryption for Lossless (k,n)-Secret Image Sharing. IEEE Trans. Image Process. 2017, 26, 5618–5631. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-J.; Chen, J.-L. Highly efficient and secure multi-secret image sharing scheme. Multimed. Tools Appl. 2016, 75, 7113–7128. [Google Scholar] [CrossRef]
- Prasetyo, H.; Jing, G.J. A note on multiple secret sharing using Chinese remainder theorem and exclusive-or. IEEE Access 2019, 7, 37473–37497. [Google Scholar] [CrossRef]
- Chattopadhyay, A.K.; Ghosh, D.; Maitra, P.; Nag, A.; Saha, H.N. A Verifiable (n, n) Secret Image Sharing Scheme Using XOR Operations. In Proceedings of the 2018 9th IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 8–10 November 2018; pp. 1025–1031. [Google Scholar]
- Kabirirad, S.; Eslami, Z. A(t,n)-multi secret image sharing scheme based on Boolean operations. J. Vis. Commun. Image Represent. 2018, 57, 39–47. [Google Scholar] [CrossRef]
- Bhattacharjee, T.; Maity, S.P.; Islam, S.R. Hierarchical secret image sharing scheme in compressed sensing. Signal Process. Image Commun. 2018, 61, 21–32. [Google Scholar] [CrossRef]
- Azza, A.A.; Lian, S. Multi-secret image sharing based on elementary cellular automata with steganography. Multimed. Tools Appl. 2020, 79, 21241–21264. [Google Scholar] [CrossRef]
- Chen, T.-H.; Wu, X.-W. Multiple secret image sharing with general access structure. Multimed. Tools Appl. 2020, 79, 13247–13265. [Google Scholar] [CrossRef]
- Yan, X.; Lu, Y.; Yang, C.-N.; Zhang, X.; Wang, S. A Common Method of Share Authentication in Image Secret Sharing. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2896–2908. [Google Scholar] [CrossRef]
- Jiang, Y.; Yan, X.; Qi, J.; Lu, Y.; Zhou, X. Secret image sharing with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities. Mathematics 2020, 8, 234. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, X.; Huang, Z.; Wang, L.; Xiang, Y. Multi-level multi-secret sharing scheme for decentralized e-voting in cloud computing. J. Parallel Distrib. Comput. 2019, 130, 91–97. [Google Scholar] [CrossRef]

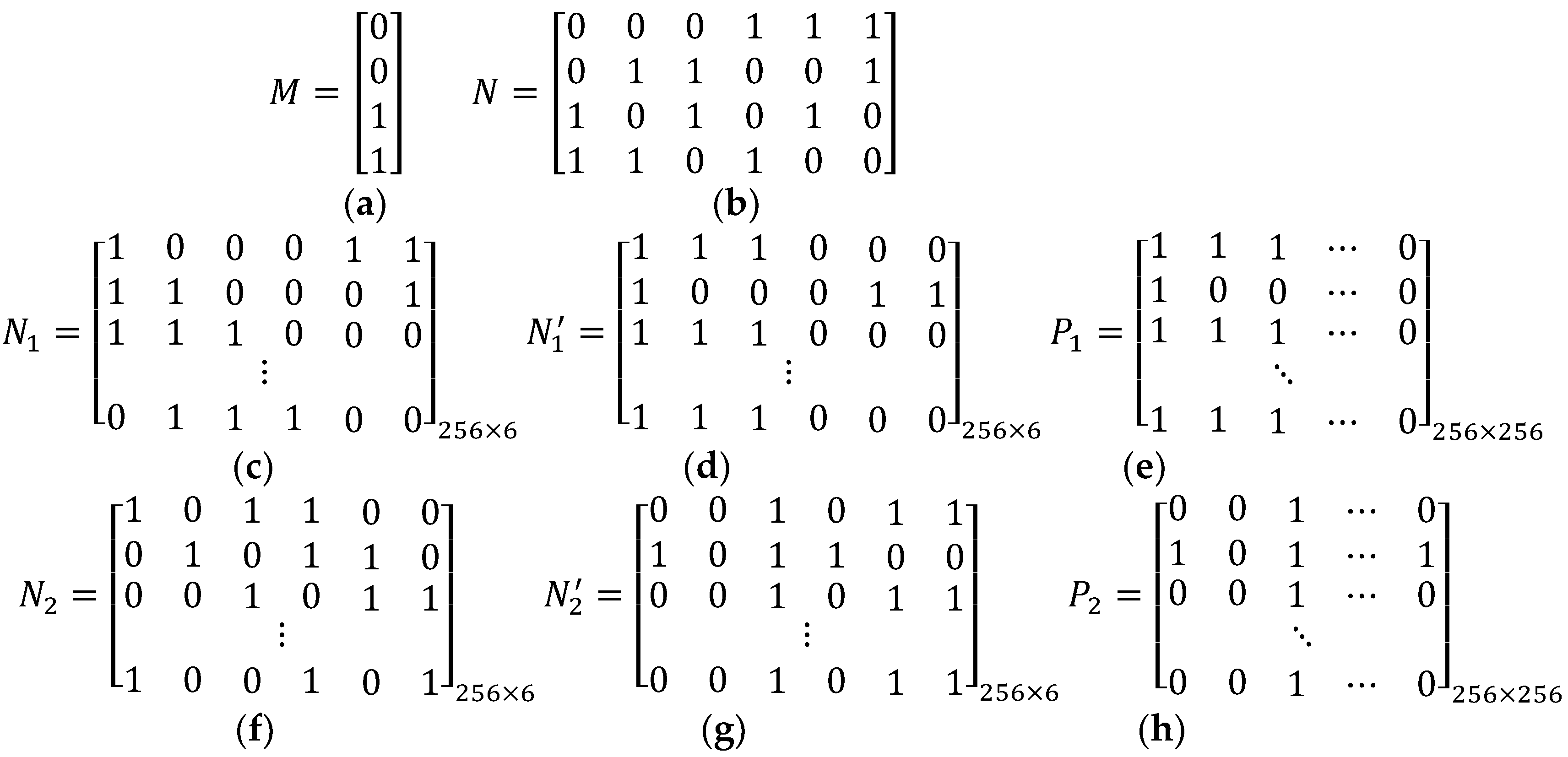








| Thresholds | Sharing Computation Time (s) | Recovery Computation Time (s) | ||
|---|---|---|---|---|
| (k, n, m) | SRM | SRS | SRM | SRS |
| (2, 3, 4) | 1.123222 | 0.377484 | 0.419478 | 0.333834 |
| (3, 4, 5) | 1.873811 | 0.521364 | 0.583452 | 0.415034 |
| (3, 5, 3) | 1.222763 | 0.539960 | 0.374655 | 0.332443 |
| Lossless Recovery | Recovery Strategy | Sharing Threshold | Multiple Sharing | Sharing Capacity | |
|---|---|---|---|---|---|
| Wu et al. [18] | No | Stacking | (2, 2) | No | |
| Chen et al. [15] | No | Stacking | (2, 2) | Yes | |
| Shyu et al. [16] | No | Stacking | (2, 2) | Yes | |
| Lin et al. [17] | No | Stacking | (2, 2) | Yes | |
| Wang et al. [6] | Yes | XOR | (n, n) | No | |
| Chen and Wu [12] | Yes | XOR | (n, n) | Yes | |
| Chen and Wu [13] | Yes | XOR | (n, n) | Yes | |
| Chen et al. [21] | Yes | XOR | (n, n) | Yes | |
| Bao et al. [20] | Yes | sharing matrix | (k, n) | No | |
| Prasetyo and Jing [22] | Yes | Chinese remainder theorem | (n, n) | Yes | |
| Chattopadhyay et. al. [23] | Yes | XOR | (n, n) | Yes | |
| Kabirirad and Eslami [24] | Yes | XOR | Consecutive (k, n) | Yes | |
| Our proposed SRM method | Yes | XOR with sharing matrix | (k, n) | Yes | |
| Our proposed SRS method | Yes | XOR with sharing matrix | (k, n) | Yes |
| Recovery Quality | (2, 2) Sharing Capacity | (2, 3) Sharing Capacity | (3, 3) Sharing Capacity | (3, 4) Sharing Capacity | |
|---|---|---|---|---|---|
| Wu et al. [18] | recognizable | ||||
| Chen et al. [15] | recognizable | ||||
| Shyu et al. [16] | recognizable | ||||
| Lin et al. [17] | recognizable | ||||
| Wang et al. [6] | 100% | ||||
| Chen and Wu [12] | 100% | ||||
| Chen and Wu [13] | 100% | ||||
| Chen et al. [21] | 100% | ||||
| Bao et al. [20] | 100% | ||||
| Our proposed SRM method | 100% | ||||
| Our proposed SRS method | 100% | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-C.; Lin, C.-S.; Chen, J.-Z. Boolean-Based (k, n, m) Multi-Secret Image Sharing. Axioms 2022, 11, 197. https://doi.org/10.3390/axioms11050197
Chen C-C, Lin C-S, Chen J-Z. Boolean-Based (k, n, m) Multi-Secret Image Sharing. Axioms. 2022; 11(5):197. https://doi.org/10.3390/axioms11050197
Chicago/Turabian StyleChen, Chien-Chang, Cheng-Shian Lin, and Jia-Zhan Chen. 2022. "Boolean-Based (k, n, m) Multi-Secret Image Sharing" Axioms 11, no. 5: 197. https://doi.org/10.3390/axioms11050197
APA StyleChen, C. -C., Lin, C. -S., & Chen, J. -Z. (2022). Boolean-Based (k, n, m) Multi-Secret Image Sharing. Axioms, 11(5), 197. https://doi.org/10.3390/axioms11050197





