Hydraulic Losses in Systems of Conduits with Flow from Laminar to Fully Turbulent: A New Symbolic Regression Formulation
Abstract
:1. Introduction
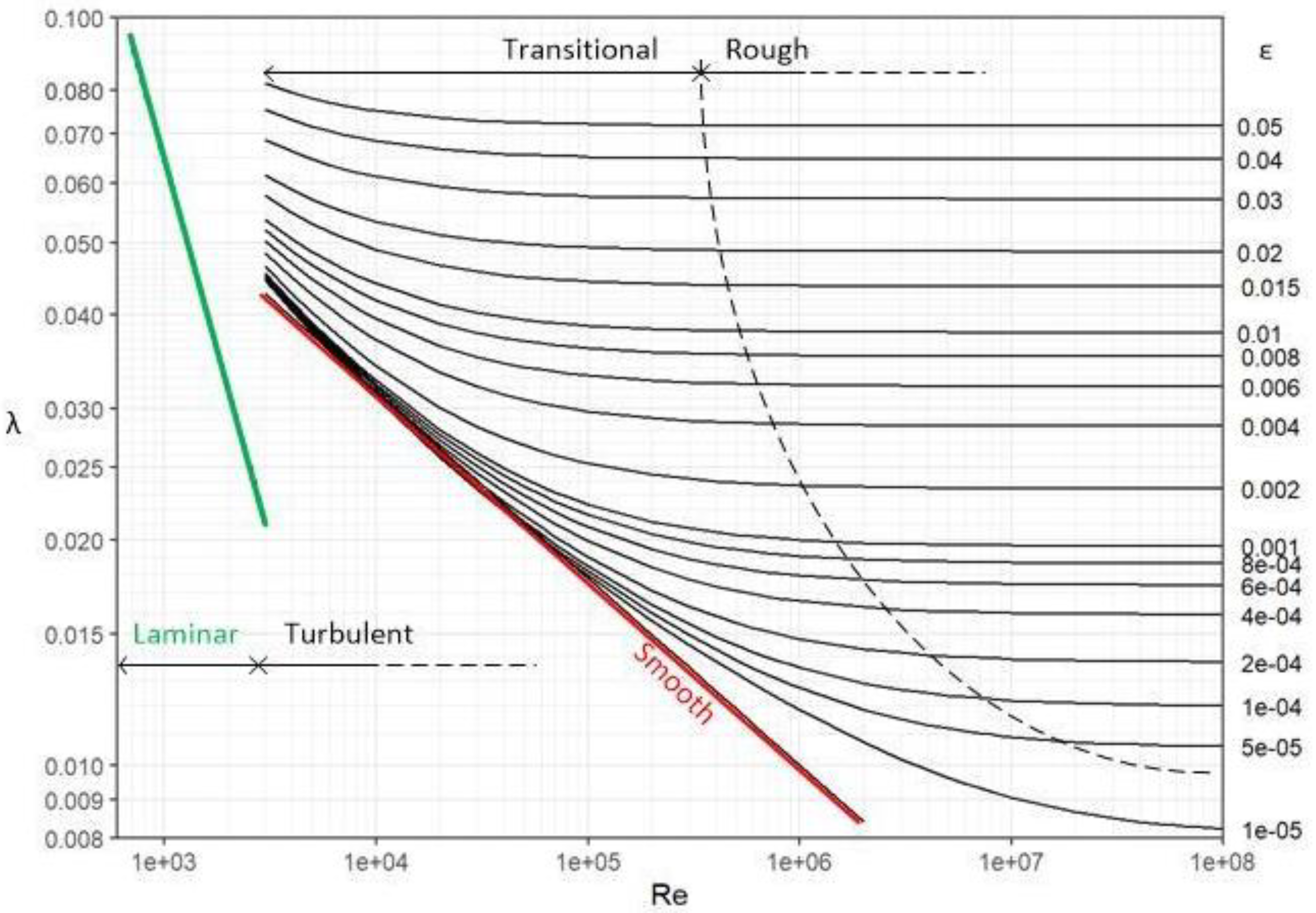
2. Hydraulic Friction
2.1. Physical Interpretation
- -
- is pressure loss in Pa;
- -
- is the length of pipe in m;
- -
- is non-dimensional Darcy’s flow friction;
- -
- is density of the fluid in kg/m3;
- -
- is flow in m3/s;
- -
- is the hydraulic diameter of the pipe in m; and
- -
- is Ludolph number; ≈ 3.1415.
- For laminar flow using theoretically founded Hagen–Poiseuille formulation as given in Equation (2):
- For turbulent flow, many empirical formulations are available, but among the most used is given by Colebrook in 1939 [11] in Equation (3), which is empirically based on an experiment with the flow of air through pipes with different inner roughness performed by Colebrook and White in 1937 [12] (while examples of other empirical equations can follow Nikuradse’s inflectional shape of curves which modify monotonic behaviour of Colebrook’s curves [13,14] or can be based on some newer experiments [15,16,17]):
- -
- is a natural logarithm;
- -
- is non-dimensional Darcy’s flow friction;
- -
- is the non-dimensional Reynolds number ( is the flow velocity of the fluid in m/s, is the hydraulic diameter of the pipe in m, and is kinematic viscosity in m2/s), and
- -
- is the non-dimensional relative roughness of the inner pipe surface (if the real absolute roughness of the pipe is , then ).
- -
- is a non-dimensional parameter that is used for determining the specific type of turbulent flow (in the case of turbulent regime, smooth turbulent flow occurs for < 16, transitional or partial turbulent flow for 16 < < 200, while fully developed rough turbulent flow occurs for > 200);
- -
- is the non-dimensional roughness of the inner pipe surface (it has no effect on laminar and smooth turbulent flow, partial effect on transitional turbulent flow, and significant effect on fully developed rough turbulent flow);
- -
- is the non-dimensional Reynolds number (the flow for < 2320 is surely laminar);
- -
- is the non-dimensional Darcy’s hydraulic flow friction factor.
2.2. Background and Related Works
- The interpolation method which is based on probability is used in [42] to develop a unified model;
- Two unified equations for flow from laminar to turbulent ape developed using symbolic regression, and they are new in this Communication.
3. Unified Equations for Laminar and Turbulent Darcy’s Flow Friction
3.1. Six Parameter Model
3.2. Unified Model Based on the Turbulent Transitional Formula
3.3. Submarine Model
3.4. Russian Formula for Transport of Crude Oil
3.5. Interpolation Method
3.6. Churchill Equation
3.7. Multisegmented Equation
3.8. Symbolic Regression-Based Unified Equation
- Quasi Monte Carlo sampling [51,52] of Equation (5) from Section 3.1 of this Communication was constructed to obtain a table of triplets with n = 65,535 combinations of the Reynolds number , the relative roughness of inner pipe surface and Darcy’s flow friction according to Praks and Brkić [53]; then,
- constants of Equation (12) were optimized in Matlab using the derivative-free method “fminsearch” [54] to minimize the absolute value of the relative error of the approximation.
4. Graphical Interpretation and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Altowayti, W.A.H.; Othman, N.; Tajarudin, H.A.; Al-Dhaqm, A.; Asharuddin, S.M.; Al-Gheethi, A.; Alshalif, A.F.; Salem, A.A.; Din, M.F.M.; Fitriani, N.; et al. Evaluating the Pressure and Loss Behavior in Water Pipes Using Smart Mathematical Modelling. Water 2021, 13, 3500. [Google Scholar] [CrossRef]
- Kraszewska, A.; Donizak, J. An Analysis of a Laminar-Turbulent Transition and Thermal Plumes Behavior in a Paramagnetic Fluid Subjected to an External Magnetic Field. Energies 2021, 14, 7972. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Air-Forced Flow in Proton Exchange Membrane Fuel Cells: Calculation of Fan-Induced Friction in Open-Cathode Conduits with Virtual Roughness. Processes 2020, 8, 686. [Google Scholar] [CrossRef]
- Billard, L.; Diday, E. Symbolic Regression Analysis. In Classification, Clustering, and Data Analysis. Studies in Classification, Data Analysis, and Knowledge Organization; Jajuga, K., Sokołowski, A., Bock, H.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Swamee, P.K. Design of a submarine oil pipeline. J. Transp. Eng. 1993, 119, 159–170. [Google Scholar] [CrossRef]
- Submarine Pipeline Systems. Offshore Standard DNV-OS-F101 by Det Norske Veritas AS, Edition 2021–08-Amended 2021–12. Available online: https://www.dnv.com/oilgas/download/dnv-st-f101-submarine-pipeline-systems.html (accessed on 21 February 2022).
- Hapanowicz, J. Two-Phase Liquid–Liquid Flow in the Aspect of Reduction of Pumping Power of Hydrophobic Substances with High Viscosity. Energies 2021, 14, 2432. [Google Scholar] [CrossRef]
- Ferro, V.; Nicosia, A. Evaluating the Effects of Sediment Transport on Pipe Flow Resistance. Water 2021, 13, 2091. [Google Scholar] [CrossRef]
- Brown, G.O. Environmental and Water Resources History Sessions. In Proceedings of the ASCE Civil Engineering Conference and Exposition 2002, Washington, DC, USA, 3–7 November 2002; pp. 34–43. [Google Scholar] [CrossRef] [Green Version]
- Brown, G.O. Henry Darcy and the making of a law. Water Resour. Res. 2002, 38, 11. [Google Scholar] [CrossRef] [Green Version]
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C.M. Experiments with fluid friction in roughened pipes. Proc. R. Soc. London. Ser. A-Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Nikuradse, J. Laws of Flow in Rough Pipes (Strömungsgesetze in Rauhen Rohren). Available online: https://ntrs.nasa.gov/citations/19930093938 (accessed on 21 February 2022).
- Thakkar, M.; Busse, A.; Sandham, N.D. Direct numerical simulation of turbulent channel flow over a surrogate for Nikuradse-type roughness. J. Fluid Mech. 2018, 837, R1. [Google Scholar] [CrossRef] [Green Version]
- McKeon, B.J.; Swanson, C.J.; Zagarola, M.V.; Donnelly, R.J.; Smits, A.J. Friction factors for smooth pipe flow. J. Fluid Mech. 2004, 511, 41–44. [Google Scholar] [CrossRef] [Green Version]
- Eck, B.J. Use of a smoothed model for pipe friction loss. J. Hydraul. Eng. 2017, 143, 06016022. [Google Scholar] [CrossRef] [Green Version]
- Basse, N.T. Turbulence Intensity and the Friction Factor for Smooth- and Rough-Wall Pipe Flow. Fluids 2017, 2, 30. [Google Scholar] [CrossRef] [Green Version]
- Rocha, H.S.D.; Marques, P.A.; Camargo, A.P.D.; Frizzone, J.A.; Saretta, E. Internal surface roughness of plastic pipes for irrigation. Rev. Bras. Eng. Agríc. Ambient. 2017, 21, 143–149. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, J.G.; Peiter, M.X.; Robaina, A.D.; Bruning, J.; Neto, M.C.; Ferreira, L.D. Simplified Scobey formula for determining head loss in pressurized pipes. Rev. Bras. Agric. Irrig. RBAI 2022, 16, 31–41. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S. Surface Roughness Modeling Using Q-Sequence. Math. Comput. Appl. 2017, 22, 33. [Google Scholar] [CrossRef] [Green Version]
- Santos-Ruiz, I.; López-Estrada, F.-R.; Puig, V.; Valencia-Palomo, G. Simultaneous Optimal Estimation of Roughness and Minor Loss Coefficients in a Pipeline. Math. Comput. Appl. 2020, 25, 56. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef] [Green Version]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- LaViolette, M. On the history, science, and technology included in the Moody diagram. J. Fluids Eng. 2017, 139, 030801. [Google Scholar] [CrossRef]
- Madeira, A.A. Major and minor head losses in a hydraulic flow circuit: Experimental measurements and a Moody’s diagram application. Eclética Quím. 2020, 45, 47–56. [Google Scholar] [CrossRef]
- McGovern, J. Friction Factor Diagrams for Pipe Flow. 2011. Available online: https://arrow.dit.ie/engschmecart/28/ (accessed on 21 February 2022).
- Abdolahi, F.; Mesbah, A.; Boozarjomehry, R.B.; Svrcek, W.Y. The effect of major parameters on simulation results of gas pipelines. Int. J. Mech. Sci. 2007, 49, 989–1000. [Google Scholar] [CrossRef]
- Díaz-Damacillo, L.; Plascencia, G. A new six parameter model to estimate the friction factor. AIChE J. 2019, 65, 1144–1148. [Google Scholar] [CrossRef]
- Plascencia, G.; Díaz–Damacillo, L.; Robles-Agudo, M. On the estimation of the friction factor: A review of recent approaches. SN Appl. Sci. 2020, 2, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Avci, A.; Karagoz, I. A new explicit friction factor formula for laminar, transition and turbulent flows in smooth and rough pipes. Eur. J. Mech. B Fluids 2019, 78, 182–187. [Google Scholar] [CrossRef]
- Avci, A.; Karagoz, I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng. 2009, 131, 061203. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Review of new flow friction equations: Constructing Colebrook explicit correlations accurately. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2020, 36, 41. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function. Mathematics 2019, 7, 34. [Google Scholar] [CrossRef] [Green Version]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef] [Green Version]
- Brkić, D.; Stajić, Z. Excel VBA-based user defined functions for highly precise Colebrook’s pipe flow friction approximations: A Comparative overview. Facta Univ. Ser. Mech. Eng. 2021, 19, 7267. [Google Scholar] [CrossRef]
- Zeyu, Z.; Junrui, C.; Zhanbin, L.; Zengguang, X.; Peng, L. Approximations of the Darcy–Weisbach friction factor in a vertical pipe with full flow regime. Water Supply 2020, 20, 1321–1333. [Google Scholar] [CrossRef]
- Naseri, A.; Nikazar, M.; Dehghani, S.M. A correlation approach for prediction of crude oil viscosities. J. Pet. Sci. Eng. 2005, 47, 163–174. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Economics and statistical evaluations of using Microsoft Excel solver in pipe network analysis”. J. Pipeline Syst. Eng. Pract. 2018, 9, 07018002. [Google Scholar] [CrossRef] [Green Version]
- Swamee, P.K.; Jain, A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div. 1976, 102, 657–664. [Google Scholar] [CrossRef]
- Чepникин, B.A.; Чepникин, A.B. Oбoбщeннaя φopмyлa для pacчeтa кoэφφициeнтa гидpaвличecкoгo coпpoтивлeния мaгиcтpaльныx тpyбoпpoвoдoв для cвeтлыx нeφтeпpoдyктoв и мaлoвязкиx нeφтeй. Hayкa И Тexнoлoгии Тpyбoпpoвoднoгo Тpaнcпopтa Нeφти И Нeφтeпpoдyктoв 2012, 4, 64–66. Available online: http://transenergostroy.ru/publications/src/20130424/Chernikin_gidrav_soprotivlenie.pdf (accessed on 22 February 2022). (In Russian).
- Aльтшyль, A.Д. Гидpaвличecкиe Coпpoтивлeния; Heдpa: Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Cheng, N.S. Formulas for friction factor in transitional regimes. J. Hydraul. Eng. 2008, 134, 1357–1362. [Google Scholar] [CrossRef]
- Churchill, S.W. Friction-factor equation spans all fluid-flow regimes. Chem. Eng. 1977, 84, 91–92. [Google Scholar]
- Churchill, S.W. Empirical expressions for the shear stress in turbulent flow in commercial pipe. AIChE J. 1973, 19, 375–376. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Unified friction formulation from laminar to fully rough turbulent flow. Appl. Sci. 2018, 8, 2036. [Google Scholar] [CrossRef] [Green Version]
- Uršič, M.; Kompare, B. Improvement of the hydraulic friction losses equations for flow under pressure in circular pipes. Acta Hydrotech. 2003, 21, 57–74. Available online: https://actahydrotechnica.fgg.uni-lj.si/en/paper/a34mu (accessed on 22 February 2022).
- Praks, P.; Brkić, D. Symbolic regression-based genetic approximations of the Colebrook equation for flow friction. Water 2018, 10, 1175. [Google Scholar] [CrossRef] [Green Version]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evol. Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef] [Green Version]
- Stoutemyer, D.R. Can the Eureqa symbolic regression program, computer algebra and numerical analysis help each other. Not. AMS 2003, 60, 713–724. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Rational approximation for solving an implicitly given Colebrook flow friction equation. Mathematics 2020, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Askar, T.; Shukirgaliyev, B.; Lukac, M.; Abdikamalov, E. Evaluation of Pseudo-Random Number Generation on GPU Cards. Computation 2021, 9, 142. [Google Scholar] [CrossRef]
- Cordero, A.; Martí, P.; Victoria, M. Optimización de topología robusta de estructuras continuas usando el método de Monte Carlo y modelos Kriging (Robust topology optimization of continuum structures using Monte Carlo method and Kriging models). Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2018, 34, 5. (In Spanish) [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Approximate flow friction factor: Estimation of the accuracy using Sobol’s quasi-random sampling. Axioms 2022, 11, 36. [Google Scholar] [CrossRef]
- Liu, H.; Huang, J.; Guan, Y.; Sun, L. Accelerated Degradation Model of Nonlinear Wiener Process Based on Fixed Time Index. Mathematics 2019, 7, 416. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, V.; Prakash, A.; Rawat, A. To Predict Frictional Pressure-Drop of Turbulent Flow of Water Through a Uniform Cross-Section Pipe Using an Artificial Neural Network. In Recent Advances in Applied Mechanics; Springer: Singapore, 2022; pp. 397–412. [Google Scholar] [CrossRef]
- Brownlie, W.R. Re-examination of Nikuradse roughness data. J. Hydraul. Div. 1981, 107, 115–119. [Google Scholar] [CrossRef]
- Beattie, D.R.H. In Defence of Nikuradse. In Proceedings of the Twelfth Australasian Fluid Mechanics Conference, The University of Sydney, Sydney, Australia, 10–15 December 1995; Available online: https://people.eng.unimelb.edu.au/imarusic/proceedings/12/Beattie.pdf (accessed on 22 February 2022).
- Hager, W.H.; Liiv, U. Johann Nikuradse–hydraulic experimenter. J. Hydraul. Res. 2008, 46, 435–444. [Google Scholar] [CrossRef]
- Yang, B.H.; Joseph, D.D. Virtual Nikuradse. J. Turbul. 2009, 10, N11. [Google Scholar] [CrossRef]
- Joseph, D.D.; Yang, B.H. Friction factor correlations for laminar, transition and turbulent flow in smooth pipes. Phys. D Nonlinear Phenom. 2010, 239, 1318–1328. [Google Scholar] [CrossRef] [Green Version]
- Choe, Y.-W.; Sim, S.-B.; Choo, Y.-M. New equation for predicting pipe friction coefficients using the statistical based entropy concepts. Entropy 2021, 23, 611. [Google Scholar] [CrossRef]
- Qiu, M.; Ostfeld, A. A head formulation for the steady-state analysis of water distribution systems using an explicit and exact expression of the Colebrook–White equation. Water 2021, 13, 1163. [Google Scholar] [CrossRef]
- Österlund, J.M.; Johansson, A.V.; Nagib, H.M.; Hites, M.H. A note on the overlap region in turbulent boundary layers. Phys. Fluids 2000, 12, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Perry, A.E.; Hafez, S.; Chong, M.S. A possible reinterpretation of the Princeton superpipe data. J. Fluid Mech. 2001, 439, 395–401. [Google Scholar] [CrossRef]
- Muzzo, L.E.; Matoba, G.K.; Ribeiro, L.F. Uncertainty of pipe flow friction factor equations. Mech. Res. Commun. 2021, 116, 103764. [Google Scholar] [CrossRef]
- Zmrhal, V.; Boháč, J. Pressure loss of flexible ventilation ducts for residential ventilation: Absolute roughness and compression effect. J. Build. Eng. 2021, 44, 103320. [Google Scholar] [CrossRef]
- Pimenta, B.D.; Robaina, A.D.; Peiter, M.X.; da Rocha, H.S.; Sobenko, L.R.; da Conceição, C.G. Use of bench and portable rugosimeters in evaluatingthe internal roughness of PVC pipes of different diameters. Rev. Bras. Ciências Agrárias 2022, 17, 1–7. [Google Scholar] [CrossRef]
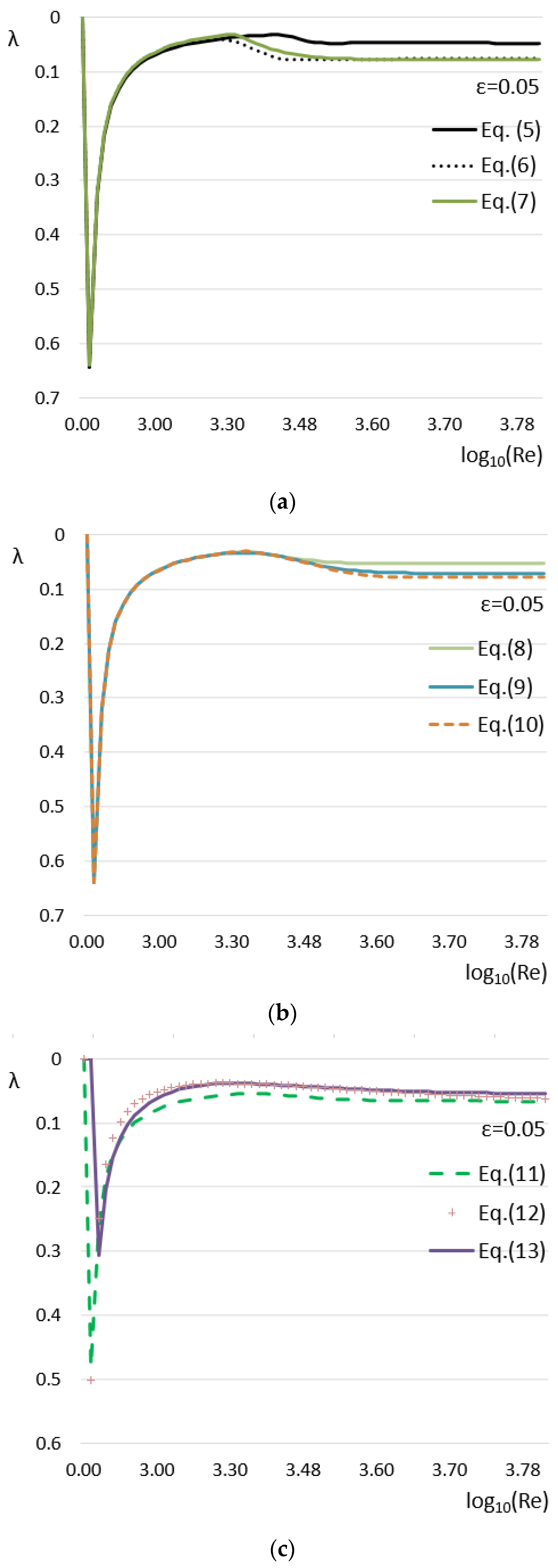
| Formulation | Type | Flexible 3 |
|---|---|---|
| Equation (5) | Inflectional | Partially |
| Equation (6) | Monotonic | Yes |
| Equation (7) | Monotonic | Yes |
| Equation (8) | Monotonic | No |
| Equation (9) | Inflectional | Partially |
| Equation (10) | Monotonic | Partially |
| Equation (11) | Inflectional | Yes |
| Equation (12) | Inflectional | No |
| Equation (13) | Inflectional | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milošević, M.; Brkić, D.; Praks, P.; Litričin, D.; Stajić, Z. Hydraulic Losses in Systems of Conduits with Flow from Laminar to Fully Turbulent: A New Symbolic Regression Formulation. Axioms 2022, 11, 198. https://doi.org/10.3390/axioms11050198
Milošević M, Brkić D, Praks P, Litričin D, Stajić Z. Hydraulic Losses in Systems of Conduits with Flow from Laminar to Fully Turbulent: A New Symbolic Regression Formulation. Axioms. 2022; 11(5):198. https://doi.org/10.3390/axioms11050198
Chicago/Turabian StyleMilošević, Marko, Dejan Brkić, Pavel Praks, Dragan Litričin, and Zoran Stajić. 2022. "Hydraulic Losses in Systems of Conduits with Flow from Laminar to Fully Turbulent: A New Symbolic Regression Formulation" Axioms 11, no. 5: 198. https://doi.org/10.3390/axioms11050198
APA StyleMilošević, M., Brkić, D., Praks, P., Litričin, D., & Stajić, Z. (2022). Hydraulic Losses in Systems of Conduits with Flow from Laminar to Fully Turbulent: A New Symbolic Regression Formulation. Axioms, 11(5), 198. https://doi.org/10.3390/axioms11050198








