A Local Density-Based Abnormal Case Removal Method for Industrial Operational Optimization under the CBR Framework

Abstract

Operational optimization is essential in modern industry and unsuitable operations will deteriorate the performance of industrial processes. Since measuring error and multiple working conditions are inevitable in practice, it is necessary to reduce their negative impacts on operational optimization under the case-based reasoning (CBR) framework. In this paper, a local density-based abnormal case removal method is proposed to remove the abnormal cases in a case retrieval step, so as to prevent performance deterioration in industrial operational optimization. More specifically, the reasons as to why classic CBR would retrieve abnormal cases are analyzed from the perspective of case retrieval in industry. Then, a local density-based abnormal case removal algorithm is designed based on the Local Outlier Factor (LOF), and properly integrated into the traditional case retrieval step. Finally, the effectiveness and the superiority of the local density-based abnormal case removal method was tested by a numerical simulation and an industrial case study of the cut-made process of cigarette production. The results show that the proposed method improved the operational optimization performance of an industrial cut-made process by 23.5% compared with classic CBR, and by 13.3% compared with case-based fuzzy reasoning.

1. Introduction

Frequent changes in operating conditions require the operating settings to change accordingly and appropriately, and unsuitable settings will bring about performance deterioration and disqualified products [1]. Therefore, operational optimization plays an essential role in industrial production since it ensures process safety and enhances economic benefit [2,3,4]. Generally, there are two kinds of operational optimization methods: model-based methods and data-based methods. In particular, the model-based methods firstly build a process model with some basic operational laws, such as material conservation and energy conservation, and then construct a constrained optimization problem with the pre-established process model [5,6]. On this basis, global optimal solutions are obtained with some optimization algorithms, such as sequential quadratic programming (SQP) [7], the genetic algorithm (GA) [8], and particle swarm optimization (PSO) [9]. Although model-based methods have been successfully applied to many fields, their shortages are inevitable when the industrial process is extremely complex. In fact, it is difficult to build an accurate model if the process is featured by a large scale, long procedure, and changeable environments [10]. Moreover, it is challenging to select an appropriate optimization algorithm to balance the efficiency and the accuracy of a certain operational optimization problems [11].

In response to the drawbacks of model-based methods, data-based methods–which are free from prior knowledge on process mechanisms [12]–have attracted much attention in both the academic and industrial community [13]. For example, Wang et al. designed an adaptive moving window convolutional neural network to extract useful information from the process time-series data, based on which the optimal decision is made according to the expected operational indices [14]. Ding et al. integrated the reinforcement learning strategy with Case-Based Reasoning (CBR) so that the optimal operational indices for a large mineral processing plant can be easily found [15]. Overall, data-based methods benefit from various kinds of sensors installed in modern industry, and they can make optimal decisions using plentiful historical data and operational experience.

Among the data-based methods, CBR does not rely on any process mechanism knowledge, so it is suitable for operational optimization problems where it is difficult to establish accurate process models. In detail, CBR solves the operational optimization problem by referring to previous operating experience, and it has been successfully applied to many processes. For example, Li et al. developed a principal component regression-based case reuse method under the CBR framework [16]. To be specific, the developed method could learn valuable experience from historical production data and finally obtain the global optimal operating settings for a coking flue gas denitration process. Ding et al. integrated a multi-objective evolutionary algorithm into the classic CBR, and the modified CBR was then employed to optimize some operating indexes of the largest hematite ore processing plant in western China [17]. Basically, since CBR could work out the optimal operating settings for certain conditions with some successful cases (also named historical optimal cases or case base), requirements of safety and stability are automatically satisfied for the acquired settings [18]. This is another advantage of CBR when it is employed to solve operational optimization problems in industry.

Conventionally, CBR includes the following steps: (1) Case retrieval; (2) Case reuse; (3) Case revision; and (4) Case retention [19]. Among them, case retrieval is one of the most important steps and its task is to retrieve the most useful cases from the pre-established case base to solve the target problem [20,21]. Currently, the majority of case retrieval is based on similarity [22], which is typically measured by various kinds of distances, such as the Euclidean distance, the Mahalanobis distance, the cosine angle distance, etc. [23]. However, similarity fails to consider the significance among different dimensions. Therefore, reference [24] employs the weighted Mahalanobis distance to measure the similarity, and reference [25] designed a new similarity measurement that combined the Euclidean distance and the cosine angle distance. To improve the accuracy of case retrieval facing nonlinearity, Li et al. introduced a new similarity index that can transfer traditional distance-based similarity into their corresponding Gaussian forms by Gaussian transformation [26]. In terms of industrial operational optimization, the Euclidean distance or the weighted Euclidean distance is adopted to calculate the similarity between two cases in most previous studies. Usually, the weights are allocated based on experience, and the allocation requires prior knowledge about the studied process. Moreover, the accuracy of case retrieval would be decreased if the process data include measuring error. Therefore, Zhang et al. utilized fuzzy logic to select the most suitable cases from a case base, and then obtained the global optimal solution for the target problem in an oil refinery [18].

Although plenty of works have improved the accuracy of case retrieval, it is still difficult to guarantee the quality of retrieved cases when applied to complex industrial processes when only using distance-based similarity. Firstly, measuring error is unavoidable in historical data [27], so it is hard to build the case base accurately. Secondly, industrial processes often run in many working conditions [28], so it is difficult to ensure the distance-based case retrieval would only retrieve cases from the same working conditions as the target problem. In this paper, these wrongly retrieved cases are named as abnormal cases because they are not helpful for the target problem. Furthermore, applying the operational settings of abnormal cases to the target problem is hazardous and may result in performance deterioration and disqualified products, or even stall the production of subsequent processes. Therefore, a local density-based abnormal case removal method is proposed in this paper to remove the abnormal cases in the case retrieval step, and finally to improve the performance of CBR for industrial operational optimization. The main contributions of this paper are summarized as follows:

(1)

The reason why historical cases in low-density areas should not be included in the case reuse step is analyzed from the perspective of safety and reliability requirements in industrial operational optimization problems.

(2)

A novel abnormal case removal method, which could effectively remove the abnormal cases before case reuse, is proposed on the basis of the Local Outlier Factor (LOF), and properly integrated into the case retrieval step.

(3)

The effectiveness and superiority of the newly proposed local density-based abnormal case removal method is verified by a numerical optimization case study and an industrial operational optimization case study.

The rest of this paper is organized as follows. Some preliminaries of the CBR framework and the distance-based similarity measurements are briefly reviewed in Section 2, then the motivations, principles, and procedures of the local density-based abnormal case removal method are systematically presented in Section 3. Section 4 exhibits the operational optimization results of a numerical case study and an industrial case study. Finally, conclusions are given in Section 5.

2. Preliminaries

In this section, some basic knowledge on the CBR framework and the distance-based similarity measurements is introduced. Unlike the model-based methods, CBR solves the target problem with several related cases stored in the case base. To be specific, the case base should be constructed with as many historical cases as possible. Each case consists of a problem description and a case solution. Figure 1 gives the basic framework of CBR (also known as the CBR cycle).

It could be seen from Figure 1 that case retrieval is the first step of the CBR cycle. The task of case retrieval is to retrieve several valuable cases from the constructed case base. Supposing the number of retrieved cases is fixed as $k$, the retrieved cases are the first $k$ cases with the most similar problem descriptions to the target problem. After the case retrieval step, the case reuse is performed to obtain a suggested solution according to the retrieved cases. If the suggested solution is not applicable to the target problem, the suggested solution needs revising to adapt to the target problem. In the last step, the experience of solving this target problem is stored to update the case base, which enable CBR to constantly learn during the CBR cycle.

In general, CBR solves the target problem by learning from historical cases with similar problem descriptions to the target problem. Therefore, case retrieval is the foundation of CBR, and the retrieval accuracy directly affects the performance of CBR [29,30,31]. In previous studies, most case retrievals are based on distance-based similarity.

Table 1. The most commonly used distances for similarity measurement in CBR.

Name	Formula
Euclidean Distance	$D(X_1,X_2)=\sqrt{(X_1-X_2){(X_1-X_2)}^T}$
Mahalanobis Distance	$D(X_1,X_2)=\sqrt{{(X_1-X_2)}^T{\sum }^{-1}(X_1-X_2)}$
Cosine angle Distance	$D(X_1,X_2)=\frac{X_1{X}_2{}^T}{\Vert X_1\Vert \Vert X_2\Vert }$
Manhattan Distance	$D(X_1,X_2)={\displaystyle \sum _{i=1}^N\left|X_{1,i}-X_{2,i}\right|}$
Chebyshev Distance	$D(X_1,X_2)=\max \left(\left|X_{1,i}-X_{2,i}\right|\right),i=1,\cdots ,N$

lists five most commonly used distances for similarity measurement in CBR.

As shown in Table 1, several distances can be applied to measure the similarity between two cases. Under the CBR framework, great attention has been paid to measure the similarity between the target problem and historical problems in the case base. However, due to the complexity of industrial processes, it is still hard to choose an appropriate similarity index that only retrieves valuable cases when facing gross measuring error and multiple working conditions. Therefore, it is necessary to develop an abnormal case removal method so as to obtain the most valuable cases in industrial operational optimization.

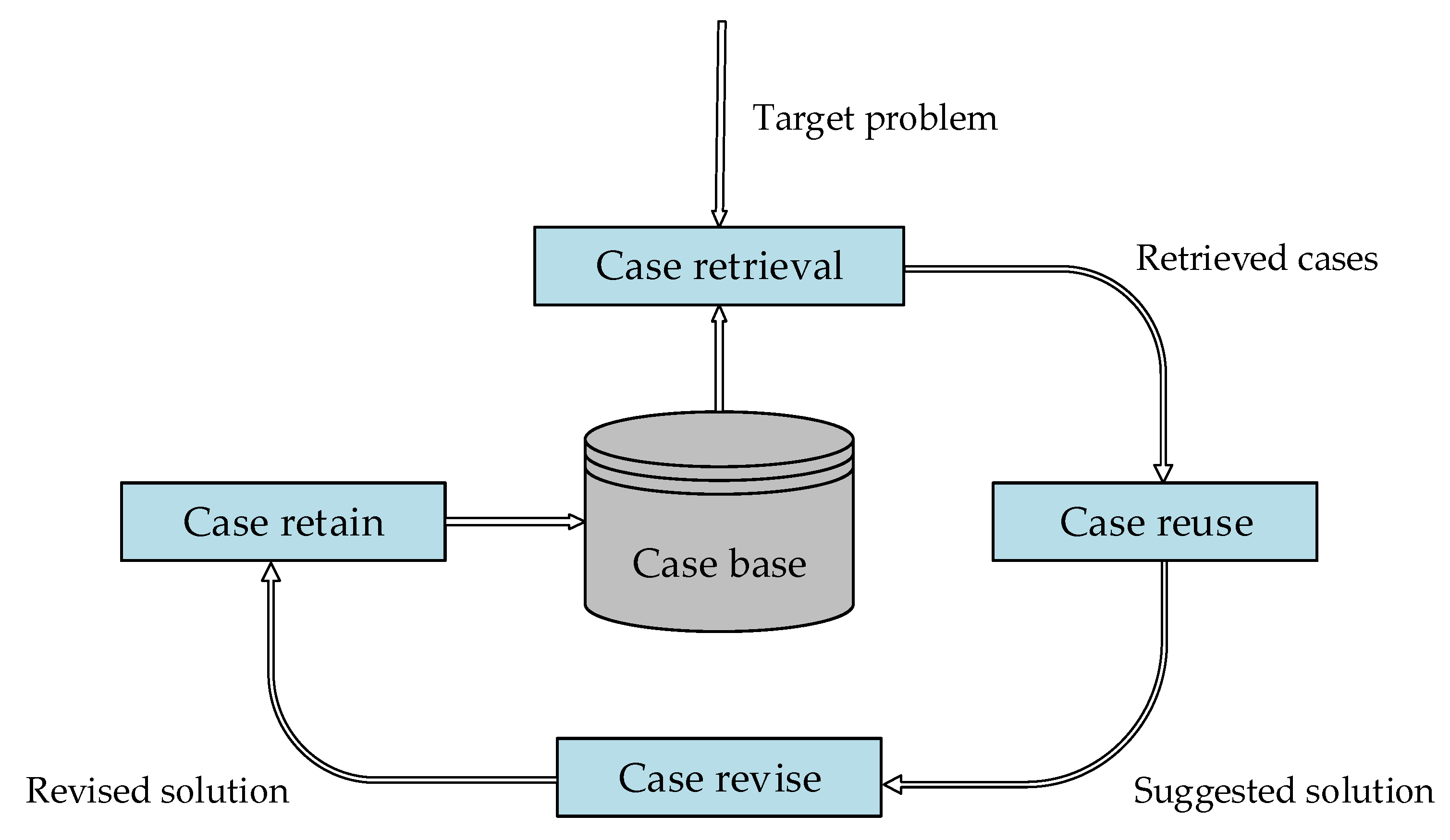
3. Methods

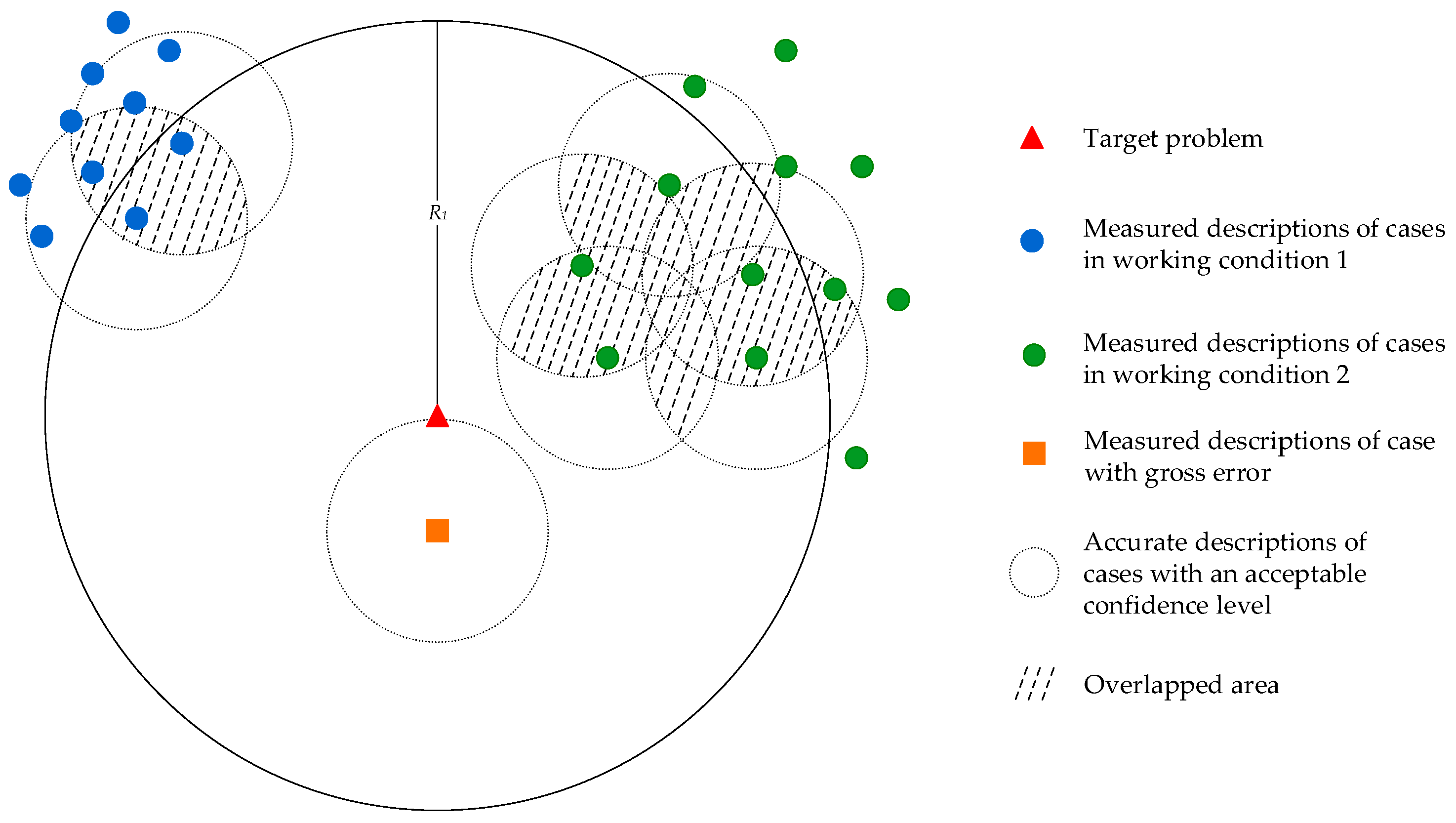
3.1. Analysis of Case Retrieval in Industrial Operational Optimization

To improve product quality and enhance economic benefits, operational optimization has been widely implemented in industrial processes. CBR can find the optimal operational settings by learning from the historical optimal operational settings in the case base, so it has been widely studied in the industrial operational optimization community. Suppose that there are $k$ cases overall retrieved from the case base, and $X_i\left(i=1,2,\cdots ,k\right)$ and $Y_i\left(i=1,2,\cdots ,k\right)$ represent the problem descriptions and the optimal solutions of the $i\mathrm{th}$ retrieved case, respectfully. Under the CBR framework, the suggested solution ${\tilde{Y}}_{\mathrm{t}}$ of the target problem $X_t$ can be determined as follows:

$${\tilde{Y}}_t=\frac{{\displaystyle \sum _{i=1}^{k}S(X_i,X_t)Y_i}}{{\displaystyle \sum _{i=1}^{k}S(X_i,X_t)}}$$

(1)

where $S(X_i,X_t)$ represents the similarity between the target problem $X_t$ and the problem description of the $i\mathrm{th}$ historical case $X_i$. In fact, the suggested solution ${\tilde{Y}}_{\mathrm{t}}$ is a weighted sum of historical optimal solutions. Concretely, $k$ historical cases are selected by the case retrieval step according to their similarity to the target problem. Moreover, Equation (1) shows that the weight of the suggested solution is only determined by the similarity between the target problem and the problem description of the selected historical case. In other words, the case retrieval step not only provides some helpful candidates for the suggested solution, but also determines their weights in the suggested solution. Hence, the accuracy of case retrieval is vital to the performance of industrial operational optimization.

Since CBR assumes that similar problem descriptions always have similar case solutions [32], most of the previous studies tend to discover the most similar cases to the target problem. Although the classic case retrieval methods have been proved effective in many fields, the accuracy of case retrieval is still inevitably affected by measuring error and by multiple working conditions. As a result, not all retrieved cases are helpful for solving the target problem. The concrete reasons are as follows.

(a)

Accuracy of case retrieval would be influenced by the measuring error

Industrial data are collected by various kinds of sensors installed in the factory. Since perturbations and noises are inevitable in industrial processes, measuring error is naturally introduced in the case base. Consequently, the descriptions of historical cases are not accurate. For the $i\mathrm{th}$ case, its measured description ${\widehat{X}}_i$ can be represented as follows:

$${\widehat{X}}_i=X_i+W_i$$

(2)

where $X_{\mathrm{i}}$ and $W_{\mathrm{i}}$ are the accurate description and the measuring error of the $i\mathrm{th}$ case, respectively. Considering the measuring error in its corresponding measured description, the true Euclidean distance between $X_i$ and $X_t$ are calculated as follows:

$$D\left(X_i,X_t\right)=\sqrt{\left(\left({\widehat{X}}_i-W_i\right)-\left({\widehat{X}}_t-W_t\right)\right){\left(\left({\widehat{X}}_i-W_i\right)-\left({\widehat{X}}_t-W_t\right)\right)}^T}$$

(3)

Then the similarity between $X_i$ and $X_t$ can be calculated as follows:

$$S\left(X_i,X_t\right)=\frac{1}{1+D\left(X_i,X_t\right)}$$

(4)

Obviously, the measuring error in industrial data would degrade the accuracy of case retrieval and make it hard to evaluate the importance of historical cases in solving the target problem. Therefore, it is necessary to eliminate negative impacts from historical cases that have gross measuring error.

(b)

Accuracy of case retrieval would be influenced by the multiple working conditions

Industrial processes always run in many working conditions, which leads to some undesirable results if the number of retrieved cases is not appropriate. That is to say, not only the similarity $S(X_i,X_t)$ but also the number $k$ have an impact on the accuracy of case retrieval. Therefore, an appropriate parameter $k$ is crucial for the success of industrial operational optimization under the CBR framework. However, for a particular process, there are different numbers of historical cases in different working conditions, suggesting that the case base is imbalanced. There are a larger number of cases in common working conditions and a smaller number of cases in uncommon working conditions. Therefore, it is easy to retrieve enough cases from a common working condition, yet difficult to do the same from an uncommon working condition. Since the parameter $k$ is fixed as a constant in classic CBR, it may perform well for some working conditions but perform poorly for others. The reason why classic CBR has a different performance in different working conditions is that some irrelevant cases from other working conditions may be retrieved if the target problem belongs to uncommon working conditions. Thus, the suggested solution may be inapplicable.

In summary, both the measuring error and the multiple working conditions would decrease the accuracy of case retrieval, which is going to affect the performance of operational optimization under the CBR framework. To decrease the negative impact from these abnormal cases, a local density-based abnormal case removal method for the case retrieval step is proposed in the following subsection.

3.2. Local Density-Based Abnormal Case Removal

Most of the previous studies on case retrieval have only focused on similarity measurement, while the distribution of retrieved cases was neglected. The goal of case retrieval is, in essence, to search the case base for valuable cases in order to solve the target problem. In Section 3.1, the reasons as to why abnormal cases commonly exist in industry are thoroughly analyzed. Consequently, the retrieval results may not be reliable and the accuracy of case retrieval needs enhancing. In contrast to the model-based methods, CBR directly uses the operational information in retrieved cases, so the accuracy of retrieved cases is vital to the performance of CBR. In another words, abnormal cases are harmful for the industrial operational optimization, so they must be removed before the case reuse. In this paper, it is believed that the distribution of retrieved cases can reflect their reliability. By eliminating low-reliability cases, the quality of the retrieved cases can be significantly enhanced. Figure 2 presents a demonstration of the relationship between the distribution and the reliability of cases.

As shown in Figure 2, the retrieved cases are not uniformly distributed in the whole space. Moreover, the accurate descriptions of historical cases are uncertain due to the existence of measuring error. In this paper, the measuring error is assumed to follow the Gaussian distribution. With a certain confidence level, accurate descriptions of historical cases lie in dashed circles centered in their corresponding measured descriptions. Since the similarity is usually calculated according to the measured descriptions, cases with the highest similarity are not necessarily the most helpful cases for the target problem. However, there exist some overlaps in the area with high-density cases, showing cases in the high-density area have higher reliability than other cases since the accurate descriptions are more likely to lie in the overlaps. Therefore, although cases in the low-density area may have a higher similarity to the target problem, they should not proceed to the case reuse step due to their lower reliability.

Another issue that impacts the accuracy of case retrieval is the multiple working conditions of industrial processes. For a target problem that lies on the edge of a working condition, its nearest neighbors probably include cases from other working conditions. Obviously, these cases will not help to solve the target problem and should not be included in the retrieved cases. This issue can be partly solved by assigning different number of retrieved cases to every working condition, but it requires identifying the working conditions in advance and setting a different $k$ parameter for every working condition. Consequently, it demands more priori knowledge and becomes much more complicated. Considering the working condition identification problem can be transformed into a classic classification problem, the K-Nearest Neighbors (KNN) classifier believes that the target problem belongs to the working condition that the majority of its nearest neighbors belongs to. That is to say, the number of retrieved cases from other working conditions is less than the number of retrieved cases from the working condition that the target problem belongs to. Since all retrieved cases belong to the same neighborhood, cases from other working conditions are more likely to be in the low-density area, so they can be identified by calculating the density of retrieved cases.

To conclude, measuring error and multiple working conditions are two inevitable problems affecting the accuracy of case retrieval and degrading the performance of CBR. Therefore, developing an abnormal case removal method is urgent and necessary. Since cases in a high-density area are more reliable than those in a low-density area, the latter should be removed from the retrieved cases. In this subsection, a local density-based abnormal case removal algorithm is designed based on the Local Outlier Factor (LOF), which is a common index showing how isolated a data point is comparing with its nearest data points. The LOF of historical case $X_i$ is defined as follows:

$$LOF(X_i)=\frac{1}{m}{\displaystyle \sum _{q=1}^m\frac{lrd(X_q)}{lrd(X_i)}}$$

(5)

where $m$ is an adjustable parameter; $lrd(X_q)$ and $lrd(X_i)$ stand for the local reachability density of case $X_q$ and $X_i$, respectively; $X_q$ is the $q\mathrm{th}$ similar cases in the retrieved cases. Particularly, the $lrd(X_i)$ can be represented as follows:

$$lrd(X_i)={\left(\frac{1}{m}{\displaystyle \sum _{q=1}^{m}D(X_i,X_q)}\right)}^{-1}$$

(6)

where $D(X_i,X_q)$ is the Euclidean distance between $X_q$ and $X_i$.

As shown in Equation (5), LOF reflects the average ratio of $lrd(X_q)$ to $lrd(X_i)$. Therefore, a bigger LOF indicates a smaller local density, and the corresponding case should be removed. Normally, the threshold of LOF is determined after the whole dataset has been analyzed, while in this paper, the threshold of LOF can be adaptively adjusted. To automatically eliminate the retrieved cases in a low-density area, the threshold of the local density-based abnormal case removal algorithm is designed as follows:

$$\xi =\mu +\alpha \sqrt{\frac{{\displaystyle {\sum }_{i=1}^k{\left(X(i)-\mu \right)}^2}}{k-1}}$$

(7)

where $\alpha$ is an adjustable parameter of the threshold $\xi$, and $\mu$ is the average LOF of the retrieved cases, which can be calculated as follows:

$$\mu =\frac{1}{k}{\displaystyle \sum _{i=1}^{k}LOF(X_i)}$$

(8)

In this paper, $k$ is optimized according to the mean absolute error of the training set; $m$ and $\alpha$ are optimized determined by orthogonal experiments. With the optimal parameter $k$, $m$, $\alpha$, pseudo-codes of the designed local density-based abnormal case removal algorithm are shown in Algorithm 1.

Algorithm 1: Local density-based abnormal case removal

Input: $k$ retrieved cases; optimal parameter $m$, $\alpha$

Output: The retrieved cases without abnormal cases

1 Calculate the local density of every retrieved case according to Equation (6)

2 Calculate the LOF of every retrieved case according to Equation (5)

3 Calculate the threshold of the retrieved cases according to Equations (7) and (8)

4 Remove the cases whose LOF are higher than the threshold

With the aforementioned local density-based abnormal case removal algorithm, procedures of the industrial operational optimization are as follows:

Step 1:

construct the case base with history data;

Step 2:

for a target problem, select $k$ most similar cases from the case base and construct the original retrieved cases $C_i=\left\{X_i,Y_i\right\}\left(i=1,\cdots ,k\right)$;

Step 3:

employ the local density-based abnormal case removal algorithm to remove wrongly retrieved cases;

Step 4:

acquire the suggested solution for the target problem according to Equation (1);

Step 5:

revise the suggested solution, if necessary;

Step 6:

store it in the case base after the target problem is solved.

4. Case Studies

In this section, the effectiveness and the superiority of the designed local density-based abnormal case removal method were validated by two case studies. Firstly, a numerical simulation was designed, where case descriptions were featured with multiple working conditions and measurement error. Then, an industrial case study, whose data were collected from a cut-made process of cigarette production, was designed to show the effectiveness and the superiority of the abnormal case removal method in industrial operation optimization under the CBR framework. In these case studies, the proposed method was compared with classic CBR and case-based fuzzy reasoning in which the fuzzy membership function and its parameters were determined according to their ability to resist measuring error [18]. The concrete hardware and software are as follows: Intel(R) Core (TM) i5-4590, ROM 8 GB, Windows 10 professional.

4.1. Numerical Simulation

In this numerical simulation, 120 operating points were generated with MATLAB 2019A to simulate the characteristics of multiple working conditions and measurement error of industrial data. Particularly, two working conditions were generated with different centers and deviations (the deviations followed Gaussian distribution to simulate the measurement error in industry). In detail, every working condition consisted of 60 operating points, and the centers of working condition 1 and working condition 2 were set as (1, 1) and (−1, −1), respectively. In addition, standard deviations of the two working conditions were both set as 0.5. It should be noted that the operating points with larger deviation from their corresponding centers were considered as operating points with gross error, and they should be removed before the case reuse. Figure 3 shows the distribution of the generated dataset, which can perfectly reflect the characteristics of industrial data.

As shown in Figure 3, the operating points lying on the edge of working condition 1 and working condition 2 were considered as operating points with gross error in this study. Moreover, the case solutions of working condition 1 and working condition 2 were designed as Equations (9) and (10), respectively.

$$Y_1(i)=0.2{\left(x_1(i)-1\right)}^2+0.3{\left(x_2(i)-1\right)}^2+\left(x_1(i)-1\right)+4$$

(9)

$$Y_2(i)=-0.2{\left(x_1(i)+1\right)}^2+0.5\left(x_2(i)+1\right)-4$$

(10)

Their parameters were designed differently to reflect diverse operating experience in different working conditions. Furthermore, Equations (9)–(12) were designed as quadratic polynomials to represent the nonlinearity in the operating experience. For operating points with gross error, their measured descriptions were heavily deviated from their accurate descriptions. Consequently, their case solutions are less helpful for operational optimization than those of normal cases. For this reason, the case solutions of working condition 1 and working condition 2 with gross error were designed as Equations (11) and (12), respectively.

$$Y_{1\mathrm{e}}(i)=0.2{\left(x_1(i)-1\right)}^2+0.3{\left(x_2(i)-1\right)}^2+\left(x_1(i)-1\right)+8$$

(11)

$$Y_{2e}(i)=-0.2{\left(x_1(i)+1\right)}^2+0.5\left(x_2(i)+1\right)-8$$

(12)

In this numerical simulation, 60 operating points were randomly chosen from the generated dataset as a case base, while the rest of 60 operating points were equally divided into two datasets. To be specific, the first was used as training dataset to pick out the optimal parameters including $k$, $m$, and $\alpha$, and the last was chosen as a testing dataset to evaluate the performance of the designed abnormal case removal method with the selected optimal parameters. The concrete evaluation criterion was Mean Absolute Error (MAE).

$$MAE=\frac{{\displaystyle \sum _{i=1}^n\left|Y_i-Y_{i,suggested}\right|}}{n}$$

(13)

where $n$ is the number of cases in the testing dataset. $Y_i$ and $Y_{i,suggested}$ are the optimal solution and the suggested solution of the $i\mathrm{th}$ cases, respectively.

Since $k$ is a crucial parameter for case retrieval and its value directly affects the performance of CBR, sensitivity analysis was firstly carried out to find the best parameter $k$. Figure 4 presents the MAE of the training dataset when $k$ changed from 1 to 15.

As shown in Figure 4, the tendency of MAE firstly decreases with $k$ changing from 1 to 6, and then generally increases with $k$ changing from 6 to 15. The minimal MAE was 0.1896 when the parameter $k$ was chosen as 6. Therefore, the number of retrieved cases was set as 6 both in classic CBR and the improved CBR with the proposed abnormal case removal method. In addition, in order to find out the best parameters $m$ and $\alpha$ for the abnormal case removal algorithm, orthogonal experiments were designed with the training dataset. In particular, the parameter $m$ was set from 1 to 5 while the parameter $\alpha$ was set from 0.2 to 2.2.

Table 2. MAE of the training dataset with different parameter combination. Bold shows the optimal number.

MAE	$\mathit{m}=1$	$\mathit{m}=2$	$\mathit{m}=3$	$\mathit{m}=4$	$\mathit{m}=5$
$\alpha =0.2$	0.1858	0.2378	0.1937	0.1984	0.2070
$\alpha =0.4$	0.1872	0.2380	0.1622	0.2001	0.1948
$\alpha =0.6$	0.1870	0.2078	0.1651	0.1675	0.1526
$\alpha =0.8$	0.1742	0.1967	0.1671	0.1475	0.1521
$\alpha =1.0$	0.1741	0.1930	0.1956	0.1457	0.1470
$\alpha =1.2$	0.1647	0.2032	0.1950	0.1458	0.1478
$\alpha =1.4$	0.1935	0.2016	0.1882	0.1541	0.1478
$\alpha =1.6$	0.1930	0.2018	0.1873	0.1893	0.1602
$\alpha =1.8$	0.1859	0.1840	0.1840	0.1877	0.1877
$\alpha =2.0$	0.1797	0.1896	0.1896	0.1896	0.1896
$\alpha =2.2$	0.1896	0.1896	0.1896	0.1896	0.1896

shows the MAE of the training dataset with different combination of parameter $m$ and parameter $\alpha$.

As shown in Table 2, the minimal MAE of the training dataset was 0.1457 when the parameter $m$ and $\alpha$ were set as 4 and 1, respectively. The reason as to why $m$ and $\alpha$ could influence the MAE of the training dataset were analyzed as follows:

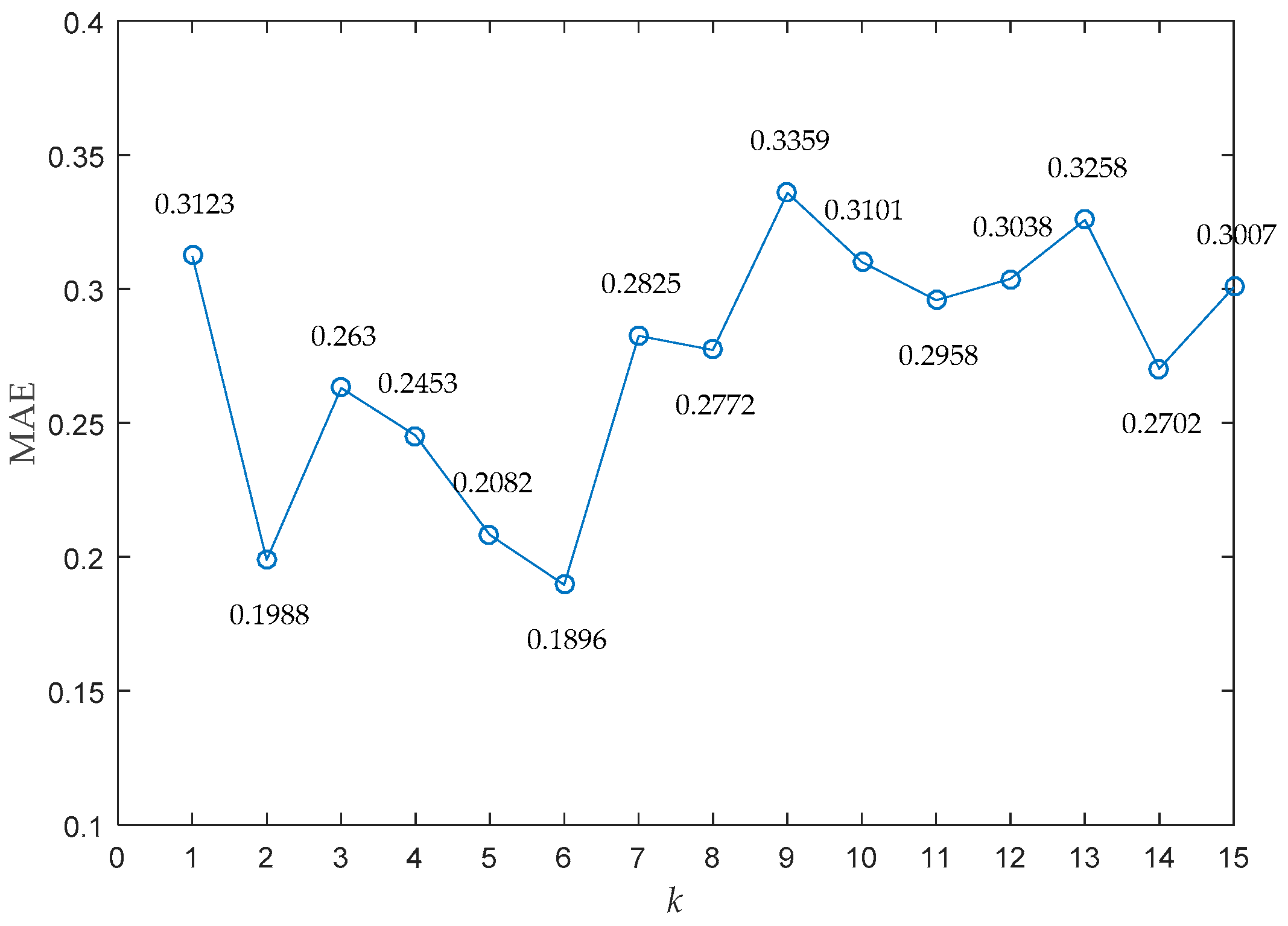
(1)

Supposing the parameter $m$ was fixed as a constant, if the selected parameter $\alpha$ was too small, it would result in a lower threshold $\xi$ and more normal cases would be removed by mistake in the retrieved cases. This would increase the MAE.

(2)

Supposing the parameter $m$ was fixed as a constant, if the selected parameter $\alpha$ was too big, it would result in a larger threshold $\xi$ and more abnormal cases would be preserved in the retrieved cases. This would increase the MAE.

(3)

Supposing the parameter $\alpha$ was fixed as a constant, if the selected parameter $m$ was too small, fewer nearest neighbors would be included in the calculation of LOF. This would make the LOF more vulnerable to uncertainty so as to increase the MAE.

(4)

Supposing the parameter $\alpha$ was fixed as a constant, if the selected parameter $m$ was too big, more nearest neighbors would be included in the calculation of LOF. This would reduce the distinguish ability of LOF so as to increase the MAE.

In the end, the best parameters of the designed abnormal case removal algorithm were set as $k=6$, $m=4$ and $\alpha =1$, respectively. With the aforementioned parameter combination, the testing dataset was finally used to show the effectiveness and the superiority of our method. Additionally, Cauchy fuzzy membership function was selected for the case-based fuzzy reasoning and its optimal parameters were 0.725 and 0.837, based on its performance against measuring error. The concrete fuzzy membership functions evaluation method and parameters optimization method can be found in reference [18]. Figure 5 presents the concrete results.

According to Figure 5, it can be found that the set values of our method are closer to their corresponding optimal set values than that of the other two methods. Specifically, there are overall five operating points (marked with red boxes) in which our method outperformed the classic CBR and case-based fuzzy reasoning. As an average, the abnormal case removal method improved the setting accuracy in the testing dataset by 20.3% compared with classic CBR, and by 8.5% compared with case-based fuzzy reasoning. The reason why our method can obtain better results is that some abnormal cases retrieved by the classic case retrieval step could be removed with Equations (5) and (7). By eliminating these abnormal cases whose LOFs are higher than the threshold, the impacts of these cases can be removed in the case reuse step, thus improving the quality of the retrieved cases. Naturally, the MAE of the testing dataset would be decreased, and the performance of operational optimization would be improved under the CBR framework.

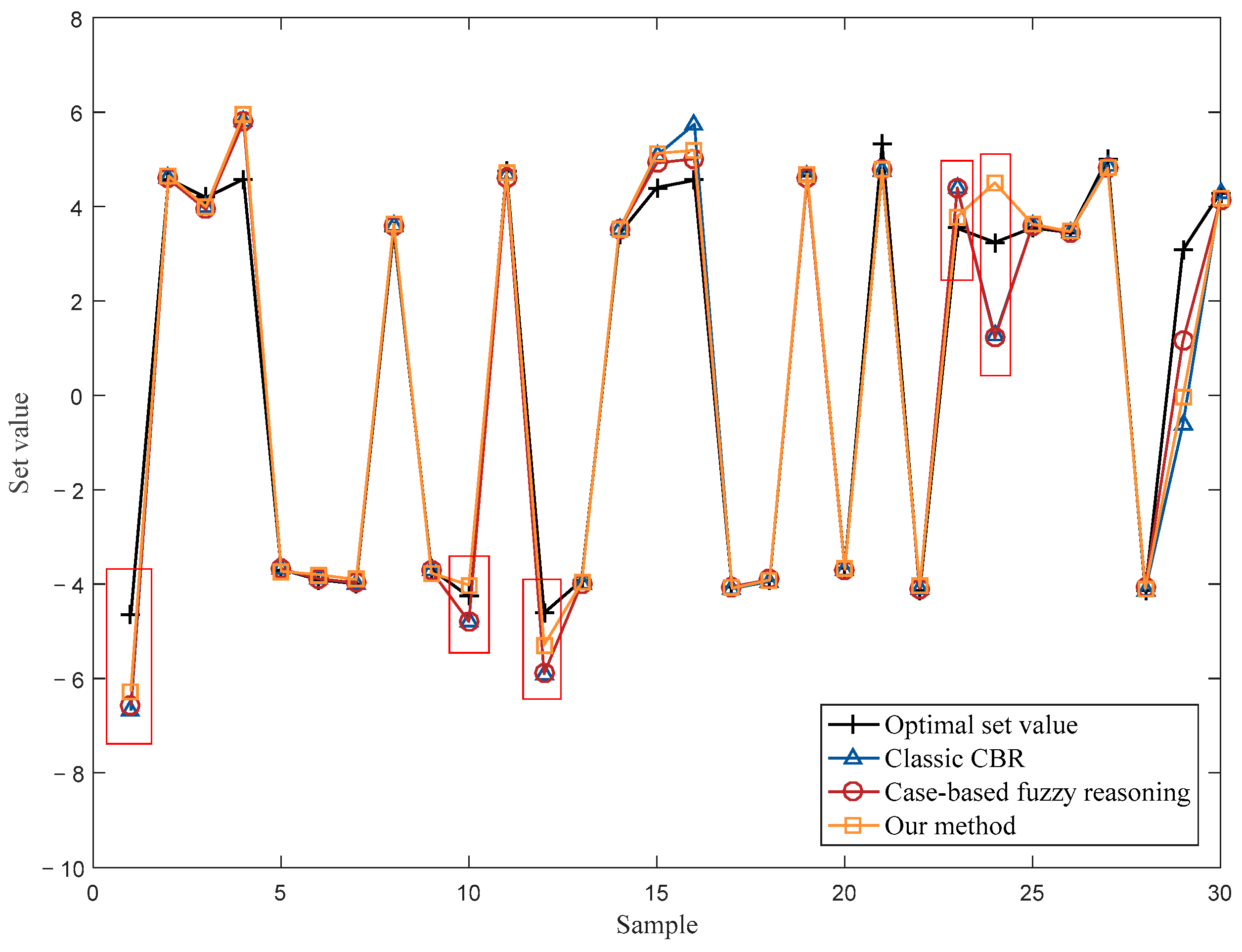
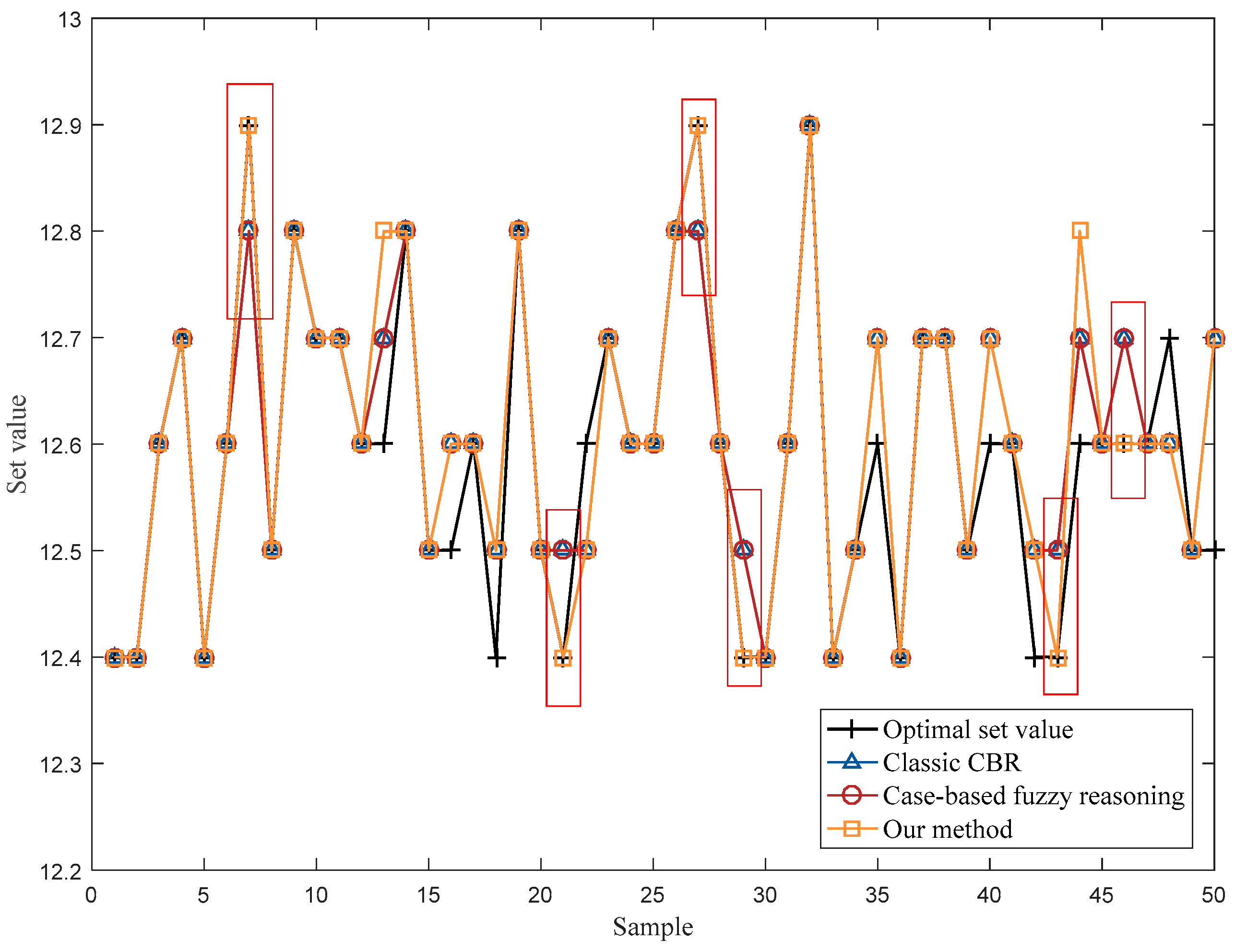
4.2. Operational Optimization of an Industrial Cut-Made Process of Cigarette Production

In this case study, the designed abnormal case removal method was tested with industrial data collected from a cut-made process of cigarette production. In this production, the operator aims to keep the moisture content of leaf-silk close to the desirable value, and the operational optimality has an impact on the quality of cigarettes. Specifically, the studied cut-made process includes the following three procedures: (1) the leaf-silk drying procedure, (2) the blending procedure, and (3) the spicing procedure. Since many operating experiences were stored in the production data, the set value of the moisture content of the leaf-silk drying procedure could be determined with historical optimal cases.

Table 3. Structure of historical case for the operational optimization of cut-made process.

Case Description	Case Solution
Average ambient temperature at the drying machine	The optimal set value of leaf-silk drying machine in production line A
Average ambient moisture at the drying machine
Average leaf-silk moisture content of production line B
Average leaf-silk moisture content of production line C
Tobacco stems moisture content
Expanded leaf-silk moisture content
Blending time
Average ambient temperature at spicing
Average ambient moisture at spicing

presents the basic structure of historical cases for the operational optimization of cut-made process of cigarette production.

After data preprocessing, a total of 200 cases were extracted for having valuable operating experience from the production data. Then, 100 cases were randomly chosen from the 200 cases as the case base, while the rest were equally divided into two datasets. The first was used as training dataset while the last was chosen as testing dataset. Similar to the numerical simulation, MAE was chosen to evaluate its operational optimization performance, and an orthogonal experiment was conducted to find the best parameter combination for the abnormal case removal algorithm and CBR. By trial and error, the best parameters of the proposed abnormal case removal algorithm were set as $k=8$, $m=5$ and $\alpha =0.6$, based on which the operational optimization performance in the training dataset was improved by 22.3% compared with classic CBR. Furthermore, the Gaussian membership function was selected, and the optimized parameters were displayed in

Table 4. Optimized parameters of Gaussian membership function in the industrial case study.

Case Description	Optimized Parameters
Average ambient temperature at the drying machine	0.4317
Average ambient moisture at the drying machine	0.3811
Average leaf-silk moisture content of production line B	0.5302
Average leaf-silk moisture content of production line C	0.3529
Tobacco stems moisture content	0.4173
Expanded leaf-silk moisture content	0.5513
Blending time	0.5556
Average ambient temperature at spicing	0.4098
Average ambient moisture at spicing	0.4885

. Figure 6 exhibits the set values provided by these methods for the industrial cut-made process in the testing dataset.

As shown in Figure 6, CBR with the designed abnormal case removal method (our method) can obtain better results in the operational optimization of moisture content of leaf-silk drying machine in production line A. In particular, overall, there are six operating points (marked with red boxes) in which our method outperformed the classic CBR and case-based fuzzy reasoning. This is due to some abnormal cases being removed by the proposed case removal method in the case retrieval step. Furthermore, the influence of multiple working conditions was not considered in the case-based fuzzy reasoning, and thus the performance of CBR with the designed abnormal case removal method was better. In summary, the MAE of classic CBR in testing dataset was 0.034 and the MAE of case-based fuzzy reasoning was 0.03, while the MAE of our method in the testing dataset was 0.026. The proposed abnormal case removal method improved the MAE by 23.5% compared to classic CBR, and by 13.3% compared to case-based fuzzy reasoning. Therefore, the effectiveness and the superiority of the local density-based abnormal case removal method was proven, and it is suitable for the operational optimization of industrial processes.

5. Conclusions

This paper proposed a local density-based abnormal case removal method for the industrial operational optimization problem. Particularly, the reason as to why abnormal cases should be removed from the case set retrieved by traditional method was analyzed in view of the safety and reliability requirements of industrial operational optimization. Then, historical cases whose LOF exceeded the corresponding threshold were removed by the designed local density-based abnormal case removal algorithm. The simulation results showed that, compared with classic CBR, the local density-based abnormal case removal method could improve the performance of operational optimization by 20.3% in the numerical case and 23.5% in the industrial case study, while improving the performance of operational optimization by 8.5% in the numerical case and 13.3% in the industrial case study compared with case-based fuzzy reasoning. In this paper, the calculation of local density increased computation cost, thus, how to obtain the local density of retrieved cases with lower computation burden would be an interesting topic in the future.