Model-Free Output-Feedback Sliding-Mode Control Design for Piezo-Actuated Stage
Abstract
:1. Introduction
2. System Modeling
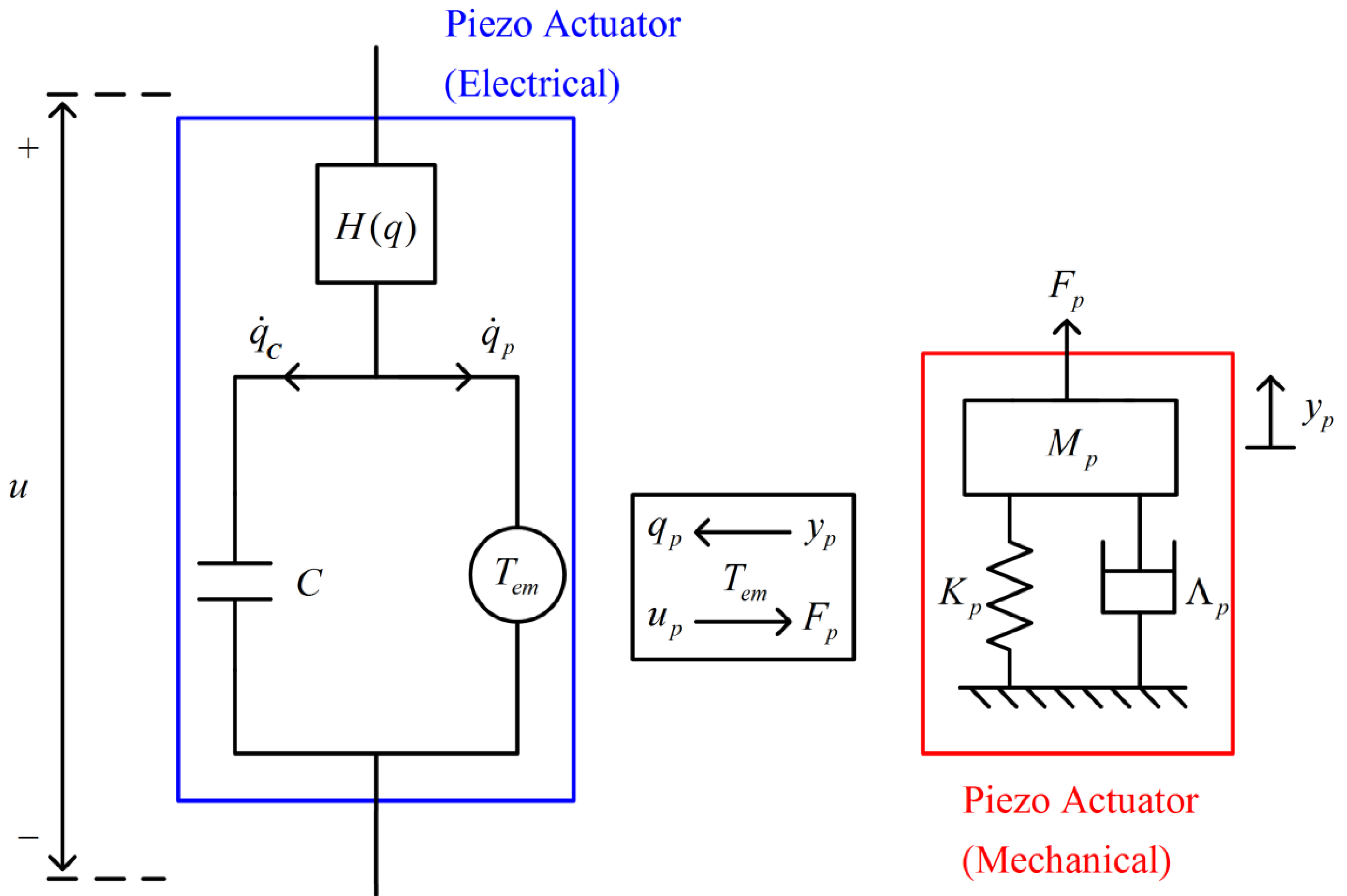
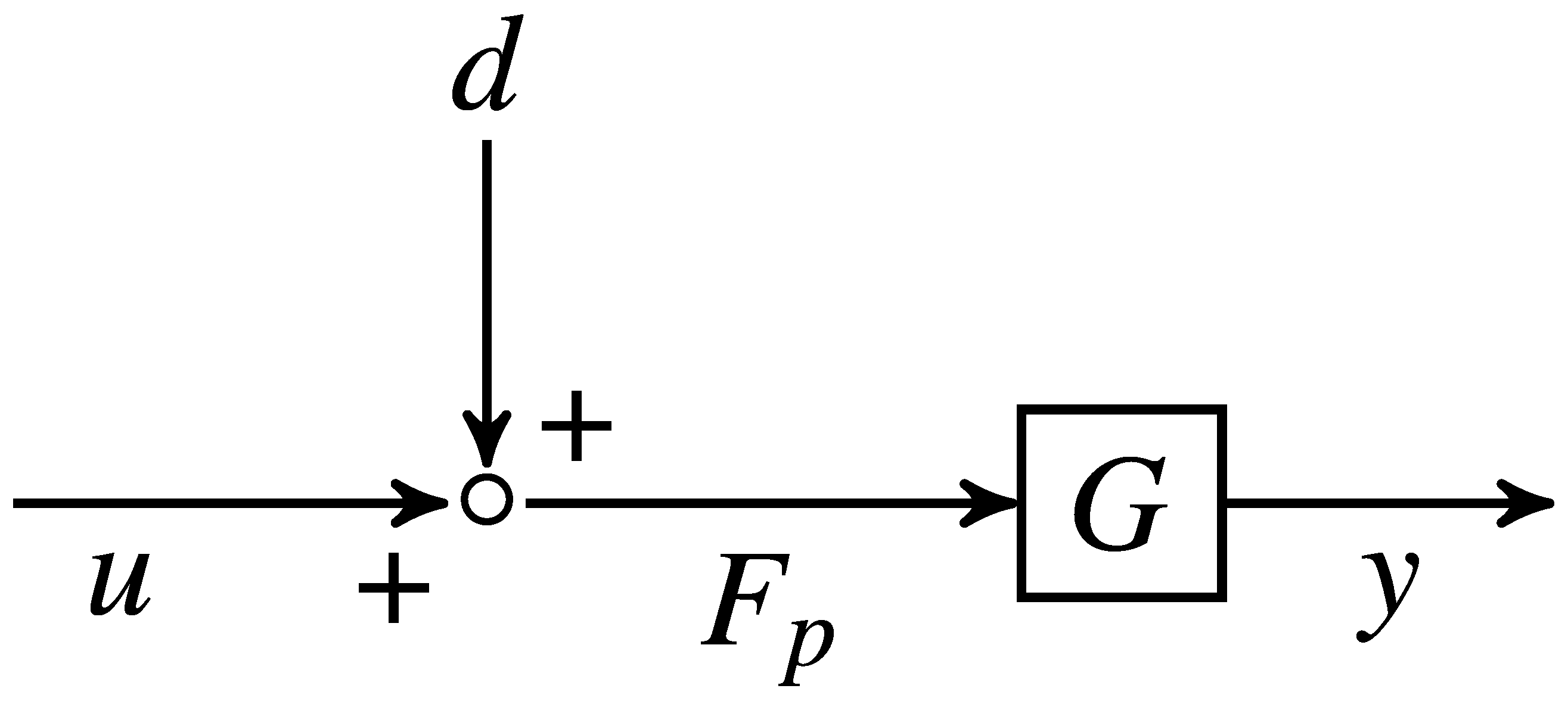
2.1. Modeling of Piezo-Actuated Stage
2.2. Upper Bound of Disturbance
3. Control Design and Stability Analysis
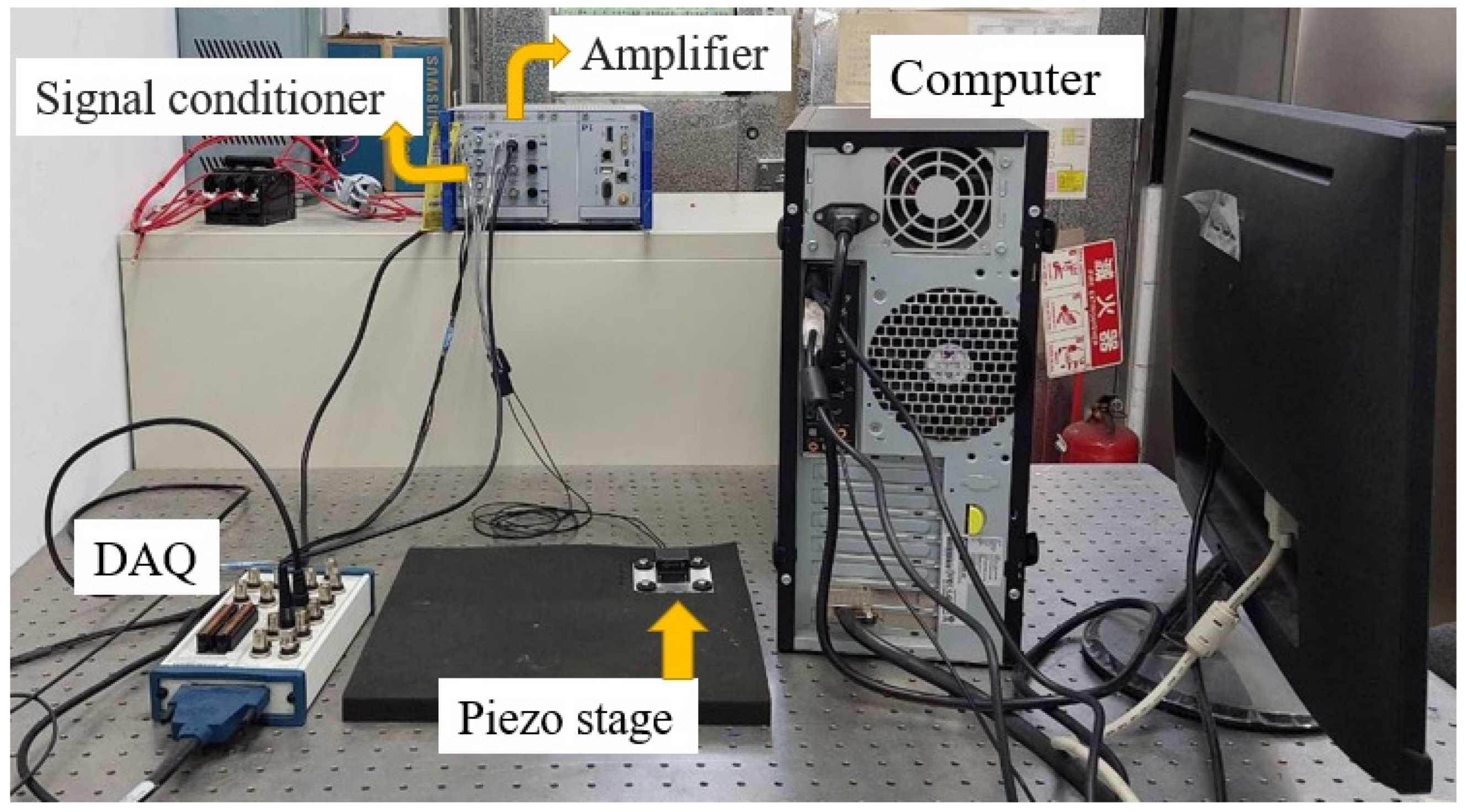
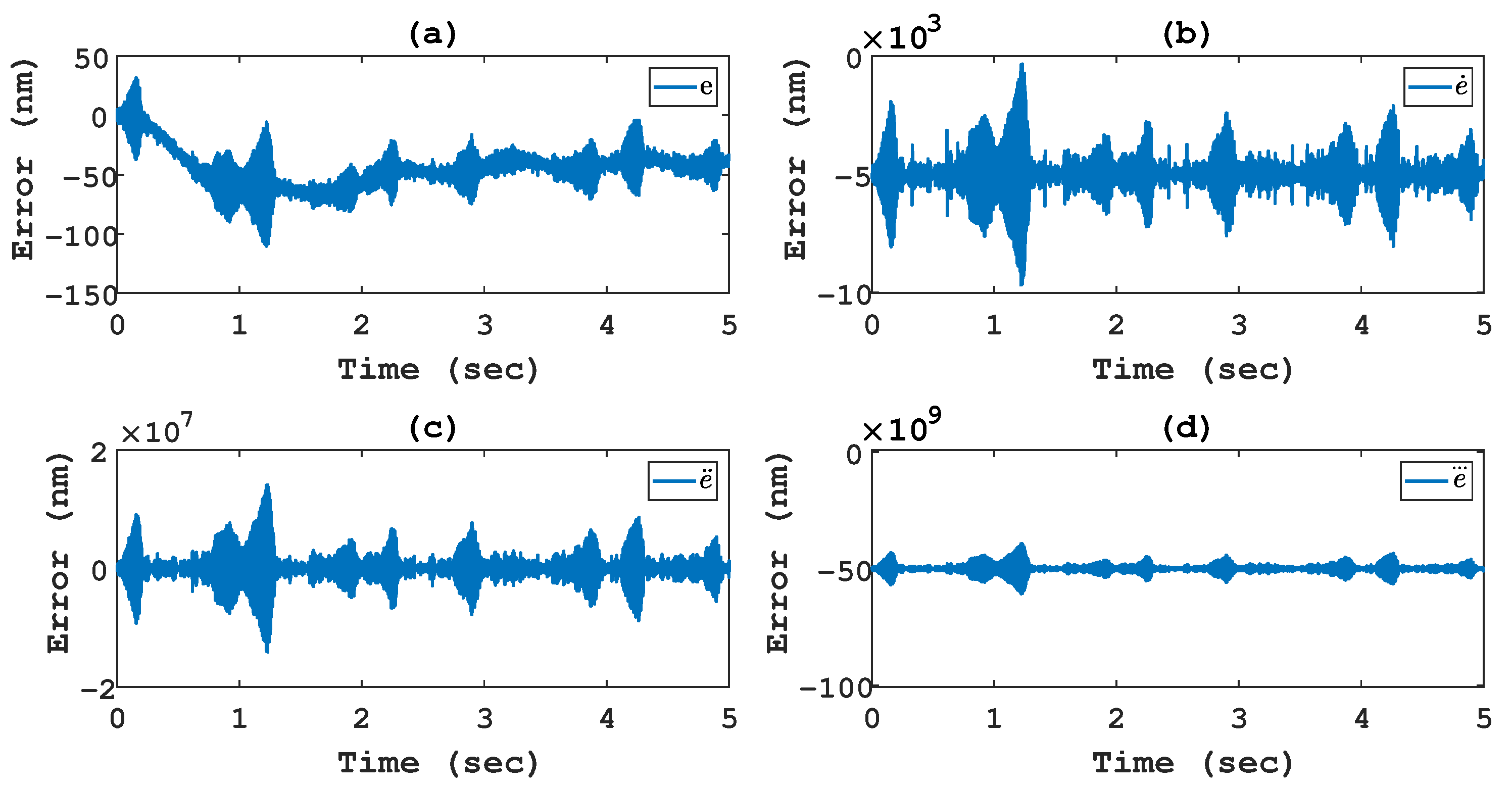
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Li, Y. A New Flexure-Based Y-θ Nanomanipulator With Nanometer-Scale Resolution and Millimeter-Scale Workspace. IEEE/ASME Trans. Mechatron. 2014, 20, 1320–1330. [Google Scholar] [CrossRef]
- Ghosh, B.; Jain, R.; Majumder, S.; Roy, S.; Mukhopadhyay, S. Experimental performance evaluation of smart bimorph piezoelectric actuator and its application in micro robotics. Microsyst. Technol. 2017, 23, 4619–4635. [Google Scholar] [CrossRef]
- Salapaka, S.M.; Salapaka, M.V. Scanning probe microscopy. IEEE Control Syst. Mag. 2008, 28, 65–83. [Google Scholar]
- Sabarianand, D.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. A totally decoupled piezo-driven XYZ flexure parallel micropositioning stage for micro/nanomanipulation. IEEE Trans. Autom. Sci. Eng. 2010, 8, 265–279. [Google Scholar] [CrossRef]
- Zhu, H.; Pang, C.K.; Teo, T.J. A flexure-based parallel actuation dual-stage system for large-stroke nanopositioning. IEEE Trans. Ind. Electron. 2017, 64, 5553–5563. [Google Scholar] [CrossRef]
- Feng, Z.; Ling, J.; Ming, M.; Liang, W.; Tan, K.K.; Xiao, X. Signal-transformation-based repetitive control of spiral trajectory for piezoelectric nanopositioning stages. IEEE/ASME Trans. Mechatron. 2020, 25, 1634–1645. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 121. [Google Scholar]
- Preisach, F. Über die magnetische Nachwirkung. Z. Phys. 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Krasnosel’skii, M.A.; Pokrovskii, A.V. Systems with Hysteresis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef] [Green Version]
- Wen, Y.K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Kodera, N.; Sakashita, M.; Ando, T. Dynamic proportional-integral-differential controller for high-speed atomic force microscopy. Rev. Sci. Instrum. 2006, 77, 083704. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Li, Y. Development and active disturbance rejection control of a compliant micro-/nanopositioning piezostage with dual mode. IEEE Trans. Ind. Electron. 2013, 61, 1475–1492. [Google Scholar] [CrossRef]
- Merry, R.J.; Holierhoek, J.L.; Van De Molengraft, M.J.; Steinbuch, M. Gain scheduling control of a walking piezo actuator. IEEE/ASME Trans. Mechatron. 2013, 19, 954–962. [Google Scholar] [CrossRef]
- Zhong, J.; Yao, B. Adaptive robust precision motion control of a piezoelectric positioning stage. IEEE Trans. Control Syst. Technol. 2008, 16, 1039–1046. [Google Scholar] [CrossRef]
- Abidi, K.; Sabanovic, A. Sliding-mode control for high-precision motion of a piezostage. IEEE Trans. Ind. Electron. 2007, 54, 629–637. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.X.; Abidi, K. Discrete-time output integral sliding-mode control for a piezomotor-driven linear motion stage. IEEE Trans. Ind. Electron. 2008, 55, 3917–3926. [Google Scholar]
- Shen, J.C.; Jywe, W.Y.; Liu, C.H.; Jian, Y.T.; Yang, J. Sliding-mode control of a three-degrees-of-freedom nanopositioner. Asian J. Control 2008, 10, 267–276. [Google Scholar] [CrossRef]
- Yeh, Y.L. Output Feedback Tracking Sliding Mode Control for Systems with State-and Input-Dependent Disturbances. Actuators 2021, 10, 117. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Chen, M.S.; Chen, C.H.; Yang, F.Y. An LTR-observer-based dynamic sliding mode control for chattering reduction. Automatica 2007, 43, 1111–1116. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Estrada, A.; Fridman, L.M. Global and exact HOSM differentiator with dynamic gains for output-feedback sliding mode control. Automatica 2017, 81, 156–163. [Google Scholar] [CrossRef]
- Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. IEEE Control Syst. Mag. 1997, 17, 69–79. [Google Scholar]
- Yeh, Y.L.; Yen, J.Y.; Wu, C.J. Adaptation-Enhanced Model-Based Control with Charge Feedback for Piezo-Actuated Stage. Asian J. Control 2020, 22, 104–116. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y. Modeling and compensation of asymmetric hysteresis nonlinearity for piezoceramic actuators with a modified Prandtl–Ishlinskii model. IEEE Trans. Ind. Electron. 2013, 61, 1583–1595. [Google Scholar] [CrossRef]
- Marquez, H.J. Nonlinear Control Systems: Analysis and Design; John Wiley: Hoboken, NJ, USA, 2003; Volume 161. [Google Scholar]
- Burton, J.; Zinober, A.S. Continuous approximation of variable structure control. Int. J. Syst. Sci. 1986, 17, 875–885. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Modeling and high dynamic compensating the rate-dependent hysteresis of piezoelectric actuators via a novel modified inverse Preisach model. IEEE Trans. Control Syst. Technol. 2012, 21, 1549–1557. [Google Scholar] [CrossRef]




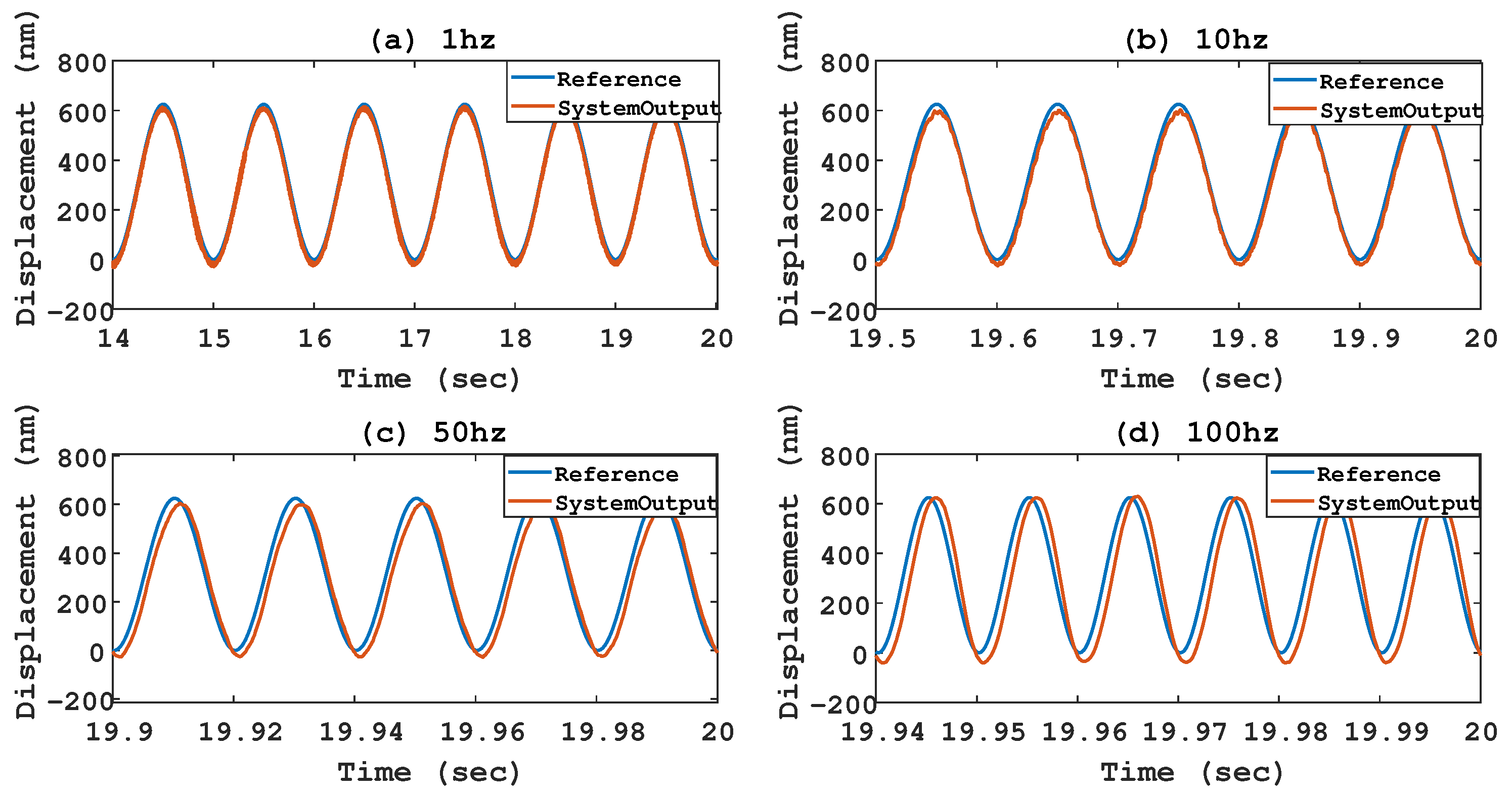
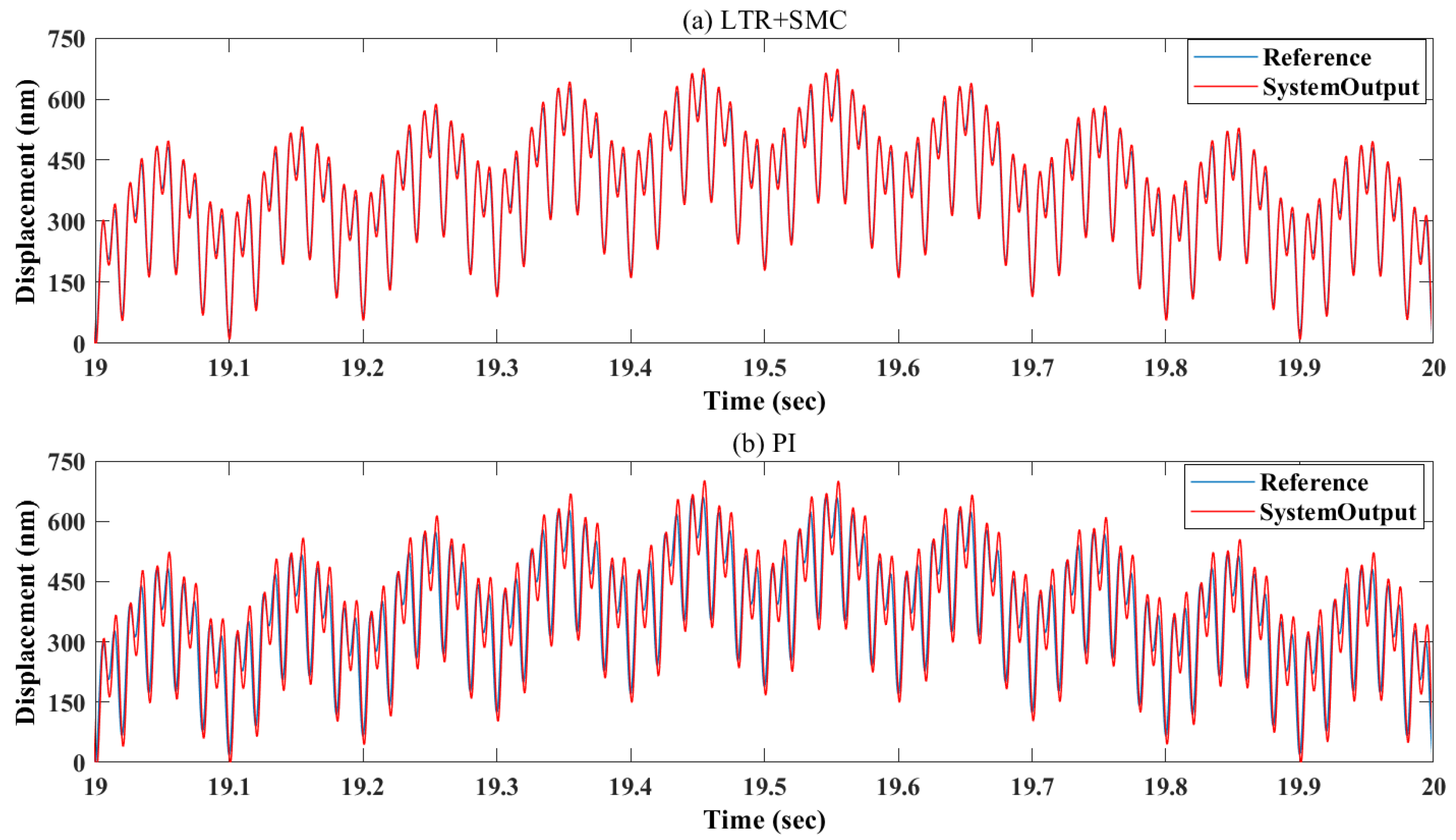
| f (Hz) | (nm) | (%) |
|---|---|---|
| 1 | 14.7 | 2.36 |
| 10 | 25.7 | 4.11 |
| 50 | 56.8 | 9.09 |
| 100 | 92.8 | 14.84 |
| Controller | (nm) | (%) |
|---|---|---|
| LTR+SMC | 97.8 | 16.5 |
| PI | 149.3 | 24.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, Y.-L.; Pan, H.-W.; Shen, Y.-H. Model-Free Output-Feedback Sliding-Mode Control Design for Piezo-Actuated Stage. Machines 2023, 11, 152. https://doi.org/10.3390/machines11020152
Yeh Y-L, Pan H-W, Shen Y-H. Model-Free Output-Feedback Sliding-Mode Control Design for Piezo-Actuated Stage. Machines. 2023; 11(2):152. https://doi.org/10.3390/machines11020152
Chicago/Turabian StyleYeh, Yi-Liang, Hsuan-Wei Pan, and Yuan-Hong Shen. 2023. "Model-Free Output-Feedback Sliding-Mode Control Design for Piezo-Actuated Stage" Machines 11, no. 2: 152. https://doi.org/10.3390/machines11020152
APA StyleYeh, Y. -L., Pan, H. -W., & Shen, Y. -H. (2023). Model-Free Output-Feedback Sliding-Mode Control Design for Piezo-Actuated Stage. Machines, 11(2), 152. https://doi.org/10.3390/machines11020152







