Portable Instruments Based on NIR Sensors and Multivariate Statistical Methods for a Semiautomatic Quality Control of Textiles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples
2.2. The Analyzed Sensors
2.3. The Proposed Multivariate Statistical Approach
3. Experimental Results and Discussion
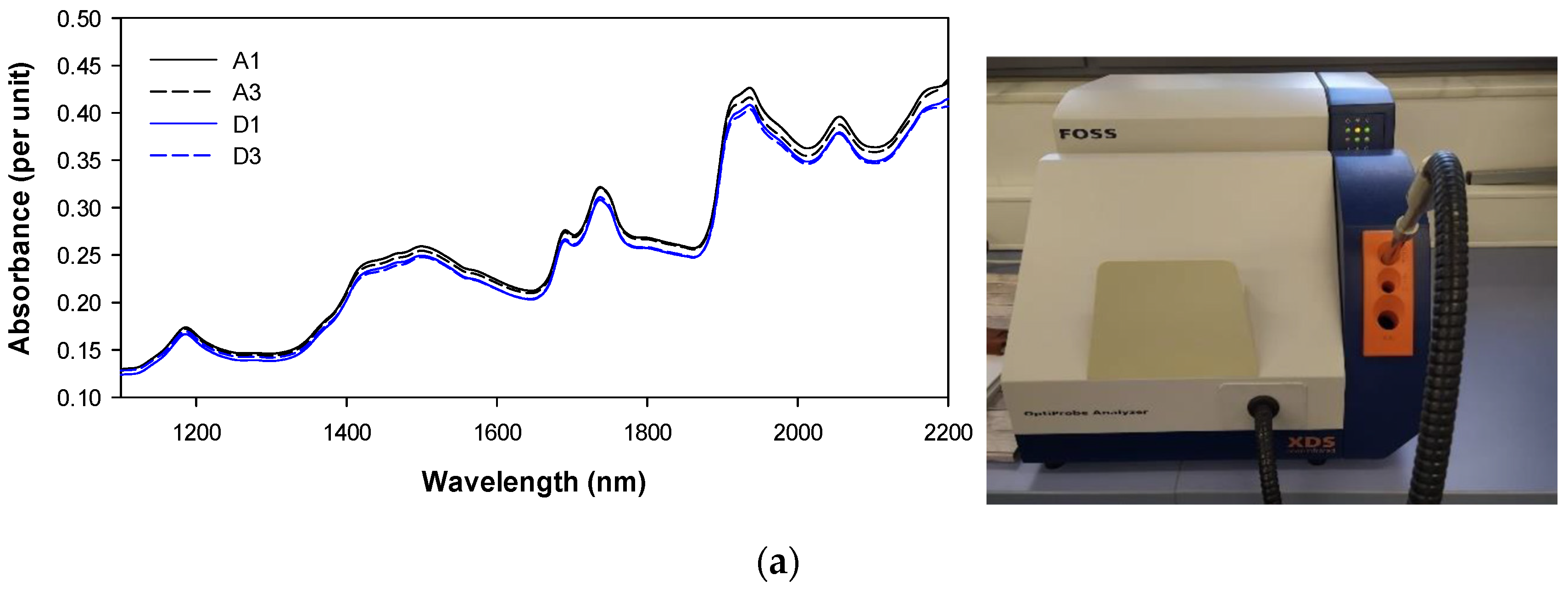
3.1. Spectra Recorded by the Different NIR Instruments
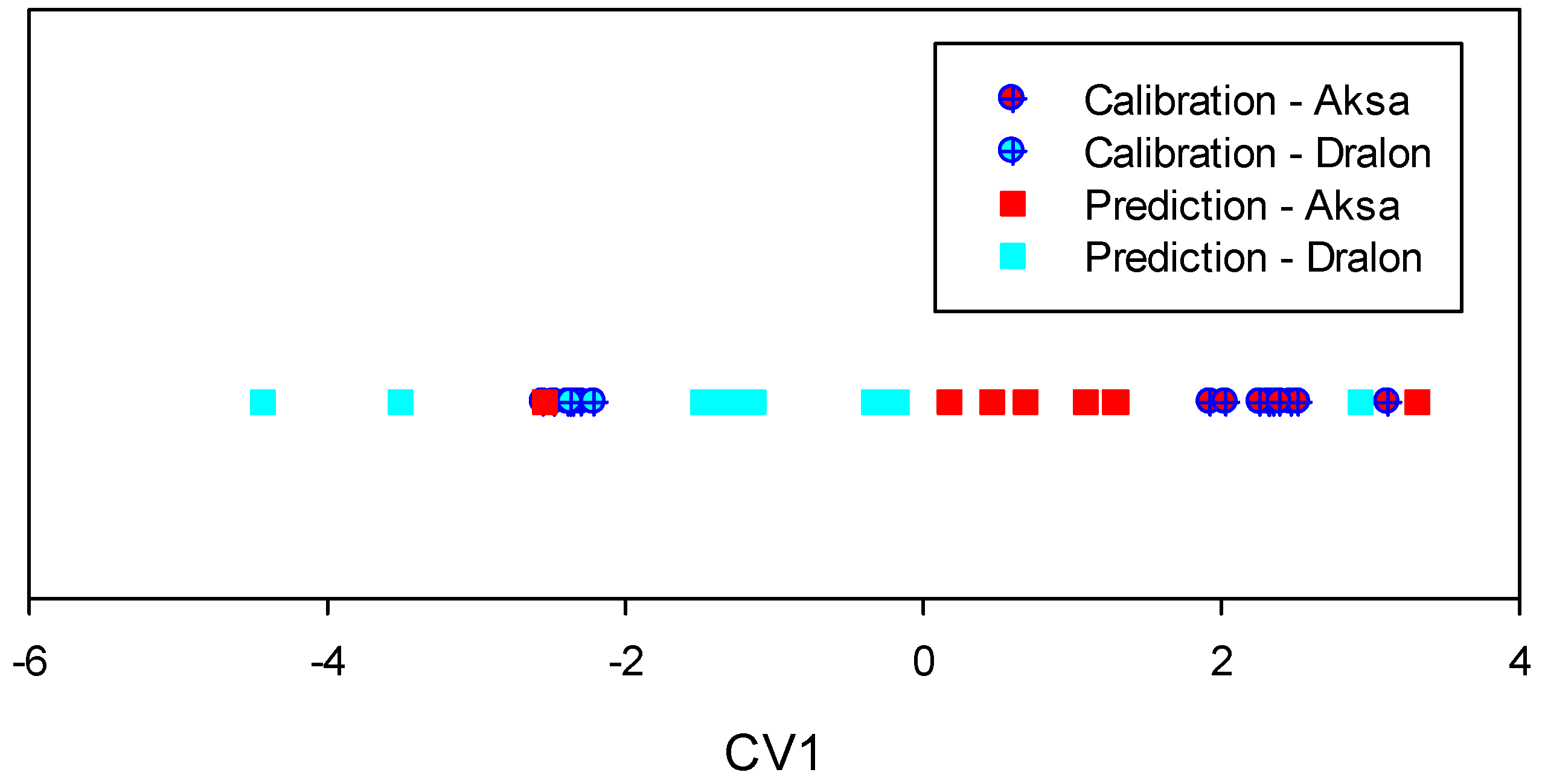
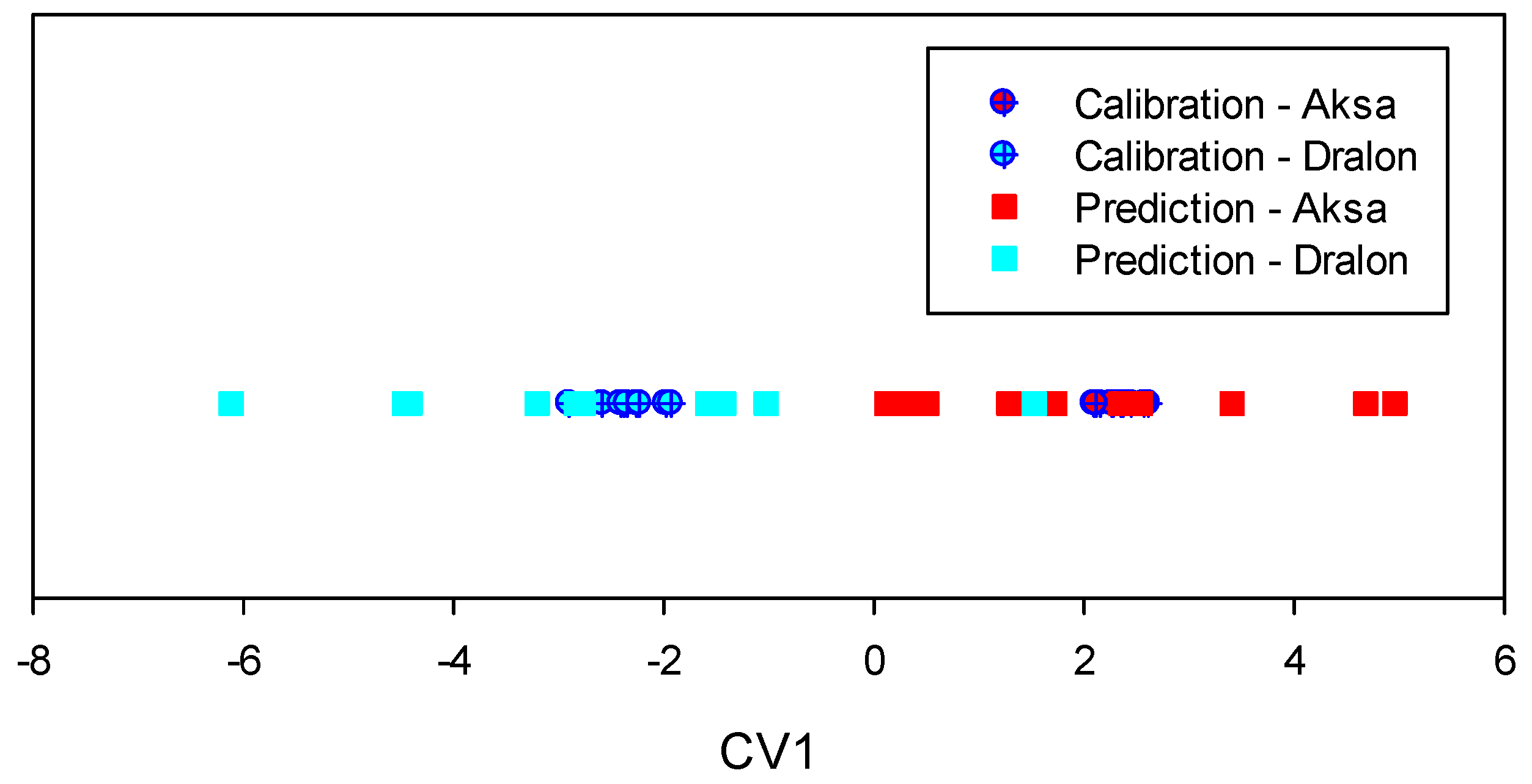
3.2. Results Obtained with the Laboratory Spectrometer
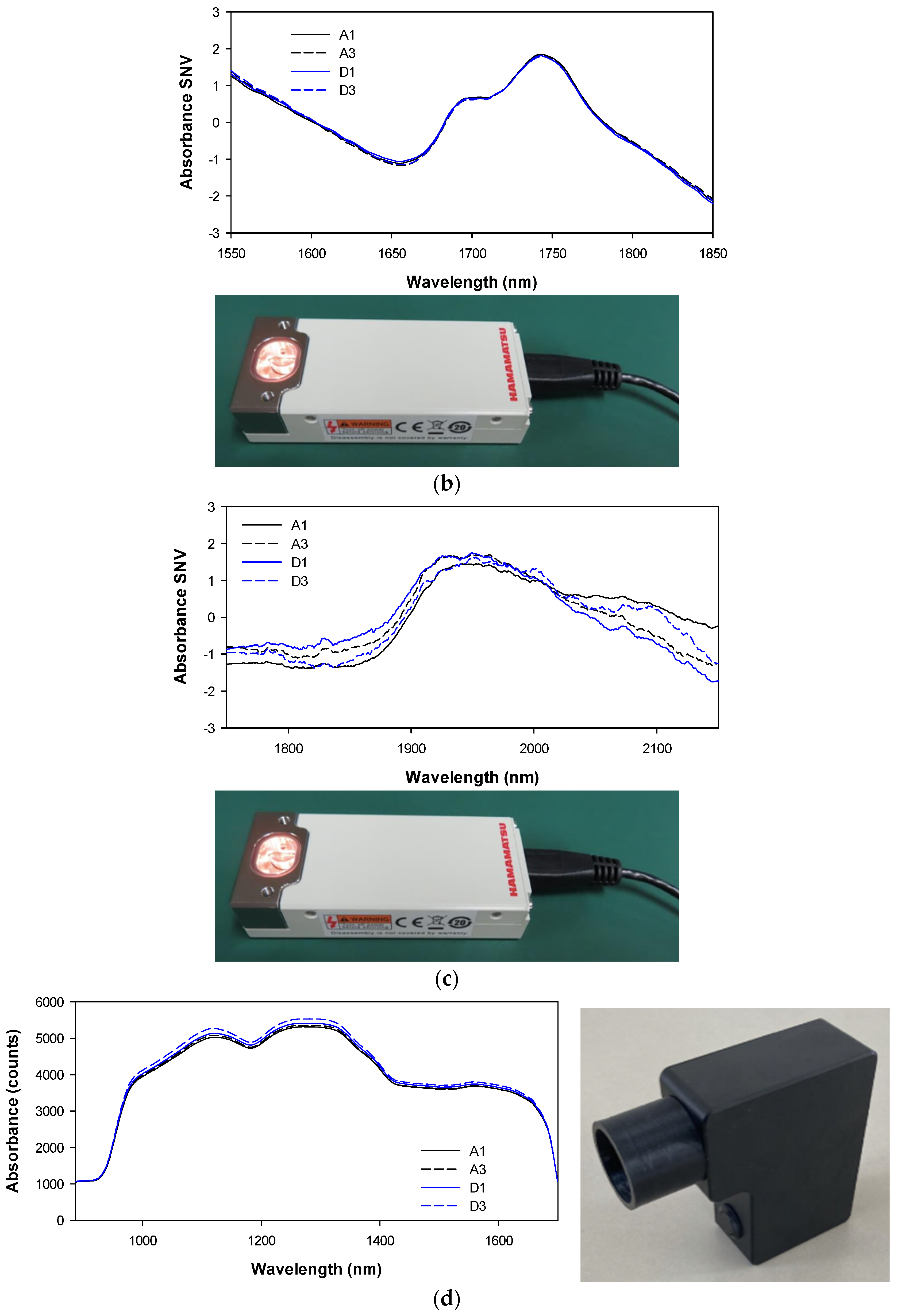
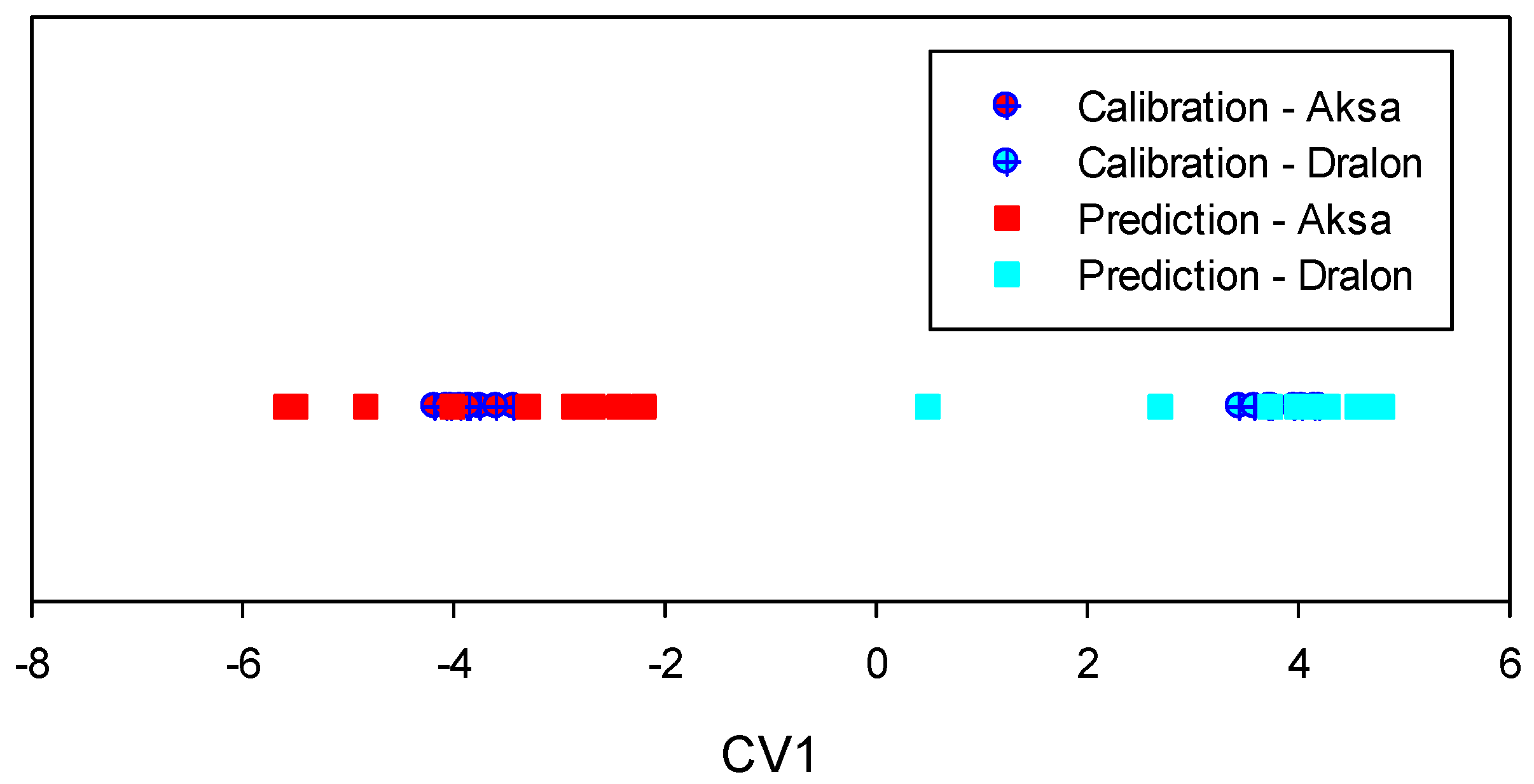
3.3. Results Obtained with the Portable NIR MEMS-FPI C15713
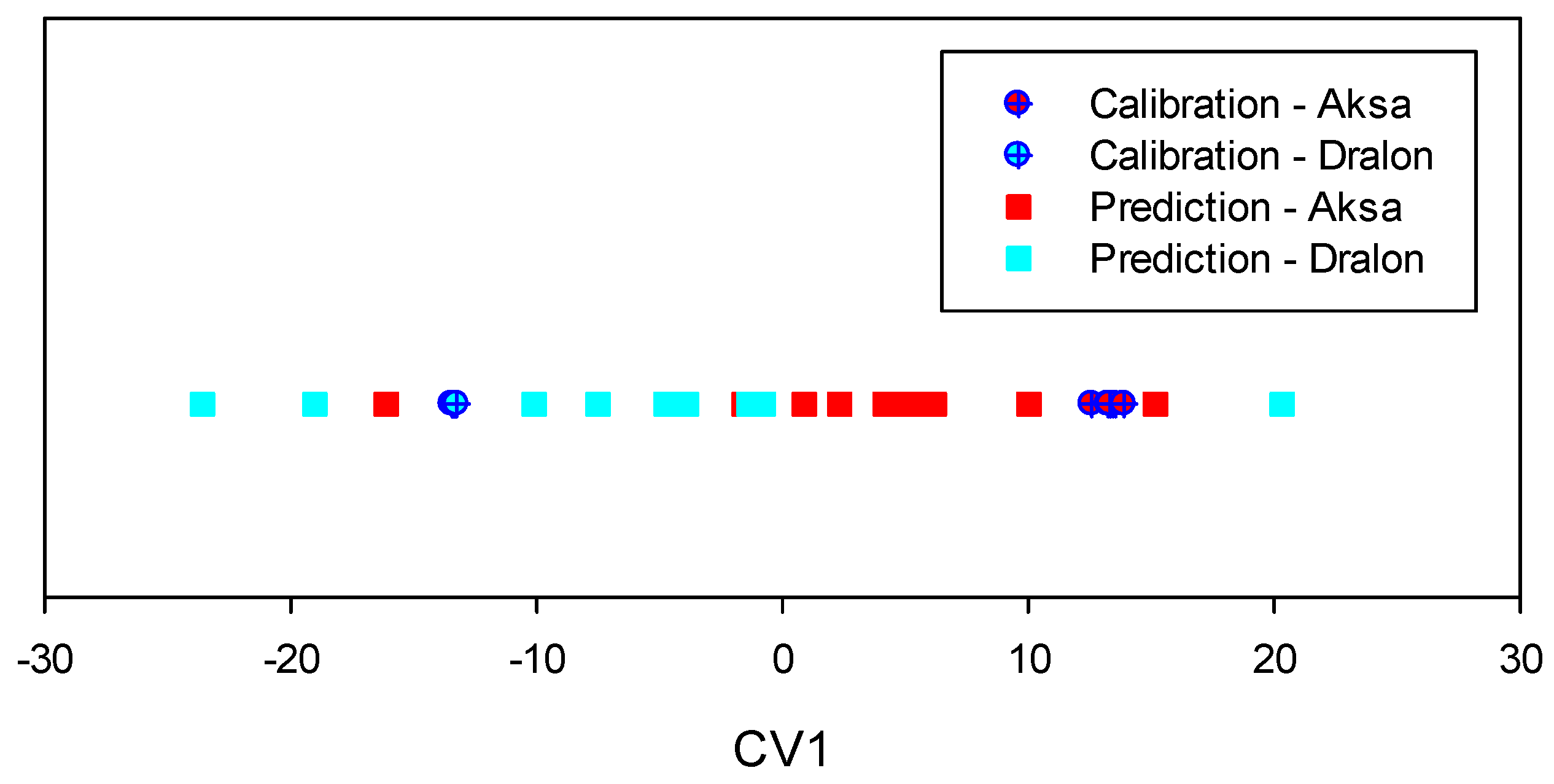
3.4. Results Obtained with the Portable NIR MEMS-FPI C15714
3.5. Results Obtained by Combining the Spectra of the Devices C15713 and C15714
3.6. Results Obtained with the Portable NIR-Q Device from Phase Photonics
3.7. Summary of Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Environment Agency. Textiles in Europe’s Circular Economy; European Environment Agency: Copenhagen, Denmark, 2019. [Google Scholar]
- Cassanelli, D.; Lenzini, N.; Ferrari, L.; Rovati, L. Partial Least Squares Estimation of Crop Moisture and Density by Near-Infrared Spectroscopy. IEEE Trans. Instrum. Meas. 2021, 70, 1004510. [Google Scholar] [CrossRef]
- Riba, J.R.; Cantero, R.; Puig, R. Classification of Textile Samples Using Data Fusion Combining Near- and Mid-Infrared Spectral Information. Polymers 2022, 14, 3073. [Google Scholar] [CrossRef] [PubMed]
- Riba, J.-R.; Canals, T.; Cantero, R. Recovered Paperboard Samples Identification by Means of Mid-Infrared Sensors. IEEE Sens. J. 2013, 13, 2763–2770. [Google Scholar] [CrossRef]
- Bonifazi, G.; Gasbarrone, R.; Palmieri, R.; Serranti, S. End-of-Life Textile Recognition in a Circular Economy Perspective: A Methodological Approach Based on Near Infrared Spectroscopy. Sustainability 2022, 14, 10249. [Google Scholar] [CrossRef]
- Riba, J.-R.; Canals, T.; Cantero, R.; Iturriaga, H. Potential of infrared spectroscopy in combination with extended canonical variate analysis for identifying different paper types. Meas. Sci. Technol. 2011, 22, 025601. [Google Scholar] [CrossRef]
- Antónia Nunes, M.; Páscoa, R.N.M.J.; Alves, R.C.; Costa, A.S.G.; Bessada, S.; Oliveira, M.B.P.P. Fourier transform near infrared spectroscopy as a tool to discriminate olive wastes: The case of monocultivar pomaces. Waste Manag. 2020, 103, 378–387. [Google Scholar] [CrossRef]
- Roldán, M.; Kyriacou, P.A. Near-Infrared Spectroscopy (NIRS) in Traumatic Brain Injury (TBI). Sensors 2021, 21, 1586. [Google Scholar] [CrossRef]
- Pasquini, C. Near infrared spectroscopy: A mature analytical technique with new perspectives—A review. Anal. Chim. Acta 2018, 1026, 8–36. [Google Scholar] [CrossRef]
- Kranenburg, R.F.; Ramaker, H.J.; Sap, S.; van Asten, A.C. A calibration friendly approach to identify drugs of abuse mixtures with a portable near-infrared analyzer. Drug Test. Anal. 2022, 14, 1089–1101. [Google Scholar] [CrossRef]
- Serrano, J.; Shahidian, S.; Carapau, Â.; Rato, A.E. Near-Infrared Spectroscopy (NIRS) and Optical Sensors for Estimating Protein and Fiber in Dryland Mediterranean Pastures. AgriEngineering 2021, 3, 73–91. [Google Scholar] [CrossRef]
- Zhao, S.; Qiu, Z.; He, Y. Transfer learning strategy for plastic pollution detection in soil: Calibration transfer from high-throughput HSI system to NIR sensor. Chemosphere 2021, 272, 129908. [Google Scholar] [CrossRef] [PubMed]
- Osborne, B.G. Near-Infrared Spectroscopy in Food Analysis. In Encyclopedia of Analytical Chemistry: Applications, Theory, and Instrumentation; Wiley Online Library: Hoboken, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Melendreras, C.; Forcada, S.; Fernández-Sánchez, M.L.; Fernández-Colomer, B.; Costa-Fernández, J.M.; López, A.; Ferrero, F.; Soldado, A. Near-Infrared Sensors for Onsite and Noninvasive Quantification of Macronutrients in Breast Milk. Sensors 2022, 22, 1311. [Google Scholar] [CrossRef] [PubMed]
- Anjos, O.; Caldeira, I.; Fernandes, T.A.; Pedro, S.I.; Vitória, C.; Oliveira-Alves, S.; Catarino, S.; Canas, S. PLS-R Calibration Models for Wine Spirit Volatile Phenols Prediction by Near-Infrared Spectroscopy. Sensors 2021, 22, 286. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Ye, Y.; Wei, L.; Yang, X.; Huang, C. Study on the Optimization of Hyperspectral Characteristic Bands Combined with Monitoring and Visualization of Pepper Leaf SPAD Value. Sensors 2021, 22, 183. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.D.; Santos, L.P.; Cunha, P.H.; Borghi, F.T.; Romao, W.; de Castro, E.V.; de Oliveira, E.C.; Filgueiras, P.R. Discrimination of oils and fuels using a portable NIR spectrometer. Fuel 2021, 283, 118854. [Google Scholar] [CrossRef]
- Riba, J.R.; Cantero, R.; Riba-Mosoll, P.; Puig, R. Post-Consumer Textile Waste Classification through Near-Infrared Spectroscopy, Using an Advanced Deep Learning Approach. Polymers 2022, 14, 2475. [Google Scholar] [CrossRef]
- Quintero Balbas, D.; Lanterna, G.; Cirrincione, C.; Fontana, R.; Striova, J. Non-invasive identification of textile fibres using near-infrared fibre optics reflectance spectroscopy and multivariate classification techniques. Eur. Phys. J. Plus 2022, 137, 85. [Google Scholar] [CrossRef]
- Cura, K.; Rintala, N.; Kamppuri, T.; Saarimäki, E.; Heikkilä, P. Textile Recognition and Sorting for Recycling at an Automated Line Using Near Infrared Spectroscopy. Recycling 2021, 6, 11. [Google Scholar] [CrossRef]
- Du, W.; Zheng, J.; Li, W.; Liu, Z.; Wang, H.; Han, X. Efficient Recognition and Automatic Sorting Technology of Waste Textiles Based on Online Near infrared Spectroscopy and Convolutional Neural Network. Resour. Conserv. Recycl. 2022, 180, 106157. [Google Scholar] [CrossRef]
- Escuredo, O.; Meno, L.; Rodríguez-Flores, M.S.; Seijo, M.C. Rapid Estimation of Potato Quality Parameters by a Portable Near-Infrared Spectroscopy Device. Sensors 2021, 21, 8222. [Google Scholar] [CrossRef]
- Crocombe, R.A. Portable Spectroscopy. Appl. Spectrosc. 2018, 72, 1701–1751. [Google Scholar] [CrossRef] [PubMed]
- Yildirim, P.; Birant, D.; Alpyildiz, T. Data mining and machine learning in textile industry. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1228. [Google Scholar] [CrossRef]
- Arora, S.; Majumdar, A. Machine learning and soft computing applications in textile and clothing supply chain: Bibliometric and network analyses to delineate future research agenda. Expert Syst. Appl. 2022, 200, 117000. [Google Scholar] [CrossRef]
- Hakkel, K.D.; Petruzzella, M.; Ou, F.; van Klinken, A.; Pagliano, F.; Liu, T.; van Veldhoven, R.P.J. Integrated near-infrared spectral sensing. Nat. Commun. 2022, 13, 103. [Google Scholar] [CrossRef] [PubMed]
- Bacon, C.P.; Mattley, Y.; DeFrece, R. Miniature spectroscopic instrumentation: Applications to biology and chemistry. Rev. Sci. Instrum. 2003, 75, 1. [Google Scholar] [CrossRef]
- Pügner, T.; Knobbe, J.; Grüger, H. Near-Infrared Grating Spectrometer for Mobile Phone Applications. Appl. Spectrosc. 2016, 70, 734–745. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cai, W.; Hasan, T. Miniaturization of optical spectrometers. Science 2021, 371, eabe0722. [Google Scholar] [CrossRef]
- Bae, B.; Park, M.; Lee, D.; Sim, I.; Lee, K. Hetero-Integrated InGaAs Photodiode and Oxide Memristor-Based Artificial Optical Nerve for In-Sensor NIR Image Processing. Adv. Opt. Mater. 2022, 11, 2201905. [Google Scholar] [CrossRef]
- Fan, D.; Lee, K.; Forrest, S.R. Flexible Thin-Film InGaAs Photodiode Focal Plane Array. ACS Photonics 2016, 3, 670–676. [Google Scholar] [CrossRef]
- Hamamatsu. Spectroscopic Modules Compact Module with MEMS-FPI Spectrum Sensor and Light Source; Hamamatsu: Shizuoka, Japan, 2022; pp. 1–7. [Google Scholar]
- Pan, J.; Nguyen, K.L. Development of the Photoacoustic Rapid-Scan FT-IR-Based Method for Measurement of Ink Concentration on Printed Paper. Anal. Chem. 2007, 79, 2259–2265. [Google Scholar] [CrossRef]
- Riba, J.-R.; Cantero, R.; García-Masabet, V.; Cailloux, J.; Canals, T.; Maspoch, M.L. Multivariate identification of extruded PLA samples from the infrared spectrum. J. Mater. Sci. 2020, 55, 1269–1279. [Google Scholar] [CrossRef]
- Lai, W.; Zeng, X.; He, J.; Deng, Y. Aesthetic defect characterization of a polymeric polarizer via structured light illumination. Polym. Test. 2016, 53, 51–57. [Google Scholar] [CrossRef]
- Riba, J.-R.; Canals, T.; Cantero, R. Supervision of Ethylene Propylene Diene M-Class (EPDM) Rubber Vulcanization and Recovery Processes Using Attenuated Total Reflection Fourier Transform Infrared (ATR FT-IR) Spectroscopy and Multivariate Analysis. Appl. Spectrosc. 2017, 71, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, N.; Bandyopadhyay, R.; Bhuyan, M.; Tudu, B.; Ghosh, D.; Jana, A. Electronic Nose for Black Tea Classification and Correlation of Measurements with “Tea Taster” Marks. IEEE Trans. Instrum. Meas. 2008, 57, 1313–1321. [Google Scholar] [CrossRef]
- Viale, L.; Daga, A.P.; Fasana, A.; Garibaldi, L. Dimensionality Reduction Methods of a Clustered Dataset for the Diagnosis of a SCADA-Equipped Complex Machine. Machines 2022, 11, 36. [Google Scholar] [CrossRef]
- Riba Ruiz, J.-R.; Canals, T.; Cantero Gomez, R. Comparative Study of Multivariate Methods to Identify Paper Finishes Using Infrared Spectroscopy. IEEE Trans. Instrum. Meas. 2012, 61, 1029–1036. [Google Scholar] [CrossRef]
- Riba, J.R.; Cantero, R.; Canals, T.; Puig, R. Circular economy of post-consumer textile waste: Classification through infrared spectroscopy. J. Clean. Prod. 2020, 272, 123011. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2007. [Google Scholar]
- Wu, Y.; Liu, X.; Zhou, Y. Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement. Machines 2023, 11, 475. [Google Scholar] [CrossRef]
- Nørgaard, L.; Bro, R.; Westad, F.; Engelsen, S.B. A modification of canonical variates analysis to handle highly collinear multivariate data. J. Chemom. 2006, 20, 425–435. [Google Scholar] [CrossRef]





| Manufacturer | Designation | Spectral Range | Resolution | Built-In Lamp |
|---|---|---|---|---|
| Hamamatsu | C15713 | 1550–1850 nm | 20 nm | Tungsten |
| Hamamatsu | C15714 | 1750–2150 nm | 22 nm | Tungsten |
| Phase Photonics | NIR-Q | 900–1700 nm | 6 nm | Tungsten |
| Prediction Samples | Classification Results | |
|---|---|---|
| Aksa | Dralon | |
| A2 | 1.000 | 0.000 |
| A4 | 1.000 | 0.000 |
| A6 | 1.000 | 0.000 |
| A8 | 1.000 | 0.000 |
| A10 | 1.000 | 0.000 |
| A12 | 1.000 | 0.000 |
| A14 | 1.000 | 0.000 |
| A16 | 1.000 | 0.000 |
| A18 | 1.000 | 0.000 |
| A20 | 1.000 | 0.000 |
| D2 | 0.000 | 1.000 |
| D4 | 0.000 | 1.000 |
| D6 | 0.000 | 1.000 |
| D8 | 0.000 | 1.000 |
| D10 | 0.000 | 1.000 |
| D12 | 0.000 | 1.000 |
| D14 | 0.000 | 1.000 |
| D16 | 0.000 | 1.000 |
| D18 | 0.000 | 1.000 |
| D20 | 0.000 | 1.000 |
| Prediction Samples | Classification Results | |
|---|---|---|
| Aksa | Dralon | |
| A2 | 1.000 | 0.000 |
| A4 | 0.000 | 1.000 |
| A6 | 0.000 | 1.000 |
| A8 | 1.000 | 0.000 |
| A10 | 0.000 | 1.000 |
| A12 | 0.000 | 1.000 |
| A14 | 1.000 | 0.000 |
| A16 | 1.000 | 0.000 |
| A18 | 1.000 | 0.000 |
| A20 | 1.000 | 0.000 |
| D2 | 0.000 | 1.000 |
| D4 | 0.000 | 1.000 |
| D6 | 1.000 | 0.000 |
| D8 | 1.000 | 0.000 |
| D10 | 0.000 | 1.000 |
| D12 | 0.000 | 1.000 |
| D14 | 0.000 | 1.000 |
| D16 | 0.000 | 1.000 |
| D18 | 0.000 | 1.000 |
| D20 | 1.000 | 0.000 |
| Prediction Samples | Classification Results | |
|---|---|---|
| Aksa | Dralon | |
| A2 | 1.000 | 0.000 |
| A4 | 1.000 | 0.000 |
| A6 | 1.000 | 0.000 |
| A8 | 1.000 | 0.000 |
| A10 | 1.000 | 0.000 |
| A12 | 1.000 | 0.000 |
| A14 | 0.000 | 1.000 |
| A16 | 0.000 | 1.000 |
| A18 | 1.000 | 0.000 |
| A20 | 1.000 | 0.000 |
| D2 | 0.000 | 1.000 |
| D4 | 0.000 | 1.000 |
| D6 | 0.000 | 1.000 |
| D8 | 1.000 | 0.000 |
| D10 | 0.000 | 1.000 |
| D12 | 0.000 | 1.000 |
| D14 | 0.000 | 1.000 |
| D16 | 0.000 | 1.000 |
| D18 | 0.000 | 1.000 |
| D20 | 0.000 | 1.000 |
| Prediction Samples | Classification Results | |
|---|---|---|
| Aksa | Dralon | |
| A2 | 1.000 | 0.000 |
| A4 | 1.000 | 0.000 |
| A6 | 1.000 | 0.000 |
| A8 | 1.000 | 0.000 |
| A10 | 0.200 | 0.800 |
| A12 | 1.000 | 0.000 |
| A14 | 1.000 | 0.000 |
| A16 | 0.000 | 1.000 |
| A18 | 1.000 | 0.000 |
| A20 | 1.000 | 0.000 |
| D2 | 0.000 | 1.000 |
| D4 | 0.000 | 1.000 |
| D6 | 0.300 | 0.700 |
| D8 | 1.000 | 0.000 |
| D10 | 0.000 | 1.000 |
| D12 | 0.000 | 1.000 |
| D14 | 0.000 | 1.000 |
| D16 | 0.000 | 1.000 |
| D18 | 0.000 | 1.000 |
| D20 | 0.000 | 1.000 |
| Prediction Samples | Classification Results | |
|---|---|---|
| Aksa | Dralon | |
| A2 | 1.000 | 0.000 |
| A4 | 1.000 | 0.000 |
| A6 | 1.000 | 0.000 |
| A8 | 1.000 | 0.000 |
| A10 | 1.000 | 0.000 |
| A12 | 1.000 | 0.000 |
| A14 | 1.000 | 0.000 |
| A16 | 1.000 | 0.000 |
| A18 | 1.000 | 0.000 |
| A20 | 1.000 | 0.000 |
| D2 | 0.000 | 1.000 |
| D4 | 0.000 | 1.000 |
| D6 | 0.000 | 1.000 |
| D8 | 1.000 | 0.000 |
| D10 | 0.000 | 1.000 |
| D12 | 0.000 | 1.000 |
| D14 | 0.000 | 1.000 |
| D16 | 0.000 | 1.000 |
| D18 | 0.000 | 1.000 |
| D20 | 0.000 | 1.000 |
| Spectrometer | Spectral Range [nm] | Resolution [nm] | Misclassification Rate |
|---|---|---|---|
| Laboratory spectrometer | 1100–2200 | 0.5 | 0% |
| MEMS-FPI C15713 | 1550–1850 | 20 | 35% |
| MEMS-FPI C15714 | 1750–2150 | 22 | 15% |
| MEMS-FPI C15713 + C15714 | 1550–2150 | 22 | 15% |
| NIR-Q | 900–1700 | 6 | 5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riba, J.-R.; Puig, R.; Cantero, R. Portable Instruments Based on NIR Sensors and Multivariate Statistical Methods for a Semiautomatic Quality Control of Textiles. Machines 2023, 11, 564. https://doi.org/10.3390/machines11050564
Riba J-R, Puig R, Cantero R. Portable Instruments Based on NIR Sensors and Multivariate Statistical Methods for a Semiautomatic Quality Control of Textiles. Machines. 2023; 11(5):564. https://doi.org/10.3390/machines11050564
Chicago/Turabian StyleRiba, Jordi-Roger, Rita Puig, and Rosa Cantero. 2023. "Portable Instruments Based on NIR Sensors and Multivariate Statistical Methods for a Semiautomatic Quality Control of Textiles" Machines 11, no. 5: 564. https://doi.org/10.3390/machines11050564
APA StyleRiba, J. -R., Puig, R., & Cantero, R. (2023). Portable Instruments Based on NIR Sensors and Multivariate Statistical Methods for a Semiautomatic Quality Control of Textiles. Machines, 11(5), 564. https://doi.org/10.3390/machines11050564








