Unveiling Inertia Constants by Exploring Mass Distribution in Wind Turbine Blades and Review of the Drive Train Parameters
Abstract
:1. Introduction
1.1. Context and Purpose of the Work
1.2. Literature Review
1.3. Research Gap and Motivation
1.4. Contribution
- Provide general expressions that allow the weight of the blade to be estimated based not only on its length, but also on the IEC wind class of the turbine and the material of the blade.
- Provide an expression that accurately estimates the blade inertia starting from the position of the CoG, its weight and its length.
- Formulate in depth a complete dimensionless framework to relate magnitudes and parameters (such as inertia, damping, stiffness and friction) with respect to their base references, valid for systems of three masses and two masses.
1.5. Paper Organization
2. Methods
2.1. Dynamics Rotor-Generator
- is the inertia of the turbine rotor due to the distribution of masses in the blades and, to a lesser extent, in the hub.
- is the coefficient of friction due to the aerodynamic resistance offered by the blades.
- is the stiffness constant in the slow axis that joins the hub and the gearbox.
- is the damping constant of the torsional movement of the slow axis.
- is the inertia of the gearbox discs, measured from the slow shaft.
- is the coefficient of friction due to friction in the gearbox, measured from the slow shaft.
- is the inertia of the rotor of the electric generator and the brake.
- is the coefficient of friction due to friction in the generator and ventilation losses.
- is the stiffness constant in the fast axis that joins the gearbox and the generator.
- is the damping constant of the torsion motion of the fast axis.
2.2. Mechanical Equations
2.3. Referring to Base Magnitudes
2.4. System of Two Masses
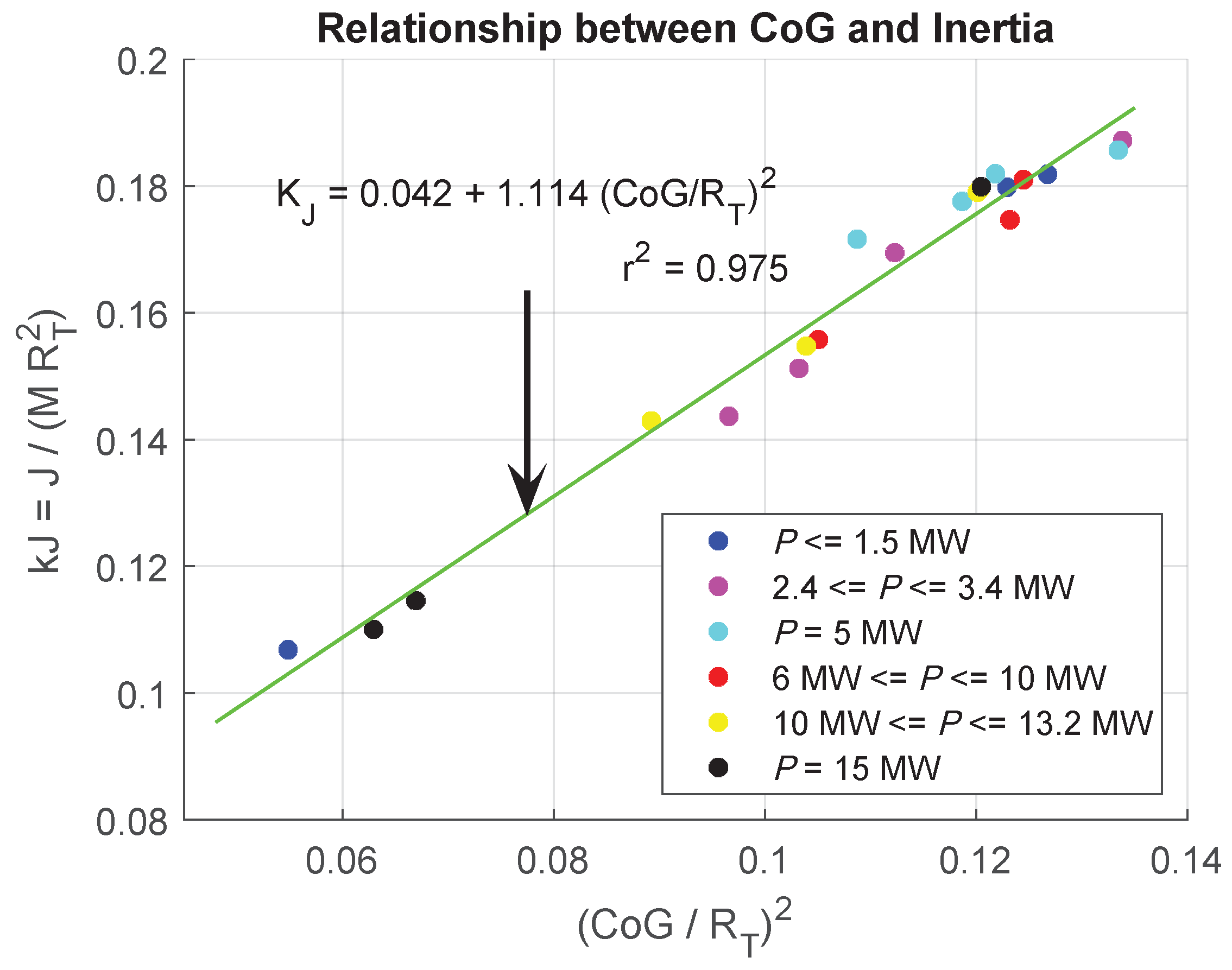
2.5. Evaluation of the Blade Inertia
2.6. Modelling the Drive Train
2.7. Generator Inertia
3. Results
3.1. Expressions Relating to Weight and Blade Length
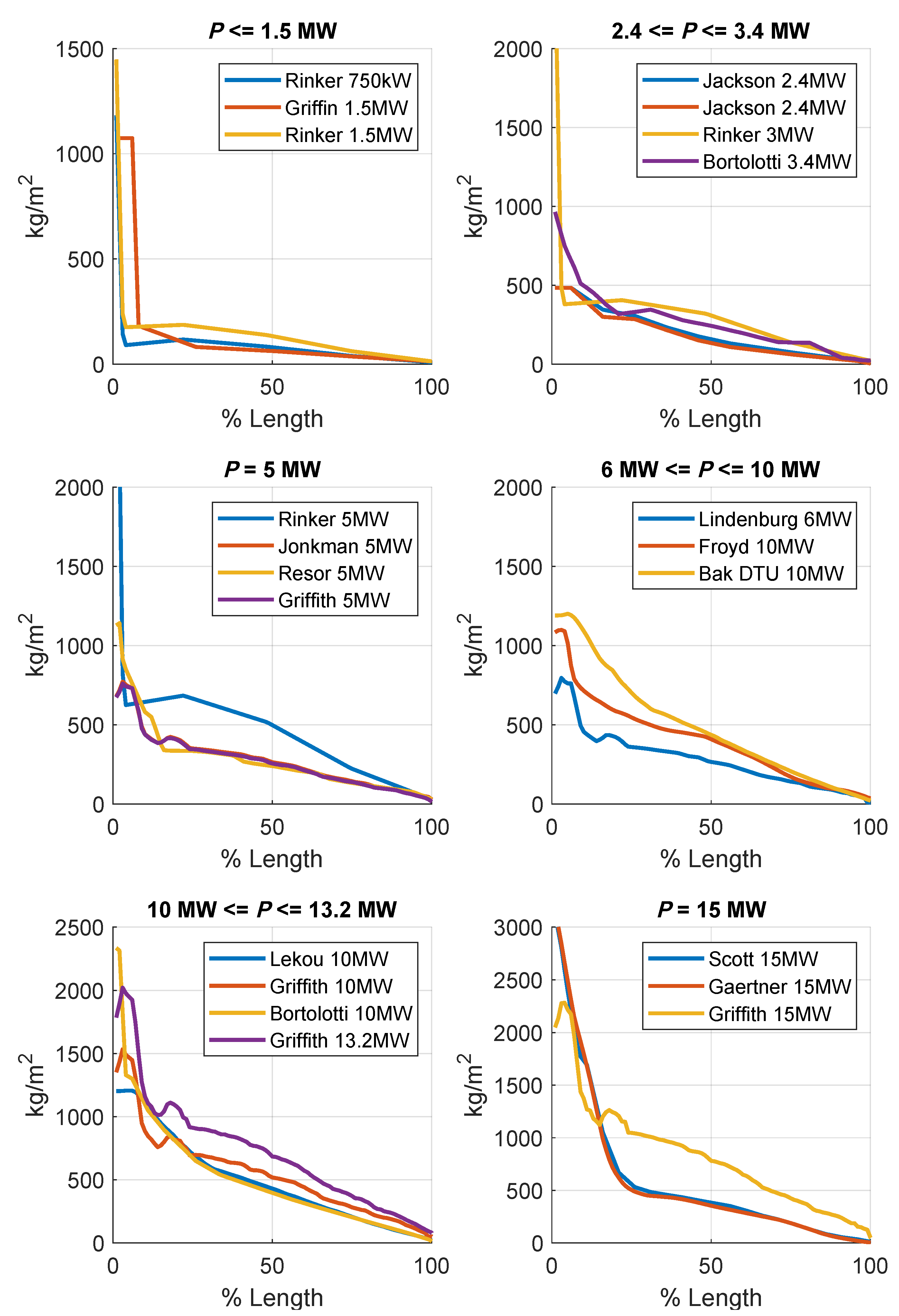
3.2. Inertia Obtained from Density Distribution
- 1.
- Capacity of the turbine for which the blade is designed.
- 2.
- Maximum rotational speed. This matches the rated rotor speed of the turbine.
- 3.
- Blade mass, as extracted from the reference (up) and calculated by the integration (down).
- 4.
- Inertia of the blade, as extracted from the reference (up) and calculated by the integration (down). A value of CoG or inertia appears in cursive when it refers to the blade root instead of the rotation axis.
- 5.
- Inertia of the three blades, as extracted from the reference (up) and calculated by the integration (down). The extracted data have been moved, where necessary, to the rotation axis.
- 6.
- Position of the CoG with respect to the rotation axis, as extracted from the reference (up) and calculated by the integration (down).
- 7.
- Calculated position of the CoG, divided by the the rotor radius.
- 8.
- Value of the coefficient .
- 9.
- Time constant of inertia H.
- 10.
- Reference where data have been obtained.
3.3. Drive Train
3.4. Hub Inertia
3.5. Generator Inertia
4. Discussion
4.1. Article Contribution
4.2. Limitations and Benefits of the Proposed Work
4.3. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AoR | Axis of rotation |
| B | Blade |
| CoG | Center of gravity |
| DD | Density distribution |
| DFIG | Doubly-fed induction generator |
| eq | Equivalent of m2 and turbine |
| G | Generator |
| GB | Gearbox |
| GBG | Shaft joining gearbox and generator |
| HGB | Shaft joining hub and gearbox |
| HSS | High-speed shaft |
| IG | Induction generator |
| LSS | Low-speed shaft |
| m2 | Components at the high-speed side |
| P | Turbine rated capacity |
| PMSG | Permanent magnet synchronous generator |
| T | Turbine or turbine rotor |
| W | Wind |
| WT | Wind turbine |
| The following variables and parameters are used in this manuscript: Magnitude | Symbol [units] | Referred to base [units] |
| Rotational speed | ||
| Torque | T | t |
| Twist angle | ||
| Inertia | J | H |
| Mutual damping | C | c |
| Shelf damping | D | d |
| Torsion stiffness | K | k |
| Kinetic energy | ||
| f | Grid frequency [Hz] | |
| P | Turbine rated capacity [W, also MW when explicitly specified] | |
| Shape coefficient, defined in (47) | ||
| Number of pole pairs | ||
| Gearbox ratio | ||
| r | Correlation index | |
| Relative damping | ||
References
- Li, H.; Zhao, B.; Yang, C.; Chen, H.W.; Chen, Z. Analysis and estimation of transient stability for a grid-connected wind turbine with induction generator. Renew. Energy 2011, 36, 1469–1476. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Vigueras-Rodríguez, A.; Molina-García, Á. Analysis of power system inertia estimation in high wind power plant integration scenarios. IET Renew. Power Gener. 2019, 13, 2807–2816. [Google Scholar] [CrossRef]
- Miao, L.; Wen, J.; Xie, H.; Yue, C.; Lee, W.J. Coordinated Control Strategy of Wind Turbine Generator and Energy Storage Equipment for Frequency Support. IEEE Trans. Ind. Appl. 2015, 51, 2732–2742. [Google Scholar] [CrossRef]
- He, X.; Geng, H.; Mu, G. Modeling of wind turbine generators for power system stability studies: A review. Renew. Sustain. Energy Rev. 2021, 143, 110865. [Google Scholar] [CrossRef]
- Ekanayake, J.; Jenkins, N. Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Morren, J.; Pierik, J.; de Haan, S.W. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M. Effects of the synthetic inertia from wind power on the total system inertia: Simulation study. In Proceedings of the 2012 2nd International Symposium On Environment Friendly Energies And Applications, Newcastle Upon Tyne, UK, 25–27 June 2012; pp. 389–395. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef]
- Girsang, I.P.; Dhupia, J.S.; Muljadi, E.; Singh, M.; Pao, L.Y. Gearbox and drivetrain models to study dynamic effects of modern wind turbines. IEEE Trans. Ind. Appl. 2014, 50, 3777–3786. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Regulski, P.; Novanda, H.; Terzija, P. Effect of the shaft stiffness on the inertial response of the fixed speed wind turbines and its contribution to the system inertia. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; Volume 2. [Google Scholar] [CrossRef]
- Akhmatov, V.; Knudsen, H. An aggregate model of a grid connected, large scale, offshore wind farm for power stability investigations - importance of windmill mechanical system. Electr. Power Energy Syst. 2002, 24, 709–717. [Google Scholar] [CrossRef]
- Rahimi, M. Drive train dynamics assessment and speed controller design in variable speed wind turbines. Renew. Energy 2016, 89, 716–729. [Google Scholar] [CrossRef]
- Frøyd, L.; Dahlhaug, O.G. Rotor design for a 10 MW offshore wind turbine. Proc. Int. Offshore Polar Eng. Conf. 2011, 8, 327–334. [Google Scholar]
- Schubel, P.; Crossley, R. Wind Turbine Blade Design Review. Wind Eng. 2012, 36, 365–388. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G. Review of mass distribution of wind turbine blades. Mendeley Data 2023, V1. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW reference wind turbine for offshore system development. Technical report, NREL, 2009. Available online: https://doi.org/https://doi.org/10.2172/947422 (accessed on 1 June 2023).
- Bywaters, G.; John, V.; Lynch, J.; Mattila, P.; Norton, G.; Stowell, J.; Salata, M.; Labath, O.; Chertok, A.; Hablanian, D. Northern Power Systems WindPACT Drive Train Alternative Design Study Report. Technical Report October 2004, NREL, 2004. Available online: http://www.osti.gov/servlets/purl/15007774/ (accessed on 1 June 2023).
- Fingersh, L.; Hand, M.; Laxson, A. Wind Turbine Design Cost and Scaling Model. NREL 2006, 29, 1–43. [Google Scholar]
- Windturbines Database. Available online: https://en.wind-turbine-models.com/turbines (accessed on 1 June 2023).
- Available online: https://4coffshore.com (accessed on 1 June 2023).
- Lekou, D.J.; Cres, D.C. Results of the benchmark for blade structural models. Technical Report November 2012, InnWind.EU, 2013. Available online: https://orbit.dtu.dk/en/publications/results-of-the-benchmark-for-blade-structural-models-part-a (accessed on 1 June 2023).
- Jackson, K.J.; Zuteck, M.D.; Van Dam, C.P.; Standish, K.J.; Berry, D. Innovative design approaches for large wind turbine blades. Wind Energy 2005, 8, 141–171. [Google Scholar] [CrossRef]
- Rinker, J.; Dykes, K. WindPACT Reference Wind Turbines, 2018. Available online: https://www.nrel.gov/docs/fy18osti/67667.pdf (accessed on 1 June 2023).
- Griffin, D.A. Evaluation of Design Concepts for Adaptive Wind Turbine Blades. Technical report, Sandia National Lab, 2002. Available online: https://doi.org/10.2172/801399 (accessed on 1 June 2023).
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy–WP2.1 Reference Wind Turbines. Available online: https://github.com/IEAWindTask37/IEA-3.4-130-RWT/tree/master/hawc2/data, (accessed on 1 June 2023).
- Resor, B.R. Definition of a 5MW/61.5 m wind turbine blade reference model. Albuquerque, New Mex. USA, Sandia Natl. Lab. SAND2013-2569 2013 2013, 2013, 50. [Google Scholar]
- Lindenburg, C. Aeroelastic Analysis of the LMH64-5 Blade Concept; Technical Report June; Energy Research Centre of the Netherlands ECN: Petten, The Netherlands, 2003. [Google Scholar]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine. Available online: https://github.com/Seager1989/DTU10MW_FAST_LIN/blob/main/Rotor/DTU_10MW_ElastoDyn_Blades.dat (accessed on 1 July 2023).
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy–WP2.1 Reference Wind Turbines. Available online: https://github.com/IEAWindTask37/IEA-10.0-198-RWT/tree/master/hawc2/data (accessed on 1 June 2023).
- Griffith, D.T.; Ashwill, T.D. The Sandia 100-meter All-glass Baseline Wind Turbine Blade: SNL100-00, 2011. https://energy.sandia.gov/wp-content/gallery/uploads/113779A.pdf. (accessed on 1 June 2023).
- IEA Wind - Offshore Reference Wind-15MW. Data. Available online: https://github.com/IEAWindTask37/IEA-15-240-RWT/blob/master/HAWC2/IEA-15-240-RWT/IEA_15MW_RWT_Blade_st_FPM.st, (accessed on 1 July 2023).
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. IEA Wind TCP Task 37, NREL Definition of the IEA Wind 15-Megawatt Offshore Reference Wind Turbine, 2020. Available online: https://www.nrel.gov/docs/fy20osti/75698.pdf (accessed on 1 June 2023).
- Scott, S.; Greaves, P.; Macquart, T.; Pirrera, A. Comparison of blade optimisation strategies for the IEA 15MW reference turbine. J. Phys. Conf. Ser. 2022, 2265. [Google Scholar] [CrossRef]
- Sørensen, P.; Madsen, P.; Vikkelsø, A.; Jensen, K.; Fathima, K.; Unnikrishnan, A.; Lakaparampil, Z. Power quality and integration of wind farms in weak grids in India, 2000. Available online: https://orbit.dtu.dk/en/publications/power-quality-and-integration-of-wind-farms-in-weak-grids-in-indi (accessed on 1 June 2023).
- Carrillo, C.; Feijoo, A.; Cidras, J.; Gonzalez, J. Power fluctuations in an isolated wind plant. IEEE Trans. Energy Convers. 2004, 19, 217–221. [Google Scholar] [CrossRef]
- Chedid, R.; F. Mrad. Intelligent Control of a Class of Wind Energy Conversion Systems. IEEE Trans. Energy Convers. 1999, 14, 1597–1604. [Google Scholar] [CrossRef]
- Garcia, H.; Segundo, J.; Rodríguez, O.; Campos-Amezcua, R.; Jaramillo, O. Harmonic Modelling of the Wind Turbine Induction Generator for Dynamic Analysis of Power Quality. Energies 2018, 11, 104. [Google Scholar] [CrossRef]
- Kayikçi, M.; Milanović, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- Licari, J.; Ekanayake, J.; Moore, I. Inertia response from full-power converter-based permanent magnet wind generators. J. Mod. Power Syst. Clean Energy 2013, 1, 26–33. [Google Scholar] [CrossRef]
- Harrison, S.; Papadopoulos, P.N.; Silva, R.D.; Kinsella, A.; Gutierrez, I.; Egea-Alvarez, A. Impact of Wind Variation on the Measurement of Wind Turbine Inertia Provision. IEEE Access 2021, 9, 122166–122179. [Google Scholar] [CrossRef]
- Mercado-Vargas, M.; Gómez-Lorente, D.; Rabaza, O.; Alameda-Hernandez, E. Aggregated models of permanent magnet synchronous generators wind farms. Renew. Energy 2015, 83, 1287–1298. [Google Scholar] [CrossRef]
- Peeters, J.L.M.; Vandepitte, D.; Sas, P. Analysis of internal drive train dynamics in a wind turbine. Wind Energy 2006, 9, 141–161. [Google Scholar] [CrossRef]
- Petru, T.; Thiringer, T. Modeling of wind turbines for power system studies. IEEE Transactions on Power Systems 2002, 17, 1132–1139. [Google Scholar] [CrossRef]
- Papathanassiou, S.; Papadopoulos, M. Dynamic behavior of variable speed wind turbines under stochastic wind. IEEE Trans. Energy Convers. 1999, 14, 1617–1623. [Google Scholar] [CrossRef]
- Vilar, C.; Usaola, J.; Amarís, H. A frequency domain approach to wind turbines for flicker analysis. IEEE Trans. Energy Convers. 2003, 18, 335–341. [Google Scholar] [CrossRef]
- Rodriguez, J.; Fernandez, J.; Beato, D.; Iturbe, R.; Usaola, J.; Ledesma, P.; Wilhelmi, J. Incidence on power system dynamics of high penetration of fixed speed and doubly fed wind energy systems: Study of the Spanish case. IEEE Trans. Power Syst. 2002, 17, 1089–1095. [Google Scholar] [CrossRef]
- Rahim, Y.; Al-Sabbagh, A. Controlled power transfer from wind driven reluctance generator. IEEE Trans. Energy Convers. 1997, 12, 275–281. [Google Scholar] [CrossRef]
- Xi, J.; Geng, H.; Yang, G.; Ma, S. Inertial response analysis of PMSG-based WECS with VSG control. J. Eng. 2017, 2017, 897–901. [Google Scholar] [CrossRef]
- Mancilla-David, F.; Domínguez-García, J.L.; De Prada, M.; Gomis-Bellmunt, O.; Singh, M.; Muljadi, E. Modeling and control of Type-2 wind turbines for sub-synchronous resonance damping. Energy Convers. Manag. 2015, 97, 315–322. [Google Scholar] [CrossRef]
- Kooijman, H.; Lindenburg, C.; Winkelaar, D.; Hooft. DOWEC 6 MW PRE-DESIGN Aero-elastic modelling of the DOWEC 6 MW pre-design in PHATAS Acknowledgement/Preface. 2003. Available online: https://api.semanticscholar.org/CorpusID:111438322 (accessed on 1 June 2023).
- Sethuraman, L.; Xing, Y.; Gao, Z.; Venugopal, V.; Mueller, M.; Moan, T. A 5MW direct-drive generator for floating spar-buoy wind turbine: Development and analysis of a fully coupled Mechanical model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 718–741. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, X.; Hu, J. Modeling of DFIG Wind Turbine Based on Internal Voltage Motion Equation in Power Systems Phase-Amplitude Dynamics Analysis. IEEE Trans. Power Syst. 2018, 33, 1484–1495. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Wong, K.P. Advanced Control Strategies of PMSG-Based Wind Turbines for System Inertia Support. IEEE Trans. Power Syst. 2017, 32, 3027–3037. [Google Scholar] [CrossRef]





| Type | Pole Pairs | Speed | Drive Train | Ratio P (kW) M (kg) |
|---|---|---|---|---|
| Squirrel cage induction | 2 ÷ 3 | 1000 ÷ 1800 rpm | Three stages, > 50 | 2 |
| Wound rotor induction | 2 ÷ 3 | 1000 ÷ 1800 rpm | Three stages, > 50 | |
| Synchronous | 5 ÷ 12 | 300 ÷ 600 rpm 1 | Two stages = 12 ÷ 45 | |
| Synchronous | 10 ÷ 40 | 100 ÷ 160 rpm | One stage = 10 | |
| Synchronous | 200 ÷ 350 | 10 ÷ 20 | Direct-drive |
| Class I (kg/m) | Class II (kg/m) | Class III (kg/m) | Class IV (kg/m) | Ref | |
|---|---|---|---|---|---|
| 1.5 MW | 163 | 159 | 143 | [22] | |
| 2 MW | 168 | 145 | 131 | [22] | |
| 3 MW | 201.7 | 164.8 | 144.1 | 119.0 | [23] |
| Designed for | Expression | Correlation |
|---|---|---|
| 0.936 | ||
| 0.865 | ||
| IEC Class I | 0.959 | |
| IEC Class II | 0.944 | |
| IEC Class III | 0.994 | |
| GFRP | 0.961 | |
| Hybrid | 0.909 |
| MW | (rpm) | M (kg) | 1 (kg m) | (kg m) | 1 (m) | (s) | Ref. | ||
|---|---|---|---|---|---|---|---|---|---|
| 0.750 | 28.65 | 1941 1940 | 1.806 2.180 | 6.786 6.540 | 8.770 8.764 | 0.351 | 0.180 | 3.924 | [24] |
| 1.500 | 22.50 | 2530 4408 | - 6.360 | - 1.908 | - 8.607 | 0.234 | 0.107 | 3.531 | [25] |
| 1.500 | 20.46 | 4336 4332 | 7.985 9.653 | 3.003 2.896 | 12.47 12.46 | 0.356 | 0.182 | 4.432 | [24] |
| 2.400 | - | 8799 9560 | - 3.910 | - 1.173 | - 16.71 | 0.321 | 0.151 | - | [23] |
| 2.400 | - | 7920 8721 | - 3.388 | - 1.016 | - 16.16 | 0.311 | 0.144 | - | [23] |
| 3.000 | 14.47 | 13,238 13,230 | 5.012 6.070 | 1.884 1.821 | 18.12 18.11 | 0.366 | 0.187 | 6.968 | [24] |
| 3.400 | 8.679 | 16,441 16,466 | - 1.179 | - 3.537 | - 21.78 | 0.335 | 0.169 | 4.297 | [26] |
| 5.000 | 11.19 | 27,854 27,880 | 1.748 2.121 | 6.579 6.362 | 23.42 23.38 | 0.365 | 0.186 | 8.737 | [24] |
| 5.000 | 12.10 | 17,740 16,838 | 1.178 1.216 | 3.896 3.648 | 21.98 21.99 | 0.349 | 0.182 | 5.857 | [17] |
| 5.000 | 11.84 | 17,700 17,012 | 1.178 1.159 | 3.876 3.477 | 0.500 20.77 | 0.330 | 0.172 | 5.348 | [27] |
| 5.000 | 12.10 | 17,740 16,430 | - 1.158 | - 3.474 | 20.50 21.70 | 0.344 | 0.178 | 5.578 | [31] |
| 6.000 | 11.84 | 17,334 17,337 | 1.284 1.330 | 3.850 3.990 | - 22.97 | 0.353 | 0.181 | 5.115 | [28] |
| 10.000 | 12.95 | 27,200 26,773 | - 2.351 | - 7.053 | - 24.75 | 0.349 | 0.175 | 6.485 | [14] |
| 10.000 | 9.600 | - 41,699 | - 5.163 | - 1.549 | - 28.89 | 0.324 | 0.156 | 7.827 | [29] |
| 10.000 | 9.600 | 42,363 41,620 | - 5.072 | - 1.522 | 31.60 28.61 | 0.322 | 0.155 | 7.690 | [22] |
| 10.000 | 8.560 | 50,184 47,104 | - 6.714 | - 2.014 | 29.00 30.91 | 0.347 | 0.180 | 8.092 | [31] |
| 10.000 | 8.680 | 47,700 47,943 | - 6.717 | - 2.015 | - 29.57 | 0.299 | 0.143 | 8.325 | [30] |
| 13.200 | 7.440 | 76,402 71,234 | - 1.340 | - 4.020 | 33.40 35.52 | 0.347 | 0.179 | 9.244 | [31] |
| 15.000 | 7.560 | 68,415 67,003 | - 1.126 | - 3.378 | - 31.34 | 0.259 | 0.115 | 7.058 | [34] |
| 15.000 | 7.560 | 65,250 65,417 | - 1.053 | - 3.160 | 2.970 30.40 | 0.251 | 0.110 | 6.603 | [33] |
| 15.000 | 6.990 | 92,131 86,626 | - 1.855 | - 5.565 | 35.60 37.87 | 0.347 | 0.180 | 9.939 | [31] |
| MW | (rpm) | J () | H (s) | Ref. | |
|---|---|---|---|---|---|
| 0.225 | 42.74 | 23.40:1 | 66,000 | 2.937 | [35] |
| 0.225 | 41.00 | 23.40:1 | 66,058 | 2.706 | [36] |
| 0.350 | 19.21 | 21.81:1 | 3.500 | 2.023 | [37] |
| 0.900 | 22.22 | 67.50:1 | 1.600 | 4.814 | [38] |
| 1.270 | 20.00 | 90.00:1 | 3.716 | 6.417 | [39] |
| 2.000 | 18.00 | 83.33:1 | 6.029 | 5.355 | [40] |
| 3.000 | 16.67 | 3.00:1 | 1.300 | 6.600 1 | [41] |
| 5.000 | 15.00 | 1.00:1 | 2.530 | 6.243 2 | [42] |
| MW | (rpm) | (Nm/rad) (pu/el.rad) | (Nm/rad) (pu/el.rad) | or (Nms/rad) or (pu) | (Nms/rad) (pu) | Ref. | |
|---|---|---|---|---|---|---|---|
| 0.180 | 42.00 | 24 | - | 2700.0 0.52 | - / - | - / - / - | [44] |
| 0.200 | 57.69 | 26 | - | - | 3.500/10.00 | 0.022/0.020/0.010 | [45] |
| 0.225 | 42.74 | 23 | 5.10 1.4 | - | -/- | -/-/- | [35] |
| 0.225 | 41.00 | 23 | - | 2242.0 0.33 | -/- | 334/-/0.61 0.027/-/0.027 | [36] |
| 0.330 | 34.00 | - | 3.181 | 2.301 | 32.19/- | 0.004/-/0.004 | [46] |
| 0.500 | - | - | 54.8 | 1834.1 | 3.500/10.00 | 0.022/0.022/0.035 | [11] |
| 0.600 | - | - | 50.0 | 1834.1 | 1.000/10.00 | 0.005/0.022/0.005 | [47] |
| 0.750 | 28.65 | 63 | 1.30 4.1 | - | 2.78 3.3 | -/-/- | [24] |
| 0.900 | 22.22 | 68 | 6.00 1.1 | - | 1.00 6 | -/-/- | [38] |
| 1.000 | 41.78 | 22 | - | 1.00 24 | -/- | -/-/- | [48] |
| 1.270 | 20.00 | 90 | 2.74 2.5 | - | 5.02 1.7 | -/-/- | [39] |
| 1.500 | 20.46 | 88 | 4.83 3.9 | - | 1.36 4.2 | -/-/- | [24] |
| 1.500 | 20.70 | 1.0 | 2.00 | - | -/- | -/-/- | [49] |
| 1.670 | 16.00 | 75 | 0.60 | - | 1.200 | -/-/- | [13] |
| 2.000 | 18.00 | 83 | 1.60 0.9 | - | 2.50 0.44 | -/-/- | [40] |
| 3.000 | 14.47 | 124.4 | 1.04 2.1 | - | 4.99 3.8 | -/-/- | [24] |
| 5.000 | 12.10 | 97 | 8.68 0.74 | - | 6.22 2/- | -/-/- | [17] |
| 5.000 | 11.19 | 160.8 | 2.30 1.7 | - | 1.49 4.1 | -/-/- | [24] |
| 5.000 | 12.37 | 145.5 | 0.30 | - | 0.00372 | -/-/- | [50] |
| 6.000 | 11.84 | 93 | 3.29 0.22 | 2.78 16 | -/- | -/-/- | [51] |
| MW | (rpm) | J () | H (s) | Ref. | |
|---|---|---|---|---|---|
| 0.750 | 28.65 | 62.832:1 | 5160 | 0.031 | [24] |
| 1.500 | 20.46 | 87.965:1 | 2.998 | 0.046 | [24] |
| 3.000 | 14.47 | 124.407:1 | 1.980 | 0.076 | [24] |
| 5.000 | 11.19 | 160.85:1 | 6.685 | 0.092 | [24] |
| 5.000 | 12.10 | 97.1:1 | 1.160 | 0.019 1 | [31] |
| 5.000 | 12.10 | 97.1:1 | 1.159 | 0.019 1 | [17] |
| 6.000 | 11.84 | 92.873:1 | 5.070 | 0.006 | [51] |
| 10.000 | 8.560 | 137.256:1 | 4.640 | 0.019 1 | [31] |
| 13.200 | 7.440 | 157.918:1 | 8.120 | 0.019 1 | [31] |
| 15.000 | 6.990 | 168.084:1 | 1.040 | 0.019 1 | [31] |
| MW | (rpm) | J () | H (s) | f (Hz) | Ref. | ||
|---|---|---|---|---|---|---|---|
| 0.180 | 42.00 | 23.75:1 | 4.500 | 0.136 | 3 | - | [44] |
| 0.225 | 41.00 | 23.40:1 | 10.00 | 0.224 | 3 | 50 | [36] |
| 0.750 | 28.65 | 62.80:1 | 16.65 | 0.394 | 2 | 60 | [24] |
| 0.900 | 22.22 | 67.50:1 | 35,184 1 | 0.106 | 2 | 50 | [38] |
| 1.270 | 20.00 | 90.00:1 | 84.08 | 1.176 | 2 | - | [39] |
| 1.500 | 20.46 | 88.00:1 | 56.44 | 0.669 | 2 | 60 | [24] |
| 2.000 | 18.00 | 83.33:1 | 416.6 | 2.570 | 2 | - | [40] |
| 3.000 | 14.47 | 124.40:1 | 177.9 | 1.053 | 2 | 60 | [24] |
| 3.000 | 16.67 | 3.00:1 2 | 1.400 | 6.397 | 60 | 50 | [41] |
| 5.000 | 12.10 | 97.10:1 | 534.1 | 0.809 | 3 | - | [17] |
| 5.000 | 11.19 | 160.80:1 | 438.9 | 1.558 | 2 | 60 | [24] |
| 5.000 | 12.10 | 97.10:1 | 534.1 | 0.809 | 3 | - | [31] |
| 5.000 | 12.10 | 1.00:1 | 3.790 | 0.061 | 248.0 | - | [52] |
| 10.000 | 8.560 | 137.26:1 | 2140 | 1.620 | 3 | - | [31] |
| 13.200 | 7.440 | 157.92:1 | 3740 | 2.145 | 3 | - | [31] |
| 15.000 | 6.990 | 168.08:1 | 4800 | 2.422 | 3 | - | [31] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Rodriguez, A.G.; Roldan-Fernandez, J.M.; Nieto-Nieto, L.M. Unveiling Inertia Constants by Exploring Mass Distribution in Wind Turbine Blades and Review of the Drive Train Parameters. Machines 2023, 11, 908. https://doi.org/10.3390/machines11090908
Gonzalez-Rodriguez AG, Roldan-Fernandez JM, Nieto-Nieto LM. Unveiling Inertia Constants by Exploring Mass Distribution in Wind Turbine Blades and Review of the Drive Train Parameters. Machines. 2023; 11(9):908. https://doi.org/10.3390/machines11090908
Chicago/Turabian StyleGonzalez-Rodriguez, Angel Gaspar, Juan Manuel Roldan-Fernandez, and Luis Miguel Nieto-Nieto. 2023. "Unveiling Inertia Constants by Exploring Mass Distribution in Wind Turbine Blades and Review of the Drive Train Parameters" Machines 11, no. 9: 908. https://doi.org/10.3390/machines11090908
APA StyleGonzalez-Rodriguez, A. G., Roldan-Fernandez, J. M., & Nieto-Nieto, L. M. (2023). Unveiling Inertia Constants by Exploring Mass Distribution in Wind Turbine Blades and Review of the Drive Train Parameters. Machines, 11(9), 908. https://doi.org/10.3390/machines11090908









