Enhanced Fatigue Resistance of Nanocrystalline Ni50.8Ti49.2 Wires by Mechanical Training
Abstract
:1. Introduction
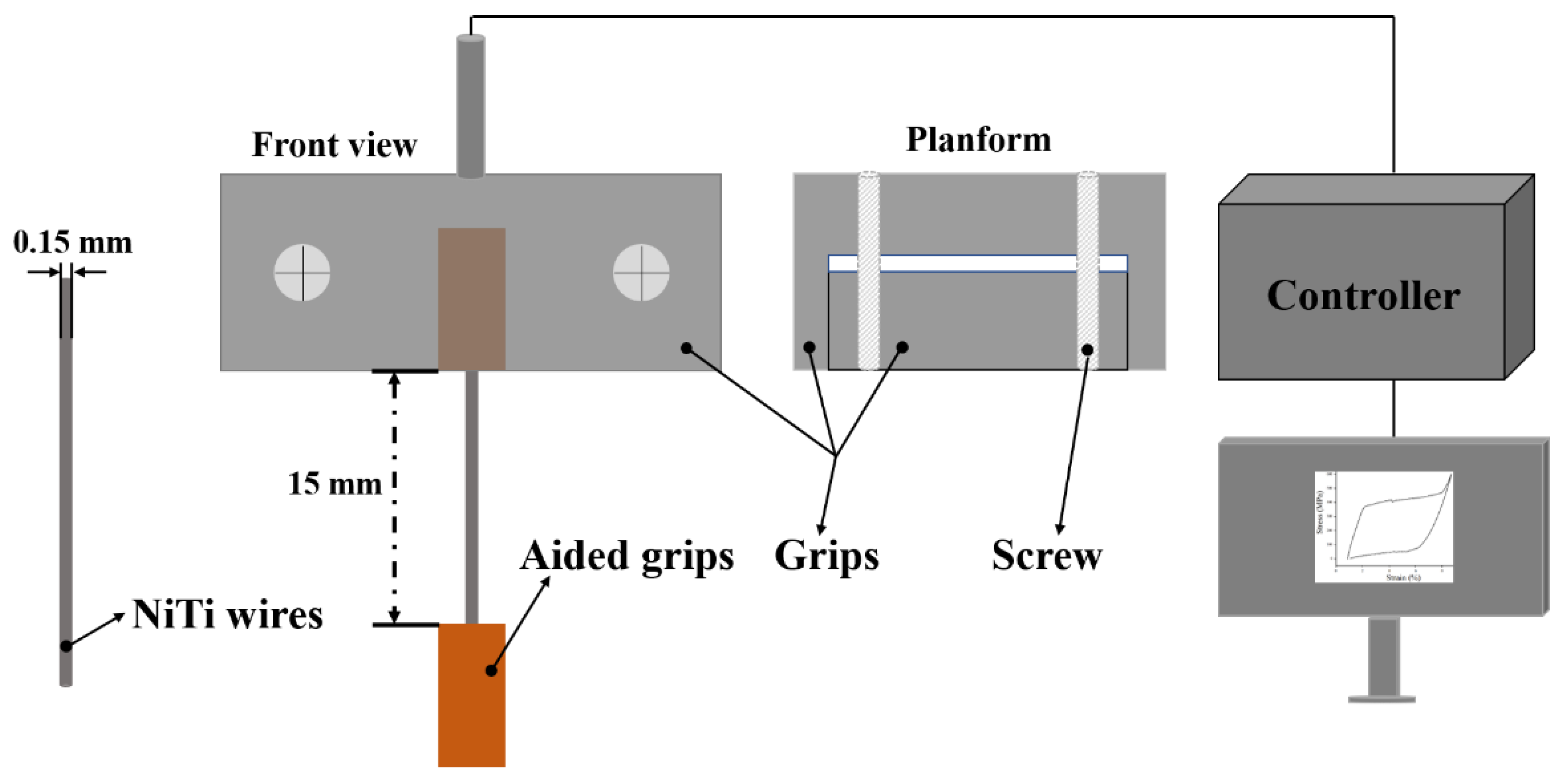
2. Materials and Methods
3. Results
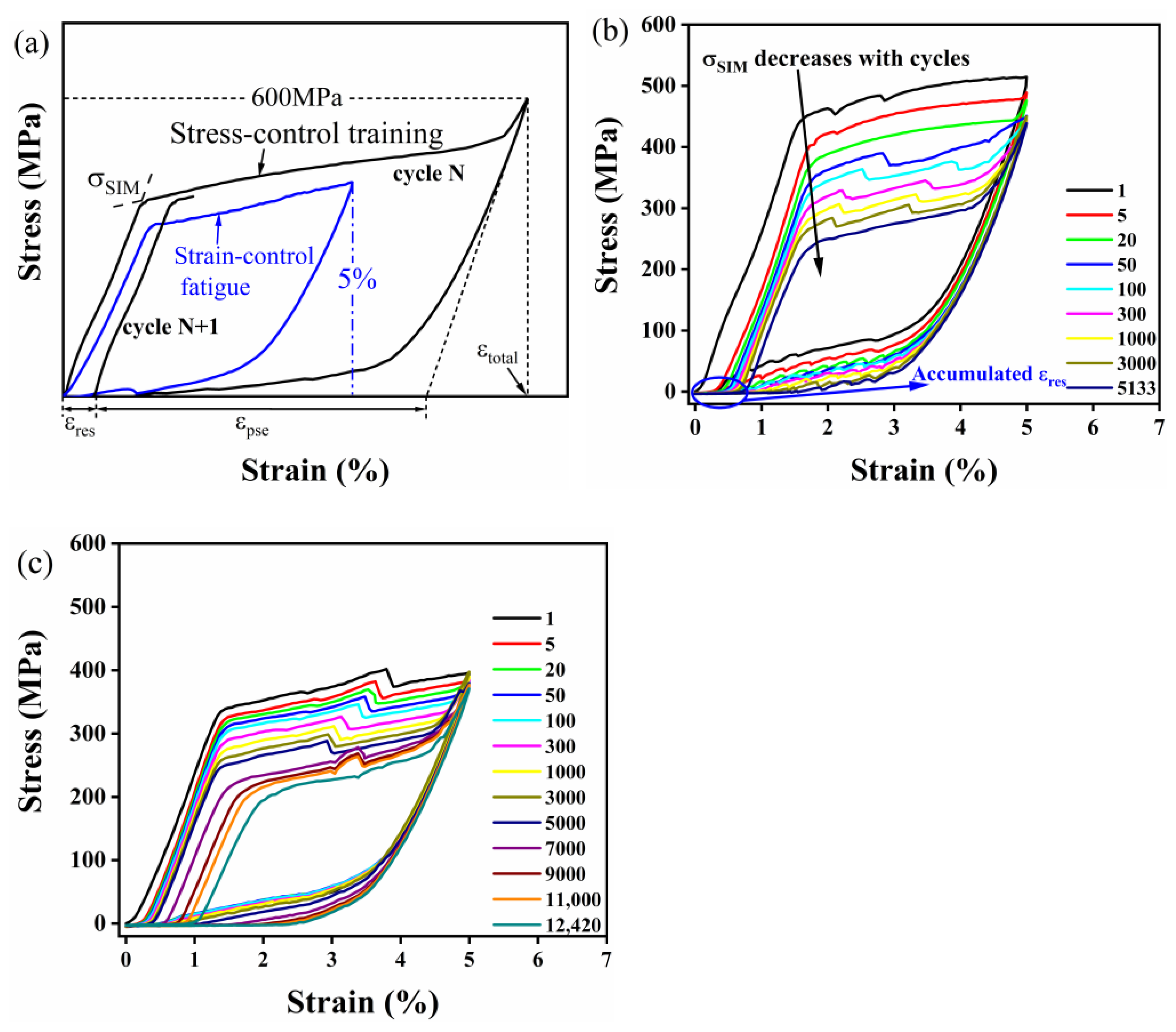
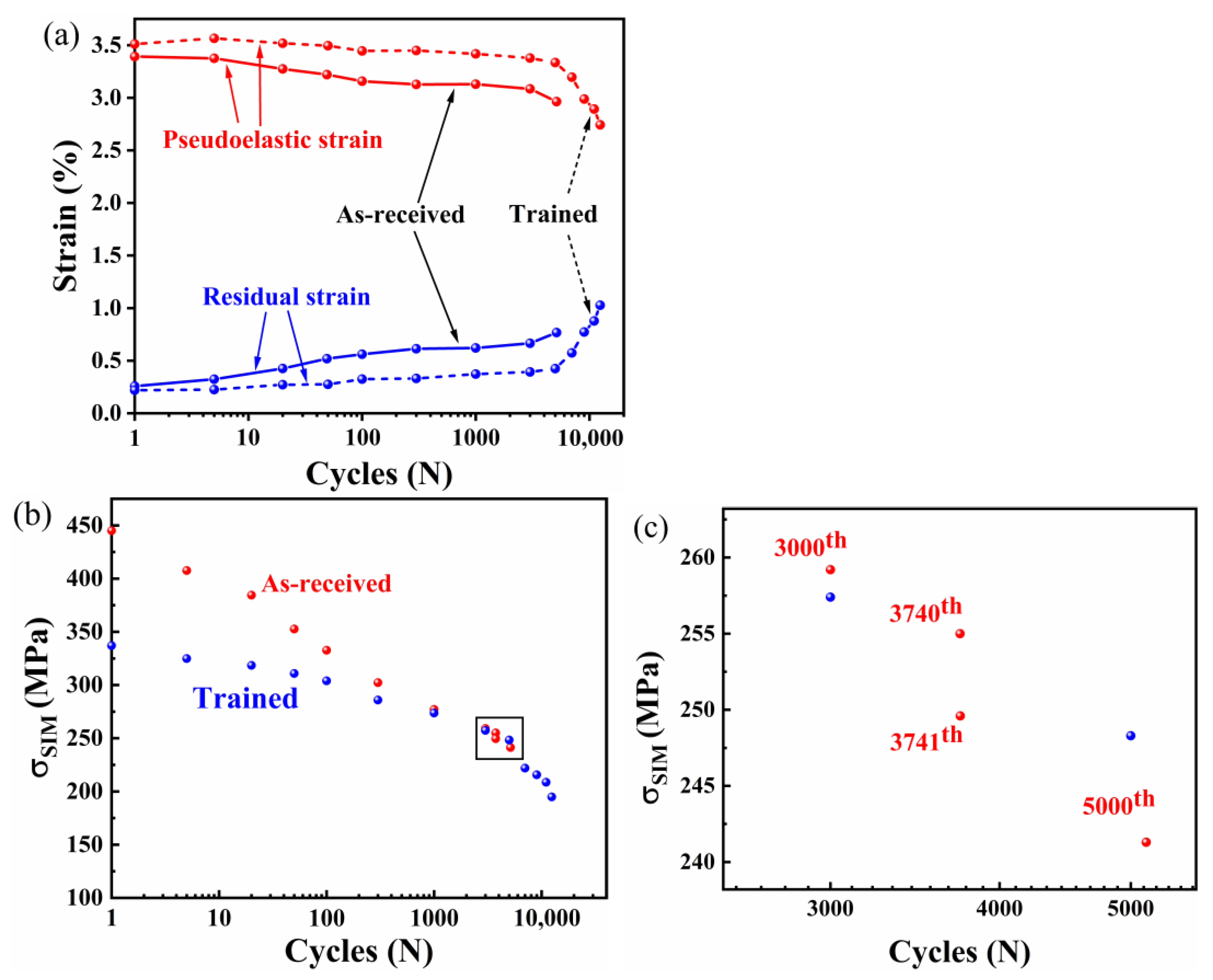
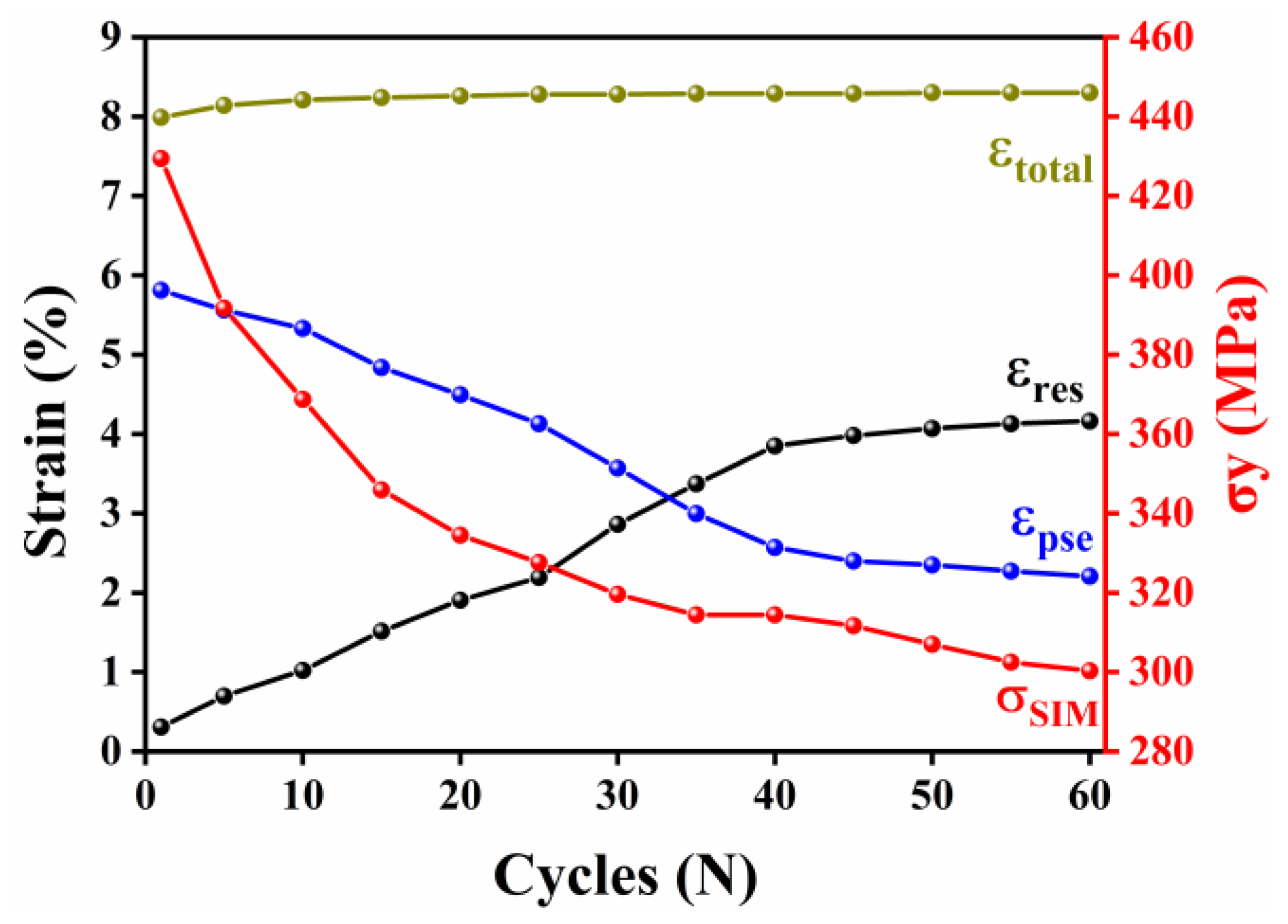
3.1. Mechanical Characterization
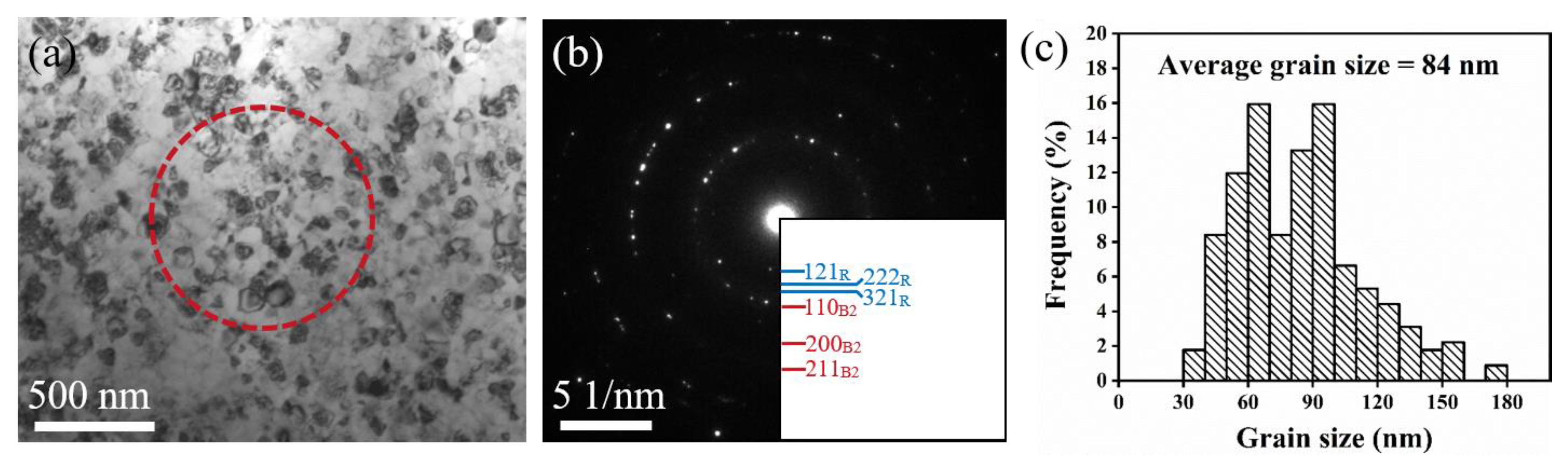
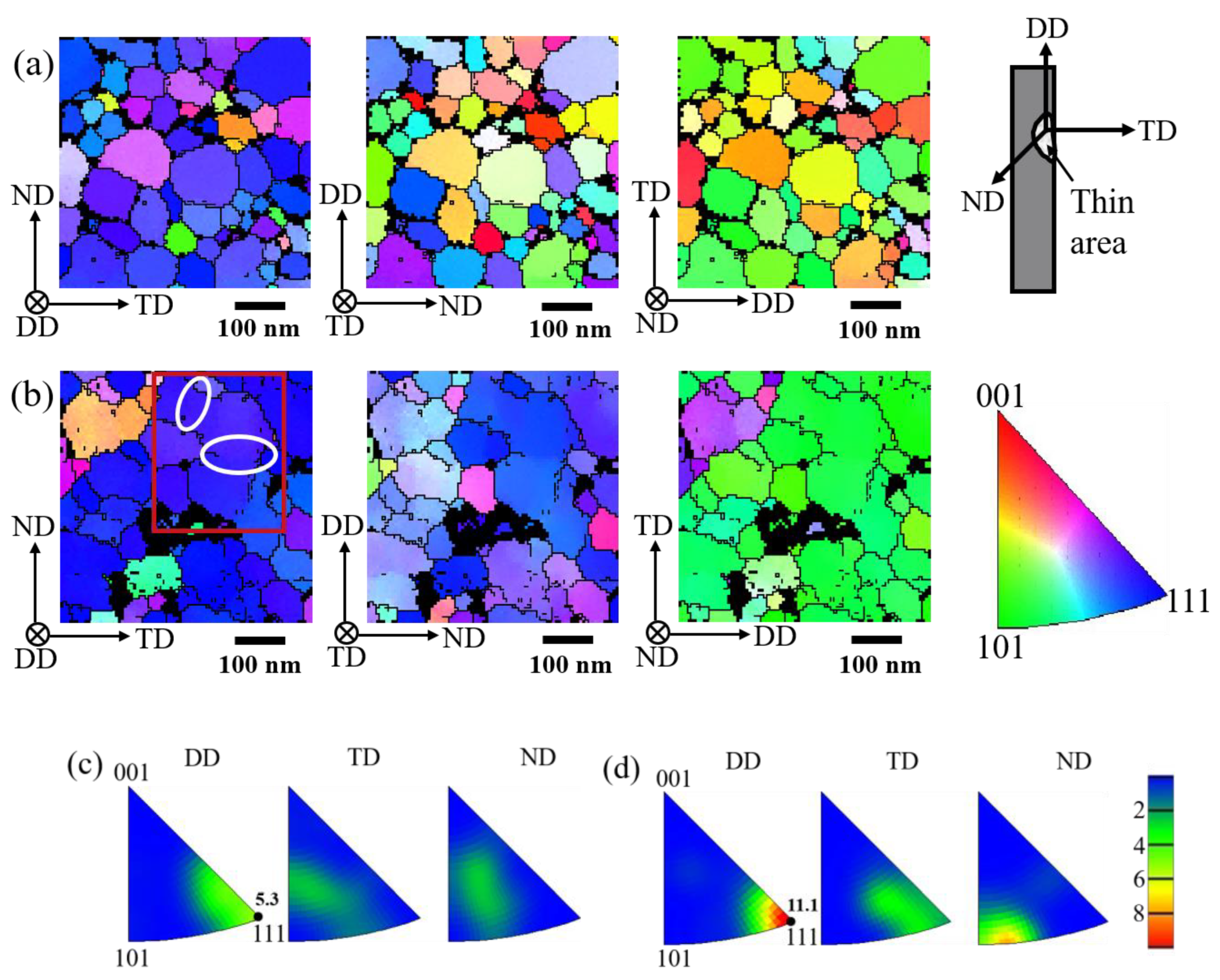
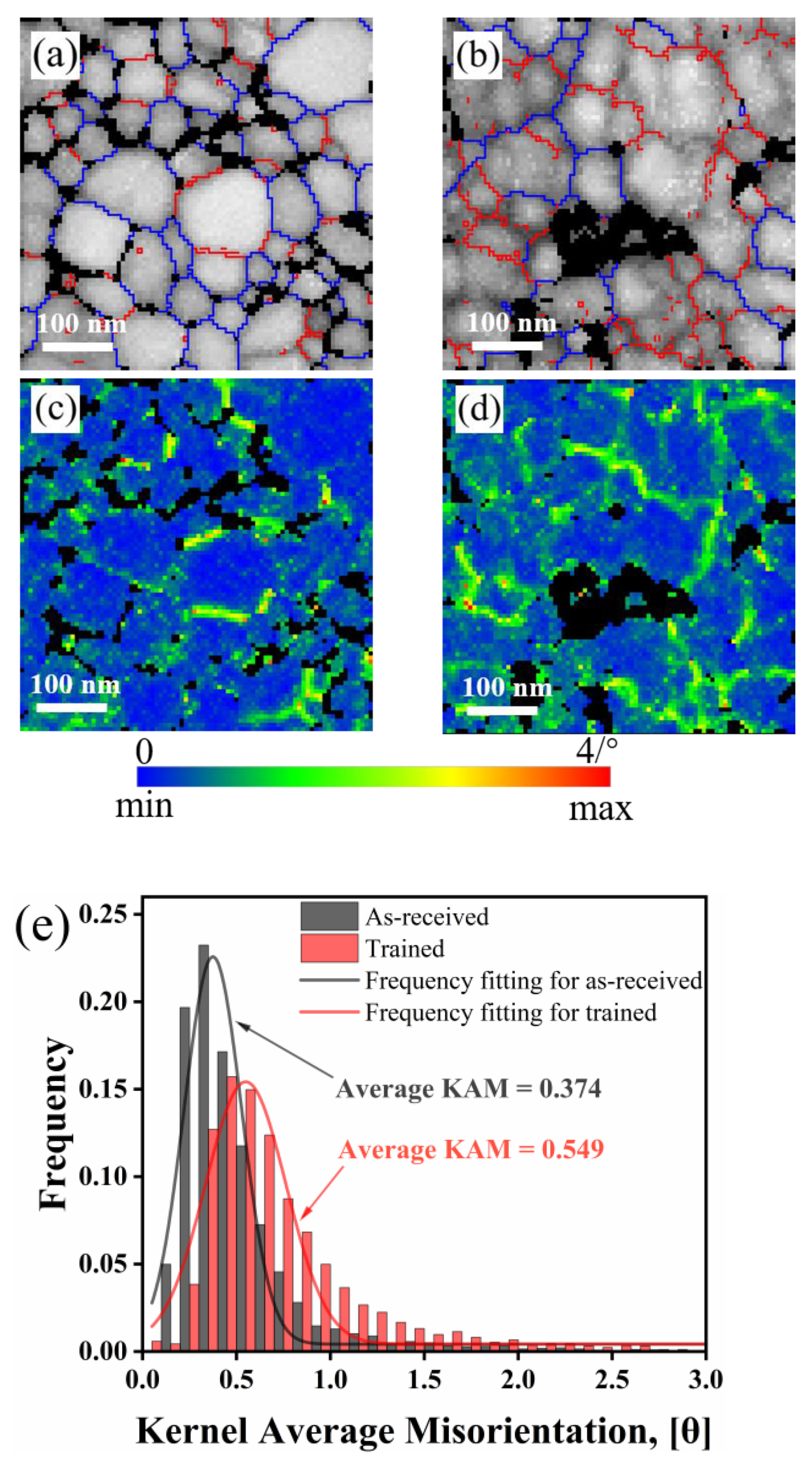
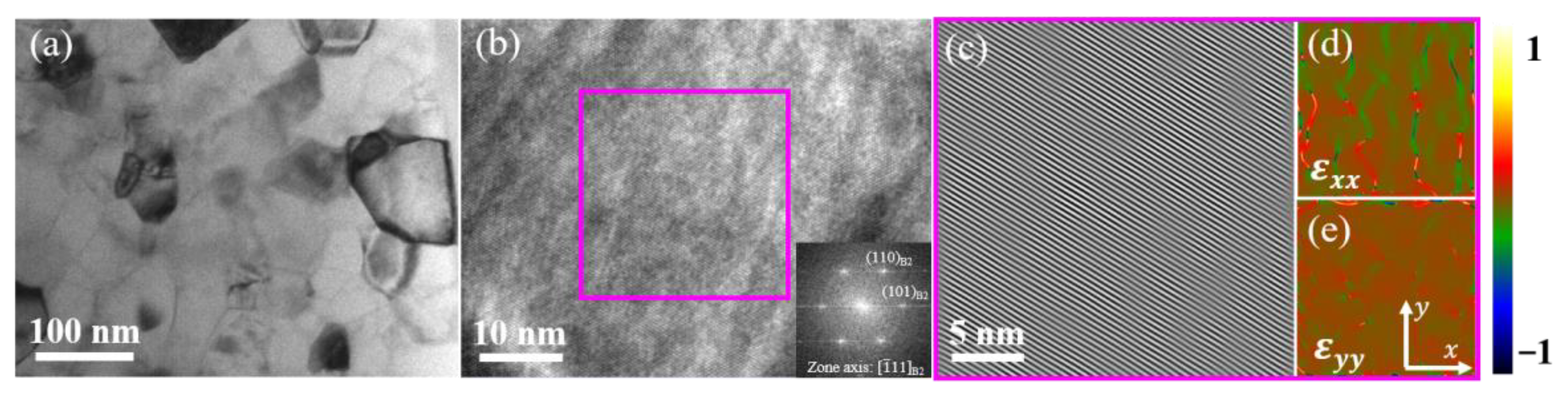
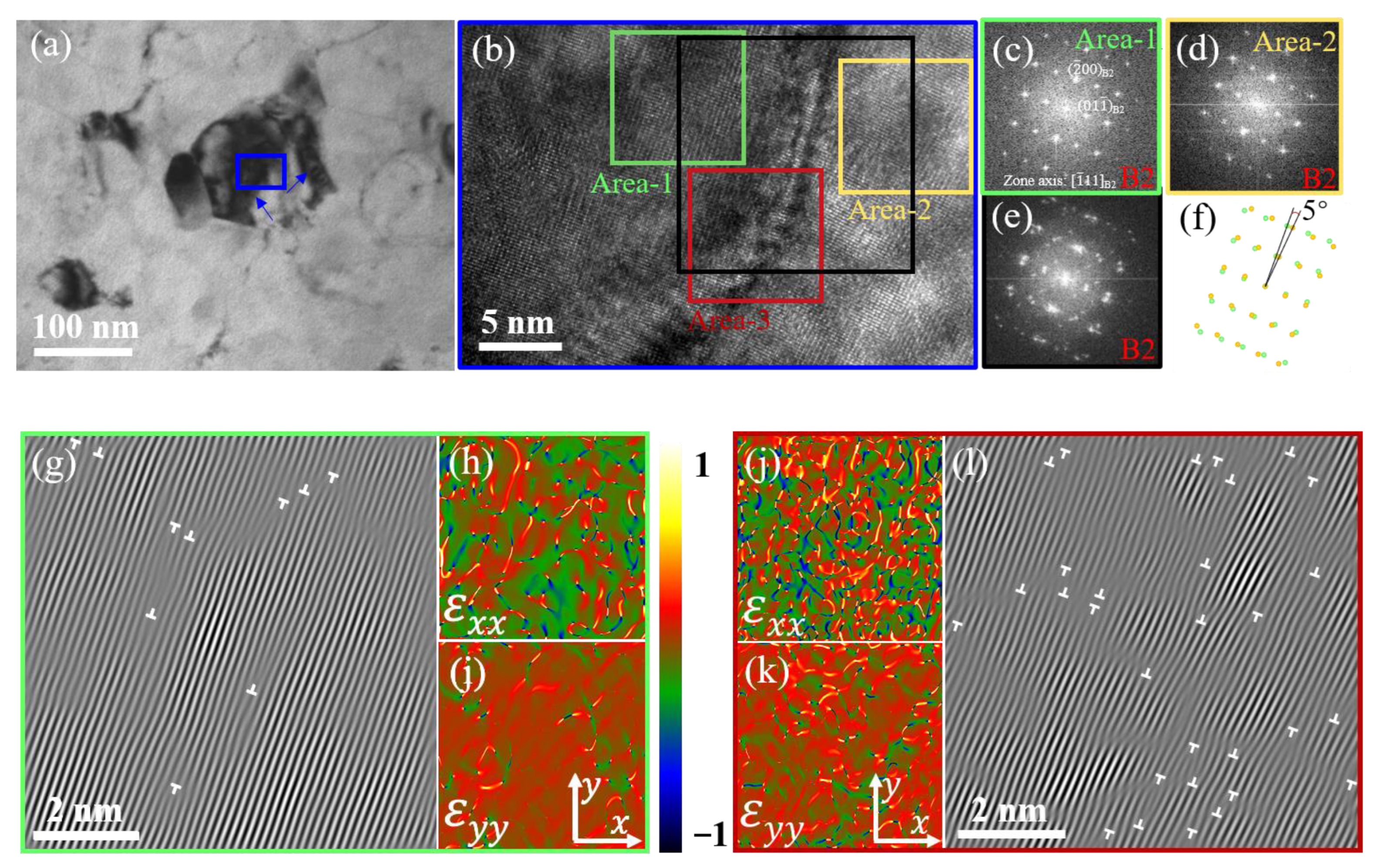
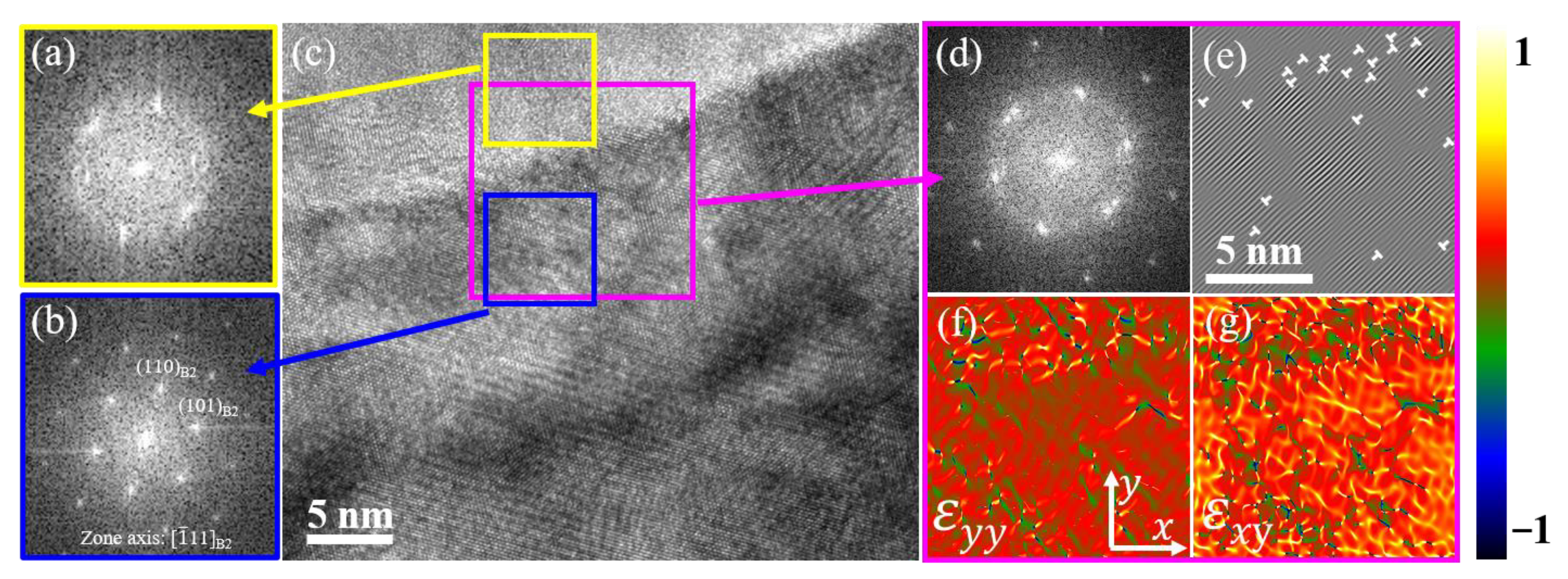
3.2. Microstructure Analysis
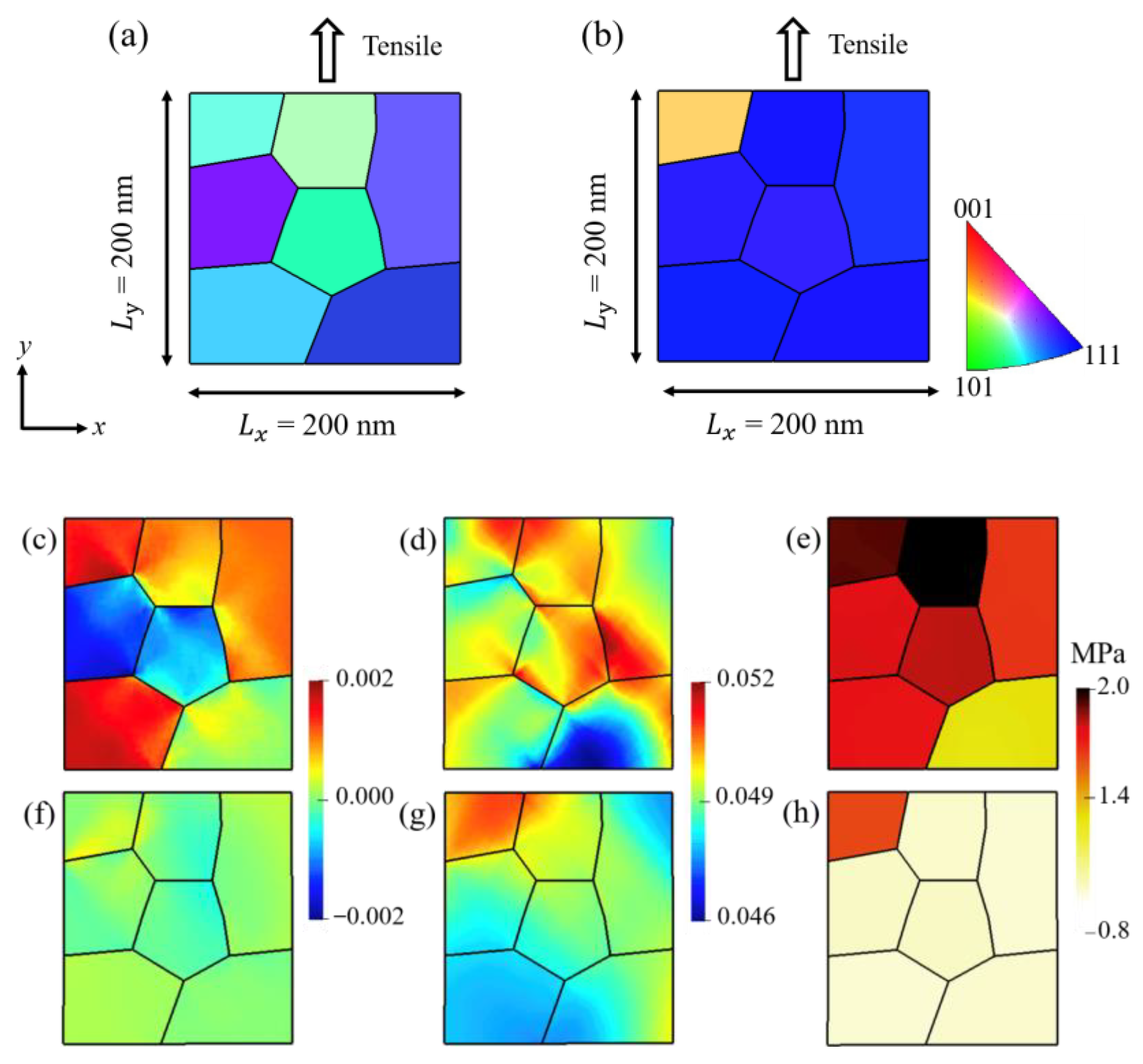
4. Discussion
4.1. Influence of Training on Functional Degradation
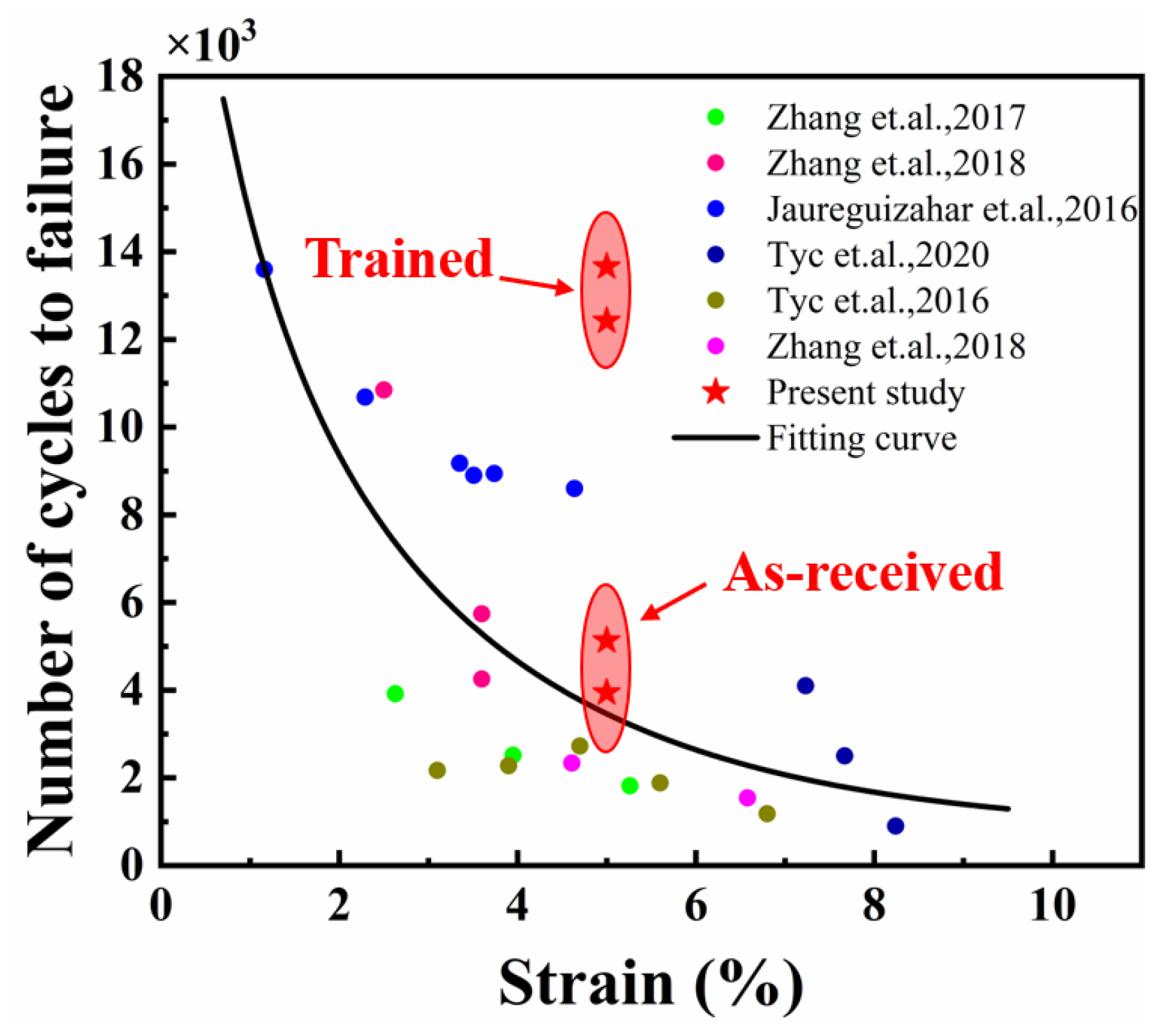
4.2. Influence of Training on Structural Fatigue
5. Conclusions
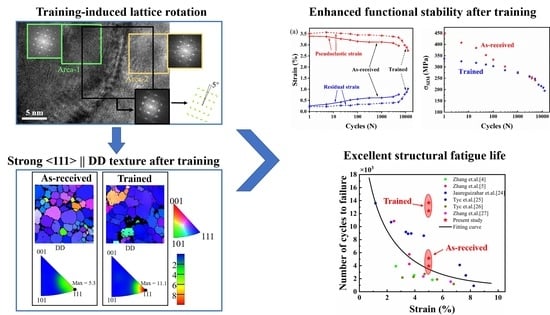
- Using a stress-control mechanical training procedure with a peak stress of 600 MPa for 60 cycles at room temperature, the average structural fatigue life increased from 4538 to 13,040 cycles in the strain-control fatigue tests, with the maximum strain of 5%, and the functional stability was also greatly enhanced.
- Microstructure characterization shows that the <111> texture has been significantly enhanced after training by using the TKD technique. TEM observations demonstrate that the lattice rotation resulting from training-induced dislocations is responsible for the evolution of texture.
- The improvement in fatigue resistance was attributed to the training-induced preferential grain orientation, which led to the reduction of the driving force and an increase in the resistance to crack propagation. Finite element method simulation results reveal that training-enhanced <111> texture contributes to reduce the incompatible deformation between different grains.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shabalovskaya, S.A. On the nature of the biocompatibility and on medical applications of NiTi shape memory and superelastic alloys. Bio-Med. Mater. Eng. 1996, 6, 267–289. [Google Scholar] [CrossRef]
- Drukteinis, S.; Peciuliene, V.; Bendinskaite, R.; Brukiene, V.; Maneliene, R.; Nedzinskiene, E. Shaping Ability, Cyclic Fatigue Resistance and Fractographic Analysis of Hybrid and Reciprocating Nickel Titanium Endodontic Instruments. Metals 2020, 10, 172. [Google Scholar] [CrossRef]
- Hartl, D.J.; Lagoudas, D. Aerospace applications of shape memory alloys. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 221, 535–552. [Google Scholar] [CrossRef]
- Mohd-Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Y.; Moumni, Z.; Anlas, G.; Zhu, J.; Zhang, W. Experimental and theoretical investigation of the frequency effect on low cycle fatigue of shape memory alloys. Int. J. Plast. 2017, 90, 1–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Moumni, Z.; Zhu, J.; Zhang, W. Effect of the amplitude of the training stress on the fatigue lifetime of NiTi shape memory alloys. Scr. Mater. 2018, 149, 66–69. [Google Scholar] [CrossRef]
- Eggeler, G.; Hornbogen, E.; Yawny, A.; Heckmann, A.; Wagner, M. Structural and functional fatigue of NiTi shape memory alloys. Mater. Sci. Eng. A 2004, 378, 24–33. [Google Scholar] [CrossRef]
- Paranjape, H.M.; Bowers, M.L.; Mills, M.J.; Anderson, P.M. Mechanisms for phase transformation induced slip in shape memory alloy micro-crystals. Acta Mater. 2017, 132, 444–454. [Google Scholar] [CrossRef]
- Delville, R.; Malard, B.; Pilch, J.; Sittner, P.; Schryvers, D. Transmission electron microscopy investigation of dislocation slip during superelastic cycling of Ni–Ti wires. Int. J. Plast. 2011, 27, 282–297. [Google Scholar] [CrossRef]
- Delville, R.; Malard, B.; Pilch, J.; Sittner, P.; Schryvers, D. Microstructure changes during non-conventional heat treatment of thin Ni–Ti wires by pulsed electric current studied by transmission electron microscopy. Acta Mater. 2010, 58, 4503–4515. [Google Scholar] [CrossRef]
- Ahadi, A.; Sun, Q. Stress-induced nanoscale phase transition in superelastic NiTi by in situ X-ray diffraction. Acta Mater. 2015, 90, 272–281. [Google Scholar] [CrossRef]
- Robertson, S.W.; Pelton, A.R.; Ritchie, R.O. Mechanical fatigue and fracture of Nitinol. Int. Mater. Rev. 2013, 57, 1–37. [Google Scholar] [CrossRef]
- Glushko, O.; Kiener, D. Initiation of fatigue damage in ultrafine grained metal films. Acta Mater. 2021, 206, 116599. [Google Scholar] [CrossRef]
- Gollerthan, S.; Young, M.; Baruj, A.; Frenzel, J.; Schmahl, W.; Eggeler, G. Fracture mechanics and microstructure in NiTi shape memory alloys. Acta Mater. 2009, 57, 1015–1025. [Google Scholar] [CrossRef]
- Robertson, S.; Mehta, A.; Pelton, A.; Ritchie, R. Evolution of crack-tip transformation zones in superelastic Nitinol subjected to in situ fatigue: A fracture mechanics and synchrotron X-ray microdiffraction analysis. Acta Mater. 2007, 55, 6198–6207. [Google Scholar] [CrossRef]
- Tyc, O.; Molnárová, O.; Šittner, P. Effect of microstructure on fatigue of superelastic NiTi wires. Int. J. Fatigue 2021, 152, 106400. [Google Scholar] [CrossRef]
- Zhang, K.; Kang, G.; Sun, Q. High fatigue life and cooling efficiency of NiTi shape memory alloy under cyclic compression. Scr. Mater. 2019, 159, 62–67. [Google Scholar] [CrossRef]
- Chen, J.; Yin, H.; Sun, Q. Effects of grain size on fatigue crack growth behaviors of nanocrystalline superelastic NiTi shape memory alloys. Acta Mater. 2020, 195, 141–150. [Google Scholar] [CrossRef]
- Xie, G.; Wang, F.; Song, B.; Cheng, J.; Wang, J.; Zeng, X. Grain size dependence of cracking performance in polycrystalline NiTi alloys. J. Alloy. Compd. 2021, 884, 161132. [Google Scholar] [CrossRef]
- Yin, H.; He, Y.; Moumni, Z.; Sun, Q. Effects of grain size on tensile fatigue life of nanostructured NiTi shape memory alloy. Int. J. Fatigue 2016, 88, 166–177. [Google Scholar] [CrossRef]
- Karakoc, O.; Atli, K.; Evirgen, A.; Pons, J.; Santamarta, R.; Benafan, O.; Noebe, R.; Karaman, I. Effects of training on the thermomechanical behavior of NiTiHf and NiTiZr high temperature shape memory alloys. Mater. Sci. Eng. A 2020, 794, 139857. [Google Scholar] [CrossRef]
- Hayrettin, C.; Karakoc, O.; Karaman, I.; Mabe, J.; Santamarta, R.; Pons, J. Two way shape memory effect in NiTiHf high temperature shape memory alloy tubes. Acta Mater. 2019, 163, 1–13. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Vokoun, D.; Hu, C.-T. Two-way shape memory effect of NiTi alloy induced by constraint aging treatment at room temperature. Met. Mater. Trans. A 2001, 32, 1629–1634. [Google Scholar] [CrossRef]
- Chu, K.; Sun, Q. Reducing functional fatigue, transition stress and hysteresis of NiTi micropillars by one-step overstressed plastic deformation. Scr. Mater. 2021, 201, 113958. [Google Scholar] [CrossRef]
- Perkins, J.; Bobowiec, P. Microstructural effects of martensitic transformation cycling of a Cu-Zn-Al alloy: Vestigial structures in the parent phase. Met. Mater. Trans. A 1986, 17, 195–203. [Google Scholar] [CrossRef]
- Trimby, P.W. Orientation mapping of nanostructured materials using transmission Kikuchi diffraction in the scanning electron microscope. Ultramicroscopy 2012, 120, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Trimby, P.W.; Cao, Y.; Chen, Z.; Han, S.; Hemker, K.J.; Lian, J.; Liao, X.; Rottmann, P.; Samudrala, S.; Sun, J.; et al. Characterizing deformed ultrafine-grained and nanocrystalline materials using transmission Kikuchi diffraction in a scanning electron microscope. Acta Mater. 2014, 62, 69–80. [Google Scholar] [CrossRef]
- Jaureguizahar, S.M.; Chapetti, M.D.; Yawny, A.A. Fatigue of NiTi shape memory wires. Procedia Struct. Integr. 2016, 2, 1427–1434. [Google Scholar] [CrossRef]
- Tyc, O.; Heller, L.; Vronka, M.; Šittner, P. Effect of temperature on fatigue of superelastic NiTi wires. Int. J. Fatigue 2020, 134, 105470. [Google Scholar] [CrossRef]
- Tyc, O.; Pilch, J.; Sittner, P. Fatigue of superelastic NiTi wires with different plateau strain. Procedia Struct. Integr. 2016, 2, 1489–1496. [Google Scholar] [CrossRef]
- Zhang, Y.; Moumni, Z.; You, Y.; Zhang, W.; Zhu, J.; Anlas, G. Multiscale TRIP-based investigation of low-cycle fatigue of polycrystalline NiTi shape memory alloys. Int. J. Plast. 2018, 115, 307–329. [Google Scholar] [CrossRef]
- Hua, P.; Lin, H.; Sun, Q. Ultrahigh cycle fatigue deformation of polycrystalline NiTi micropillars. Scr. Mater. 2021, 203, 114108. [Google Scholar] [CrossRef]
- Cai, X.; Handwerker, C.A.; Blendell, J.E.; Koslowski, M. Shallow grain formation in Sn thin films. Acta Mater. 2020, 192, 1–10. [Google Scholar] [CrossRef]
- Jahedi, M.; Ardeljan, M.; Beyerlein, I.J.; Paydar, M.H.; Knezevic, M. Enhancement of orientation gradients during simple shear deformation by application of simple compression. J. Appl. Phys. 2015, 117, 214309. [Google Scholar] [CrossRef]
- Motz, C.; Schöberl, T.; Pippan, R. Mechanical properties of micro-sized copper bending beams machined by the focused ion beam technique. Acta Mater. 2005, 53, 4269–4279. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y.; Nix, W.; Hutchinson, J. Mechanism-based strain gradient plasticity? I. Theory. J. Mech. Phys. Solids 1999, 47, 1239–1263. [Google Scholar] [CrossRef]
- Xiao, Y.; Zeng, P.; Lei, L.; Zhang, Y. In situ observation on temperature dependence of martensitic transformation and plastic deformation in superelastic NiTi shape memory alloy. Mater. Des. 2017, 134, 111–120. [Google Scholar] [CrossRef]
- Gao, Y.; Casalena, L.; Bowers, M.; Noebe, R.; Mills, M.; Wang, Y. An origin of functional fatigue of shape memory alloys. Acta Mater. 2017, 126, 389–400. [Google Scholar] [CrossRef]
- Šittner, P.; Molnárová, O.; Kaderavek, L.; Tyc, O.; Heller, L. Deformation twinning in martensite affecting functional behavior of NiTi shape memory alloys. Materialia 2020, 9, 100506. [Google Scholar] [CrossRef]
- Chen, Y.; Tyc, O.; Kadeřávek, L.; Molnárová, O.; Heller, L.; Šittner, P. Temperature and microstructure dependence of localized tensile deformation of superelastic NiTi wires. Mater. Des. 2019, 174, 107797. [Google Scholar] [CrossRef]
- Polatidis, E.; Šmíd, M.; Kuběna, I.; Hsu, W.-N.; Laplanche, G.; Van Swygenhoven, H. Deformation mechanisms in a superelastic NiTi alloy: An in-situ high resolution digital image correlation study. Mater. Des. 2020, 191, 108622. [Google Scholar] [CrossRef]
- Belyaev, S.; Resnina, N.; Ponikarova, I.; Iaparova, E.; Rakhimov, T.; Ivanova, A.; Tabachkova, N.; Andreev, V. Damage of the martensite interfaces as the mechanism of the martensite stabilization effect in the NiTi shape memory alloys. J. Alloy. Compd. 2022, 921, 166189. [Google Scholar] [CrossRef]
- Polatidis, E.; Zotov, N.; Bischoff, E.; Mittemeijer, E. The effect of cyclic tensile loading on the stress-induced transformation mechanism in superelastic NiTi alloys: An in-situ X-ray diffraction study. Scr. Mater. 2015, 100, 59–62. [Google Scholar] [CrossRef]
- Li, H.; Chen, T.; Li, W.; Zhang, H.; Han, S.; Zhou, C.; Chen, Z.; Flores-Johnson, E.A.; Shen, L.; Lian, J.; et al. Grain size dependent microstructure and texture evolution during dynamic deformation of nanocrystalline face-centered cubic materials. Acta Mater. 2021, 216, 117088. [Google Scholar] [CrossRef]
- Madhavan, R.; Ray, R.; Suwas, S. Texture transition in cold-rolled nickel–40wt.% cobalt alloy. Acta Mater. 2014, 74, 151–164. [Google Scholar] [CrossRef]
- Madhavan, R.; Suwas, S. Micro-mechanisms of deformation texture evolution in nanocrystalline nickel-cobalt alloys. Acta Mater. 2016, 121, 46–58. [Google Scholar] [CrossRef]
- Buchheit, T.E.; Wert, J.A. Predicting the orientation-dependent stress-induced transformation and detwinning response of shape memory alloy single crystals. Met. Mater. Trans. A 1996, 27, 269–279. [Google Scholar] [CrossRef]
- Ono, N.; Satoh, A.; Ohta, H. A Discussion on the Mechanical Properties of Shape Memory Alloys Based on a Polycrystal Model. Mater. Trans. JIM 1989, 30, 756–764. [Google Scholar] [CrossRef]
- Alger, B.; Andrš, D.; Carlsen, R.W.; Gaston, D.R.; Kong, F.; Lindsay, A.D.; Miller, J.M.; Permann, C.J.; Peterson, J.W.; Slaughter, A.E.; et al. MOOSE Web Page. 2020. Available online: https://mooseframework.org (accessed on 2 August 2021).
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity: Volume 7 of Interdisciplinary Applied Mathematics; Springer: Secaucus, NJ, USA, 1998. [Google Scholar]
- Xu, L.; Solomou, A.; Baxevanis, T.; Lagoudas, D. Finite strain constitutive modeling for shape memory alloys considering transformation-induced plasticity and two-way shape memory effect. Int. J. Solids Struct. 2020, 221, 42–59. [Google Scholar] [CrossRef]
- Wagner, M.F.-X.; Windl, W. Elastic anisotropy of Ni4Ti3 from first principles. Scr. Mater. 2009, 60, 207–210. [Google Scholar] [CrossRef]
- Lackmann, J.; Niendorf, T.; Maxisch, M.; Grundmeier, G.; Maier, H. High-resolution in-situ characterization of the surface evolution of a polycrystalline NiTi SMA-alloy under pseudoelastic deformation. Mater. Charact. 2011, 62, 298–303. [Google Scholar] [CrossRef]
- Griffith, A.A. VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A 1920, 221, 163–198. [Google Scholar]
- Paranjape, H.; Anderson, P.M. Texture and grain neighborhood effects on Ni–Ti shape memory alloy performance. Model. Simul. Mater. Sci. Eng. 2014, 22, 075002. [Google Scholar] [CrossRef]
- Rahim, M.; Frenzel, J.; Frotscher, M.; Pfetzing-Micklich, J.; Steegmüller, R.; Wohlschlögel, M.; Mughrabi, H.; Eggeler, G. Impurity levels and fatigue lives of pseudoelastic NiTi shape memory alloys. Acta Mater. 2013, 61, 3667–3686. [Google Scholar] [CrossRef]
- Cervellon, A.; Hémery, S.; Kürnsteiner, P.; Gault, B.; Kontis, P.; Cormier, J. Crack initiation mechanisms during very high cycle fatigue of Ni-based single crystal superalloys at high temperature. Acta Mater. 2020, 188, 131–144. [Google Scholar] [CrossRef]
- Frenzel, J. On the Importance of Structural and Functional Fatigue in Shape Memory Technology. Shape Mem. Superelasticity 2020, 6, 213–222. [Google Scholar] [CrossRef]
- Hua, P.; Chu, K.; Ren, F.; Sun, Q. Cyclic phase transformation behavior of nanocrystalline NiTi at microscale. Acta Mater. 2020, 185, 507–517. [Google Scholar] [CrossRef]
- Karakoc, O.; Hayrettin, C.; Canadinc, D.; Karaman, I. Role of applied stress level on the actuation fatigue behavior of NiTiHf high temperature shape memory alloys. Acta Mater. 2018, 153, 156–168. [Google Scholar] [CrossRef]
- Hou, H.; Simsek, E.; Ma, T.; Johnson, N.S.; Qian, S.; Cissé, C.; Stasak, D.; Al Hasan, N.; Zhou, L.; Hwang, Y.; et al. Fatigue-resistant high-performance elastocaloric materials made by additive manufacturing. Science 2019, 366, 1116–1121. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Cai, X.; Min, N.; Liu, Y.; Wang, Z.; Jin, M.; Jin, X. Enhanced Fatigue Resistance of Nanocrystalline Ni50.8Ti49.2 Wires by Mechanical Training. Metals 2023, 13, 361. https://doi.org/10.3390/met13020361
Chen P, Cai X, Min N, Liu Y, Wang Z, Jin M, Jin X. Enhanced Fatigue Resistance of Nanocrystalline Ni50.8Ti49.2 Wires by Mechanical Training. Metals. 2023; 13(2):361. https://doi.org/10.3390/met13020361
Chicago/Turabian StyleChen, Peng, Xiaorong Cai, Na Min, Yunfan Liu, Zhengxiong Wang, Mingjiang Jin, and Xuejun Jin. 2023. "Enhanced Fatigue Resistance of Nanocrystalline Ni50.8Ti49.2 Wires by Mechanical Training" Metals 13, no. 2: 361. https://doi.org/10.3390/met13020361
APA StyleChen, P., Cai, X., Min, N., Liu, Y., Wang, Z., Jin, M., & Jin, X. (2023). Enhanced Fatigue Resistance of Nanocrystalline Ni50.8Ti49.2 Wires by Mechanical Training. Metals, 13(2), 361. https://doi.org/10.3390/met13020361