Estimating the Cowper–Symonds Parameters for High-Strength Steel Using DIC Combined with Integral Measures of Deviation
Abstract
:1. Introduction
- Multi-phase high yield strength steel (MP800HY), according to [28],
- The selected testing method and the achieved strain rates have a significant influence on the estimated parameters. In general, the higher the strain rates achieved, the higher the parameter C.
- The two parameters C and p are not independent but are strongly correlated.
- The considered strain-rate range influences the estimated parameters C and p.
- The forms of the applied Cowper–Symonds model may be different.
- How the cost function for estimating the strain-rate dependent parameters is defined is important.
2. Materials and Methods
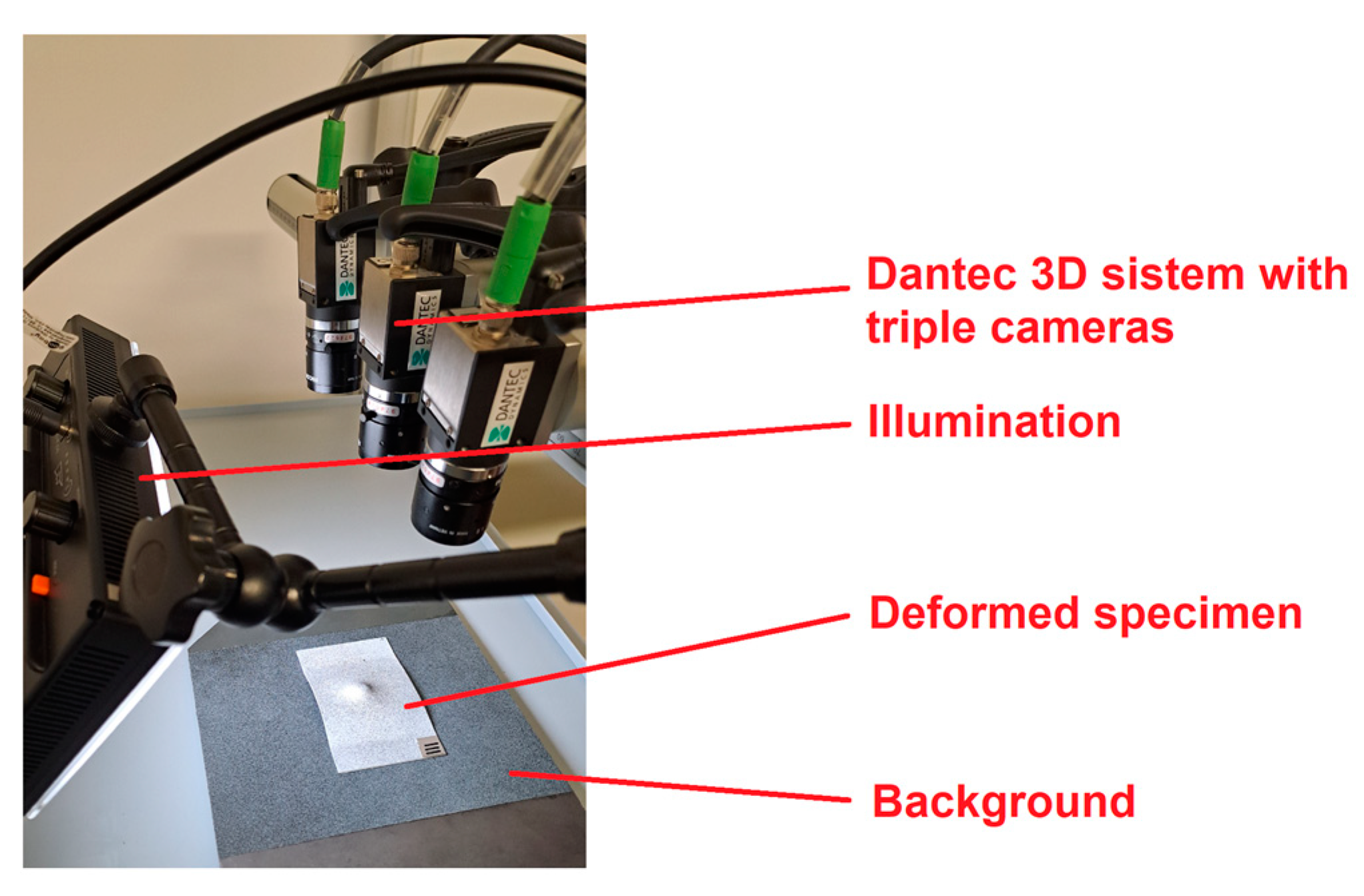
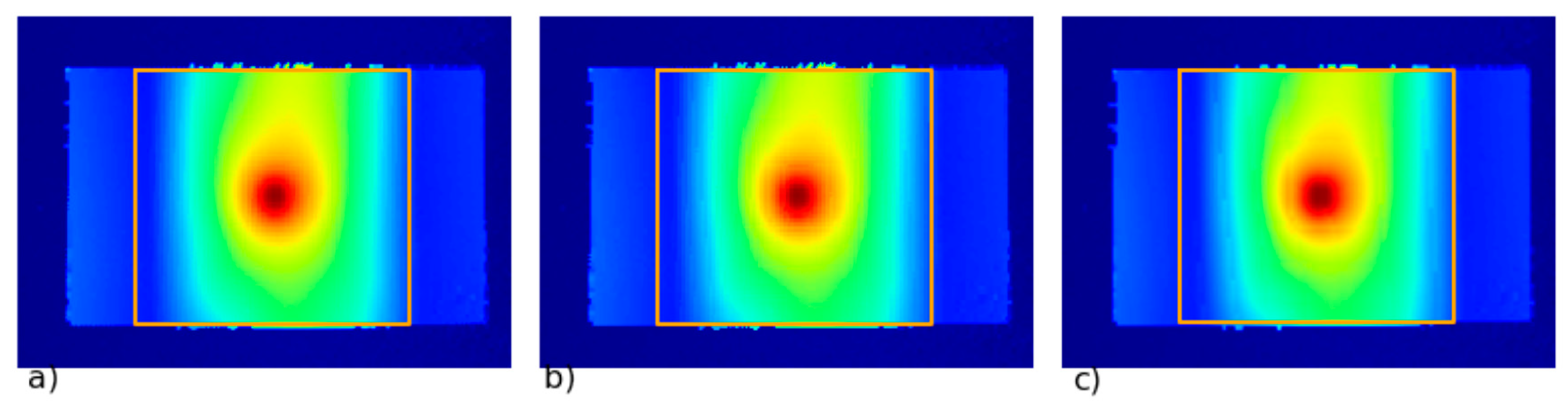
2.1. Experimental Setup
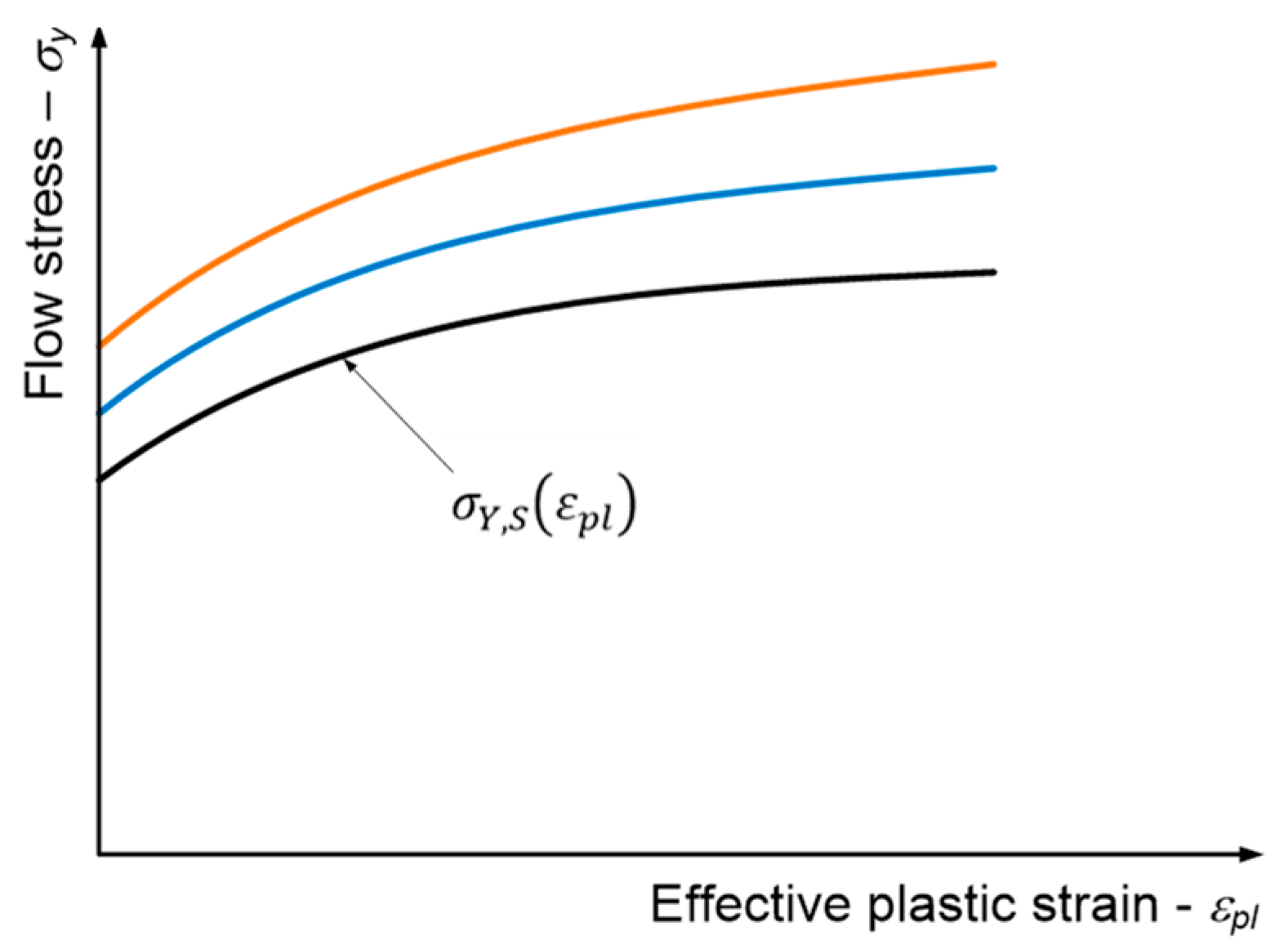
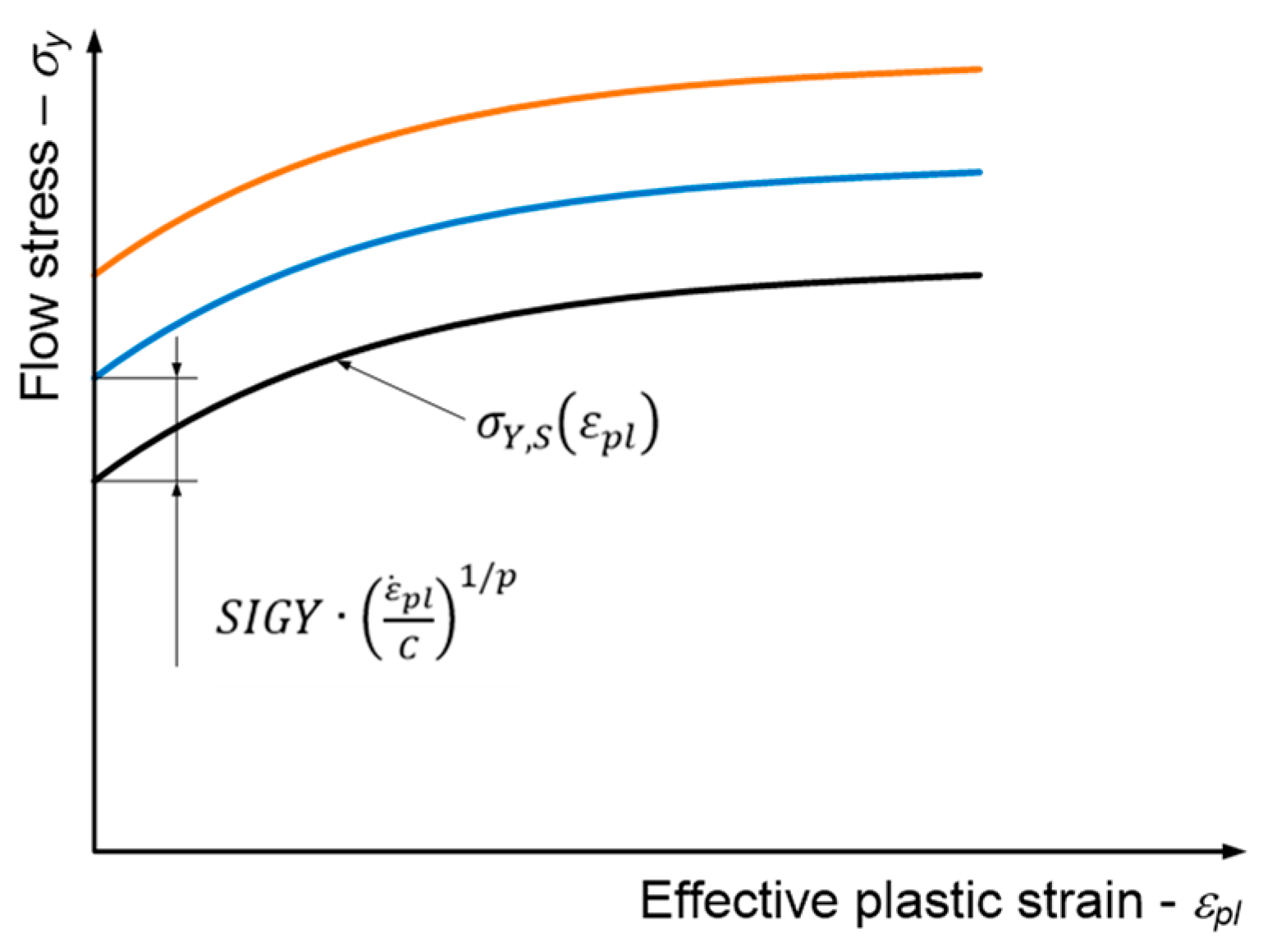
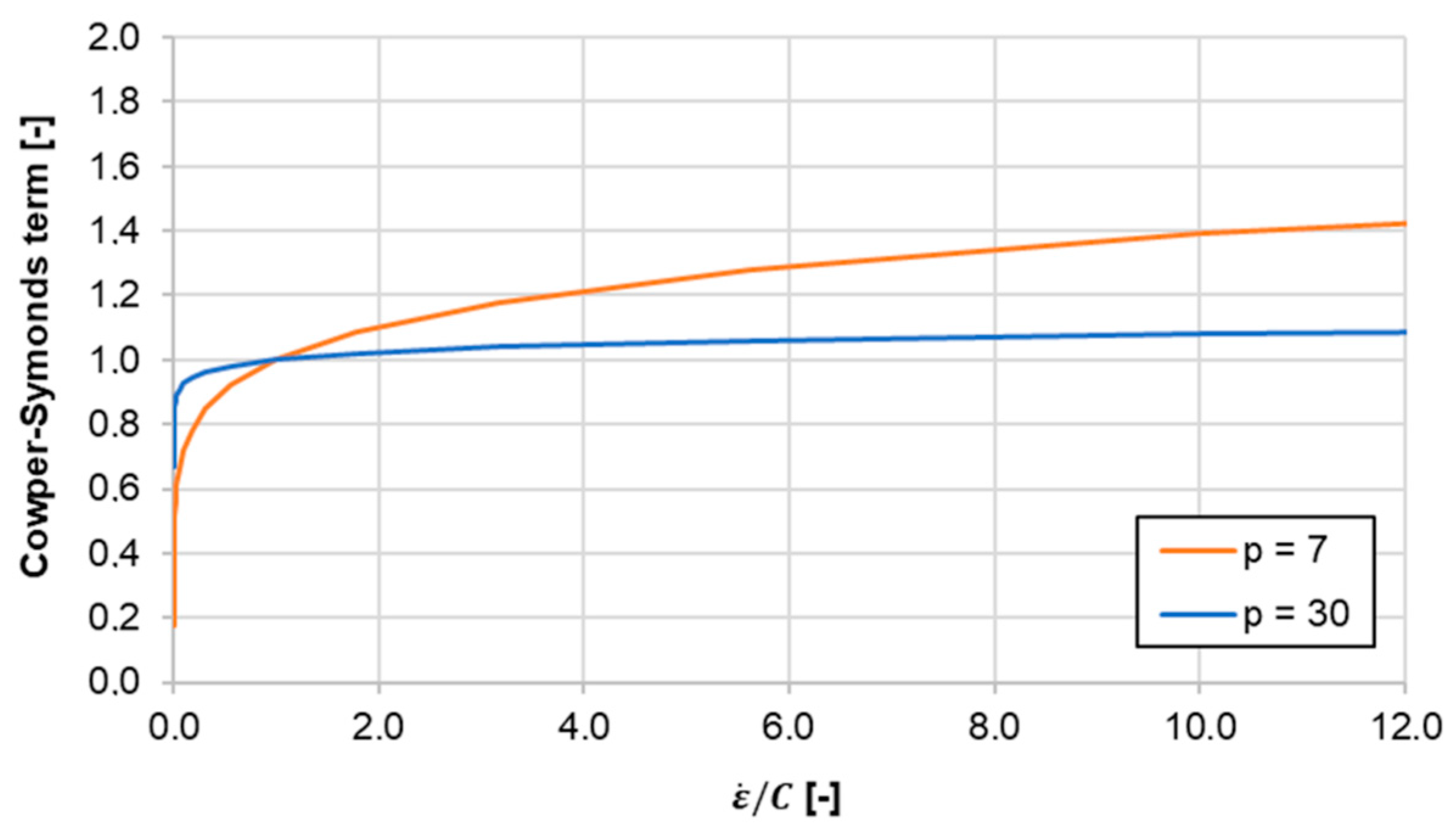
2.2. Modelling the Strain-Rate-Dependent Material Response
2.3. Estimating the Material Parameters from the Experimental Data
- Phase 1: a rough estimation of the three parameters that is based on the low strain-rate tensile tests.
- Phase 2: fine-tuning of the C and p parameters using multi-criterion cost function combined with numerical optimisation and reverse engineering. In this phase, low-strain rate and high-strain rate experiments are considered.
3. Results
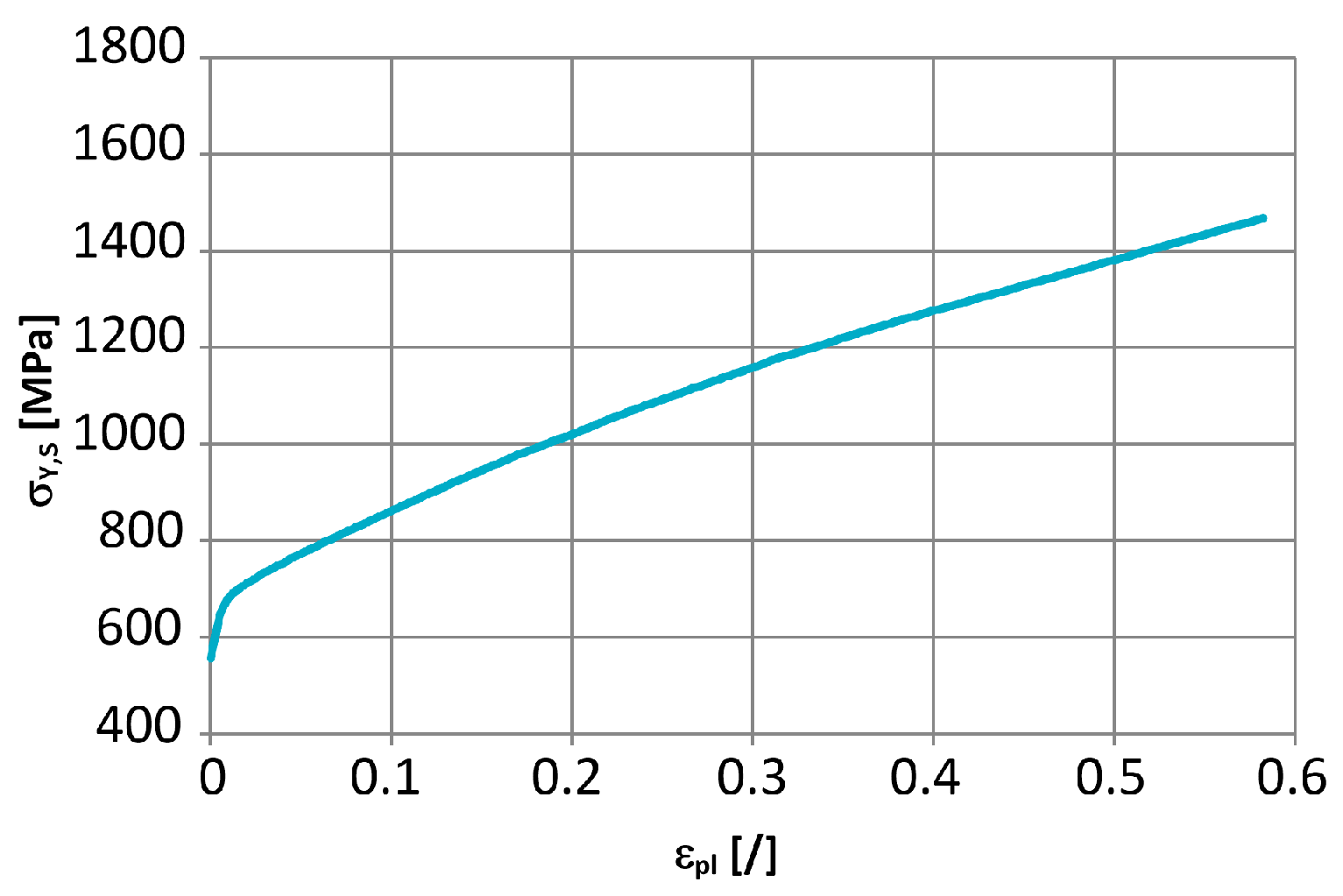
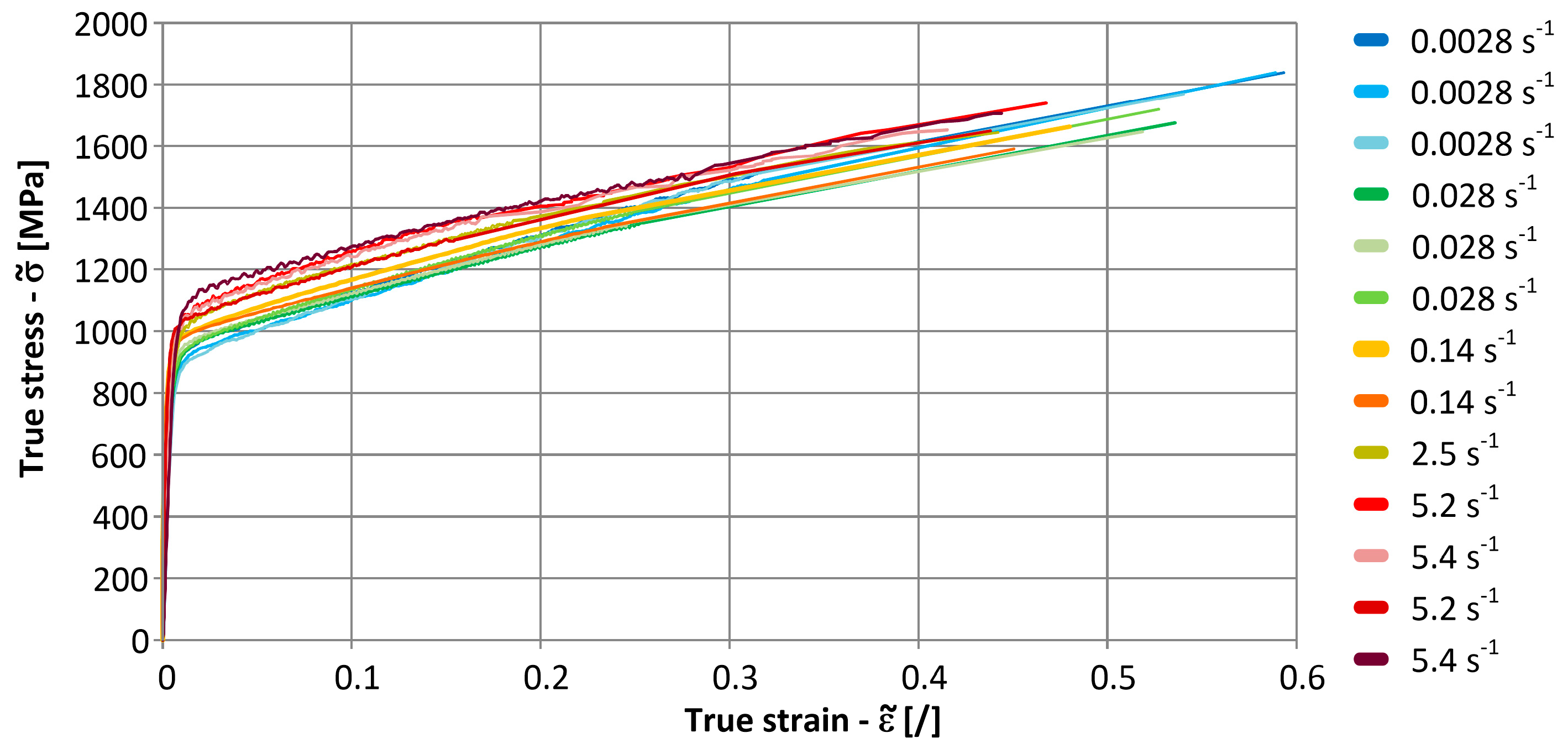
3.1. Tensile Stress-Strain Curves at Different Low-Strain Rates
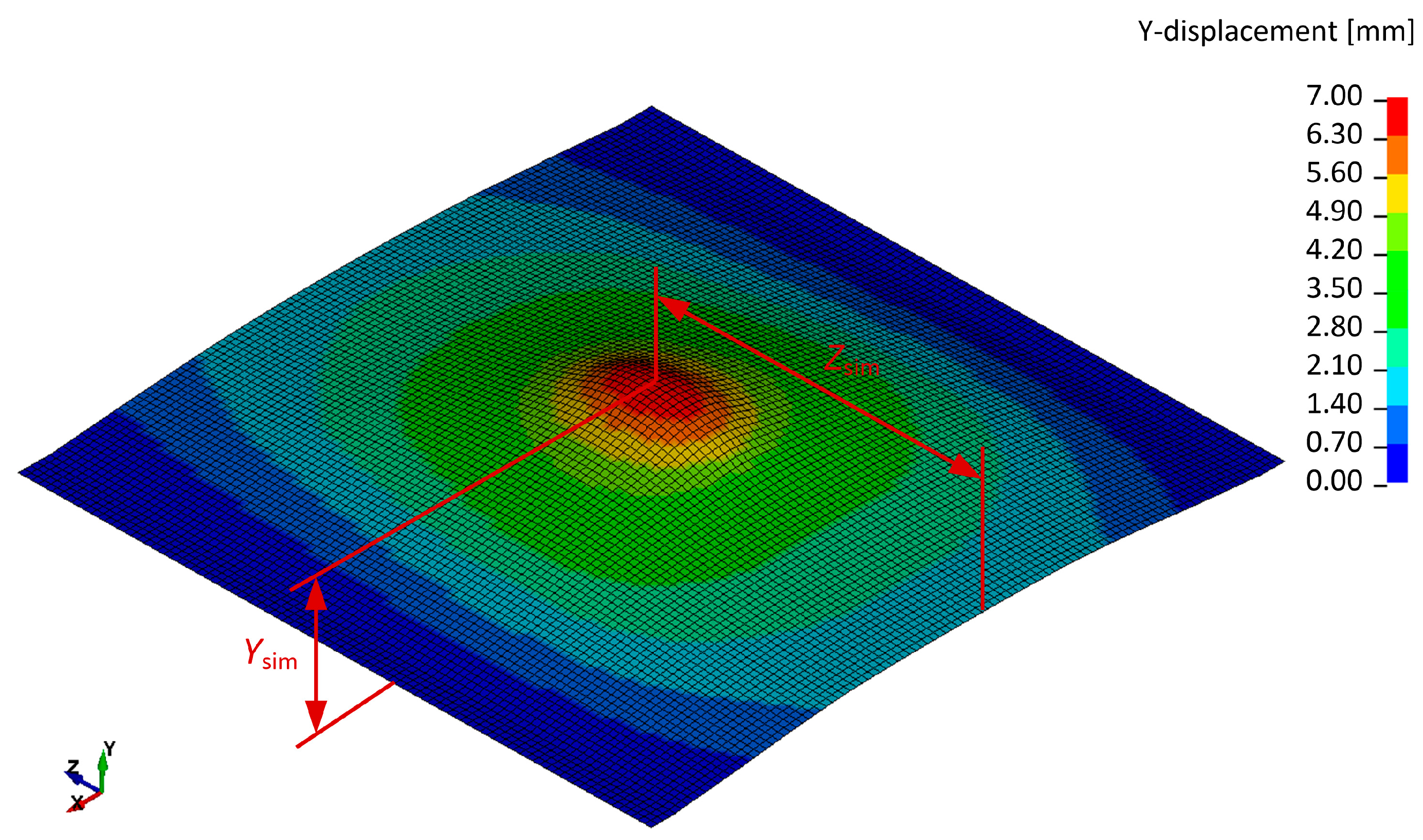
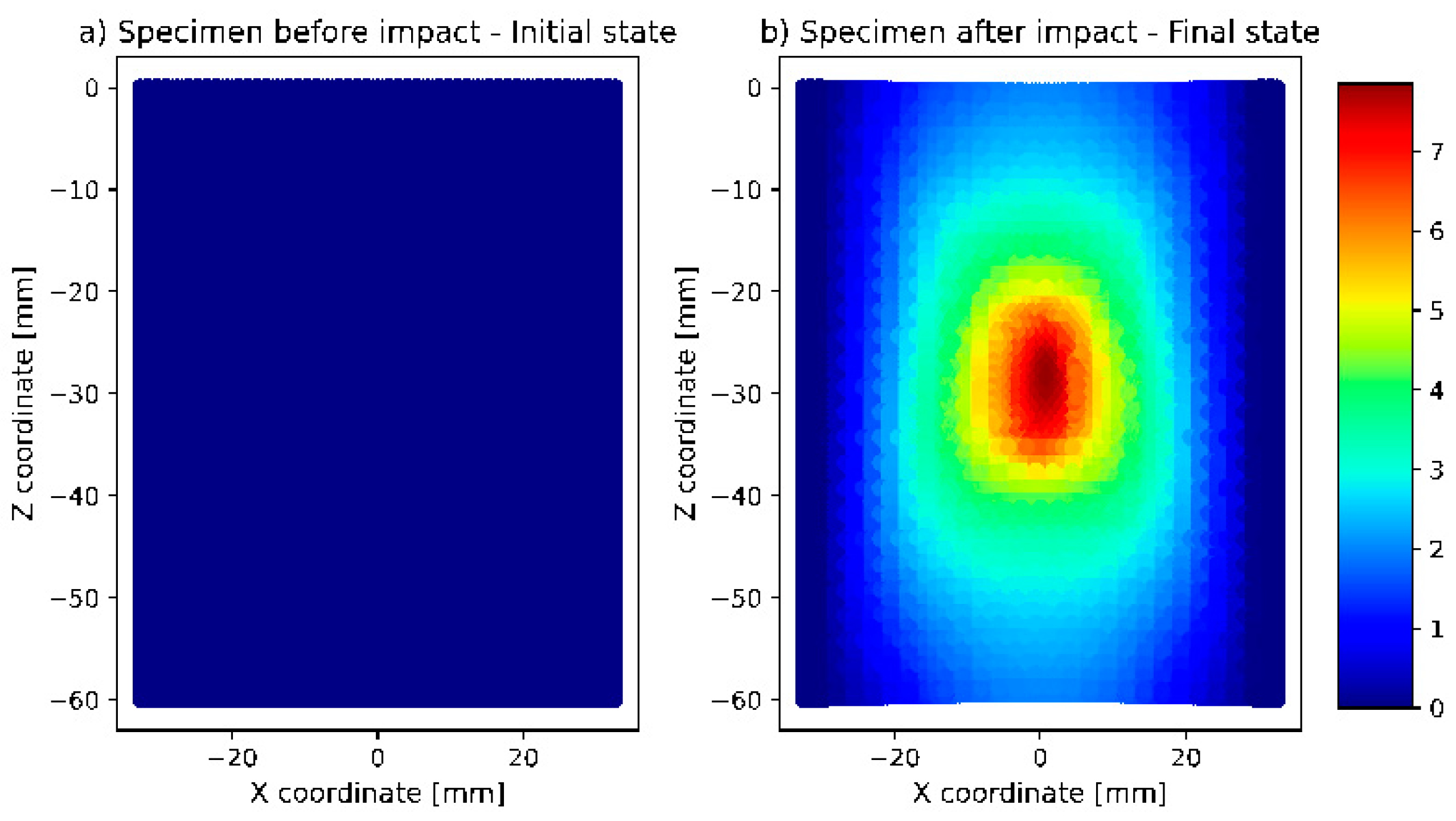
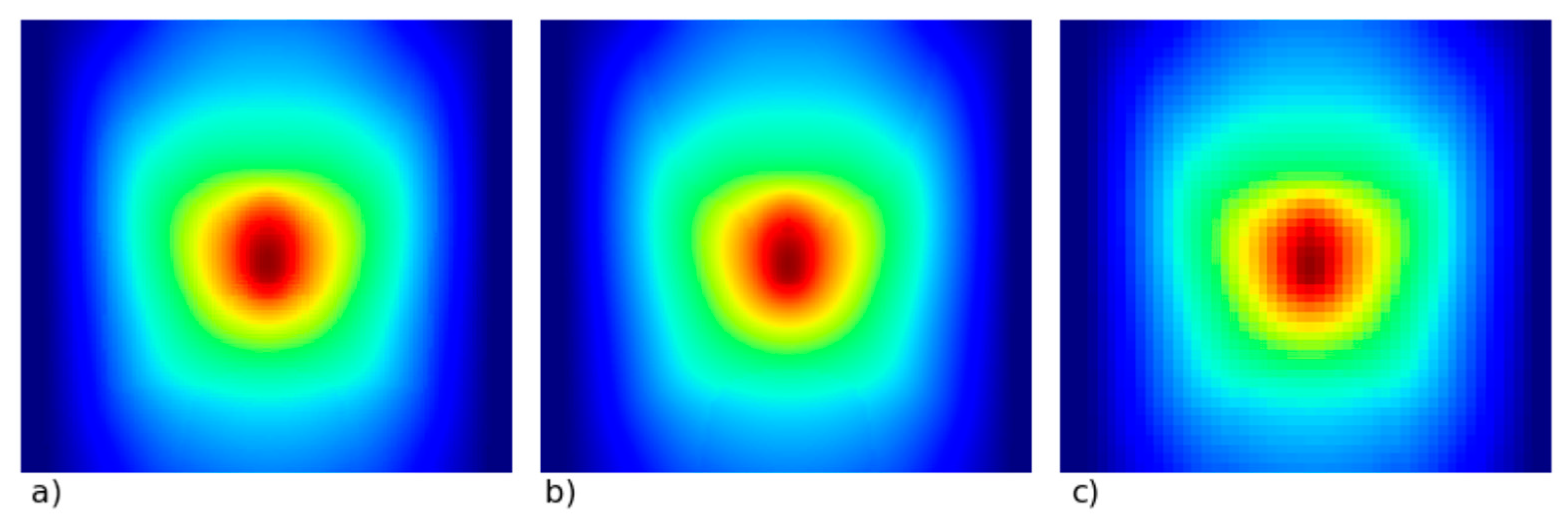
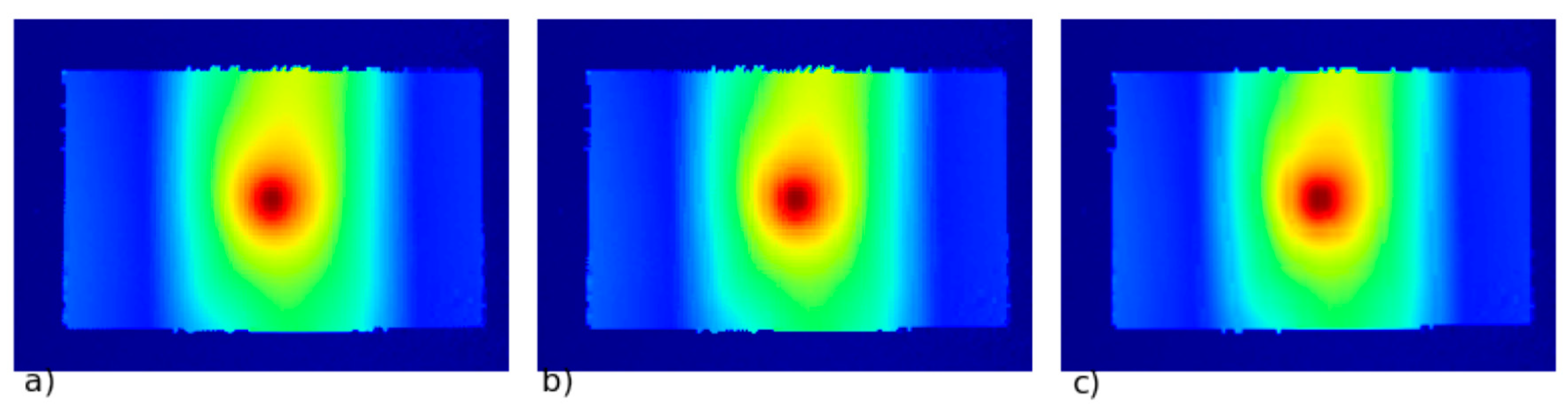
3.2. High Strain-Rate Experiments with a Shooting Ball Test
3.3. Estimating the Cowper–Symonds Parameters from the Experiments
4. Discussion
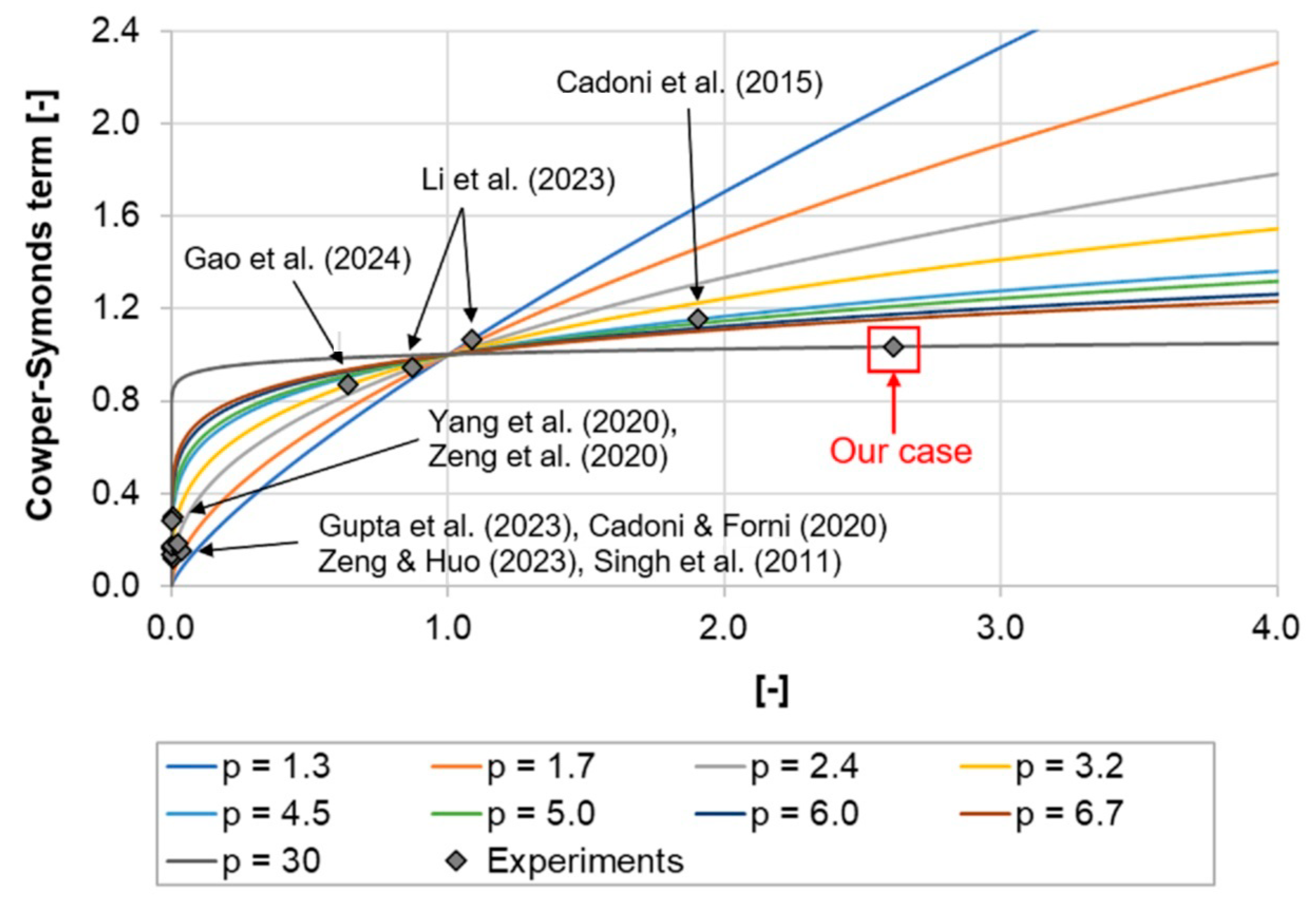
- Most scholars applied the conventional formulation for the MAT_24 material, as shown in Equation (2), despite the fact that such a formulation is sometimes not appropriate for the studied steel alloys.
- Furthermore, it is not optimal if the parameters C and p are estimated only on the basis of the high-strain rate experiments (e.g., Taylor test, split Hopkinson bar test, etc.). In the past [49], we also followed such an approach and obtained similar parameters. However, as soon as the optimisation process is extended to a wide range of strain rates, it turns out that the parameter values of C > 100,000 are not the best estimates. Despite the fact that different scholars have performed tests at different strain rates it is not clear how they considered the experimental data at various strain rates when estimating the parameters C and p.
5. Conclusions
- The obtained results were compared to the values from the literature. It turned out that the estimated optimal values of the parameters C and p sometimes deviate significantly from the literature. After a careful analysis of our results and the published results from the literature, it can be concluded that some estimates in the literature are not very reliable due to different reasons that are explained in the article. This critical evaluation of our results and references presents another novelty of this article.
- Yet another result of this study is a conclusion that it is immensely important is how the cost function is defined, which measures a deviation between the experimental results and numerical simulations for the high strain-rate experiments. It turns out that the integral measure of deviation is much better than the point-wise measure of deviation.
- Finally, we can also conclude that the high-strength steel SZBS800 is not very sensitive to the strain, which is indicated by a rather high value of the Cowper–Symonds parameter p. However, such results are not surprising because it was previously discovered by other scholars that high-strength steels are often insensitive to the high strain-rate effects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hallquist, J.O. LS-DYNA Theoretical Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006; Available online: https://lsdyna.ansys.com/manuals/ (accessed on 26 August 2024).
- Hallquist, J.O. LS-DYNA Keyword User’s Manual R11.0. Volume I; Livermore Software Technology Corporation: Livermore, CA, USA, 2018; Available online: https://lsdyna.ansys.com/manuals/ (accessed on 26 August 2024).
- Taylor, G. The Use of Flat-Ended Projectiles for Determining Dynamic Yield Stress I. Theoretical Considerations. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 194, 289–299. [Google Scholar] [CrossRef]
- Rohr, I.; Nahme, H.; Thoma, K. Material Characterization and Constitutive Modelling of Ductile High Strength Steel for a Wide Range of Strain Rates. Int. J. Impact Eng. 2005, 31, 401–433. [Google Scholar] [CrossRef]
- Deng, Y.; Wu, H.; Zhang, Y.; Huang, X.; Xiao, X.; Lv, Y. Experimental and Numerical Study on the Ballistic Resistance of 6061-T651 Aluminum Alloy Thin Plates Struck by Different Nose Shapes of Projectiles. Int. J. Impact Eng. 2022, 160, 104083. [Google Scholar] [CrossRef]
- Hopkinson, B.X. A Method of Measuring the Pressure Produced in the Detonation of High, Explosives or by the Impact of Bullets. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Or Phys. Character 1914, 213, 437–456. [Google Scholar] [CrossRef]
- Chen, W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Mechanical Engineering Series; Springer: Boston, MA, USA, 2011; ISBN 978-1-4419-7981-0. [Google Scholar]
- Forni, D.; Mazzucato, F.; Valente, A.; Cadoni, E. High Strain-Rate Behaviour of as-Cast and as-Build Inconel 718 Alloys at Elevated Temperatures. Mech. Mater. 2021, 159, 103859. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials, 1st ed.; Wiley: Hoboken, NJ, USA, 1994; ISBN 978-0-471-58262-5. [Google Scholar]
- Froustey, C.; Lambert, M.; Charles, J.L.; Lataillade, J.L. Design of an Impact Loading Machine Based on a Flywheel Device: Application to the Fatigue Resistance of the High Rate Pre-Straining Sensitivity of Aluminium Alloys. Exp. Mech. 2007, 47, 709–721. [Google Scholar] [CrossRef]
- Meram, A. Dynamic Characterization of Elastomer Buffer under Impact Loading by Low-Velocity Drop Test Method. Polym. Test. 2019, 79, 106013. [Google Scholar] [CrossRef]
- Hernandez, C.; Buchely, M.F.; Maranon, A. Dynamic Characterization of Roma Plastilina No. 1 from Drop Test and Inverse Analysis. Int. J. Mech. Sci. 2015, 100, 158–168. [Google Scholar] [CrossRef]
- Song, B.; Sanborn, B.; Heister, J.; Everett, R.; Martinez, T.; Groves, G.; Johnson, E.; Kenney, D.; Knight, M.; Spletzer, M. Development of “Dropkinson” Bar for Intermediate Strain-Rate Testing. EPJ Web Conf. 2018, 183, 02004. [Google Scholar] [CrossRef]
- Othman, R.; Guégan, P.; Challita, G.; Pasco, F.; LeBreton, D. A Modified Servo-Hydraulic Machine for Testing at Intermediate Strain Rates. Int. J. Impact Eng. 2009, 36, 460–467. [Google Scholar] [CrossRef]
- Škrlec, A.; Kocjan, T.; Nagode, M.; Klemenc, J. Modelling a Response of Complex-Phase Steel at High Strain Rates. Materials 2024, 17, 2302. [Google Scholar] [CrossRef] [PubMed]
- D20 Committee. Test Method for Impact Resistance of Flat, Rigid Plastic Specimen by Means of a Striker Impacted by a Falling Weight (Gardner Impact); ASTM International: West Conshohocken, PA, USA, 2007. [Google Scholar]
- GB/T 1591-2018; High Strength Low Alloy Structural Steels (English Version). SAMR, SAC: Beijing, China, 2018.
- Li, H.; Li, F.; Zhang, R.; Zhi, X. High Strain Rate Experiments and Constitutive Model for Q390D Steel. J. Constr. Steel Res. 2023, 206, 107933. [Google Scholar] [CrossRef]
- EN 10088-4:2009; Stainless Steels—Part 4: Technical Delivery Conditions for Sheet/Plate and Strip of Corrosion Resisting Steels for Construction Purposes. Technical Committee ECISS/TC 105. CEN Management Centre: Brussels, Belgium, 2009.
- Gupta, M.K.; Singh, N.K.; Gupta, N.K. Deformation Behaviour and Notch Sensitivity of a Super Duplex Stainless Steel at Different Strain Rates and Temperatures. Int. J. Impact Eng. 2023, 174, 104494. [Google Scholar] [CrossRef]
- EN 10025-6:2019; Hot Rolled Products of Structural Steels—Part 6: Technical Delivery Conditions for Flat Products of High Yield Strength Structural Steels in the Quenched and Tempered Condition. Technical Committee ECISS/TC 103. CEN Management Centre: Brussels, Belgium, 2019.
- Yang, X.; Yang, H.; Lai, Z.; Zhang, S. Dynamic Tensile Behavior of S690 High-Strength Structural Steel at Intermediate Strain Rates. J. Constr. Steel Res. 2020, 168, 105961. [Google Scholar] [CrossRef]
- Cadoni, E.; Forni, D. Strain-Rate Effects on S690QL High Strength Steel under Tensile Loading. J. Constr. Steel Res. 2020, 175, 106348. [Google Scholar] [CrossRef]
- EN 10083-3:2006; Steels for Quenching and Tempering—Part 3: Technical Delivery Conditions for Alloy Steels. Technical Committee ECISS/TC 105. CEN Management Centre: Brussels, Belgium, 2006.
- Gao, S.; Yu, X.; Li, Q.; Sun, Y.; Hao, Z.; Gu, D. Research on Dynamic Deformation Behavior and Constitutive Relationship of Hot Forming High Strength Steel. J. Mater. Res. Technol. 2024, 28, 1694–1712. [Google Scholar] [CrossRef]
- DGJ32/TJ 202-2016; Technical Specification for Application of Heat-Treatment High-Strength Ribbed Bar in Concrete Structures. Jiangsu Phoenix Science and Technology Press: Nanjing, China, 2016.
- Zeng, X.; Huo, J.S. Rate-Dependent Constitutive Model of High-Strength Reinforcing Steel HTRB600E in Tension. Constr. Build. Mater. 2023, 363, 129824. [Google Scholar] [CrossRef]
- Singh, N.K.; Cadoni, E.; Singha, M.K.; Gupta, N.K. Dynamic Tensile Behavior of Multi Phase High Yield Strength Steel. Mater. Des. 2011, 32, 5091–5098. [Google Scholar] [CrossRef]
- EN 1992-1-1:2005; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. Technical Committee CEN/TC 250. CEN Management Centre: Brussels, Belgium, 2004.
- Cadoni, E.; Dotta, M.; Forni, D.; Tesio, N. High Strain Rate Behaviour in Tension of Steel B500A Reinforcing Bar. Mater. Struct. 2015, 48, 1803–1813. [Google Scholar] [CrossRef]
- GB/T 1499.2-2018; Steel for the Reinforcement of Concrete—Part 2: Hot Rolled Ribbed Bars (English Version). AQSIQ, SAC: Beijing, China, 2018.
- Zeng, X.; Huo, J.; Wang, H.; Wang, Z.; Elchalakani, M. Dynamic Tensile Behavior of Steel HRB500E Reinforcing Bar at Low, Medium, and High Strain Rates. Materials 2020, 13, 185. [Google Scholar] [CrossRef]
- Nahme, H.; Lach, E. Dynamic Behavior of High Strength Armor Steels. Le J. De Phys. IV 1997, 7, C3–C373. [Google Scholar] [CrossRef]
- Børvik, T.; Hopperstad, O.S.; Dey, S.; Pizzinato, E.V.; Langseth, M.; Albertini, C. Strength and Ductility of Weldox 460 E Steel at High Strain Rates, Elevated Temperatures and Various Stress Triaxialities. Eng. Fract. Mech. 2005, 72, 1071–1087. [Google Scholar] [CrossRef]
- Trajkovski, J.; Kunc, R.; Pepel, V.; Prebil, I. Flow and Fracture Behavior of High-Strength Armor Steel PROTAC 500. Mater. Des. 2015, 66, 37–45. [Google Scholar] [CrossRef]
- Huang, Y.H. Shape Measurement by the Use of Digital Image Correlation. Opt. Eng. 2005, 44, 087011. [Google Scholar] [CrossRef]
- Aktepe, R.; Guldur Erkal, B. State-of-the-Art Review on Measurement Techniques and Numerical Modeling of Geometric Imperfections in Cold-Formed Steel Members. J. Constr. Steel Res. 2023, 207, 107942. [Google Scholar] [CrossRef]
- Tarigopula, V.; Hopperstad, O.S.; Langseth, M.; Clausen, A.H.; Hild, F. A Study of Localisation in Dual-Phase High-Strength Steels under Dynamic Loading Using Digital Image Correlation and FE Analysis. Int. J. Solids Struct. 2008, 45, 601–619. [Google Scholar] [CrossRef]
- Tiwari, V.; Sutton, M.A.; McNeill, S.R.; Xu, S.; Deng, X.; Fourney, W.L.; Bretall, D. Application of 3D Image Correlation for Full-Field Transient Plate Deformation Measurements during Blast Loading. Int. J. Impact Eng. 2009, 36, 862–874. [Google Scholar] [CrossRef]
- Borkowski, Ł.; Grudziecki, J.; Kotełko, M.; Ungureanu, V.; Dubina, D. Ultimate and Post-Ultimate Behaviour of Thin-Walled Cold-Formed Steel Open-Section Members under Eccentric Compression. Part II: Experimental Study. Thin-Walled Struct. 2022, 171, 108802. [Google Scholar] [CrossRef]
- Shin, W.; Yoo, C. Application of the Digital Image Correlation Technique in Wide Width Tensile Test of Geogrids. Geotext. Geomembr. 2024, 52, 1087–1098. [Google Scholar] [CrossRef]
- SZBS800 Multiphase Steels: Bainitic Grade. Salzgitter Flachstahl GmbH. Available online: https://www.salzgitter-flachstahl.de/fileadmin/footage/media/gesellschaften/szfg/informationsmaterial/produktinformationen/warmgewalzte_produkte/eng/szbs800.pdf (accessed on 26 February 2024).
- E28 Committee. Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Rolling Elements|Schaeffler Medias. Available online: https://medias.schaeffler.hu/en/rolling-elements (accessed on 23 August 2024).
- EN-ISO 683-17:2023(En); Heat-Treated Steels, Alloy Steels and Free-Cutting Steels—Part 17: Ball and Roller Bearing Steels. ISO: Geneva, Switzerland, 2023.
- Besseling, J.F. A Theory of Elastic, Plastic, and Creep Deformations of an Initially Isotropic Material Showing Anisotropic Strain-Hardening, Creep Recovery, and Secondary Creep. J. Appl. Mech. 1958, 25, 529–536. [Google Scholar] [CrossRef]
- Škrlec, A.; Klemenc, J. Estimating the Strain-Rate-Dependent Parameters of the Johnson-Cook Material Model Using Optimisation Algorithms Combined with a Response Surface. Mathematics 2020, 8, 1105. [Google Scholar] [CrossRef]
- Mirone, G.; Barbagallo, R.; Bua, G.; De Caro, D.; Ferrea, M.; Tedesco, M.M. A Simple Procedure for the Post-Necking Stress-Strain Curves of Anisotropic Sheet Metals. Metals 2023, 13, 1156. [Google Scholar] [CrossRef]
- Škrlec, A.; Klemenc, J. Estimating the Strain-Rate-Dependent Parameters of the Cowper-Symonds and Johnson-Cook Material Models Using Taguchi Arrays. Stroj. Vestn. J. Mech. Eng. 2016, 62, 220–230. [Google Scholar] [CrossRef]






| C | Si | Mn | P | S | Al | B | Cu |
|---|---|---|---|---|---|---|---|
| max. | max. | max. | max. | max. | min. | max. | max. |
| 0.18% | 1.00% | 2.20% | 0.05% | 0.01% | 0.015–1.2% | 0.005% | 0.2% |
| Parameter | Values |
|---|---|
| C [s−1] | 10, 30, 50, 70, 90, 1110, 130, 150, 170, 190, 210, 230, 250, 270, 300, 600 |
| p [/] | 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100 |
| Parameter | Values |
|---|---|
| C [s−1] | 70, 150, 230, 310, 390, 470, 550, 630, 710, 790, 870, 950, 1030, 1110, 1190, 1270, 1350 |
| p [/] | 15, 20, 25, 30, 35, 40, 45 |
| Parameter | Values |
|---|---|
| Impact angles α [°] | 0, 0, 0, 20, 20, 20, 35, 35, 35 |
| Impact velocity v [m/s] | 111.5, 133.3, 155.3, 111.2, 132.6, 154.2, 113.1, 131.9, 153.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Škrlec, A.; Panić, B.; Nagode, M.; Klemenc, J. Estimating the Cowper–Symonds Parameters for High-Strength Steel Using DIC Combined with Integral Measures of Deviation. Metals 2024, 14, 992. https://doi.org/10.3390/met14090992
Škrlec A, Panić B, Nagode M, Klemenc J. Estimating the Cowper–Symonds Parameters for High-Strength Steel Using DIC Combined with Integral Measures of Deviation. Metals. 2024; 14(9):992. https://doi.org/10.3390/met14090992
Chicago/Turabian StyleŠkrlec, Andrej, Branislav Panić, Marko Nagode, and Jernej Klemenc. 2024. "Estimating the Cowper–Symonds Parameters for High-Strength Steel Using DIC Combined with Integral Measures of Deviation" Metals 14, no. 9: 992. https://doi.org/10.3390/met14090992





