2. Acoustic Emissions and Martensitic Transformations in Shape Memory Alloys
The dynamics of first-order phase transitions in shape memory alloys exhibit plentiful variety, since such transformations hardly occur in thermal equilibrium [
4]. The energy barriers against the transition are typically large as compared to thermal fluctuations, and this leads to an athermal character. These barriers are typically quenched disorders (dislocations, deviations from stoichiometry, impurities, precipitates, etc.) that strongly affect the metastable path, and the corresponding order parameter follows metastable trajectories; instead of having a sharp jump, the transitions extend over a broad range of the driving parameter (e.g., the temperature, if the transformation is thermally induced) and a hysteresis is observed. This hysteresis (and the energy dissipation connected with it) is often rate-independent, i.e., it is not related to the delayed response of the system. In addition, in martensitic transformations, the order parameter is the strain, and the symmetry differences between the austenite and martensite also have an influence on the metastable trajectory and on the hysteresis.
According to the above picture, during athermal evolution of the system, smooth driving results in a sequence of discontinuous jumps (avalanches) of the order parameter (strain) are separated by inactive periods. Since the energy landscape usually contains an enormous number of energy minima, and the thermal fluctuations play a negligible role, the system moves by jumps between metastable states. This means that, when the external control parameter is changed, and the given state in which the system was trapped becomes unstable, an extended irreversible jump occurs to a different metastable state [
3]. Thus, avalanches related to the jumps between metastable states are observed, and are connected with the motion of the interface and/or with the nucleation of the embryos of the new phase. The avalanches are very fast as compared to the rate of the external field, and it can be assumed that a so-called adiabatic limit can be a good description (the driving rate is close to zero). The advance of an interface that separates the parent and product phases produces elastic waves, which propagate through the material and can be recorded at the surface by an appropriate transducer. Thus, AE events are inherently related to elementary steps of the phase transition. For more details on the theoretical interpretation of the intermittent character of the transformation and of AE experiments, we refer to the review by Rosinberg and Vives [
4] as well as the papers [
3,
10,
12,
13,
14]. In any case, it was shown theoretically in [
12] that there can exist a certain critical value of disorder (and a corresponding driving field) at which avalanches of all sizes are observed, and this leads to power-law behaviour of the avalanche size distribution that is like that given by Equation (1). In addition, it was also shown that the avalanche criticality depends on the driving mechanism [
15,
16,
17], and it can be different from the above (when the driving is due to fine tuning of the field, i.e., of an intensive parameter, such as the temperature or stress; soft driving). If the transition is hard-driven, i.e., if it is driven by controlling the displacement (which is thermodynamically conjugated to the stress), a self-organized type of criticality occurs. The two cases are characterized by different critical exponents, and, in the second case, the control of the displacement induces an effective long-range effect that results in self-organization of the system into the critical point [
3,
4]. In this case, the critical point is independent of the amount of the disorder (e.g., there are no “training effects” observed [
3], which are typical for soft driving and are naturally related to the reorganization of the disorder). It was also shown experimentally, in Cu–Zn–Al single crystals, that the entire hysteresis loop was enclosed within the stress-driven one [
16], indicating that the dissipated energy is much smaller for the hard-driving case. In addition, it was also pointed out that the exponents belonging to the stress-driven case were in very good agreement with those determined by thermal driving [
3,
16] (even if, in the first case, the system transforms to a single variant martensite structure, in contrast to the multivariant structure that typically forms in the second case). This means that the macroscopic avalanche dynamics are very similar in both soft-driven cases [
3].
From the point of view of experimental investigations of AE during martensitic transformations, the emitted elastic waves typically have frequency components that are in the ultrasonic range (20 kHz–2 MHz), and their sources can be, in a simplified manner, considered as sudden creations of displacement jumps. However, our knowledge on the dynamics of such jumps (acceleration, duration, etc.) is very restricted, and, thus, it is very difficult to recover the information about the source [
4], although, by the simultaneous use of two sensors, the localization of the position of the moving fronts is already possible [
18]. There is a generally accepted simple idea that the maximum amplitude of the detected signal is proportional to the velocity of the advancing front [
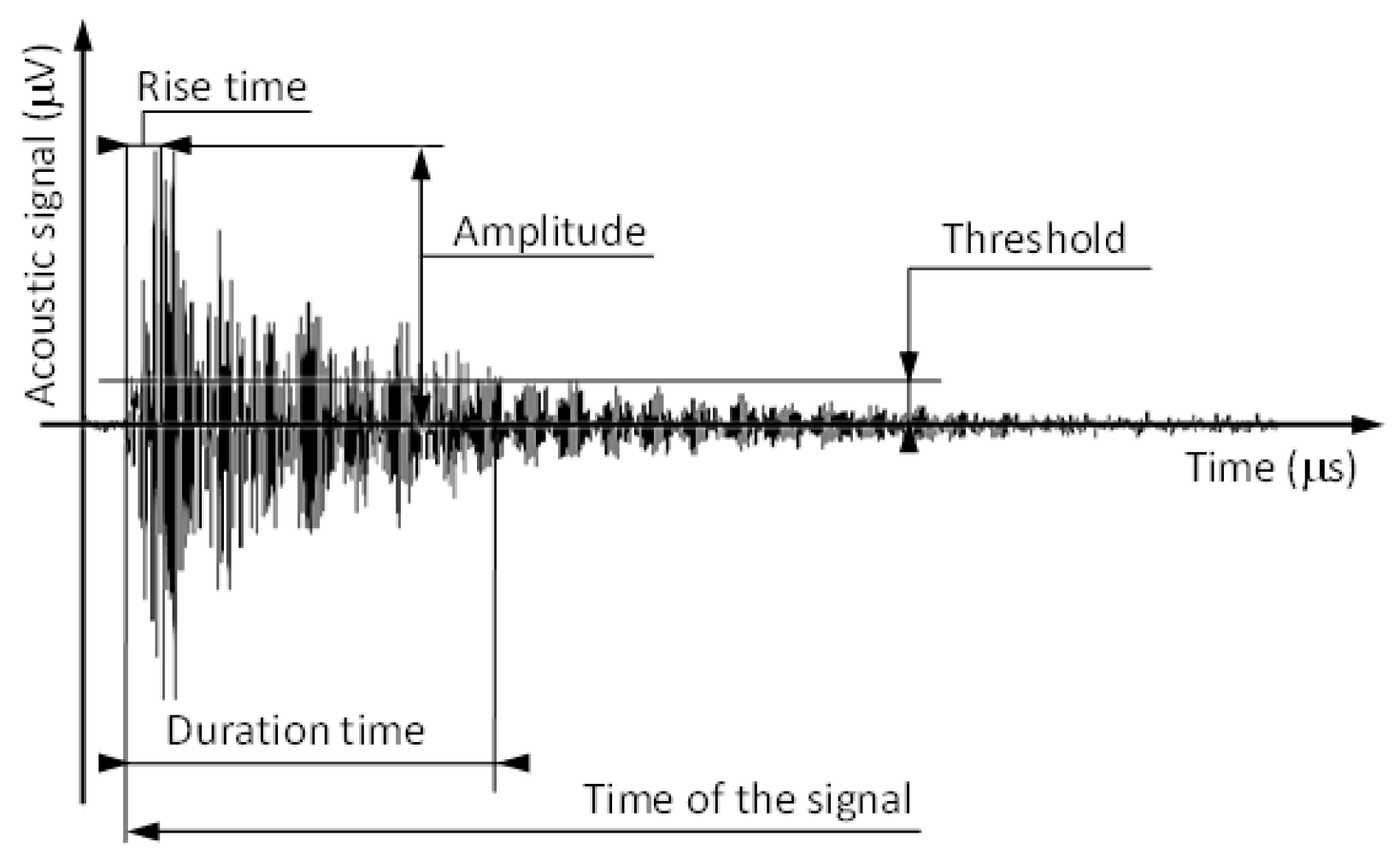
19]. The resonant transducers that are usually used have high sensitivity to detect very small (down to tens of nanometers) displacement discontinuities. An individual voltage,
U(
t), produced by the transducer has a typical form shown in
Figure 1 schematically. The energy of the
ith peak can be calculated by using the expression
where
U2(
t) is the square of the measured signal and
R is an arbitrary chosen resistance.
The two important basic techniques in the study of structural changes by AE are the (i) pulse-counting techniques and (ii) statistical analysis of single events [
4]. In the first technique, the number of avalanches (events or hits) per unit time (
dN/
dt) is determined (hits with an amplitude above the threshold, as shown in
Figure 1, are counted). For a constant driving rate,
dT/
dt (in the case of changing the temperature), the so-called activity, is determined as follows:
A(T) = (
dN/
dt)/(
dT/
dt). A typical example is shown in
Figure 2 for a temperature-driven transition in Ni
2MnGa single crystal [
8], which also illustrates that the main AE and DSC activity correlates very well with each other. This suggests proportionality between the energies of AE events and the heat released during these events [
20]. In addition, from the hysteresis loop determined from the DSC results (taking the ratio of the partial integral and the full integration of the Q/T ratio, which is in fact the fraction of the transformed entropy [
21]), the value of the martensite volume fraction,
η, as the function of the temperature was also determined (
Figure 3).
The second basic technique, which recently has been more and more extensively used, is based on the detection of a large number of AE signals and the statistical analysis of their amplitude, energy, or duration (see also
Figure 1) according to Equation (1). Thus, the main goal is to check whether the probability densities follow the power law or not and, if yes, to determine the corresponding exponents. In most cases, they indeed show a power-law behaviour, with exponents typically ranging from 1.5 to 4 (see, as an example,
Figure 4 [
8]). Sometimes, there is a problem with the number of events: if it is small, the statistics are not good enough. Thus, the collection of data is performed by taking into account the signals recorded during the whole transition, and neglecting the non-homogeneous character reflected in the activity curves (see
Figure 2 and
Figure 3). In addition, averaging over heating and cooling runs is also frequently done. We will turn back to these points in
Section 3,
Section 4,
Section 5 and
Section 6. Once the exponents are determined, it is also possible to check the validity of the so-called scaling rules that establish relations between the exponents [
3,
4]. Indeed, it was shown [
22] that, e.g., the energy
E and the amplitude
A are statistically related through
E~
Az, leading to the following scaling rule [
3,
4,
22]
where
α is the amplitude exponent. It was found that
z ≅ 2 for martensitic transformations [
3].
In addition, trials to answer the following questions are also important: are there time correlations between the subsequent events in the AE spectra, or not. Two types of correlations can be investigated [
8]. In the first, one can check whether there exists any interdependence between closely recorded signals or not by creating the waiting time distributions
P(
τ) (with
τ = (
tk+1) −
tk, the waiting time, or the time between consecutive jerks) [
23,
24]. It was shown [
23,
24] that
P(
τ) fulfils a scaling law
where
is the mean waiting time and
is a universal function of its argument. This is usually different from the Poisson-type behaviour,
(where
is the Poissonian rate) describing uncorrelated behaviour.
Figure 5 shows, as an illustration, the normalized probability distribution function for both AE and magnetic emission (ME) events in Ni
2MnGa single crystal [
8]. We will turn back to the second type of analysis and to the details of time correlations in
Section 4; what we emphasize here is that the fitted curves at both small and large arguments for AE deviate from the Poisson-type uncorrelated behaviour.
Closing this section, the recognition made by the authors of [
3] is worth mentioning. They recognized that the energy and amplitude exponents collected from a number data obtained in different shape memory alloys can be grouped into universality classes according to the symmetry of the martensite (
Table 1). This means that the multiplicity (i.e., the ratio of symmetry operations of the parent and martensite phases) has an influence on the exponents; the large variant multiplicity should decrease the numbers of big events, which results in a larger exponent. This suggests, according to the last sentence of the first paragraph of this Section, that the nucleation and growth dynamics are indeed influenced by the symmetry change during the transition. Due to this dependence of the exponents (and also due to the dependence of the exponents on the driving mechanism), this avalanche criticality is called weak universality [
25].
3. On the Asymmetry of the Forward and Reverse Martensitic Transformations
There is a long-standing debate about the interpretation of the asymmetry, namely that AE activities and DSC runs, taken during martensitic phase transformations in shape memory alloys, often look different during cooling and heating. This is especially striking if the cooling/heating rates are low enough (and the mass of the sample is also small enough), i.e., the transition is adiabatic, but still athermal.
Figure 6 and
Figure 7 show such examples of DSC results. As was already mentioned above, besides the above thermal avalanches, avalanches of magnetic emission signals can also be detected during martensitic transformations in ferromagnetic alloys (see, e.g., [
5,
6,
7,
8] and [
26,
27,
28] and
Figure 8). Thus, it is not surprising that the above asymmetry is also manifested in differences of AE and ME activities or numbers of hits as well as in the power-law exponents of the probability densities of the peak energy and amplitude [
4,
5,
6,
7,
8,
17,
25,
26,
27,
28,
29,
30,
31] for cooling and heating. It is worth noting that the fingerprints of the above asymmetry were recognized very early on in acoustic emission measurements in shape memory alloys by a pulse-counting technique (see, e.g., [
29,
32,
33]). The results of these early investigations can be summarized as follows:
- (i)
There was a significant asymmetry between the AE parameters obtained during cooling and heating.
- (ii)
The AE activity depended on the morphology of both phases (single or polycrystalline samples, formation of a single or multivariant martensite structure, transformation by a single interface or multiple interface motion).
- (iii)
The lack of well-defined Mf and Af temperatures.
- (iv)
The rate of AE activity was larger at the beginning of the forward and at the end of the reverse transformation.
- (v)
It was also concluded that the AE activity must be a function of the transformed quantity and the formation velocity, and the difference in the formation velocity for cooling and heating is probably very important in understanding the asymmetry.
- (vi)
There was a good correlation between the thermal peaks (in the thermal power measured) and the AE peaks, signifying that the physical origin of both is the same.
It was argued that most of the above observations can be qualitatively interpreted by the differences in stress accumulation/release and relaxation (reorientation of marensite variants) during heating and cooling [
29]. It was also concluded [
32] that the formation of the first martensite plates produced a larger AE intensity than the following plates, and the formation and vanishing kinetics of the first martensite plates were much faster than that of the other ones.
The interpretation of this phenomenon has recently evoked a renewed interest [
7,
25,
34] in carrying out a statistical analysis of a large number of AE signals and determining the exponents of the energy, amplitude, area, or duration distributions. This will be discussed in more detail below.
First, it was proposed in [
25] that the asymmetry is a consequence of the fact that, while nucleation is required for the forward transformation, during the reverse transformation only the fast shrinkage of the martensite domains occurs, i.e., the dynamic mechanisms are different for cooling than heating. It was shown that, while no significant differences between the forward and reverse transitions were observed in Fe–Pd single crystals (in fact, the AE activity was slightly larger for the forward transition), in the Cu–Zn–Al single crystalline samples the AE activity was much larger for the reverse transition. In addition, although for the reverse transition in Cu–Zn–Al an energy exponent of about ε ≅ 2 was obtained (being the same as for the forward transition and in agreement with the value shown in
Table 1 for monoclinic martensite), a strong disturbing effect of the exponential damping factor was identified (it was diffcult to identify the plateau region in the maximum likelihood method to find the reliable power exponent). The authors mentioned the possibility that the damping was due to the overlapping of small events. Nevertheless, their final conclusion was that the different dynamics during cooling and heating can be responsible for the exponentially damped behaviour in the Cu–Zn–Al samples in the reverse transformation. It is worth noting that, according to [
25], it would be expected that (due to the required nucleation and its absence of the forward and reverse transitions, respectively) the asymmetry should be the same in all cases (e.g., the AE activity should be larger for cooling than heating). The deviation from this expectation for the Cu–Zn alloy was due to the deviation from the criticality during heating. In addition, this “nucleation” model explains the observations (i) and (iv) listed above.
In a set of recent papers from our group [
5,
6,
7,
8,
34], it was recognized, from experimental data obtained in Ni
2MnGa and Ni
49Fe
18Ga
27Co
6 [
6] alloys, that the distributions indeed followed the power law with large cutoff values over 3–5 orders of magnitude of the given variable (i.e., the criticality was confirmed) in both directions. In addition, the asymmetry did not change if the numbers of pinning points were changed by surface roughening of the samples; only the numbers of hits were increased [
5,
6,
7,
8].
Furthermore, the asymmetries observed could be classified into two groups: (a) the number of hits and the whole energy of AE is larger while the energy and amplitude exponents (ε and α, respectively) were smaller for cooling (positive asymmetry), and (b) the situation is just the reverse (negative asymmetry). Thus, the following asymmetry parameters were introduced:
γε = (
εh −
εc)/
εc,
γα = (
αh −
αc)/
αc,
μ =
Nh/
Nc, and
η =
EhAE/
EcAE, where N is the number of hits and, e.g.,
EcAE is the total energy of the acoustic emission for cooling:
EcAE = ∑
jE
cj (E
cj denotes the energy of an individual acoustic event). Note that the asymmetry is positive if
γα and
γε > 0 while μ and
η < 0.
Table 2 illustrates that the asymmetry is positive for Ni
2MnGa single crystal and negative for homogeneous Ni
49Fe
18Ga
27Co
6. It can also be seen that, in accordance with conclusion (ii), the presence of γ-precipitates of different sizes has also a strong influence on the asymmetry. The transformation took place by a single interface motion, as is illustrated in
Figure 9, in Sample 1, while the formation of many needles in Samples 2 and 3, as shown in
Figure 10, was observed. It is remarkable that non-zero asymmetry was observed for transformations by a single interface motion in Ni
49Fe
18Ga
27Co
6 single crystal, i.e., asymmetry exists, even if there are no nucleation effects.
On the basis of the above observations, we attempted to provide a quantitative interpretation of the above asymmetry [
34]. We agreed with the general conclusion of [
28], namely that the asymmetry is related to the differences in the dynamics of forward and reverse transformations; however, instead of emphasizing the role of nucleation (there was an asymmetry for the single interface motion too, where the nucleation effects can be certainly neglected, and both positive and negative asymmetry were observed), we turned back to the original idea of Baram and Rosen [
29]. Thus, the central role of the differences in stress accumulation/release and relaxation (the reorientation of martensite variants) during heating and cooling was analysed in [
34].
It is clear that the storage/release of the elastic energy during the forward and reverse transformation itself is not an irreversible process, whereas the presence of local free-energy barriers leads to irreversible and intermittent dynamics (noises) [
35]. Consider that during cooling and heating, three types of AE sources (local free-energy barriers) are operative (see, e.g., [
29,
35,
36]):
- (a)
nucleation events;
- (b)
pinning/depinning effects; and
- (c)
during cooling or heating, partial relaxations of the stored elastic energy (due to interaction/competitive growth of different martensitic variants) can occur in the form of acoustic emissions.
The first two can be called frictional-type interactions, and these are active in both directions. We will assume that the dissipated energy related to them is the same in both directions:
(surface roughening of samples did not change the asymmetry). Regarding the relative roles of these sources, while in [
29] only the frictional interactions were mentioned, in Ni
2MnGa single crystalline samples it was demonstrated [
36] that contributions to AE from classical nucleation events could be excluded, and the majority of the energy relaxations originated from the variant–variant interactions and from the interaction of martesite variants with grain boundaries (jamming effect), and pinning/deepening effects played only a minor role. On the other hand, if the transformation took place towards a single variant martensite structure, the pinning and depinning were identified as dominant mechanisms of the generation of AE (see, e.g., [
30]).
Thus, one can write, also using (6), for the total energies measured by acoustic emissions:
for cooling and heating, respectively. Here
δ < 1 is the detected fraction of the acoustic energy emitted (assuming that this fraction is the same for cooling and heating),
Erc is the relaxed elastic energy during cooling,
Erh is the relaxed elastic energy during heating, and
Et is the total elastic energy (that would be stored without its relaxation). Furthermore,
In the denominator of the expression for
βh,
Et −
Erc appears because this difference is the actual elastic energy stored during cooling and part of it can be relaxed by AE during heating. Thus, from (7) and (8), one obtains
This gives the condition for zero asymmetry (
η = 1) as
In the above expressions, the Erc and Erh energies (or the βc and βh(1 − βh) ratios) can be different because the elastic interactions at the moving interfaces as well as the development/regression of different martensite variants (leading to overlapping/disintegration of their elastic field) can be different for cooling and heating, and, thus, different parts of the elastic energy can be relaxed by the emission of elastic waves (acoustic emissions).
On the basis of (9) and (10), we can conclude that [
34]: if the relaxed fraction of the total elastic energy during cooling,
Erc, is larger/smaller than the corresponding relaxed fraction during heating,
Erh, then the asymmetry is positive/negative (
η < 1 or
η > 1). The same statement is valid for the total energy of the acoustic emission peaks.
In addition to the expression for
η, it was also shown in [
34] that the following correlations exist between the asymmetry parameters defined above: if
η is less than unity,
μ is also less than unity, while
γε and
γα should be negative; see also
Table 1. The correlation between
γε and
γα is a consequence of the scaling law Equation (3), while the relation between, e.g.,
γε and
μ can be obtained from the fact that the numbers of hits should be the integral of
ni(
E)~
E−εi, where
ni(
E) is the number of peaks of energy E [
34].
In [
34], it was concluded that, in the majority of the samples investigated until the end of 2017 (Tables 1 and 3 in [
34]), the asymmetry is positive in accordance with the expectation that, during cooling, the elastic energy relaxations by AE are more considerable (due to the rearrangements of the newly formed martensite variants) than those during heating (when a more or less stable martensite structure transforms back). In the case of transformation by the single interface motion, less elastic energy accumulation/release is expected (there is only a minor stress accumulation during cooling due to the easy formation of the surface step at the moving interface), and it is expected that both
μ and
η will be close to unity. Thus, a negative asymmetry should be accompanied by some deviations from the above main tendency.
There are indications in the literature (see e.g., [
8,
17,
28,
29]) that AE and ME activities can also be observed after the martensite finish temperature during cooling (see also point iii and the insert of
Figure 2). This indicates possible stress relaxations inside the freshly formed martensite even during the cooling [
8,
29]. This fact can have an influence on the above-presented analysis. Indeed, in this case, the values of
Erc and
Erh can be different and depend on the rate of change of the temperature and on the time that the sample spent in the martensitic state before being heated. Thus, the
η ratio can also depend on this time.
It was also concluded recently [
37] that the energy exponents obtained from thermal, acoustic, and magnetic emission noises in ferromagnetic shape memory alloys (Ni
2MnGa, Ni
49Fe
18Ga
27Co
6, and Ni
45Co
5Mn
36.6In
13.4) were almost the same within the error bars in the same direction, which can be an indication that the origin of all types of the above noises is the displacement discontinuities during the transformation.
Closing this Section, we mention some questions that remain open:
4. Correlations between Subsequent Events or between Acoustic and Magnetic Noise Events in Ferromagnetic Shape Memory Alloys
As was mentioned in
Section 2, investigations of time correlations between subsequent events (e.g., statistical distributions of waiting times) can be useful because they may contain a lot of information complementing that extracted from amplitude and energy distributions [
4,
38]. This topic has not been explored before, and the relatively small number of publications related to time correlations has appeared only in the last 10 years [
8,
23,
24,
28,
38].
Three types of correlations have been investigated so far in shape memory alloys. The first two are related to correlations between subsequent events within a given set of noise data (either in thermal [
23], AE [
8,
23,
28], or ME [
8,
28] avalanches). The third one is the investigation of correlations between (simultaneously measured) AE and ME events, which gives information about the time delay between the two types of signals [
8,
28].
As an illustrative example,
Figure 5 in
Section 2 shows the probability distribution function of waiting times
τ (Equation (4)) for AE and ME events in Ni
2MnGa single crystal [
8]. Besides this, given that it deviates from the Poisson-type uncorrelated behaviour, it can be seen that it follows a power-law behaviour with different exponents for small and large arguments of the normalized waiting time. Furthermore, it can also be seen that the points belonging to AE and ME events fall on the corresponding straight lines with approximately the same exponents. This collapse of the distribution of data on the two types of noise is good, and, regarding the exponents, there is a very good agreement between these and those obtained from simultaneous calorimetric and AE measurements on polycrystalline Cu
67.64Zn
16.71Al
15.65 samples [
23]. Thus, the universal character of the
function in relation (4) is also confirmed by these data, especially if we take into account that the values of the above slopes are also in good agreement with those obtained from earthquakes and the compression of porous materials [
23] (corresponding to the Omori-like correlations at small arguments and to temporal non-homogeneity, connected to deviation of the activity curves from a single Gaussian function [
23], at large arguments).
The second type of investigation of time correlations between subsequent events is based on a recent paper [
39]. It was pointed out in [
39] that if temporal correlations exist in the sequences of discrete events (inhomogeneous temporal processes)—as suggested by the power-law behaviour of the
function for large arguments—it is also useful to make comparisons between the experimentally determined
P (
n;
τm) functions with the
Pind (
n;
τm) distributions
belonging to a sequence of
n successive independent events within a burst [
40]. Here,
and
τ <
τm, where
τm is the maximum time difference between subsequent events in a burst. In [
41], a long sequence of AE events was called a “burst”, and
τm was typically about 2 orders of magnitude longer than the characteristic time for a single event, 0.1–10 ms. For independent events,
an−1 is the probability that
n − 1 events follow the first event with
τ <
τm, and (1 −
a) is the probability that, for the subsequent event,
τ >
τm [
41].
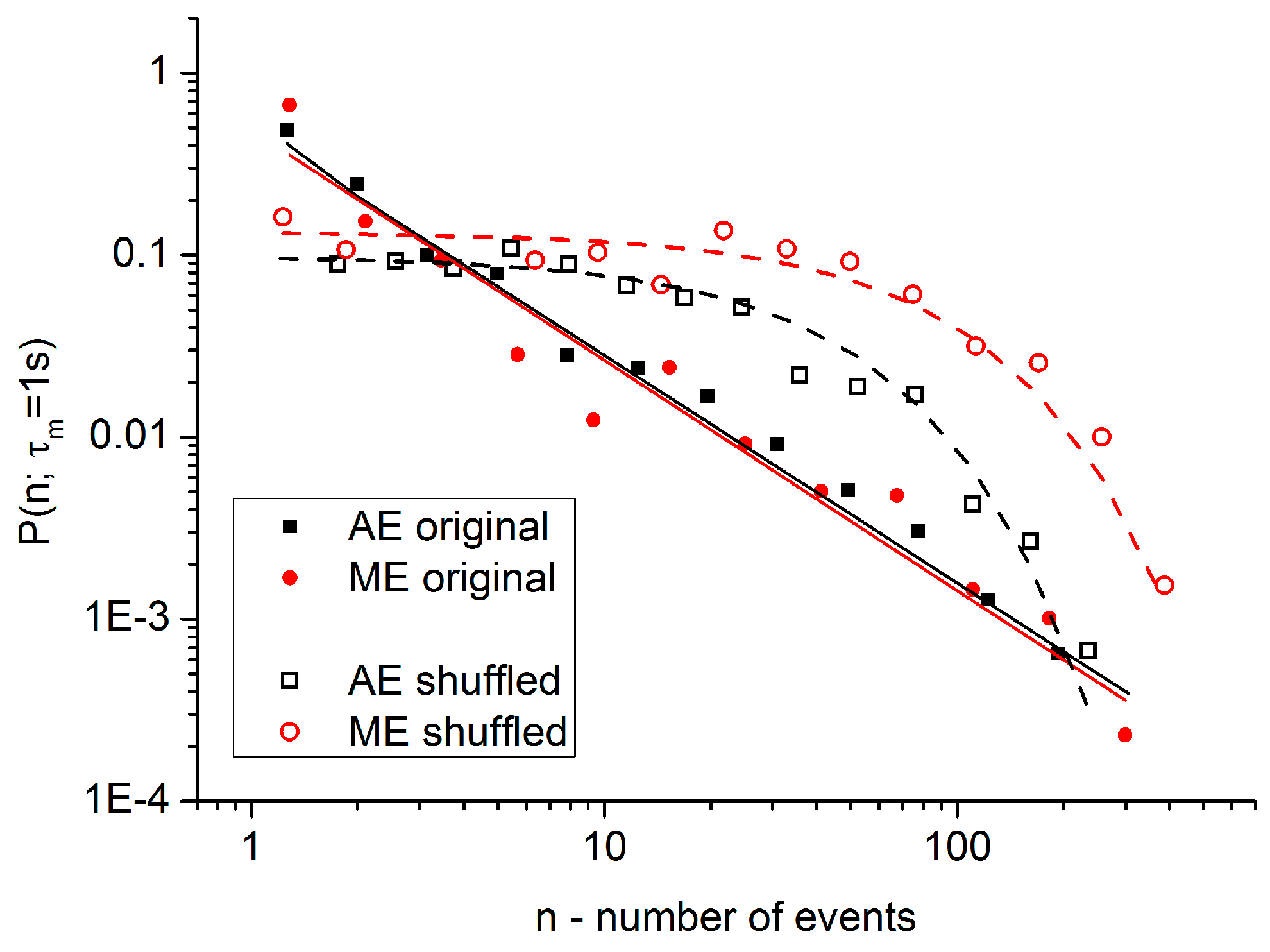
Figure 12 shows the
P(
n;
τm) functions of the acoustic and magnetic events at
B = 0 T for heating and cooling in Ni
2MnGa single crystal [
8] with
τm = 0.5 s. The
P(
n;
τm = 0.5 s) distributions follow a power-law behaviour,
P(
n) ∼
nβ, with a
β = −1.9 exponent. The dashed line indicates in
Figure 12 the
Pind(
n;
τm) distribution according to Equation (11), with
a = 0.6 for independent events. Thus, we can conclude that the
P(
n;
τm) distributions are clearly different from
Pind(
n;
τm), demonstrating that correlations exist between the AE as well as between the ME events. Note again that all AE and ME points, belonging to both heating and cooling, lie on a common straight line, indicating the universal character of the
P(
n;
τm) distributions.
In addition to the above time correlations, simultaneous measurements of AE and ME signals also enable the study of time correlations between these two signals. Let
δME→AE denote the time delay between consecutive signals when a magnetic avalanche is followed by an acoustic one, and
δAE→ME the time delay when an acoustic event is followed by a magnetic one. If the two signals are correlated, the two types of delays should have different probability distributions [
28]. For uncorrelated signals, the two delays have the same distribution, which can be described by the Poisson function given by the relation (5).
Figure 13 shows the results of such an analysis made in [
8] in Ni
2MnGa single crystal. It can be seen that, at intermediate values of
δ, the AE and ME events are uncorrelated; the probability functions are close to the exponential function with
λ ≅ 150 s
−1, while there are deviations from this behaviour both at small and high values of
δ. Deviations at high arguments were explained in [
8] and [
28] by the nonhomogeneous character of the process (see also above), while for
δ < 10
−4 s, the
P(
δME→AE) and
P(
δAE→ME) curves are also diverging. This means that it is more probable that an acoustic signal is followed by a magnetic one than inversely. This is in accordance with the plausible expectation that the AE, accompanied by the jerky phase transition, is the primary effect, and the magnetic domain rearrangement occurs as a consequence of the structural transformation. Below about
δ = 5 μs, the sequence of the two signals is the opposite, i.e., it seems more probable that a magnetic signal is followed by an acoustic one. This can be due to the fact that, while the time necessary for the magnetic signals to reach the detector is negligible, the acoustic propagation delay of the AE signals is considerable.
5. Acoustic and Magnetic Emissions during Variant Rearrangements in the Martensitic State (Plastic, Superelastic, and Rubber-Like Behaviour)
Besides the intermittent character of martensitic transformations, rearrangements of the martensitic variants have also a jerky character in shape memory alloys, and, thus, the AE technique (and the ME measurements, if the alloy is ferromagnetic) is a very good tool for the investigation of such processes. The properties of variant rearrangements are closely related to important practical properties of shape memory alloys, such as superplasticity, superlasticity, or rubber-like behaviour. For example, magnetic shape memory (MSM) alloys are capable of producing a large magnetic-field-induced strain (MFIS, due to the rearrangement of martensite variants) with relatively high frequency, which makes them good candidates for actuators and sensors [
41]. In general, the multivariant martensitic structure, which is formed during cooling of the austenite, can be transformed into a single variant one by application of either uniaxial stress or a magnetic field. It was shown in [
17] that acoustic emission activity can indeed be detected during stress-induced martensite reorientation, indicating the jerky character of the detwinning process. However, no statistical analysis of the stress-induced AE noises was presented in [
17], and only a qualitative description was given. Furthermore, in previous studies of magnetic-field-induced detwinning, no noise measurements were implemented, but rather the emphasis was put on the observation of the initial and/or final magnetic domain structure [
42,
43,
44,
45,
46,
47]. A detailed analysis of simultaneously measured AE and ME jerks was carried out during magnetic-field-induced superplastic deformation in a single-crystalline Ni
2MnGa shape memory alloy with a 10 M modulated martensite structure [
9]. For the details of this work, we refer the reader to the original article. Here, we summarize only those results that are related to the noises related to the twin rearrangements.
Figure 14 shows the ME and AE as well as the relative length change as a function of the applied magnetic field (in the initial state, the sample had an almost single variant martensitic structure, which was produced by compression from the single variant state established earlier by the application of the external magnetic field). It can be seen that, in the low-field range (below the critical field value necessary to start the variant rearrangements, see the Δ
L/
L curve) there are no AE signals, while the ME is due to the simple classical Barkhausen noise related to the rearrangements of magnetic domains. In the high-field range (0.35–0.95 T), sporadic ME noise, together with intense AE activity, is present. A macroscopic shape change of about 6% also takes place in this high-field range.
Figure 15 shows the corresponding energy probability distribution function, illustrating the validity of a power-law behaviour (Equation (1)). It can be seen that the energy exponents of the two types of signals are the same within the experimental errors, in accordance with the fact that the origin of both emissions is the variant rearrangement. It is worth noting that these values are also in very good agreement with the energy exponents (
ε ≅ 1.5) of ME determined from noises induced by cyclic bending deformations in the same alloy [
48,
49].
The time correlations between subsequent events were also analysed in [
9] according to the relation (11).
Figure 16 shows the
P(
n;
τm) functions for
τm = 1 s, together with the distributions of a randomized data set (shuffled data). It can be seen that the original AE and ME experimental points fit very well to a common straight line (power-law behaviour) with
β = −1.25. Thus, we arrive at a similar conclusion as drawn from the analysis of noises obtained during the martensitic transformation: the character of the
P(
n;
τm) distributions is universal (the exponent is the same for AE and ME). At the same time, these common exponents are different for the noises belonging to the austenite/martensite transition and for the superplastic deformation by variant rearrangements.
The above results belong to noises emitted during superplastic deformations by variant rearrangements. On the other hand, there is an interesting superelastic deformation that is also related to martensite rearrangements. This is the so-called rubber-like behaviour in the martensitic state, which can be observed when stress-induced martensite variants are produced from a single variant martensite structure, and, after the removal of the stress, the sample (partly) turns back to the original shape. This rubber-like behaviour is produced due to the energy mismatch between the stress-induced martensitic variants and the original variants, so that the induced variants are less stable than the original ones, and this is why the original variants are restored when the stress is removed. The explanation of this difference is based on the short-range symmetry conforming model [
50]: a certain stress-induced variant can be stabilized by temperature-induced aging, during which the short-range order gradually develops from the one corresponding to the quenched in the short-range order of the martensite to the short-range order according to the martensite symmetry [
51,
52]. Sometimes, such a rubber-like behaviour can also be observed even without the above temperature aging (e.g., training for a two-way shape memory behaviour can also result in giving a preference for a certain martensite variant). Indeed, it was observed [
53] that, in a single-crystalline Ni
2MnGa shape memory alloy with a 10 M modulated martensite structure, after creating a single variant martensite and then (without carrying out any special heat treatment for martensite stabilization) making a superplastic deformation by uniaxial stress, about 0.7% rubber-like behaviour appeared after relieving the load (
Figure 17 and
Figure 18). In addition, in [
53], AE and ME noises were detected during both the first superplastic part of the deformation and the rubber-like region. It was obtained that the energy exponents for the stress-induced rearrangements (superplasticity) were again the same as the error bars (
ε = 1.7 ± 0.1 and
ε = 1.6 ± 0.1 for AE and ME, respectively) and also agreed well with these values for magnetic-field-induced superplasticity (
ε = 1.5 ± 0.1) [
9]. Interestingly, the energy exponents obtained from the rubber-like regime were also the same as those belonging to the stress-induced superplasticity. These results nicely illustrate that, although the driving forces for the rearrangements of the martensite variant structure were different (magnetic field, stress field, or the lower energy of one of the variants), the characteristic exponents have a universal value.
6. Application of the Clustering Method for Identification of Different Contributions to Martensitic Transformations
In the last decade, a new method, the so-called AE cluster analysis method, was developed [
10,
11,
54], which allows us to distinguish between the sources of different origin in AE data and to obtain a deeper insight into the interrelation between the underlying processes (such as dislocation slip, twinning, interface shift, etc.) during martensitic transformations. This method, instead of reducing the AE waveform to a set of time-dependent parameters, such as peak amplitude, number of counts, rise time, and duration, uses a “spectrum-based” analysis in a frequency domain after a Fourier or wavelet transformation. There is a generally accepted assumption based on fundamental theoretical considerations: different sources produce AE signals with different waveforms, and, thus, different power spectral density (PSD) functions. Therefore, AE signals originating from different sources will belong to different clusters, which are identified by the average PSD functions of the AE events.
One can find several clustering algorithms for categorizing the AE events. Most of them are iterative processes, where the number of clusters must be predetermined. The most efficient method for clustering of AE events is the Adaptive Sequential k-means algorithm (ASK) described in [
10]. The ASK is a real-time categorization method, where the number of clusters can vary during the data processing depending on the coarsening and refining parameters [
10].
There is a plausible expectation that the asymmetry of the martensitic transformations (as treated in
Section 3) should be related to different AE source activities during heating and cooling, and, thus, the performance of the AE cluster analysis for data collected during heating and cooling can provide information on the details. Thus, acoustic emission measurements were carried out during the forward and reverse transformation of a single crystalline Ni
2MnGa shape memory alloy [
55], and some of the results of [
55]—as an illustration—are reviewed here. The normalized PSD function, the peak energy, and the median frequency were determined for each AE event. The ASK method was applied for clustering the AE events, which was based on the dissimilarity between the normalized PSD functions. As a measure of dissimilarity, we used, in the framework of our own program [
55], the correlation distance between two discrete PSD functions,
and
, each of which consists of n elements:
where the upper bar denotes the average of the normalized PSD functions.
The ASK clustering in Ni
2MnGa single crystal indicated that most of the events (≈95 %) can be classified into three clusters for heating, and into four clusters for cooling. The remaining events form several other clusters with a negligible number of events in each cluster.
Table 3 contains the number of events in each cluster.
Figure 19 and
Figure 20 show the representation of the clusters in two-dimensional (2D) (median frequency–energy) feature spaces.
Figure 19 and
Figure 20 clearly show the similarities and the differences between heating and cooling runs. The first three clusters are common for the forward and reverse transformations. In the case of cooling, there is an additional cluster, C4, with a relatively low median frequency, which deviates from all the previous clusters. The first clusters for heating and cooling (H1 and C1) were identified as belonging to the austenite–martensite transformation itself (they contain most of the events). The other clusters can belong to stress relaxations in the martensite phase, the friction between the parts of the measurement setup due to the slight shape change of the sample during the transformation, as well as to the nucleation of the martensite phase during cooling. For the details, we refer the reader to [
55].
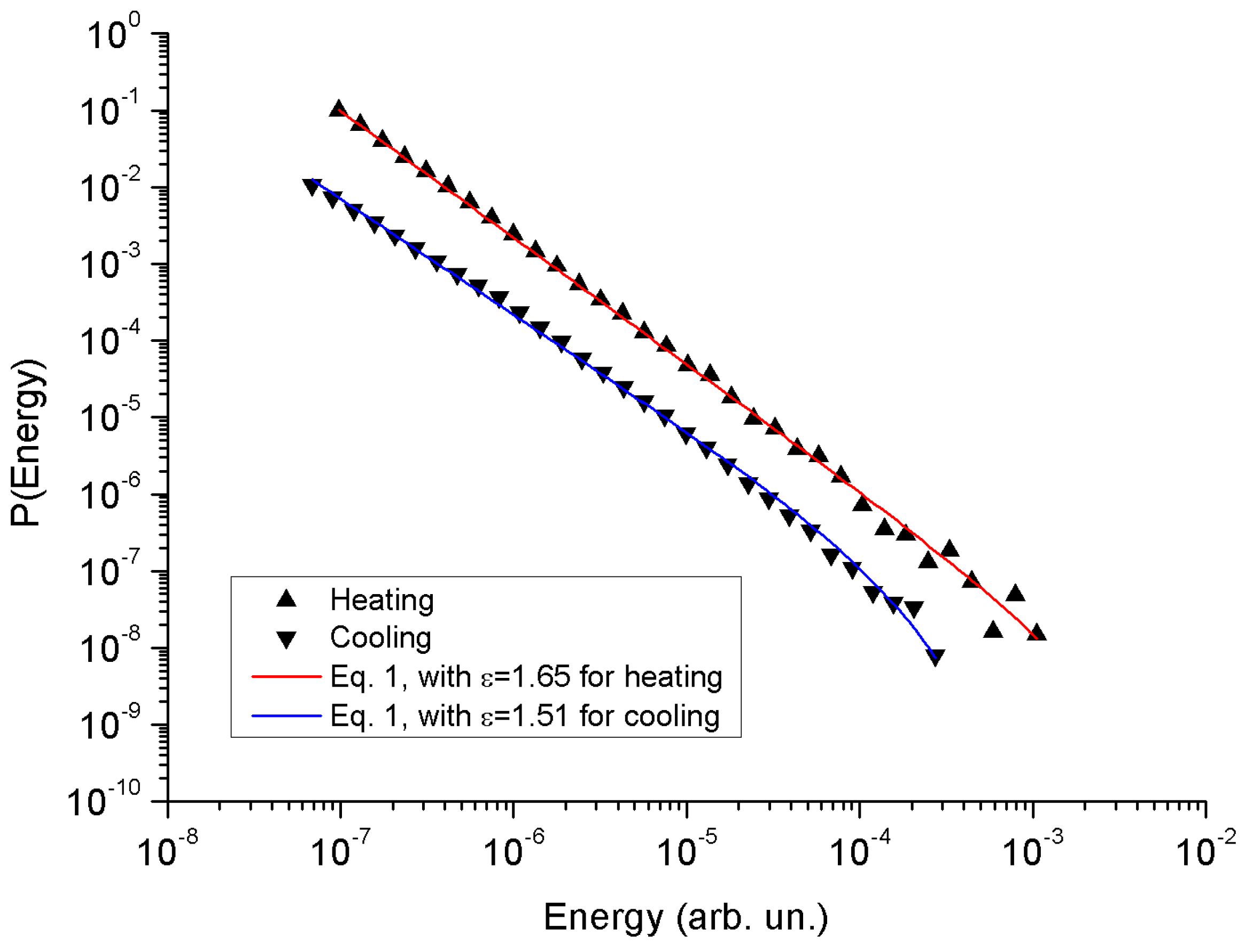
Figure 21 shows the energy probability density functions for heating and cooling (including all data points measured) as well as the fitted curves using Equation (1). The fitted values are
εh = 1.65 ± 0.05 and
εc = 1.51 ± 0.05 for heating and cooling, respectively, which means positive asymmetry, as was expected from the previous measurements [
5,
8] on the same alloy. Furthermore, the H1 and C1 clusters contain more than 80% of the AE events, and their exponents are very similar to the exponents of the full data sets (for the other clusters, the energy exponents had error bars that were too high due to the small number of events).
In summary, the ASK clustering analysis showed that the detected AE events originate from different sources, and there is an important difference between heating and cooling (see the presence of the C4 additional cluster during cooling, which has high noise activity at the end of the transformation; see
Figure 22 for an illustration and [
55] for the details).). On the other hand, the clustering did not resolve the asymmetry of the energy exponents. Thus, the reason for the asymmetry is still an open question from this point of view. A plausible explanation can be that the energy distributions of the same type of source(s) are different for heating and cooling.